1 Introduction

Spark plasma sintering (SPS) [1,2,3,4,5], also known as field assisted sintering technique (FAST) [5] or pulsed electric current sintering (PECS) [4], is a promising technology for innovative processing in the field of new and advanced materials’ production. The SPS technique is based on pressure-driven powder consolidation accompanied by heating of the compact using a pulsed direct electric current passing—in case of an electrical conducting material—through the sample. The direct way of passing the electric current through the sample volume that induces Joule heating allows the application of very high heating rates and reduced sintering temperatures. Therefore, SPS is an energy-saving technology due to shorter production times in comparison with hot isostatic pressing (HIP) or hot pressing (HP). The shorter material production time is also beneficial for retaining a fine microstructure, since grain coarsening can be avoided due to shorter dwell times.

Spark plasma sintering is used for manufacturing of various materials such as hard metals, Ni-based and Ti-based alloys, metal matrix nanocomposites, ceramics and diamond-based materials, thermoelectric as well as magnetic materials or high-entropy alloys [6]. It is also an attractive technique for the development of nanocomposites reinforced with carbon fibers and nanotubes, graphite and graphene, as it is possible to achieve a high level of densification without damaging the structural integrity of the nanofillers.

SPS involves a complex interplay of thermo-electro-chemo-mechanical processes. Its description requires coupled nonlinear models of the material behavior. The available models of sintering can be classified based on the modeling scale. They include the atomic level, the particle level and the continuum level as well as multiscale level approaches [7, 8]. For continuum material models, there exist two types: microscopic [9,10,11,12,13,14] and phenomenological [9, 15,16,17] models. Microscopic models take into consideration different mass transport mechanisms involved in sintering: (i) surface diffusion, (ii) grain boundary diffusion, (iii) volume (lattice) diffusion, (iv) plastic flow and (v) vapor transport (evaporation/condensation) [18].

Analytical models [9, 11, 13, 18,19,20,21,22] play a key role in understanding of the sintering process, but drastic simplifications have to be assumed (e.g. oversimplified geometry, isothermal sintering and neglected grain growth) that limit their ability to quantitatively predict the densification of real powder compacts. Analytical models only provide a qualitative understanding of sintering. Using the approximations underlying these simple approaches of sintering, expressions for the growth of the neck radius x can be obtained as a function of time t, which are generally of the power-law type \(\left( \frac{x}{R} \right)^{n} = BR^{ - m} t\), where R is the particle radius, B, m, n are material/process constants. These expressions can be used for the verification of the numerical solution and for the identification of the dominant neck growth mechanism based on the experimentally obtained constants m and n.

The limitations of analytical models can be overcome by numerical models [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], which offer a powerful tool for the sintering analysis for various stages and scales taking into account complex geometry and concurrent mechanisms. Different solution methods of the sintering problems exist: the kinetic Monte-Carlo method [34, 35], finite difference method [23, 24, 33], finite-element method [36,37,38,39], phase field method [25, 26, 40], discrete element method [27,28,29,30,31] and a cellular automaton approach [32].

Variational principles that can serve as the basis for numerical methods were developed for grain-boundary diffusion by Needleman and Rice [41], for volume (lattice) diffusion by Cocks [42] and for surface diffusion by Suo [43].

The finite-element method is usually used for the simulation at the component level for a part of or for the whole sintering machine. Typically, such modeling is limited to a thermal or thermoelectric analysis [44,45,46,47,48,49,50,51,52], although, multi-physics simulations of powder systems are getting more widespread for various technological processes involving powders [53]. The finite-element simulation of the three-way coupling of thermal, electrical and mechanical behavior with spatial distribution of the stress and strain fields was analyzed only in a few works [54,55,56,57,58]. The more complex problem of coupled diffusion and mechanics is considered in the work of Pino-Munoz et al. [38], where the analysis of sintering processes is carried out at the microstructural level, taking into account the heterogeneity of the stress state. However, in this work [38] the Euler-based formulation, the level set method and the fictitious non-compressible interparticle fluid were considered, which requires the development of original software and is not available to most users. In addition, variational principles are not used in that work.

The goal of the present research is to develop a widely available engineering method for solving boundary value problems of coupled diffusion and thermo-electro-mechanics. The present work describes the sintering processes at the particle (microscopic) level taking into account (i) improved models of plasticity and creep, (ii) frictional contact, (iii) grain boundary and (iv) surface diffusion, (v) thermal gradient and (vi) electric field. A Lagrange-based formulation is used here to deal with the detailed description of history of plastic and creep strain accumulation, which is important for the initial stage of sintering.

In order to verify and to better understand the interaction of surface diffusion and inelastic deformation, the cases in which diffusion and creep are the dominant mechanisms are separately analyzed. For verification, a staggered solution method of the four-way coupled thermal, electrical, chemical and mechanical fields is carried out. The numerically obtained results for the evolution of the interparticle neck radius during the SPS process are compared with experimental results for copper powder.

2 Governing equation of sintering

In the present section the mechanisms and the resulting equations for diffusion in general as well as the thermo-electro-mechanical material behavior model used for the sintering simulations are given.

2.1 Different mechanisms of diffusion at the sintering model

During the sintering process, the mass is transported through multiple mechanisms involving (i) surface diffusion, (ii) grain boundary diffusion, (iii) volume (lattice) diffusion, and (iv) vapor phase transport.

The diffusion flux j (atoms per unit area per unit time) of surface, grain boundary, and volume diffusion is defined on the basis of chemical potentials of the atoms μa and of the vacancies μv by [59]:

$$ {\mathbf{j}} = - \frac{{Dn_{a} }}{kT}\nabla \left( {\upmu_{a} - \upmu_{v} } \right), $$
(1)

where D is the effective diffusion coefficient, which depends on the temperature by the Arrhenius exponential relation \(D = D_{0} e^{{ - \frac{Q}{RT}}}\). k = 1.380649 × 10−23 J/K is the Boltzmann constant, R = k·NA = 8.314463 J K−1 mol−1 is the ideal gas constant, T the absolute temperature and Q the activation energy. For volume diffusion, \(n_{a}\) is the number of atoms per unit volume (\(n_{a} = 1/\Omega\), where \(\Omega\) is the atomic volume); for surface and grain boundary diffusion, \(n_{a}\) is the number of atoms per area of interface participating in the drift (\(n_{a} = \updelta /\Omega\)) and \(\updelta\) is the effective thickness of the high diffusivity interface. It is assumed that the transport can take place only by the vacancy mechanism. The different types of diffusion (surface, grain boundary, volume diffusion) have different mass transfer routes. Their driving forces are defined by different chemical potentials.

2.1.1 Surface diffusion

Neglecting strain energy terms, the surface diffusion is defined by the following chemical potentials [59, 60]:

$$ \upmu_{a} = \upmu_{a0} + p\Omega ,\quad \upmu_{v} = p\Omega + \gamma_{s} \upkappa \Omega , $$
(2)

where \(\gamma_{s}\) is the specific free surface energy of a crystalline solid, \(\upkappa = 1/R^{I} + 1/R^{II}\) is the mean curvature with \(R^{I}\) and \(R^{II}\) being the two principal radii of surface curvature (the curvature is positive for a convex pore), \(p = - 1/3tr{{\varvec{\upsigma}}}\) is the hydrostatic pressure (scaled first invariant of the stress tensor) and \(\mu_{a0}\) is the chemical potential of the atoms in a stress-free state. In the stress tensor \({{\varvec{\upsigma}}}\), tensile stresses have positive values. Substitution of Eq. (2) in the equation for the diffusion current (1) leads to the atomic flux density vector expression:

$$ {\mathbf{j}}_{s}^{\upkappa } = \frac{{D_{s} \updelta_{s} \gamma_{s} }}{kT}\nabla_{s} \upkappa . $$
(3)

The upper index of j stands for the driving force (here: the surface curvature \(\upkappa\)), the lower index for the transport route (here: the (free) surface s). The equation clarifies the surface curvature \(\upkappa\) as driving force for the surface diffusion. In the case of the surface diffusion, the matter transport leads to a deposition or removal of material over the free surface that can be described by the normal displacement rate \({\mathbf{v}}_{s}^{\upkappa }\). A matter balance condition provides the equation for the surface movement rate vector \({\mathbf{v}}_{s}^{\upkappa }\) on the base of surface diffusion flux \({\mathbf{j}}_{s}^{\upkappa }\):

$$ {\mathbf{v}}_{s}^{\upkappa } = - {\mathbf{n}}\Omega \nabla_{s} \cdot {\mathbf{j}}_{s}^{\upkappa } , $$
(4)

where the operator \(\nabla_{s} = \left( {{\mathbf{1}} - {\mathbf{nn}}} \right) \cdot \nabla\) is the surface gradient, \({\mathbf{1}}\) is the unit tensor and \({\mathbf{n}}\) the outer normal vector of the surface. Surface diffusion produces geometric changes through rearrangement of matter, i.e. neck growth, without causing shrinkage.

2.1.2 Grain boundary diffusion

For the grain boundary diffusion the difference of chemical potentials is given accordingly to [61, 62] by:

$$ \upmu_{a} - \upmu_{v} = \upsigma_{nn} \Omega , $$
(5)

so that the stress-induced atomic flux density vector can be represented by

$$ {\mathbf{j}}_{gb}^{\upsigma } = - \frac{{D_{gb} \updelta_{gb} }}{kT}\nabla_{gb} \upsigma_{nn} , $$
(6)

where \(\nabla_{gb} = \left( {{\mathbf{1}} - {\mathbf{nn}}} \right) \cdot \nabla\) is a surface gradient that was calculated on the grain boundary and \(\upsigma_{nn} = {\mathbf{n}} \cdot {{\varvec{\upsigma}}} \cdot {\mathbf{n}}\) is the normal stress on the grain boundary. It is assumed that the grain boundary remains straight during sintering.

The grain boundary velocity vector \({\mathbf{v}}_{gb}^{\upsigma } = v_{gb}^{\upsigma } {\mathbf{n}}\) is normal to the interface and is defined by:

$$ {\mathbf{v}}_{gb}^{\upsigma } = - {\mathbf{n}}\Omega \nabla_{gb} \cdot {\mathbf{j}}_{gb}^{\upsigma } . $$
(7)

The scalar normal velocity \(v_{gb}^{\upsigma }\) is positive when the grains move apart. Removal of material from the grain boundary region leads to shrinkage (densification) during sintering.

2.2 Thermo-electro-mechanical model of the material behavior

For the description of the coupled thermo-electro-mechanical problem, the following balance equations in volume are considered.

The equation of heat conduction resulting from the energy balance and Fourier's law

$$ \rho C_{p} \frac{\partial T}{{\partial t}} - \nabla \cdot \left[ {\lambda \,\nabla T} \right] = q_{V} . $$
(8)

Maxwell's equation, simplified for a conducting material to the law of conservation of charge

$$ \nabla \cdot \left[ {\frac{1}{{\rho_{e} }}\nabla \phi } \right] = 0, $$
(9)

the equation for the mechanical equilibrium

$$ \nabla \cdot {{\varvec{\upsigma}}} = {\mathbf{0}} $$
(10)

are used. In Eqs. (8)–(10), T represents the temperature, φ is the scalar electric potential (assuming \({\varvec{E}} = - \nabla \varphi\) for the electric field intensity vector \({\varvec{E}}\)), t is the time, \(\nabla (...)\) is the nabla operator, \(\rho\) is the density, Cp denotes the specific heat capacity at constant pressure and \(\lambda\) represents the thermal conductivity (assuming isotropic material properties). Regarding the electrical properties \(\rho_{e}\) indicates the electrical resistivity, providing the link between the electric field intensity to the current density \({\varvec{E}} = \rho_{e} {{\bf J}}\)). The generated heat due to the current flow per unit volume and unit time is given by

$$ q_{V} = {\mathbf{J}} \cdot {\mathbf{E}} = 1/\rho_{e} \nabla \varphi \cdot \nabla \varphi . $$
(11)

In Eq. (10) \({{\varvec{\upsigma}}}\) is the Cauchy stress tensor, which is related to the Kirchhoff stress tensor by \({{\varvec{\uptau}}} = J{{\varvec{\upsigma}}},\) with \(J = \det {\mathbf{F}}\), where \({\mathbf{F}}\) is the deformation gradient. For the analyzed sintering problem at the microscopic scale, large plastic strains and small elastic strains take place. An additive decomposition of the strain rate tensor \({\mathbf{d}} = \left( {\nabla {\mathbf{v}}} \right)^{S} = {\mathbf{d}}^{e} + {\mathbf{d}}^{p}\) is used. Taking into account the presence of temperature and of viscous effects, the additive decomposition of the strain rate tensor takes the form

$$ {\mathbf{d}} = {\mathbf{d}}^{e} + {\mathbf{d}}^{T} + {\mathbf{d}}^{p} + {\mathbf{d}}^{v} . $$
(12)

In the case of small elastic strains, the elastic response can be characterized by a hypoelastic rate constitutive equation (ad hoc extension of the infinitesimal theory)

$$ {\mathbf{d}}^{e} = {}^{4}{\mathbf{C}}^{ - 1} \cdot \cdot \,{{\varvec{\uptau}}}^{J} , $$
(13)

where \({{\varvec{\uptau}}}^{J} = {\dot{\varvec{\uptau }}} - {\mathbf{w}} \cdot \,{{\varvec{\uptau}}} - {{\varvec{\uptau}}} \cdot {\mathbf{w}}\) is the Jaumann–Zaremba (objective) rate of the Kirchhoff stress, and \({\mathbf{w}} = \left( {{\mathbf{v}}\nabla } \right)^{A}\) is the spin tensor. Concerning the elastic properties of the material, \(^{4} {\mathbf{C}} = \frac{Ev}{{(1 + v)(1 - 2v)}}{\mathbf{1}} \otimes {\mathbf{1}} + \frac{E}{2(1 + v)}\left( {{\mathbf{1}}\overline{ \otimes } {\mathbf{1}} + {\mathbf{1}}\underline{ \otimes } {\mathbf{1}}} \right)\) denotes the fourth-order tensor of elasticity, where E is the Young’s modulus and v is the Poisson’s ratio. In Eqs. (8)–(10) and (13) the symbol ‘\(\cdot\)’ denotes the dot product, ‘\(\cdot \cdot\)’ is a double contraction, \(\left( {{\mathbf{A}} \otimes {\mathbf{B}}} \right)_{ijkl} = A_{ij} B_{kl}\) is the direct dyadic product and \(\left( {{\mathbf{A}}\,\overline{ \otimes } \,{\mathbf{B}}} \right)_{ijkl} = A_{ik} B_{jl}\), \(\left( {{\mathbf{A}}\,\underline{ \otimes } \,{\mathbf{B}}} \right)_{ijkl} = A_{il} B_{jk}\) are indirect dyadic products.

The thermal strain rate tensor is defined by

$$ {\mathbf{d}}^{T} = \alpha (T)\,\dot{T}\,{\mathbf{1}}, $$
(14)

where \(\alpha\) is the thermal expansion coefficient.

The viscoelastic/viscoplastic material model that takes into account both plastic and viscous properties (above and below the yield stress) [63] is used in the simulation for the description of the inelastic deformation under high temperature. The plastic strain rate tensor is defined by the associative flow rule

$$ {\mathbf{d}}^{p} = \lambda \frac{\partial f}{{\partial {{\varvec{\uptau}}}}}, $$
(15)

where the von Mises criterion with linear isotropic hardening \(f = \sqrt {\tfrac{3}{2}{\mathbf{s}} \cdot \cdot \;{\mathbf{s}}} - \sigma_{Y} - H(T)\varepsilon_{i}^{p}\) is used. \({\mathbf{s}} = {{\varvec{\uptau}}} - \tfrac{1}{3}{\mathbf{1}}tr{{\varvec{\uptau}}}\) is the Kirchhoff stress deviator and \(\varepsilon_{i}^{p} = \int\limits_{0}^{t} {\sqrt {\tfrac{2}{3}{\mathbf{d}}^{p} \cdot \cdot \;{\mathbf{d}}^{p} } dt}\) is the Odquist parameter. The plastic multiplayer \(\lambda\) satisfies the loading/unloading conditions in the classical Kuhn–Tucker form \(\lambda \ge 0,\;f({{\varvec{\uptau}}}) \le 0,\,\;\lambda f({{\varvec{\uptau}}}) = 0\) along with the consistency requirement \(\lambda \dot{f}({{\varvec{\uptau}}}) = 0\).

The viscous (creep) strain rate tensor is defined by a Norton power-type constitutive equation

$$ {\mathbf{d}}^{v} = A_{0} e^{{ - \,\;\frac{Q}{RT}}} \sigma_{i}^{n - 1} {\mathbf{s}}. $$
(16)

In Eqs. (13)–(16) \(E\), \(v\), \(\alpha\), \(H\), \(A_{0}\), \(Q\), \(n\), \(\sigma_{Y}\), are material parameters.

The temperature dependence of the thermo-electro-elasto-plastic properties (see Table 1), the creep properties (see Table 2) and the diffusion constants (see Table 3) for copper are taken from literature [14, 64,65,66,67,68,69] and used in the numerical simulations presented in Sect. 4.

Table 1 Thermo-electro-elasto-plastic properties [see Eqs. (8)–(15)] of copper used in the numerical study
Full size table
Table 2 Creep properties [see Eq. (16)] of copper used in the numerical study
Full size table
Table 3 Diffusion properties [see Eqs. (2)–(7) and \(D = D_{0} \updelta e^{{ - \frac{Q}{RT}}}\)] of copper used in the numerical study
Full size table

3 Staggered solution

The equations of surface diffusion and grain boundary diffusion use the two-dimensional differential operators \(\nabla_{s}\) and \(\nabla_{gb}\), respectively [see Eqs. (3), (4), (6), (7)]. In contrast, for volume diffusion, thermal conductivity, electrostatics and viscoelastoplasticity, the three-dimensional differential operator \(\nabla\) is used [see Eqs. (6), (8), (9), (10)]. Also, the different problems have different driving forces, of which that for surface diffusion, the surface curvature, is purely geometrical. It is therefore more convenient to solve a coupled thermo-electro-chemo-mechanical problem in a staggered way. The finite-element (FE) method is used for the solution of the coupled thermo-electro-mechanical problem while the finite-difference (FD) method is applied for the solution of surface and grain boundary diffusion problems. Those staggered schemes are widely used in the computational mechanics literature, e.g. by Zienkiewicz et al. [70, 71] for coupled fluid–structure problem, by Schrefler et al. [72, 73] for coupled thermo-fluid–structure problem, by Martins et al. [74] in thermoplasticity, by Zohdi [75] for thermo-electro-magnetically coupled problems.

In the proposed staggered approach, a step-by-step incremental procedure is used for solving the coupled nonlinear system of Eqs. (1)–(16) (see Fig. 1). At each loading step, first the thermo-electro-mechanical problem is solved for a given time increment. The calculated temperature T, the stresses \({{\varvec{\upsigma}}}\) and the geometry of the free surface \({\mathbf{r}}^{\prime}_{s}\) (changing due to the growing contact caused by viscous and plastic strains) are used as an input for the following surface and grain boundary diffusion simulation. At the next loading step, a new configuration of the free surface \({\mathbf{r}}^{\prime\prime}_{s}\), obtained from the solution of the coupled surface and grain boundary diffusion problems, is used as input parameter for the solution of the thermo-electro-mechanical problem. For an implicit type of staggering, the process can be repeated in an iterative manner at the current loading step, while for an explicit type one moves to the next time step after one pass through the system. An analysis of practical convergence for all the examples discussed below showed that an explicit scheme is sufficient.

Fig. 1
figure 1

Staggered iterative approach (explicit scheme) for the solution of coupled thermo-electro-mechanical (TEM) problem with surface and grain boundary diffusion (D)

Full size image

The solution of the coupled transient nonlinear thermo-electro-mechanical problem is described in [58]. For the solution of surface and grain boundary diffusion problem the approach proposed by Bouvard and McMeeking [76] is used here.

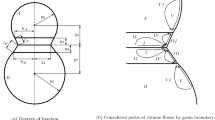
The steady-state grain boundary diffusion problem (6)–(7) for the two-particle model system (see Fig. 2) under the assumptions of absent influence of volume and surface diffusion can be solved analytically. The radial atomic flux density \(j_{gb} (r)\) along the grain boundary (OA in Fig. 2) and the grain boundary normal displacement rate \(v_{gb}\) are defined by the expressions [62, 76,77,78,79]:

$$ j_{gb} (r) = \frac{{4D_{gb} r}}{{kTx^{2} }}\left( {\gamma_{s} \kappa_{tip} - \sigma_{eff} + \frac{{2\gamma_{s} }}{x}\sin \frac{\psi }{2}} \right), $$
(17)
$$ v_{gb} = - \frac{{8\delta_{gb} D_{gb} \Omega }}{{kTx^{2} }}\left( {\gamma_{s} \kappa_{tip} - \sigma_{eff} + \frac{{2\gamma_{s} }}{x}\sin \frac{\psi }{2}} \right) = - \frac{{2j_{gb} (x)\Omega }}{x}, $$
(18)

where x is the radius of the contact zone (i.e. the half of neck diameter), \(\upkappa_{tip}\) is the mean curvature at the edge of the neck, and \(\sigma_{eff} = \overline{F}/(\pi x^{2} )\) is the effective (mean) normal stress on the grain boundary due to outer mechanical loading (\(\overline{F}\)) on a particle (\(\sigma_{eff} < 0\) for compression). \(\psi = 2\arccos \frac{{\gamma_{gb} }}{{2\gamma_{s} }}\) is the equilibrium dihedral angle, and \(\gamma_{s}\) and \(\gamma_{gb}\) are the specific free surface and grain boundary energies, respectively.

Fig. 2
figure 2

Geometry of the two-particle model

Full size image

As the Eqs. (3) and (4) for the surface diffusion could not be solved generally in closed form, the finite-difference method is used for the solution of the one-dimensional axisymmetric surface diffusion problem:

$$ {\mathbf{v}}_{s}^{\kappa } = {\dot{\mathbf{r}}}_{s} = {\mathbf{n}}v_{s}^{\kappa } = - {\mathbf{n}}\frac{{\delta_{s} D_{s} \gamma_{s} \Omega }}{kT}\Delta_{s} \kappa = - {\mathbf{n}}B\frac{1}{r}\frac{\partial }{\partial s}\left( {r\frac{\partial \kappa }{{\partial s}}} \right), $$
(19)

where s is arc-length along the free surface of a particle measured from the neck edge (see Fig. 2), \(B = \frac{{\delta_{s} D_{s} \gamma_{s} \Omega }}{kT}\) and \({\mathbf{r}}_{s}\) is the radius vector of the particle boundary. Equation (19) is obtained by substituting Eq. (3) in Eq. (4). Note: Equation (19) contains the first derivative in time and the fourth derivative with respect to the spatial coordinate (arc-length) of the radius vector \({\mathbf{r}}_{s}\).

The curvilinear free surface of the particle is discretized by an array of points (nodes) from the neck point A to the point B (Fig. 2). By using a cylindrical coordinate system (see Fig. 2) the axisymmetric free surface is defined by the two coordinates \(r_{i}\) and \(z_{i}\) (\(1 \le i \le N\), where N is the number of discretization points along curve AB) in the meridian plane. The arc-length is defined by

$$ s_{i} = s_{i - 1} + \sqrt {(r_{i} - r_{i - 1} )^{2} + (z_{i} - z_{i - 1} )^{2} } . $$
(20)

At each time step the new coordinates of point i after a time increment \(\Delta t\) are obtained by the explicit Euler method procedure

$$ r_{i}^{t + \Delta t} = r_{i}^{t} + v_{i} \sin \varphi_{i} \Delta t,\quad z_{i}^{t + \Delta t} = z_{i}^{t} - v_{i} \cos \varphi_{i} \Delta t, $$
(21)

where the displacement rate normal to the surface in the ith node \(v_{i}\) is calculated by using Eq. (4):

$$ v_{i} = \Omega \frac{{j_{i} (r_{i} + r_{i - 1} ) - j_{i + 1} (r_{i + 1} + r_{i} )}}{{r_{i} (s_{i + 1} - s_{i - 1} )}}. $$
(22)

The diffusion flux in ith node \(j_{i}\) is defined on the basis of Eq. (3) by:

$$ j_{i} = \frac{B}{\Omega }\frac{{\kappa_{i} - \kappa_{i - 1} }}{{s_{i} - s_{i - 1} }}. $$
(23)

The mean curvature in ith node \(\upkappa_{i}\) is defined by two principal radii of surface (\(R_{i}^{I}\) and \(R_{i}^{II} = - \frac{{r_{i} }}{{\sin \varphi_{i} }}\)):

$$ \kappa_{i} = \frac{1}{{R_{i}^{I} }} - \frac{{\sin \varphi_{i} }}{{r_{i} }}, $$
(24)

where the non-convex curvature radius \(R_{i}^{I}\) and the angle between the normal and the symmetry axis \(\varphi_{i}\) are found by approximating the free surface as a circle going through the three points: \(i - 1\), \(i\) and \(i + 1\):

$$ R_{i}^{I} = \sqrt {(r_{i} - r_{{C_{i} }} )^{2} + (z_{i} - z_{{C_{i} }} )^{2} } ,\quad \varphi_{i} = - arctg\frac{{r_{i} - r_{{C_{i} }} }}{{z_{i} - z_{{C_{i} }} }}, $$
(25)
$$ \begin{aligned} r_{{C_{i} }} & = \frac{{k_{i} (r_{i + 1} + r_{i} ) - k_{i + 1} (r_{i} + r_{i - 1} ) + k_{i + 1} k_{i} (z_{i + 1} - z_{i - 1} )}}{{2(k_{i} - k_{i + 1} )}}, \\ z_{{C_{i} }} & = \frac{{k_{i + 1} (z_{i + 1} + z_{i} ) - k_{i} (z_{i} + z_{i - 1} ) + r_{i + 1} - r_{i - 1} }}{{2(k_{i} - k_{i + 1} )}}. \\ \end{aligned} $$
(26)

The slope of the boundary \(k_{i}\), which is necessary for calculating of curvature centre coordinates \(r_{{C_{i} }}\) and \(z_{{C_{i} }}\), is defined by the difference relation

$$ k_{i} = \frac{{z_{i} - z_{i - 1} }}{{r_{i} - r_{i - 1} }}. $$
(27)

The initial values of the coordinates of the surface points come from the finite element solution of the coupled thermo-electro-mechanical (TEM) problem. The slope in the first node (point A in Fig. 2) \(k_{1}\) is defined by dihedral angle \(\psi\). The surface diffusion flux in the first node (point A in Fig. 2) \(j_{1}\) is defined by the grain boundary diffusion flux \(j_{1} = j_{s} (s = 0) = 1/2j_{gb} (x)\). The coefficient 1/2 is due to symmetry. The flux \(j_{gb} (x)\) is defined by Eq. (17).

4 Numerical examples

In this section, neck growth and shrinkage, i.e. the geometric changes associated with sintering, are analysed by using the two-particle model [9, 14, 62, 76, 77] as a representative volume element of powder. The two test cases employ sintering conditions that are supposed to result in creep dominance (Sect. 4.1) and surface diffusion dominance (Sect. 4.2). For an intermediate case, the comparison with experimental data is presented in Sect. 4.3. The results of the Sects. 4.1 and 4.3 are obtained by the proposed staggered procedure including (i) a finite-element (FE) solution of the coupled thermo-electro-mechanical problem and (ii) a finite-difference (FD) solution for the surface diffusion problem. In Sect. 4.2, for a step in the staggered scheme, the finite-difference method for the surface diffusion is applied. The FE solution of the thermo-electro-mechanical problem was obtained using the FE tool ANSYS. The FD solution of the surface and grain boundary diffusion problem (17)–(27) was realized in an in-house C++ code tool.

4.1 Model test for creep dominance case

The boundary conditions and the finite-element mesh for the axisymmetric two-particle model—used for the solution of the thermo-electro-mechanical (TEM) problem—are shown in Fig. 3. Due to the symmetry, only the lower half of the upper particle of the two-particle representative volume element is considered. The fine regular mesh is used for the potential contact zone of the particle.

Fig. 3
figure 3

a Boundary conditions for TEM problem and b axisymmetric FE mesh (due to symmetry only the lower half of the upper particle is considered) for two-particle model of powder

Full size image

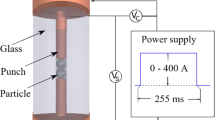
The magnitude of the electric current I(t) is obtained from sintering experiments on a miniature FAST-machine—as described in a previous publication by the authors [22] and related to the current through a single contact between two particles. During the first 70s the current I(t) heats up the sample from room temperature to a preset value of 600 °C or 800 °C. Then the temperature remains constant until t = 1200 s.

The pressure \(p\) on the cylindrical sample of the powder remained almost constant throughout the process, whereby minimal changes represent the correct experimental values. A mean pressure in the equatorial cross section of the particle \(\overline{p} = \frac{p}{{N_{particles} }}\frac{{\pi R_{sample}^{2} }}{{\pi R_{particle}^{2} }}\) is defined (i) by the applied mechanical pressure \(p\) acting on the sample, (ii) by the number of particles \(N_{particles}\) in the sample cross section—which is related with the porosity—and (iii) by the particle radius \(\left. {R_{particle} } \right|_{t = 0} = R\), which can be changed in the sintering process due to large plastic and creep strains. In the performed finite-element computations the constant force \(\overline{F} = \overline{p}\pi R_{particle}^{2} = \frac{p}{{N_{particles} }}\pi R_{sample}^{2}\) instead of variable pressure \(\overline{p}\) is applied in the particle center (see also Fig. 2). Simultaneous, a symmetry requirement—due to periodicity of the arrangement—is prescribed, i.e. the upper boundary of the particle model remains straight and horizontal (see Fig. 3).

The material properties of the particles used in the FE simulations are given in Tables 1 and 2.

Selected results of the FE simulations of a copper two-particle representative volume element are given in Fig. 4. The vertical stress field \(\sigma_{zz}\) (Fig. 4a), plastic strain intensity \(\varepsilon_{i}^{p}\) (Fig. 4b) and creep strain intensity \(\varepsilon_{i}^{v}\) (Fig. 4c) are shown for a particle radius of R = 50 μm under an electric current I = 0.14 A and a pressure of p = 5 MPa at t = 1200 s. The temperature field in the particle after 1200 s is close to being homogeneous with a mean temperature of approximately 600 °C. The relative variation of the steady-state temperature in the particle is approximately 0.0002%.

Fig. 4
figure 4

Results of FE TEM simulations of a copper two-particle representative volume element (R = 50 μm) under electric current I = 0.14 A and pressure of p = 5 MPa at t = 1200 s (Tmax = 600 °C): a vertical stress field σzz distribution; b plastic strain von Mises intensity \(\varepsilon_{i}^{p}\); c creep strain von Mises intensity \(\varepsilon_{i}^{v}\)

Full size image

The contact radius x is very sensitive to the applied mechanical pressure. It nonlinearly increases with increasing pressure p as shown as a function of sintering time in Fig. 5. Note, that the difference between linear and nonlinear solutions for the neck radius is more than 5% for p = 5, 10 and 15 MPa.

Fig. 5
figure 5

Neck radius evolution for various pressures in the TEM problem. Tmax = 600 °C

Full size image

The character of the neck radius evolution is defined by plastic and creep strains, see Fig. 6. The graph shows the maximum values of inhomogeneous fields in the particle; the localization of these extremes can change over time.

Fig. 6
figure 6

Plastic and creep strain evolution for various constant pressure in TEM problem. Tmax = 600 °C

Full size image

The maximum value of the plastic strain does not change largely during sintering. A slight increase of the plastic strain is observed during the temperature increase due to thermal dependency of yield stress and hardening modulus. The rapid growth of the creep strain begins at t = 60 s, when the temperature exceeds 460 °C. Up to t = 100 s (T = 600 °C) plastic strain dominates over creep. After t = 200 s (T = 600 °C) for all considered pressures, the creep strain begins to dominate. This determines the subsequent neck growth. For the considered loading conditions, the growth of the neck radius due to surface diffusion is 80 times lower than due to creep.

Under the considered loading regime, when creep dominates over diffusion, the latter one has no practical effect on neck growth. The obtained results shown that the intensive creep may even prevent the formation of nonconvex curvature at the edge of the contact zone, which is the main driving force of surface diffusion.

4.2 Model test for diffusion dominance case

For low mechanical pressure or very small particles (nanoparticles), the diffusion process is—at least initially—supposed to dominate over the creep process. In the present test case, only the neck growth due to surface/grain boundary diffusion is investigated for the initial neck radius obtained from the thermo-electro-mechanical FE solution of the contact problem. In Fig. 7 the free surface evolution and corresponding neck growth by pure surface/grain boundary diffusion is shown for a low pressure of p = 0.5 MPa. A copper particle of radius R = 50 μm is considered in the computations. In the numerical simulation of the diffusion process, the initial conditions have been taken from the prior FE solution: i.e. the initial neck radius was x = 5.05 μm and the maximal initial temperature was Tmax = 800 °C. The initial configuration of the particle surface (t = 0 s) is shown in Fig. 7 by a thin black line. Both, surface and grain boundary diffusion processes are simulated with the material properties given in Table 3.

Fig. 7
figure 7

Neck configuration evolution with time by pure surface/grain boundary diffusion. p = 0.5 MPa. T = 800 °C

Full size image

The model gives surface configurations for different sintering times for a temperature T = 800 °C (Fig. 7) and for different sintering temperatures between 500 and 1000 °C at time t = 1 h (Fig. 8) as they are known from the sintering theory and point out the considerable influence of the temperature T on the neck formation.

Fig. 8
figure 8

Neck configurations at fixed time under different temperatures (surface/grain boundary diffusion). p = 0.5 MPa

Full size image

The evolution of the neck radius x(t) is shown for different temperatures in Fig. 9.

Fig. 9
figure 9

Neck radius evolution due to surface/grain boundary diffusion for various temperatures. p = 0.5 MPa

Full size image

Comparing the obtained numerical results with the analytical evaluation [23]

$$ \frac{x}{R} = \left( {\frac{25t}{{t_{s} }}} \right)^{1/6} , $$
(28)

where

$$ t_{s} = \frac{{kTR^{4} }}{{\delta_{s} D_{s} \gamma_{s} \Omega }} = \frac{{R^{4} }}{B} $$
(29)

shows an excellent agreement (see Fig. 10) at large times. The analytical approximation is given in Fig. 10 by a black dashed line.

Fig. 10
figure 10

Numerically obtained neck radius evolution due to surface and grain boundary diffusion for various initial neck radii x0 compared with analytical expression by [23]. p = 0.5 MPa. T = 800 °C

Full size image

Results of computations with different values of the initial neck radii x0 (see Fig. 10) show that diffusive neck growth is practically absent until a specified time, which can be evaluated by Eq. (28) for a given neck radius x = x0. This neck growth retardation for large initial radii (which can be caused, for example, by plasticity) indicates a weak influence of the mechanical behavior on the interparticle neck growth when diffusion mechanism dominates. In other words, using the limitations implied in the two-particle model applied for the numerical evaluation of the sintering process, the initial neck radius has only little effect on the configuration after long times.

4.3 Comparison with experiment

A comparison with the results of spark plasma sintering experiments using copper powder (produced by Ecka Granules) having a radius R = 50 μm and applying a sintering temperature Tmax = 600 °C as well as a pressure p ≈ 4.3 MPa is given in Fig. 11. The mean neck radius of the particles is measured by means of a scanning electron microscope after t = 300 s, 600 s and 1200 s. A comparison of the values of the experimentally measured and calculated neck radius—using the coupled thermo-electro-mechanical problem accounting for surface diffusion—show a very good agreement, confirming the reliability of the modeling approach.

Fig. 11
figure 11

Comparison results of simulation with experiment for neck radius evolution. p ≈ 4.3 MPa. Tmax = 600 °C

Full size image

5 Conclusion

In the present research, a method for solving nonlinear boundary value problems of coupled diffusion and thermo-electro-mechanics is proposed. Within this formulation, improved models of plasticity and creep, frictional contact, grain boundary and surface diffusion, real thermal gradient and electric field are taken into account.

Different conclusions can be drawn from the results of the performed numerical simulations:

  • In the case of creep domination (for high mechanical pressure or/and large particles) the neck growth due to mechanical contact prevents the formation of negative neck curvature and therefore the contribution from surface diffusion is practically absent.

  • In the case of diffusion dominance (for low mechanical pressure or/and small particles), the contribution of plasticity affects the neck radius only at the initial stage. For a large initial neck radius, a neck growth retardation is obtained, leading to nearly equal geometries for different initial radii after sufficiently long process times.

Both, experimental results of the neck growth in the SPS process of copper powder sintering and numerical results for a coupled thermo-electro-mechanical problem accounting for surface diffusion are given. A very good agreement between numerically and experimentally obtained values for the evolution of the neck radius has been obtained.