Toward an explainable machine learning model for claim frequency: a use case in car insurance pricing with telematics data

Abstract

In this paper, we suggest an explainable machine learning approach to model the claim frequency of a telematics car dataset. In fact, we use a data-driven method based on tree ensembles, namely, the random forest, to create a claim frequency model. Then, we present a method to build a tree that faithfully synthesizes the predictions of a tree ensemble model such as those derived from the random forest or gradient boosting. This tree serves as a global explanation of the predictions of the black-box. Thanks to this surrogate model, we can extract knowledge from a black-box tree ensemble model. Then, we provide an application to improve the performance of a generalized linear model. Indeed, we integrate this new knowledge into a generalized linear model to increase the predictive power.

Appendices

Appendix

A Results on partitions

Proof

The proof is organized in two parts. First, we prove that the reunion of $\tilde{{\mathcal {R}}}_g$ elements covers ${\mathbb {R}}^p$, i.e.,

• For each $x \in {\mathbb {R}}^p$, there exists $i \in \{1,..,I_1\}$ and $k \in \{1,..,I_2\}$ such that $x \in \tilde{R}_{1, i} \cap \tilde{R}_{2, k}$.

Subsequently, we prove that the elements of $\tilde{{\mathcal {R}}}_g$ are pairwise disjoint, i.e.,

• if $\tilde{R}_{g, 1} \in \tilde{R}_g$ and $\tilde{R}_{g, 2} \in \tilde{R}_g$ then $\tilde{R}_{g, i_1} \cap \tilde{R}_{g, i_2} = \emptyset$.

Let $x \in {\mathbb {R}}^p$, $\tilde{{\mathcal {R}}}_1$ be a partition of ${\mathbb {R}}^p$, so there exists $i \in \{ 1, I_1 \}$ such that $x \in \tilde{R}_{1, i}$. Symmetrically, there exists $k \in \{ 1, I_2 \}$ such that $x \in \tilde{R}_{2, k}$. Hence, $x \in \tilde{R}_{1, i} \cap \tilde{R}_{2, k}$. It means that $\tilde{R}_{1, i} \cap \tilde{R}_{2, k} \ne \emptyset$ and prove the first point.

Now, let us suppose that $\tilde{R}_{g, 1} \in \tilde{{\mathcal {R}}}_{g}$ and $\tilde{R}_{g, 2} \in \tilde{{\mathcal {R}}}_{g}$. There exists $i_1, i_2 \in \{ 1, I_1 \}$ and $k_1, k_2 \in \{ 1, I_2 \}$ such that $\tilde{R}_{g, 1} = \tilde{R}_{1, i_1} \cap \tilde{R}_{2, k_1}$ and $\tilde{R}_{g, 2} = \tilde{R}_{1, i_2} \cap \tilde{R}_{2, k_2}$ where $\tilde{R}_{1, i_1}, \tilde{R}_{1, i_2} \in \tilde{{\mathcal {R}}}_{1}$ and $\tilde{R}_{2, k_1}, \tilde{R}_{2, k_2} \in \tilde{{\mathcal {R}}}_{2}$. Suppose that $\tilde{R}_{g, 1} \cap \tilde{R}_{g, 2} \ne \emptyset$, then there exists $x \in {\mathbb {R}}^p$ such that

$$\begin{aligned} x \in \tilde{R}_{g, 1} \cap \tilde{R}_{g, 2} = \left( \tilde{R}_{1, i_1} \cap \tilde{R}_{1, i_2}\right) \cap (\tilde{R}_{2, k_1} \cap \tilde{R}_{2, k_2}) \end{aligned}$$

It means that $x \in \tilde{R}_{1, i_1} \cap \tilde{R}_{1, i_2}$ and hence that $\tilde{R}_{1, i_1} \cap \tilde{R}_{1, i_2} \ne \emptyset$. However, $\tilde{{\mathcal {R}}}_1$ is a partition. Therefore, the only way that $\tilde{R}_{1, i_1} \cap \tilde{R}_{1, i_2} = \emptyset$ is that $\tilde{R}_{1, i_1} = \tilde{R}_{1, i_2}$. The same argument holds for $\tilde{R}_{2, k_1} \cap \tilde{R}_{2, k_2}$. It follows directly that $\tilde{R}_{g, 1} = \tilde{R}_{g, 2}$. Hence, we prove that if two elements of $\tilde{{\mathcal {R}}}_g$ are not disjoint, they are equal. This concludes the proof. $\square$

B Exploratory data analysis

Table 7 Table of predictors

1.1 Exposure variable selection

Fig. 25

Time as exposure

Fig. 26

Distance as exposure

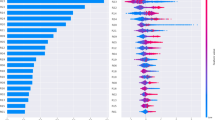
To visualize the relationships between the claim frequency and explanatory variables, we represent a scatter plot of the log claim frequency as a function of each continuous policy predictor: License seniority, Age, and Age registration. Those graphs allow us to see immediately that there is no log-linear relationship between these variables and the target. Hence, we need to discretize continuous predictors to utilize the complex relationship between predictors and the target. As we can see, there is a clear trend for License seniority: the more experienced the driver is, the lower the claim frequency. This is less obvious for Age and Age registration. This is why we choose to discretize our variables with a tree- based method described below.

Remark 14

This dataset contains very few points. Sometimes, for the highest values of continuous predictors, the claim frequency is null because no claim was reported. To represent this in Fig. 3, we remove those points because the log is not defined for these observations. Moreover, the Kwatt variable has too many zeros to be useful in a scatter plot. Therefore, we decided to represent only the discretized variable.

C Grid search

Table 8 Table of allowed random forest hyperparameters for grid search

Table 9 Table of allowed gradient boosting hyperparameters for grid search