Abstract
For a continuous map on the unit interval or circle, we define the bifurcation set to be the collection of those interval holes whose surviving set is sensitive to arbitrarily small changes of (some of) their endpoints. By assuming a global perspective and focusing on the geometric and topological properties of this collection rather than the surviving sets of individual holes, we obtain a novel topological invariant for one-dimensional dynamics. We provide a detailed description of this invariant in the realm of transitive maps and observe that it carries fundamental dynamical information. In particular, for transitive non-minimal piecewise monotone maps, the bifurcation set encodes the topological entropy and strongly depends on the behavior of the critical points.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr Mark F Demers
Footnotes
- 4
The assumption that a and b avoid the boundary points {0, 1} simply reduces certain technicalities and is not of any further importance. For an explicit study of general continuous maps on [0, 1] with interval holes of the form [0, t) and (t, 1] where t ∈ [0, 1], see [22].
- 5
For
 , this is true for all segments. For
, this is true for all segments. For ![$\mathbb{I}=\left[0,1\right]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , this is true for all but those lines in
, this is true for all but those lines in  with arbitrarily small first or second coordinate, see also the previous footnote.
with arbitrarily small first or second coordinate, see also the previous footnote. - 6
As in theorem A (f), we consider the space of all continuous maps
 equipped with the uniform topology, and the space of all non-empty closed subsets of Δ endowed with the Hausdorff metric.
equipped with the uniform topology, and the space of all non-empty closed subsets of Δ endowed with the Hausdorff metric. - 7
More precisely, in the interval case, proposition 2.2 yields transitivity for all points except 0 and 1. Yet, denseness of periodic points for transitive maps implies minimality of f, see the remark before proposition 3.12. Further, recall that there are no minimal continuous maps on [0, 1], i.e.,
 is always non-empty for
is always non-empty for ![$\mathbb{I}=\left[0,1\right]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) .
. - 8
Note that formally speaking, as our present definition of
 excludes points with coordinate entries equal to zero, we could not apply lemma 4.9. However, this issue is of a rather formal nature (see also the remark in the introduction) and will further not play a role in the discussion of the discontinuity of
excludes points with coordinate entries equal to zero, we could not apply lemma 4.9. However, this issue is of a rather formal nature (see also the remark in the introduction) and will further not play a role in the discussion of the discontinuity of  as this discussion has to be carried out explicitly anyway.
as this discussion has to be carried out explicitly anyway. - 9
Note that s0 is necessarily different from
 , since
, since  coincides with the unique fixed point of
coincides with the unique fixed point of  which gives that
which gives that  is not periodic. Hence,
is not periodic. Hence,  is always an interval which has a non-trivial intersection with
is always an interval which has a non-trivial intersection with ![$\left[\sqrt{2},2\right]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) .
.




![$\mathbb{I}=\left[0,1\right]$](https://content.cld.iop.org/journals/0951-7715/34/3/1366/revision2/nonabb78cieqn52.gif)
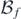
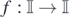
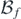
![$\mathbb{I}=\left[0,1\right]$](https://content.cld.iop.org/journals/0951-7715/34/3/1366/revision2/nonabb78cieqn97.gif)
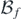
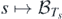

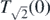


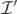
![$\left[\sqrt{2},2\right]$](https://content.cld.iop.org/journals/0951-7715/34/3/1366/revision2/nonabb78cieqn574.gif)