Near optimal minimal convex hulls of disks

Abstract

The minimal convex hulls of disks problem is to find such arrangements of circular disks in the plane that minimize the length of the convex hull boundary. The mixed-integer non-linear programming model, named MinPerim [17], works only for small to moderate-sized problems. Here we propose a polylithic framework of the problem for big problem instances by combining the following algorithms and models: (i) A fast disk-packing algorithm VOROPACK-D based on Voronoi diagrams, non-linear programming (NLP) models for packing disks, and an NLP model minDPCH for minimizing the discretized perimeter of convex hull; (ii) A fast convex-hull algorithm QuickhullDisk to compute the convex hulls of disk arrangements and their perimeter lengths; (iii) A mixed-integer NLP model MinPerim taking the output of QuickhullDisk as its input. We present complete analytic solutions for small problems up to four disks and a semi-analytic mixed-integer linear programming model which yields exact solutions for strip packing problems with up to one thousand congruent disks. It turns out that the proposed polylithic approach works fine for large problem instances containing up to 1,000 disks. Monolithic and polylithic solutions using minDPCH usually outperform other approaches. The polylithic approach yields better solutions than the results in [17] and provides a benchmark suite for further research.

1 Introduction

The minimal convex hull of disks problem in the plane, hereafter referred to the minimal convex hull problem, is to find arrangements of a finite set of 2D circular disks in the plane so that the perimeter length of the convex hull of the disks is minimized. The disks, either congruent or non-congruent, are placed in the arrangements in such a way that they do not overlap each other although two disks may contact. Some problems in logistics, such as the container loading [4] and placement of cylindrical drums on trucks [17], require computing minimal convex hulls of disks. Instead of packing objects into a container of explicitly specified shape such as rectangle and circle, the container in this study is implicitly defined: It is the convex hull of the objects.

The minimal convex hull problem was formally introduced by [17], hereafter abbreviated as KF19, and that of minimal convex hulls of 3D spheres by [16]. The problem was solved by formulating a mixed-integer non-linear programming (MINLP) model named MinPerim and approached from the deterministic global optimization point of view. However, as a MINLP problem is NP-hard, the MinPerim model can only be solved for small problem instances. In this paper, we want to find near optimal solutions of the minimal convex hull problems of considerably large problem instances using a polylithic approach by combining techniques from both mathematical programming and computational geometry. The motivation is to combine the advantages of both disciplines: computational efficiency of computational geometry techniques and solution quality of mathematical programming. Two computational geometry algorithms are employed: VOROPACK-D for packing a set of disks [35, 39] and QuickhullDisk for constructing the convex hulls of the arrangements of disks [26, 33].

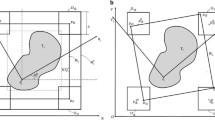
The idea of this study is simple as follows (Fig. 1). Given a large set of input disks, it first makes an initial disk arrangement by solving the disk packing problem with VOROPACK-D or an NLP model (in Step I) and constructs its convex hull with QuickhullDisk (in Step III). The convex hull is then used to build an MINLP model to minimize the perimeter of the convex hull boundary (in Step IV). If the input disk set is of a small-to-moderate size, Step I is followed by an improvement step (in Step II) with an NLP model based on the discretization of the boundary of an approximated convex hull (in Step II) before reaching Step III. The discretization is based on a finite set of rays emanating from a common interior point of the convex hull. The length of each ray, i.e., the terminating point on each ray, follows from the tangential condition that all disks are “below” that tangential line, i.e., the union of all tangentials provide an outer approximation of the boundary of the convex hull.

Fig. 1

Overview of the proposed polylithic approach. Given a set of input disks, it first makes an initial disk arrangement (in Step I) which may be used to improve the solution by solving an NLP model to minimize a discretized perimeter of the approximated convex hull (in Step II). The convex hull of the output from Step II is constructed (in Step III) which is then used to build an MINLP model to minimize the convex hull boundary. The NLP model of Step II can work without an initial disk arrangement in Step I. For small to mid-sized problems, this could be more efficient

Contributions

The major contributions and highlights of this paper are three-fold.

• 1. A combined view of solving the minimal convex hull problems from both computational geometry and mathematical programming for problem instances containing up to 1,000 disks:

  • Polylithic approaches computing the arrangement of non-overlapping disks based on VOROPACK-D or non-linear programming (NLP).

  • Output of VOROPACK-D providing input for QuickhullDisk, possibly through minDPCH (minimum discretized perimeter of convex hull).

  • Output of QuickhullDisk providing initial values for an MINLP model MinPerim.

• 2. Introducing a novel NLP model minDPCH which provides initial values for MinPerim via QuickhullDisk.

• 3. Analytic solutions for smaller cases up to four non-congruent disks and semi-analytic solutions involving a mixed-integer linear programming (MILP) model to solve strip packing problems with congruent disks.

The term polylithic has been coined by [13, 14] to refer to tailor-made modeling and solution approaches to solve optimization problems exploiting several models where output of one is input to another. Hence, polylithic methods consist of a set of models which are linked to each other with regard to their inputs and outputs, i.e., model i+1 can use the results of the first i models. This can be used, for instance, to initialize variables or to put tighter bounds on variables. On the other hand, a monolithic model consists of a model with data, variables and constraints and a call to a solution algorithm to solve optimization problems, i.e., one model with one solve statement. This keeps the structure of the model and its solution relatively simple and clear. Let ${\mathcal {C}}$ be a container hosting all input disks and ${\mathcal {H}}$ be the convex hull of the input disks. Suppose that ${\mathcal {C}}$ is convex. Then, ${\mathcal {H}} \subseteq {\mathcal {C}}$. Circular, elliptic, oval, and rectangular containers are typical examples of such convex containers. We call a container a design container if we seek a disk arrangement which determines the parameters of the container in such a way that an objective function is minimized. The area of the container is an example objective function. This optimization problem could be constrained by a target domain $\varOmega$ in which both the disks and the container have to fit. Hence, ${\mathcal {C}} \subseteq \varOmega$. Usual target domains are also of a convex shape such as circular, elliptic, oval, and rectangular. In this paper, both disk and circle denote a circular object and its boundary, respectively.

Two computational geometry algorithms are used to take advantage of the geometric nature of the problem, particularly for large problem instances. First, the VOROPACK-D algorithm packs circular disks in a container of circular or rectangular shape [35]. There were many studies on packing and cutting problems with mathematical programming and/or heuristic methods [6, 8, 11, 27, 34, 37, 41]. This study uses VOROPACK-D which can quickly find sufficiently good solutions for big problem instances. VOROPACK-D takes an argument denoting the container shape: CC or RC for a circular or rectangular container, respectively. Hence, with a slight abuse of notation, VOROPACK-D(CC) and VOROPACK-D(RC) pack input disks in a circular and rectangular container, respectively. Note that VOROPACK-D(CC) actually executes the Shrink&Shake algorithm which shrinks a sufficiently big circular container and shakes the disks intersecting the container, if any, by repositioning in the container [35, 39]. Taking advantage of the powerful spatial reasoning property of the Voronoi diagram of disks, Shrink&Shake can quickly reach a local optimum. VOROPACK-D(RC) uses a similar algorithm. Secondly, the QuickhullDisk algorithm constructs the convex hulls of disk arrangements by adapting the idea of the well-known quick sort algorithm [26]. VOROPACK-D and QuickhullDisk are freely available as both web servers and standalone programs (for both Linux and MS Windows) from the Voronoi Diagram Research Center, Hanyang University (http://voronoi.hanyang.ac.kr/voropack, http://voronoi.hanyang.ac.kr/quickhulldisk).

The remainder of the paper is organized as follows. Section 2 introduces the ordinary and minimal convex hull of disks and their related notations. Section 3 presents the non-linear programming basis for the minimal convex hull problems. Section 4 derives analytic solutions for small problems up to four disks and provides a semi-analytic mixed-integer linear programming model for a special strip packing problem. Section 5 presents theoretical bounds and gaps. Section 6 presents the proposed polylithic framework and Sect. 7 its validation with numerical experiments. Section 8 concludes this paper.

2 The ordinary and minimal convex hulls of disks

Let ${\mathbf {x}}\in \mathbb {R}^{2}$ be a column vector and ${\mathbf {x}}^{\mathrm {T}}$ be its transpose. The two dimensions of the plane are referenced by $d\in {\mathcal {D}}=\{{1,2\}}$, where 1 and 2 represent the first (x-axis) and second dimension (y-axis), respectively. Let ${\mathcal {I}}$ be a finite set of n disks in the plane where the center of each disk $i \in {\mathcal {I}}$ is ${\mathbf {x}}_{i}^{\mathrm {0}}=(x_{i1},x_{i2})^{\mathrm {T}}$ and its a radius $R_{i}$. Two coordinate frames are employed depending on the situation. The first one uses only the positive quadrant with vectors ${\mathbf {x}}\in \mathbb {R}^{2}$, ${\mathbf {x}}$ $\ge {\mathbf {0}}$. On the other hand, in the second one, we enforce

$$\begin{aligned} {\mathbf {x}}_{\mathrm {c}}=\frac{1}{\sum _{i}R_{i}}\sum _{i}R_{i}{\mathbf {x}}_{i}^{\mathrm {0}} = {\mathbf {0}}. \end{aligned}$$

(2.1)

This implies that ${\mathbf {x}}_{\mathrm {c}}$ coincides the origin of the coordinate system and relaxes the non-negativity constraint. Given two points ${\mathbf {x}}_{1}=(x_{11},x_{12})^{\mathrm {T}}$ and ${\mathbf {x}}_{2}=(x_{21},x_{22})^{\mathrm {T}}$ in the plane, the distance between ${\mathbf {x}}_{1}$ and ${\mathbf {x}}_{2}$ in this study is defined by the $L_2$-norm, i.e., the ordinary Euclidean distance, $\left\| {\mathbf {x}}_{1}-{\mathbf {x}}_{2}\right\| _{2}=\sqrt{\sum _{d\in {\mathcal {D}}}\left( x_{1d}-x_{2d}\right) ^{2}}$.

Suppose that a convex hull boundary of a set of disks is represented by $\partial {\mathcal {H}} = \{ a_1,l_1, a_2,l_2, \ldots , a_M,l_M \}$, where $a_i$ and $l_i$ denote an arc and a line segment on the boundary, respectively. As illustrated in Fig. 2, $\partial {\mathcal {H}}$ is counterclockwise oriented and thus every arc and line segment are also accordingly oriented. Particularly, each arc $a_i \in \partial {\mathcal {H}}$ is counterclockwise oriented around its center. According to the convex hull condition, arcs and line segments tangentially contact if they contact. An oriented line segment $l_j\in \partial {\mathcal {H}}$ is represented by an ordered tuple (${\mathbf {s}}_j$,${\mathbf {e}}_j$) for the start and end vertices, respectively. Note that ${\mathbf {s}}_{j}$ and ${\mathbf {e}}_{j}$ are points on two adjacent disks on $\partial {\mathcal {H}}$. Let $d_k$ be a disk which contributes to $\partial {\mathcal {H}}$. An oriented arc a of disk $d_k$ is represented by an ordered triplet (${\mathbf {x}}_{k}^{\mathrm {0}}$, ${\mathbf {s}}_{k}$, ${\mathbf {e}}_{k}$) of the disk center, the start and end vertices of a on $\partial d_k$, respectively.

Fig. 2

Illustration of a convex hull of six disks. $d_1$, $d_2$, and $d_3$ are outer (or extreme) disks and $d_4$, $d_5$, and $d_6$ are inner (or non-extreme) disks. Be aware of the orientations. $a_1$, $a_2$, and $a_3$ are arcs and $l_1$, $l_2$, and $l_3$ are line segments contributing to the convex hull boundary

Suppose that a subset ${\mathcal {I}}^{\mathrm {out}}\subseteq {\mathcal {I}}$ of disks contributes to $\partial {\mathcal {H}}$. Then, the disks in ${\mathcal {I}}^{\mathrm {out}}$ are called outer disks (or extreme disks), while all other disks are inner disks (non-extreme disks). In Fig. 2, $d_1$, $d_2$, and $d_3$ are outer (or extreme) disks and $d_4$, $d_5$, and $d_6$ are inner (or non-extreme) disks. The arcs $a_1$, $a_2$, and $a_3$ contribute to the convex hull boundary. Note that all entities are oriented. If $|{\mathcal {I}}^{\mathrm {out}}|=k$ and $|{\mathcal {I}}|=n$, $n-k$ disks are either in the interior of ${\mathcal {H}}$ or just touch $\partial {\mathcal {H}}$ from the inside of ${\mathcal {H}}$. A disk touching $\partial {\mathcal {H}}$ is not an outer disk but an inner one.

In a general setting, a disk d can contribute more than one arc to $\partial {\mathcal {H}}$. Consider the case that tiny disks are placed around a big one in the center in such a way that the tangential line between each tiny one and the big one is a supporting hyperplane of the entire disk set. In this case, given n tiny disks, the big disk can contribute to the convex hull boundary with up to n arcs and in such a case, there are 2n line segments on ${\mathcal {H}}$. In Fig. 3a, we have a big disk, say $d_1$, in the middle and two small disks, say $d_2$ and $d_3$, are tangentially placed around $d_1$ in such a way that $d_2$ and $d_3$ are antipodal.

However, in the minimal convex hull, a disk contributes to $\partial {\mathcal {H}}$ at most once if a domain $\varOmega$ does not constrain the placement of disks. See Fig. 3b: $d_2$ and $d_3$ are clustered together. It is easy to prove that the length of $\partial {\mathcal {H}}$ in Fig. 3b is shorter than that in Fig. 3a. In addition, it is not difficult to prove that the placement in Fig. 3b is the minimal convex hull. This observation extends to an arbitrary number of tiny disks. For details, see KF19 [17]. Hence, minimal perimeter length convex hulls have outer disks which contribute one and only one arc to the convex hull boundary. Be aware that, however, there are alternative solutions as the rotation of the arrangement in Fig. 3b with an arbitrary angle around the center of the big disk $d_1$ results in an identical length.

Suppose that there is a constraint such that disks can be placed within a rectangular domain $\varOmega$ as shown in Fig. 3c. Here we have a big disk $d_1$ in the center of $\varOmega$ so that the disk is inscribed in $\varOmega$. Suppose that $\partial d_1 \cap \partial \varOmega$ yields four distinct points, i.e., the center of $d_1$ is equidistant from $\partial \varOmega$ and $\partial \varOmega$ is in fact a square. Suppose that we have four more disks $d_2$, $d_3$, $d_4$, and $d_5$, where no two disks can be placed in a single corner of $\varOmega$ without violating the non-overlapping constraint, i.e., unless the interior of two disks have a non-empty intersection. In such a case, $d_1$ contributes to the minimal convex hull boundary with four arcs. Hence, it can be easily proved that a disk d can contribute to the minimal convex hull boundary with M arcs if and only if $\partial d \cap \partial \varOmega$ has M points. Figure 3d shows that the placement of two non-clustered tiny disks in a single corner cannot be the solution of the minimal convex hull. Here the same reasoning in Fig. 3a and b holds. This discussion results in the following observation: If a disk d has M tangential contacts with a domain $\varOmega$, d contributes to $\partial {\mathcal {H}}$ with M arcs.

Fig. 3

The number of arcs that a disk can contribute to the convex hull boundary. a Two tiny disks, not clustered. The convex hull is not minimal and the big disk contributes to the convex hull boundary with two arcs. b Two tiny disks clustered together. The convex hull is minimal and every disk contributes to the convex hull boundary with one arc. c The domain $\varOmega$ is rectangular. There are four disconnected regions at the corners where each can host only one small disk. The big disk ($d_1$) contributes to the boundary of minimal convex hull with four arcs. Note that $\partial d_1 \cap \partial \varOmega$ has four points. d Two tiny disks separated by a tangential point around a corner. The convex hull is not minimal. In this case the big disk contributes to the convex hull boundary with an additional arc between the two tiny disks

3 Non-linear programming for the minimal convex hull problems

Sections 3.1 and 3.2 discuss an NLP model called minDPCH to minimize the discretized perimeter of an approximated convex hull. The output of minDPCH is used to construct the convex hull using QuickhullDisk algorithm which is then used to build an MINLP model to minimize the convex hull boundary. Section 3.3 presents various NLP models to initialize minDPCH for larger problem instances.

3.1 The idea of minDPCH

Similarly to the idea developed in [16] using polar coordinates, we cover the perimeter of convex hull by a grid of points distributed uniformly on the boundary $\partial {\mathcal {H}}$ of the convex hull. Suppose that we define a coordinate origin as the averaged radius-weighted center ${\mathbf {x}}_{\mathrm {c}}$ using Eq. (2.1). Over the angular index domain $\varphi$ we generate a uniform grid of unit direction vectors ${\mathbf {m}}_{\varphi }$ using ${\mathbf {x}}_{\mathrm {c}}$. Then each point is sampled considering the radial distance from ${\mathbf {x}}_{\mathrm {c}}$ as shown in Fig. 4.

Fig. 4

The geometric idea of minDPCH. A coordinate origin ${\mathbf {x}}_{\mathrm {c}}$ is defined as the averaged radius-weighted center using Eq. (2.1). Then a set of points are sampled using polar coordinates. Given coordinate origin ${\mathbf {x}}_{\mathrm {c}}$, a uniform grid of unit direction vectors ${\mathbf {m}}_{\varphi }$ is defined onto the tangent line at point ${\mathbf {x}}_{\varphi }$ using polar coordinates. ${\mathbf {r}}_{\varphi } = r{\mathbf {m}}_{\varphi }$ is the radial vector which corresponds to ${\mathbf {m}}_{\varphi }$. ${\mathbf {n}}_{\varphi }$ is a normal vector of tangent plane at the point ${\mathbf {x}}_{\varphi }$ which corresponds to ${\mathbf {r}}_{\varphi }$. Note that the orange curve is not the convex hull perimeter but an inner approximation

To each ${\mathbf {m}}_{\varphi }$ we associate a non-negative variable $r_{\varphi }$ and we describe $\partial {\mathcal {H}}$ based on this polar coordinate ${\mathbf {x}}_{\varphi }=(r_{\varphi }, \varphi )$. The points on $\partial {\mathcal {H}}$ are subject to the condition that the distance of all disk centers ${\mathbf {x}}_{i}^{\mathrm {0}}$ is greater or equal to their radii,

$$\begin{aligned} \mathbf {n}_{{\varvec{\varphi }}}^{\mathrm {T}}{\mathbf {x}}_{i}^{\mathrm {0}}-n^{\mathrm {D}}\ge R_{i}, \end{aligned}$$

(3.1)

where the normal vector $\mathbf {n}_{\varvec{\varphi }}$ and origin-distance $n^{\mathrm {D}}$ describe the tangent plane at ${\mathbf {x}}_{\varphi }$,

$$\begin{aligned} \mathbf {n}_{\varvec{\varphi }}^{\mathrm {T}}{\mathbf {x}}_{\varphi }=n^{\mathrm {D}}. \end{aligned}$$

(3.2)

Note that the angle between $\mathbf {n}_{\varphi }$ and ${\mathbf {m}}_{\varphi }$ has to be in the range of 90 and 180 degrees, or

$$\begin{aligned} \mathbf {n}_{\varvec{\varphi }}^{\mathrm {T}}{\mathbf {m}}_{\varphi }\le 0, \end{aligned}$$

(3.3)

which means that the normal vector of the tangential plane points into the interior of the convex hull. We minimize the line integral $\int _{0}^{2\pi }r_{\varphi }\mathrm {d}\varphi \mathbf {,}$ or its discretized version

$$\begin{aligned} \sum _{\nu =1} ^{N_{{\upvarphi }}}r_{\varphi _{\nu }}{ \Delta }\varphi , \end{aligned}$$

(3.4)

with $N_{{\upvarphi }}$ equidistant $\varphi$-angles, the $\varphi$-increments ${\Delta }\varphi =\frac{2\pi }{N_{{\varphi }}}$, and the $\varphi$-grid points $\varphi _{\nu }=\left( \nu -\frac{1}{2}\right) {\Delta }\varphi$. To keep the non-convex NLP problem computationally tractable, we maintain the total number of grid points at a reasonable level of no more than forty points. However, if we want to integrate only the unit disk (i.e., $r_{\varphi _{\nu }}=1$), we need about a hundred grid points to obtain the approximate value of 6.2831853 for $2\pi$. The approach has been implemented and works for up to two hundred disks. Beyond this size we cannot find feasible points. In such cases, we compute initial arrangements of disks using the disk packing models in Sect. 3.3.

Sampling of grid points For convex hulls with near-circular boundaries (with no target domain), the equidistant angular grid is fine. However, for rectangular target domain, it is more efficient to use non-equidistant angular grid. We have applied a few individual numerical tests and see an improved efficiency due to the smaller number of grid points. However, due to the complexity and various technical complications (distribution of the grid points, filling degree of the rectangle, smoothing effects in the non-zero curvature part of the convex hull boundary), we have not systematically followed this track.

3.2 NLP formulation of minDPCH

The ideas in Sect. 3.1 yield the following intuitive NLP formulation. The key decision variables are the center coordinates ${\mathbf {x}}_{i}^{\mathrm {0}}=(x_{i1},x_{i2})^{\mathrm {T}}\in \mathbb {R}^{2}$ of the disks. Consider the disks $i, j \in {\mathcal {I}}$ with radii $R_{i}$ and $R_{j}$, where $R_{i}\ge R_{j}$ for $i>j$. The non-overlap condition for disks i and j produces the following non-convex constraints.

$$\begin{aligned} \left\| {\mathbf {x}}_{i}^{\mathrm {0}}-{\mathbf {x}}_{j}^{\mathrm {0}}\right\| _{2}^{2}=\sum _{d\in {\mathcal {D}}}\left( x_{id}^{\mathrm {0}}-x_{jd}^{\mathrm {0}}\right) ^{2}\ge \left( R_{i}+R_{j}\right) ^{2}\mathbf {,}\quad \forall \{(ij)|i<j\}. \end{aligned}$$

(3.5)

Note that there are $n(n-1)/2$ inequalities of type Eq. (3.5) for n disks. For each direction vector ${\mathbf {m}}_{\varphi }$ with its center at ${\mathbf {x}}_{c}$ using Eq. (2.1), we seek the value of the non-negative variable $r_{\varphi }$ which describes the boundary $\partial {\mathcal {H}}$ of the convex hull based on the polar coordinate ${\mathbf {x}}_{\varphi }=(r_{\varphi }, \varphi )$. The convex hull vector points are subject to the condition that the distances of disk centers ${\mathbf {x}}_{i}^{0}$ is greater or equal to their radii using the constraints (3.1), (3.2), and (3.3). We minimize the discretized perimeter length $\ell _{\mathrm {D}} =\sum _{\nu =1} ^{N_{{\upvarphi }}}\left\| \mathbf {x} _{\varphi }-\mathbf {x} _{\varphi +1}\right\| {\Delta }\varphi$ of $\partial {\mathcal {H}}$ in Eq. (3.4).

The structure of the problem This NLP model contains bilinear and square root relations. It does not provide strong lower bounds. The only strict lower bound we can provide is the radius of the smallest disk: $r_{\varphi }\ge \min _{i}R_{i}, \ \forall \varphi$.

Symmetry and optimality Symmetry is a problem when using deterministic global solver and trying to close the gap between the upper and lower bounds, and thus proving global optimality. Therefore, we want to reduce the observed symmetries: translational, rotational, and mirror symmetry. We can partially reduce translational symmetry by fixing ${\mathbf {x}}_{\mathrm {c}}$. We can destroy these symmetries by selecting the coordinate frame 2 without fixing ${\mathbf {x}}_{\mathrm {c}}$ and instead placing the disk 1 at the origin to break translational symmetry, i.e., ${\mathbf {x}}_{1}=0$. We place disk 2 on the positive $x_{2}$-axis such that $x_{21}=0, \ x_{22}\ge 2R_{1}+R_{2}$ to destroy rotational symmetry. We break mirror symmetry by requesting the third disk to be placed above the $x_{1}$-axis, i.e., $x_{32}\ge 0$. This approach helps us to at least solve small instances with only congruent disks to optimality when we use MinPerim directly and only minimize the sum $\ell _{\mathrm {L}}$ of line segments. However, there is always a trade-off with deterministic global solvers. Without symmetry reducing techniques, i.e., with fewer constraints, they find better initial solutions in shorter time. Symmetry reducing techniques only pay out when one wants to close the gap, which is usually possible only for smaller problems.

3.3 NLP models for disk packing

This section discusses the NLP models for disk packing arrangements to initialize either minDPCH or MinPerim. The disk packing arrangements have to satisfy two constraints: i) the non-overlap constraint and ii) if a rectangular target domain $\varOmega$ is given, all input disks should fit into $\varOmega$. The non-overlap constraints for disks i and j with arbitrary radii $R_{i}$ and $R_{j}$ correspond to Eq. (3.5). For congruent disks, we add the symmetry breaking inequality

$$\begin{aligned} x_{i1}^{\mathrm {0}}\le x_{j1}^{\mathrm {0}}, \quad \forall \{(i,j)|i<j\}. \end{aligned}$$

(3.6)

Fitting the disks inside the rectangular target domain requires

$$\begin{aligned} x_{id}^{\mathrm {0}}\ge R_{i}, \quad \forall \{i,d\} \end{aligned}$$

(3.7)

and

$$\begin{aligned} x_{id}^{\mathrm {0}}+R_{i}\le x_{d}^{\mathrm {p}}\le E_{d}, \quad \forall \{i,d\}. \end{aligned}$$

(3.8)

$E_{d}$ specifies the length ($d=1$) and width ($d=2$) of the rectangle. $x_{d}^{\mathrm {p}}$ is the free length and width of the rectangle if the rectangle is considered as a design container whose area or length of perimeter is to be minimized. Inequality (3.7) assumes that the rectangular container has its lower-left corner at the origin.

Inequalities in Eqs. (3.7) and (3.8) will only be used in the coordinate frame 1; in this case all disks are hosted in a target domain located in the first octant; ${\mathbf {x}}\ge 0$. The model established by Eqs. (3.5), (3.6), (3.7) and (3.8) is called CutDisks which uses either the area $a=x_{1}^{\mathrm {p}}x_{2}^{\mathrm {p}}$ or perimeter length $\ell _{\mathrm {R}}=2(x_{1}^{\mathrm {p}}+x_{2}^{\mathrm {p}})$ of the rectangle hosting the disks. If we want to fit the disks into a circular container of minimal radius $r^{\mathrm {cc}}_{\mathrm {minR}}$, it is better to use the coordinate frame 2 with $-\infty \le {\mathbf {x}}\le +\infty$. For practical reasons one tries to locate the radius-weighted center ${\mathbf {x}}_{\mathrm {c}}$ of the disks near or in the origin of the coordinate system as discussed in Eq. (2.1). The condition for fitting all disks into the circular container of radius $r^{\mathrm {cc}}_{\mathrm {minR}}$ is

$$\begin{aligned} \left\| {\mathbf {x}}_{i}^{\mathrm {0}}\right\| _{2}+R_{i}=\sqrt{ \sum _{d}\left( x_{id}^{\mathrm {0}}\right) ^{2}}+R_{i}\le r^{\mathrm {cc}}_{\mathrm {minR}}. \end{aligned}$$

(3.9)

Rotational symmetry is broken by placing disk 1 in the first quadrant, i.e., ${\mathbf {x}}_{1}\ge 0$. The model established by Eqs. (3.5), (3.6), (3.9), and ${\mathbf {x}}_{1}\ge 0$ is called minRadiusCC; we use it to compute disk arrangements with minimal $r^{\mathrm {cc}}_{\mathrm {minR}}$. It produces good disk arrangements for computing minimal convex hulls of a large number of disks.

In the coordinate frame 2, we also consider a packing problem in which we minimize the sum of distances from all disks to the center ${\mathbf {x}}_{\mathrm {c}}$. That model with (3.5), (3.6) and the objective function

$$\begin{aligned} \min \sum _{i}\left\| {\mathbf {x}}_{i}^{\mathrm {0}}-{\mathbf {x}}_{\mathrm {c} }\right\| _{2} \end{aligned}$$

(3.10)

is called minSDC for a circular container. minSDC can be applied to the rectangular domain using the additional constraints (3.7) and (3.8). The MINLP and NLP models for polylithic approaches of Sect. 7 are summarized in Table 1.

Table 1 Summary of non-linear programming models

4 Analytic and semi-analytic solutions

In this section, we provide various analytic solutions and a semi-analytic solution based on an MILP model to solve the examples in Sect. 7.2.2 to global optimality within seconds—even for instances up to one thousand disks. For the evaluation of numerical experiments in Sect. 7, it helps us to compare the numerical results to analytic solutions.

4.1 Analytic methods for optimal solutions

4.1.1 Two disks

Suppose that two disks with radii $R_{1}$ and $R_{2}$, $R_{1}\ge R_{2}$, are given. We find the disk sector angles, $\alpha _{1}$ and $\alpha _{2}$, in KF19 as

$$\begin{aligned} \alpha _{1}=2\pi -2\arccos \frac{R_{1}-R_{2}}{R_{1}+R_{2}},\quad \alpha _{2}=2\arccos \frac{R_{1}-R_{2}}{R_{1}+R_{2}} \end{aligned}$$

(4.1)

or, alternatively,

$$\begin{aligned} \alpha _{1,2}=\pi \pm 2\arccos \frac{2\sqrt{R_{1}R_{2}}}{R_{1}+R_{2}}. \end{aligned}$$

Thus the length $\ell _{2}$ of $\partial {\mathcal {H}}$ of two touching disks is given by

$$\begin{aligned} \ell _{2}=\ell _{\mathrm {L}2}+\ell _{\mathrm {A}2}=4\sqrt{R_{1}R_{2}}+R_{1}\alpha _{1}+R_{2}\alpha _{2}. \end{aligned}$$

(4.2)

Note that $R_{2}=R_{1}=R$ implies that $\alpha _{2}=\alpha _{1}=\pi$, i.e., the contributed length $\ell _{\mathrm {A}2}$ of the arcs is $2\pi R$ as geometrically expected.

4.1.2 Three disks

For three disks with radii $R_{1},R_{2}$ and $R_{3}$, $R_{1}\ge R_{2}\ge R_{3}$, we need to distinguish two cases to compute the length of the perimeter $\ell _{3}$: In case 1, the radius $R_{3}$ of the smallest disks is so small that this disk does not contribute an arc to $\partial {\mathcal {S}}$ (they may touch $\partial {\mathcal {H}}$); in this case we have $\ell _{3}=\ell _{2}$, where $\ell _{2}$ depends only on $R_{1}$ and $R_{2}$.

In case 2, all three disks contribute an arc to $\partial {\mathcal {H}}$ and establish the tour 1-2-3-1. The minimal sum of the lengths of the line segments is given by

$$\begin{aligned} \ell _{\mathrm {L}3}=2\left[ \sqrt{R_{1}R_{2}}+\sqrt{R_{2}R_{3}}+\sqrt{R_{3}R_{1}}\right] . \end{aligned}$$

(4.3)

To calculate the contribution of the three arcs, we need the sector angles $\alpha _{i}$. As displayed in Fig. 5, they can be obtained as

$$\begin{aligned} \alpha _{i}=2\pi -{\bar{\alpha }}_{i}-\theta _{i,i-1}-\theta _{i,i+1}, \end{aligned}$$

where ${\bar{\alpha }}_{i}$ is the inner triangle angle (opposite to the sector angle $\alpha _{i}$) corresponding to $\alpha _{i}$. Those angles ${\bar{\alpha }}_{i}$ are established by the center coordinates of the disks i, $i-1$, and $i+1$, or, equivalently, sides of size $R_{1}+R_{2}$, $R_{2}+R_{3}$, and $R_{3}+R_{1}$. The angles $\theta _{i,i-1}$ and $\theta _{i,i+1}$ are the trapezoid angles at the center of disk i to the adjacent disks $i-1$ and $i+1$ (similar to Fig. 4 of KF19) obtained by

$$\begin{aligned} \theta _{i,i-1}=\arccos \frac{R_{i}-R_{i-1}}{R_{i}+R_{i-1}},\quad \theta _{i,i+1}=\arccos \frac{R_{i}-R_{i+1}}{R_{i}+R_{i+1}}, \end{aligned}$$

in detail

$$\begin{aligned} \theta _{13}= & {} \arccos \frac{R_{1}-R_{3}}{R_{1}+R_{3}},\quad \theta _{31}=\pi -\theta _{13},\\ \theta _{12}= & {} \arccos \frac{R_{1}-R_{2}}{R_{1}+R_{2}},\quad \theta _{21}=\pi -\theta _{12},\\ \theta _{23}= & {} \arccos \frac{R_{2}-R_{3}}{R_{2}+R_{3}},\quad \theta _{32}=\pi -\theta _{23}. \end{aligned}$$

The angles ${\bar{\alpha }}_{i}$ – their sum adds up to $\pi$ – are given as

$$\begin{aligned} {\bar{\alpha }}_{i}=\arccos \frac{(R_{i}+R_{i-1})^{2}+(R_{i}+R_{i+1})^{2}-(R_{i-1}+R_{i+1})^{2}}{2(R_{i}+R_{i-1})(R_{i}+R_{i+1})}, \end{aligned}$$

(4.4)

in detail

$$\begin{aligned} {\bar{\alpha }}_{1}= & {} \arccos \frac{(R_{1}+R_{3})^{2}+(R_{1}+R_{2})^{2}-(R_{3}+R_{2})^{2}}{2(R_{1}+R_{3})(R_{1}+R_{2})},\\ {\bar{\alpha }}_{2}= & {} \arccos \frac{(R_{2}+R_{1})^{2}+(R_{2}+R_{3})^{2}-(R_{1}+R_{3})^{2}}{2(R_{2}+R_{1})(R_{2}+R_{3})}, \end{aligned}$$

and

$$\begin{aligned} {\bar{\alpha }}_{3}=\arccos \frac{(R_{3}+R_{2})^{2}+(R_{3}+R_{1})^{2}-(R_{2}+R_{1})^{2}}{2(R_{3}+R_{2})(R_{3}+R_{1})}. \end{aligned}$$

Finally, the length $\ell _{3}$ of $\partial {\mathcal {H}}$ of three touching disks is given by

$$\begin{aligned} \ell _{3}=\ell _{\mathrm {L}3}+\ell _{\mathrm {A}3}=\ell _{\mathrm {L} 3}+R_{1}\alpha _{1}+R_{2}\alpha _{2}+R_{3}\alpha _{3}. \end{aligned}$$

(4.5)

Fig. 5

Derivation of the sector angles for three arbitrary disks

4.1.3 Four disks

For four disks with radii $R_{1},R_{2},R_{3}$ and $R_{4}$, where $R_{1}\ge R_{2}\ge R_{3}\ge R_{4}$, we only compute the length of the perimeter $\ell _{4}$ for the case in which all four disks contribute an arc to the convex hull. All other cases can be reduced to two or three disks. As shown in KF19 we need to consider three possible counter-clockwise tours: 1–2–3–4–1, 1–2–4–3–1, and 1–3–2–4—1. The lengths of the lines segments had been given by KF19. To use the idea illustrated in Fig. 1 of KF19, we arrange the disks 1 and 2 horizontally, disk 3 on top touching disks 1 and 2, and disks 4 below disks 1 and 2. This can be understood as tour 1-4-2-3-1, which is the return tour corresponding to 1-3-2-4-1. For the upper part with disks 1, 2 and 3, we can use the formulae for three disks provided in Sect. 4.1.2 to compute ${\bar{\alpha }}_{i}$ and $\theta _{13}$, $\theta _{23}$ as well as $\theta _{31}$ and $\theta _{32}$. For the lower part with disks 1, 2, and 4, we denote the angles ${\bar{\alpha }}_{i}$ by ${\bar{\gamma }}_{i}$ and replace $R_{3}$ by $R_{4}$ leading to similar formulae as in Sect. 4.1.2:

$$\begin{aligned} {\bar{\gamma }}_{1}= & {} \arccos \frac{ (R_{1}+R_{2})^{2}+(R_{1}+R_{4})^{2}-(R_{1}+R_{4})^{2}}{2(R_{1}+R_{2})(R_{1}+R_{4})},\\ {\bar{\gamma }}_{2}= & {} \arccos \frac{(R_{2}+R_{1})^{2}+(R_{2}+R_{4})^{2}-(R_{1}+R_{4})^{2}}{2(R_{2}+R_{1})(R_{2}+R_{4})}, \end{aligned}$$

and

$$\begin{aligned} {\bar{\gamma }}_{4}=\arccos \frac{(R_{4}+R_{2})^{2}+(R_{4}+R_{1})^{2}-(R_{2}+R_{1})^{2}}{2(R_{4}+R_{2})(R_{4}+R_{1})}. \end{aligned}$$

Now we get

$$\begin{aligned} \alpha _{1}= & {} 2\pi -{\bar{\alpha }}_{1}-{\bar{\gamma }}_{1}-\theta _{13}-\theta _{14},\\ \alpha _{2}= & {} 2\pi -{\bar{\alpha }}_{2}-{\bar{\gamma }}_{2}-\theta _{23}-\theta _{24},\\ \alpha _{3}= & {} 2\pi -{\bar{\alpha }}_{3}-\theta _{32}-\theta _{31},\\ \alpha _{4}= & {} 2\pi -{\bar{\gamma }}_{4}-\theta _{42}-\theta _{41}, \end{aligned}$$

with

$$\begin{aligned} \theta _{13}= & {} \arccos \frac{R_{1}-R_{3}}{R_{1}+R_{3}},\quad \theta _{31}=\pi -\theta _{13},\\ \theta _{14}= & {} \arccos \frac{R_{1}-R_{4}}{R_{1}+R_{4}},\quad \theta _{41}=\pi -\theta _{14},\\ \theta _{23}= & {} \arccos \frac{R_{2}-R_{3}}{R_{2}+R_{3}},\quad \theta _{32}=\pi -\theta _{23},\\ \theta _{24}= & {} \arccos \frac{R_{2}-R_{4}}{R_{2}+R_{4}},\quad \theta _{42}=\pi -\theta _{24}. \end{aligned}$$

The minimal sum of the lengths of the line segments is given by

$$\begin{aligned} \ell _{\mathrm {L}4}=2\left[ \sqrt{R_{1}R_{4}}+\sqrt{R_{4}R_{2}}+\sqrt{R_{2}R_{3}}+\sqrt{R_{3}R_{1}}\right] . \end{aligned}$$

(4.6)

Finally, the length $\ell _{4}$ of $\partial {\mathcal {H}}$ of four extreme disks is given by

$$\begin{aligned} \ell _{4}=\ell _{\mathrm {L}4}+\ell _{\mathrm {A}4}=\ell _{\mathrm {L}4}+\sum _{i}R_{i}\alpha _{i}. \end{aligned}$$

(4.7)

The analytic solutions have been compared to the numerical results of the test instances DC04, TC04, TC04a and TC04c defined in Tables 9 and 10. Note that TC04b cannot be used for this comparison as the rectangular target constraints become active; in this case, the optimal analytic solution is not feasible.

4.2 Minimal convex hulls for congruent disks in a strip packing problem

The task of this problem is to arrange a set of congruent disks of radius $R=0.5$ in a rectangle with width $W=4$ and arbitrary, or at least non-limiting length L in such a way that the length of the perimeter of the convex hull becomes minimal. As the disks have radius $R=0.5$, we can have at most four disks in a layer. The solutions are established by a first block (bottom) which consists of layers with one, two, three, or four disks, and a final block (upper) embracing a main body of layers consisting of three or four disks. We have seven dominant configurations for the first block as demonstrated in Fig. 6. The upper block is just the up-side-down configuration of the first block.

Fig. 6

Block configurations 1 to 7 with 4, 5, 6, 7, 8, 9, and 6 congruent disks

Let us now build the model for the optimal configuration. Basically, this model is a partitioning model which covers n disks by the first block, the layers of the main body and the last block. For each block b we derive a priori its contribution $L_{b}$ to the length of perimeter of ${\mathcal {H}}$, if it is selected as first or last block. The binary variables $\delta _{b}^{\mathrm {FB}}$ and $\delta _{b}^{\mathrm {LB}}$ indicate their selection. Note that different blocks can be selected as the first and the last block. The length contribution of blocks has been worked out in Appendix C.2.

Table 2 Lengths $L_b/R-\pi$ of the lower and upper blocks as worked out in Appendix C. The specification parameter S indicates the number of disks in the last layer (seen from bottom or top)

The selection of layers inside the main body is governed by the binary variables $\delta _{l}^{\mathrm {3}}$ and $\delta _{l}^{\mathrm {4}}$ indicating whether layer l contains three or four disks. The objective function of the model, hereafter named minLSP, is to minimize the length of the perimeter of the convex hull.

$$\begin{aligned} \ell =\sum _{b}L_{b}\delta _{b}^{\mathrm {FB}}+\sum _{l}L_{\mathrm {3D}}\delta _{l}^{\mathrm {3}}+\sum _{l}L_{\mathrm {4D}}\delta _{l}^{\mathrm {4} }+\sum _{b}L_{b}\delta _{b}^{\mathrm {LB}}, \end{aligned}$$

(4.8)

where $L_b$ follows from Table 2 and $L_{\mathrm {3D}}=2(\sqrt{3}-1)R,\ L_{\mathrm {4D}}=2\cdot 2R=4R$.

$L_{\mathrm {3D}}$ and $L_{\mathrm {4D}}$ denote the lengths of a layer with three or four disks, respectively, contributed to the length $\ell$. The number of disks in all layers equals the number n of disks to be placed, i.e.,

$$\begin{aligned} \sum _{b}L_{b}\delta _{b}^{\mathrm {FB}}+\sum _{l}3\delta _{l}^{\mathrm {3} }+\sum _{l}4\delta _{l}^{\mathrm {4}}+\sum _{b}L_{b}\delta _{b}^{\mathrm {LB}}=n. \end{aligned}$$

(4.9)

Select one block for the first layer and the other for the last layer, i.e., $\sum _{b}\delta _{b}^{\mathrm {FB}}=1$ and $\sum _{b}\delta _{b}^{\mathrm {LB}}=1$. A layer $l>1$ can be a 3-layer, a 4-layer, or the last layer (last block): $\delta _{l}^{\mathrm {3}}+\delta _{l}^{\mathrm {4}}+\delta _{l}^{\mathrm {L} }=\delta _{l}^{\mathrm {A}}, \ \forall l$, where binary variable $\delta _{l}^{\mathrm {A}}$ indicates whether layer l is active. Active layers are established by

$$\begin{aligned} \delta _{l}^{\mathrm {A+1}}\le \delta _{l}^{\mathrm {A}},\quad \forall l. \end{aligned}$$

(4.10)

The last active layer is identified by $\delta _{l}^{\mathrm {L}}=\delta _{l}^{\mathrm {A}}-\delta _{l}^{\mathrm {A+1}},\ \forall l$. We also need to connect the number $n_{l}$ of disks in layer l to the activity of that layer. As there are not more than 9 disks in an active layer (including blocks), we have

$$\begin{aligned} n_{l}\le 9\delta _{l}^{\mathrm {A}},\quad \forall l. \end{aligned}$$

(4.11)

Note that the first layer is always active, i.e., $\delta _{l}^{\mathrm {A}}=1$ as it is associated with the first block. The last layer is associated with the last block.

It is never optimal if a 3-layer follows a 3-layer. Therefore we exclude two subsequent 3-layers by

$$\begin{aligned} \delta _{l}^{\mathrm {3}}+\delta _{l+1}^{\mathrm {3}}\le 1,\quad \forall l. \end{aligned}$$

(4.12)

Following the same argument it is never optimal if a 3-layer follows first block 7 (the highest layer of that block has three disks) and therefore we require

$$\begin{aligned} \delta _{7}^{\mathrm {FB}}+\delta _{2}^{\mathrm {3}}\le 1,\quad \forall l. \end{aligned}$$

(4.13)

Similarly, it is never optimal if the second-last layer is a 3-layer and that one is followed by last block 7, i.e.,

$$\begin{aligned} \delta _{l-1}^{\mathrm {3}}+\delta _{l}^{\mathrm {L}}+\delta _{7}^{\mathrm {LB}}\le 2,\quad \forall l. \end{aligned}$$

(4.14)

Comments on the implementation Initially, for each block b we store $x_{b}^{\mathrm {0}}$, the $x_{1}$-coordinate of the highest layer of disks (seen from bottom), and the number $N_{b}^{\mathrm {S}}$ of disks at this highest layer. To initialize the computation of the $x_{1}$-coordinate of the main body we compute $x_{1}^{\mathrm {L}}=\sum _{b}x_{1b}^{\mathrm {0}}\delta _{b}^{\mathrm {FB}}$ and then iterate subsequently

$$\begin{aligned} x_{1}^{\mathrm {L}}\rightarrow \left\{ \begin{array}{lc} x_{1}^{\mathrm {L}}+\sqrt{3}R&{},\ S=3 \\ x_{1}^{\mathrm {L}}+2R&{},\ S=4 \end{array} \right. , \end{aligned}$$

(4.15)

where S is a specification parameter indicating the number of disks in the previous layer. The $x_{1}$-coordinates of the layer of disks in the upper block b are computed by a transformation which sets the $x_{1}$-coordinates of the last layer to zero, the second-last layer to $x_{b,\mathrm {LAST}}^{\mathrm {0}}-x_{b,\mathrm {LAST-1}}^{\mathrm {0}}$, and the first layer to $x_{b,\mathrm {LAST}}^{\mathrm {0}}-x_{b,\mathrm {LAST-1}}^{ \mathrm {0}}$. Then we use (4.15) to compute the $x_{1}$-coordinates of all disks in the very layer. This model is solved easily even for large instances of several hundred disks within seconds. Figure 7 shows the selected configurations up to 100 disks.

Fig. 7

Selected configurations for 13 to 100 disks

5 Theoretical bounds and gaps

In this section, we provide some theoretical bounds and gaps for the perimeter length of minimal convex hull. We solve the disk packing problem which minimizes the radius of the circular container hosting all not necessarily congruent disks using minRadiusCC, minSDC, or VOROPACK-D(CC). These initial arrangements of disks are input to minDPCH producing a minimal discretized perimeter of the convex hull ${\mathcal {H}}$, or directly input to QuickhullDisk (Refer to PL4 in Sect. 6). QuickhullDisk computes the perimeter length $\ell ^{\mathrm {QH}}$ of ${\mathcal {H}}$ and generates the extreme disks and vertices which are required to initialize the binary variables $\delta _{j}^{\mathrm {A}}$, $\delta _{ij}^{\mathrm {S}}$, $\delta _{ij}^{\mathrm {D}}$, and $\delta _{ij}$ and to establish $\partial {\mathcal {H}}$ for MinPerim as described in Appendix C.1. With these input we follow up with MinPerim to compute $\ell ^{\mathrm {MP}}$.

As expected, we observe ${\mathcal {L}}^{\mathrm {II}}\le \ell ^{\mathrm {MP}}\le \ell ^{\mathrm {QH}}\le l^{\mathrm {CC}}$, where $l^{\mathrm {CC}}$ is the length of circumference for smallest circular container from minRadiusCC, VOROPACK-D(CC), or benchmark data from Packmomania (Refer to Sect. 7). $\ell ^{\mathrm {QH}}$ is the length of the perimeter of the convex hull constructed by QuickhullDisk and $\ell ^{\mathrm {MP}}$ is the length of the perimeter of the convex hull obtained by MinPerim. ${\mathcal {L}}^{\mathrm {II}}$ is the lower bound derived from the isoperimetric inequality $4\pi a\le \ell ^{2}$ [30] relating the square of the circumference $\ell$ of a closed curve and the area a of the region it encloses on the plane. Let $a=Area({\mathcal {H}})$, i.e., the area of a convex hull ${\mathcal {H}}$, and $A=\pi \sum _{i}R_{i}^{2} < a$, where $R_i$’s are the radii of input disks. Hence, the following weak lower bound ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ can be easily established:

$$\begin{aligned} {\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}=\sqrt{4\pi A}=2\pi \sqrt{\sum _{i}R_{i}^{2}}. \end{aligned}$$

(5.1)

Especially, for n disks with $R_{i}=n-i+1$, $i=1,2,\ldots$, the lower bound ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ on the length of $\partial {\mathcal {H}}$ is reduced to

$$\begin{aligned} {\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}=2\pi \sqrt{\frac{n(n+1)(2n+1)}{6}}. \end{aligned}$$

(5.2)

For congruent disks, on the other hand, a tighter lower bound can be derived from Wegner’s inequality which establishes a lower bound of the area A of the convex hull ${\mathcal {H}}$ of n unit disks (i.e., every disk has a unit radius) as follows: $A \ge \sqrt{12}(n-1)+\left( 2-\sqrt{3}\right) \left\lceil \sqrt{12n-3} -3\right\rceil +\pi$ [3, 18]. Let $\ell$ be the length of the boundary $\partial {\mathcal {H}}$ of the convex hull ${\mathcal {H}}$. Given the isoperimetric inequality $4 \pi A \le \ell ^{2}$, we get the Wegner lower bound ${\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}$ on $\ell$ as follows.

$$\begin{aligned} {\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}=\sqrt{4\pi \left[ \sqrt{12}(n-1)+\left( 2-\sqrt{3}\right) \left\lceil \sqrt{12n-3}-3\right\rceil +\pi \right] } \end{aligned}$$

(5.3)

which is much stronger than the lower bound ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ derived from isoperimetric inequality. For the congruent disks with radius 0.5, divide both sides of Eq. (5.3) by $\sqrt{4.0}$. For instance, if we have $n=13$ such disks, we get ${\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}\approx 12.2017$. Table 5 shows two lower bounds ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ and ${\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}$ for some congruent disks with radius 0.5 using Eqs. (5.1) and (5.3).

Let $\ell _{tot}$ be the total length of the convex hull perimeter. Let $\ell _{\mathrm {L}}$ and $\ell _{\mathrm {A}}$ be the subtotal lengths of the linear and circular segments on the convex hull boundary, respectively. Hence, $\ell _{tot} =\ell _{\mathrm {L}}+\ell _{\mathrm {A}}$. Let ${\mathcal {L}}^{\mathrm {best}}_{\mathrm {lb}}$ be the best lower bound of the length of the convex hull boundary. Let

$$\begin{aligned} \varDelta =\frac{\ell _{tot} - {\mathcal {L}}^{\mathrm {best}}_{\mathrm {lb}}}{ {\mathcal {L}}^{\mathrm {best}}_{\mathrm {lb}} }. \end{aligned}$$

(5.4)

Then, $\varDelta$ defines the gap between the best solution obtained for the perimeter and the best lower bound. The column D($\varDelta ^\mathrm {ii}(\%)$) of Table 5 shows the gap between the best solution G($\ell _{*}$) in analytic form and B(${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$). Note that the optimal solution in column G($\ell _{*}$) of Table 5 for $n=13$ is $8 + \sqrt{3} + \pi = 12.8736$. Hence, the corresponding gap is $\varDelta = \frac{12.8736-11.3272}{11.3272} \times 100 = 13.6521\%$. Similarly, the column E($\varDelta ^{\mathcal {W}}(\%)$) shows the gap between the best solution G($\ell _{*}$) obtained and C(${\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}$). See columns ${\mathcal {L}}^\mathrm {ii}_\mathrm {lb}$, ${\mathcal {L}}^{\mathcal {W}}_\mathrm {lb}$, $\varDelta ^\mathrm {ii}(\%)$, and $\varDelta ^{\mathcal {W}}(\%)$ in Table 5.

6 Polylithic framework of the minimal convex hull problems

In this section, we propose a polylithic approach to modeling and solving the minimal convex hull problems using the MINLP and NLP models in Table 1, VOROPACK-D, and QuickhullDisk. We recommend readers to refer to Appendix B for VOROPACK-D, QuickhullDisk, and Voronoi diagrams. Figure 1 is redrawn in Fig. 8 with algorithmic details. Step I constructs an initial disk arrangement and Step II minimizes the discretized perimeter of the approximated convex hull using minDPCH. This minimization can be from scratch, using minDPCH on its own, or by initializing minDPCH with the initial arrangement of the disks obtained in Step I. Step III constructs the convex hull of the disk arrangement and computes the perimeter length of the convex hull, and Step IV constructs the minimal convex hulls of the disks via an MINLP model MinPerim. Step I finds a non-overlapping disk arrangement. Depending on the existence of a target domain, Step I may use NLP model(s) or either VOROPACK-D(CC) or VOROPACK-D(RC). Step II minimizes the discretized perimeter of the approximated convex hull using an NLP model minDPCH. There are two alternatives in Step II: minDPCH may take the output of Step I as its input or minDPCH may be used as a monolith for Step III. In Step III, QuickhullDisk is used to construct the convex hull of the disk arrangement resulting from Step I or II. QuickhullDisk provides the initial values for MinPerim in Step IV. Note that two different versions of minSDC appear in Step I: One model with Eqs. (3.5), (3.6), and (3.10) used for a circular container (with no target domain), and the other with Eqs.(3.5), (3.6), (3.7), (3.8), and (3.10) for a rectangular target domain. We have validated the proposed PolyLithic approach (PL) using the following algorithmic settings:

• PL1. Verification of VOROPACK-D algorithm: We have done this by comparing its solutions to those of the NLP models.

  • (a) VOROPACK-D(CC) (circular container, i.e. no target domain): Comparing the solutions to the global minima of minRadiusCC; Table 3.

  • (b) VOROPACK-D(RC) (rectangular target domains): Comparing the solutions to the global minima of CutDisks; Table 5.

• PL2. Initial disk arrangements: We have obtained from the following NLP models and algorithm.

  • (a) NLP models with various objective functions minimizing

    • i. the radius of a circular container using minRadiusCC (good for larger numbers of disks),

    • ii. the sum of radius weighted distances from all disks to the averaged center using minSDC,

    • iii. the area of a rectangle using CutDisks, and

    • iv. the perimeter length of a rectangle using CutDisks.

  • (b) minDPCH for the minimal discretized perimeter of the convex hull (in monolithic or polylithic version).

  • (c) VOROPACK-D algorithm.

• PL3. Monolithic version of minDPCH: Output of minDPCH is provided for input of QuickhullDisk; Tables 4, 5,  6, 7, 8 (Flow C2–C3 in Fig. 8).

• PL4. Polylithic versions of minDPCH: NLP model(s) or VOROPACK-D precedes minDPCH as follows.

  • (a) minRadiusCC: Table 4 (Flow A11-A21-A3).

  • (b) minSDC: Table 4 (Flow A12-A21-A3).

  • (c) CutDisks: Tables 6, 7, and 8 (Flow B11-B12-B21-B3).

  • (d) VOROPACK-D(CC): Tables 3 (Flow A13-A22-A3) and 4 (Flow A13-A21-A3).

  • (e) VOROPACK-D(RC): Tables 6, 7, and 8 (Flow B13-B22-B3).

• PL5. Polylithic for solving MinPerim (The first polylithic approach P1 proposed in KF19): We solve the disk packing problem minimizing the area or perimeter length of the design rectangle hosting all disks. Then this initial disk arrangement is used for initializing MinPerim. We provide this to compare the results of P1 with those of this paper (Tables 5, 6, 7, 8).

Fig. 8

The proposed polylithic framework consisting of up to four computational steps: (I) Initial disk arrangement, (II) discretized perimeter of the approximated convex hull, III) convex hull of the disk arrangement computed by QuickhullDisk, and IV) perimeter minimization of convex hulls using MinPerim. Depending on the existence of a target domain, Step I uses either VOROPACK-D(CC) or VOROPACK-D(RC) as well as NLP models. They may be used to initialize minDPCH to compute the discretized perimeter, or minDPCH is used as a monolith in Step II. In Step III, QuickhullDisk is used to compute the convex hull of the initial disk arrangement available after Step I or II. Step III finishes with providing intermediate data allowing to compute initial values for MinPerim in Step IV. Note that minSDC comes in two slightly different versions: One model with (3.5), (3.6), and (3.10) used in the circular container context, and the other with (3.5), (3.6), (3.7), (3.8), and (3.10) subject to a rectangular target domain

7 Validation of the polylithic framework via numerical experiments

We have verified and validated the solution quality and performance of the polylithic approach comparing its experimental results to analytic solutions, theoretical bounds, and some benchmark data including the best known results from both KF19 and the Packomania website (www.packomania.com, visited on Jun 29, 2018, maintained by E. Specht). Good initial disk arrangements for the polylithic approach were obtained using both the NLP models and VOROPACK-D. minDPCH is the strongest NLP model and thus almost all experiments contain the results obtained by minDPCH. The congruent disk experiments summarized in Table 5 enable us to evaluate and compare the quality of minDPCH to the analytic solutions.

7.1 Experimental environment: data, software, and computing platforms

Data sets

We have performed the computational tests for both circular containers (no target domain) and rectangular domains. For circular containers, we used one of the Packomania data sets where the disk radii are defined as $R_{i}=n-i+1$, $n=1, 2, \ldots 1,000$. This data enables us to compare our results with those of Packomania for $n\le 200$. Note that the original Packomania set has $R_i=i$, but some of our models and algorithms require that the radii of the disks are sorted in descending order. The computational resources used for getting the best-known solutions of Packomania are not known. For rectangular domains, two different instance types Cx or Dx were used in KF19. Instances with congruent disks start with the prefix “C” while instances with non-congruent disks start with “D”. The parameter x stands for the number of disks in each instance, e.g., D03 represents an instance with three non-congruent disks. If the final gap for the minimization is smaller than $10^{-4}$, the instance is labeled with an $^{*}$. We used the following data sets for experiments.

• SET-P: Packomania data.

• SET-A: C05-C90 (in Table 5).

• SET-B: DC03-DC10 (in Table 9).

• SET-C: TC03-TC28 (in Table 10).

• SET-D: D series (in Table 11).

The instances in SET-D of Table 11 are established by combining some disk sets of B and C, e.g., D21 = 3 $\times$ TC07 (Refer to Appendix D for Tables 9, 10, and 11). Note that only SET-B and SET-C have been used by KF19.

Software and hardware

The mathematical optimization models as well as the polylithic approaches were implemented in GAMS 28.2 using two global solvers, BARON (with CPLEX for the LP relaxation and MINOS for the NLP problem) and LINDO. VOROPACK-D was used to pack circular disks in a container of circular or rectangular shape [35] and QuickhullDisk was used to construct the convex hulls of disk arrangements [26]. Computations were executed on three similar machines: i) PC1: a 64 bit machine with an Intel(R) Core(TM) i7 CPU 2.8 GHz, 16 GB, RAM running Windows 7, ii) PC2: a 64 bit machine with an Intel(R) Core(TM) i7-7700 (3.6 GHz), 16GB RAM running Windows 10 Pro, iii) PC3: a 64 bit machine with an Intel(R) Core(TM) i7-7700 (3.6 GHz), 16GB RAM running Windows 10 Pro. All computations were done using a single core processor. However, the proposed polylithic approaches could exploit parallel computer hardware (multi-core system, clusters of computers, etc.) by applying the technique introduced by Kallrath et al. [15]. This allows us to select a polylithic method and its parameters and to solve it on a selected core or computer. By doing this in parallel, we may pick the best solution obtained within a given time limit.

Computation time limits

Computation time limits for minRadius, CutDisks, and minSDC were set to 3,600 sec; Those of MinPerim and minDPCH were set to 36,000 sec. An algorithm terminated when the gap was reached. The computation times for VOROPACK-D and QuickhullDisk were negligible (i.e. a few seconds, at most). For details on their computation time, see [35] and [26]. The computation times for the best-known solutions of the Packomania data SET-P are not publicly available.

Assumption

Let $N_{i}^{\mathrm {ls}}$ be the maximal number of line segments of the convex hull boundary which is incoming (ending) to disk i or outgoing (starting) from disk i. For example, a disk $d_1$ of Fig. 2 has an incoming line segment $l_3$ and outgoing line segment $l_1$. All numerical experiments in this section have been performed with $N_{i}^{\mathrm {ls}}=1$, i.e., each disk has at most one incoming and one outgoing line segment on the convex hull boundary unless we explicitly express some different setting.

7.2 Experiments and discussions

7.2.1 Circular container (No target domain)

We performed experiments for the circular container problem using the Packomania data SET-P. Tables 3 and 4 summarize the results. For smaller number of disks, as is expected, the minimal circular container solutions are not strong initial solutions for minimal convex hulls. However, for 20 or more disks they are reasonable initial solutions. From about $n=50$, VOROPACK-D(CC) provides better initial solutions than the NLP models based on minRadiusCC and minSDC. The monolithic approach works only reasonably well up to a certain problem size of 170 disks in Table 4. Within the polylithic approach (PL4 in Sect. 6), minRadiusCC and minSDC - in terms of the quality of the configuration—are competitive up to 40 disks; for larger problem instances VOROPACK-D(CC) outperforms them.

Figure 9 shows the arrangements of non-congruent disks in circular container which are produced by applying different methods to Packomania data SET-P (n=5, 10, 15, 20, 30, 50, and 100). The columns of the table are as follows. Column (A): n: The number of disks. Columns (B - E): The disk arrangements by four different methods and their convex hull boundaries as follows. Column (B): $\texttt {VOROPACK-D(CC)}$ (This column corresponds to Column B of Table 3). Column (C): $\textsf {minRadiusCC}$ (Column D of Table 3). Column (D): $\texttt {VOROPACK-D(CC)}\rightarrow \texttt {QuickhullDisk}\rightarrow \textsf {MinPerim}$ (Column G of Table 3). Column (E): $\textsf {minRadiusCC}\rightarrow \texttt {QuickhullDisk}\rightarrow \textsf {MinPerim}$ (Column H of Table 3). We have the following observations.

• In all cases except two (Column (D) of $n=50, 100$), MinPerim improves initial solutions from both $\texttt {VOROPACK-D(CC)}$ and $\textsf {minRadiusCC}$.

• Improvements become smaller as the problem size increases.

• The methods using only NLP and MINLP models do not work for the large problem instances (Refer to Tables 3 and 4). In this case, the computational geometry algorithm such as $\texttt {VOROPACK-D(CC)}$ could be a good alternative.

Monolithic experiments

Table 3 reports the radii of the containers obtained from VOROPACK-D(CC) ($r^{\mathrm {cc}}_{{\mathbf{V}}}$), the best-known radii reported in Packomania ($r^{\mathrm {cc}}_{{\mathbf{P}}}$), and those of minRadiusCC ($r^{\mathrm {cc}}_{\mathrm {minR}}$) followed by the relative gap ($\varDelta ^{\mathrm {ii}}$) in percent between column D($r^{\mathrm {cc}}_{\mathrm {minR}}$) and the best lower bound, $\ell _{lb}$, provided by BARON (not in the table) ,i.e., (D($r^{\mathrm {cc}}_{\mathrm {minR}}$) - $\ell _{lb}$) / $\ell _{lb}$ * 100. The next column shows the length $l^{\mathrm {cc}}_{\mathrm {peri}}=2\pi \min \{r^{\mathrm {cc}}_{{\mathbf{V}}},r^{\mathrm {cc}}_{{\mathbf{P}}},r^{\mathrm {cc}}_{\mathrm {minR}}\}$ of the perimeter of the smallest circular container. Columns $\ell (r^{\mathrm {cc}}_{{\mathbf{V}}})$ and $\ell (r^{\mathrm {cc}}_{\mathrm {minR}})$ show the lengths of perimeters of the convex hull when feeding the initial solutions obtained by VOROPACK-D(CC) or minRadiusCC through QuickhullDisk into MinPerim, respectively (i.e., $\texttt {VOROPACK-D(CC)} \rightarrow \texttt {QuickhullDisk} \rightarrow \textsf {MinPerim}$ or $\textsf {minRadiusCC} \rightarrow \texttt {QuickhullDisk} \rightarrow \textsf {MinPerim}$). The last two columns display $\ell (\text {KF19})$, the value obtained by MinPerim using the polylithic mode P1 described in KF19 and the lower bound ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ derived from the isoperimetric inequality in Eq. (5.2). The entry marked green in each row indicates the smallest perimeter length found for that problem instance.

Note that for smaller problem instances $n\le 8$, the followings were observed: (i) we are able to close the gap and prove the global optimality of $r^{\mathrm {cc}}_{\mathrm {minR}}$; (ii) $r^{\mathrm {cc}}_{\mathrm {minR}}=r^{\mathrm {cc}}_{{\mathbf{P}}}$; (iii) the monolithic computations of the minimal length of the perimeter using minRadiusCC produce disk arrangements which fit into a circular container of the radius $r^{\mathrm {cc}}_{\mathrm {minR}}=r^{\mathrm {cc}}_{{\mathbf{P}}}$. The computed radius is proven to be optimal. This leads us to formulating a conjecture in Appendix E which relates the optimal solution of minimal circular container to that of the minimal convex hull.

Polylithic experiments The first column $\ell _{\mathrm {b}}$ of Table 4 is the best perimeter length of Table 3, i.e., $\ell _{\mathrm {b}} = \min \{ \ell (r^{\mathrm {cc}}_{{\mathbf{V}}}), \ell (r^{\mathrm {cc}}_{\mathrm {minR}}), \ell (\text {KF19}) \}$. The column $\ell _{\mathrm {m}}$ is obtained by initializing MinPerim (through QuickhullDisk) by the monolithic solution found by minDPCH (i.e., minDPCH $\rightarrow$ QuickhullDisk $\rightarrow$ MinPerim). The next column $\ell ^1_{\mathrm {p}}$ is the polylithic value which is obtained by initializing minDPCH with minSDC (i.e., minSCD $\rightarrow$ minDPCH $\rightarrow$ QuickhullDisk $\rightarrow$ MinPerim). The following two columns $\ell ^2_{\mathrm {p}}$ and $\ell ^3_{\mathrm {p}}$ are identical to $\ell ^1_{\mathrm {p}}$ except that minSDC is replaced by VOROPACK-D(CC) and minRadiusCC, respectively. The last column is the lower bound ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ of the length of the convex hull perimeter derived from the isoperimetric inequality and is a duplication of the last column of Table 3. For most cases, $\ell ^2_{\mathrm {p}}$ using VOROPACK-D(CC) provides the best initialization of minDPCH. For many instances in the circular container experiments we found that the arrangements of disks leading to the minimal circular container radius also had the minimal perimeter convex hulls and vice versa. This observation inspired us to attempt to formulate the conjecture in Appendix E.

Table 3 Circular container

Table 4 Circular container

7.2.2 Rectangular domain

We performed experiments for rectangular domain against SET-A, SET-B, SET-C, and SET-D of Sect. 7.1.

The experimental results are compiled as follows: Table 5 for congruent disks, Tables 6, 7, and 8 for non-congruent disks. For congruent disks, in most cases, the monolithic solutions using minDPCH and polylithic solutions using VOROPACK-D outperform the previous results reported in KF19. For non-congruent disks except SET-C (Table 7), the monolithic solutions using minDPCH (PL3 of Sect. 6) outperform others in most cases. For SET-C, the polylithic solutions using minDPCH based on CutDisks and minSDC (PL4 of Sect. 6) outperform others.

Congruent disks Table 5 shows the results for the congruent disks of radius $R=0.5$. The width W of a rectangular domain is fixed by $W=4$ and its length $L=8$ for $n \le 30$, $L=14$ for $30 < n \le 60$, and $L=25$ for $n > 60$. The columns of the table are as follows. Column Instance: The instance of congruent disk models as named in KF19 (e.g., C20 involves 20 congruent disks). ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$: The lower bound of the primeter length derived from the isoperimetric inequality as ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}=\sqrt{n} \pi$. ${\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}$: The Wegner lower bound in Eq. (5.3). $\varDelta ^\mathrm {ii}(\%)$: The gap between the analytic solution $\ell _{*}$ in Column G and ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ using Eq. (5.4). $\varDelta ^{\mathcal {W}}(\%)$: The gap between the analytic solution $\ell _{*}$ and ${\mathcal {L}}^{{\mathcal {W}}}_{\mathrm {lb}}$. $\varDelta (\%)$: The gap between the analytic solution $\ell _{*}$ and $\min \{\ell _{\mathrm {m}},\ell ^{{\mathbf{V}}}_{\mathrm {p}},\ell ^{\mathrm {P1}}_{\mathrm {p}}\}$. $\ell _{*}$: The best solution (analytic and MILP solution of minLSP are identical up to 9 decimal places). CPU: The CPU time in seconds to compute the monolith solution $\ell _{\mathrm {m}}$ using minDPCH. $\ell _{\mathrm {m}}$: The monolithic length of the convex hull perimeter obtained by solving the grid model using minDPCH. $\ell ^{{\mathbf{V}}}_{\mathrm {p}}$: The polylithic length of the convex hull perimeter using VOROPACK-D(RC). $\ell ^{\mathrm {P1}}_{\mathrm {p}}$: The polylithic length of the convex hull perimeter using homotopy P1 in MinPerim. $\ell (\mathrm {KF19})$: The perimeter reported in KF19. In most cases, $min[\ell _{\mathrm {m}},\ell ^{{\mathbf{V}}}_{\mathrm {p}}] \le \ell (\mathrm {KF19})$. Thus the current approach improves the results by KF19. The numerical solutions of the instances marked with an $*$, e.g., C13*, are identical to the analytic results or semi-analytic ones based on the partitioning model. Zeros of column F($\varDelta (\%)$) also shows the same information.

Fig. 9

Circular container. The arrangements of non-congruent disks of Packomania data SET-P produced by different methods. Column (A): n: The number of disks. Columns (B–E): The disk arrangements by four different methods and their convex hull boundaries as follows. Column (B): $\texttt {VOROPACK-D(CC)}$ (This column corresponds to Column B of Table 3). Column (C): $\textsf {minRadiusCC}$ (Column D of Table 3). Column (D): $\texttt {VOROPACK-D(CC)}\rightarrow \texttt {QuickhullDisk}\rightarrow \textsf {MinPerim}$ (Column G of Table 3). Column (E): $\textsf {minRadiusCC}\rightarrow \texttt {QuickhullDisk}\rightarrow \textsf {MinPerim}$ (Column H of Table 3). 1st row: n=5. 2nd row: n=10. 3rd row: n=15. 4th row: n=20. 5th row: n=30. 6th row: n=50. 7th row: n=100. $\ell$ is the length of minimal convex hull boundary which is computed by each method. In all cases except two (Column (D) of $n=50, 100$), MinPerim improves initial solutions from both $\texttt {VOROPACK-D(CC)}$ and $\textsf {minRadiusCC}$. Improvements become smaller as the problem size increases. * means no improvement. As shown in Tables 3 and 4, the methods using only NLP and MINLP models do not work for the large problem instances. In this case, the computational geometry algorithm such as $\texttt {VOROPACK-D(CC)}$ could be a good alternative

The last column (Best Arrangement): Layer arrangements for congruent disks (C05 through C20). As the target rectangle has width $W=4$, at most 4 disks can find place in the width direction. Therefore, we are facing a sort of a strip packing problem for more than five disks in which disks are arranged in layers. The last column of Table 5 and Fig. 10 symbolically and graphically reveal the best arrangement patterns for up to 20 disks, respectively; see also other columns of Table 5 for the analytic and numeric results. For instance, to understand Table 5 better, read configuration C20 in Fig. 10 from left to right vertically. The first column of disks at the very left contains two disks, followed by a column of three disks, then three times four disks, and finally three disks at the very right.

Table 5 Rectangular domain

Fig. 10

Congruent disk configurations up to 20 disks. All instances from SET-A

Non-congruent disks

Tables 6, 7, and 8 show the results for non-congruent disks in a rectangular domain for SET-B, SET-C, and SET-D, respectively. The tables report the lower bound ${\mathcal {L}}^{\mathrm {ii}}_{\mathrm {lb}}$ derived from the isoperimetric inequality Eq. (5.2) followed by the best known solution $\ell _{b}$. The CPU-column gives the time in seconds to compute the length $\ell _{\mathrm {m}}$ using the monolith version of minDPCH. $\ell ^{\mathrm {0}}_{\mathrm {p}}$ is obtained by using the polylithic version of minDPCH which starts with CutDisks yielding input into minSDC, which in turn feeds into minDPCH followed by QuickhullDisk and, finally, MinPerim. Then we see the length $\ell ^{\mathrm {P1}}_{\mathrm {p}}$ computed by the polylithic mode P1 of MinPerim described in KF19. The next column labeled $\ell ^{{\mathbf{V}}}_{\mathrm {p}}$ displays the convex hull perimeter obtained when feeding the configuration computed by VOROPACK-D(RC) into MinPerim. The last column of Table 7 displays $\ell (\mathrm {KF19})$, the best value reported by KF19 using MinPerim. Figure 11 shows the best configurations for the non-congruent disks problem of SET-B, SET-C, and SET-D.

Some entries in the $\ell ^{{\mathbf{V}}}_{\mathrm {p}}$-column, in Tables 7 and 8, show nsf, which indicates that VOROPACK-D(RC) does not find a feasible configuration. It does not strictly mean the problem is infeasible, as the Voronoi approach embedded in VOROPACK-D(RC) is a heuristic. We expect this to happen when the target domain has not much more capacity than just hosting the disks to be placed. This weakness can possibly be overcome by connecting it with a metaheuristic such as simulated annealing.

Table 6 Rectangular domain

Table 7 Rectangular domain

Table 8 Rectangular domain

Fig. 11

Configurations for the non-congruent disks problems of SET-B, SET-C, and SET-D. a, b, c: from SET-B. (d through k): from SET-C. (l through o): from SET-D

8 Conclusions and outlook

This paper studies solution methods for the minimal convex hull of disks problem which is to find the arrangement of a finite set of 2D circular disks such that the perimeter length of the convex hull of the disks is minimized. In the arrangement, disks are not allowed to overlap each other but may contact. To solve the problem, we have developed a polylithic framework which combines various NLP models and computational geometry algorithms to provide good initial disk arrangements. These arrangements - the best ones result from minimizing the discretized perimeter or from minimal circular containers obtained by the VOROPACK-D algorithm (which is based on the Voronoi diagram) - have been fed into the QuickhullDisk algorithm to construct the convex hull and to compute the length of its perimeter. The output of QuickhullDisk is transformed into initial values which are used by MinPerim to improve the solution. For up to 1,000 disks, VOROPACK-D was used to compute the non-overlapping disk arrangement with convex hulls of almost circular shape. Monolithic and polylithic solutions using minDPCH usually outperform other approaches. Analytic and semi-analytic solutions helped us to verify that the NLP based algorithm and VOROPACK-D produce near optimal solutions over a broad range of test cases. It turns out that the polylithic approach yields better solutions than the results in [17] and the test cases and results could serve as a benchmark suite for further research.

From circular container experiments, we observed that the disk arrangement with minimal circular container radius gave the minimal perimeter convex hull. Thus one of the future researches would be to apply the techniques used in VOROPACK-D to the computation of minimal convex hull. Another research path is to extend the current activities to 3D problems, i.e., computing the convex hull of spheres, ellipsoids, and polytopes. We believe that the polylithic framework can be similarly applied to other hard optimization problems.

Appendices

Notation

We provide the symbols which is introduced in the derivation of the models and is used in the Voronoi diagrams (Appendix B); they are not necessarily used in the models directly.

VD(P):

the ordinary Voronoi diagram of a point set P in ${\mathbb {R}}^2$.

VD(D):

the Voronoi diagram of a circular disk set D in ${\mathbb {R}}^2$.

${\mathcal {VD}}(\kappa ,D)$:

the Voronoi diagram of a set D of non-intersecting circular disks contained in a container $\kappa$

$\varDelta$:

the difference between the upper and lower bound from the LP relaxation for the MINLP provided by the solver.

$\partial {\mathcal {H}}$:

the perimeter of the convex hull hosting all disks.

${\mathcal {H}}_{ij}$:

hyperplane induced by the circular line segment of disk i connecting a pair of incoming (ending) and outgoing (starting) vertices ${\mathbf {v}}_{j}^{ \mathrm {la}}$ and ${\mathbf {v}}_{j++1}^{\mathrm {al}}$ located on that disk.

${\mathcal {H}}_{j}$:

hyperplane induced by line segment j connecting and tangential to two adjacent disks.

m:

the number of disks touching the convex hull; $m\le n$.

n:

the number of disks to be placed.

$N_{i}^{\mathrm {ls}}$:

for disk i, the maximal number of incoming or outgoing line segments on the convex hull boundary.

${\mathbf {n}}_{j}^{\mathrm {H}}$:

the normal vector onto hyperplane ${\mathcal {H}}_{j}$ induced by line segment j connecting two disks.

${\mathcal {H}}$:

the convex hull hosting all disks.

$S_{ij}$:

specifying whether arc on disk i induced by line segment j is a major ($S_{ij}=1$) or minor sector ($S_{ij}=0$); $S_{ij}\in \{0,1\}$.

${\mathbf {v}}_{j}^{\mathrm {al}}$:

vertex connecting a source arc to line segment j; ${\mathbf {v}}_{j}^{\mathrm {al}}=(v_{1j}^{\mathrm {al}},v_{2j}^{ \mathrm {al}})$

${\mathbf {v}}_{j}^{\mathrm {an}}$:

vertex connecting a source arc line segment $j+1$; ${\mathbf {v}}_{j}^{\mathrm {an}}=(v_{1j}^{\mathrm {an}},v_{2j}^{ \mathrm {an}})$.

${\mathbf {v}}_{j}^{\mathrm {la}}$:

vertex connecting line segment j to a destination arc; ${\mathbf {v}}_{j}^{\mathrm {la}}=(v_{1j}^{\mathrm {la} },v_{2j}^{\mathrm {la}})$.

${\mathbf {x}}^{\mathrm {c}}$:

radius-weighted center of all disks.

The symbols used in the explanations of the models are summarized in the following subsections.

1.1 Indices and sets

$d\in {\mathcal {D}}$ :

index for the dimension with ${\mathcal {D}}=\{1,2\}$; $d=1$ represents the length-axis, and $d=2$ the width-axis of the rectangle.

$i\in {\mathcal {I}}$ :

objects (disks) to be packed; ${\mathcal {I}} {:}{=}\{1,\ldots ,n\}$.

$j\in {\mathcal {J}}$ :

line segments potentially connecting disks and tangential to the convex hull; ${\mathcal {J}}{:}{=}\{1,\ldots ,m\le N^{\mathrm {J} }\le n\}$. Note that the number m of active line segments is identical to the number of circular arcs contributed to $\partial {\mathcal {H}}$.

1.2 Data

$E_{d}$ :

length ($d=1$) and width ($d=2$) of the rectangle.

L :

length of the rectangle; also called $E_{1}$.

$R_{i}$ :

radius of disk i to be packed.

$S_{i}$ :

indicator specifying to use a major ($S_{i}=1)$ or minor ($S_{i}=0)$ sector of disk i contributing an arc to the boundary of the convex hull.

W :

width of the rectangle; also called $E_{2}$.

1.3 Decision variables

$d_{j}^{\mathrm {H}}$ :

distance of hyperplane ${\mathcal {H}}_{j}$ induced by line segment j to the origin of the coordinate system.

$m_{ij}^{ \mathrm {D}}$ :

distance of hyperplane ${\mathcal {H}}_{ij}$ induced by circle segment i to the origin of the coordinate system.

${\mathbf {m}}_{dij}^{ \mathrm {H}}$ :

a specific orthogonal vector onto the circle line segment of disk i connecting ${\mathbf {v}}_{j}^{\mathrm {la}}$ and ${\mathbf {v}}_{j}^{\mathrm {an}}$.

$n_{dj}^{\mathrm {H}}$ :

the normal vector onto hyperplane ${\mathcal {H}}_{j}$ induced by line segment j connecting two disks (direction d).

$x_{d}^{\mathrm {R}}$ :

(continuous) extension of the rectangle in dimension d.

$x_{id}^{0}$ :

(continuous) coordinates of the center vector of disk i to be packed.

1.4 Decision variables used in MinPerim

$d_{j}^{\mathrm {H}}$ :

distance of hyperplane ${\mathcal {H}}_{j}$ induced by line segment j to the origin of the coordinate system.

$m_{ij}^{\mathrm {D}}$ :

distance of hyperplane ${\mathcal {H}}_{ij}$ induced by circle segment i to the origin of the coordinate system.

${\mathbf {m}}_{dij}^{\mathrm {H}}$ :

a specific orthogonal vector onto the circle line segment of disk i connecting ${\mathbf {v}}_{j}^{\mathrm {la}}$ and ${\mathbf {v}}_{j}^{\mathrm {an}}$ .

$n_{dj}^{\mathrm {H}}$ :

the normal vector onto hyperplane ${\mathcal {H}} _{j}$ induced by line segment j connecting two disks (direction d).

$x_{d}^{\mathrm {R}}$ :

(continuous) extension of the rectangle in dimension d.

$x_{id}^{0}$ :

(continuous) coordinates of the center vector of disk i to be packed.

$\alpha _{ij}$ :

(continuous) sector angle of disk i induced by line segment j.

$\delta _{ij}$ :

(binary) indicates whether disk i has incoming (ending) or outgoing (starting) line segment j.

$\delta _{j}^{\mathrm {A}}$ :

(binary) indicates whether vertices ${\mathbf {v}}_{j}^{\mathrm {al}}$ and ${\mathbf {v}}_{j}^{\mathrm {la}}$ are active, i.e., line segment j is used.

$\delta _{ij}^{\mathrm {D}}$ :

(binary) indicates whether disk i is the destination of line segment j.

$\delta _{j}^{\mathrm {L}}$ :

(binary) indicates whether line segment j is the last active one used.

$\delta _{ij}^{\mathrm {S}}$ :

(binary) indicates whether disk i is the origin of line segment j.

$\ell$ :

(continuous) length of the convex hull perimeter.

$\mu$ :

(integer) the number of active line segments.

Computational geometry basis for the minimal convex hull problems

If the size of a given problem becomes so large that it cannot be solved analytically, semi-analytically, or by mathematical programming alone, we resort to different computational methods. For this purpose, we use two computational geometry algorithms: The VOROPACK-D algorithm for packing circular disks in a container [35], and the QuickhullDisk algorithm for constructing the convex hulls of disk arrangements [26].

The VOROPACK-D algorithm

VOROPACK-D can pack input disks in a circular or rectangular design container by taking advantage of the powerful spatial reasoning capability of the Voronoi diagram of disks in a container. With the Voronoi diagram, VOROPACK-D can locate the vacancy information in a container such that no disk intersects both other disks and the container. In literature, the phi-function [5, 31, 34, 37] and no-fit polygon [2, 6, 8] were exploited to incorporate the non-overlap condition among disks and container for packing and cutting problems. VOROPACK-D takes an argument denoting the container shape: A circular or rectangular design container. VOROPACK-D(CC) and VOROPACK-D(RC) are for a circular and rectangular container, respectively. The VOROPACK-D(CC) algorithm actually implements the Shrink&Shake algorithm which packs circular disks in a circular container by taking advantage of the Voronoi diagram of disks in the container [35, 39]. The method solves a disk packing problem of either congruent or non-congruent disks. The idea of the algorithm is, beginning with a sufficiently large container, to repeat shrinking the container and shaking mutually disjoint disks to reposition in the shrunken container. With the correct implementation of the Voronoi diagram of disks in a circular container, the algorithm is extremely fast compared to the other reported algorithms. The algorithm, during the shake process, pushes each protruding disk by repositioning every disk at a new position through an average O(1) time decremental and incremental operations from and to the existing Voronoi diagram. With these enhancements, Shrink&Shake takes an $O(Mn \log n)$ time for each container shrinkage where $M \le n$ represents the number of protruding disks which intersect the boundary of the shrunken container. M depends on input data and tends to increase until it reaches some constant as the algorithm iterates. The number of shrinkage also depends on input data. We note that Shrink&Shake takes full advantage of the vacancy information among the generators in the container.

In this study, we also use the VOROPACK-D(RC) algorithm for packing disks in a rectangular container. VOROPACK-D(RC) is designed to handle a rectangular container case using the basic idea of Shrink&Shake. VOROPACK-D(RC) begins with a sufficiently large container and repeatedly shrink the container and reposition all disks in the shrunken container. Due to the correct implementation of the Voronoi diagram of non-congruent circular disks in a rectangular container, the algorithm can take full advantage of the vacancy information among the generators in the container. Hereafter, if necessary, we will use VOROPACK-D(CC) to name an algorithm for packing disks in a circular container and VOROPACK-D(RC) for packing disks in a rectangular container instead of Shrink&Shake.

The QuickhullDisk algorithm

Convex hull is one of the most fundamental concepts in geometry and its construction has been extensively studied, particularly the convex hull of points. Here, we use the recently reported simple and fast QuickhullDisk algorithm for the construction of the convex hull of a set of disks in ${\mathbb {R}}^2$ by generalizing the quickhull algorithm for points [26]. The QuickhullDisk algorithm is a divide-and-conquer algorithm and is based on the idea of the well-known quick sort algorithm. It constructs the convex hull of a disk set D by dividing it into two subsets and quickly conquering the results of the subsets to get the solution of the entire set D. The algorithm recurs until one or two disks are left in the set so that a stopping-condition for a further recursion is encountered. QuickhullDisk takes $O(n \log n)$ time on average and O(mn) time in the worst case where m represents the number of extreme disks which contribute to the boundary of the convex hull of n disks. Experimental result shows that the proposed QuickhullDisk algorithm runs significantly faster than the $O(n \log n)$ time incremental algorithm, proposed by [7], particularly for big data. QuickhullDisk is approximately 2.6 times faster than the incremental algorithm for random disks.

Voronoi diagrams

Voronoi diagrams are powerful geometric constructs which are used to solve diverse problems related with spatial reasoning. We briefly introduce Voronoi diagrams because of their critical uses in the proposed algorithm. For Voronoi diagrams in general, we recommend readers to refer to [1, 29]. Hereafter “V-” denotes “Voronoi” for notation simplicity. We limit the discussion in ${\mathbb {R}}^2$ unless otherwise stated. We store all Voronoi diagrams in ${\mathbb {R}}^2$ in the winged-edge or half-edge data structure which takes O(n) memory for n entities because the Voronoi diagram is a planar subdivision [1, 28, 29, 32]. The geometry of the V-edges in this paper is either linear, parabolic, hyperbolic, or elliptic which are in fact quadratic polynomial curves that can be all represented as a rational quadratic Bézier curve in a unified manner [21].

The ordinary Voronoi diagram of points

The ordinary Voronoi diagram VD(P) of a point set P in ${\mathbb {R}}^2$ is a tessellation where each V-cell of the tessellation is a set of locations in the plane which is closer to the associated point, called a generator, in P than to the other generators. Each V-edge is equidistant from two generators, is a subset of a line, and is the boundary between two adjacent V-cells; Some V-edges may be unbounded to emanate to infinity while the others are bounded. Each V-vertex is equidistant from three points. Figure 12a shows an example of VD(P).

In the ordinary Voronoi diagram VD(P) of n point generators in ${\mathbb {R}} ^2$, there are O(n) V-vertices, O(n) V-edges, and n V-cells. VD(P) can be constructed in the optimal $O(n \log n)$ time using the divide-and-conquer algorithm [1, 29, 32]. However, we prefer to use the robust topology-oriented incremental algorithm which was introduced by [38] which takes O(n) time on average (although $O(n^2)$ time in the worst case). Ordinary Voronoi diagrams of approximately 50,000 points in the plane can be robustly constructed in a second on an ordinary desktop computer.

The Voronoi diagram of disks

The Voronoi diagram VD(D) of a circular disk set $D=\{d_1,d_2,\ldots ,d_n\}$ in ${\mathbb {R}}^2$ is a tessellation of the plane so that every location in a V-cell is closer to its generating disk than to other disks. Each V-edge is the locus of the center of circular probe that simultaneously contacts the boundaries of two generating disks: If the generating disks are of different sizes, the V-edge is hyperbolic and if they are of an identical size, it is linear. Hence, they can be all represented as a rational quadratic Bézier curve. The Voronoi diagram of congruent disks is identical to the ordinary Voronoi diagram of disk centers. A V-vertex is the center of circular probe that simultaneously contacts three generating disks. If two generator disks intersect each other, their V-edge passes through the two intersection points between the boundaries of the two disks. Figure 12b shows an example of VD(D).

VD(D) has O(n) V-vertices, O(n) V-edges, and n V-cells and can be constructed by an optimal $O(n \log n)$ time for n disks using the plane sweep method [12, 40] or the divide-and-conquer method [24, 36]. However, we prefer to use the topology-oriented incremental algorithm which guarantees robustness [25] (or the edge-flipping algorithm [22, 23]) for its robust construction. Both algorithms take $O(n^2)$ time in the worst case but O(n) time on average. VD for approximately 15,000 disks can be robustly constructed in a second on an ordinary desktop computer.

The Voronoi diagram of disks in a container

Let ${\mathcal {VD}}(\kappa ,D)$ be the Voronoi diagram of a set D of non-intersecting circular disks contained in a container $\kappa$ [19]. In this paper, $\kappa$ is either a circle or a rectangle. We define ${\mathcal {VD}}$ only in $\partial \kappa$, i.e., the interior of the container. ${\mathcal {VD}}$ shares many similarities with the Voronoi diagram VD of D but it also has some differences, particularly near $\partial \kappa$.

${\mathcal {VD}}$ is a tessellation of the interior of $\kappa$, where every location of each V-cell is closer to its generating disk. The container $\kappa$ itself is regarded as a generator but its interior is considered to be the outside of $\kappa$. In other words, the interior of $\partial \kappa$ is regarded as the entire Euclidean space of the outside of $\kappa$. Hence, a V-cell can also be well-defined for the container as the set of locations closer to $\partial \kappa$ than to boundaries of any input disks.

If $\kappa$ is a circle, a rectangle, or a polygon [9, 10, 20], the V-edge defined between $\partial \kappa$ and an input disk is elliptic or parabolic, respectively. Note that both ellipse and parabola are quadratic. The V-edges between input disks are hyperbolic. Hence, all V-edges can be represented by a rational quadratic Bézier curve [21]. Figure 12c, d shows the examples of ${\mathcal {VD}}(\kappa ,D)$, where $\kappa$ is a circular and a rectangular container, respectively.

Both ${\mathcal {VD}}$ and VD can be constructed with a similar efficiency. Even if an optimal algorithm taking $O(n \log n)$ time is known, we prefer to use the topology-oriented incremental algorithm (with an average O(n) time and the worst case $O(n^2)$ time) [25] with the winged-edge data structure. This is because of the guaranteed robustness with a sufficiently good efficiency - actually significantly faster than the optimal algorithm for large problem instances. We skip the details of the combinatorial properties of ${\mathcal {VD}}$ because they are identical or similar to VD.

Incremental maintenance of Voronoi diagram

Removing a disk $d \in D$ from one location and inserting it to another location, both in the container, is essential to Shrink&Shake. If we reconstruct the entire Voronoi diagram for each removal or insertion of d, it takes an optimal $O(n \log n)$ time for each reconstruction. As the removal and insertion of disks occur very frequently in Shrink&Shake, it is desirable to do it efficiently. We developed an average O(1)-time (but a worst case O(n) time) algorithms for the maintenance of Voronoi diagram in an incremental manner.

The insertion of a disk into a Voronoi diagram is done as follows. Let ${\mathcal {VD}}_{i-1}$ be the Voronoi diagram of $i-1$ disks in the container. We want to compute ${\mathcal {VD}}_{i}$ including a new disk $d_i$. We try to reuse the information in ${\mathcal {VD}}_{i-1}$ as much as possible. ${\mathcal {VD}}_{i-1}$ is a planar subdivision: i.e., the network of V-edges of ${\mathcal {VD}}_{i-1}$ forms a planar graph. The basic idea of the topology-oriented increment is to maintain the planarity of the V-edge graph of ${\mathcal {VD}} _{i}$ after the incremental insertion of $d_i$. Therefore, the topology-oriented increment is to consistently maintain the planarity of ${\mathcal {VD}}_{i}$ by (i) identifying a tree subset of V-edge graph of ${\mathcal {VD}}_{i-1}$ contained in the V-cell of the incrementing disk $d_i$, (ii) trimming the tree from ${\mathcal {VD}}_{i-1}$, (iii) creating new V-vertex(es), V-edge(s), and a new V-face corresponding to $d_i$, and (iv) properly establishing topology connections among the Voronoi entities remaining in ${\mathcal {VD}}_{i}$. While an insertion (and a delete, too) can be done in O(i) time in the worst case for i disks in the container, its average time complexity is O(1). This average O(1) time holds particularly well during the disk packing process because most disks are in contact with a constant number of other disks on average. For details, see [25].

The removal of a disk from a Voronoi diagram is, roughly speaking, the reverse of the insertion of a disk to a particular location in a given Voronoi diagram and a removal can be done in O(1) on average and in O(i) time in the worst case for i disks in the container. In the incremental insertion, however, identifying the proper location for disk packing in the Voronoi diagram and the bookkeeping after the insertion requires at least $O(\log n)$ time with a priority queue.

Fig. 12

Voronoi diagrams used in the proposed algorithm. a VD(P): The ordinary Voronoi diagram of a point set P. b VD(D): The Voronoi diagram of a disk set D. c VD(D, CC): The Voronoi diagram in a circular container. d VD(D, RC): The Voronoi diagram in a rectangular container

Detailed derivations and proofs

1.1 Importing results from QuickhullDisk

Here we provide analytic expression for importing the result of QuickhullDisk as an initial value to MinPerim. The analytic expression improves the usage of the solver BARON and LINDO, especially, if all variables used in MinPerim are initialized. QuickhullDisk provides a list of hull disk vertices, ${\mathbf {v}}_{j}^{\mathrm {al}}$ and ${\mathbf {v}}_{j}^{\mathrm {la}}$. A subset of hull disk is called extreme disks in the context of QuickhullDisk. These extreme disks ${\mathcal {I}}_{\mathrm {e}}$ correspond to outer disks of MinPerim. Therefore, QuickhullDisk could provide more vertices than those required in MinPerim because some hull disk vertices can touch the boundary $\partial {\mathcal {H}}$ of the convex hull ${\mathcal {H}}$. In order to cope with this situation we consider those hull disks as well by adjusting $\varepsilon =0$ in inequality (2.42) of KF19. Vertex ${\mathbf {v}}_{j}^{\mathrm {al}}$ is the outgoing (starting) vertex and tangential to the arc of that disk from which line segment j leaves. Line segment j ends in an ingoing (ending) vertex ${\mathbf {v}}_{j}^{\mathrm {la}}$ which is the extreme vertex of the arc of the adjacent outer disk. The arc ends in vertex ${\mathbf {v}}_{j+1}^{\mathrm {al}}$ which is then the outgoing vertex for line segment $j+1$. The line segment ends in an incoming vertex ${\mathbf {v}}_{j+1}^{\mathrm {la}}$ which is the start vertex for the arc of the neighbored outer disk. We continue the construction in anti-clockwise order until line segment $j=m$ ends in vertex ${\mathbf {v}}_{m}^{\mathrm {la}}$ which is the start vertex of the arc ending in vertex ${\mathbf {v}}_{1}^{\mathrm {al}}$. This construction closes $\partial {\mathcal {H}}$. From ${\mathbf {v}}_{j}^{\mathrm {al}}$ and ${\mathbf {v}}_{j}^{\mathrm {la}}$ we derive

$$\begin{aligned} \delta _{j}^{\mathrm {A}}=\left\{ \begin{array}{c} 1, \\ 0, \end{array} \begin{array}{c} \sum _{d}\left| {\mathbf {v}}_{j}^{\mathrm {al}}\right| \ne 0\wedge \sum _{d}\left| {\mathbf {v}}_{j}^{\mathrm {la}}\right| \ne 0 \\ else \end{array} \right. ,\quad \forall j. \end{aligned}$$

Note that for importing the results of QuickhullDisk into MinPerim, at first, we fix all binary variables, i.e., we keep the selected hull disks, arc, and line segments. Once, we have an accepted initial point in LINDO, we relax this fixation. The last active line segment is computed by

$$\begin{aligned} \delta _{j}^{\mathrm {L}}=\delta _{j}^{\mathrm {A}}-\delta _{j+1}^{\mathrm {A} },\quad \forall j. \end{aligned}$$

Whether disk $i\in {\mathcal {I}}_{\mathrm {e}}$ is the source of line segment j is traced by

$$\begin{aligned} \delta _{ij}^{\mathrm {S}}=\left\{ \begin{array}{c} 1, \\ 0, \end{array} \begin{array}{c} \left| \sum _{d}\left( x_{id}-{\mathbf {v}}_{j}^{\mathrm {al}}\right) ^{2}-R_{i}^{2}\right| <\varepsilon _{\mathrm {R}} \\ else \end{array} \right. \quad ,\quad \forall \{(ij)|i\in {\mathcal {I}}_{\mathrm {e}}\} \end{aligned}$$

which measures whether ${\mathbf {v}}_{j}^{\mathrm {al}}$ is a point on the circumference of disk i. For numerical purposes we set $\varepsilon _{ \mathrm {R}}=10^{-4}$. Similarly, we proceed for tracing whether disk $i\in {\mathcal {I}}_{\mathrm {e}}$ is the destination of line segment j

$$\begin{aligned} \delta _{ij}^{\mathrm {D}}=\left\{ \begin{array}{c} 1, \\ 0, \end{array} \begin{array}{c} \left| \sum _{d}\left( x_{id}-{\mathbf {v}}_{j}^{\mathrm {la}}\right) ^{2}-R_{i}^{2}\right| <\varepsilon _{\mathrm {R}} \\ else \end{array} \right. ,\quad \forall \{(ij)|i\in {\mathcal {I}}_{\mathrm {e}}\}. \end{aligned}$$

This allows us to derive

$$\begin{aligned} \delta _{ij}=\left\{ \begin{array}{r} 1, \\ 0, \end{array} \begin{array}{c} \delta _{ij}^{\mathrm {D}}>0.5\vee \delta _{ij}^{\mathrm {S}}>0.5 \\ else \end{array} \right. ,\quad \forall \{(ij)|i\in {\mathcal {I}}_{\mathrm {e}}\}. \end{aligned}$$

The vertex on the circular arc, which is the source of line segment $j+1$, is given by

$$\begin{aligned} {\mathbf {v}}_{j}^{\mathrm {an}}={\mathbf {v}}_{j}^{\mathrm {al}}+ {\mathbf {v}}_{v01}^{\mathrm {al}}\delta _{j}^{\mathrm {L}},\quad \forall j, \end{aligned}$$

where v01 denotes the first line segment counted counterclockwise. In case we have more than 99 line segments, the first one would be named v001. Note that it is also necessary to define upper bounds on the variables ${\mathbf {v}}_{j}^{\mathrm {al}}$, ${\mathbf {v}}_{j}^{ \mathrm {la}}$, and ${\mathbf {v}}_{j}^{\mathrm {an}}$. For simplicity, we put the dimension of the rectangle as upper bounds (the coordinate frame 1). The normal vector on line segment j (pointing into the interior of the convex hull) is given by

$$\begin{aligned} n_{dj}^{\mathrm {H}}=-\sum _{i\in {\mathcal {I}}}\frac{x_{id}^{\mathrm {0}}-v_{dj}^{\mathrm {al}}}{R_{i}}\delta _{ij}^{\mathrm {S}},\quad \forall \{dj\}. \end{aligned}$$

(C.1)

The distance to the origin is

$$\begin{aligned} d_{j}^{\mathrm {H}}={\mathbf {n}}_{j}^{\mathrm {H}}{\mathbf {v}}_{j}^{\mathrm {al}},\quad \forall j. \end{aligned}$$

(C.2)

The orthogonal vector ${\mathbf {m}}_{ij}^{\mathrm {H}}$ onto the circle line segment of disk i connecting ${\mathbf {v}}_{j}^{\mathrm {la}}$ and ${\mathbf {v}}_{j}^{\mathrm {an}}$ is constructed as the vector from the center of disk i to the midpoint of the chord

$$\begin{aligned} m_{dij}^{\mathrm {H}}=\frac{1}{2}\left( v_{dj}^{\mathrm {an}}+v_{dj}^{\mathrm {la}}\right) \delta _{ij}^{\mathrm {D}}-x_{di}^{\mathrm {0}}\delta _{ij}^{\mathrm {D}},\quad \forall \{i,j\}. \end{aligned}$$

(C.3)

In the half-space inequality we use the negated vector pointing into the interior of ${\mathcal {H}}$. If norm $\left\| {\mathbf {m}} _{ij}^{\mathrm {H}}\right\| _{2}>0$, the right-hand side value $m_{ij}^{ \mathrm {D}}$ of the Hessian normal form ${\mathbf {m}}_{ij}^{\mathrm {H}} {\mathbf {x}}=m_{ij}^{\mathrm {D}}$ is computed as

$$\begin{aligned} m_{ij}^{ \mathrm {D}}=\frac{1}{\left\| {\mathbf {m}}_{ij}^{\mathrm {H}}\right\| _{2}} \sum _{d}m_{dij}^{\mathrm {H}}v_{dj}^{\mathrm {la}}\delta _{ij}^{\mathrm {D} },\quad \forall \{i,j\}. \end{aligned}$$

(C.4)

The angles $\alpha _{ij}$ of the circular arcs follow from

$$\begin{aligned} \sin \frac{\alpha _{ij}}{2}=\frac{\left\| {\mathbf {v}}_{j}^{\mathrm {an}}-v_{j}^{\mathrm {la}}\right\| _{2}\delta _{ij}^{\mathrm {D}}}{2R_{i}},\quad \forall \{i,j\}\mathrm {\ } \end{aligned}$$

(C.5)

and

$$\begin{aligned} \alpha _{ij}=2\pi S_{ij}\delta _{ij}^{\mathrm {D} }+2(1-2S_{ij})\arcsin \left( \frac{\left\| {\mathbf {v}}_{j}^{\mathrm {an}}-v_{j}^{\mathrm {la}}\right\| _{2}\delta _{ij}^{\mathrm {D}}}{2R_{i}}\right) ,\quad \forall \sum \{i,j\}. \end{aligned}$$

(C.6)

Finally, we also need to initialize the objective function variable, i.e., the length $\ell$ of the perimeter of the convex hull

$$\begin{aligned} \ell =\sum _{j\in {\mathcal {J}}}\sqrt{\sum _{d\in {\mathcal {D}}}\left[ v_{dj}^{\mathrm {al}}-v_{dj}^{\mathrm {la}}\right] ^{2}}+\sum _{i\in {\mathcal {I}}}\sum _{j\in {\mathcal {J}}}R_{i}\alpha _{ij}. \end{aligned}$$

(C.7)

1.2 Computing the length in the partition model

To demonstrate how to compute the length contribution of blocks, let us inspect the solution corresponding to C13 of Table 5 in the main text. This solution is composed by block 3, which is a little complicated, and by block 4 (upside down). If we inspect block 3 as an independent arrangement of six congruent disks with radius R, the length $\ell _{3}$ of its complete perimeter is given by

$$\begin{aligned} \ell _{3}=\ell _{\mathrm {L}}+2\pi R, \end{aligned}$$

where $\ell _{\mathrm {L}}$ is the sum of lengths of all line segments given by

$$\begin{aligned} \ell _{\mathrm {L}}=5\cdot (2R)+\left\| (R,4R)-(R+[\sqrt{3}R],R+3\cdot 2R)\right\| . \end{aligned}$$

The term $\left\| ((R,4R))-(R+[ \sqrt{3}R],R+3\cdot 2R)\right\|$ represents the length of the line segment from the very right disk of the block’s lower layer with origin at (R, 4R) to the very right disk of its upper layer centered at $(R+[\sqrt{3} R],R+3\cdot 2R)$. This length is identical to the distance of these disks. Disks in contact have line segments of length 2R. Therefore, we have

$$\begin{aligned} \ell _{\mathrm {L}}=\left[ 10+\left\| (-\sqrt{3},-3)\right\| \right] R=\left[ 10+\sqrt{12}\right] R. \end{aligned}$$

From this, inspecting the geometry, we further derive

$$\begin{aligned} \ell _{3}=R+\left( \ell _{\mathrm {L}}+2\pi R\right) -(3\cdot 2R+\pi R)+R. \end{aligned}$$

The summands R’s at the very left and very right are the contributions of a half layer while the term $-(3\cdot 2R+\pi R)$ reflects that the upper layer of the block does not fully contribute to the length of the perimeter in the partition model; only the lower layer of block 3 and half the upper layer of disks contribute. Therefore, the total contribution of block 3 is

$$\begin{aligned} \ell _{3}=\left[ 6+\sqrt{12}+\pi \right] R. \end{aligned}$$

(C.8)

Similarly, for the upper blocks $\ell _{4}$ and $\ell _{5}$ we obtain

$$\begin{aligned} \ell _{4}=\left[ 10+\pi \right] R\quad , \quad \ell _{5}=\left[ 2+\sqrt{12}+\pi \right] R. \end{aligned}$$

(C.9)

Tables for input disks

We provide Tables 9, 10, and 11 for non-congruent disks in SET-B (DC03-DC10), SET-C (TC03-TC28), and SET-D (D series) of Sect. 7 in the main text, respectively.

Table 9 Non-congruent disks in SET-B (Called Set B in KF19)

Table 10 Non-congruent disks in SET-C (Called Set C in KF19)

Table 11 Non-congruent disks in SET-D (Called Set D in KF19)

Conjecture

Let ${\mathcal {C}}$ be set of all arrangements of disks fitting into the minimal convex container (with radius $r_{*}$ in the case of a circular container, otherwise in more general situations with a finite set of variables ${\mathbf {x}}_{*}^{s}$ for rectangular, polygonal, ellipse, or oval containers) and let ${\mathcal {P}}$ be the set of all arrangements of disks whose convex hull has minimal perimeter with length $\ell _{*}$. In both sets ${\mathcal {C}}$ and ${\mathcal {P}}$ we only consider irreducible arrangements, i.e., not translated, rotated or arrangements obtained by symmetry operations.

Then the following statements hold:

• ST1: The intersection of ${\mathcal {C}}$ and ${\mathcal {P}}$ is not empty, i.e., ${\mathcal {C}}\cap {\mathcal {P}}$ $\ne \varnothing$.

• ST2: There exists at least one element ${\mathfrak {c}}\in {\mathcal {C}}$, which is also an element of ${\mathcal {P}}$, i.e., ${\mathfrak {c}}\in {\mathcal {C}}\wedge {\mathfrak {c}}\in {\mathcal {P}}$.

• ST3: There exists at least one element ${\mathfrak {p}}\in {\mathcal {P}}$, which is also an element of ${\mathcal {C}}$, i.e., ${\mathfrak {p}}\in {\mathcal {P}}\wedge {\mathfrak {p}}\in {\mathcal {C}}$.

• ST4: There exists an arrangement ${\mathfrak {a}}$, whose convex hull has minimal perimeter $\ell _{*}$ and fits into the minimal convex container, ${\mathfrak {a}}\in {\mathcal {C}}\cap {\mathcal {P}}$, i.e.,

  $$\begin{aligned} \ell _{*}=\min _{{\mathfrak {c}}\in {\mathcal {C}}}\ell _{{\mathfrak {c}}}. \end{aligned}$$

While the equivalences are obvious, it is not easy to see how to prove one of them easily. ST1 through ST4 basically express that minimal container configurations can be found within the set of minimal perimeter length configurations, and, the other way round, that minimal perimeter length configurations can be found within the set of minimal container configurations.

Note that ${\mathcal {C}}$ and ${\mathcal {P}}$ may have the dimensionality of the continuum if smaller disks (named orphans in this context) can be placed anywhere into the empty areas between other disks with changing the shape and size of either ${\mathcal {C}}$ and ${\mathcal {P}}$. The other extremes we expect to find are the cases with cardinalities $\left| {\mathcal {C}} \right| =1$, $\left| {\mathcal {P}}\right| =1$, or $\left| {\mathcal {C}}\right| =$ $\left| {\mathcal {P}}\right| =1$. If we neglect the orphans in the arrangements, we almost always found $\left| {\mathcal {C}}\right| =$ $\left| {\mathcal {P}}\right| =1$, i.e., the minimal perimeter length configuration and the minimal container configuration coincide for the unique arrangement ${\mathfrak {a}}$. In one case, we found $\left| {\mathcal {C}}\right| =1$ and $\left| {\mathcal {P}}\right| >1$ (Refer to Fig. 13).

In the formulation of the conjecture we have implicitly used the assumption that minimal configurations are really realized and not only approached in the sense of the infimum. This assumption is justified by the extreme value theorem on compact sets (Weierstraß). It is important to note that while the disks do not overlap they are allowed to touch in one common point. Without this possibly touching point we would not have a compact set. If the conjecture is true, we have the following two conclusions:

• 1. In an iterative procedure, we could compute the minimal radius of the container (not necessarily optimal), and add this as an constraint to the minimal perimeter problem extended by the inequalities of the minimal container problem. For the convex hull obtained that way (not necessary optimal), we can compute the minimal radius (very cheaply), and see whether that improves what we have.

• 2. If we are able to compute the solution of the minimal convex hull problem and know for some reason that it is unique (problems with all disks having different radii are good candidates), all the other specific-type minimal convex container follow immediately from the arrangements of the convex objects within the minimal convex hull. We just need to solve the minimal container problem with the variables describing the container but not the positions of the convex objects hosted. Examples are: The radius $r^{\mathrm {cc}}_{\mathrm {minR}}$ of the circular container, the sides a and b of the rectangular container as well as the angle $\theta$ of its orientation, the semi-major axis a and b of the ellipse container as well as the angle $\theta$ of its orientation.

If the opposite of the conjecture was true, the implication

$$\begin{aligned} \ell _{*}<\min _{{\mathfrak {c}}\in {\mathcal {C}}}\ell _{{\mathfrak {c}}}, \end{aligned}$$

would hold, i.e., all arrangements with the perimeters of the minimal convex hull are outside the set of minimal container arrangements. Of course, it could also be that for some problem instances we have $\ell _{*}=\min _{ {\mathfrak {c}}\in {\mathcal {C}}}\ell _{{\mathfrak {c}}}$, and for others $\ell _{*}<\min _{{\mathfrak {c}}\in {\mathcal {C}}}\ell _{{\mathfrak {c}}}$.

Let us focus a little more on the special case of uniqueness. If an arrangement ${\mathcal {A}}_{*}$ of disks is the only arrangement which leads to the minimal perimeter length convex hull, then the smallest enclosing circle of ${\mathcal {A}}_{*}$ is the minimal enclosing circle of all possible arrangements ${\mathcal {A}}$ of those disks in the plane. In other words, a unique disk arrangements with the minimal convex hull is also the disk arrangement with minimal circular containers, i.e.,

$$\begin{aligned} \min \ell \Rightarrow \min r^{\mathrm {cc}}_{\mathrm {minR}}. \end{aligned}$$

Equivalently, a necessary condition for $\ell$ to be minimal is that $r^{\mathrm {cc}}_{\mathrm {minR}}$ is minimal. Note that this holds only when the disk arrangement is not subject to any target container constraint. The conjecture does not hold if we allow several arrangements leading to the same minimal $\ell _{*}$ as seen in the counter example displayed in Fig. 13. Both have minimal length $\ell _{*}=4+\pi$, but the radius of arrangement in Fig. 13a is $r^{\mathrm {cc}}_{\mathrm {minR}}=1.2062$ (the global minimum of $r^{\mathrm {cc}}_{\mathrm {minR}}$) while the one in the oblique arrangement (Fig. 13b) has radius $1.3608>r^{\mathrm {cc}}_{\mathrm {minR}}$.

Fig. 13

The left figure shows the square arrangement of four congruent disks with radius $R=0.5$, $\ell =\ell _{*}=4+\pi$, and circular container with radius 1.2062. The right one: An oblique arrangement of the same disks, the same $\ell =\ell _{*}=4+\pi$ but larger, circular container with radius 1.3608

If this conjecture holds, we can check easily whether a given disk arrangement is not minimal w.r.t. $\ell$. For a given disk arrangement with perimeter length $\ell$ (quickly computed by QuickhullDisk) we compute $r^{\mathrm {cc}}_{\mathrm {minR}}(\ell )$ for this disk arrangement using minRadiusCC (this problem has only two free variables, $r^{\mathrm {cc}}_{\mathrm {minR}}=r^{\mathrm {cc}}_{\mathrm {minR}}(\ell )$ and $x_{\mathrm {c}}$, and solves in seconds to global optimality). Then we compare $r^{\mathrm {cc}}_{\mathrm {minR}}(\ell )$ by the value $r^{\mathrm {cc}}_{\mathrm {minR}}$ obtained for the free disk arrangement obtained by minRadiusCC or VOROPACK-D(CC). If $r^{\mathrm {cc}}_{\mathrm {minR}}(\ell )>r^{\mathrm {cc}}_{\mathrm {minR}}$, $\ell$ is not minimal. If $r^{\mathrm {cc}}_{\mathrm {minR}}(\ell )=r^{\mathrm {cc}}_{\mathrm {minR}}$, we cannot conclude anything as the minimal circular container property is not sufficient for $\ell$ to be minimal.

This conjecture, if true, can also be the basis for an efficient heuristic iteration scheme for larger problem instances in which we are not able to compute $r^{\mathrm {cc}}_{\mathrm {minR}}$ to global optimality by minRadiusCC: We plan to develop a simulated annealing enhanced version of VOROPACK-D(CC) and subsequently solve for $\ell$ subject to $r^{\mathrm {cc}}_{\mathrm {minR}}(\ell )\le r^{\mathrm {cc}}_{{\mathbf{V}}}$. VOROPACK-D(CC) might follow up on a disk arrangement produced by MinPerim and further improve w.r.t. to $r^{\mathrm {cc}}_{\mathrm {minR}}$ producing a new value $r^{\mathrm {cc}}_{{\mathbf{V}}}$. The conjecture motivates us to perform also a few numerical experiments using the discrete perimeter approach with the objective function $z=r^{\mathrm {cc}}_{\mathrm {minR}}+\ell$ and inequality (3.9). For CC05, ..., CC10 of SET-P in Sect. 7.1 of the main text, this simultaneous minimization of $r^{\mathrm {cc}}_{\mathrm {minR}}$ and $\ell$ yields indeed the minimal circular container and perimeter minimal convex hull. For CC11 and higher this is not the case as the values of $r^{\mathrm {cc}}_{\mathrm {minR}}$ are larger than the Packomania values $r^{\mathrm {cc}}_{\mathrm {Pack}}$. Authors would welcome the opportunity for other researchers to either prove or disprove the conjecture.