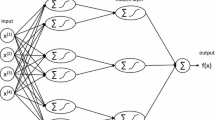
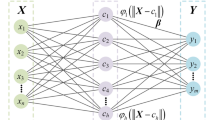
Abstract
Quantification of uncertainty of a technical system is often based on a surrogate model of a corresponding simulation model. In any application, the simulation model will not describe the reality perfectly, and consequently the surrogate model will be imperfect. In this article, we combine observed data from the technical system with simulated data from the imperfect simulation model in order to estimate an improved surrogate model consisting of multilayer feedforward neural networks, and we show that under suitable assumptions, this estimate is able to circumvent the curse of dimensionality. Based on this improved surrogate model, we show a rate of the convergence result for density estimates. The finite sample size performance of the estimates is illustrated by applying them to simulated data. The practical usefulness of the newly proposed estimates is demonstrated by using them to predict the uncertainty of a lateral vibration attenuation system with piezo-elastic supports.



Similar content being viewed by others
References
Anthony, M., Bartlett, P. L. (1999). Neural networks and learning: Theoretical foundations. Cambridge: Cambridge University Press.
Bauer, B., Kohler, M. (2019). On deep learning as a remedy for the curse of dimensionality in nonparametric regression. The Annals of Statistics, 47, 2261–2285.
Bayarri, M. J., Berger, J. O., Cafeo, J., Garcia-Donato, G., Liu, F., Palomo, J., Parthasarathy, R. J., Paulo, R., Sacks, J., Walsh, D. (2007). Computer model validation with functional output. The Annals of Statistics, 35, 1874–1906.
Bichon, B., Eldred, M., Swiler, M., Mahadevan, S., McFarland, J. (2008). Efficient global reliability analysis for nonlinear implicit performance functions. AIAA Journal, 46, 2459–2468.
Bott, A. K., Felber, T., Kohler, M. (2015). Estimation of a density in a simulation model. Journal of Nonparametric Statistics, 27, 271–285.
Bourinet, J.-M., Deheeger, F., Lemaire, M. (2011). Assessing small failure probabilities by combined subset simulation and support vector machines. Structural Safety, 33, 343–353.
Bucher, C., Bourgund, U. (1990). A fast and efficient response surface approach for structural reliability problems. Structural Safety, 7, 57–66.
Choi, S.-K., Grandhi, R. V., Canfield, R. A. (2007). Reliability-based structural design. London: Springer.
Coombs, C. H. (1964). A theory of data. New York: Wiley.
Das, P.-K., Zheng, Y. (2000). Cumulative formation of response surface and its use in reliability analysis. Probabilistic Engineering Mechanics, 15, 309–315.
Deheeger, F., Lemaire, M. (2010). Support vector machines for efficient subset simulations: \(^2\)SMART method. In Proceedings of the 10th international conference on applications of statistics and probability in civil engineering (ICASP10), Tokyo, Japan.
Devroye, L., Felber, T., Kohler, M. (2013). Estimation of a density using real and artificial data. IEEE Transactions on Information Theory, 59(3), 1917–1928.
Devroye, L., Györfi, L., Lugosi, G. (1996). A probabilistic theory of pattern recognition. New York: Springer.
Felber, T., Kohler, M., Krzyżak, A. (2015a). Adaptive density estimation based on real and artificial data. Journal of Nonparametric Statistics, 27, 1–18.
Felber, T., Kohler, M., Krzyżak, A. (2015b). Density estimation with small measurement errors. IEEE Transactions on Information Theory, 61, 3446–3456.
Goh, J., Bingham, D., Holloway, J. P., Grosskopf, M. J., Kuranz, C. C., Rutter, E. (2013). Prediction and computer model calibration using outputs from mulitfidelity simulators. Technometrics, 55, 501–512.
Götz, B., Schaeffner, M., Platz, R., Melz, T. (2016). Lateral vibration attenuation of a beam with circular cross-section by a support with integrated piezoelectric transducers shunted to negative capacitances. Smart Materials and Structures, 25(9), 1–10.
Györfi, L., Kohler, M., Krzyżak, A., Walk, H. (2002). A distribution-free theory of nonparametric regression. New York: Springer.
Han, G., Santner, T. J., Rawlinson, J. J. (2009). Simultaneous determination of tuning and calibration parameters for computer experiments. Technometrics, 51, 464–474.
Haykin, S. O. (2008). Neural networks and learning machines3rd ed. New York: Prentice-Hall.
Hertz, J., Krogh, A., Palmer, R. G. (1991). Introduction to the theory of neural computation. Redwood City, CA: Addison-Wesley.
Higdon, D., Gattiker, J., Lawrence, E., Jackson, C., Tobis, M., Pratola, M., Habib, S., Heitmann, K., Price, S. (2013). Computer model calibration using the ensemble kalman filter. Technometrics, 55, 488–500.
Hurtado, J. (2004). Structural reliability—Statistical learning perspectives. Vol. 17 of Lecture Notes in Applied and Computational Mechanics. Berlin: Springer.
Kaymaz, I. (2005). Application of Kriging method to structural reliability problems. Strutural Safety, 27, 133–151.
Kennedy, M. C., O’Hagan, A. (2001). Bayesian calibration of computer models (with discussion). Journal of the Royal Statistical Society: Series B, 63, 425–464.
Kim, S.-H., Na, S.-W. (1997). Response surface method using vector projected sampling points. Structural Safety, 19, 3–19.
Kohler, M., Krzyżak, A. (2017a). Nonparametric regression based on hierarchical interaction models. IEEE Transaction on Information Theory, 63, 1620–1630.
Kohler, M., Krzyżak, A. (2017b). Improving a surrogate model in uncertainty quantification by real data. Submitted for publication.
Kohler, M., Krzyżak, A., Mallapur, S., Platz, R. (2018). Uncertainty quantification in case of imperfect models: A non-Bayesian approach. Scandinavian Journal of Statistics, 45(3), 729–752.
Li, S., Götz, B., Schaeffner, M., Platz, R. (2017). Approach to prove the efficiency of the Monte Carlo method combined with the elementary effect method to quantify uncertainty of a beam structure with piezo–elastic supports. In Proceedings of the 2nd international conference on uncertainty quantification in computational sciences and engineering (UNCECOMP 2017) (pp. 441–455).
Papadrakakis, M., Lagaros, N. (2002). Reliability-based structural optimization using neural networks and Monte Carlo simulation. Comput Methods Appl Mech Eng, 191, 3491–3507.
Parzen, E. (1962). On the estimation of a probability density function and the mode. Annals of Mathematical Statistics, 33, 1065–1076.
Ripley, B. D. (2008). Pattern recognition and neural networks. Cambridge: Cambridge University Press.
Rosenblatt, M. (1956). Remarks on some nonparametric estimates of a density function. Ann Math Stat, 27, 832–837.
Santner, T. J., Williams, B. J., Notz, W. I. (2003). The design and analysis of computer experiments. New York: Springer.
Schmidt-Hieber, J. (2017). Nonparametric regression using deep neural networks with ReLU activation function. arXiv:1708.06633v2.
Stone, C. J. (1985). Additive regression and other nonparametric models. Annals of Statistics, 13, 689–705.
Tuo, R., Wu, C. F. J. (2015). Efficient calibration for imperfect computer models. Annals of Statistics, 43, 2331–2352.
Wang, S., Chen, W., Tsui, K. L. (2009). Bayesian validation of computer models. Technometrics, 51, 439–451.
Wong, R. K. W., Storlie, C. B., Lee, T. C. M. (2017). A frequentist approach to computer model calibration. Journal of the Royal Statistical Society, Series B, 79, 635–648.
Acknowledgements
The authors would like to thank the German Research Foundation (DFG) for funding this project within the Collaborative Research Center 805. Furthermore, the authors would like to thank an anonymous Associate Editor and two anonymous referees for their invaluable comments improving an early version of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
About this article
Cite this article
Götz, B., Kersting, S. & Kohler, M. Estimation of an improved surrogate model in uncertainty quantification by neural networks. Ann Inst Stat Math 73, 249–281 (2021). https://doi.org/10.1007/s10463-020-00748-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10463-020-00748-1