A review of cooperative rules and their associated algorithms for minimum-cost spanning tree problems

Abstract

Minimum-cost spanning tree problems are well-known problems in the operations research literature. Some agents, located at different geographical places, want a service provided by a common supplier. Agents will be served through costly connections. Some part of the literature has focused, mainly, in studying how to allocate the connection cost among the agents. We review the papers that have addressed the allocation problem using cooperative game theory. We also relate the rules defined through cooperative games with rules defined directly from the problem, either through algorithms for computing a minimal tree, either through a cone-wise decomposition.

1 Introduction

Several problems involving network formation have been studied in operations research and economics. The operations research literature is more focused in efficient algorithm designs and computational complexity. The economic literature focuses on aspects such as cost sharing within networks. In this paper, we focus on the cost sharing aspect. Hence, this review belongs to the well-known literature of cost allocation.

In this paper, we consider minimum-cost spanning tree problems, briefly mcstp. A group of agents, which are located at different geographical places, want a particular service which can only be provided by a common supplier, called the source. Agents will be served through costly connections. Agents are indifferent between being connected directly or indirectly to the source. There are many situations that can be modeled in this way. For instance, several towns may draw power from a common power plant, and hence have to share the cost of the distribution network (Dutta and Kar 2004). Bergantiños and Lorenzo (2004, 2005, 2008) study a real situation where villagers had to pay the cost of constructing pipes from their respective houses to a water supplier. Other examples include communication networks, such as telephone, Internet, or cable television.

The literature on mcstp starts by defining algorithms for constructing minimal (cost spanning) trees (mt for short). We can mention, for instance, the papers of Borůvka (1926), Kruskal (1956), Prim (1957). However, constructing an mt is only part of the problem. Another important issue is how to allocate the cost associated with mt among agents. Claus and Kleitman (1973) were the first to address the cost sharing aspect, and Bird (1976) proposed a rule, now known as the Bird’s rule, through Prim’s algorithm. Bird (1976) also associated a cooperative game with any mcstp . He proved that this rule belongs to the core of the cooperative game. Many papers have followed addressing the cost allocation problem arising from mcstp. Early works and reviews are due to Aarts (1994), Feltkamp (1995), Curiel (1997), Borm et al. (2001). Trudeau (2013) reviews some cost sharing rules focusing on two rules (to be addressed below): the folk rule and the Kar’s rule, comparing several axiomatic characterizations. Trudeau and Vidal-Puga (2019) review the main axiomatic characterizations of the rules based on the Shapley value in mcstp.

There are two possible ways for defining rules in mcstp. The first way is the direct approach, which defines rules directly from the structure of the problem. In this review, we describe rules that are defined through the algorithms for computing the mt defined above (namely Boruvka, Prim, and Kruskal). The idea of such rules is as follows: the algorithm selects the arc, and the rule decides how to divide its cost between the agents. Each agent pays the sum of the assigned costs over all selected arcs by the algorithm.

We also review the rules that are defined through a cone-wise decomposition. Each mcstp can be decomposed as a linear combination of the so called elementary problems, where each cost is either 0 or 1. The rule states how to divide the cost of each elementary problem between the agents. Each agent pays the sum of the assigned costs over all elementary problems.

The second way is an indirect approach through cooperative games. First, we associate with each problem a cooperative game. Second, we compute a solution for cooperative games (Shapley value, core, ...) in the associated cooperative game. Third, we define the rule in the original problem as the solution applied to the cooperative game associated with the original problem. This indirect approach is quite standard and has been considered in many economic problems. Some classical examples are the airport problem (Littlechild and Owen 1973), where the cost of a runway has to be divided among different airplanes, and bankruptcy problems (O’Neill 1982; Aumann and Maschler 1985) where an estate should be divided among several claimants. Other recent examples are the museum pass problem (Ginsburgh and Zang 2003; Bergantiños and Moreno-Ternero 2015), where the revenue generated by the sale of museum cards has to be divided among the museums, and the broadcasting problem (Bergantiños and Moreno-Ternero 2020), where the revenues from broadcasting sport league events must be divided among the teams. Other examples regarding the Shapley value are in Algaba et al. (2019).

In this second approach, the most studied case in the literature is the case of private nodes. It is assumed that, when computing the value of a coalition, agents in such coalition can use only the nodes of such coalition. However, there are other possible approaches, as, for example, the case of public nodes, where it is assumed that agents in a coalition can use nodes outside the coalition.

So far, there have been at least five cooperative games in the literature of mcstp: the private game, the irreducible game, the optimistic game, the public game, and the cycle-complete game.

Private game:

Bird (1976) associates with each mcstp a cooperative game with transferable utility where the worth of each coalition S is computed assuming that agents in $N\setminus S$ are not participating. It is a pessimistic approach because agents in $N\setminus S$ are supposed not to cooperate. The private assumption makes their nodes unavailable.

Irreducible game:

Given an mcstp $\left( N_{0},C\right) ,$ Bird (1976) defines the irreducible associated problem $\left( N_{0},C^{*}\right) .$ The idea is to reduce the costs of C as much as possible without reducing the cost of the minimal tree of C. The irreducible game associated with a mcstp $\left( N_{0},C\right)$ is the private game associated with the irreducible problem $\left( N_{0},C^{*}\right) .$

Optimistic game:

Bergantiños and Vidal-Puga (2007b) associate with each mcstp a cooperative game with transferable utility where the cost of each coalition S is computed assuming that agents in $N\setminus S$ are already connected. This game is called optimistic because agents in $N\setminus S$ are already connected to the source and agents in S can connect to the source through agents in $N\setminus S$ for free.

Public game:

Bogomolnaia and Moulin (2010) were the first to formally consider the case where the cost of each coalition S is computed assuming that even though agents in $N\setminus S$ are not connected to the source, agents in S can connect to the source through agents in $N\setminus S$ by paying the costs of the arcs they use.

Cycle-complete game:

Given an mcstp $\left( N_{0},C\right) ,$ Trudeau (2012) defines the associated cycle-complete problem $\left( N_{0},C^{**}\right) .$ The idea is to achieve concavity by reducing the costs of C as much as possible without reducing the cost of any minimal cycle. The cycle-complete game associated with a mcstp $\left( N_{0},C\right)$ is the private game associated with the cycle-complete problem $\left( N_{0},C^{**}\right) .$

The most studied solutions in the five cooperative games we review are the core and the Shapley value. Nevertheless, some other solutions, for instance, the nucleolus (Schmeidler 1969) and weighted Shapley values (Shapley 1953a; Kalai and Samet 1987), have also been considered. We have tried to be exhaustive and to mention all papers studying deeply some aspect of the five cooperatives games.

In this survey, we discuss the relation between both approaches. Actually, all the rules mentioned which are defined through some algorithm or the cone-wise decomposition are related to some of the cooperative rules. We give two examples. First, a rule obtained through Kruskal’s algorithm coincides with the Shapley value of the irreducible game. Second, in the irreducible game, the convex combination of the payoffs given by rules obtained through Prim’s algorithm coincides with the core.

There also a third approach, which is not discussed in this paper, which is the non-cooperative approach. Instead of providing a rule for dividing the cost, we provide a bargaining protocol to the agents. Thus, agents bargain among themselves, following such bargaining protocol, how to divide the cost. Papers using this approach in mcstp are Bergantiños and Lorenzo (2004, 2005, 2008), Moulin and Velez (2013), Hernández et al. (2016). Other non-cooperative results are part of a relevant research agenda known as the Nash program for cooperative games. The Nash program arises from Nash (1953) as a tool to bridge the gap between cooperative and non-cooperative games by finding non-cooperative procedures yielding cooperative solutions as their equilibrium payoff allocations (Serrano 2005, 2020). Papers which show how the folk rule arises in equilibrium following different non-cooperative protocols are Bergantiños and Vidal-Puga (2010), Hougaard and Tvede (2012), Hernández et al. (2020).

The paper is organized as follows. In Sect. 2, we introduce mcstp. In Sect. 3, we review the rules obtained through algorithms and the cone-wise decomposition. In Sect. 4, we review the rules obtained through cooperative games and discuss the relations with the rules defined in Sect. 3. In Sect. 5, we conclude.

2 Preliminaries

In this section, we formally define minimum-cost spanning tree problems.

Let $\mathbb {N}_+=\left\{ 1,2,...\right\}$ be the set of possible agents (nodes). We denote by N a general finite subset of $\mathbb {N}_+,$ usually assumed to be $N=\left\{ 1,...,n\right\} .$

Given a non-empty, finite subset $N\subset \mathbb {N}_+$, let $\Pi _{N}$ denote the set of all orders in N. Given $\pi \in \Pi _{N}$, let $Pre\left( i,\pi \right)$ denote the set of nodes in N which come before node i in the order given by $\pi$, i.e.,

$$\begin{aligned} Pre\left( i,\pi \right) =\left\{ j\in N\mid \pi \left( j\right) <\pi \left( i\right) \right\} . \end{aligned}$$

For notational simplicity, given $\pi \in \Pi _{N}$ and $s\in N$, we denote by $\pi _s$ the unique node $i\in N$ such that $\pi \left( i\right) =s$. Moreover, given $\pi \in \Pi _{N}$ and $S\subset N$, let $\pi _{S}$ denote the order induced by $\pi$ among agents in S.

For each non-empty, finite $N\subset \mathbb {N}_+$, let $\Delta (N)=\left\{ x\in \mathbb {R}_{+}^{N} : \sum _{i\in N}x_{i}=1\right\}$.

We consider networks whose nodes are elements of a set $N_{0}=N\cup \left\{ 0\right\}$, where $N\subset \mathbb {N}_+$ is non-empty and finite, and 0 is a special node called the source.

A cost matrix $C=\left( c_{ij}\right) _{i,j\in N_{0}}$ represents the cost of direct link between any pair of nodes. We assume that $c_{ij}=c_{ji}\ge 0$ for each $i,j\in N_{0}$ and $c_{ii}=0$ for each $i\in N_{0}$. Since $c_{ij}=c_{ji}$, we work with undirected arcs, i.e., $\left( i,j\right) =\left( j,i\right)$.

We denote the set of all cost matrices over N as $\mathcal {C}^{N}$. Given C,  $C^{\prime }\in \mathcal {C}^{N},$ we say $C\le C^{\prime }$ if $c_{ij}\le c_{ij}^{\prime }$ for all $i,j\in N_{0}.$

A minimum-cost spanning tree problem, briefly an mcstp,  is a pair $\left( N_{0},C\right)$ where $N\subset \mathbb {N}_+$ is a finite set of agents, 0 is the source, and $C\in \mathcal {C}^{N}$ is the cost matrix.

Given an mcstp $\left( N_{0},C\right)$, we define the mcstp induced by C for $S\subset N$ as $\left( S_{0},C\right)$.

A network g over $N_{0}$ is a subset of $\left\{ \left( i,j\right) :i,j\in N_{0}\right\} .$ The elements of g are called $arcs .$

Given a network g and a pair of nodes i and j, a path from i to j in g is a sequence of different arcs $\left\{ \left( i_{h-1},i_{h}\right) \right\} _{h=1}^{l}$ satisfying $\left( i_{h-1},i_{h}\right) \in g$ for all $h\in \left\{ 1,2,...,l\right\}$, $i=i_{0}$, and $j=i_{l}$. A cycle is a path from i to i in g with $i \in N_0$ and at least two different arcs.

Let $\mathcal {G}^{N}$ denote the set of all networks over $N_{0}$, and let $\mathcal {G}_{0}^{N}$ denote the set of all networks where every agent $i\in N$ is connected to the source, i.e., there exists a path from agent i to the source.

Given a network $g \in \mathcal {G}^{N},$ let $P(g) = \{S_{k}(g)\}_{k=1}^{n(g)}$ denote the partition of $N_{0}$ in connected components induced by g. Formally, P(g) is the only partition of $N_{0}$ satisfying the following two properties:

• 1. If $i,j\in S_{k}(g)$, then agent i and agent j are connected in g.

• 2. If $i\in S_{k}(g)$, $j\in S_{l}(g)$ and $k\ne l$, then agent i and agent j are not connected in g.

Given a network $g\in \mathcal {G}^{N}$ and $i\in N_{0},$ let S(P(g), i) denote the set in P(g) to which agent i belongs to.

Given an mcstp $\left( N_{0},C\right)$ and $g\in \mathcal {G}^{N}$, we define the cost associated with g as

$$\begin{aligned} c\left( N_{0},C,g\right) =\sum _{\left( i,j\right) \in g}c_{ij}. \end{aligned}$$

When there is no ambiguity, we write $c\left( g\right)$ or $c\left( C,g\right)$ instead of $c\left( N_{0},C,g\right)$.

A spanning tree is a network such that for all $i\in N$ there is a unique path from agent i to the source. A minimal tree for $\left( N_{0},C\right)$, briefly an mt, is a spanning tree $t^*$ over $N_{0}$ such that

$$\begin{aligned} c\left( t^*\right) =\min _{g\in \mathcal {G}_{0}^{N}}c\left( g\right) . \end{aligned}$$

It is well known that an mt exists, even though it is not necessarily unique. Borůvka (1926), Kruskal (1956), Prim (1957) provide algorithms for computing an mt. Given an mcstp $\left( N_{0},C\right) ,$ we denote the cost associated with any mt for $\left( N_{0},C\right)$ as $m\left( N_{0},C\right)$.

Given an mcstp $\left( N_{0},C\right)$ and an mt $t^*$, Bird (1976) defines the minimal network $\left( N_{0},C^{t^*}\right)$ associated with $t^*$ as follows: $c_{ij}^{t^*}=\max _{\left( k,l\right) \in g^*_{ij}}\left\{ c_{kl}\right\} ,$ where $g^*_{ij}$ denotes the unique path in $t^*$ from agent i to agent j. It is well known that $C^{t^*}$ is independent from the chosen $t^*.$ Hence, we can define the irreducible form $\left( N_{0},C^{*}\right)$ of an mcstp $\left( N_{0},C\right)$ as the minimal network $\left( N_{0},C^{t^*}\right)$ associated with any mt $t^*.$

Given an mcstp $\left( N_{0},C\right)$, Trudeau (2012) defines the cycle-complete network $\left( N_{0},C^{**}\right)$ as follows: $c_{ij}^{**}=\max _{\left( k,l\right) \in g_{ij}^{**}}\left\{ c_{kl}\right\} ,$ where $g_{ij}^{**}$ denotes the cycle with minimal cost containing both agent i and agent j. It is clear that $c_{ij}^{**}=c_{ij}$ whereas (i, j) belongs to a cycle with minimal cost (among those containing both agent i and agent j), and hence $C^{**}$ is independent of the criterion used to choose minimal cycles, in case there are more than one.

Next example illustrates some of the concepts introduced above.

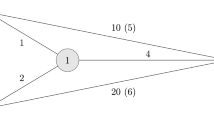
Example 2.1

Figure 1(a) depicts a minimum-cost spanning tree problem. There are three agents 1,  2,  and 3. The source is denoted by 0. These nodes are represented by circles, where the connection between them are represented by straight lines. Numbers by the lines represent the cost of each connection. The minimal tree is $\left\{ \left( 0,1\right) , \left( 1,2\right) , \left( 1,3\right) \right\}$. The irreducible form (b) and the cycle-complete network (c) are also depicted.

Fig. 1

Example of a mcstp a and its irreducible b and cycle-complete c forms

A (cost sharing) rule is a function f such that $f\left( N_{0},C\right) \in \mathbb {R}^{N}$ and $\sum _{i\in N}f_{i}\left( N_{0},C\right)$ $=m\left( N_{0},C\right)$ for each mcstp $\left( N_{0},C\right)$. As usual, $f_{i}\left( N_{0},C\right)$ represents the cost assigned to agent i.

3 Rules defined through the problem

In this subsection, we mention some rules of the literature that are defined directly through the problem, without using cooperative games. We have focused on the rules that are related to cooperative games, even though cooperative games are not used in their definition. Hence, we have not been exhaustive. In particular, we mention all the rules defined through algorithms and are related to some cooperative game rule. There are rules in the literature defined through algorithms that are not related to any cooperative game rule.

We first consider rules defined through algorithms for computing an mt. The idea is as follows. The algorithm selects the arc we construct and the rule decides how the cost of the selected arc is divided between the agents. Finally, each agent pays the sum of the costs over the arcs selected by the algorithm.

We also consider rules that are defined through a cone-wise decomposition. The idea is as follows. We first decompose the original problem as the sum of elementary problems. We solve these elementary problems. The solution to the original problem is obtained by adding the solutions to the elementary problems. As in the case of algorithms, we focus on rules related to some cooperative game rule.

3.1 Rules defined through Prim’s algorithm

Prim (1957) provides an algorithm for computing a minimal tree. The idea is as follows. Starting from the source, we sequentially add arcs with the lowest cost and without introducing cycles.

Formally, we start with $S^{0}=\left\{ 0\right\}$ and $g^{0}=\emptyset .$

Stage 1: Take an arc $\left( 0,i\right)$ such that $c_{0i}=\min _{j\in N}$ $\left\{ c_{0j}\right\}$. If there are several arcs satisfying this condition, select any of them. Now, $S^{1}=\left\{ 0,i\right\}$ and $g^{1}=\left\{ \left( 0,i\right) \right\}$.

Stage $p+1$: Assume we have defined $S^{p}\subset N_{0}$ and $g^{p}\in G^{N}$ . We now define $S^{p+1}$ and $g^{p+1}$. Take an arc $\left( j,i\right)$ with $j\in S^{p}$ and $i\in N_{0}\backslash S^{p}$ such that $c_{ji}=\min _{k\in S^{p},l\in N_{o}\setminus S^{p}}\left\{ c_{kl}\right\}$. If there are several arcs satisfying this condition, select any of them. Now, $S^{p+1}=S^{p}\cup \left\{ i\right\}$ and $g^{p+1}=g^{p}\cup \left\{ \left( j,i\right) \right\}$.

This process is completed in n stages. We say that $g^{n}$ is a tree obtained following Prim’s algorithm. Notice that this algorithm leads to a tree, but it is not always unique.

The Bird’s rule, denoted as $B\left( N_{0},C\right) ,$ was introduced by Bird (1976) in mcstp with a unique mt, and further studied in Granot and Huberman (1981), Feltkamp et al. (2000), Gómez-Rúa and Vidal-Puga (2011). The idea is the following. Agents connect sequentially to the source paying their connection cost. Let $\left( N_{0},C\right)$ be an mcstp with a unique mt,  denoted by $t^*.$ Given $i\in N$, let $i^{0}$ be the first node in the unique path in $t^*$ from agent i to the source. Then, for each $i\in N,$ we define

$$\begin{aligned} B_{i}\left( N_{0},C\right) =c_{i^{0}i}. \end{aligned}$$

Later on, Dutta and Kar (2004) extend this definition for any $mcstp\$ as an average of the trees associated with Prim’s algorithm. Given $\pi \in \Pi _{N},$ they defined $B^{\pi }\left( N_{0},C\right)$ as the allocation obtained when applied Prim’s algorithm to $\left( N_{0},C\right)$ and solved the indifferences by selecting the first agent given by $\pi$. Then, they defined

$$\begin{aligned} B\left( N_{0},C\right) =\frac{1}{n!}\sum _{\pi \in \Pi _{N}}B^{\pi }\left( N_{0},C\right) . \end{aligned}$$

Chun and Lee (2012) introduce the family of sequential contributions rules for mcstp with a unique mt. The connection cost of each agent is paid by this agent and the agents that connect to the source through this agent. Notice that the Bird’s rule is a member of this family.

We now introduce this family formally following Chun and Lee (2012). Let $t^{*}$ and $i^{0}$ be defined as in the case of Bird’s rule. Given $i\in N$, we define the set of followers of agent i as

$$\begin{aligned} F\left( i,t^{*}\right) =\left\{ j\in N_{0}:i\text { belongs to the unique path in }t^{*}\text { from }j\text { to 0}\right\} . \end{aligned}$$

Besides, we define the set of predecessors of agent i as

$$\begin{aligned} P\left( i,t^{*}\right) =\left\{ j\in N_{0}:j\text { belongs to the unique path in }t^{*}\text { from }i\text { to 0}\right\} . \end{aligned}$$

An agent $i\in N$ is a leaf if $F\left( i,t^{*}\right) =\varnothing$ and a first link agent if $P\left( i,t^{*}\right) =\left\{ 0\right\} .$ Let $Z\left( C\right)$ denote the set of leaves in $\left( N_{0},C\right)$ and $Y\left( C\right)$ denote the set of first link agents in $\left( N_{0},C\right) .$

Given a set of agents N,  a contributions function $\alpha ^{N}=\left( \alpha _{i}^{N}\right) _{i\in N}$ is defined as follows. For each $i\in N,$ $\alpha _{i}^{N}$ is a function from the set of cost matrices with a unique mt on $\mathbb {R}$ satisfying the following conditions.

$\left( i\right)$ For each $\left( N_{0},C\right) ,$ $0\le \alpha _{i}^{N}\left( C\right) \le c_{i^{0}i}.$

$\left( ii\right)$ For each $\left( N_{0},C\right)$, if $i\in Z\left( C\right) ,$ then $\alpha _{i}^{N}\left( C\right) =c_{i^{0}i}.$

$\left( iii\right)$ For each $\left( N_{0},C\right)$ and $\left( N_{0}^{\prime },C^{\prime }\right)$ such that $i\in N\cap N^{\prime }$, if $i\in F\left( i,t^{*}\right) =F\left( i,t^{\prime *}\right)$ and $c_{i^{0}i}=c_{i^{\prime 0}i}^{\prime },$ then $\alpha _{i}^{N}\left( C\right) =\alpha _{i}^{N^{\prime }}\left( C^{\prime }\right) .$

We say that $\varphi ^{\alpha }$ is the sequential contributions rule with contributions function $\alpha ^{N}$ if, for each $\left( N_{0},C\right) ,$

$$\begin{aligned} \varphi _{i}^{\alpha }\left( N_{0},C\right) =\alpha _{i}^{N}\left( C\right) +\sum _{j\in P\left( i,t^{*}\right) }\frac{c_{j^{0}j}-\alpha _{j}^{N}\left( C\right) }{\left| F\left( j,t^{*}\right) \right| } . \end{aligned}$$

The Dutta–Kar’s rule, denoted as $DK\left( N_{0},C\right)$, was introduced by Dutta and Kar (2004). It is also defined through Prim’s algorithm. Let $\left( N_{0},C\right)$ be an mcstp with a unique mt. Agents connect to the source via Prim’s algorithm, but with a pivotal switch in the allocation cost at each step. We now introduce it formally following Dutta and Kar (2004).

Let $S^{0}=\left\{ 0\right\}$, $g^{0}=\varnothing ,$ and $x^{0}=0.$

Stage 1. Select the unique arc $\left( i^{1},j^{1}\right)$ such that

$$\begin{aligned} c_{i^{1}j^{1}}=\min \left\{ c_{ij}:i\in A^{0}\text { and }j\in N_{0}\backslash A^{0}\right\} . \end{aligned}$$

Define,

$$\begin{aligned} x^{1}=\max \left\{ x^{0},c_{i^{1}j^{1}}\right\} ,\text { }S^{1}=S^{0}\cup \left\{ j^{1}\right\} ,\text { and }g^{1}=g^{0}\cup \left\{ \left( i^{1},j^{1}\right) \right\} . \end{aligned}$$

Stage $p+1.$ Assume we have defined $S^{p},$ $g^{p},$ and $x^{p}.$ Select the unique arc $\left( i^{p+1},j^{p+1}\right)$ such that

$$\begin{aligned} c_{i^{p+1}j^{p+1}}=\min \left\{ c_{ij}:i\in S^{p}\text { and }j\in N_{0}\backslash S^{p}\right\} . \end{aligned}$$

Define

$$\begin{aligned} x^{p+1}{=}\max \left\{ x^{p},c_{i^{p+1}j^{p+1}}\right\} ,\text { } S^{p+1}{=}S^{p}\cup \left\{ j^{p+1}\right\} , \text { and }g^{p+1}{=}g^{p}\cup \left\{ \left( i^{p+1},j^{p+1}\right) \right\} . \end{aligned}$$

The algorithm finishes in n stages. For each $i\in N$, there exists an stage $p\left( i\right)$ such that $i=j^{p\left( i\right) }$. We define

$$\begin{aligned} DK_{i}\left( N_{0},C\right) =\min \left\{ x^{p\left( i\right) -1},c_{i^{p\left( i\right) },j^{p\left( i\right) }}\right\} . \end{aligned}$$

When there are more than one mt, several arcs $\left( i^{p+1},j^{p+1}\right)$ could satisfy the condition. In this case, we define a rule $DK^{\pi }$ for each $\pi \in \Pi _{N},$ obtained by selecting the arc $\left( i^{p+1},j^{p+1}\right)$ where $j^{p+1}$ is the first agent given by $\pi$.

Dutta and Kar (2004) extend this definition for any mcstp similarly to the Bird’s rule. Namely,

$$\begin{aligned} DK\left( N_{0},C\right) =\frac{1}{n!}\sum _{\pi \in \Pi _{N}}DK^{\pi }\left( N_{0},C\right) . \end{aligned}$$

3.2 Rules defined through Kruskal’s algorithm

Kruskal (1956) defines another algorithm for computing an mt. The mt is constructed by sequentially adding arcs with the lowest cost without introducing cycles.

Formally, we start with $A^{0}(C) = \left\{ (i,j)\mid i,j\in N_{0},i\ne j\right\}$ and $g^{0}(C)=\emptyset .$

Stage 1: Take an arc $\left( i^1(C),j^1(C)\right) \in A^{0}\left( C\right)$ such that $c_{i^1(C) j^1(C)} = \min _{\left( i,j\right) \in A^{0}\left( C\right) }\left\{ c_{ij}\right\} .$ If there are several arcs satisfying this condition, select one of them. We then update $A^{1}\left( C\right) = A^{0}\left( C\right) \setminus \left\{ \left( i^1(C),j^1(C)\right) \right\} ,$ and $g^{1}\left( C\right) =\left\{ \left( i^{1}\left( C\right) ,j^{1}\left( C\right) \right) \right\}$.

Stage $p+1$: Given $A^{p}\left( C\right)$ and $g^{p}\left( C\right) ,$ consider an arc $\left( i,j\right) \in A^{p}\left( C\right)$ such that $c_{ij}=\min _{\left( k,l\right) \in A^{p}\left( C\right) }\left\{ c_{kl}\right\} .$ If there are several arcs satisfying this condition, select one of them. Two cases are possible:

• 1. If $g^{p}\left( C\right) \cup \left\{ \left( i,j\right) \right\}$ has a cycle, then repeat Stage $p+1$ with $A^{p}\left( C\right) \setminus \left\{ \left( i,j\right) \right\}$ instead of $A^{p}\left( C\right)$ and the same $g^{p}\left( C\right)$.

• 2. If $g^{p}\left( C\right) \cup \left\{ \left( i,j\right) \right\}$ has no cycles, then take $\left( i^{p+1}\left( C\right) ,j^{p+1}\left( C\right) \right) =\left( i,j\right) ,$ $A^{p+1}\left( C\right) =A^{p}\left( C\right) \setminus \left\{ \left( i,j\right) \right\}$, and $g^{p+1}\left( C\right) =g^{p}\left( C\right) \cup \left\{ \left( i ,j \right) \right\}$.

This process is completed in $\left| N\right|$ stages. Let $g^{\left| N\right| }(C)$ be the tree obtained following Kruskal’s algorithm. This algorithm leads to a tree, which is not always unique. When no confusion arises, we write $A^{p},$ $g^{p}$, and $(i^{p},j^{p})$ instead of $A^{p}(C)$, $g^{p}(C)$, and $(i^{p}(C),j^{p}(C))$.

Norde et al. (2004) present a subtraction algorithm, closely related to Kruskal’s, for the determination of minimum-cost spanning trees.

Bergantiños et al. (2010, 2011) consider a family of rules through Kruskal’s algorithm. At each step of the algorithm, an arc is added to the network. The cost of the arc is divided between the agents according to a function $\varrho$ specifying the part of the cost paid by each agent. Each agent pays the sum of the costs of the arcs selected by Kruskal’s algorithm.

We now introduce this family formally.

Let $\mathcal {P}(N_{0})$ denote the set of all partitions over $N_{0}$. Let $P=\{S_{0},S_{1},\ldots ,S_{m}\}$ be a generic element of $\mathcal {P}(N_{0})$ such that $0\in S_{0}$. We assume that for all $k=0,\dots ,m,$ $S_{k}\ne \emptyset .$ Given $P,P^{\prime }\in \mathcal {P}(N_{0}),$ we say that P is 1-finer than $P^{\prime }$ if $P^{\prime }$ is obtained from P by merging two elements of P.

A sharing function $\varrho$ associates with each pair of partitions $\left( P,P^{\prime }\right) ,$ where P is 1-finer than $P^{\prime },$ a vector $\varrho \left( P,P^{\prime }\right) \in \Delta \left( N\right)$ satisfying the path independence condition (see Bergantiños et al. (2010) for the definition of this condition). For each sharing function $\varrho ,$ we define the rule $f^{\varrho }$ as follows. Given an mcstp $\left( N_{0},C\right)$ and $i\in N$, we define

$$\begin{aligned} f_{i}^{\varrho }(N_{0},C) = \sum _{p=1}^{\left| N\right| }c_{i^{p}j^{p}} \cdot \varrho _{i}\left( P\left( g^{p-1}\right) ,P\left( g^{p}\right) \right) . \end{aligned}$$

These functions are called Kruskal’s sharing rules. We now consider some rules and a family of rules in the literature which are members of the family of Kruskal’s sharing rules.

Obligation rules, introduced by Tijs et al. (2006a), are defined through obligation functions, that specify the obligation of each agent in each coalition.

An obligation function for N is a map o that assigns to each $S\in 2^{N_{0}}\setminus \{\emptyset \}$ a vector $o(S)\in \mathbb {R}^{S}$ satisfying the following three conditions:

• For each $S\in 2^{N_{0}}\setminus \{\emptyset \}$ such that $0\notin S$ , $o(S)\in \Delta (S).$

• For each $S\in 2^{N_{0}}\setminus \{\emptyset \}$ such that $0\in S$, $o_{i}(S)=0$ for each $i\in S.$

• For each $S,T\in 2^{N_{0}}\setminus \{\emptyset \}$ with $S\subset T$ and $i\in S$, $o_{i}(S)\ge o_{i}(T).$

Given an obligation function o, we can define the Kruskal sharing rule $f^{\varrho ^{o}}$ where for each $i\in N,$

$$\begin{aligned} \varrho _{i}\left( P\left( g^{p-1}\right) ,P\left( g^{p}\right) \right) =o_{i}(S(P(g^{p-1}),i))-o_{i}(S(P(g^{p}),i)). \end{aligned}$$

Bergantiños et al. (2011) prove that the set of obligation rules is given by

$$\begin{aligned} \left\{ f^{\varrho ^{o}}\left( N_{0},C\right) :o\text { is an obligation function}\right\} . \end{aligned}$$

We now introduce some distinguished elements of the family of obligation rules.

The folk rule, denoted by $F\left( N_{0},C\right)$, was firstly considered in Feltkamp et al. (1994). It can be seen as a Kruskal sharing rule where $\varrho$ satisfies the following principles:

• Only agents who benefit directly when adding an arc pay for that arc.

• All agents in the same group pay the same.

• The amount paid by the members of a group $G_{1}$ is proportional to the number of agents of the group $G_{2}$ to whom this group $G_{1}$ is connected.

Formally, the folk rule corresponds with the obligation function o where for each $S\subset N$ and each $i\in S,$

$$\begin{aligned} o_{i}(S)=\frac{1}{\left| S\right| }. \end{aligned}$$

The folk rule is, probably, the most studied rule in this literature. It can be defined in several ways, different from the Kruskal’s algorithm approach considered above. Besides, it has also been studied through the axiomatic approach and the non-cooperative approach. Some papers studying the folk rule are Branzei et al. (2004), Bergantiños and Vidal-Puga (2009, 2010), Ciftci and Tijs (2009), Bergantiños et al. (2014), Subiza et al. (2016), Norde (2019), Giménez-Gómez et al. (2020), Hernández et al. (2020).

Optimistic weighted Shapley rules are introduced in Bergantiños and Lorenzo-Freire (2008b, 2008a). Each agent i has a weight $w_{i}>0.$ The sharing function $\varrho$ is defined proportionally to such weights. Formally, for each weight system $w=\left( w_{i}\right) _{i\in N},$ the optimistic weighted Shapley rule $f^{\varrho ^{ow}}$ is the Kruskal sharing rule associated with the obligation function o where for each $S\subset N$ and each $i\in S,$

$$\begin{aligned} o_{i}(S)=\frac{w_{i}}{\sum _{j\in S}w_{j}}. \end{aligned}$$

Pessimistic weighted Shapley rules are introduced in Lorenzo and Lorenzo-Freire (2009). Each agent i has a weight $w_{i}>0.$ The sharing function $\varrho$ is defined through such weights as follows. For each weight system $w=\left( w_{i}\right) _{i\in N},$ the pessimistic weighted Shapley rule $f^{\varrho ^{pw}}$ is the Kruskal sharing rule associated with the obligation function o where for each $S\subset N$ and each $i\in S,$

$$\begin{aligned} o_{i}(S)=\sum _{\pi \in \Pi \left( S\backslash \left\{ i\right\} \right) }\prod _{j=1}^{s-1}\frac{w_{\pi ^{-1}\left( j\right) }}{\sum _{k=1}^{j}w_{\pi ^{-1}\left( k\right) }+w_{i}}. \end{aligned}$$

3.3 Rules defined through Boruvka’s algorithm

Borůvka (1926) provides an algorithm for computing an mt. Bergantiños and Vidal-Puga (2011) introduce a rule based on Boruvka’s algorithm. We first provide an informal definition of Boruvka’s algorithm and the rule associated with it. We start with an empty network. Besides, each agent is a single component. Then, sequentially, for each connected component, we add the cheapest arc joining this connected component with some agent outside this connected component but without introducing cycles. The cost of each arc selected by Boruvka’s algorithm is divided among the agents following three principles. First, each agent only pays the arc selected by the component it belongs to. Second, all agents pay the same proportion of the arc selected by the component. Third, the proportion paid should be as large as possible.

We now introduce formally Boruvka’s algorithm and the associated rule following Bergantiños and Vidal-Puga (2011).

Let $\pi$ be an order over the set of all arcs. Namely,

$$\begin{aligned} \pi :\left\{ \left( i,j\right) :i,j\in N_{0},i\ne j\right\} \rightarrow \left\{ 1,2,\dots ,\left( \begin{array}{c} \left| N\right| \\ 2 \end{array} \right) \right\} . \end{aligned}$$

We first introduce the Boruvka’s algorithm associated with the order $\pi$.

Stage 1: Let $g^{\pi ,0}=\emptyset$. Notice that the set of connected components is $\left\{ \left\{ 0\right\} ,\left\{ 1\right\} ,\dots ,\left\{ \left| N\right| \right\} \right\}$.

Assume we have reached Step s ($s=1,2,\dots$) and we have defined $g^{\pi ,s-1}$.

Stage s: For each connected component T, $0\notin T$, let $\left( i^{\pi ,T},j^{\pi ,T}\right) \in T\times \left( N_{0}\backslash T\right)$ be the cheapest arc connecting T and $N_{0}\backslash T$. In case there are more than one possible arc, we select the one with the lowest position in the order $\pi$. We then add this arc to the graph, i.e.,

$$\begin{aligned} g^{\pi ,s}=g^{\pi ,s-1}\cup \left\{ \left( i^{\pi ,T},j^{\pi ,T}\right) :T \text { is a connected component},0\notin T\right\} . \end{aligned}$$

Following this algorithm, $g^{\pi ,s}$ is a graph with no cycles.

If the set of connected components becomes $\left\{ N_{0}\right\}$, then $g^{\pi ,s}$ is a tree and the process is over. Otherwise, we move to Step $s+1$.

The process finishes in a finite number of steps. The tree obtained by this procedure is an mt, and we denoted it as $t^{\pi }$. When no confusion arises, we write $g^{s},$ $i^{T},\dots$ instead of $g^{\pi ,s},$ $i^{\pi ,T},\dots$, respectively.

We now introduce the rule based on Boruvka’s algorithm.

Let $\pi$ be some order of the arcs, let $\left( N_{0},C\right)$ be a cost matrix, and let $t^{\pi }$ (or simply t) be the arc selected following Boruvka’s algorithm associated with $\pi .$ We now define the rule $\beta ^{\pi }$ as follows:

Stage 0. We define $a_{i}^{0,\pi }=\emptyset$ for all $i\in N$, $p^{0,\pi }=0$, $\varrho _{ij}^{0,\pi }=0$ for all $\left( i,j\right) \in t$, $A^{0,\pi }=t$, and $f_{i}^{0,\pi }=0$ for all $i\in N.$

In general, $a_{i}^{s,\pi }$, or simply $a_{i}^{s}$, denotes the arc in t that agent i pays partially in Stage s; $p^{s,\pi }$, or simply $p^{s}$, denotes the proportion of the cost of the arc that each agent pays in Stage s; $\varrho _{ij}^{s,\pi }$, or simply $\varrho _{ij}^{s}$, denotes the proportion of the cost of arc $\left\{ i,j\right\}$ already paid in Stage s; $A^{s,\pi }$, or simply $A^{s}$, denotes the set of non-completely paid arcs in Stage s, i.e. $A^{s}=\left\{ \left( i,j\right) \in t:\varrho _{ij}^{s}<1\right\}$; $f_{i}^{s,\pi }$, or simply $f_{i}^{s}$, denotes the cost that agent i pays in Stage s, i.e.,  $f_{i}^{s}=p^{s}c_{a_{i}^{s}}$.

We denote $\overline{A}^{s}=t\backslash A^{s}=\left\{ \left( i,j\right) \in t:\varrho _{ij}^{s}=1\right\}$. Let $\mathcal {P}^{s}$ be the set of connected components of $N_{0}$ associated with $\overline{A}^{s}$.

Assume that we have defined Stage r for all $r<s$. We now define Stage s . For simplicity, we omit reference to the order $\pi$.

Given a connected component $T\in \mathcal {P}^{s-1}$, $0\notin T$, we select the arc $\left( i^{T},j^{T}\right)$ as in Boruvka’s algorithm, so that $\left( i^{T},j^{T}\right) \in t$. Moreover, if component T selects $\left( i^{T},j^{T}\right)$ in Stage $s-1$ and $\left( i^{T},j^{T}\right)$ is not completely paid at the beginning of Stage s, then component T also selects $\left( i^{T},j^{T}\right)$ in Stage s.

Given $k\in T\in \mathcal {P}^{s-1}$, we define $a_{k}^{s}=\left( i^{T},j^{T}\right)$. That is, each agent will pay the cost of the arc selected by Boruvka’s algorithm for the component he belongs to.

For each arc $\left( i,j\right) \in A^{s-1}$, let $N_{ij}^{s}=\left\{ k\in N:a_{k}^{s}=\left( i,j\right) \right\}$ be the set of agents that will pay the cost of arc $\left( i,j\right)$. We define

$$\begin{aligned} p^{s}=\min \left\{ \frac{1-\varrho _{ij}^{s-1}}{\left| N_{ij}^{s}\right| }:\left( i,j\right) \in A^{s-1},N_{ij}^{s}\ne \emptyset \right\} . \end{aligned}$$

Notice that, assuming that all agents must pay the same proportion of the cost for each arc, $p^{s}$ is the maximum proportion that agents can pay in Stage s.

For each $\left\{ i,j\right\} \in A^{s-1},$ we define $\varrho _{ij}^{s}=\varrho _{ij}^{s-1}+\left| N_{ij}^{s}\right| p^{s}$ . Thus, $\varrho _{ij}^{s}\le 1$ for each $\left\{ i,j\right\} \in A^{s-1}$. Moreover, there exists at least one $\left( i,j\right) \in A^{s-1}$ such that $\varrho _{ij}^{s}=1$. Thus, $A^{s}\varsubsetneq A^{s-1}$ and $\overline{A}^{s-1}\varsubsetneq \overline{A}^{s}$. That is, there are more arcs completely paid.

This process finishes when $\overline{A}^{s}=t$. Since $a_{i}^{s}\in t$ for each agent i and each Stage s,  and $\overline{A}^{s-1}\varsubsetneq \overline{A}^{s}$, this process finishes in a finite number of Stages (at most $\left| N\right|$), say $\gamma$.

Moreover, by definition, the process finishes when $\sum _{s=1}^{ \gamma }p^{s}=1$.

Given an order $\pi$ of the set of arcs and a cost matrix C, we define the Boruvka’s rule induced by the order $\pi$ as

$$\begin{aligned} \beta _{i}^{\pi }\left( N_{0},C\right) =\sum \limits _{s=1}^{\gamma }f_{i}^{s} \text { for each }i\in N. \end{aligned}$$

Even this allocation could depend on $\pi ,$Bergantiños and Vidal-Puga (2011) prove that, for each order $\pi$, $\beta ^{\pi }$ coincides with the folk rule.

3.4 Rules defined through a cone-wise decomposition

Norde et al. (2004) prove that every mcstp can be written as a nonnegative combination of the so-called elementary mcstp,  in which the costs of the arcs are 0 or 1.

Formally, for each mcstp $(N_{0},C)$, there exists a family $\{C^{q}\}_{q=1}^{m(C)}$ of cost matrices and a family $\{x^{q} \}_{q=1}^{m(C)}$ of nonnegative real numbers satisfying three conditions:

• 1. $C=\sum _{q=1}^{m(C)}x^{q}C^{q}.$

• 2. For each $q\in \{1,\dots ,m(C)\}$, there exists a network $g^{q}$ such that $c_{ij}^{q}=1$ if $(i,j)\in g^{q}$ and $c_{ij}^{q}=0$ otherwise.

• 3. Let $q\in \{1,\ldots ,m(C)\}$ and $\{i,j,k,l\}\subset N_{0}$. If $c_{ij}\le c_{kl}$, then $c_{ij}^{q}\le c_{kl}^{q}.$

Assume we know how a rule R should share the cost in any elementary problem. Then, we can extend the rule R for elementary problems to any general mcstp by using the decomposition given by Norde et al. (2004) as follows:

$$\begin{aligned} R\left( N_{0},C\right) =\sum _{q=1}^{m(C)}x^{q}R\left( N_{0},C^{q}\right) . \end{aligned}$$

Several authors have followed this approach for defining rules or family of rules. We mention some of them.

Branzei et al. (2004) proved that the folk rule can be obtained in this way. Given an elementary problem $\left( N_{0},C^{q}\right) ,$ agents in the same component as the source (and hence connected to the source through a path of cost 0) pay 0. Agents in any other component equally divide the cost of connecting them to the source, which is 1. Formally,

$$\begin{aligned} F\left( N_{0},C^{q}\right) =\left\{ \begin{array}{ll} \frac{1}{S(P(g^{q}),i)} &{}\quad \hbox {if } 0\notin S(P(g^{q}),i) \\ 0 &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

Bergantiños and Lorenzo-Freire (2008b) prove that optimistic weighted Shapley rules can also be obtained in this way by taking

$$\begin{aligned} f^{\varrho ^{ow}}\left( N_{0},C^{q}\right) =\left\{ \begin{array}{ll} \frac{w_{i}}{\sum _{j\in S(P(g^{q}),i)}w_{j}} &{}\quad \hbox {if } 0\notin S(P(g^{q}),i)\\ 0 &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

Bogomolnaia and Moulin (2010) consider the following family of rules. Given an elementary problem $\left( N_{0},C^{q}\right)$ and agent $i\in N,$ let $\delta _{i}$ denote the number of non-null arcs in $C^{q}$ containing agent i. For each $\lambda \in \left[ 0,+\infty \right) ,$

$$\begin{aligned} R^{\lambda }\left( N_{0},C^{q}\right) =\left\{ \begin{array}{ll} \frac{\lambda ^{\delta _{i}}}{\sum _{j\in S(P(g^{q}),i)}\lambda ^{\delta _{j}}} &{}\quad \hbox {if } 0\notin S(P(g^{q}),i) \\ 0 &{}\quad \hbox {otherwise} \end{array} \right. \end{aligned}$$

and for $\lambda =+\infty$

$$\begin{aligned} R^{\lambda }\left( N_{0},C^{q}\right) =\left\{ \begin{array}{ll} \arg \max _{j\in S(P(g^{q}),i)}\delta _{j} &{}\quad \hbox {if } 0\notin S(P(g^{q}),i)\\ 0 &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

4 Rules defined through cooperative games

We first review some concepts of cooperative games used in this paper. In some cases, we simply give an informal definition, the notation, and a reference where it is possible to find the formal definition.

A cooperative game with transferable utility, briefly a TU game, is a pair $\left( N,v\right)$ where $v:2^{N}\rightarrow \mathbb {R}$ satisfies that $v\left( \emptyset \right) =0$.

We say that $\left( N,v\right)$ is concave if, for all $S,T\subset N$ and $i\in N$ such that $S\subset T$ and $i\notin T$,

$$\begin{aligned} v\left( S\cup \left\{ i\right\} \right) -v\left( S\right) \ge v\left( T\cup \left\{ i\right\} \right) -v\left( T\right) . \end{aligned}$$

The core is defined as

$$\begin{aligned} core\left( N,v\right) =\left\{ x\in \mathbb {R}^{N} : \sum _{i\in N}x_{i}=v\left( N\right) \text { and }\sum _{i\in S}x_{i}\le v\left( S\right) \text {, }\forall S\subset N\right\} . \end{aligned}$$

The Shapley value (Shapley 1953b), denoted as $Sh\left( N,v\right) ,$ is defined as the average of marginal contributions over all possible orders in which agents may appear. Namely, for each $i\in N,$

$$\begin{aligned} Sh_{i}\left( N,v\right) =\frac{1}{\left| N\right| !}\sum _{\pi \in \Pi \left( N\right) }\left[ v\left( Pre\left( i,\pi \right) \cup \left\{ i\right\} \right) -v\left( Pre\left( i,\pi \right) \right) \right] . \end{aligned}$$

An alternative to marginal contributions are the reduced marginal contributions (Vidal-Puga 2004) defined as

$$\begin{aligned} s^\pi _i(v) = v_s\left( N \setminus Pre(i,\pi ) \right) - v_s\left( N \setminus \left( Pre(i,\pi ) \cup \{i\} \right) \right) \end{aligned}$$

where $s = \left( s^\pi _j(v)\right) _{j\in Pre(i,\pi )}$ and $(N\setminus Pre(i,\pi ),v_s)$ is the reduced game defined as

$$\begin{aligned} v_s(T) =\left\{ \begin{array}{ll} 0 &{}\quad \text {if }T = \emptyset \\ \max _{S\subseteq Pre(i,\pi )}\left\{ v(T \cup S) - \sum _{j\in S}s_i \right\} &{}\quad \text {otherwise} \end{array} \right. \end{aligned}$$

for all $T \subseteq N\setminus Pre(i,\pi ).$

Shapley (1953a) introduced the family of weighted Shapley values for TU games. Each agent $i\in N$ has positive weight $w_{i}$. These weights are the proportions in which the players share in unanimity games. Kalai and Samet (1987) further studied this family. We denote by $Sh^{w}\left( N,v\right)$ the weighted Shapley value associated with the weight system $w=\left( w_{i}\right) _{i\in N}.$ For each $i\in N,$

$$\begin{aligned} Sh_{i}^{w}(N,v)={\sum _{\pi \in \Pi \left( N\right) }}p_{w}(\pi )\left[ v(Pre(\pi ,i)\cup \left\{ i\right\} )-v(Pre(\pi ,i))\right] \end{aligned}$$

where $p_{w}(\pi )={\prod _{j=1}^{\left| N\right| }}\frac{w_{\pi \left( j\right) }}{{\sum _{k=1}^{j}}w_{\pi \left( k\right) }}$.

Owen (1977) introduced a value for TU games with a group structure. Agents are partitioned into different groups. We denote by P such partition. We should divide $v\left( N\right)$ among the agents taking into account the partition P. Owen (1977) proved that his value generalizes the Shapley value. We call it the Owen value and denote it as $Ow\left( N,v,P\right)$.

We say that a permutation $\pi \in \Pi _{N}$ is admissible with respect to P if given $i,i^{\prime }\in P^{k}\in P$ and $j\in N$ with $\pi (i)<\pi (j)<\pi (i^{\prime })$, then $j\in P^{k}.$ We denote by $\Pi ^{G}$ the set of all permutations over N admissible with respect to P. Given $\left( N,v,P\right)$ and $i\in P^{k}\in P,$

$$\begin{aligned} Ow_{i}\left( N,v,G\right) =\dfrac{1}{\left| \Pi ^{G}\right| } \sum _{\pi \in \Pi ^{G}}\left[ v\left( Pre\left( i,\pi \right) \cup \left\{ i\right\} \right) -v\left( Pre\left( i,\pi \right) \right) \right] . \end{aligned}$$

Weber (1988) introduced the marginalistic values of a cooperative game as generalizations of the Shapley value. Weber considers that agent i ’s marginal contribution to a coalition S is weighted by an exogenously specified factor. Let $p^{i}$ be a weight scheme for agent $i\in N$, where negative weights are also allowed. Formally, $p^{i}\in \mathbb {R}^{|\left\{ S:S\subset N\setminus \left\{ i\right\} \right\} |}$ and $\sum _{S\subset N\setminus \left\{ i\right\} }p^{i}\left( S\right) =1.$ We define the marginalistic value $f^{p}$ associated with a collection of weight schemes $p={\left\{ p^{i}\right\} }_{i\in N}$ as follows. Given the TU game $\left( N,v\right)$ and $i\in N,$

$$\begin{aligned} f_{i}^{p}\left( N,v\right) =\sum _{S\subset N\backslash \left\{ i\right\} }p^{i}\left( S\right) \left( v\left( S\cup \left\{ i\right\} \right) -v\left( S\right) \right) . \end{aligned}$$

4.1 The private game

Bird (1976) associated with each mcstp $\left( N_{0},C\right)$ a TU game $\left( N,v_{C}^{p}\right)$ where the cost of each coalition S is computed under the assumption that agents in $N\setminus S$ are not available. We call this game private because the nodes in $N\setminus S$ belong to these agents, and hence, their participation is needed in order to use their nodes.

Formally, the TU game $\left( N,v_{C}^{p}\right)$ associated with each mcstp $\left( N_{0},C\right)$ is defined as follows. For each coalition $S\subseteq N$,

$$\begin{aligned} v_{C}^{p}\left( S\right) =m\left( S_{0},C\right) . \end{aligned}$$

(1)

When no confusion arises, we write $v^{p}$ instead of $v_{C}^{p}.$

We compute $v^{p}$ in Example 2.1.

S	$\left\{ 1\right\}$	$\left\{ 2\right\}$	$\left\{ 3\right\}$	$\left\{ 1,2\right\}$	$\left\{ 1,3\right\}$	$\left\{ 2,3\right\}$	N
$v^{p}\left( S\right)$	12	15	20	16	18	23	22

Hence, $v^{p}\left( \left\{ 2,3\right\} \right)$ is computed using only nodes 2 and 3. Thus, the minimal tree in the problem $\left( \left\{ 2,3\right\} _{0},C\right)$ is $\left\{ ( 0,3),( 2,3) \right\}$.

Kobayashi and Okamoto (2014) provide sufficient and necessary conditions for $v^{p}$ to be a concave game. Moreover, when the costs are restricted to two possible values: low and high (as in elementary problems), $v^{p}$ is concave if and only if the cycles formed by arcs of low cost are either adjacent to the source or pairwise adjacent. This condition can be verified in polynomial time.

Bird (1976) proved that, for each mcstp $\left( N_{0},C\right) ,$ the core of $v^{p}$ is non-empty. Later on, the core was studied by other authors. We mention some other results about the core.

Theorem 4.1

• 1. (Bird 1976) For each mcstp $\left( N_{0},C\right)$, the Bird’s rule $B\left( N_{0},C\right)$ belongs to the core of $v^{p}$.

• 2. (Feltkamp et al. 1994) For each mcstp $\left( N_{0},C\right)$, the folk rule $F\left( N_{0},C\right)$ belongs to the core of $v^{p}$.

• 3. (Dutta and Kar 2004) For each mcstp $\left( N_{0},C\right)$, the Dutta–Kar’s rule $DK\left( N_{0},C\right)$ belongs to the core of $v^{p}$.

• 4. (Tijs et al. 2006a) For each mcstp $\left( N_{0},C\right)$, each obligation rule $f^{\varrho ^{o}}\left( N_{0},C\right)$ belongs to the core of $v^{p}$.

• 5. (Bogomolnaia and Moulin 2010) For each mcstp $\left( N_{0},C\right)$ and each $\lambda \in \left[ 0,+\infty \right)$, $R^{\lambda }\left( N_{0},C\right)$ belongs to the core of $v^{p}$.

• 6. (Trudeau and Vidal-Puga 2017) For each mcstp $\left( N_{0},C\right)$, the core of $v^{p}$ is the convex hull of the reduced marginal contributions vectors.

Since optimistic weighted Shapley rules are obligation rules (Bergantiños and Lorenzo-Freire 2008a, b) and pessimistic weighted Shapley rules are also obligation rules (Lorenzo and Lorenzo-Freire 2009), both belong to the core of $v^{p}.$

Moreover, Moretti et al. (2002) study some monotonicity properties of the core of $v^p$.

Next result applies to mcstp with a unique mt : 

Theorem 4.2

(Chun and Lee 2012) The unique sequential contributions rule that selects a core allocation in the private game $v^p$ for each mcstp with a unique mt is the Bird’s rule.

Next result applies to elementary mcstp:

Theorem 4.3

(Kuipers 1993)

• 1. For each elementary mcstp,  there exists an associated concave elementary graph game, which has the same core as $v^p$.

• 2. For each elementary mcstp,  its extreme core allocations are marginal allocation vectors of the game $v^p$.

We now mention, briefly, some single values for mcstp that have been defined through the game $v^{p}.$

Granot and Huberman (1981, 1984) study the core and the nucleolus of $v^{p}.$ They prove that the core and the nucleolus can be obtained as a Cartesian product of the core and the nucleolus of some subproblems. They also provide efficient algorithms for the computation of the core and the nucleolus.

Faigle et al. (1998) prove that computing the nucleolus is NP-hard.

Kar (2002) defines a rule as the Shapley value of $v^{p}$. Namely, for each mcstp $\left( N_{0},C\right)$, he considers $Sh\left( N,v^{p}\right) .$ He obtains an axiomatic characterization of this value. Ando (2012) proves that computing this Shapley value is NP-hard, even for elementary games.

Trudeau and Vidal-Puga (2017, 2020) study the permutation-weighted average of extreme points of the core in elementary cost matrices. Moreover, Trudeau and Vidal-Puga (2020) provide a necessary condition for the coincidence of these three values, i.e., the nucleolus, the Shapley value, and the permutation-weighted average of extreme points of the core of $v^p$.

4.2 The irreducible game

We associate with each mcstp $\left( N_{0},C\right)$ a TU game $\left( N,v_{C}^{i}\right)$ defined as the private game associated with the irreducible form $\left( N_{0},C^{*}\right) .$ Thus, for each coalition $S\subseteq N$,

$$\begin{aligned} v_{C}^{i}\left( S\right) =m\left( S_{0},C^{*}\right) . \end{aligned}$$

(2)

This game was already considered in Bird (1976). When no confusion arises, we write $v^{i}$ instead of $v_{C}^{i}.$

We compute $v^{i}$ in Example 2.1.

S	$\left\{ 1\right\}$	$\left\{ 2\right\}$	$\left\{ 3\right\}$	$\left\{ 1,2\right\}$	$\left\{ 1,3\right\}$	$\left\{ 2,3\right\}$	N
$v^{i}\left( S\right)$	12	12	12	16	18	18	22

Now, $v^{i}\left( \{2,3\}\right)$ is also computed using only the nodes 2 and 3,  but considering $C^{*}$ instead of C. Thus, the minimal tree in problem $\left( \left\{ 2,3\right\} _{0},C^{*}\right)$ is $\left\{ \left( 0,3\right) ,\left( 2,3\right) \right\} ,$ but the cost is 18 (instead of 23).

Bird (1976) proved that for each mcstp $\left( N_{0},C\right)$ the core of $v^{i}$ (usually called the irreducible core) is non-empty and it is a subset of the core of $v^{p}$. Later on, the core of $v^{i}$ was studied by other authors.

We mention some other results about the irreducible core.

Theorem 4.4

• 1. (Bird 1976) For each mcstp $\left( N_{0},C\right)$, the irreducible core is the convex combination of the set of allocations induced by Prim’s algorithm.

• 2. (Aarts and Driessen 1993) For each mcstp $\left( N_{0},C\right)$, $v^{i}$ is concave.

• 3. (Bird 1976) For each mcstp $\left( N_{0},C\right) ,$ the Bird’s rule $B\left( N_{0},C\right)$ belongs to the core of $v^{i}$.

• 4. (Feltkamp et al. 1994) For each mcstp $\left( N_{0},C\right) ,$ the folk rule $F\left( N_{0},C\right)$ belongs to the core of $v^{i}$.

• 5. (Tijs et al. 2006a) For each mcstp $\left( N_{0},C\right) ,$ each obligation rule $f^{\varrho ^{o}}\left( N_{0},C\right)$ belongs to the core of $v^{i}$.

• 6. (Tijs et al. 2006b) The core of $v^i$ is the largest solution which is efficient, nonnegative, upper-bounded by the stand-alone costs, and cone-wise positive linear.

• 7. (Bergantiños and Vidal-Puga 2015) For each mcstp $\left( N_{0},C\right) ,$ the core of $v^{i}$ coincides with the set of allocation induced by the set of all monotonic rules over the cost matrix and the set of agents.

Since optimistic weighted Shapley rules are obligation rules (Bergantiños and Lorenzo-Freire 2008a, b), and pessimistic weighted Shapley rules are also obligation rules (Lorenzo and Lorenzo-Freire 2009), both belong to the core of $v^{i}.$

We now consider the Shapley value of $v^{i}.$ We also consider other values of TU closely related to the Shapley value.

Bergantiños and Vidal-Puga (2007a) define a rule as the Shapley value of $v^{i}$ . Namely, or each mcstp $\left( N_{0},C\right) ,$ they consider $Sh\left( N,v^{i}\right) .$

Theorem 4.5

• 1. (Bergantiños and Vidal-Puga 2007a) For each mcstp $\left( N_{0},C\right) ,$ the folk rule of $\left( N_{0},C\right)$ coincides with $Sh\left( N,v^{i}\right) .$

• 2. (Bergantiños and Vidal-Puga 2007a) For each mcstp $\left( N_{0},C \right) ,$ the Bird’s rule of $\left( N_{0},C^{*}\right)$ coincides with $Sh\left( N,v^{i}\right) .$

• 3. (Lorenzo and Lorenzo-Freire 2009) The family of pessimistic weighted Shapley rules coincides with the family of weighted Shapley values of $v^{i}.$

• 4. (Bergantiños and Kar 2010) For each mcstp $\left( N_{0},C\right) ,$ the set of obligation rules is a subset of the set of marginalistic values of $v^{i}.$

A comparative of the Shapley value in the irreducible game (folk solution) and in the private game (Kar solution) can be found in Trudeau (2014b). Ando and Kato (2010) prove that the Shapley value in the irreducible game, as well as the egalitarian solution and the nucleolus, can be computed in time $O(|N|^2).$ For irreducible cost matrices, Trudeau and Vidal-Puga (2020) show that the Shapley value, the nucleolus and the permutation-weighted average of extreme points of the core of $v^i$ coincide.

Moreover, Bergantiños and Gómez-Rúa (2010, 2015) study the rule given by the Owen value of $v^{i}.$

4.3 The optimistic game

As an alternative to Bird’s approach, Bergantiños and Vidal-Puga (2007b) associate with each mcstp $\left( N_{0},C\right)$ a cooperative game $\left( N,v_{C}^{o}\right)$ where the worth of each coalition S is computed assuming that agents in $N\setminus S$ are already connected. We call this game optimistic because agents in S can connect to the source through agents in $N\setminus S$ for free.

Let $\left( N_{0},C\right)$ be an mcstp, and $S,T\subset N$ with $S\cap T=\emptyset .$ We define the associated mcstp $\left( S_{0},C^{T}\right)$ assuming that agents in S have to be connected to the source, agents in T are already connected, and the agents in S can connect to the source through agents in T. Formally, $c_{ij}^{T}=c_{ij}$ for all $i,j\in S$ and $c_{0i}^{T}=\min _{j\in T_{0}}c_{ji}$ for all $i\in S$.

Bergantiños and Vidal-Puga (2007b) defined the TU game $\left( N,v^{o}_C\right)$ associated with each mcstp $\left( N_{0},C\right)$. For each coalition $S\subseteq N$,

$$\begin{aligned} v_{C}^{o}\left( S\right) =m\left( S_{0},C^{N\setminus S}\right) . \end{aligned}$$

(3)

When no confusion arises, we write $v^{o}$ instead of $v_{C}^{o}.$

We compute $v^{o}$ in Example 2.1.

S	$\left\{ 1\right\}$	$\left\{ 2\right\}$	$\left\{ 3\right\}$	$\left\{ 1,2\right\}$	$\left\{ 1,3\right\}$	$\left\{ 2,3\right\}$	N
$v^{o}\left( S\right)$	4	4	6	10	10	10	22

Hence, $v^{o}\left( \left\{ 2,3\right\} \right)$ is computed assuming that agent 1 is already connected. Thus, agents 2 and 3 connect to the source through tree $\left\{ \left( 1,2\right) ,\left( 1,3\right) \right\} ,$ which has a cost of 10.

We say that two mcstp $\left( N_{0},C\right)$ and $\left( N_{0},C^{\prime }\right)$ are tree-equivalent if there exists a spanning tree $t^*$ such that $t^*$ is an mt for both $\left( N_{0},C\right) ,$ and $\left( N_{0},C^{\prime }\right)$ and $c_{ij} = c_{ij}^{\prime }$ for all $\left( i,j\right) \in t^*.$

In the next theorem, we summarize some results obtained for $v^{o}.$

Theorem 4.6

• 1. (Bergantiños and Vidal-Puga 2007b) If $\left( N_{0},C^*\right)$ is irreducible, then $v^p$ and $v^o$ are dual, i.e.,

  $$\begin{aligned} v^{p}\left( S\right) +v^{o}\left( N\setminus S\right) =m\left( N_{0},C\right) \end{aligned}$$

  for all $S\subset N.$

• 2. (Bergantiños and Vidal-Puga 2007b) If $\left( N_{0},C\right)$ and $\left( N_{0},C^{\prime }\right)$ are tree-equivalent, then $v_{C}^{o}=v_{C^{\prime }}^{o}.$

• 3. (Bergantiños and Vidal-Puga 2007b) The optimistic game associated with any mcstp (N, C) coincides with the optimistic game associated with its irreducible form $(N,C^*)$, i.e., $v_C^{o} = v_{C^*}^{o}.$

In the next theorem, we summarize some results obtained for the Shapley value (and other related values) of $v^{o}.$

Theorem 4.7

• 1. Bergantiños and Vidal-Puga (2007b) For all mcstp $\left( N_{0},C\right) ,$

  $$\begin{aligned} Sh\left( N,v_C^{o}\right) =Sh\left( N,v_C^{i}\right) =Sh\left( N,v_{C^*}^{o}\right) . \end{aligned}$$

• 2. (Bergantiños and Lorenzo-Freire 2008b) The family of optimistic weighted Shapley rules coincides with the family of weighted Shapley values of $v^{o}.$

Since $Sh\left( N,v^{o}\right) =Sh\left( N,v^{i}\right)$, and the folk rule coincides with $Sh\left( N,v^{i}\right)$, the Shapley value of $v^{o}$ is just another way for obtaining the folk rule.

The family of optimistic weighted Shapley rules is studied from an axiomatic point of view in Bergantiños and Lorenzo-Freire (2008a). Moreover, Gómez-Rúa and Vidal-Puga (2017) prove that a version of such an optimistic weighted Shapley rule is immune to manipulation by merging or splitting of nodes in a slightly more general model.

4.4 The public game

A natural alternative to the private case is to assume that there are no property rights on nodes and agents in S can use, paying their cost, the nodes of their neighbors in $N\setminus S$ to connect to the source. This approach was first explicitly studied by Bogomolnaia and Moulin (2010).

We compute $v^{u}$ in Example 2.1.

S	$\left\{ 1\right\}$	$\left\{ 2\right\}$	$\left\{ 3\right\}$	$\left\{ 1,2\right\}$	$\left\{ 1,3\right\}$	$\left\{ 2,3\right\}$	N
$v^{u}\left( S\right)$	12	15	18	16	18	22	22

Now, $v^{u}\left( \{2,3\}\right)$ is computed assuming that agent 1 is available. Thus, agents 2 and 3 connect to the source through tree $\left\{ \left( 0,1\right) , \left( 1,2\right) ,\left( 1,3\right) \right\} ,$ which has a cost of 22.

The public game has not received much attention in the literature, and it has been limited to the contrast with the private game (Trudeau 2013; Trudeau and Vidal-Puga 2017, 2019). A possible reason for this lack of attention is that the private game is more tractable. Notice, for example, that $v^u(S) = \min _{S\subseteq T}v^p(T),$ i.e., it requires much more effort to compute $v^u(S).$ Moreover, the core allocations of the public game coincide with the core allocations of the private game with nonnegative cost shares, as first noted by Bogomolnaia and Moulin (2010) and formally proved by Trudeau and Vidal-Puga (2017):

Theorem 4.8

(Trudeau and Vidal-Puga 2017) $core(N,v^u) = core(N,v^p) \cap \mathbb {R}_+^N.$

Additionally, the public game associated with the irreducible form of a mcstp coincides with the private game associated with this irreducible form. Hence, the irreducible game can be defined from either the private or the public approach.

As a consequence, most of the results for the private game also hold for the public game. For the sake of completeness, we replicate these results for the public game. The proof is an immediate consequence of Theorem 4.1 and the nonnegativity of the rules mentioned in the respective item.

Theorem 4.9

• 1. For each mcstp $\left( N_{0},C\right)$, the Bird’s rule $B\left( N_{0},C\right)$ belongs to the core of $v^{u}$.

• 2. For each mcstp $\left( N_{0},C\right)$, the folk rule $F\left( N_{0},C\right)$ belongs to the core of $v^{u}$.

• 3. For each mcstp $\left( N_{0},C\right)$, the Dutta–Kar’s rule $DK\left( N_{0},C\right)$ belongs to the core of $v^{u}$.

• 4. For each mcstp $\left( N_{0},C\right)$, each obligation rule $f^{\varrho ^{o}}\left( N_{0},C\right)$ belongs to the core of $v^{u}$.

• 5. (Bogomolnaia and Moulin 2010) For each mcstp $\left( N_{0},C\right)$ and each $\lambda \in \left[ 0,+\infty \right)$, $R^{\lambda }\left( N_{0},C\right)$ belongs to the core of $v^{u}$.

• 6. (Trudeau and Vidal-Puga 2017) For each mcstp $\left( N_{0},C\right)$, the core of $v^{u}$ is the convex hull of the reduced marginal contributions vectors.

The Shapley value of the public game may not belong to the core. See Trudeau and Vidal-Puga (2019) for an example of a three-agent problem in which the Shapley value of the public game lies outside both the core of $v^u$ and the core of $v^p.$ Since the folk rule is a core selector, it does not coincide with the Shapley value of the public game.

Next result applies to mcstp with a unique mt : 

Theorem 4.10

The unique sequential contributions rule that selects a core allocation in the public game $v^u$ for each mcstp with a unique mt is the Bird’s rule.

Proof

Under Theorem 4.9(1), we know that the Bird rule is a sequential contribution rule that select a core allocation in the public game. Under Theorem 4.8, the core of $v^u$ is a subset of the core of $v^p.$ Hence, any sequential contribution rule that select a core allocation in the public game does so also in the private game. Under Theorem 4.2, such a rule coincides with the Bird’s rule. $\square$

Next result applies to elementary mcstp:

Theorem 4.11

(Trudeau and Vidal-Puga 2017) For elementary mcstp problems, the folk solution is the permutation-weighted average of extreme core allocations of the game $v^u.$

4.5 The cycle-complete game

The last alternative to be considered is to associate with each mcstp $\left( N_{0},C\right)$ a TU game $\left( N,v_{C}^{c}\right)$ defined as the private game associated with the cycle-complete network $\left( N_{0},C^{**}\right) .$ Thus, for each coalition $S\subseteq N$,

$$\begin{aligned} v_{C}^{c}\left( S\right) = v_{C^{**}}^{i}\left( S\right) = m\left( S_{0},C^{**}\right) . \end{aligned}$$

(4)

As usual, we write $v^{c}$ instead of $v_{C}^{c}.$

This approach was studied by Trudeau (2012).

We compute $v^{c}$ in Example 2.1.

S	$\left\{ 1\right\}$	$\left\{ 2\right\}$	$\left\{ 3\right\}$	$\left\{ 1,2\right\}$	$\left\{ 1,3\right\}$	$\left\{ 2,3\right\}$	N
$v^{c}\left( S\right)$	12	15	15	16	18	23	22

Now, $v^{c}\left( \{2,3\}\right)$ is again computed using only the nodes 2 and 3,  but considering $C^{**}.$ In this case, there are two minimal trees in problem $\left( \left\{ 2,3\right\} _{0},C^{**}\right) ,$ which are $\left\{ \left( 0,3\right) ,\left( 2,3\right) \right\}$ and $\left\{ \left( 0,2\right) ,\left( 2,3\right) \right\} ,$ both with cost 23.

Theorem 4.12

(Trudeau 2012) The game $(N,v^c)$ is concave.

Theorem 4.12 is not tight in the sense that there are concave mcstp which are not cycle-complete. However, this result is tight if we look only at elementary mcstp.

It is well known that the Shapley value of a concave cost game belongs to its core. Moreover, it is clear that $core(N,v^c) \subseteq core(N,v^p).$ Hence, the Shapley value of $(N,v^c),$ which Trudeau (2012) calls cycle-complete solution, belongs to both cores.

Theorem 4.13

(Trudeau 2012) For each mcstp $\left( N_{0},C\right) ,$ the cycle-complete solution belongs to the core of the game $v^{c}$.

Next result applies to elementary mcstp:

Theorem 4.14

(Trudeau and Vidal-Puga 2017) For elementary problems, the cycle-complete solution is the permutation-weighted average of extreme core allocations of the game $v^c.$

A comparative of the Shapley value in the cycle-complete game (cycle-complete solution) and in the irreducible game (folk solution) can be found in Trudeau (2014a).

4.6 Relation between cores

It is clear from their definition that the cost of the grand coalition in all the games coincide, i.e., $v^{p}(N)=v^{i}(N)=v^{o}(N)=v^{u}(N)=v^{c}(N)={m(N_{0},C)},$ whereas for each coalition $S\subset N,$

$$\begin{aligned} v^{o}(S)\le v^{i}(S)\le v^{u}(S)\le v^{p}(S) \end{aligned}$$

and

$$\begin{aligned} v^{o}(S)\le v^{i}(S)\le v^{c}(S)\le v^{p}(S). \end{aligned}$$

Notice that both $v^u(S)$ and $v^c(S)$ lie between $v^i(S)$ and $v^p(S).$ They are not related though.

As an implication, we have the following relations:

$$\begin{aligned} core(N,v^o) \subseteq core(N,v^i) \subseteq core(N,v^u) \subseteq core(N,v^p) \end{aligned}$$

and

$$\begin{aligned} core(N,v^o) \subseteq core(N,v^i) \subseteq core(N,v^c) \subseteq core(N,v^p). \end{aligned}$$

The core of $v^o$ is, in general, empty. The rest of the cores are always non-empty. This implies that any stable cost allocation for $v^i$ is stable in all the other games except $v^o$ and that we can always find such an allocation. As a counterpart, focusing on the core of $v^i$ rules out other relevant properties for the private game, such as strict monotonicity and strict ranking (Trudeau 2012).

5 Conclusions and future research

In this paper, we have reviewed the contribution of cooperative game theory to the problem of sharing the cost of mcstp between the agents. This contribution is, however, far from being closed, as there are numerous natural extensions, many of them deriving in balanced games, that have not been fully explored yet.

Some examples of extensions with non-empty core that have received some attention in the literature are the following:

• Minimum-cost spanning tree problems where some agents are indifferent (Trudeau 2014c), i.e., they can connect to the source (and get rewarded for it) if it helps others agents.

• Arborescences (Dutta and Mishra 2012; Bahel and Trudeau 2017), where the costs are not symmetric, i.e., $c_{ij} \ne c_{ji}$ in general.

• Minimum-cost spanning tree problems where the costs are uncertain and represented by closed intervals (Moretti et al. 2011).

• Minimum-cost spanning tree problems with multiple sources (Bergantiños and Navarro-Ramos 2019b, a; Bergantiños and Lorenzo 2020; Bergantiños et al. 2020) where agents want to be connected to several sources.

• Multi-period shorted path problems (Streekstra and Trudeau 2020) generalize mcstp to several periods, so that the agents should receive from the source different amount of services in different periods.

Some examples of extensions with empty core are the following:

• Steiner tree problems (Megiddo 1978), where agents can use some special (Steiner) nodes, if needed, to connect to the source. However, some special cases are always balanced (Skorin-Kapov 1995), as, for example, when all Steiner nodes belong to an optimal tree (Skorin-Kapov and Skorin-Kapov 2012).

• Multi-criteria minimum-cost spanning tree games (Fernández et al. 2004), where the cost of the arcs are vectors instead of numbers. In this extended class of games, the dominance core (where inequalities apply to at least some dimension) is non-empty, whereas the preference core (where inequalities apply to all dimensions) may be empty.

• Minimum-cost spanning tree problems with revenues (Bergantiños and Lorenzo 2008; Estévez-Fernández and Reijnierse 2014) are games where some agents have a limited budget, i.e., they connect if their assigned payment is not more than their connection revenue, or budget. These problems also generalize minimum-cost spanning tree problems where some agents are indifferent.

• k-Hop minimum-cost spanning tree problems (Bergantiños et al. 2012, 2014), where no agent can be more than k nodes away from the source.

• Directed acyclic graph games (Sziklai et al. 2016) arise from problems where some directions are unfeasible, so that the graph is directed, it has no cycles, and there always exists at least one path from each agent to the source. Moreover, some nodes are optional (Steiner nodes) and hence these problems also generalize Steiner tree problems.

• Minimum-cost spanning tree problems with priced nodes (Trudeau and Vidal-Puga 2017) generalize Steiner tree problems in the sense that each Steiner node has assigned a price, so that players should pay the price of the nodes they use.

In the other direction, some limited results have been obtained for some relevant subclasses of mcstp,  as, for example, information graph games, which are characterized by elementary mcstp. Kuipers (1993) studies the core and Núñez and Vidal-Puga (2020) study the stable sets (von Neumann and Morgenstern 1944) of these games. Since stable sets may exist for non-balanced games, this research is also a promising open field of study in games where the core is empty.