1 Introduction

In the additive manufacturing process known as selective laser melting (SLM), a moving high-power laser beam selectively melts the deposited powder material, which is solidified after the laser beam moves further scanning the required area, layer by layer, to build a three-dimensional solid component reflecting a preliminary prepared CAD model. The components currently manufactured by SLM can be made of different materials, both metallic and not metallic, such as ceramic and polymers [1,2,3,4]. The component is manufactured on a movable platform located in a chamber that adjusts its height equal to the thickness of the forming layer. The powder material is added from a powder feed device and spread with a roller or using other methods. Many of existing SLM processes using flat powder bed spreading techniques are only suitable for manufacturing single material components. Following rising industrial demands for advanced aero-engine components, dies, moulds, advanced biomedical implants among other applications, more advanced SLM techniques are also being intensively developed aiming for manufacturing multiple material components required for specific applications where different materials with different properties are required at different locations [5,6,7]. There are examples of processing 316L SS/C18400 and ALSi10Mg/C18400 copper alloys, Fe/Al-12Si dual material structure, and also silver/copper components using different SLM systems designed for deposition of at least two powder materials [8,9,10,11]. More sophisticated SLM methods were reported recently combining powder bed deposition, point by point multiple nozzles ultrasonic dry powder delivery, and point by point single layer powder removal to obtain multiple material fusion both within the same layer and across different layers at required locations to achieve real three-dimensional multi-material structures [12, 13].

The fast and growing development of the sophisticated additive manufacturing processes characterized by changes of state of matter, such as melting and solidification, brings current need in reliable predictive modelling. Further development of such technologies points to serious technical problems that have to be solved for the achievement of the reliable manufacturing process combining different materials and obtaining desirable properties of the final components. One of the ways to solve the technical problems is an appropriate application of physically based mathematical modelling that capable to support the necessary quantitative analysis and optimization of the whole manufacturing process. The mathematical models should be able to take into consideration changes of state of matter including melting and solidification among other physical phenomena. The lack of through process models allowing such optimization is the serious obstacle on the way towards reliable manufacturing and successful use of the produced components. For instance, the effect of powder compact conversion into a densified solid has not been properly considered in the existing mathematical models. The stress values derived from the solid model predictions are lower than those are from the powder one due to the smaller thermal gradients in the fabricated part [14, 15]. The degree of warpage is decreased when the material is changed from powder to solid during the SLM process. In many cases, research on SLM technologies is done by empirical investigations on individual materials, gaining expertise with proceeding examinations. Most of the current multiscale modelling approaches rely on combinations of several models operating either on different principles or on different scales. For instance, the application of cellular automata (CA) and discrete element (DE) methods allows for the simulation of the powder bed generation [16, 17]. Thermal processes can be modelled by using finite element (FE) while DE and Lattice Boltzmann methods (LBM) are applied to simulate liquid flows [18,19,20]. FE or CA may also apply for modelling of melting and solidification [21, 22]. Most of the combinations are significantly inhomogeneous or heterogeneous multiscale numerical approaches that would require complicated interfaces between different components. The interfaces almost eliminate the possibility to complete full-scale calculations within a single numerical model without running the individual modules independently and combining them afterwards. These difficulties present serious obstacles for the implementation of such numerical methods rising limitations and questioning the feasibility of such approaches. As yet, there is very little or no information available on robust holistic numerical models, systems or calculation platforms, which are capable of comprehensive modelling of the entire SLM process considering particle movement, heat exchange and transfer, melting, wetting, oxidation effects, free flow of melted material and solidification. While the above-mentioned individual physical processes can be developed by using different numerical methods discussed above, the main difficulties appear when a holistic model of the whole SLM process is considered. Development of simulation techniques based entirely on one or two homogeneous methods will allow for both modelling very complex multi-physical phenomena accompanying the manufacturing process and elimination of the complicated interfaces.

Authors in the first article have discussed the idea of such a modelling approach based on the coupling of CA and LBM [23]. Four main stages can be distinguished in a powder bed fusion technology known as SLM. These for stages are powder material delivery, heating and melting of the deposited powder, free or directed flow of the material in a liquid or semi-liquid state, and also cooling and solidification [24]. Heat transfer accompanies the last three stages between solid, liquid and gas phases and by heat conduction. The diagram shown in the top of Fig. 1 can represent the SLM process and describes the following sequence of the basic stages: powder deposition, pause, laser treatment, pause that are repeated multiple times throughout the technological process. As can be seen in the bottom of Fig. 1, corresponding mathematical models cannot always exactly represent the mentioned technological stages. Instead, the appropriate physically based models consider key physical processes taking place during the SLM. The middle block of the diagram in Fig. 1 illustrates the following five main associated physical processes:

  • Particles movement during powder bed generation (PBG);

  • Laser beam heat exchange and transfer (LBHE&T);

  • Melting (M);

  • Free flow of melted material—liquid flow (LF);

  • Solidification (S).

Fig. 1
figure 1

Block diagram of SLS/SLM technological process including associated physical processes and models

Full size image

The mentioned physical processes can take place in a sequence or simultaneously. The associated individual mathematical models can require additional physical events and can be more complicated. The results of the powder bed generation stage, where only spherical particles with different size distributions are considered, have been presented elsewhere [16]. However, many aspects of the integrated numerical approach were omitted for further consideration and analysis.

In this study, the following four models are considered:

  • PBG model extended to random shape particles based on CA;

  • Heat exchange and transfer (HE&T) model including laser treatment based on LBM;

  • Phase transition model (solid–liquid transformation) based on LBM and CA;

  • Model of fluid flow with free surface flow based on LBM.

The present paper addresses development of multiphysics simulation approach to SLM modelling based entirely on two homogeneous numerical methods, such as CA and LBM, dealing mainly with energy transfer problems including solid–liquid phase transformation. The following physical events are taken into consideration: powder bed deposition, laser energy absorption and heating of the powder bed by the moving laser beam leading to powder melting, fluid flow in the melted pool and flow through partly or not melted materials and solidification. The mentioned events can occur in sequence or simultaneously. It is important, because the holistic numerical model is generic and can be applied to different multi-material additive manufacturing processes where energy transfer including solid–liquid phase transformation is essential. The presented results concern melting and solidification of the powder bed including free surface flow, wettability and surface tension among other associated phenomena. The discussed models operate in the common domain allowing for linking them into a more complex holistic numerical model with the possibility to complete full-scale calculations within the integrated model.

2 LBM-based computational fluid dynamics models

The central element of the proposed holistic model is fluid flow. For the simulation, fluid flow can be described by incompressible Navier–Stokes equations. Application of the traditional simulation methods, such as FE or finite difference (FD) methods, are inherently fraught with difficulties, particularly dealing with advection component. Lattice Gas Automaton (LGA) can be considered as an alternative numerical solution for such simulations [25,26,27]. LGA operates in discrete space and time when particles move along the lines on a regular lattice and can collide with each other on each lattice site or a cell according to appropriate rules. The first LGA models were referenced as a class of cellular automata (CA). Those models did not take into consideration some physical laws and were not initially accurate [25]. Then later, the simulation technique based on lattice Boltzmann equation (LBE) was derived from the LGA [28, 29] followed by the development of the lattice Boltzmann method (LBM) [30, 31]. At present, the LBM is a useful tool for multiscale modelling and considered as one of the most powerful numerical methods for solving engineering problems of modern computational fluid dynamics (CFD). Although LBM is a relatively new method for CFD, it has already been proved as a stable, accurate and computationally efficient numerical method that can be particularly effective for considering problems related to complex and multiphase media [32,33,34]. LBM can be applied by modelling flows in non-ideal, binary, and ternary complex fluids, micro-fluids, free-surface flows and flows in porous media achieving significant success in simulations of fluid flows and associated transport phenomena [34, 35]. The method allows for the modelling of laminar and turbulent flows taking into consideration diffusion and thermal problems. It is applicable for simulation of heat transfer in multicomponent or multiphase systems in heterogeneous media [36,37,38]. Several models of liquid–vapour phase transitions based on LBM models have also been developed recently [39,40,41,42].

3 CA-LBM model of energy transfer

The absorbed by the powder bed thermal energy initially spreads by heat diffusion [43, 44]. A solid–liquid phase transformation starts when the temperature in the affected zone exceeds the solidus temperature. After consuming latent heat, when the volume of liquid phase exceeds a threshold, the solid particulate material exhibits signs of liquid behaviour, where heat transport is described by diffusion or convection including radiation and convection heat transfer from the liquid surface. The excess heat in the area of the liquid phase is dissipated by heat conduction into the deeper layers of the powder bed leading to re-solidification of the melt pool. Different aspects and fragments of the combined CA-LBM model concerning simulation of the mentioned above stages of energy transfer during the process are discussed beneath.

The flowchart of the algorithm for the numerical calculation of energy transfer within the representative domain using CA-LBM is schematically presented in Fig. 2. A regular lattice is applied to the modelling space. In LBM, intersections are treated as nodes or sites. While in CA, they are considered as cells. Initially, the macroscopic variables, such as density, momentum, temperature, and others, are calculated based on the initially assumed input distribution functions. Then, the macroscopic variables are used for calculation of the equilibrium distribution functions in each site. The input and equilibrium distribution functions define output distribution functions in the block ‘Collision’. In the block ‘Streaming’, each component of the output distribution functions is transferred directly to the neighbouring site according to the appropriate direction and velocity. Finally, the boundary conditions are taken into account. For both hydrodynamic and thermal tasks, the same velocity model D2Q9 is applied (b = bT = 8), where b and bT are numbers of vectors in the velocity model, or components of the distribution function, for flow and temperature, respectively [45, 46].

Fig. 2
figure 2

Schematic representation of the algorithm for CA-LBM-based model

Full size image

Different materials in a different state of matter can fill the representative space. It is easier to perform the relevant calculations when the state of matter is explicitly defined by an appropriate state variable. Then, the state variable should be attached to every cell. The following three fundamental states of matter are considered in the model: solid (S), liquid (L) and gas (G). Contacts of the different materials or the same material in the different state of matter are considered as boundaries with the appropriate mechanical and thermal properties. The boundaries divide the whole space into different subdomains, which are treated as homogeneous. All interactions between domains take place at the boundaries. The boundaries can move and do not remain in the same place. The cells can be partly filled with material(s) in different states, because every site or cell represents some finite volume. Therefore, mixed states are introduced. The developed state diagram is shown in Fig. 3. Solid (S), liquid (L), and gas (G) are inside main subdomains, while liquid–gas (LG), solid–gas (SG), solid–liquid (SL), and solid–liquid–gas (SLG) interfaces represent boundaries. Moreover, there should not be direct contacts between S, L and G but only through an interface (boundary). The cells containing gas are illustrated as white, or they have a white segment. Correspondingly, the cells containing liquid are shown as blue while those containing solid material are highlighted as grey.

Fig. 3
figure 3

The state diagram considered in the model

Full size image

The presented state diagram includes three kinds of state changes. Arrows in different colours mark them. The blue arrows represent a hydrodynamic component, i.e. flow of a liquid with a free surface. There are two following transitions here: L–LG–G and SL–SLG–SG. The first transition represents the movement of the liquid under the surface tension, gravity and inertia, etc. While the second one, besides, takes into account wettability. The submodel of the fluid flow with the free surface represents the transitions. This part of the state diagram is completely considered in the model. The second kind of transition is shown in the state diagram by red arrows. They represent phase transitions, in other words, changes in the state of matter. At this stage, the only transition assumed in the model is a solid–liquid transition with the presence of gas, such as SG–SLG–LG; and without one, S–SL–L. They are described by the submodel of the phase transition (melting-solidification). The third kind of transition presented in the state diagram is connected with the movement of the solid phase. They are represented by grey arrows and will be considered in the further investigation on an extended PBG model.

3.1 Model of fluid flow with free surface

The whole holistic model is developed on the principles of the LBM with elements of CA [47, 48]. The LBM is a discrete numerical method applied for the solution of the Boltzmann transport equation:

$$ \frac{\partial f}{{\partial t}} + \frac{\partial f}{{\partial x}}{\varvec{e}} + \frac{{\varvec{F}}}{m}\frac{\partial f}{{\partial e}} = \Omega $$
(1)

where f(x, v, t) is the particles distribution function, i.e. the number of particles of mass m at time t positioned between x and x + dx which have velocities between v and v + dv, e is the phase space variable—velocity (vector), x is the phase space variable-coordinates, F is the external force (e.g. gravity), Ω is the collision operator. The particle velocity space can be reduced to a set of discrete velocities {ei, i = 0,…,b} and to the lattice on which the calculations are carried out. The equation is approximated along characteristic velocity vectors using the trapezoidal rule in space and explicit Euler scheme for the time derivative becoming Lattice Boltzmann Equation (LBE):

$$ f_{i} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t + \Delta t} \right) = f_{i} \left( {{\varvec{x}},t} \right) + \Omega_{i} + F_{i} $$
(2)

where the subscript i is ith component of the velocity model. By using Bhatnagar–Gross–Krook (BGK) collision operator Ω [49], Eq. (2) can be rewritten in the following form:

$$ f_{i} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t + \Delta t} \right) = f_{i} \left( {{\varvec{x}},t} \right) + \frac{\Delta t}{\tau }\left[ {f_{i}^{{{\text{eq}}}} - f_{i} \left( {{\varvec{x}},t} \right)} \right] + F_{i} $$
(3)

where fieq = \(f_{i}^{{{\text{eq}}}} \left( {{\mathbf{x}},t} \right) \equiv f_{i}^{{{\text{eq}}}} \left( {\rho ,{\mathbf{v}}} \right)\) is the equilibrium distribution function of ith discrete velocity, ρ is the macroscopic fluid density and τ is the relaxation time for velocity problem. Equation (3) is solved in two stages, collision (4) and streaming (5), according to the algorithm presented in Fig. 2:

$$ f_{i}^{{{\text{out}}}} = f_{i}^{{{\text{in}}}} + \Omega_{i} = f_{i}^{{{\text{in}}}} + \frac{\Delta t}{\tau }\left[ {f_{i}^{{{\text{eq}}}} - f_{i}^{{{\text{in}}}} } \right] $$
(4)
$$ f_{i}^{{{\text{in}}}} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t + \Delta t} \right) = f_{i}^{{{\text{out}}}} \left( {{\varvec{x}},t} \right) $$
(5)

where the superscripts in and out are input and output stream, respectively. The equilibrium distribution function appearing in (4) is calculated according to the following:

$$ f_{i}^{{{\text{eq}}}} = w_{i} \rho \left[ {1 + 3{\varvec{e}}_{i} \cdot {\varvec{v}} + 4.5\left( {{\varvec{e}}_{i} \cdot {\varvec{v}}} \right)^{2} - 1.5{\varvec{v}} \cdot {\varvec{v}}} \right] $$
(6)

where wi are the weights for calculation of the function. The macroscopic density ρ and momentum ρv in a cell are the 0th and 1st moments of the distribution functions:

$$ \rho = \mathop \sum \limits_{i = 0}^{b} f_{i} $$
(7)
$$ \rho {\varvec{v}} = \mathop \sum \limits_{i = 0}^{b} f_{i} {\varvec{e}}_{i} $$
(8)

where the macroscopic velocity is calculated as v = ρv/ρ. Equations (1)–(8) are only applied for the liquid domain. It is assumed in the model that the distribution functions are unavailable outside the liquid domain (fluid). The assumption means the cells on the boundary do not receive appropriate components of distribution functions fi outside from the external cells (solid, obstacles or gas). The main goal of the boundary condition algorithm is a reconstruction of the unavailable components for these cells.

The oldest but still the most widely used boundary condition for solid or obstacles in LBM is the bounce-back rule. The reversion of the velocity takes place on the boundary nodes x in such node-based implementation:

$$ f_{i} \left( {{\varvec{x}} + {\varvec{e}}_{{\varvec{i}}} ,t + \Delta t} \right) = f_{{\overline{i}}} \left( {{\varvec{x}},t} \right) $$
(9)

where ī defines reverse direction: eī = − ei. The reconstruction of the missing distribution functions for the liquid–gas interface (LG and SLG) can be made with the use of Eq. [50]:

$$ f_{i} \left( {{\varvec{x}} - {\varvec{e}}_{i} ,t} \right) = f_{i}^{{{\text{eq}}}} \left( {\rho_{g} ,{\varvec{v}}} \right) + f_{{\overline{i}}}^{{{\text{eq}}}} \left( {\rho_{g} ,{\varvec{v}}} \right) - f_{{\overline{i}}} \left( {{\varvec{x}},t} \right) $$
(10)

where v is the velocity of a liquid on the boundary.

The gas density is influenced by the gas pressure pg and the surface curvature κ, which depends on the local shape of the surface and surface tension σs:

$$ \rho_{g} = 3p_{g} + 6\sigma_{s} \kappa $$
(11)

where ρg is the gas density. The mass exchange Δmi between an LG cell and its neighbouring cell depends on the type of the neighbouring cell. No mass transfer is possible between an interface and gas/obstacle (solid) cells:

$$ \Delta m_{i} = 0 $$
(12)

The mass transfer between fluid and interface cells is the difference between flows inward fī and outward fi the interface cell:

$$ \Delta m_{i} = f_{{\overline{i}}} \left( {{\varvec{x}},t} \right) - f_{i} \left( {{\varvec{x}} + {\varvec{e}}_{{\varvec{i}}} ,t} \right) $$
(13)

Additionally, the mass transfer between two interface cells takes into consideration their average liquid fractions φ:

$$ \Delta m_{i} = 0.5\left[ {f_{{\overline{i}}} \left( {{\varvec{x}},t} \right) - f_{i} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t} \right)} \right]\left[ {\varphi \left( {{\varvec{x}},t} \right) + \varphi \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t} \right)} \right] $$
(14)

After the mass exchange, the new liquid fraction for interface cells is calculated according to the expression: φ = m/ρ. A vector normal to the surface and curvature κ is calculated as described elsewhere [51, 52].

3.2 Thermal model

The distribution function gi for the thermal problem is expressed in the following form:

$$ g_{i} \left( {{\varvec{x}} + {\mathbf{e}}_{{\text{i}}} ,t + \Delta t} \right) = g_{i} \left( {{\varvec{x}},t} \right) + \frac{\Delta t}{{\tau_{T} }}\left[ {g_{i}^{{{\text{eq}}}} \left( {{\varvec{x}},t} \right) - g_{i} \left( {{\varvec{x}},t} \right)} \right] + S_{i} $$
(15)

where S is the heat source/sink and the τT is the relaxation time concerning heat conduction. The temperature T and the equilibrium distribution function \(g_{i}^{{{\text{eq}}}}\) are expressed as the following:

$$ T = \mathop \sum \limits_{i = 0}^{{b_{T} }} g_{i} $$
(16)
$$ g_{i}^{{{\text{eq}}}} = w_{i} T\left[ {1 + 3{\mathbf{e}}_{i} \cdot {\varvec{v}}} \right] $$
(17)

The energy exchange (heat transfer) on the boundaries depends on the type of the neighbouring cell. There are three kinds of boundary conditions considered in the model. The first kind is the Dirichlet boundary condition that specifies the value of the temperature, for example, the constant temperature on the boundary Tb (mainly on the boundary of the considered domain). This boundary condition is applied in the model using the anti-bounce-back scheme:

$$ g_{{\overline{i}}} \left( {{\varvec{x}}_{b} ,t} \right) = - g_{i} \left( {{\varvec{x}}_{b} ,t} \right) + 2w_{i} T_{b} $$
(18)

where \(g_{i}\) is the value after the collision. The second kind of the boundary conditions is Neumann boundary condition that specifies a normal gradient, or a normal flux, on the boundary. The only one variant of such conditions is considered in the model, namely an adiabatic (isolated) boundary, where the flux is equal to zero. Then, the bounce-back rule is applied:

$$ g_{i} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t + \Delta t} \right) = g_{{\overline{i}}} \left( {{\varvec{x}},t} \right) $$
(19)

The more important is the boundary condition of the third kind, i.e. Robin boundary condition. This condition prescribes the dependence of the heat flux due to conduction at the surface of a body based on temperatures of both the surface of the body and the surrounding medium. To obtain such a condition, the equation for streaming without boundaries is used:

$$ g_{i} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t + \Delta t} \right) = g_{i} \left( {{\varvec{x}},t} \right) $$
(20)

Then, it is combined with the adiabatic boundary condition (19) using the heat transfer coefficient h, which depends on both the cell size Δx and the time step Δt:

$$ g_{i} \left( {{\varvec{x}} + {\varvec{e}}_{i} ,t + \Delta t} \right) = hg_{i} \left( {{\varvec{x}},t} \right) + \left( {1 - h} \right)g_{{\overline{i}}} \left( {{\varvec{x}},t} \right) $$
(21)

The method applied for phase transition modelling has been previously described in details [23].

4 Case studies

In this section, the results concerning different aspects of the modelling approach are discussed. They cover key stages of the considered powder bed fusion SLM process. The presented results are mainly qualitative and are intended to stimulate and induce new contributions. The case studies allow for evaluation of the quality and correctness of the solution. Quantitative adaptation and complete model verification will be done gradually after gathering results of comparison with reliable data and using the developed simulation code for modelling of different aspects concerning the specific SLM processes.

4.1 Liquid flow with free surface

The changing shape of a liquid drop from rectangular to round predicted under the effect of surface tension is shown in Fig. 4 illustrating the initial (a), transient (b) and final (c) stages. Figure 5 shows the predicted shape of the liquid surface considering several factors, namely surface tension, gravity and wettability showing liquid drops on a horizontal surface (Fig. 5a–c) and a liquid in the container with vertical walls (Fig. 5d and e). Wettability is related to the attempt of a solid to form a common interface with a liquid that comes into contact with the solid and can be measured by the contact angle α. The corresponding values of cos α presented in Fig. 5 are equal to − 0.5 (Fig. 5a, d); 0 (Fig. 5b), and 0.5 (Fig. 5c, e). Figure 6 illustrates the next stages of the simulation, such as liquid flow along with a more complex pattern compared with an obstacle-free flow. The examples of such modelling results presented in Fig. 6 demonstrate the effects of surface tension, gravity and wettability on the flow of a liquid into a container.

Fig. 4
figure 4

Modelling results illustrating the influence of surface tension on the shape of a drop of liquid: a—initial, b—transient, c—final

Full size image
Fig. 5
figure 5

Modelling results related to the influence of wettability on the shape of liquid surface illustrating the shape of the liquid drops on the horizontal surface with lyophobic (a), neutral (b) and lyophilic (c) surface properties as well as the shape of the liquid surface in contact with lyophobic (d) and lyophilic (e) vertical walls

Full size image
Fig. 6
figure 6

Simulation results illustrating three consecutive stages of the flow of a liquid into a container

Full size image

4.2 Phase transition

The next stage is a consideration of the applicability of the LBM-based model for thermal applications. With this aim, a solid–liquid interface was implemented into the model. The interface allows for the simulation of the phase transition and changes of the state of matter considering the enthalpy of transition as the enthalpy change accompanying the phase transition. The thermal model is connected with the previously developed hydrodynamic model. It means that the liquid phase model takes into account surface tension, gravity, and wettability during the simulation. Additionally, the hydrodynamic part of the model includes into consideration convection induced by temperature difference in the various areas of the liquid.

To illustrate the ability of the method, the following two cases are presented in Fig. 7. The first case is related to modelling of the melting sample assuming convection without consideration of heat transfer between gas and liquid (Fig. 7a) while the second one represents the simulation results obtained assuming convection with such heat transfer (Fig. 7b). Each case is represented by a set of four images. In each set, the first image (top left) shows the temperature distribution with white and black isotherms. The temperature distribution within the liquid is represented using warm colours while the temperature of the solid phase is shown using a light blue colour. The black isotherm indicates the transition temperature. The second picture (top right) shows velocity distribution within the liquid phase, while the third and fourth pictures present horizontal (bottom left) and vertical (bottom right) components of the velocity. The temperature of the left wall of the sample is constant and is maintained above the transition temperature, while the right wall has a temperature below the transition temperature. It should be mentioned that the calculations based on LBM models were performed using dimensionless variables. The length of the cells, the average density and temperature, the maximum macroscale velocity, the time step and the discrete characteristic velocities have all been assumed to be equal to 1. Figure 7 clearly illustrates the effect of convection on the boundary shape between liquid and solid phases, and also the influence of the boundary conditions on the simulation results. Point 1.0 of the temperature scale corresponds to the melting point of the material. Thus, the presented temperature range is between 0.9 and 1.1. The dimensionless temperature data can be recalculated to give real temperature values. For example, assuming the melting temperature presented in Fig. 7 equals to Tm = 0 °C, the temperature of the left wall will be equal to Tl = 40 °C and the right wall temperature will be Tr =  − 10 °C. In these calculations, the basic dimensionless velocity in the modelled material was assumed to be equal to the velocity of sound, vs = 1/3.

Fig. 7
figure 7

Modelling results related to melting considering convection without (a) and with (b) heat transfer between gas and liquid illustrating distribution of the temperature (top left) and velocity (top right) within liquid as well as horizontal (bottom left) and vertical (bottom right) components of the velocity

Full size image

The results based on the application of CA-LBM related to phase transition are presented in Fig. 8. A material in a solid-state is heated by hot gas with a temperature above its melting temperature. The molten material flows down and is collected into small drops. The drops gradually grow and come off the surface reaching a critical size. They fall on the bottom surface of a container. The results illustrate two cases where the temperature of the bottom surface of the container is above and below the transition temperature (Fig. 8a and b). The solidification of the molten material on the bottom surface of the container is visible in the second case.

Fig. 8
figure 8

Modelling results illustrating melting material falling on the surface without (a) and followed by (b) subsequent solidification

Full size image

4.3 CA-LBM model of laser heating

In the SLM process, a laser beam scans the powder bed as a source of heat coursing powder bed radiation, light-absorbing, scattering, dispersion, and diffraction of light. The interaction between the powder bed and the laser beam is very complicated and its understanding is key to correct description of the laser energy penetration and powder bed absorption.

The model of light propagation applied in this work combines elements of both LBM and CA. The algorithm similar to particle tracing methods for visualization and computer graphics is used in the modelling approach. It is assumed that the laser radiation transmits light energy in gas as straight beam without scattering. Striking the surface of the liquid or solid phase, the energy is divided into the following three parts: reflected, absorbed, and transmitted. If the material is opaque, the beam is not transmitted and the radiation is reflected and absorbed. The reflected energy is not considered further in the present version of the model. The light energy penetrating the material is subjected to scattering and absorption. Both transmission and absorption depend on a variety of chemical and physical characteristics of the powder bed material and also on the wavelength of the incident radiation. In the model, the laser energy entering the cell is divided into the following parts. The absorbed part of the energy is transferred into heat and used in the holistic model as a heat source S, Eq. (15). The second part is considered as output energy, which is defined by a transferred distribution function and describes a fraction of the output light energy depending on the angle between directions of entering and exiting beams. It is assumed in the model that the material can be opaque, translucent or transparent. For instance, gas is assumed as transparent, metals are opaque and bio-active glasses are translucent materials. In terms of bio-active glasses, the coefficient of material transparency depends on both the state of matter and the temperature, from low values for the cold solid to high values related to the hot molten bio-active glass. Some of the simulation results are presented in Figs. 9, 10, 11, where the intensity of light or the power of the light transferred per unit area, is presented by the intensity of green colour. The heat source, as an absorbed part of the light energy, is shown by pink-red colour. Following the colour scheme, the point source of light energy is applied and shown in Figs. 9 and 10 as a point of red colour in the first two results of the simulation. The solid material is shown in the figures as the grey area while the liquid one is presented as the blue one. In Fig. 11, the source of light energy is a laser beam striking and penetrating material. In the current calculations using LBM, the maximal intensity of the light energy is assumed to be equal to 1.0 at the point source (Figs. 9 and 10). The maximum is also observed in the middle part of the area within the material affected by the laser beam (Fig. 11). In the first simulation (Fig. 9), the material is melted and is flowing down as the assumed temperature conditions do not allow for solidification. The second example differs from the first one by the temperature, which allowed for the material solidification (Fig. 10). The simulation result presented in Fig. 11 illustrates melting by the laser beam. The two following areas of more intensive heat absorption can be noticed. The first area is located near the liquid surface, where the maximum energy flux density is observed, despite high transparency of the molten material. The second area is seen near the phase transition boundary accompanied by a decrease in material transparency. Figure 12 illustrates both the temperature and state of mater change during melting by a laser beam. Initially, the temperature of the whole material is slightly below the melting point (blue colour) while the ambient temperature is somewhat above the melting temperature (pink colour) (Fig. 12a). The absorbed energy for this particular case is shown in Fig. 12c.

Fig. 9
figure 9

Simulation results of melting by the light energy

Full size image
Fig. 10
figure 10

Simulation results of melting by the light energy followed by flow and solidification

Full size image
Fig. 11
figure 11

Simulation results of melting by a laser beam illustrating distribution of the absorbed energy

Full size image
Fig. 12
figure 12

Simulation results related to melting by a laser beam illustrating: a initial temperature distribution, b state of matter change and c intensity of laser beam and heat transfer

Full size image

4.4 SLM process simulation

The results presented above demonstrate certain possibilities and benefits of the holistic homogeneous approach to modelling of the entire SLM process characterized by melting and solidification of the deposited particulate material. Figure 13 presents the examples of such simulation for two consecutive time moments of the process when the vertically orientated laser beam moves from the left to the right of the domain showing two layers of the deposited spherical particles. The particles have varied transparency. They are assumed almost opaque in the solid-state and much more transparent when the state is changed from solid to liquid. The transparency is changed near the transformation temperature. The colour scheme is the same as above. The laser power was assumed twice as higher for the second case, presented in Fig. 13c, d, comparing with the first simulation case (Fig. 13a, b). It can be seen that the amount of melted material is very sensitive to the applied laser power. The size of the melted pool, its depth and length, depends on the power of the laser beam. The modelling space was 160 × 100 cells or nodes. A single simulation case lasted about 3 h using PC with Intel Core i7-3930 K and CPU with sequential code. Several sub-models have been recoded for parallel computations on GPU with CUDA technology using the graphic card GeForce 1060 with 1280 CUDA cores. Application of such parallel calculations allows for at least 100 times acceleration. The simulations do not require complicated interfaces between different sub-models and allow for continuous simulation of the whole processing cycle.

Fig. 13
figure 13

Simulation results illustrating a single SLM cycle predicted for two different laser power and time moments

Full size image

5 Model verifications

The metallic and non-metallic materials for SLM processes are supplied in powder form. Particle sizes play an important role in the thermal properties of the powder bed. Moreover, its thermal properties strongly depend on the packing density of the deposited particles, particularly for the cases when not only single-sized particles but also a mixture of different powders with different particle sizes and shapes is deposited depending on the specific SLM process requirements (Fig. 14). The density of the powder layers is a key factor influencing the performance of SLM processes. It is recognized that quantification of the packing density and its correlation to process outcomes is one of the important challenges towards the improvement of process reliability [53]. The verification of all different predictive aspects of the holistic model is a relatively long and time-consuming process. This process has started from verification of the predictive abilities of powder bed formation including effects of particle size distributions, the speed and sequence of powder delivery during deposition indicating improvement of the prediction accuracy concerning the powder bed packing density and morphology [16]. The chosen from the powder feedstock 14,523 particles with measured size distribution using X-ray Computer Tomography technique (Fig. 15a) were mixed and randomly deposited across the cylinder area of 1.82 mm diameter. The height of the cylinder filled with particles being inversely proportional to the deposit density was used for comparison showing only 3.2% discrepancy between the experimental and predicted results (Fig. 15b and c). Since CA and LBM are homogeneous numerical techniques, the numerical module developed for powder bed generation based on CA has been currently linked with the developed LBM module.

Fig. 14
figure 14

Simulation results illustrating a cross section of the generated powder bed predicted of solid granular particles

Full size image
Fig. 15
figure 15

Size distribution of solid spherical particles (a), X-ray Computer Tomography image (b) and the corresponding image of the powder deposit predicted within the same diameter cylinder (c) [after 25]

Full size image

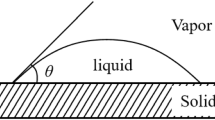
Contact angle hysteresis between advancing and receding angles is a well-known phenomenon in physics [54]. It allows for a liquid drop remains unmovable on the inclined surface. The drop changes its shape to compensate for an external or internal force. Hysteresis is defined by the range of advanced θA and receding θR angles that cannot exceed some critical values. In the developed model, the contact angles can be set directly. The angles are the same on both sides of the drop (θA = θR = θ0) for a state without force components parallel to the surface line. In such case, θ0 is defined by the ability of a liquid to maintain contact with the solid surface, i.e. by wettability, being lyophobic, lyophilic or neutral. The angles are changed under the applied forces on the same value: θA = θ0 + Δθ, θR = θ0 − Δθ, where Δθ is the contact angle. Introduction of the different angles θA ≠ θR influences deformation of the drop shape redistributing the effect of the surface tension. The drop starts moving when a horizontal component of the force is close to zero. The horizontal component Fh is increasing during such movement until the drop stops moving (Fh = Fr) or starts moving in the opposite direction (Fh = Fl), where Fr and Fl are horizontal components of the force when drop starts moving right and left, respectively. The values of Fr and Fl are not the same in the model (Fr ≠ Fl). There is friction at the solid–liquid interface due to the bounce-back rule at the interface causing some small hysteresis, about 3–5°, which is useful for a stable solution.

Eotvos (Eötvös) Eo or Bond Bo dimensionless number stating the importance of the gravitational forces compared to the surface tension forces. The number is used to characterize the shape of the moving drops and is given by equation [54]:

$$ {\text{Eo}} = {\text{Bo}} = \frac{{\Delta \rho gL^{2} }}{\sigma } $$
(22)

where Δρ is the difference in density between two phases, g is the gravitational acceleration and σ is the surface tension. The gas density can be neglected for calculation of Δρ. The drop radius can be assumed as the characteristic length L. The balance between gravity and tension defines a change of the contact angle:

$$ {\text{sin}}\Delta \theta = \frac{\rho gA}{{2\sigma }}{\text{sin}}\alpha = \frac{{\pi {\text{Eo}} }}{4} {\text{sin}}\alpha$$
(23)

where A is the area of the two-dimensional drop and α is the inclination angle. For verification purposes, several variants with different Eotvos numbers were considered in the modelling. The drop area A, the contact angle Δθ, and the gravitational acceleration g were varied to change the Eotvos number Eo. Two critical values of the force component (gr = Fr and gl = Fl) were determined during the simulations. The results are shown in Fig. 16. The squares correspondingly represent gr and the circles distinguish gl values that have been obtained using the developed model. The straight line illustrates the theoretical dependence according to Eq. (23). The presented simulation results are in good agreement with the theoretical dependency confirming that the developed numerical model provides an acceptable degree of accuracy.

Fig. 16
figure 16

The dependency between inclination α and contact angles Δθ predicted using Eq. (23) (straight line) and the numerical model

Full size image

Following the simulations described in Sect. 4.1 (Fig. 6) and the procedure discussed elsewhere [55], the deformation of a drop placed on a slowly inclined wall has been predicted. Initially, the 2D model of the drop was applied on the horizontally placed wall. Then, after the equilibrium between surface tension, gravity, and the assumed contact angle condition at the wall is achieved, the wall is inclined gradually ensuring that the shape of the drop adopts to the changes in the wall position following a quasi-static evolution. In other words, the capillarity times of the liquid are significantly less than a characteristic time of such a process. The drop starts sliding when the balance between gravity and capillarity is achieved. Two drop sizes were considered in the simulation. The results are presented in Fig. 17a and b, where all the drop surface normals are shown in the first picture while the consecutive ones include only normals near the contact with the wall. Assuming the same hysteresis, the critical inclination angles for the bigger and smaller drops were predicted to be 32° and 56° correspondingly. It can also be seen that for the bigger drop the contact angle increases faster than for the smaller one.

Fig. 17
figure 17

The bigger and smaller liquid drops predicted on the inclined wall for the different inclination angles correspondingly: a—0, 11, 22 and 31°; b—0, 11, 22, 31, 39, 45 and 55°

Full size image

6 Further development

The model of powder bed generation (PBG) based on CA has been discussed and presented earlier [16]. The PBG model has been combined with the models developed in this study for simulation of the whole SLM process to prove the concept of the proposed multiphysics simulation approach. The significant part of further development is a validation of the completely integrated model against observations from the relevant physical systems. The most difficult part seems to be testing of the model structure making quantitative comparisons with empirical results, or numerical results obtained by applying other methods, to make sure that the modelled features are not spurious leading to imperfect predictions. Although the presented modelling results have been validated at each step of the current development against simple analytical solutions showing their lattice independence, further validation using the relevant physical systems has yet to be done. Ideally, the model assumptions, structure, parameters and predictions should be tested and validated against experimental observations in the laboratory or industrial conditions opening further stages of the investigation. Among the reasons, leading to imperfect predictions of such complicated physical systems can also be natural variability in the system and its environment. Such variability has to be distinguished from the effects of important factors that have been ignored or the errors, which are attributable to misspecification of the developed numerical models.

7 Conclusions

A novel approach to numerical modelling of multi-material SLM processes characterized by melting and solidification of the deposited particulate material is presented. The multiphysics simulation is based entirely on two homogeneous methods, CA and LBM. Such combination allows for efficient modelling of multi-physical phenomena accompanying the manufacturing process, but at the same time, it eliminates the complicated interfaces between different components of the model. Operating in the common domain, the model components are linked into a complex holistic numerical model with the possibility to complete the full-scale calculations within the single integrated model. Such full-scale modelling focusing on energy transfer problems including solid–liquid phase transformation has been executed for the first time to prove the concept. It differs the proposed approach from the existing multiscale models based on heterogeneous numerical methods, where the possibility to simulate the entire SLM process within a single numerical model is almost eliminated without running the individual modules independently and combining them afterwards.

Considering physical processes in this study, which can occur in sequence or simultaneously, include powder bed deposition, laser energy absorption, heating of the powder bed by the moving laser beam leading to powder melting, fluid flow in the melted pool, flow through partly or not melted materials and solidification. The presented integrated holistic model consists of a combination of four models linked together for simulation of the mentioned-above physical phenomena within the proposed framework. Among them are powder bed generation, heat exchange and transfer, phase transition (solid–liquid transformation) and fluid flow with free surface models. The possibilities and benefits of the proposed approach are demonstrated through a series of benchmark cases, as well as model verifications dealing mainly with melting and solidification of the deposited powder bed including the free surface flow, wettability and surface tension. The approach is generic and can be applied to different multi-material SLM processes, where energy transfer including solid–liquid phase transformation is essential. Some aspects of the obtained modelling results have been validated showing their lattice independence and good agreement with available experimental results and theoretical predictions. More work should be done, including both modelling and experimental trials, to achieve reliable predictability of the entire integrated model to specific SLM processes. The significant part of this work is validation against observations from the relevant physical systems in the laboratory or industrial conditions. Nevertheless, the development shows a great potential of the numerical approach in terms of becoming a trustworthiness attribute of the new technology.