Homotopy analysis Shehu transform method for solving fuzzy differential equations of fractional and integer order derivatives

Abstract

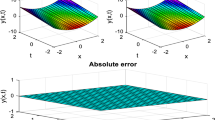
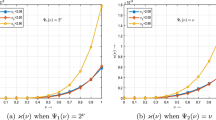
In this paper, we propose the fuzzy Shehu transform method (FSTM) using Zadeh’s decomposition theorem and fuzzy Riemann integral of real-valued functions on finite intervals. As an alternative to standard fuzzy Laplace transform and the fuzzy Sumudu integral transform, we established some potential useful (new or known) properties of the FSTM and validate their applications. Furthermore, the FSTM is coupled with the well-known homotopy analysis method to obtain the approximate and exact solutions of fuzzy differential equations of integer and non-integer order derivatives. The convergence analysis and the error analysis of the suggested technique are provided and supported by graphical solutions. Comparison of the numerical simulations of exact and approximate solutions of two fuzzy fractional partial differential equations are tabulated to further justify the reliability and efficiency of the proposed method.

Appendix

In this section, we proof some basic properties of fuzzy Shehu transform.

Property 1

Linearity property. Suppose $\tilde{f}(t)$ and $\tilde{g}(t)$ be continuous fuzzy-valued functions, and $\vartheta$ and $\beta$ be constants, and then:

$$\begin{aligned} \mathbf{S} \left[ \vartheta \odot \tilde{f}(t)\oplus \beta \odot \tilde{g}(t)\right] =\vartheta \odot \mathbf{S} \left[ \tilde{f}(t)\right] \oplus \beta \odot \mathbf{S} \left[ \tilde{g}(t)\right] . \end{aligned}$$

(107)

Proof

Let $r\in [0,1]$ be arbitrary fixed. Then, using Eq. (21), we have:

$$\begin{aligned}&\mathbf{S} \left[ \vartheta \odot \tilde{f}(t)\oplus \beta \odot \tilde{g}(t)\right] \\&\quad =\int _{0}^{\infty }(\vartheta \odot \tilde{f}(t)\oplus \beta \odot \tilde{g}(t))\odot \exp \left( \frac{-p}{q}t\right) \mathrm{d}t\\&\quad =\int _{0}^{\infty }\vartheta \odot \tilde{f}(t)\odot \exp \left( \frac{-p}{q}t\right) \mathrm{d}t\oplus \int _{0}^{\infty }\beta \odot \tilde{g}(t)\odot \exp \left( \frac{-p}{q}t\right) \mathrm{d}t\\&\quad =\left( \vartheta \odot \int _{0}^{\infty }\tilde{f}(t)\odot \exp \left( \frac{-p}{q}t\right) \mathrm{d}t\right) \oplus \left( \beta \odot \int _{0}^{\infty }\tilde{g}(t)\odot \exp \left( \frac{-p}{q}t\right) \mathrm{d}t\right) \\&\quad =\vartheta \odot \left( \int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \underline{f}(t;r)\mathrm{d}t,\int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \bar{f}(t;r)\mathrm{d}t\right) \\&\qquad \oplus \beta \odot \left( \int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \underline{g}(t;r)\mathrm{d}t,\int _{0 }^{\infty }\exp \left( \frac{-p}{q}t\right) \bar{g}(t;r)\mathrm{d}t\right) \\&\quad =\vartheta \odot \mathbf{S} \left[ \tilde{f}(t)\right] \oplus \beta \odot \mathbf{S} \left[ \tilde{g}(t)\right] . \end{aligned}$$

The proof is complete. $\square$

Property 2

Scaling property. Let $\vartheta$ be an arbitrary constant and $\tilde{f}(\vartheta t)$ be an integrable fuzzy-valued functions, and then:

$$\begin{aligned} \mathbf{S} \left[ \tilde{f}(\vartheta t)\right] =\frac{1}{\vartheta }F\left( \frac{p}{\vartheta },q\right) . \end{aligned}$$

(108)

Proof

Using the Definition 9 of fuzzy Shehu transform, we obtain:

$$\begin{aligned} \mathbf{S} \left[ \tilde{f}(\vartheta t)\right]= & {} \int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot \tilde{f}(\vartheta t)\mathrm{d}t. \end{aligned}$$

(109)

Let $r\in [0,1].$ Substituting $\zeta =\vartheta t$ and $\mathrm{d}t=\frac{\mathrm{d}\zeta }{\vartheta }$ in Eq. (109) yields:

$$\begin{aligned} \mathbf{S} \left[ \tilde{f}(\vartheta t)\right]= & {} \frac{1}{\vartheta }\odot \int _{0 }^{\infty }\exp \left( \frac{-p\zeta }{q\vartheta }\right) \odot \tilde{f}(\zeta )\mathrm{d}\zeta =\frac{1}{\vartheta }\odot \int _{0 }^{\infty }\exp \left( \frac{-pt}{q\vartheta }\right) \odot \tilde{f}\left( t\right) \mathrm{d}t\\= & {} \frac{1}{\vartheta }\odot \int _{0 }^{\infty }\exp \left( \frac{-pt}{\vartheta }\right) \odot \tilde{f}(qt)\mathrm{d}t\\= & {} \left( \frac{1}{\vartheta }\int _{0 }^{\infty }\exp \left( \frac{-pt}{\vartheta }\right) \underline{f}(qt;r)\mathrm{d}t,\frac{1}{\vartheta }\int _{0 }^{\infty }\exp \left( \frac{-pt}{\vartheta }\right) \bar{f}(qt;r)\mathrm{d}t\right) \\= & {} \left( \frac{1}{\vartheta }{\underline{F}}\left( \frac{p}{\vartheta },q\right) ,\frac{1}{\vartheta }\bar{F}\left( \frac{p}{\vartheta },q\right) \right) =\frac{1}{\vartheta }\odot F\left( \frac{p}{\vartheta },q\right) . \end{aligned}$$

This complete the proof. $\square$

Property 3

Exponential shifting property. Let the $\tilde{f}(t)$ be a continuous fuzzy-valued function on $[0,\infty )$ and $\vartheta$ be an arbitrary constant, and then:

$$\begin{aligned} \mathbf{S} \left[ \exp \left( \vartheta t\right) \odot \tilde{f}(t)\right] (p,q)=F(p-\vartheta q,q). \end{aligned}$$

(110)

Proof.

From Eq. (21), we get:

$$\begin{aligned}&\mathbf{S} \left[ \tilde{f}(t)\right] (p,q)= q\odot \int _{0 }^{\infty }\exp \left( -pt\right) \odot \tilde{f}(qt)\mathrm{d}t. \end{aligned}$$

(111)

Then, for any fixed $r\in [0,1]$, we have:

$$\begin{aligned}&\mathbf{S} \left[ \exp \left( \vartheta t\right) \odot \tilde{f}(t)\right] (p,q)=\int _{0}^{\infty }\exp \left( (\vartheta t)\right) \odot \exp \left( \frac{-pt}{q}\right) \odot \tilde{f}(t)\mathrm{d}t\nonumber \\&\quad =\int _{0 }^{\infty }\exp \left( -\frac{(p-\vartheta q)}{q}\right) \odot \tilde{f}(t)\mathrm{d}t=q\odot \int _{0}^{\infty }\exp \left( -(p-\vartheta q)t\right) \odot \tilde{f}(qt)\mathrm{d}t\nonumber \\&\quad =\left( \int _{0 }^{\infty }\exp \left( -(p-\vartheta q)t\right) \underline{f}(qt;r)\mathrm{d}t,\int _{0 }^{\infty }\exp \left( -(p-\vartheta q)t\right) \bar{f}(qt;r)\mathrm{d}t\right) \nonumber \\&\quad =\left( {\underline{F}}(p-\vartheta q,q),\bar{F}(p-\vartheta q,q)\right) =\mathbf{S} \left[ f(t)\right] (p-\vartheta q)=F(p-\vartheta q,q). \end{aligned}$$

(112)

Property 4

Multiple shift property. Let $\tilde{f}(t)$ be a continuous fuzzy-valued function on $[0,\infty )$ and $\mathbf{S} \left[ \tilde{f}(t)\right] (p,q)=F(p,q)$, and then:

$$\begin{aligned} \mathbf{S} \left[ t^n\odot \tilde{f}(t)\right] (p,q)=(-q)^n\odot \frac{d^n}{dp^n}F(p,q). \end{aligned}$$

(113)

Proof.

Applying Eq. (21) and Leibniz’s rule, we obtain:

$$\begin{aligned}&\frac{d}{d p}F(p,q)=\frac{d}{d p}\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot \tilde{f}(t)\mathrm{d}t=\int _{0 }^{\infty }\frac{\partial }{\partial p}\left( \exp \left( \frac{-pt}{q}\right) \right) \odot \tilde{f}(t)\mathrm{d}t\nonumber \\&\quad =-\frac{1}{q}\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot t\odot \tilde{f}(t)\mathrm{d}t=\mathbf{S} \left[ t\odot \tilde{f}(t)\right] (p,q)\nonumber \\&\quad =-q\odot \frac{d}{d p}F(p,q)\,\,\,(for\,\, n=1). \end{aligned}$$

(114)

Besides, to generalize the result of Eq. (114), we assume Eq. (113) holds for $n=k$, and then:

$$\begin{aligned}&\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot t^k\odot \tilde{f}(t)\mathrm{d}t=(-q)^k\odot \frac{d^k}{dp^k}F(p,q). \end{aligned}$$

(115)

Thus:

$$\begin{aligned}&\frac{d}{d p}\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot t^k\odot \tilde{f}(t)\mathrm{d}t=(-q)^k\odot \frac{d^{k+1}}{dp^{k+1}}F(p,q). \end{aligned}$$

(116)

Thanks to Leibniz’s rule which help us to get:

$$\begin{aligned}&\frac{d}{d p}\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot t^k\odot \tilde{f}(t)\mathrm{d}t=\int _{0 }^{\infty }\frac{\partial }{\partial p}\left( \exp \left( \frac{-pt}{q}\right) \right) \odot t^k\odot \tilde{f}(t)\mathrm{d}t\nonumber \\&\quad =-\frac{1}{q}\odot \int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot t^{k+1}\odot \tilde{f}(t)\mathrm{d}t=(-q)^k\odot \frac{d^{k+1}}{dp^{k+1}}F(p,q). \end{aligned}$$

(117)

The above result yields:

$$\begin{aligned}&\int _{0 }^{\infty }\exp \left( \frac{-pt}{q}\right) \odot t^{k+1}\odot \tilde{f}(t)\mathrm{d}t=(-q)^{k+1}\odot \frac{d^{k+1}}{dp^{k+1}}F(p,q). \end{aligned}$$

(118)

Finally, Eq. (117) validates the result of Eq. (113) holds for $n=k+1$. The proof is complete. $\square$