Dynamic Modeling of Heated Oscillatory Layer of Non-Newtonian Liquid

Abstract—

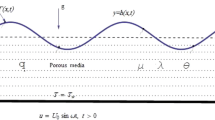
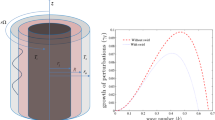
In this work, we have effectively used the numerical inversion of the Laplace transform to study the time-dependent thin heated film flow of a viscoelastic fluid flowing on an infinitely long flat substrate. Exact and analytical solutions are obtained in some limiting cases. The model describing this problem is a system of equations, coupling the linearized Navier–Stokes equation of the viscoelastic fluid with regard for gravity as an external force and the temperature relation for the energy profile. By assuming that the fluids are incompressible, we first derive a new system of equations, by taking into account additional terms, due to the insoluble surfactants and the viscoelastic properties. The velocity and temperature profiles are shown and the influence of coupling constant, viscoelastic parameters and the interfacial surfactants on the liquid film are discussed in detail. The validity of our solutions is verified by the numerical results to show the effects of different parameters involved and to show how the fluid flow evolves with time.

APPENDIX

The quantities ${{c}_{1}},{{c}_{2}},...,{{c}_{6}}$ given in Eqs. (2.24)–(2.26) may be formulated as follows:

$${{c}_{1}} = \frac{{A\bar {U}(s)}}{{{{M}_{0}}}}((k{{M}_{2}} - \gamma {{M}_{4}}){{J}_{6}}{{\mathfrak{M}}_{0}} + {{M}_{6}}(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}}))),$$

$${{M}_{0}} = A({{J}_{1}} - {{J}_{3}})((k{{M}_{2}} - \gamma {{M}_{4}}){{J}_{6}}{{\mathfrak{M}}_{0}} + {{M}_{6}}(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}})))$$

$$ + \,\gamma {{J}_{4}}\left( {{{M}_{6}}\left( {A{{J}_{3}}{{\mathfrak{M}}_{0}} - A{{J}_{1}}{{\mathfrak{M}}_{0}} + k\left( {A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}\left( {{{\Lambda }_{K}} - \Lambda } \right)} \right)} \right)} \right.$$

$$\, + {{J}_{6}}{{\mathfrak{M}}_{0}}(A{{M}_{1}} - A{{M}_{3}} + k{{A}_{1}}{{P}_{e}}{{M}_{5}}(\Lambda - {{\Lambda }_{K}}))) + k{{J}_{2}}({{J}_{6}}{{\mathfrak{M}}_{0}}(A{{M}_{3}} - A{{M}_{1}}$$

$$\left. { + \,k{{A}_{1}}{{P}_{e}}{{M}_{5}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right) + {{M}_{6}}(A{{J}_{1}}{{\mathfrak{M}}_{0}} - A{{J}_{3}}{{\mathfrak{M}}_{0}} - k(A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}})$$

$$\left. {\left. {\left. { + \,{{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}({{\Lambda }_{K}} - {{\Lambda }_{\gamma }})} \right)} \right)} \right),\quad A = ({{k}^{2}} - {{\delta }^{2}})({{\gamma }^{2}} - {{\delta }^{2}}),\quad {{A}_{1}} = - \frac{{{{B}_{i}}}}{{1 + {{B}_{i}}}},$$

$${{\Lambda }_{K}} = {{k}^{2}} - {{\delta }^{2}},\quad {{\Lambda }_{\gamma }} = {{\gamma }^{2}} - {{\delta }^{2}},$$

$${{J}_{1}} = \frac{1}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}}({{k}^{4}}\cosh(\gamma ) - {{C}_{a}}({{k}^{2}}\cosh(\gamma ) + {{k}^{4}}\cosh(\gamma ){{A}_{1}}{{M}_{a}} - {{s}^{2}}\gamma \sinh(\gamma ){{R}_{e}}$$

$$\, - 3{{k}^{2}}s\gamma \sinh(\gamma )F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) + s{{\gamma }^{3}}\sinh(\gamma )F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right))),$$

$${{J}_{2}} = \frac{1}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}}({{k}^{4}}\sinh(\gamma ) - {{C}_{a}}({{k}^{2}}\sinh(\gamma ) + {{k}^{4}}\sinh(\gamma ){{A}_{1}}{{M}_{a}} - {{s}^{2}}\gamma \cosh(\gamma ){{R}_{e}}$$

$$ - \,3{{k}^{2}}s\gamma \cosh(\gamma )F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) + s{{\gamma }^{3}}\cosh(\gamma )F({{\lambda }_{1}},{{\lambda }_{2}},s))),$$

$${{J}_{3}} = \frac{{k({{k}^{3}}\cosh(k) + {{C}_{a}}({{s}^{2}}\sinh(k){{R}_{e}} + 2{{k}^{2}}s\sinh(k)F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) - k\cosh(k) - {{k}^{3}}\cosh(k){{A}_{1}}{{M}_{a}}))}}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}},$$

$${{J}_{4}} = \frac{{k({{k}^{3}}\sinh(k) + {{C}_{a}}({{s}^{2}}\cosh(k){{R}_{e}} + 2{{k}^{2}}s\cosh(k)F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right) - k\sinh(k) - {{k}^{3}}\sinh(k){{A}_{1}}{{M}_{a}}))}}{{2{{s}^{2}}{{C}_{a}}{{R}_{e}}}},$$

$${{J}_{1}} = \frac{{\cosh(\gamma )({{k}^{2}}{{A}_{1}}{{M}_{a}}(A + s{{P}_{e}}{{\Lambda }_{K}}) + sA({{k}^{2}} + {{\gamma }^{2}})F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right))}}{{sA}},$$

$${{J}_{2}} = \frac{{\sinh(\gamma )({{k}^{2}}{{A}_{1}}{{M}_{a}}(A + s{{P}_{e}}{{\Lambda }_{K}}) + sA({{k}^{2}} + {{\gamma }^{2}})F\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right))}}{{sA}},$$

$${{J}_{3}} = \frac{{{{k}^{2}}\cosh(k)\left( {{{A}_{1}}{{M}_{a}}\left( {A + s{{P}_{e}}{{\Lambda }_{\gamma }}} \right) + 2sAF\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right)} \right)}}{{sA}},$$

$${{J}_{4}} = \frac{{{{k}^{2}}\sinh(k)\left( {{{A}_{1}}{{M}_{a}}\left( {A + s{{P}_{e}}{{\Lambda }_{\gamma }}} \right) + 2sAF\left( {{{\lambda }_{1}},{{\lambda }_{2}},s} \right)} \right)}}{{sA}},\quad {{J}_{5}} = k\cosh(\delta ){{M}_{a}},\quad {{J}_{6}} = k\sinh(\delta ){{M}_{a}},$$

$${{\mathfrak{M}}_{0}} = s + \frac{{{{k}^{2}}}}{{{{P}_{{{\text{es}}}}}}},\quad {{\mathfrak{M}}_{1}} = - k\gamma \sinh(\gamma ),\quad {{\mathfrak{M}}_{2}} = - k\gamma \cosh(\gamma ),\quad {{\mathfrak{M}}_{3}} = - {{k}^{2}}\sinh(k),\quad {{\mathfrak{M}}_{4}} = - {{k}^{2}}\cosh(k),$$

$${{M}_{1}} = \frac{{k{{A}_{1}}(\gamma \sinh(\gamma ) + \cosh(\gamma ){{B}_{i}}){{P}_{e}}{{\Lambda }_{K}}}}{A},\quad {{M}_{2}} = \frac{{k{{A}_{1}}(\gamma \cosh(\gamma ) + \sinh(\gamma ){{B}_{i}}){{P}_{e}}{{\Lambda }_{K}}}}{A},$$

$${{M}_{3}} = \frac{{k{{A}_{1}}(k\sinh(k) + \cosh(k){{B}_{i}}){{P}_{e}}{{\Lambda }_{\gamma }}}}{A},\quad {{M}_{4}} = \frac{{k{{A}_{1}}(k\cosh(k) + \sinh(k){{B}_{i}}){{P}_{e}}{{\Lambda }_{\gamma }}}}{A},$$

$${{M}_{5}} = \delta \sinh(\delta ) + \cosh(\delta ){{B}_{i}},\quad {{M}_{6}} = \delta \cosh(\delta ) + \sinh(\delta ){{B}_{i}},$$

$${{c}_{2}} = \frac{{ - k\bar {U}(s)}}{{{{M}_{0}}}}({{M}_{6}}\left( {A{{J}_{3}}{{\mathfrak{M}}_{0}} - A{{J}_{1}}{{\mathfrak{M}}_{0}} + k\left( {A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right)} \right)$$

$$ + \;{{J}_{6}}{{\mathfrak{M}}_{0}}(A{{M}_{1}} - A{{M}_{3}} + k{{A}_{1}}{{P}_{e}}{{M}_{5}}({{\Lambda }_{\gamma }} - {{\Lambda }_{K}}))),$$

$${{c}_{3}} = - {{c}_{1}},\quad {{c}_{4}} = - (\gamma {\text{/}}k){{c}_{2}},$$

$${{c}_{5}} = \frac{{k{{A}_{1}}{{P}_{e}}\bar {U}(s)({{\Lambda }_{\gamma }} - {{\Lambda }_{K}})}}{{{{M}_{0}}}}((k{{M}_{2}} - \gamma {{M}_{4}}){{J}_{6}}{{\mathfrak{M}}_{0}} + {{M}_{6}}(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}}))),$$

$${{c}_{6}} = \frac{{\bar {U}(s)}}{{{{M}_{0}}}}(k{{M}_{2}}\left( {A{{J}_{3}}{{\mathfrak{M}}_{0}} - A{{J}_{1}}{{\mathfrak{M}}_{0}} + k\left( {A{{N}_{e}}({{\mathfrak{M}}_{1}} - {{\mathfrak{M}}_{3}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right)} \right)$$

$$ + \;(\gamma {{J}_{4}}{{\mathfrak{M}}_{0}} - k{{J}_{2}}{{\mathfrak{M}}_{0}} + k{{N}_{e}}(k{{\mathfrak{M}}_{2}} - \gamma {{\mathfrak{M}}_{4}}))\left( {A{{M}_{3}} - A{{M}_{1}} + k{{A}_{1}}{{P}_{e}}{{M}_{5}}\left( {{{\Lambda }_{K}} - {{\Lambda }_{\gamma }}} \right)} \right)$$

$$ + \;\gamma {{M}_{4}}(A{{J}_{1}}{{\mathfrak{M}}_{0}} - A{{J}_{3}}{{\mathfrak{M}}_{0}} + k(A{{N}_{e}}({{\mathfrak{M}}_{3}} - {{\mathfrak{M}}_{1}}) + {{A}_{1}}{{P}_{e}}{{J}_{5}}{{\mathfrak{M}}_{0}}({{\Lambda }_{\gamma }} - {{\Lambda }_{K}})))).$$