1 Introduction

We are concerned with models coming from a special type of hydrodynamical systems, that do not include the effects of the internal pressure. The simplest example is the motion of dust, that is, of free particles evolving in the space like, e.g. in astrophysics [17], or in multi-fluid systems [4, 6]. Leaving the world of inanimate matter, one can also mention models that describe collective behavior, where particles or rather agents exhibit some intelligence, and for which having a force like internal pressure is not so natural. A well-known example in this area is given by the equations of traffic flow [5, 25], where particles are just cars.

In order to specify and understand this class of models, let us go back to the kinetic description of a collective behavior. Consider equations of the following form

$$\begin{aligned} f_t +v\cdot \nabla _x f + \mathrm{div}_{v} K(f)f=0 \ \ \text{ in } \ (0,T)\times {\mathbb {R}}^d_x \times {\mathbb {R}}^d_v, \end{aligned}$$
(1.1)

where \(f=f(t,x,v)\) is a distribution function of a gas in the phase-space. Classically, if the operator K comes from the Poisson potential, then we find the Vlasov system. If taking a less singular operator, then one may obtain for example the Cucker–Smale system that models collective behavior like flocking of birds [7]. Assuming a very special form of f, the so-called mono-kinetic ansatz, one can pass formally from the kinetic model (1.1) to the hydrodynamical system, putting just

$$\begin{aligned} f(t,x,v)=\rho (t,x) \delta _{v=u(t,x)}. \end{aligned}$$
(1.2)

This amounts to saying that the distribution of the gas under consideration is located on the curve \(v=u(t,x)\). Although one cannot expect this simplification to be a correct description of a gas, it is relevant for modelling some collective behavior phenomena as one can expect a crowd of individuals to have the same speed (or tendency) at one point [32, 34].

Formally, plugging (1.2) in (1.1) leads to the following general form of hydrodynamical system:

$$\begin{aligned} \begin{array}{l} \rho _t + {\mathrm{div}}\, (\rho u)=0,\\ \rho u_t + \rho u\cdot \nabla u = A(\rho ,u). \end{array} \end{aligned}$$
(1.3)

The two equations may be seen as the mass and momentum balances, respectively. If \(A\equiv 0,\) then one just recovers the pressureless compressible Euler system, and there is no interaction whatsoever between the individuals. Relevant examples where \(A\not \equiv 0\) can be found in [31, 37, 38].

In our note, we would like to put our attention on the following two cases:

$$\begin{aligned} A(\rho ,u)= \mu \Delta u \ \hbox { or }\ A(\rho ,u)=\mu \Delta u + \mu '\nabla {\mathrm{div}}\, u,\qquad \mu>0,\quad \mu +\mu '>0.\nonumber \\ \end{aligned}$$
(1.4)

The first case is a viscous regularization of (1.3) that can be viewed as a simplification of the Euler alignment system. It corresponds to the hydrodynamical version of the Cucker–Smale model, namely

$$\begin{aligned} \begin{array}{l} \rho _t +{\mathrm{div}}\, (\rho u)=0,\\ \displaystyle \rho u_t + \rho u \cdot \nabla u = \int _{{\mathbb {R}}^d} \frac{u(t,y)-u(t,x)}{|x-y|^{d+\alpha }} \rho (t,y)\rho (t,x)\,\mathrm{d}y,\qquad \alpha \in (0,2). \end{array} \end{aligned}$$
(1.5)

The right-hand side of (1.5) involves the fractional Laplacian \((-\Delta )^{\alpha /2}\) (see details in [16, 20]) and the first case in (1.4) thus meets \(\alpha = 2\). The second case of (1.4) is the Lamé operator that can be obtained from the Vlasov–Boltzmann equation (for more explanation, one may refer to the introduction of [36]). The form of (1.4) does not take into account the effects of internal pressure. From the mathematical viewpoint, the lack of the pressure term P causes serious problems. In particular, all techniques for the compressible viscous systems based on the properties of the so-called effective viscous flux, namely \(F:= {\mathrm{div}}\, u - P,\) which has better regularity than \({\mathrm{div}}\, u\) and P taken separately, are bound to fail. Recall that using F is one of the keys to the theory of weak solutions of the compressible Navier–Stokes equations [21, 22, 26,27,28], as it allows to exhibit compactness properties of the set of weak solutions. In the theory of regular solutions [9, 13, 30, 33], the effective viscous flux provides the decay properties for the density that are needed for establishing global existence for small data.

In the case of pressureless systems, there is no such a possibility, so that we need to resort to more sophisticated techniques to control the density. This may partially explain the reason why the mathematical theory of pressureless models is poorer than the classical one. The aim of this note is to present a novel technique coming from the maximal regularity theory for analytic semi-groups, allowing to prove global-in-time properties of solutions to (1.3), (1.4). It will enable us to show existence and uniqueness results under rough assumptions on the density (only bounded), even though one cannot take advantage of the effective viscous flux. More precisely, by combining interpolation arguments, subtle embeddings, suitable time weighted norms and the magic properties of Lorentz spaces, we succeed in obtaining the \(L_1({\mathbb {R}}_+;L_\infty )\) regularity for the gradient of the solution to the linearized momentum equation in (1.3) and, eventually, produce global-in-time strong solutions. Our main results concern global-in-time solvability for the two dimensional case for large velocity, and the three dimensional case in the small data regime.

2 Functional framework

This note aims at presenting an interesting application of Lorentz spaces for parabolic type systems. Lorentz spaces can be defined on any measure space \((X,\mu )\) via real interpolation between the classical Lebesgue spaces, as follows:

$$\begin{aligned} L_{p,r}(X,\mu ) := (L_\infty (X,\mu ),L_1(X,\mu ))_{1/p,r} \ \hbox { for }\ p\in (1,\infty )\quad \mathrm{and}\quad r \in [1,\infty ].\nonumber \\ \end{aligned}$$
(2.1)

Lorentz spaces may be endowed with the following (quasi)-norm (see, e.g., [24, Prop. 1.4.9]):

$$\begin{aligned} \Vert f\Vert _{L_{p,r}}:=\left\{ \begin{array}{ll} p^{\frac{1}{r}}\biggl (\displaystyle \int _0^\infty \bigl (s\, |\{|f|>s\}|^{\frac{1}{p}}\bigr )^r\,\frac{\mathrm{d}s}{s}\biggr )^{\frac{1}{r}} &{}\quad \hbox {if }\ r<\infty ,\\ \displaystyle \sup _{s>0} s\, |\{|f|>s\}|^{\frac{1}{p}}&{}\quad \hbox {if }\ r=\infty .\end{array}\right. \end{aligned}$$
(2.2)

The reason for the pre-factor \(p^{\frac{1}{r}}\) is to have \(\Vert f\Vert _{L_{p,p}}=\Vert f\Vert _{L_p},\) according to Cavalieri’s principle. The following classical properties of Lorentz spaces may be found in, e.g., [3, 24]:

  • Embedding : \(L_{p,r_1}\hookrightarrow L_{p,r_2}\) if \(r_1\le r_2,\) and \(L_{p,p}=L_p.\)

  • Hölder inequality : for \(1<p,p_1,p_2<\infty \) and \(1\le r,r_1,r_2\le \infty \), we have

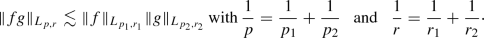    (2.3)

    Inequality (2.3) still holds for couples (1, 1) and \((\infty ,\infty )\) with the convention \(L_{1,1}=L_1\) and \(L_{\infty ,\infty }=L_\infty .\)

  • For any \(\alpha >0\) and nonnegative measurable function f,  we have

    $$\begin{aligned} \Vert f^\alpha \Vert _{L_{p,r}}=\Vert f\Vert _{L_{p\alpha ,r\alpha }}^\alpha . \end{aligned}$$

It must be highlighted that Lorentz spaces have the following two interesting and useful properties:

  • If \(f\in L_\infty (\Omega )\) and \(g\in L_{p,q}(\Omega )\), then \(fg \in L_{p,q}(\Omega )\) for all \(p,q\in [1,\infty ]\).

  • If \(\Omega \subset {\mathbb {R}}^d\) is open and if \(f\in L_{d,1}(\Omega )\) and \(\nabla f \in L_{d,1}(\Omega )\), then \(f \in C_b(\Omega )\).

However the class of Lorentz spaces possesses also “false friends”:

  • There is no “Fubini property”, that is if (I, J) is a couple of nontrivial intervals, then (see [8]):

    $$\begin{aligned} L_{p,q}(I\times J)\ne L_{p,q}(I;L_{p,q}(J)) \quad \hbox {whenever }\ p \ne q. \end{aligned}$$

  • Being not reflexive, the space \(L_{p,1}(\Omega )\) does not have the UMD property, and the general theory of deducing maximal regularity in \(L_q(0,T;L_{p,1}(\Omega ))\) via \({{\mathcal {R}}}\)-boundedness and Fourier multiplier theory developed in [18] cannot be applied.

Owing to their definition by real interpolation, Lorentz spaces have some connections with homogeneous and nonhomogeneous Besov spaces. Recall that those spaces may be defined, respectively (for all \(s\in (0,1)\) and \(1\le p,q\le \infty \)) by

$$\begin{aligned} \dot{B}^s_{p,q}(\Omega )=(L_p(\Omega );\dot{W}^1_p(\Omega ))_{s,q}\quad \mathrm{and}\quad B^s_{p,q}(\Omega )=(L_p(\Omega ); W^1_p(\Omega ))_{s,q}. \end{aligned}$$
(2.4)

For more properties of Besov spaces, we refer to Bahouri et al. [2].

The main results of the paper strongly rely on a family of maximal regularity estimates for the heat equation, where the time regularity is measured in Lorentz spaces of type \(L_{q,r}(0,T;L_p)\). Those estimates come up as a consequence of \(L_q(0,T;L_p)\) maximal regularity estimates from the general theory [1, 18, 23, 29, 35].

Proposition 2.1

Let \(1<p,q<\infty \) and \(1\le r \le \infty .\) Then, for any \(u_0\in \dot{B}^{2-2/q}_{p,r}({\mathbb {R}}^d)\) and \(f\in L_{q,r}({\mathbb {R}}_+;L_p({\mathbb {R}}^d)),\) the following heat equation:

$$\begin{aligned} \begin{aligned} u_t-\mu \Delta u&=f\quad&\hbox {in }\ {\mathbb {R}}_+\times {\mathbb {R}}^d,\\ u|_{t=0}&=u_0&\quad \hbox {in }\ {\mathbb {R}}^d\end{aligned} \end{aligned}$$
(2.5)

has a unique solution in the spaceFootnote 1

$$\begin{aligned} \dot{W}^{2,1}_{p,(q,r)}({\mathbb {R}}^d\times {\mathbb {R}}_+):=\Bigl \{u\in {{\mathcal {C}}}_b\bigl ({\mathbb {R}}_+;\dot{B}^{2-2/q}_{p,r}({\mathbb {R}}^d)\bigr ): u_t,\nabla ^2 u\in L_{q,r}({\mathbb {R}}_+;L_p({\mathbb {R}}^d))\Bigr \}, \end{aligned}$$

and the following inequality holds true:

(2.6)

Furthermore, if \(2/q + d/p>2\), then for all \(q< s<\infty \) and \(p\le m\) such that \(1+\frac{d}{2}(\frac{1}{m}-\frac{1}{p})>0,\) interrelated by

$$\begin{aligned} \frac{d}{2m}+\frac{1}{s}=\frac{1}{q}+\frac{d}{2p}-1, \end{aligned}$$

it holds that

The proof of the above result is given in appendix.

3 Results

Let us first present our results pertaining to the case where \(A(\rho ,u)=\mu \Delta u + \mu '\nabla {\mathrm{div}}\, u\) if the gas domain is the whole plane \({\mathbb {R}}^2.\) So, we consider:

$$\begin{aligned} \begin{array}{ll} \rho _t +{\mathrm{div}}\, (\rho u)=0 &{}\quad \text{ in } \ {\mathbb {R}}_+\times {\mathbb {R}}^2,\\ \rho u_t +\rho u \cdot \nabla u = \mu \Delta u + \mu '\nabla {\mathrm{div}}\, u &{}\quad \text{ in } \ {\mathbb {R}}_+\times {\mathbb {R}}^2,\\ \rho |_{t=0} =\rho _0,\qquad u|_{t=0}=u_0 &{}\quad \text{ at } \ {\mathbb {R}}^2. \end{array} \end{aligned}$$
(3.1)

Following recent results of the first two authors in [12, 14, 15] (in different contexts, though), we strive for global results for general initial velocities provided the volume (bulk) viscosity \(\mu '\) is large enough. As our approach is based on a perturbative method, we need moreover the density to be close to some positive constant.

Our solution space will be the set \(\dot{W}^{2,1}_{4/3,(4/3,1)}({\mathbb {R}}^2\times {\mathbb {R}}_+)\) of functions \(z:{\mathbb {R}}_+\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}\) such that

$$\begin{aligned} z\in {{\mathcal {C}}}_b({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1})\quad \mathrm{and}\quad \partial _tz,\, \nabla ^2_xz \in L_{4/3,1}({\mathbb {R}}_+; L_{4/3}({\mathbb {R}}^2)). \end{aligned}$$

As shown in appendix, the corresponding trace space on fixed times is the homogeneous Besov space \(\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2),\) which is ‘critical’ in terms of regularity, and embedded in \(L_2({\mathbb {R}}^2).\) Our first statement is a global existence and uniqueness result for (3.1) for large data in the two dimensional case, provided the volume viscosity \(\nu \) is sufficiently large.

Theorem 3.1

Let \(M\ge 1.\) Denote by \({{\mathcal {P}}}\) and \({{\mathcal {Q}}}\) the Helmholtz projectors on divergence-free and potential vector fields, and set \(\nu :=\mu +\mu '.\)

There exist two constants c and C (independent of M) such that if the initial density \(\rho _0\) satisfies

$$\begin{aligned} \Vert \rho _0-1\Vert _{L_\infty ({\mathbb {R}}^2)}\le c \end{aligned}$$
(3.2)

and if the initial velocity \(u_0\) has components in \(\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)\) and satisfies,

$$\begin{aligned} C\bigl (\Vert {{\mathcal {P}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}+(\nu /\mu )^{1/4}\Vert {{\mathcal {Q}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}\bigr )\exp \bigl \{C\mu ^{-1}\Vert u_0\Vert _{L^2({\mathbb {R}}^2)}^2\bigr \}\le M\mu \nonumber \\ \end{aligned}$$
(3.3)

then, for all \(\nu \ge \nu _0:= \max (C M^{1 / 2} e^{CM^4} , \mu ),\) system (3.1) admits a global finite energy solution \((\rho ,u)\) with \(\rho \in {{\mathcal {C}}}_w^*({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2))\) and \(u\in \dot{W}^{2,1}_{4/3,(4/3,1)},\) satisfying

$$\begin{aligned} \Vert \rho -1\Vert _{L_\infty ({\mathbb {R}}_+\times {\mathbb {R}}^2)}\le 2c \quad \mathrm{and}\quad \Vert u\Vert _{\dot{W}^{2,1}_{4/3,(4/3,1)}({\mathbb {R}}^2\times {\mathbb {R}}_+)}\le C\Vert u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}. \end{aligned}$$
(3.4)

Furthermore, \(\nabla u\in L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2))\) and the following decay property holds:

(3.5)

Finally, the solution \((\rho ,u)\) is unique in the above regularity class.

Some comments are in order:

  • Condition (3.3) means that global existence holds true for large \(\nu ,\) provided the divergence part of the velocity is \({{\mathcal {O}}}(\nu ^{-1/4}).\) A similar restriction (with other exponents, though) was found in our prior works dedicated to the global existence of strong solutions for the compressible Navier-Stokes equations with increasing pressure law [12, 14, 15].

  • The above statement involves only quantities that are scaling invariant for system (3.1).

  • Having Lorentz spaces with second index equal to 1 allows us to capture limit cases of Sobolev embeddings. Other choices than \(L_{4/3,1}\) and \(L_{4,1}\) might be possible.

In the three-dimensional case, the energy space \(L_2({\mathbb {R}}^3)\) is super-critical by half a derivative, and there is no chance (so far) to prove a general result for large data, assuming only that one of the viscosity coefficients is large. Therefore, for simplicity, we focus on the first case of (1.4), that is on the following system:

$$\begin{aligned} \begin{array}{ll} \rho _t+{\mathrm{div}}\, (\rho u)=0 &{} \quad \hbox { in }\ {\mathbb {R}}_+\times {\mathbb {R}}^3,\\ \rho u_t +\rho u \cdot \nabla u = \mu \Delta u &{}\quad \hbox { in }\ {\mathbb {R}}_+\times {\mathbb {R}}^3,\\ u|_{t=0}=u_0, \qquad \rho |_{t=0}=\rho _0 &{}\quad \hbox { at }\ {\mathbb {R}}^3. \end{array} \end{aligned}$$
(3.6)

To simplify our analysis, we choose a functional framework for the velocity that is well beyond critical regularity (actually, we ask for one more derivative). In the same spirit as in the 2D case, we will use the following class of functional spaces:

Our global existence result in the three dimensional case reads:

Theorem 3.2

Take initial data \(\rho _0 \in L_\infty ({\mathbb {R}}^3)\) and \(u_0\in \dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)\cap \dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3).\) There exists a constant \(c>0\) such that if

$$\begin{aligned} \Vert \rho _0-1\Vert _{L_\infty ({\mathbb {R}}^3)}<c \quad \mathrm{and}\quad \Vert u_0\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)}^{1/3} \Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)}^{2/3}<c\mu , \end{aligned}$$
(3.7)

then (3.6) has a global-in-time unique solution \((\rho ,u)\) with

$$\begin{aligned} \rho \in {{\mathcal {C}}}_w({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3))\quad \mathrm{and}\quad u \in (\dot{W}^{2,1}_{5/2,(5/2,1)}\cap \dot{W}^{2,1}_{10/7,(10/7,1)})({\mathbb {R}}^3\times {\mathbb {R}}_+). \end{aligned}$$

Furthermore, that solution has finite energy,

$$\begin{aligned} \Vert \rho -1\Vert _{L_\infty ({\mathbb {R}}^3)} < 2c, \end{aligned}$$
(3.8)

functions tu and \(\nabla u\) belong to \(\dot{W}^{2,1}_{10/3,(10/3,1)}({\mathbb {R}}^3\times {\mathbb {R}}_+)\) and \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3)),\) respectively, and the following inequalities are valid:

$$\begin{aligned} \begin{aligned}&\mu ^{3/5}\sup _{t\ge 0} \Vert u(t)\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)} + \Vert \mu \nabla ^2u,u_t\Vert _{L_{5/2,1}({\mathbb {R}}_+;L_{5/2}({\mathbb {R}}^3))} \le C \mu ^{3/5}\Vert u_0\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)},\\&\mu ^{3/10}\sup _{t\ge 0} \Vert u(t)\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)} + \Vert \mu \nabla ^2u,u_t\Vert _{L_{10/7,1}({\mathbb {R}}_+;L_{10/7}({\mathbb {R}}^3))} \le C \mu ^{3/10}\Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)},\\&\mu ^{7/10}\sup _{t\ge 0} \Vert tu(t)\Vert _{\dot{B}^{7/5}_{10/3,1}({\mathbb {R}}^3)} + \Vert \mu \nabla ^2(tu),(tu)_t\Vert _{L_{10/3,1}({\mathbb {R}}_+;L_{10/3}({\mathbb {R}}^3))} \le C \mu ^{7/10}\Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)}\\&\mathrm{and}\quad \mu \int _0^\infty \Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^3)}\,\mathrm{d}x \le C \Vert u_0\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)}^{1/3} \Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)}^{2/3}. \end{aligned} \end{aligned}$$

Remark 3.1

That \(u_0\) belongs to \(\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)\) may be seen as a low frequency assumption that exactly corresponds to the critical embedding in \(L_2({\mathbb {R}}^3)\) (hence our solutions have finite energies). Other choices of exponents might be possible both for low and high regularity.

We also want to stress the fact that the smallness condition (3.7) is scaling invariant.

The rest of the paper is structured as follows. In the next section, we prove our two-dimensional global result for (3.1). Section 5 is devoted to the proof of Theorem 3.2. In Appendix, we establish a maximal regularity estimate involving Lorentz spaces, of independent interest.

We shall use standard notations and conventions. In particular, C will always designate harmless constants that do not depend on ‘important’ quantities, and we shall sometimes note \(A\lesssim B\) instead of \(A\le CB.\)

4 The two dimensional case

This part is dedicated to the proof of Theorem 3.1. The key observation is that combining the energy balance associated to (3.1) with Proposition 2.1 supplies a bound of the norm of

$$\begin{aligned} u \text{ in } \dot{W}^{2,1}_{4/3,(4/3,1)}({\mathbb {R}}^2\times {\mathbb {R}}^+) \text{ and } \text{ in } L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2)) \text{ in } \text{ terms } \text{ of } u_0, \end{aligned}$$

provided the density is close to 1. The latter information will enable us to bound tu in \(\dot{W}^{2,1}_{4,(4,1)}({\mathbb {R}}^2\times {\mathbb {R}}^+)\) and to get a control on \({\mathrm{div}}\, u\) in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2)).\) Next, reverting to the mass conservation equation, one can ensure that \(\rho -1\) remains small provided \(\nu :=\mu +\mu '\) is large enough. Then, we observe that the very same arguments leading to the control of \({\mathrm{div}}\, u\) also allow to bound \(\nabla u\) in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2)).\) From that point, we follow the energy method of [11, Sec. 4] going to Lagrangian coordinates in order to prove uniqueness, and the rigorous proof of existence is obtained by compactness arguments, after constructing a sequence of smoother solutions (see the next section).

Let us now go to the details of the proof. In the first five steps, we assume we are given a smooth enough solution \((\rho ,u)\) of (3.1) and we concentrate on the proof of a priori estimates. We suppose that \(\mu '\ge 0\) and, to simplify the computations, we take \(\mu =1.\) That latter assumption is not restrictive, since \((\rho ,u)\) satisfies (3.1) with coefficients \((\mu ,\mu ')\) if and only if

$$\begin{aligned} (\widetilde{\rho },\widetilde{u})(t,x):= (\rho , \mu ^{-1}u)(\mu ^{-1}t,x) \end{aligned}$$
(4.1)

satisfies (3.1) with coefficients 1 and \(\mu '/\mu .\)

4.1 Step 1. The energy balance

As already pointed out, the space for \(u_0\) is continuously embedded in \(L_2({\mathbb {R}}^2).\) Hence the initial data have finite energy. Now, the energy balance for (3.1) reads

$$\begin{aligned} \frac{1}{2} \frac{\mathrm{d}}{\mathrm{d}t} \int _{{\mathbb {R}}^2} \rho |u|^2 \mathrm{d}x + \int _{{\mathbb {R}}^2} \bigl ( |\nabla u|^2 + \mu ' ({\mathrm{div}}\, u)^2\bigr )\,\mathrm{d}x =0. \end{aligned}$$
(4.2)

Provided the first part of (3.4) is fulfilled with small enough c,  we thus have, denoting \(\nu :=1+\mu ',\)

$$\begin{aligned} \Vert u\Vert _{L_\infty ({\mathbb {R}}_+;L_2({\mathbb {R}}^2))}^2 + 2\Vert \nabla {{\mathcal {P}}}u\Vert _{L_2({\mathbb {R}}_+;L_2({\mathbb {R}}^2))}^2+2\nu \Vert {\mathrm{div}}\, u\Vert _{L_2({\mathbb {R}}_+;L_2({\mathbb {R}}^2))}^2 \le 2\Vert u_0\Vert _{L_2}^2.\nonumber \\ \end{aligned}$$
(4.3)

4.2 Step 2. Control of the norm of the solution in \(\dot{W}^{2,1}_{4/3,(4/3,1)}\)

Rewrite the velocity equation as:

$$\begin{aligned} u_t-\Delta u- \mu '\nabla {\mathrm{div}}\, u= f:=(1-\rho )u_t-\rho u\cdot \nabla u. \end{aligned}$$

Projecting the equation by means of the Helmholtz projectors \({{\mathcal {P}}}\) and \({{\mathcal {Q}}},\) we get

$$\begin{aligned} ({{\mathcal {P}}}u)_t-\Delta {{\mathcal {P}}}u = {{\mathcal {P}}}f\quad \mathrm{and}\quad ({{\mathcal {Q}}}u)_t-\nu \Delta {{\mathcal {Q}}}u={{\mathcal {Q}}}f. \end{aligned}$$

Applying Proposition 2.1 with \(d=2,\) \(p=q=4/3,\) \(m=s=4\) and \(r=1\) yields

$$\begin{aligned}&\Vert {{\mathcal {P}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2))} + \Vert \nabla ^2{{\mathcal {P}}}u,{{\mathcal {P}}}u_t\Vert _{L_{4/3,1}({\mathbb {R}}_+\!;L_{4/3}({\mathbb {R}}^2))} +\Vert {{\mathcal {P}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))} \nonumber \\&\quad \lesssim \Vert {{\mathcal {P}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)} + \Vert {{\mathcal {P}}}f\Vert _{L_{4/3,1}({\mathbb {R}}_+\!;L_{4/3}({\mathbb {R}}^2))} \end{aligned}$$
(4.4)

andFootnote 2

$$\begin{aligned}&\nu ^{1/4}\Vert {{\mathcal {Q}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1} ({\mathbb {R}}^2))} + \Vert \nu \nabla {\mathrm{div}}\, u, {{\mathcal {Q}}}u_t\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))}\nonumber \\&\quad +\nu ^{1/2} \Vert {{\mathcal {Q}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))} \nonumber \\&\quad \lesssim \nu ^{1/4}\Vert {{\mathcal {Q}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)} + \Vert {{\mathcal {Q}}}f\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))}. \end{aligned}$$
(4.5)

To bound \({{\mathcal {P}}}f\) and \({{\mathcal {Q}}}f,\) we use the fact that \({{\mathcal {P}}}\) and \({{\mathcal {Q}}}\) are continuous on \(L_{4/3,1}({\mathbb {R}}_+ ; L_{4/3} ({\mathbb {R}}^2)),\) so that it is enough to estimate f in \(L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2)).\) Now, using Hölder inequality in Lorentz spaces (see (2.3)), we find that

$$\begin{aligned}&\Vert f\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} \le \Vert 1-\rho \Vert _{L_\infty ({\mathbb {R}}_+\times {\mathbb {R}}^2)} \Vert u_t\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))}\\&\quad +\Vert \rho \Vert _{L_\infty ({\mathbb {R}}_+\times {\mathbb {R}}^2)}\Vert \nabla u\Vert _{L_{2}({\mathbb {R}}_+\times {\mathbb {R}}^2)} \Vert u\Vert _{L_{4,1}({\mathbb {R}}_+;L_{4}({\mathbb {R}}^2))}. \end{aligned}$$

Hence, summing up (4.4) and (4.5), and assuming smallness of \(\rho -1\), one gets

$$\begin{aligned}&\Vert {{\mathcal {P}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1} ({\mathbb {R}}^2))} + \nu ^{1/4}\Vert {{\mathcal {Q}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2))}+ \Vert u_t\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} \\&\qquad +\, \Vert \nabla ^2{{\mathcal {P}}}u,\nu \nabla {\mathrm{div}}\, u\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} +\Vert {{\mathcal {P}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))}\\&\quad + \nu ^{1/2} \Vert {{\mathcal {Q}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))} \\&\qquad \lesssim \Vert {{\mathcal {P}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)} + \nu ^{1/4}\Vert {{\mathcal {Q}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)} + \Vert \nabla u\Vert _{L_{2}({\mathbb {R}}_+\times {\mathbb {R}}^2)} \Vert u\Vert _{L_{4,1}({\mathbb {R}}_+;L_{4}({\mathbb {R}}^2))}. \end{aligned}$$

In the case \(\nu \ge 1,\) it is now clear that there exists a constant \(\eta >0\) independent of \(\nu \) such that, if

$$\begin{aligned} \Vert \nabla u\Vert _{L_{2}({\mathbb {R}}_+\times {\mathbb {R}}^2)}\le \eta , \end{aligned}$$
(4.6)

then we eventually have

$$\begin{aligned}&\Vert {{\mathcal {P}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2))} + \nu ^{1/4}\Vert {{\mathcal {Q}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2))}+ \Vert u_t\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} \\&\qquad +\, \Vert \nabla ^2{{\mathcal {P}}}u,\nu \nabla {\mathrm{div}}\, u\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} +\Vert {{\mathcal {P}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))}\\&\qquad + \nu ^{1/2} \Vert {{\mathcal {Q}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))} \\&\quad \lesssim \Vert {{\mathcal {P}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)} + \nu ^{1/4}\Vert {{\mathcal {Q}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}. \end{aligned}$$

If (4.6) is not satisfied, then the idea is to split the time line into a finite number K of intervals \([T_{k-1},T_{k})\) with \(T_0 = 0\) and \(T_K=\infty ,\)

$$\begin{aligned}&\Vert \nabla u \Vert _{L_2 ((T_{k - 1} , T_k) \times {\mathbb {R}}^2)} = \eta \ \hbox { for all }\ 1\\&\le k \le K - 1,\quad \mathrm{and}\quad \Vert \nabla u \Vert _{L_2 ((T_{K - 1} , T_K) \times {\mathbb {R}}^2)} \le \eta . \end{aligned}$$

For given \(\eta \), we now calculate how many time intervals are needed for this splitting. We have

$$\begin{aligned} K\eta ^2\ge & {} \sum _{k = 1}^{K } \Vert \nabla u \Vert _{L_2 ((T_{k - 1} , T_k) \times {\mathbb {R}}^2)}^2 = \Vert \nabla u \Vert _{L_2 ({\mathbb {R}}_+ \times {\mathbb {R}}^2)}^2\\\ge & {} \sum _{k = 1}^{K - 1} \Vert \nabla u \Vert _{L_2 ((T_{k - 1} , T_k) \times {\mathbb {R}}^2)}^2 = (K - 1) \eta ^2, \end{aligned}$$

whence

$$\begin{aligned} K=\lceil \eta ^{-2} \Vert \nabla u \Vert _{L_2 ({\mathbb {R}}_+ \times {\mathbb {R}}^2)}^2\rceil . \end{aligned}$$
(4.7)

Having this information at hand, we adapt (4.4) and (4.5) to the finite time interval setting, getting, for each \(k\in \{0,\ldots K-1\},\)

(4.8)

Arguing by induction and remembering that K is estimated by (4.7) and (4.3), we conclude that

$$\begin{aligned}&\Vert {{\mathcal {P}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2))}+\nu ^{1/4}\Vert {{\mathcal {Q}}}u\Vert _{L_\infty ({\mathbb {R}}_+;\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2))} + \Vert {{\mathcal {P}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))} \nonumber \\&\quad +\,\nu ^{1/2}\Vert {{\mathcal {Q}}}u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))} + \Vert u_t\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} + \Vert \nabla ^2{{\mathcal {P}}}u\Vert _{L_{4/3,1}( {\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} \nonumber \\&\quad +\, \nu \Vert \nabla {\mathrm{div}}\, u\Vert _{L_{4/3,1}( {\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))} \le C\big ( \Vert {{\mathcal {P}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}\nonumber \\&\quad + \nu ^{1/4}\Vert {{\mathcal {Q}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)} \big )e^{C\Vert u_0\Vert _{L_2({\mathbb {R}}^2)}^2}. \end{aligned}$$
(4.9)

4.3 Step 3. A time weighted estimate

We now look at the momentum equation in the form

(4.10)

By definition, the initial datum for tu is zero, and (4.9) provides us with a bound for the term \(\rho u\) in the space \(L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2)).\) This gives us some hint on the regularity of the whole right-hand side. Now, projecting (4.10) by means of \({{\mathcal {P}}}\) and \({{\mathcal {Q}}},\) using the maximal regularity estimates of Proposition 2.1, and still assuming the first part of (3.4), one gets for all \(0\le T\le T'\le \infty ,\)

(4.11)

Since we have \(\dot{B}^{1/2}_{4,1}({\mathbb {R}}^2)\hookrightarrow L_\infty ({\mathbb {R}}^2),\) the term with \(u\cdot \nabla u\) may be bounded as follows:

$$\begin{aligned} \Vert tu\cdot \nabla u\Vert _{L_{4,1}(T,T';L_4({\mathbb {R}}^2))} \le C\Vert u\Vert _{L_{4,1}(T,T';L_4({\mathbb {R}}^2))} \Vert t u\Vert _{L_\infty (T,T'; \dot{B}^{3/2}_{4,1}({\mathbb {R}}^2))}. \end{aligned}$$
(4.12)

Consequently, if \(\nu \ge 1\) there exists a constant \(\eta >0\) independent of \(\nu \) such that, if

$$\begin{aligned} \Vert u\Vert _{L_{4,1}(T , T' ; L_4 ({\mathbb {R}}^2))}\le \eta , \end{aligned}$$
(4.13)

then Inequality (4.11) reduces to

(4.14)

Clearly, if one can take \(T=0\) and \(T'=\infty \) in (4.13), then we control the left-hand side of (4.11) on \({\mathbb {R}}_+,\) so assume from now on that \( \Vert u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))}>\eta .\) We claim that there exists a finite sequence \(0=T_0<T_1<\cdots< T_{K-1}< T_{K}=\infty \) such that (4.13) if fulfilled on \([T_k,T_{k+1}]\) for each \(k\in \{0,\ldots , K-1\}.\) In order to prove our claim, we introduce

$$\begin{aligned} U(t):=\Vert u(t,\cdot )\Vert _{L_{4}({\mathbb {R}}^2)} \end{aligned}$$

and recall that

$$\begin{aligned} \Vert U\Vert _{L_{4,1}({\mathbb {R}}_+)} = 4 \int _0^\infty |\{t\in {\mathbb {R}}_+: |U(t)|>s\}|^{1/4}\, \mathrm{d}s. \end{aligned}$$
(4.15)

From Lebesgue dominated convergence theorem, we have

$$\begin{aligned} \Vert U\Vert _{L_{4,1}(T',T'')} = 4 \int _0^\infty |\{t\in (T',T''): |U(t)|>s\}|^{1/4}\,\mathrm{d}s \rightarrow 0\quad \hbox {as}\quad T''-T'\rightarrow 0.\nonumber \\ \end{aligned}$$
(4.16)

Hence one can construct inductively a family \(0=T_0<T_1<\cdots<T_{k}<\cdots < T_K = \infty \) such that

$$\begin{aligned} \Vert U\Vert _{L_{4,1}(T_{k - 1},T_{k})}=\eta \quad \text {for} \quad 1 \le k \le K - 1 \quad \mathrm{and}\quad \Vert U\Vert _{L_{4,1}(T_{K - 1},T_{K})} \le \eta .\qquad \end{aligned}$$
(4.17)

By simple Hölder inequality on series, we have

$$\begin{aligned}&\sum _{k=1}^{K - 1} | \{ t\in (T_{k-1},T_k): |U(t)|>s\} |^{1/4} \le (K - 1)^{3/4}\\&\biggl ( \sum _{k=1}^{K - 1} |\{ t \in (T_{k-1},T_k): |U(t)|>s\}|\biggr )^{1/4}. \end{aligned}$$

Hence, integrating with respect to s,  and using (4.17), we get

$$\begin{aligned} (K-1)\eta \le (K-1)^{3/4}\int _0^\infty |\{t\in (0,T_{K-1}): |U(t)|>s\}|^{1/4}\,\mathrm{d}s, \end{aligned}$$

whence

$$\begin{aligned} (K-1)^{1/4}\eta \le \Vert U\Vert _{L_{4,1}({\mathbb {R}}_+)}. \end{aligned}$$

Now, remembering the definition of U and (4.9), one may conclude that there exists some constant C such that

$$\begin{aligned} K=[ C \bigl (\Vert {{\mathcal {P}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}^4 + \nu \Vert {{\mathcal {Q}}}u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}^4\bigr ) e^{C\Vert u_0\Vert _{L_2({\mathbb {R}}^2)}^2}]+1. \end{aligned}$$
(4.18)

Let \(X_k:=\sup _{t\in (T_k,T_{k+1})} \bigl (\Vert t{{\mathcal {P}}}u(t)\Vert _{\dot{B}^{3/2}_{4,1}({\mathbb {R}}^2)} + \nu ^{3/4} \Vert t{{\mathcal {Q}}}u(t)\Vert _{\dot{B}^{3/2}_{4,1}({\mathbb {R}}^2)}\bigr )\). Then, (4.14) and (4.17) ensure that \(X_0\le C\eta \) and that

$$\begin{aligned} X_k \le C(\eta + X_{k-1})\quad \hbox {for all }\ k\in \{1,\ldots ,K-1\}. \end{aligned}$$
(4.19)

So, arguing by induction, we eventually get for all \(m\in \{0,\ldots ,K-1\},\)

$$\begin{aligned} X_m \le C\eta \sum _{\ell =0}^mC^\ell \le \frac{C^{K+1}}{C-1}\,\eta . \end{aligned}$$
(4.20)

Reverting to (4.14), then using (4.18), we conclude that for some universal constant \(C\ge 1,\)

(4.21)

4.4 Step 4. Bounding \({\mathrm{div}}\, u\)

In order to keep the density close to 1,  we have to bound \({\mathrm{div}}\, u\) in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2)).\) The key observation is that

$$\begin{aligned} {\mathrm{div}}\, (t u) \in L_{4,1}({\mathbb {R}}_+;\dot{W}^1_{4}({\mathbb {R}}^2)) \quad \mathrm{and}\quad {\mathrm{div}}\, u \in L_{4/3,1}({\mathbb {R}}_+;\dot{W}^{1}_{4/3}({\mathbb {R}}^2)). \end{aligned}$$
(4.22)

Now, from Gagliardo–Nirenberg inequality and Sobolev embedding, we see that

$$\begin{aligned} \Vert z\Vert _{L_\infty ({\mathbb {R}}^2)} \le C \Vert \nabla z\Vert ^{1/2}_{L_4({\mathbb {R}}^2)} \Vert \nabla z\Vert ^{1/2}_{L_{4/3}({\mathbb {R}}^2)}. \end{aligned}$$
(4.23)

So we have, thanks to Hölder inequality in Lorentz spaces,Footnote 3

$$\begin{aligned} \begin{aligned} \int _0^\infty \Vert {\mathrm{div}}\, u\Vert _{L_\infty }\, dt&\le C \int _0^\infty t^{-1/2} \Vert t\nabla {\mathrm{div}}\, u\Vert _{L_4}^{1/2} \Vert \nabla {\mathrm{div}}\, u\Vert ^{1/2}_{L_{4/3}}\,\mathrm{d}t \\&\le C \Vert t^{-1/2}\Vert _{L_{2,\infty }({\mathbb {R}}_+)} \bigl \Vert \Vert t\nabla {\mathrm{div}}\, u\Vert _{L_{4}({\mathbb {R}}^2)}^{1/2}\bigr \Vert _{L_{8,2}({\mathbb {R}}_+)} \bigl \Vert \Vert \nabla {\mathrm{div}}\, u\Vert _{L_{4/3}({\mathbb {R}}^2)}^{1/2}\bigr \Vert _{L_{8/3,2}({\mathbb {R}}_+)}\\&\le C \Vert t\nabla {\mathrm{div}}\, u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))}^{1/2} \Vert \nabla {\mathrm{div}}\, u\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))}^{1/2}. \end{aligned} \end{aligned}$$

Hence, thanks to (4.9) and (4.21),

(4.24)

4.5 Step 5. Bounding the density

The discrepancy of the density to 1 (that is \(a:=\rho -1\)) may be controlled by means of the mass equation:

$$\begin{aligned} \partial _ta +u\cdot \nabla a + (1+a){\mathrm{div}}\, u=0, \end{aligned}$$

which gives

$$\begin{aligned}&\Vert a(t)\Vert _{L_\infty ({\mathbb {R}}^2)}\le \Vert a_0\Vert _{L_\infty ({\mathbb {R}}^2)} + \int _0^t\Vert {\mathrm{div}}\, u\Vert _{L_\infty ({\mathbb {R}}^2)}\,\mathrm{d}\tau \\&+ \int _0^t\Vert a\Vert _{L_\infty ({\mathbb {R}}^2)}\Vert {\mathrm{div}}\, u\Vert _{L_\infty ({\mathbb {R}}^2)}\,d\tau , \end{aligned}$$

and thus, owing to the integral version of Gronwall lemma,

$$\begin{aligned} \begin{aligned} \Vert a(t)\Vert _{L_{\infty }({\mathbb {R}}^2)}&\le \bigg ( \Vert a_0 \Vert _{L_{\infty }({\mathbb {R}}^2)} + \int _0^t e^{-\int _0^s \Vert \mathrm{div}\, u \Vert _{L_{\infty }({\mathbb {R}}^2)}\,\mathrm{d}s} \Vert {\mathrm{div}}\, u\Vert _{L_{\infty }({\mathbb {R}}^2)}\, d\tau \bigg ) e^{\int _0^t \Vert \mathrm{div}\, u \Vert _{L_{\infty }({\mathbb {R}}^2)}\,\mathrm{d}t}\\&= \displaystyle \Vert a_0 \Vert _{L_{\infty }({\mathbb {R}}^2)}e^{\int _0^t \Vert \mathrm{div}\, u \Vert _{L_{\infty }({\mathbb {R}}^2)}\,\mathrm{d}t}\; + \;e^{\int _0^t \Vert \mathrm{div}\, u \Vert _{L_{\infty }({\mathbb {R}}^2)}\,\mathrm{d}t}-1.\end{aligned} \end{aligned}$$

Hence, provided we have (3.2) and \(c \le 1\) and

$$\begin{aligned} \int _0^T\Vert {\mathrm{div}}\, u\Vert _{L_\infty ({\mathbb {R}}^2)}\,\mathrm{d}\tau \le \log (1+c/2), \end{aligned}$$
(4.25)

the smallness property (3.4) is satisfied on [0, T]. Bearing in mind Inequality (4.24) and the assumption (3.3), we get

$$\begin{aligned} \nu \int _0^{\infty } \Vert {\mathrm{div}}\, u \Vert _{L_{\infty }({\mathbb {R}}^2)} \, \mathrm{d}t \le C M^{\frac{1}{2}} e^{C M^4}. \end{aligned}$$

Consequently, in order to have (4.25) satisfied, it suffices that

$$\begin{aligned} \nu ^{-1} C M^{\frac{1}{2}} e^{C M^4}\le \log (1+c/2), \end{aligned}$$

which corresponds to the condition on \(\nu \) given in the statement of the theorem.

4.6 Step 6: Uniqueness

The key to uniqueness is that \(\nabla u\) is in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2)).\) To get that property, one may proceed exactly as for bounding \({\mathrm{div}}\, u,\) writing that

$$\begin{aligned} \int _0^\infty \Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^2)}\, \mathrm{d}t \le C \Vert t^{-1/2}\Vert _{L_{2,\infty }({\mathbb {R}}_+)} \Vert t\nabla ^2u\Vert _{L_{4,1}({\mathbb {R}}_+;L_4({\mathbb {R}}^2))}^{1/2}\Vert \nabla ^2 u\Vert _{L_{4/3,1}({\mathbb {R}}_+;L_{4/3}({\mathbb {R}}^2))}^{1/2},\nonumber \\ \end{aligned}$$
(4.26)

and using that the right-hand side is bounded in terms of \(u_0\) according to (4.9) and (4.21). Because of the hyperbolic nature of the continuity equation, the uniqueness issue is not straightforward, as the regularity of the density is very low. However, knowing that \(\nabla u\) is in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2))\) enables us to rewrite our system in Lagrangian coordinates. More precisely, for all \(y\in {\mathbb {R}}^2,\) consider the following ODE:

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}(t,y)=u(t,X(t,y)), \qquad X|_{t=0}=y. \end{aligned}$$
(4.27)

Having (4.26) at hand guarantees that (4.27) defines a \(C^1\) flow X on \({\mathbb {R}}_+\times {\mathbb {R}}^2.\)

Let us express the density and velocity in the new coordinates:

$$\begin{aligned} \eta (t,y)=\rho (t,X(t,y)), \qquad v(t,y)=u(t,X(t,y)). \end{aligned}$$
(4.28)

Then, the system for \((\eta ,v)\) reads (see details in, e.g., [10]):

$$\begin{aligned} \begin{array}{l} (J_v\eta )_t=0, \\ \rho _0 v_t -{\mathrm{div}}_{\!v}\, (\nabla _vv + \mu ' ({\mathrm{div}}_{\!v}\, v)\mathop \mathrm{Id}\nolimits ) =0, \end{array} \end{aligned}$$
(4.29)

where \(\nabla _v:=A_v^\top \nabla _y\), \({\mathrm{div}}\, _v:= {\mathrm{div}}\, (J_v^{-1}A_v\cdot )= A_v^\top :\nabla _y\) with \(A_v=(DX_v)^{-1}\) and \(J_v=\det (DX_v).\) One points out that \(J_v^{-1}A_v=\mathop \mathrm{adj}\nolimits (DX_v)\) (the adjugate matrix of \(DX_v\)). Since, in our framework the Lagrangian and Eulerian formulations are equivalent (see, e.g., [10, 33]), it suffices to prove uniqueness at the level of Lagrangian coordinates. Therefore, consider two solutions \((\eta ,v)\) and \(({\bar{\eta }}, {\bar{v}})\) of (4.29) emanating from the data \((\rho _0,u_0).\) Then, the difference of velocities \(\delta \!v: = {{\bar{v}}}- v\) satisfies

$$\begin{aligned}&\rho _0 \delta \!v_t -{\mathrm{div}}_{\!v}\, (\nabla _v\delta \!v+ \mu ' ({\mathrm{div}}_{\!v}\, \delta \!v)\mathop \mathrm{Id}\nolimits ) \nonumber \\&\quad =\bigl ({\mathrm{div}}\, _{\!{{\bar{v}}}}\nabla _{{\bar{v}}}-{\mathrm{div}}\, _v\nabla _v\bigr ){{\bar{v}}}+\mu '\bigl ({\mathrm{div}}\, _{\!{{\bar{v}}}}\mathop \mathrm{Id}\nolimits {\mathrm{div}}\, _{\!{{\bar{v}}}}-{\mathrm{div}}_{\!v}\, \mathop \mathrm{Id}\nolimits {\mathrm{div}}_{\!v}\, \bigr ){{\bar{v}}}. \end{aligned}$$
(4.30)

Note that

Now, taking the \(L^2\) scalar product of (4.30) with \(\delta \!v\) and integrating by parts delivers

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\Vert \sqrt{\rho _0}\,\delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2 +\Vert \nabla _v\delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2+\mu '\Vert {\mathrm{div}}_{\!v}\, \delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2\\&\quad \le \nu \bigl \Vert \bigl (\mathop \mathrm{adj}\nolimits (DX_{{\bar{v}}})A_{{\bar{v}}}^\top - \mathop \mathrm{adj}\nolimits (DX_v)A_v^\top \bigr )\cdot \nabla {{\bar{v}}}\bigr \Vert _{L^2({\mathbb {R}}^2)}\Vert \nabla \delta \!v\Vert _{L_2({\mathbb {R}}^2)}. \end{aligned}$$

Let us take an interval [0, T] for which

$$\begin{aligned} \max \biggl (\int _0^T\Vert \nabla v\Vert _{L_\infty ({\mathbb {R}}^2)}\,\mathrm{d}t,\int _0^T\Vert \nabla {{\bar{v}}}\Vert _{L_\infty ({\mathbb {R}}^2)}\,\mathrm{d}t\biggr ) \quad \hbox {is small.} \end{aligned}$$
(4.31)

All terms like \(\mathop \mathrm{Id}\nolimits -A_w,\) \(1-J_w\) or \(\mathop \mathrm{Id}\nolimits -\mathop \mathrm{adj}\nolimits (DX_w)\) (with \(w=v,{{\bar{v}}}\)) may be computed by using Neumann series expansions, and we end up with pointwise estimates of the following type:

$$\begin{aligned}&|\mathop \mathrm{Id}\nolimits - A_w|\lesssim \int _0^t |\nabla w|\, \mathrm{d}t', \qquad |\mathop \mathrm{Id}\nolimits -\mathop \mathrm{adj}\nolimits (DX_w)|\lesssim \int _0^t |\nabla w| \, \mathrm{d}t',\\&\quad |1-J_w|\lesssim \int _0^t|\nabla w| \, \mathrm{d}t'. \end{aligned}$$

From this, we deduce that

$$\begin{aligned}&\frac{d}{dt}\Vert \sqrt{\rho _0}\,\delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2 +\Vert \nabla \delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2\lesssim (\Vert \nabla v\Vert _{L_\infty ({\mathbb {R}}^2)}\\&+\!\Vert \nabla {{\bar{v}}}\Vert _{L_\infty ({\mathbb {R}}^2)}) \Vert \nabla \delta \!v\Vert _{L_2({\mathbb {R}}^2)}\biggl \Vert \int _0^t \nabla \delta \!v\,\mathrm{d}\tau \biggr \Vert _{L_2({\mathbb {R}}^2)}. \end{aligned}$$

Because we have, by Cauchy–Schwarz inequality,

$$\begin{aligned} t^{-1/2} \biggl \Vert \int _0^t \nabla \delta \!v\,\mathrm{d}\tau \biggr \Vert _{L_2({\mathbb {R}}^2)} \le \Vert \nabla \delta \!v\Vert _{L_2((0,t)\times {\mathbb {R}}^2)}, \end{aligned}$$

integrating the above inequality (and using again Cauchy–Schwarz inequality) yields

$$\begin{aligned}&\Vert \sqrt{\rho _0}\,\delta \!v(t)\Vert _{L_2({\mathbb {R}}^2)}^2+\int _0^t \Vert \nabla \delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2\,\mathrm{d}\tau \\&\le C\biggl (\int _0^t \tau \Vert (\nabla v,\nabla \bar{v})(\tau )\Vert _{L_\infty ({\mathbb {R}}^2)}^2\mathrm{d}\tau \biggr )^{1/2} \int _0^t \Vert \nabla \delta \!v\Vert _{L_2({\mathbb {R}}^2)}^2\,\mathrm{d}\tau . \end{aligned}$$

Hence, there exists \(c>0\) such that if, in addition to (4.31), we have

$$\begin{aligned} \Vert t^{1/2}\nabla w\Vert _{L_2(0,T;L_\infty ({\mathbb {R}}^2))}\le c\quad \hbox {for }\ w=v,{{\bar{v}}}, \end{aligned}$$
(4.32)

then we have \(\delta \!v\equiv 0\) on [0, T],  that is to say \({{\bar{v}}}=v.\) Since \(\delta \!\eta =(J_{{{\bar{v}}}}^{-1}-J_v)\rho _0,\) we get \({\bar{\eta }}=\eta ,\) too. In light of the above arguments, in order to get uniqueness on the whole \({\mathbb {R}}_+,\) it suffices to show that our solutions satisfy not only \(\nabla u\in L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^2)),\) but also

$$\begin{aligned} \int _0^\infty t\Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^2)}^2\,\mathrm{d}t<\infty . \end{aligned}$$
(4.33)

This is a consequence of (4.23), as it gives

4.7 Step 7: Proof of existence

The idea is to smooth out the data, and to solve (3.1) supplemented with those data, according to the local-in-time existence result of Danchin et al. [11] (that just requires the initial velocity to be smooth enough, and the initial density to be close to 1 in \(L_\infty \)). Then, the previous steps provide uniform bounds that allow to show that those smoother solutions are actually global, and one can eventually pass to the limit. The reader may refer to the end of the next part where more details are given on the existence issue, both for Theorems 3.1 and 3.2.

5 The three dimensional case

Our aim here is to prove a global existence result in the small data regime case for system (3.6). In order to get the optimal dependency of the smallness condition in terms of the viscosity coefficient, it is wise to resort again to the rescaling (4.1). So we assume from now on that \(\mu =1.\)

The bulk of the proof consists in exhibiting global-in-time bounds in terms of the data for

$$\begin{aligned} \Xi:= & {} \sup _{t\ge 0} \Vert u(t) \Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)} + \Vert \nabla ^2u, u_t\Vert _{L_{5/2,1}({\mathbb {R}}_+;L_{5/2}({\mathbb {R}}^3))} \end{aligned}$$
(5.1)
$$\begin{aligned} \quad \mathrm{and}\quad \Psi:= & {} \sup _{t\ge 0} \Vert u(t) \Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)} + \Vert \nabla ^2u, u_t\Vert _{L_{10/7,1}({\mathbb {R}}_+; L_{10/7}({\mathbb {R}}^3))}. \end{aligned}$$
(5.2)

From that control and Proposition 2.1, we will estimate u in the space \(L_{10/3,1}({\mathbb {R}}_+; L_{10/3}({\mathbb {R}}^3))\) (that will play the same role as \(L_{4,1}({\mathbb {R}}_+; L_4({\mathbb {R}}^2))\) for (3.1)), and exhibit a bound for tu in the space \(\dot{W}^{2,1}_{10/3,(10/3,1)}({\mathbb {R}}_+ \times {\mathbb {R}}^3).\) This will eventually enable us to bound \(\nabla u\) in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3)).\) From that stage, the proof of uniqueness follows the lines of the two-dimensional case.

5.1 Step 1. Control by the energy

Remembering that our assumptions imply that \(u_0\) is in \(L_2({\mathbb {R}}^3),\) we start with the basic energy balance:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} \int _{{\mathbb {R}}^3} \rho |u|^2 \,dx + \int _{{\mathbb {R}}^3} |\nabla u|^2\, \mathrm{d}x =0. \end{aligned}$$
(5.3)

By Sobolev embedding and provided that (3.8) is satisfied, this implies the following bound on u:

$$\begin{aligned} \Vert u\Vert _{L_\infty ({\mathbb {R}}_+;L_2({\mathbb {R}}^3))} + \Vert u\Vert _{L_2({\mathbb {R}}_+;\dot{H}^1({\mathbb {R}}^3))}\lesssim \Vert u_0\Vert _{L_2({\mathbb {R}}^3)}. \end{aligned}$$
(5.4)

That relation will enable us to control higher norms of the solution, globally in time, provided some scaling invariant quantity involving \(u_0\) is small enough.

5.2 Step 2. Control of the high norm

This step is somehow standard: we want to construct smooth solutions like for the classical Navier-Stokes system. Now, assuming (3.8) and taking advantage of the maximal regularity estimate for the heat equation in \(L_{5/2,1}({\mathbb {R}}_+ ; L_{5/2}({\mathbb {R}}^3))\) stated in Proposition 2.1 yields (recall the definition of \(\Xi \) in (5.1)):

We see by Hölder inequality and Sobolev embedding \(\dot{W}^1_{5/2}({\mathbb {R}}^3) \hookrightarrow L_{15}({\mathbb {R}}^3)\) that

$$\begin{aligned} \begin{aligned} \Vert u\cdot \nabla u \Vert _{L_{5/2,1}({\mathbb {R}}_+; L_{5/2}({\mathbb {R}}^3))}&\le C\Vert u\Vert _{L_\infty ({\mathbb {R}}_+;L_{3}({\mathbb {R}}^3))} \Vert \nabla u \Vert _{L_{5/2,1}({\mathbb {R}}_+;L_{15}({\mathbb {R}}^3))}\\&\le C\Vert u\Vert _{L_\infty ({\mathbb {R}}_+;L_{3}({\mathbb {R}}^3))} \Vert \nabla ^2u\Vert _{L_{5/2,1}({\mathbb {R}}_+;L_{5/2}({\mathbb {R}}^3))}. \end{aligned} \end{aligned}$$

Moreover, we note that by Hölder inequality, Sobolev embedding and (5.4), we have

$$\begin{aligned} \Vert u\Vert _{L_{3}({\mathbb {R}}^3)} \le C\Vert u\Vert _{L_2({\mathbb {R}}^3)}^{2/3}\Vert u\Vert _{L_\infty ({\mathbb {R}}^3)}^{1/3}\le C\Vert u_0\Vert ^{2/3}_{L_2({\mathbb {R}}^3)} \Vert u\Vert ^{1/3} _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)}. \end{aligned}$$
(5.5)

Hence, altogether, this gives

From this, we deduce that

(5.6)

5.3 Step 3. Control of the low norm

It is now a matter of bounding the functional \(\Psi \) defined in (5.2). Thanks to Proposition 2.1, we have

(5.7)

By Hölder inequality and Sobolev embedding \(\dot{W}^1_{10/7}({\mathbb {R}}^3) \hookrightarrow L_{30/11}({\mathbb {R}}^3),\) we discover that

$$\begin{aligned} \begin{aligned} \Vert u\cdot \nabla u \Vert _{L_{10/7,1}({\mathbb {R}}_+;L_{10/7}({\mathbb {R}}^3))}&\le C\Vert u\Vert _{L_\infty ({\mathbb {R}}_+;L_{3}({\mathbb {R}}^3))} \Vert \nabla u \Vert _{L_{10/7,1}({\mathbb {R}}_+;L_{30/11}({\mathbb {R}}^3))}\\&\le C\Vert u\Vert _{L_\infty ({\mathbb {R}}_+;L_{3}({\mathbb {R}}^3))} \Vert \nabla ^2u\Vert _{L_{10/7,1}({\mathbb {R}}_+;L_{10/7}{\mathbb {R}}^3))}. \end{aligned} \end{aligned}$$

Hence, thanks to (5.5),

$$\begin{aligned} \Vert u\cdot \nabla u \Vert _{L_{10/7,1}({\mathbb {R}}_+;L_{10/7}({\mathbb {R}}^3))} \le C\Vert u_0\Vert _{L_2({\mathbb {R}}^3)}^{2/3} \Xi ^{1/3}\Psi . \end{aligned}$$

Therefore, using (5.6) and reverting to (5.7) yields

$$\begin{aligned} \Psi \le C\bigl (\Psi _0 + \Vert u_0\Vert _{L_2({\mathbb {R}}^3)}^{2/3} \Xi _0^{1/3}\Psi \bigr ), \end{aligned}$$

whence, thanks to the smallness condition in (5.6) (changing C if need be),

$$\begin{aligned} \Psi \le 2C\Psi _0. \end{aligned}$$
(5.8)

Let us emphasize that, since \(u_0\) is in \(\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)\cap \dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3),\) it also belongs to all intermediate spaces, and in particular to \(\dot{B}^{4/5}_{5/3,1}({\mathbb {R}}^3)\) with estimate \( \Vert u_0\Vert _{\dot{B}^{4/5}_{5/3,1}({\mathbb {R}}^3)}\lesssim \Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)}^{2/3} \Vert u_0\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)}^{1/3}.\) Hence, mimicking the proof of (5.8), we discover that, up to an irrelevant change of C,  we have

$$\begin{aligned} \Vert u\Vert _{\dot{W}^{2,1}_{5/3,(5/3,1)}} \le C \Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)}^{2/3} \Vert u_0\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)}^{1/3}. \end{aligned}$$
(5.9)

5.4 Step 4. Time weight

In order to get eventually the desired control on \(\nabla u\) in \(L_1({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3))\) that is needed to ensure (3.8) provided we have (3.7) for \(\rho _0,\) and, later on, uniqueness, we mimic the sharp approach of the two dimensional case, considering the momentum equation in the following form

$$\begin{aligned} (tu)_t - \Delta (tu) =(1-\rho )(tu)_t -t \rho u \cdot \nabla u + \rho u \ \ \text{ in } \ {\mathbb {R}}_+ \times {\mathbb {R}}^3. \end{aligned}$$
(5.10)

We observe that using Proposition 2.1 with \(m=s=10/3\) delivers

$$\begin{aligned} \Vert u\Vert _{L_{10/3,1}({\mathbb {R}}_+;L_{10/3}({\mathbb {R}}^3))} \lesssim \Psi . \end{aligned}$$
(5.11)

Since the term \(\rho u\) appears in the right-hand side of (5.10), it is natural to look for a control of tu in the space \(\dot{W}^{2,1}_{10/3,(10/3,1)}({\mathbb {R}}^3 \times {\mathbb {R}}_+).\)

Let \(\Pi := \sup _{t\ge 0} \Vert tu\Vert _{\dot{B}^{7/5}_{10/3,1}} + \Vert \nabla ^2 (tu), (tu)_t\Vert _{L_{10/3,1}({\mathbb {R}}_+;L_{10/3}({\mathbb {R}}^3))}.\) Proposition 2.1 and (3.8) give us

$$\begin{aligned} \Pi \lesssim \Vert t u\cdot \nabla u \Vert _{L_{10/3,1}({\mathbb {R}}_+;L_{10/3}({\mathbb {R}}^3))} + \Vert u\Vert _{L_{10/3,1}({\mathbb {R}}_+; L_{10/3}({\mathbb {R}}^3))}. \end{aligned}$$

In order to estimate the nonlinear term, we first use Hölder inequality to get:

$$\begin{aligned} \Vert u\cdot \nabla t u \Vert _{L_{10/3,1}({\mathbb {R}}_+ ; L_{10/3}({\mathbb {R}}^3))} \le C \Vert u\Vert _{L_{5,1}({\mathbb {R}}_+ ; L_5({\mathbb {R}}^3))} \Vert t\nabla u\Vert _{L_{10}({\mathbb {R}}_+\times {\mathbb {R}}^3)}. \end{aligned}$$
(5.12)

From Gagliardo–Nirenberg inequality and Sobolev embedding, we know that

$$\begin{aligned} \Vert \nabla z\Vert _{L_{10}({\mathbb {R}}^3)}\lesssim \Vert \nabla ^2z\Vert _{L_{10/3}({\mathbb {R}}^3)}^{1/3}\Vert \nabla z\Vert _{\dot{W}^{2/5}_{10/3}({\mathbb {R}}^3)}^{2/3}. \end{aligned}$$

Therefore, using Hölder inequality,

$$\begin{aligned} \Vert \nabla z\Vert _{L_{10}({\mathbb {R}}_+\times {\mathbb {R}}^3)}\lesssim \Vert \nabla ^2z\Vert _{L_{10/3}({\mathbb {R}}_+\times {\mathbb {R}}^3)}^{1/3}\Vert z\Vert _{L_\infty ({\mathbb {R}}_+;\dot{W}^{7/5}_{10/3}({\mathbb {R}}^3))}^{2/3}. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert t\nabla u\Vert _{L_{10}({\mathbb {R}}_+\times {\mathbb {R}}^3)} \lesssim \Pi . \end{aligned}$$
(5.13)

In order to bound u in \(L_{5,1}({\mathbb {R}}_+;L_5({\mathbb {R}}^3)),\) we use Proposition 2.1 with \(p=q=5/3,\) and \(m=s=5,\) and Inequality (5.9). This gives

$$\begin{aligned} \Vert u\Vert _{L_{5,1}({\mathbb {R}}_+;L_5({\mathbb {R}}^3))} \lesssim \Vert u_0\Vert _{\dot{B}^{3/5}_{10/7,1}({\mathbb {R}}^3)}^{2/3} \Vert u_0\Vert _{\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)}^{1/3}. \end{aligned}$$

Putting together with (5.13) and reverting to (5.12), we end up with

$$\begin{aligned} \Vert u\cdot \nabla t u \Vert _{L_{10/3,1}({\mathbb {R}}_+ \times {\mathbb {R}}^3)} \lesssim \Psi _0^{2/3} \,\Xi _0^{1/3}\,\Pi . \end{aligned}$$

Therefore, using also (5.11) and (5.8), we get the following inequality for \(\Pi \):

Consequently, assuming \(C \Psi _0^{2/3} \,\Xi _0^{1/3}\le 1/2,\) a condition that implies (5.6) (up to a change of the constant maybe), we obtain

(5.14)

5.5 Step 5. Bounding \(\nabla u\)

It is now easy to get the desired control on \(\nabla u\): we start from the following combination of the Gagliardo–Nirenberg inequality with Sobolev embedding:

$$\begin{aligned} \Vert \nabla u \Vert _{L_\infty ({\mathbb {R}}^3)} \le C\Vert \nabla u\Vert ^{2/3}_{\dot{W}^{1}_{10/3}({\mathbb {R}}^3)} \Vert \nabla u\Vert ^{1/3}_{ \dot{W}^{1}_{5/2}({\mathbb {R}}^3)}, \end{aligned}$$
(5.15)

which implies

$$\begin{aligned} \int _0^\infty \Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^3)}\,\mathrm{d}t\le C\int _0^{\infty } t^{-2/3} \Vert t \nabla u\Vert _{\dot{W}^{1}_{10/3}({\mathbb {R}}^3)}^{2/3} \Vert \nabla u \Vert ^{1/3}_{\dot{W}^1_{5/2}({\mathbb {R}}^3)}\,\mathrm{d}t. \end{aligned}$$
(5.16)

Using Hölder inequality (2.3) with respect to time in Lorentz spaces, we find that

$$\begin{aligned} \int _0^\infty \Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^3)}\, \mathrm{d}t\le C\Vert t^{-2/3}\Vert _{L_{3/2,\infty }({\mathbb {R}}_+)} \Vert t\nabla u\Vert ^{2/3}_{L_{10/3,1}({\mathbb {R}}_+;\dot{W}^{1}_{10/3}({\mathbb {R}}^3))} \Vert \nabla u \Vert ^{1/3}_{L_{5/2,1}({\mathbb {R}}_+;\dot{W}^1_{5/2}({\mathbb {R}}^3))}. \end{aligned}$$

As the right-hand side is bounded, owing to (5.6) and (5.14), one may conclude that

$$\begin{aligned} \int _0^\infty \Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^3)}\, \mathrm{d}t\le C \Psi _0^{2/3}\, \Xi _0^{1/3}\ll 1. \end{aligned}$$
(5.17)

Therefore, arguing on the mass equation exactly as in the 2D case, one can justify (3.8), and thus all the previous steps provided (3.7) is satisfied.

5.6 Step 6. Uniqueness

Arguing as in the previous section and knowing (5.17) (so as to put our system in Lagrangian coordinates), it suffices to establish the additional property that \(t^{1/2}\nabla u\) is in \(L_2(0,T;L_\infty ({\mathbb {R}}^3)).\) Now, one may write, owing to (5.15), that

$$\begin{aligned} \begin{aligned} \int _0^\infty t\Vert \nabla u\Vert _{L_\infty ({\mathbb {R}}^3)}^2\,\mathrm{d}t&\lesssim \int _0^\infty t^{-1/3} \Vert t \nabla u\Vert _{\dot{W}^{1}_{10/3}({\mathbb {R}}^3)}^{4/3} \Vert \nabla u \Vert ^{2/3}_{\dot{W}^1_{5/2} ({\mathbb {R}}^3)}\,\mathrm{d}t\\&\lesssim \Vert t^{-1/3}\Vert _{L_{3,\infty }({\mathbb {R}}_+)} \bigl \Vert \Vert t \nabla u\Vert _{\dot{W}^{1}_{10/3}({\mathbb {R}}^3)}^{4/3} \bigr \Vert _{L_{5/2,1}({\mathbb {R}}_+)} \bigl \Vert \Vert \nabla u \Vert ^{2/3}_{\dot{W}^1_{5/2} ({\mathbb {R}}^3)}\bigr \Vert _{L_{15/4}({\mathbb {R}}_+)}\\&\lesssim \Vert t \nabla ^2 u\Vert _{L_{10/3,1}({\mathbb {R}}_+; L_{10/3}({\mathbb {R}}^3))}^{4/3} \Vert \nabla ^2 u \Vert ^{2/3}_{L_{5/2}({\mathbb {R}}_+\times {\mathbb {R}}^3)}. \end{aligned} \end{aligned}$$

Because \(t\nabla ^2 u\) is in \(L_{10/3,1}({\mathbb {R}}_+; L_{10/3}({\mathbb {R}}^3))\) and \(\nabla ^2 u\) is in \(L_{5/2}({\mathbb {R}}_+\times {\mathbb {R}}^3),\) the right-hand side is indeed bounded. This completes the proof of uniqueness.

5.7 Step 7. Existence

Here, we sketch the proof of the existence of a global solution under our assumptions on the data. The overall strategy is essentially the same in dimensions \(d=2\) and \(d=3.\)

As a first, we truncate \(\rho _0\) and smooth out \(u_0\) to meet the conditions of the local-in-time existence theorem of [11]: we fix a sequence \((\rho _0^n,u_0^n)_{n\in {\mathbb N}}\) that converges weakly to \((\rho _0,u_0)\) and satisfy the conditions therein. Let \((\rho ^n,u^n)_{n\in {\mathbb N}}\) be the corresponding sequence of maximal solutions, defined on \([0,T_n)\times {\mathbb {R}}^d\) and belonging for all \(T<T_n\) to the classical maximal regularity space

$$\begin{aligned} \dot{W}^{2,1}_{p,r}(T):= \bigl \{z\in {{\mathcal {C}}}([0,T];\dot{B}^{2-2/r}_{p,r}({\mathbb {R}}^d)): \partial _tz,\nabla ^2_xz\in L_r(0,T;L_p({\mathbb {R}}^d))\bigr \}, \end{aligned}$$

with, e.g. \(p=2d\) and \(r=7/6.\)

It is shown in [11] that those solutions satisfy the energy balance and (3.8). Since the computations of the previous step just follow from the properties of the heat flow and basic functional analysis, each \((\rho ^n,u^n)\) satisfies the estimates therein. In particular, \(\Vert \nabla u^n\Vert _{L_1(0,T_n;L_\infty ({\mathbb {R}}^d))}\) is uniformly bounded like in (5.17), which ensures control of (3.8). Now, applying the standard maximal regularity estimates toFootnote 4

$$\begin{aligned} \partial _tu^n-\Delta u^n-\mu '\Delta u^n=(1-\rho ^n)\partial _tu^n+\rho ^n u^n\cdot \nabla u^n, \end{aligned}$$

one gets for all \(T<T_n,\)

$$\begin{aligned} \Vert u^n\Vert _{\dot{W}^{2,1}_{p,r}(T)}\lesssim \Vert u_0^n\Vert _{\dot{B}^{2-2/r}_{p,r}({\mathbb {R}}^d)} + \Vert u^n\cdot \nabla u^n\Vert _{L_r(0,T;L_p({\mathbb {R}}^d))}, \end{aligned}$$

whence

$$\begin{aligned} \Vert u^n\Vert _{\dot{W}^{2,1}_{p,r}(T)}^r\lesssim \Vert u_0^n\Vert _{\dot{B}^{2-2/r}_{p,r}({\mathbb {R}}^d)} ^r + \int _0^T \Vert u^n\Vert _{L_\infty ({\mathbb {R}}^d)}^r \Vert \nabla u^n\Vert _{L_p({\mathbb {R}}^d)}^r\,\mathrm{d}t. \end{aligned}$$
(5.18)

Gagliardo–Nirenberg inequality reveals that

$$\begin{aligned} \Vert \nabla u^n\Vert _{L_p({\mathbb {R}}^d)}\lesssim \Vert u^n\Vert _{\dot{B}^{2-2/r}_{p,r}({\mathbb {R}}^d)}^{r/2}\Vert \nabla ^2 u^n\Vert _{L_p({\mathbb {R}}^d)}^{1-r/2}. \end{aligned}$$

Therefore, plugging that inequality in (5.18) then using Young inequality, we discover that for all \(T<T_n\) and all \(\varepsilon >0,\)

$$\begin{aligned}&\Vert u^n\Vert _{\dot{W}^{2,1}_{p,r}(T)}^r\le C\Vert u_0^n\Vert _{\dot{B}^{2-2/r}_{p,r}({\mathbb {R}}^d)}^r\\&+ C_\varepsilon \int _0^T \Vert u^n\Vert _{L_\infty ({\mathbb {R}}^d)}^2\Vert u^n\Vert _{\dot{B}^{2-2/r}_{p,r}({\mathbb {R}}^d)}^r\,\mathrm{d}t +\varepsilon \int _0^T \Vert \nabla ^2 u^n\Vert _{L_p({\mathbb {R}}^d)}^r\,\mathrm{d}t. \end{aligned}$$

Then, taking \(\varepsilon \) small enough and using Gronwall inequality, we end up with

Now, in the 2D case, we observe that \(\Vert u^n\Vert _{L_\infty ({\mathbb {R}}^2)}\lesssim \Vert u^n\Vert _{L_2({\mathbb {R}}^2)}^{1/3} \Vert \nabla ^2u^n\Vert _{L_{4/3}({\mathbb {R}}^2)}^{2/3},\) and thus, by Hölder inequality,

$$\begin{aligned} \Vert u^n\Vert _{L_2(0,T_n;L_\infty ({\mathbb {R}}^2))}\lesssim \Vert u^n\Vert _{L_\infty (0,T_n;L_2({\mathbb {R}}^2))}^{1/3} \Vert \nabla ^2u^n\Vert _{L_{4/3}((0,T_n)\times {\mathbb {R}}^2)}^{2/3}\lesssim \Vert u_0\Vert _{\dot{B}^{1/2}_{4/3,1}({\mathbb {R}}^2)}, \end{aligned}$$

and one can thus bound \(u^n\) in \(\dot{W}^{2,1}_{p,r}(T_n)\) independently of \(T_n.\)

In the framework of Theorem 3.2, we use the following Gagliardo–Nirenberg inequality:

$$\begin{aligned} \Vert u^n\Vert _{L_\infty ({\mathbb {R}}^3)}\lesssim \Vert u^n\Vert _{\dot{W}^2_{5/2}({\mathbb {R}}^3)}^{1/9}\Vert u^n\Vert _{\dot{W}^2_{10/7}({\mathbb {R}}^3)}^{8/9} \end{aligned}$$

that implies

$$\begin{aligned} \Vert u^n\Vert _{L_{3/2}({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3))} \lesssim \Vert u^n\Vert _{L_{5/2}({\mathbb {R}}_+;\dot{W}^2_{5/2}({\mathbb {R}}^3))}^{1/9} \Vert u^n\Vert _{L_{10/7}({\mathbb {R}}_+;\dot{W}^2_{10/7}({\mathbb {R}}^3))}^{8/9}, \end{aligned}$$

then the fact that \(L_2({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3))\subset L_{3/2}({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3))\cap L_\infty ({\mathbb {R}}_+;L_\infty ({\mathbb {R}}^3))\) and that \(\dot{B}^{6/5}_{5/2,1}({\mathbb {R}}^3)\hookrightarrow L_\infty ({\mathbb {R}}^3),\) to get the desired control of \( \Vert u^n\Vert _{L_2(0,T;L_\infty ({\mathbb {R}}^3))}\) in terms of \(u_0\) only.

In short, in both cases, one can bound \(u^n\) in \(\dot{W}^{2,1}_{p,r}(T_n)\) independently of \(T_n.\) Then, applying standard continuation arguments allows to prove that \((\rho ^n,u^n)\) is actually global, and may be bounded in terms of the original data \((\rho _0,u_0)\) in the spaces of our main theorems, independently of n.

From this stage, passing to the limit in the slightly larger (but reflexive) space

$$\begin{aligned} \dot{W}^{2,1}_{5/2}({\mathbb {R}}^3\times {\mathbb {R}}_+)\cap \dot{W}^{2,1}_{10/7}({\mathbb {R}}^3\times {\mathbb {R}}_+)\quad \bigl (\hbox {or in }\ \dot{W}^{2,1}_{4/3}({\mathbb {R}}^2\times {\mathbb {R}}_+)\bigr ) \end{aligned}$$

for the velocity can be done as in [11] (passing to the limit directly in the nonreflexive spaces \(\dot{W}^{2,1}_{p,(p,1)}({\mathbb {R}}^d\times {\mathbb {R}}_+)\) would require more care). The mass conservation equation may be handled according to Di Perna and Lions’ theory [19] (see details in [11]) and the momentum equation does not present any difficulty compared to works on global weak solutions, since a lot of regularity is available on the velocity and there is no pressure term.

Next, once we know that \((\rho ,u)\) is a solution, one can recover all the additional regularity, that are just based on ‘linear’ properties like interpolation or parabolic maximal regularity. \(\square \)