1 Introduction

The run-up of water waves on a sloping beach is an important phenomenon. A basic challenge is to predict the transient run-up from a given solitary wave at a beach with a constant slope. A classical paper that addressed transient run-up was written by Carrier and Greenspan [1]. Nonlinear numerical analysis on run-up of solitary waves came several decades later [2,3,4].

Synolakis [5] presented experiments supported by asymptotic theory for the nonlinear run-up. He explored the differences between breaking run-up and non-breaking run-up, which is a crucial distinction. Non-breaking run-up may evolve into breaking run-up when a wave starts breaking during its early stages of run-up. As long as the bulk flow in the run-up mass remains irrotational, there is non-breaking run-up. Breaking run-up will induce macroscopic vorticity in the bulk fluid. Tsunami run-up tends to be turbulent since it usually represents the mature stage of a breaking bore. Any bore approaching a sloping beach will develop breaking because its influx of energy cannot be stopped [6, 7]. A tsunami entering a sloping beach may occasionally start with a draw-down. A more common type of tsunami run-up comes as a turbulent bore with positive elevation, advancing into almost still water.

We will now propose and develop an elementary model with relevance for the highest possible run-up configuration of stagnant fluid at a sloping beach. The present model applies only to non-breaking run-up. It assumes an idealized situation where the instantaneous kinetic energy is zero, and the fluid is in a state of pure acceleration where all its energy is gravitational potential energy. Just at the motionless instant, the acceleration field is governed by an acceleration potential that satisfies the Laplace equation. The underlying synchronicity assumption that the irrotational inviscid fluid flow comes completely to rest at one single instant is, of course, vulnerable. We are aware that our simplified point of view does not describe the narrow wedge tip of fluid that typically climbs along the slope in the final stages of a run-up process. The phrase run-up is associated with the commonly observed tip of fluid climbing to maximal height along the slope, but in this paper, we use it in a wider sense.

The present approach to transient free-surface flows along a slope was first suggested by Spielvogel [8]. He took stagnant configurations of narrow wedge-shaped run-up along the beach as initial condition for modeling the flow backward in time. Thereby he modeled the late stages of wave motion before the final state of maximal run-up, with a model sharing our admittedly vulnerable synchronicity assumption. One dilemma of Spielvogel [8] is that any gravitational flow released from rest is highly dispersive, so the Laplace equation applies to the initial acceleration field and its subsequent oscillatory stages of wave motion. Spielvogel [8] compromised dispersion by his shallow-water approximation, and his model included no other boundary than the uniform slope. Therefore, he limited his study to the amplification of the single wave from the shoreline and up to its final stage of stagnant run-up. He was aware that his computations could not come close to maximal non-breaking run-up. Our model follows that of Spielvogel [8] in the geometry of a uniform slope where an initially deformed fluid mass is released from rest under gravity. Our class of surface shapes for which we assume zero kinetic energy is different from [8]. We consider a peaked surface shape, which is possible by applying the Laplace equation, while Spielvogel considered a gently sloping initial surface ending as a narrow wedge tip along the slope. We will not cover the early wave motion like Spielvogel [8] as we study only the initial stage of pure acceleration. Our chosen configuration of a stagnant peaked fluid mass is to be regarded as an idealized limit case that can never be fully reached in a practical run-up process.

It is likely that a solitary wave at uniform depth will make a candidate for approaching the idealized limit that we present. In our analysis, we will consider only the slope where stagnant fluid finally piles up. The absence of channel bottom in our model makes it impossible to include a solitary wave in the present model.

The present model may be linked to an incoming wave only indirectly through the energy content in the stagnant fluid. Our approach relates to the analytical tradition of the previous generations [6, 7]. It contrasts recent progress on nonlinear dispersive run-up, applying heavy numerical computations based on smoothed particle hydrodynamics [9].

The present work is a contribution to the analysis of finite-amplitude initiation of water waves, which is an emerging field. The classical Cauchy–Poisson theory of water wave initiation is limited to linear theory. A pioneering calculation of nonlinear water waves was given by Penney and Price [10]. The harmonic time dependence in their model makes it possible to interpret their theory as a nonlinear standing water wave released from rest. They investigated the highest standing periodic deep-water wave, but could not predict precisely the right-angle surface peak where the entire fluid is at rest. This was achieved later by Grant [11]. Tyvand [12] outlined the different classes of finite-amplitude Cauchy–Poisson problems, suggesting dipole potentials for representing stagnant run-up, which we will pursue in the present paper.

2 Basic assumptions and formulation

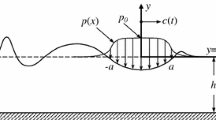
We will now develop an elementary model relevant for maximal run-up. We look at a situation where the fluid has come to rest with a deformed free surface. We will look at the situation just before or just after the instant \(t=0\) where the velocity field is assumed to be zero everywhere. We, therefore, consider an inviscid and incompressible fluid (liquid) which is initially at rest with deformed free surface \(y=\eta (x,0)\). The constant fluid density is \(\rho \), and g is the gravitational acceleration. The 2D fluid domain is represented in the x, y plane, which is a vertical plane. There is a rigid boundary with a constant slope angle \(\alpha \) and a free surface subject to constant atmospheric pressure. Time is denoted by t. Cartesian coordinates x, y are introduced, where the y axis is directed upwards in the gravity field, and the horizontal x axis defines the undisturbed free surface. The origin of our coordinate system is thus placed in the shoreline according to Spielvogel [8] who introduce the present physical model for run-up. The fluid is of semi-infinite extent in the \(+x\) direction, where the depth goes to infinity along the sloping bottom. The gravitational acceleration is g, and \(\rho \) denotes the constant fluid density. The components of the velocity vector \(\mathbf {v}\) are denoted by (u, v). The surface elevation is \(\eta (x,t)\).

No vorticity is generated within the inviscid fluid, which implies that the flow is irrotational according to Lord Kelvin’s theorem

$$\begin{aligned} \nabla \times \mathbf {v} = 0, \end{aligned}$$
(1)

but there is zero velocity initially. We must take the time derivative of Lord Kelvin’s constraint (1) to get

$$\begin{aligned} \nabla \times \frac{\partial \mathbf {v}}{\partial t} = 0. \end{aligned}$$
(2)

The local acceleration is the total acceleration at \(t=0^+\). The released flow at \(t=0^+\) will, therefore, be an irrotational acceleration field, implying the existence of an initial acceleration potential \(\phi (x,y)\) so that \(\partial \mathbf {v}/\partial t\vert _{t=0^+} = \nabla \phi \). The incompressible flow of the homogeneous fluid implies the validity of Laplace’s equation

$$\begin{aligned} \nabla ^2 \phi = 0 \end{aligned}$$
(3)

in the entire fluid domain.

From conservation of momentum Bernoulli’s equation follows:

$$\begin{aligned} \frac{p-p_\mathrm{{atm}}}{\rho } + \phi + g y = 0, \end{aligned}$$
(4)

since the convective term is identically zero for this motionless state. The atmospheric pressure \(p_\mathrm{{atm}}\) appears as an integration constant. The flow decays to zero at infinite distance of a disturbance taking place around the origin, which means that \(p=p_\mathrm{{atm}}\) at \(z=0\) as \(\vert \nabla \varPhi \vert \rightarrow 0\) in the far field (\( x^2 + y^2 \rightarrow \infty \)) for finite time t. From now on we will disregard the reference pressure \(p_\mathrm{{atm}}\) (which corresponds to making the transformation \(p-p_\mathrm{{atm}} \rightarrow p\)). Since there is zero initial velocity, the initial (nonlinear) dynamic free-surface condition is

$$\begin{aligned} \phi + g y = 0~~\text {on}~~y=\eta (x,0). \end{aligned}$$
(5)

Our idealized model represents a state of rest where the energy content can be interpreted as incoming kinetic energy in a solitary wave has been converted to potential energy in the gravity field. The initial-value problem must be formulated. From a state of rest with a deformed free surface, the early flow for \(t>0\) is the same as the late flow for small negative values of t. The state of rest at \(t=0\) represents a state of maximal potential energy because of the conservation of energy in inviscid flow. Any nonzero kinetic energy in the waves will lead to a reduction in the potential energy compared with the initial motionless state at \(t=0\).

We consider a uniformly sloping beach with slope angle \(\alpha \), measured with respect to the horizontal x axis. Our analysis will start with the case \(\alpha = 45^{\circ }\). Our model is, in principle, the same as that suggested by Spielvogel [8], but our approach differs from him in that we emphasize the initial acceleration potential \(\phi (x,y,0)\). While he selected his initial surface shapes based on common but crude observations of run-up phenomena, we will select a class of surface shapes systematically from the general family of multipole acceleration potentials.

2.1 A small-time expansion

The mathematical model developed above can be put into the context of a small-time expansion. The flow for small time (\(t\ge 0\)) can be described as follows:

$$\begin{aligned} (\varPhi , \eta , p) = (0, \eta _0, p_0) + t (\varPhi _1, 0, p_1) + t^2 (\varPhi _2, \eta _2, p_2) + \cdots \end{aligned}$$
(6)

for a flow with initially deformed free surface which is released from rest under gravity. Here we consider the complex velocity potential \(\varPhi \), the surface elevation \(\eta \) (measured vertically with respect to the undisturbed fluid level \(y=0\)) and the pressure p. There is no zeroth-order flow, and there is no first-order elevation. We are studying only the leading-order contributions \(\eta _0 = \eta (x,0)\), \(\varPhi _1 = \partial \varPhi /\partial t\vert _{t=0}\) and \(p_0 = p(x,y,0)\) in the present paper. The small-time expansion scheme is here formulated for the sake of providing a general overview, and it will not be in practical use in the subsequent analysis.

3 A dipole potential representing an initial fluid shape

The length scale L is basic for a dimensionless description, but it cannot be stated explicitly. We leave the definition of the length scale open until we have established results from which we may calibrate a length scale. We introduce gravitational dimensionless quantities, achieved in a simple way by putting \(g=1\). This means that gravity sets the scale of acceleration. It is obvious that any sharp surface peak will experience a free fall with the gravitational acceleration. The unit of length can only be given implicitly by the parameters in the acceleration potential \(\varPhi \). From now on we work with a complex acceleration potential which we will denote as \(\varPhi = \phi + \mathrm{{i}} \psi \), where its real part \(\phi (x,y)\) is the flow potential and \(\psi (x,y)\) is the streamfunction. The potential \(\varPhi _1\) in the small-time expansion is thus written as \(\varPhi \) from now on.

From the dynamic free-surface condition (5) we have the dimensionless free-surface condition valid for the initial flow

$$\begin{aligned} \phi + y = 0,~~y=\eta (x,0), \end{aligned}$$
(7)

since the velocity field is initially zero. The dimensionless Bernoulli equation is therefore

$$\begin{aligned} p + \phi + y = 0, \end{aligned}$$
(8)

where the unit of dimensionless pressure p is \(\rho g L\). As already mentioned, the unit length L which will be specified implicitly in each computed case.

Among possible scenarios for non-breaking run-up, flows with mild gradients are the best candidates. Dipole potentials are the best candidates among multipoles, as they give single surface peaks without any neighboring surface trough. Thus, the natural case to investigate is the dipole with its image to satisfy the kinematic boundary condition along the slope. The single dipole has the complex potential with unit amplitude

$$\begin{aligned} \varPhi _\mathrm{{dipole}}(x,y;\alpha ) = \frac{\mathrm{{e}}^{\mathrm{{i}} \theta }}{z} \end{aligned}$$
(9)

where we introduce \(\theta \) as the angle of orientation of the single dipole. We introduce the complex variable

$$\begin{aligned} z = x + \mathrm{{i}} y, \end{aligned}$$
(10)

where i is the imaginary unit.

3.1 A pair of dipoles at a slope with angle \(\pi /4\)

We choose to start with explicit formulas for the dipole potential at a uniformly sloping beach with angle \(\pi /4\) measured with respect to the \(-x\) axis. An alternative definition of the same slope angle is \(3\pi /4\) if it is measured with respect to the \(+x\) axis.

By definition, the slope goes through the origin and is defined as \(y=-x\). The simplest dipole acceleration field that satisfies the boundary condition at the slope is given by the complex function

$$\begin{aligned} \varPhi _\mathrm{{parallel}}(z) = A \mathrm{{e}}^{3 \mathrm{{i}} \pi /4}\left( \frac{1}{z-Z} + \frac{1}{z+iZ^*}\right) , \end{aligned}$$
(11)

where the dimensionless amplitude A is real by definition. This function is the sum of two equal dipoles with the same orientation, which is parallel to the slope. The complex orientation factor for each dipole is \(\mathrm{{e}}^{3 \mathrm{{i}} \pi /4}\), which means that these two parallel dipoles are oriented in a direction that makes an angle of \((3 \pi )/4\) with the \(+x\) axis. Again we emphasize that the orientation of each dipole is measured with respect to the \(+x\) axis, while the slope angle is measured with respect to the \(-x\) axis.

The dipole that gives the flow is located in the point with the complex coordinate \(Z = X + \mathrm{{i}} Y\). Its image dipole is located in the point \(- \mathrm{{i}} Z^* = - Y - \mathrm{{i}} X\), to satisfy the kinematic boundary condition of zero normal velocity along the slope. Here \(Z^* = X - \mathrm{{i}} Y\) denotes the complex conjugate.

As a primary choice we use \((X,Y) = (0.2, 2)\) for the dipole location in the following figures. These choices give a length scale of order one for the run-up shapes and their dimensionless area S above the undisturbed water level \(y=0\).

Figure 1a shows the isobars for this acceleration potential of two parallel dipoles (11) aligned with the slope. According to Eq. (8) the isobars are defined by

$$\begin{aligned} \phi + y = - p = \mathrm{{constant}}. \end{aligned}$$
(12)

The free surface is included in this definition as the isobar of zero pressure. The free-surface peak has an angle of \(\pi /2\). This follows from complex function theory because the free surface represents an isoline for the real part of a complex function \(\varPhi - \mathrm{{i}} z\) in the complex z plane

$$\begin{aligned} Re(\varPhi - \mathrm{{i}} z) = 0. \end{aligned}$$
(13)

As we will demonstrate below, the surface peak represents a point where a closed loop branches out from this isoline.

Figure 1a also shows the initial streamline pattern represented by \(\psi = \mathrm{{constant}}\). We note that the peak is not very high compared with the water level outside the peak. The surface slope at the inside of the peak is, in fact, steeper than the surface slope at the outside of the peak. This is opposite to what we expect from a peaked run-up, revealing that Fig. 1a based on parallel dipoles cannot represent localized run-up along the sloping beach. By definition, the free surface level tends to \(y=0\) as \(x \rightarrow \infty \), but the domain with a quite high elevation in Fig. 1a) is much wider than it should be for run-up at a slope. We must, therefore, allow the dipole and its image to have other directions than parallel to the slope, attempting to model the highest possible run-up where a heap of fluid is concentrated along the sloping beach. We will generalize the formula (11) to allow an arbitrary direction of the dipole, so we introduce an angle \(\theta \) for a clockwise rotation of the dipole located in the point \(Z=X+\mathrm{{i}} Y\), giving the complex potential

$$\begin{aligned} \varPhi (z; \theta ) = A \left( \frac{\mathrm{{e}}^{\mathrm{{i}}(3 \pi /4-\theta )}}{z-X - \mathrm{{i}} Y} + \frac{\mathrm{{e}}^{\mathrm{{i}}(3 \pi /4+\theta )}}{z + \mathrm{{i}} X + Y }\right) = A \left( \frac{\mathrm{{e}}^{\mathrm{{i}}(3 \pi /4-\theta )}}{z-Z} + \frac{\mathrm{{e}}^{\mathrm{{i}}(3 \pi /4+\theta )}}{z + \mathrm{{i}} Z^* }\right) , \end{aligned}$$
(14)

since we have to rotate the image dipole an angle \(\theta \) in the counterclockwise direction to satisfy the kinematic condition at the slope.

Fig. 1
figure 1

Initial streamlines with isobars for two different dipole orientations when the slope angle is \(\pi /4\). The peaked free surface is the zero-pressure isobar. The locations of the dipoles are \((x, y) = (0.2, 2)\) and \((x, y) = (-2, -0.2)\). The flow amplitude A is given in the figure for each case. a The directions of both dipoles are parallel to the slope. b The directions of both dipoles are perpendicular to the slope (normal dipoles)

Full size image

3.1.1 The normal dipoles perpendicular to a slope with angle \(\pi /4\)

The dipole orientation perpendicularly to the slope deserves special attention because it gives the strongest spatial decay in the far field. We call this configuration where \(\theta =\pi /2\) the normal dipoles. It consists of the set of dipoles (14) where \(\theta =\pi /2\), given by the formula

$$\begin{aligned} \varPhi (z) = A \left( \frac{\mathrm{{e}}^{\mathrm{{i}} \pi /4}}{z-Z} + \frac{\mathrm{{e}}^{5 \mathrm{{i}} \pi /4}}{z+ \mathrm{{i}} Z^*}\right) = A \mathrm{{e}}^{\mathrm{{i}} \pi /4} \left( \frac{1}{z-Z} - \frac{1}{z + \mathrm{{i}} Z^*}\right) , \end{aligned}$$
(15)

where again the amplitude A has a real value so that the exponential factor takes case of the direction of the two dipoles with opposite sign. These two dipoles point along the same line. They are directed oppositely to one another, both perpendicular to the slope.

3.1.2 On normal dipoles giving an optimal configuration

We note the differences between the parallel dipoles potential (11) and the normal dipoles potential (15). The normal dipoles are given with an orientation factor \(\pi /4\), perpendicular to the slope, with opposite signs since they are directed oppositely along the same line. The parallel dipoles have a common orientation factor \((3 \pi )/4\); both directed parallel to the slope.

We do not intend to prove mathematically that the normal dipoles give the most relevant configuration for peaked run-up, but we can deliver physical arguments for it. Concerning the parallel dipoles, we first note their far-field behavior as \(\vert x \vert \rightarrow \infty \): they tend to merge into one single dipole located at the shoreline. This single-dipole far field tends too slowly to zero in the fluid. This has to do with the fact that a single dipole surrounds itself with a directionally biased far field, which is well-known from magnetism. The initial acceleration field from two parallel dipoles would not only be too strong along at the distant free surface, it would be even stronger along the sloping bottom. Two dipoles that have different directions, is the superposition of a parallel pair and a normal pair of dipoles. Only the strictly normal dipoles oppositely directed along the same line will avoid this anisotropic bias. Their merged quadrupole far-field is isotropic in this sense, that it has no bias with respect to any two orthogonal directions. Two normal dipoles serve to lift the free surface gently locally, avoiding strong gradients. Moreover, they will give the isotropic type of quadrupole far-field behavior, avoiding the artificially slow decay of parallel dipoles. We do not consider higher multipoles as an option. Thus no further physical arguments in favor of the normal dipoles are needed, since their behavior is fully satisfying.

In Fig. 1, we show the initial isobars and streamlines for these two cases with different dipole orientations, where the slope angle is \(\pi /4\). As already mentioned, Fig. 1a shows the parallel dipoles, represented by the complex potential (11). Figure 1b shows the normal dipoles, represented by the complex potential (15). The far-field behavior is very different because the two parallel dipoles have a dipole far field, while the two normal dipoles produce a quadrupole far field. The quadrupole gives the strongest far-field decay, which we see from Fig. 1a and b by comparing the far-field convergence towards zero surface elevation for these two cases with one another. The set of two oppositely directed normal dipoles is the only option available for generating a quadrupole far-field, which means that it represents an optimal concentration of fluid along the slope.

The peaked free surface is the zero-pressure isobar. There is a positive normal derivative of the pressure at the surface, being directed into the fluid, with one exception: At the surface peak, the pressure gradient is zero, implying that the fluid particle at the peak experiences initial free fall under gravity. The initial streamline at the surface peak must, therefore, be vertical, which is what we see in Fig. 1. There is a dividing streamline that approaches a stagnation point at the slope, meeting the slope at a right angle. When this stagnation point exists within the fluid domain, it separates the bulk of fluid in downward acceleration from a small amount of fluid with opposite initial motion, in the upward direction along the slope. The parallel dipoles (Fig. 1a) sum up to generate a curved dividing streamline. The normal dipoles (Fig. 1b) have a straight dividing streamline from one dipole to the other, meeting the slope at a right angle halfway between the two dipole locations.

In Fig. 1, we have marked the two dipoles, with their orientations. The flow is driven by the primary dipole above the free surface, located in the point \(z = X + \mathrm{{i}} Y\). The image dipole in the point \(z = - Y - \mathrm{{i}} X\) serves the purpose of satisfying the boundary condition at the sloping beach \(y = - x\) with a slope angle of \(\pi /4\). The dipoles in Fig. 1 are marked with double arrows, to illustrate the situation just before and just after the stagnant situation with a peaked free surface at \(t=0\). Each light blue arrow represents the dipole direction for the terminating upward flow at \(t=0^-\), where the deceleration of the upward flow is finished so that the fluid motion stops everywhere. Each dark blue arrow represents the dipole direction for the starting downward acceleration at \(t=0^+\).

Figure 1a shows the stagnant peaked surface shape for two parallel dipoles, where there is a dividing streamline with a circular shape meeting the slope at a right angle. This circular streamline goes through the primary dipole and continues as a circular image streamlines on the other side of the slope, where it intersects the image dipole. All streamlines have their origin in the dipole outside the fluid domain, but only the dividing streamline has this simple circular shape in Fig. 1a. Figure 1b depicts an even simpler situation, where the dividing streamline is part of the straight line joining the primary dipole to the image dipole, and its path outside the fluid domain is included in the figure as a dashed line.

Physically, this straight dividing streamline is important because it separates the dominating fluid mass in downward acceleration (for \(t=0^+\)) from a small fluid mass near its tip, which will actually start an early upward sliding along the slope, against the gravitational pull. There is an angle limit for the sloping beach, above which no upward sliding is possible, and it will be discussed below.

3.1.3 The stagnant fluid model of normal dipoles

We have now selected the normal dipoles, which we consider as the most relevant class of acceleration potentials for representing the highest non-breaking fluid shapes to be released from rest along a uniform slope.

The assumption that the entire fluid flow stops at \(t=0\) is, of course, an idealization, but it does not have to be far from reality for a wave packet that does not break without vorticity being generated in the bulk of the fluid (disregarding vorticity diffusion from the rigid bottom). If the surface itself comes to a complete halt with zero surface velocity at \(t=0\), we know from potential theory that the bulk fluid will also be motionless everywhere. Less realistic than the assumption of zero surface velocity is the assumption that a sharp surface peak exists at \(t=0\), since this is a singular and inherently unstable situation, just at the edge of breaking. Any situation beyond the peaked surface will imply surface breaking since the peaked surface represents a situation which is as close to breaking as possible. The isobars just below the peaked shape will also represent possible situations of free surfaces for the almost highest non-breaking wave. We focus on the peaked surface shape because it gives a one parameter problem for the normal dipoles, where the angle of the sloping beach is the only parameter.

The set of normal dipoles share by Eq. (15) an orientation factor \(\mathrm{{e}}^{\mathrm{{i}} \pi /4}\), which is convenient since it represents an angle of direction for the dipole, which is equal to the slope angle. The normal dipoles have a quadrupole-type far-field, which is an exclusive case with the strongest spatial decay. The normal dipoles, therefore, represents an optimal situation of concentrated run-up, i.e., the fluid mass piles up as much as possible along the slope. All the other dipole directions yield a dipole decay in the far-field, much less concentrated. We work exclusively with normal dipoles, and we will allow an arbitrary slope angle.

The dimensionless area S of the elevated fluid above the undisturbed free surface \(y=0\) is defined by

$$\begin{aligned} S = \int _{x_1}^\infty (\eta (x,0) - \mathrm{{max}}(-x,0)) \mathrm{{d}}x, \end{aligned}$$
(16)

where the integral includes all positive values of \(\eta (x,0)\), while \(\eta (x.0)\) is put equal to zero if there are values of x where it is negative. The lower limit of integration \(x=x_1\) is the waterline point where the initial free surface meets the slope. This definition means that the elevated fluid area is constricted by the slope \(y=-x\) for \(x<0\), while it is constricted by the undisturbed free surface \(y=0\) for \(x>0\). For the slope angle \(\pi /4\) in Fig. 1, the elevation \(\eta (x,0)\) represented in this figure is always positive, extending all the way to infinity. The normal dipoles represented in Fig. 1b give a rapid spatial decay of the quadrupole type, so we may truncate the area integral (16) by an approximation

$$\begin{aligned} S = \int _{x_1}^{x_\mathrm{{tr}}} (\eta (x,0) - \mathrm{{max}}(-x,0)) \mathrm{{d}}x, \end{aligned}$$
(17)

and in Table 1 we show how the numerical values for the area S converges with increasing truncation length \(x_\mathrm{{tr}}\). Table 1 also includes the coordinates \((x_c, y_c)\) of the centre of gravity for the elevated domain with area S. These coordinates are defined by

$$\begin{aligned}&x_c = S^{-1} \int _S x \left[ \eta (x,0) - \mathrm{{max}}(-x,0)\right] \mathrm{{d}}x, \end{aligned}$$
(18)
$$\begin{aligned}&y_c = \frac{1}{2} S^{-1} \int _S \left[ \eta (x,0)^2 - \mathrm{{max}}(-x,0)^2\right] \mathrm{{d}}x, \end{aligned}$$
(19)
$$\begin{aligned}&(x_c, y_c) = S^{-1} \int _S (x, y) \mathrm{{d}}x \, \mathrm{{d}}y, \end{aligned}$$
(20)

and these integrals are also truncated in Table 1, by applying \(x_\mathrm{{tr}}\) as an upper limit for x in the integration.

Figure 2 shows the stagnant free surface for normal dipoles with slope angle \(\pi /4\), repeating the configuration in Fig. 1b adding geometric parameters. We display the elevated area with color, and we mark three calculated points: The area centre \((x_c, y_c)\) which is needed for calculating the potential energy in the stagnant domain above the undisturbed water level \(y=0\). The waterline point \((x_1, y_1)\), which is the highest point of elevated fluid at the sloping beach. The peak \((x_2, y_2)\) where the surface has a right-angle peak. We prolong the isoline for the free surface in the complex z plane (\(z=x + i y\)), showing that this curve has a loop that intersects the upper dipole point \((X, Y) = (0.2, 2)\).

3.1.4 Earlier studies of run-up for the slope angle \(\pi /4\)

We have noted that a slope angle \(\alpha = \pi /4\) is exceptional, giving an elevated mass with the strongest far-field decay of its surface elevation, according to our theory. Several numerical studies have dealt with this particular slope angle.

Kim et al. [3] studied numerically run-up on a beach with the slope angle \(\pi /4\). However, the solitary waves that they studied are quite long shallow-water waves, keeping their contact with the uniform channel depth while the wavefront advances along the sloping beach. The influence from the horizontal channel on the run-up prevents a direct comparison with our model since we work with a slope that extends down to infinite depth.

Table 1 Convergence of area S and centre of gravity \((x_c, y_c)\) as a function of numerical truncation length (\(x_\mathrm{{tr}}\)) for normal dipoles at a slope angle \(\pi /4\)
Full size table
Fig. 2
figure 2

Illustration of the calculated geometric parameters for the peaked surface shape with a slope angle \(\pi /4\), for normal dipoles located in \((x, y) = (0.2000, 2.0000)\) and \((x, y) = (-2.0000, -0.2000)\). These geometric parameters are: The waterline coordinates \((x_1, y_1) = (-1.0200, 1.0200)\). The surface peak \((x_2, y_2) = (-0.1750, 1.2250)\). The area centre \((x_c, y_c) = (1.0104, 0.5992)\). This figure extends the mathematical zero-pressure isobar (free surface contour) outside the fluid domain, where it goes in a closed loop through the dipole point \((X, Y) = (0.2000, 2.0000)\)

Full size image

Maiti and Sen [13] performed numerical simulations for the same slope angle \(\pi /4\). They used the boundary integral equation method introduced in [14], which allows an accurate description of overturning waves leading to breaking. Maiti and Sen [13] calculated snapshots of the elevation of a non-breaking run-up in their Fig. 9. Their Fig. 9a showed the stages of a relatively short solitary wave climbing to maximal run-up along the slope, while Fig. 9b showed the reflected wave in its run-down, starting from the maximal run-up along the slope. Their result for the last snapshot before maximal run-up is reasonably similar to our almost-highest wave in Fig. 1b, which is the isobar next to the peaked zero-pressure isobar. Our highest wave of stagnant peaked run-up is an idealized limit case at the edge of surface breaking when the wave motion stops. It cannot be reproduced exactly in a time-dependent nonlinear simulation. Nevertheless, the reasonable agreement between our Fig. 1b supports our claim that the pair of normal dipoles represents the physically preferred run-up. Thus the parallel dipoles of our Fig. 1a are of no other use than exposing their shortcomings, so we select exclusively the pair of normal dipoles from now on. The simulations in [13] agree much better with our predicted family of stagnant run-up than those in [3], because Maiti and Sen [13] considered relatively short solitary waves, which lose their contact with the channel bottom during the run-up.

A narrowing triangular wedge along the slope emerges in the late stages of run-up, as we see from the final snapshots in [13], their Fig. 9a. This is not necessarily in conflict with our Fig. 1b, since this climbing wedge may emerge from the fluid mass above the dividing streamline. Around the instant of stagnant run-up (when \(\vert t \vert \) is small), the fluid flow along the slope above the dividing streamline will be opposite to the gravitational pull on the fluid mass below the dividing streamline.

3.2 The normal dipoles at an arbitrary slope

We now consider more general slope angles, \(\alpha = \pi /4 + \beta \), allowing values of \(\alpha \) between 0 and \(\pi /2\).

From now on, we will consider only a set of normal dipoles, which we express in a modified coordinate system \((\hat{x}, \hat{y})\), rotated an angle \(\beta \) with respect to the original system. The slope keeps its slope angle \(\pi /4\) in the \((\hat{x},\hat{y})\) system, measured with respect to the \(\hat{x}\) axis. We introduce the new complex plane \(\hat{z} = \hat{x} + \mathrm{{i}} \hat{y}\). From Eq. (15) we have the potential of the normal dipoles in the new system

$$\begin{aligned} \varPhi (z;\beta ) = A \mathrm{{e}}^{\mathrm{{i}} \pi /4} \left( \frac{1}{\hat{z}(z;\beta )-\hat{Z}} - \frac{1}{\hat{z}(z;\beta )- \mathrm{{i}} \tilde{Z}}\right) , \end{aligned}$$
(21)

where we have introduced the notation \(\hat{z}(z;\beta )\) for the rotational transformations that we use to change the slope angle in a convenient way mathematically. By increasing the boundary slope angle \(\pi /4\) by an amount \(\beta \), we rotate each dipole the same angle \(\beta \) in the clockwise direction. This transformation formula is

$$\begin{aligned} \hat{x} = x \cos \beta - y \sin \beta ,~~ \hat{y} = x \sin \beta + y \cos \beta , \end{aligned}$$
(22)

rewritten in the complex form as

$$\begin{aligned} \hat{z}(z;\beta ) = z \mathrm{{e}}^{\mathrm{{i}} \beta }. \end{aligned}$$
(23)

The transformed dipole positions are

$$\begin{aligned} \hat{Z}= Z \mathrm{{e}}^{\mathrm{{i}} \beta },~~\tilde{Z} = Z^* \mathrm{{e}}^{\mathrm{{i}} \beta }. \end{aligned}$$
(24)

A is still a real amplitude in the formula for the potential (21), and by performing the rotation by an angle \(\beta \) we do not change the direction of gravity, which is still in the negative y direction so that the dimensionless dynamic condition (7) remains unchanged while we change the slope angle and the formula for the potential by the rotational transformation (23), which does not apply to the fixed direction of gravity.

Figure 3 shows the stagnant surface shapes with a peaked surface for the slope angles \(\alpha = 22.5^{\circ }\), \(45.0^{\circ }\), \(67.5^{\circ }\) and \(90.0^{\circ }\). The initial streamlines are displayed, with corresponding isobars, and the generating normal dipoles leave their signature by the straight dividing streamline in the first two cases. The last two cases have a too steep slope and no dividing streamline, which means that the entire fluid starts sliding in the downward direction at \(t=0^+\). In all four cases, the right-angle surface peak has a greater slope on the outside, steeper than its slope on the inside. Figure 3b repeats the solution from Fig. 1b.

By restricting our analysis to pairs of normal dipoles, the problem of released fluid shapes with a peaked surface becomes a one-parameter problem, where the angle \(\alpha \) is the only parameter. To arrive at a one-parameter family of surface shapes is a seemingly remarkable achievement, but one must keep in mind that the assumption of a completely motionless instantaneous state is highly idealized. Our choice of dipole position \((\hat{x},\hat{y}) = (0.2, 2)\) is arbitrary to the extent that it cannot give a consistent length scale. In the final section, we will therefore complete the rescaling of the tabulated lengths and area in Table 2 in order to provide a consistency of length scale, with dimensionless length based on total wave energy.

Fig. 3
figure 3

Initial isobars and streamlines for peaked stagnant fluid domiains, generated by a pair of normal dipoles. We show four different slope angles: a \(\alpha = 22.5^{\circ }\). b \(\alpha = 45.0^{\circ }\). c \(\alpha = 67.5^{\circ }\). d \(\alpha = 90.0^{\circ }\). The angles are marked in degrees. The respective flow amplitudes A are given

Full size image

3.3 On the far-field decay

The importance of a strong far-field decay has already been illustrated in Fig. 1. With a mild decay, the mass piled up along the slope will not be sufficiently concentrated in space. The surface elevation from parallel dipoles in Fig. 1a tends to zero as \(x^{-1}\) in the far field, and this very weak decay does not represent the empirical run-up phenomenon. The two normal dipoles is the only possible option for a dipole pair, since it gives a far field of the quadrupole type. The quadrupole far field in Fig. 1b has a convincing appearance, but it should be noted that the normal dipoles at the exact slope angle \(\pi /4\) is exceptional because of its \(x^{-4}\) far-field decay for the surface elevation. Other slope angles give milder far-field decay, of order \(x^{-3}\) as \(x \rightarrow \infty \).

There will always be a power-law far-field decay for multipole fields, which are acceleration fields with the gentle gradients suitable for describing non-breaking run-up. Among the multipole fields, the local dipoles are best suited for modeling a concentrated fluid mass along a slope.

Table 2 Dimensionless geometric parameters for the elevated fluid domains computed as functions of the slope angle \(\alpha = \pi /4 + \beta \)
Full size table

There is an apparent conflict between this power law for run-up along a slope, and an incoming solitary wave surrounded by its exponential decay. Tyvand and Storhaug [15] studied similar source flows in connection with free-surface Green functions for impulsive bottom deflections, and their analysis can easily be extended to dipoles. Their section 3 D treated a uniform slope ending at a constant depth. It is the same geometric configuration that we would have to consider in order to model the full run-up process of a solitary wave. Tyvand and Storhaug [15] illustrated the smooth transition from power-law decay to exponential decay through the corner where the slope ends and continues as a horizontal bottom.

3.4 Numerical results and analysis for very steep slopes

The vertical wall is a limit case where the run-up seems to be equivalent to the reflection of an incoming wave. Decent experimental and theoretical work has been published [16], for an incoming solitary wave. However, Fig. 3d defies comparisons with wave reflection on finite depth, since a shallow-water wave cannot be the cause of a stagnant run-up along a wall that extends to infinite depth.

The numerical results in Table 2 show that steep slopes will give run-up shapes that do not tend monotonically to zero elevation at infinity, as they experience a sign change at finite value of x before their far-field spatial decay takes place. We will now investigate this type of behavior for the simple case of a vertical wall, where the slope angle is \(\pi /2\). Zero elevation means that \(\phi (x,0,0) = 0\) according to Eq. (7), and for the normal dipoles at a vertical wall the condition \(\phi = 0\) at \(y=0\) can be written as

$$\begin{aligned} A \frac{x-X}{(x-X)^2 + (y-Y)^2} - A \frac{x+X}{(x+X)^2 + (y-Y)^2} = 0, \end{aligned}$$
(25)

which reduces to the simple relationship for the point (x, 0) where \(\eta (x,0,0) = 0\)

$$\begin{aligned} x = \sqrt{X^2 + Y^2} = \sqrt{4.04} = 2.00998, \end{aligned}$$
(26)

where we insert the chosen position \((\pm 0.2, 2)\) in the (x, y) coordinate system. This result is in excellent agreement with Table 2, where the table caption gives the points where the surface elevation changes sign and gives a finite upper limit for the area integration. Thereby, we have confirmed explicitly that the elevated fluid domain has a finite horizontal extension when the slope is sufficiently steep.

The slope is steep if all the fluid particles share the same sign in their vertical acceleration component. A precise definition of a steep slope is that its peaked stagnant fluid mass does not contain a dividing streamline. Figure 4 shows the limit case with slope angle \(\alpha _c = 54.7^{\circ }\), where the dividing streamline coincides with the waterline point. All steeper slopes with \(\alpha > \alpha _c\) will have downward motion of all fluid particles at \(t=0^+\). All milder slopes with \(\alpha < \alpha _c\) will contain a straight dividing streamline perpendicular to the slope, and the fluid above this dividing streamline start moving in the upward direction at \(t=0^+\).

Fig. 4
figure 4

Streamlines with isobars for the special case where the dividing streamline coincides with the waterline point \((x_1, y_1)\) at the sloping beach. The dashed line is a fictitious dividing streamline that connects the pair of normal dipoles generating the flow. The slope angle for this special case is \(\alpha _c = 54.7^{\circ }\). The surface peak coordinates \((x_2, y_2)\) and the flow amplitude A are included in the figure

Full size image

3.5 Perspectives for small slope angles

Moderate and small slope angles contain a straight dividing streamline intersecting the two normal dipoles. We will now discuss the stagnant fluid domains for the small slope angles displayed in Fig. 5, where we have stretched the vertical coordinate in the three first subfigures. Thereby all subfigures are given an appearance of having the same slope angle, for improved visual comparison. The respective slope angles represented in Fig. 5a–d are \(\alpha = 22.5^{\circ }, 15^{\circ }, 7.5^{\circ }, 2.88^{\circ }\). The last case is chosen because it is the slope angle for which Synolakis [5] reported good experimental results.

Fig. 5
figure 5

Initial streamlines with corresponding isobars for peaked stagnant surface shapes, showing four cases of small slope angles: a \(\alpha = 22.5^{\circ }\). b \(\alpha = 15^{\circ }\). c \(\alpha = 7.5^{\circ }\). d \(\alpha = 2.88^{\circ }\). The peaked free surface is the zero-pressure isobar, which decays to the undisturbed fluid level \(y=0\) as \(x \rightarrow \infty \). The flow is generated by a pair of normal dipoles at \((\hat{x},\hat{y} = (0.2, 2)\). The slope angles are given in degrees, with the associated flow amplitudes. Only the slope with angle \(7.5^{\circ }\) is shown in correct scaling, as the other subfigures are compressed or stretched to give equal apparent slopes. For the smallest slope \(\alpha = 2.88^{\circ }\) we calculate the waterline coordinates (\(x_1\), \(y_1\)) \(=\) (\(-8.300\), 0.418) and the surface peak coordinates (\(x_2\), \(y_2\)) \(=\) (\(-1.205\), 1.080)

Full size image

Figure 5d shows much higher amplitudes of stagnant fluid shapes than those of Fig. 9 in [5], which represents the greatest wave amplitude in the experiments by Synolakis. Experimentally, it is even more difficult to reproduce an idealized full conversion of wave energy into potential energy, than it is in purely numerical simulations. Figure 9c shown by Synolakis [5] is the last snapshot before breaking, where the crest amplitude is at its highest away from the sloping beach. It may be compared with the middle internal isobar in Fig. 5d, but the steepness of the experimental wave is very much smaller than the steepness of our postulated stagnant configuration.

There are a number of reasons that experimental waves do not proceed to stagnant run-up but start breaking at much lower steepness. One reason is that time-dependent nonlinearities at the free surface become relatively more important, the smaller the slope of the beach. Another closely related reason is that there cannot be a synchronized situation where kinetic energy converts simultaneously to potential energy everywhere in the elongated wave, as it climbs the slope. For the lowest interval of small slope angles, \(0<\alpha \le 15^{\circ }\), all internal isobars that can be reinterpreted as smooth surface shapes, contain a crest intersected by the dividing streamline. This means that our stagnant shapes would release a thin wedge of fluid (above the dividing streamline) to advance higher along the slope as the entire stagnant mass is released from rest under gravity. This peculiar behavior at small angles agrees with the observations by Synolakis [5] in his experiments: The highest run-up along the wall does not take place in synchronicity with the maximum surface crest in the bulk fluid, but this climbing fluid wedge seems to be catapulted out from the crest as it starts decaying. This bullwhip phenomenon is not compatible with our assumption of zero kinetic energy. Final stages of wetting run-up along the slope will then contain less potential energy than preceding stages where the highest elevation is located at a finite distance from the slope.

3.6 Rescaling the results with unit of energy as basis

The results so far are given in terms of a somewhat arbitrary length scale L, primarily governed by our choices of dimensionless coordinates for the dipoles. We will now pick a redefined precise length scale by rescaling the results in Tables 2 and 3, from which we choose a new length unit L so that the dimensionless potential energy in the elevated fluid mass is unity by definition.

Table 3 Dimensionless data from Table 2 applied for rescaling of geometric parameters, given for increasing slope angles \(\alpha = \pi /4 + \beta \)
Full size table
Table 4 Rescaled dimensionless geometric parameters for the elevated fluid domains computed as functions of the slope angle
Full size table

For a moment, we return to dimensional quantities for the purpose of rescaling the problem with new dimensionless quantities. The energy per length in the 2D stagnant elevated fluid is now denoted by E, given with dimension and measured in \(N = \mathrm{{kg}}~\mathrm{{m}}~\mathrm{{s}}^{-2}\). This energy is a potential energy in the gravity field and can be given as \(m g y_c^*\), where m is the stagnant mass of fluid per unit length and the vertical coordinate of the mass centre \(y_c^*\) is now given with dimension (marked with star to distinguish it from the dimensionless version). The dimensionless energy is now taken to be one by definition

$$\begin{aligned} \frac{E}{\rho g L^3} = \frac{m g y_c^*}{\rho g L^3} = 1, \end{aligned}$$
(27)

whereby we introduce a new dimensional length unit L defined by

$$\begin{aligned} L = \left( \frac{E}{\rho g}\right) ^{1/3}. \end{aligned}$$
(28)

Table 2 shows calculated values of dimensionless energy based on the previous arbitrary length unit, which was based on our choices of dimensionless dipole coordinates. Table 3 serves to calculate factor that we need for the final rescaling.

Table 4 shows the complete rescaled results that emerge from introducing the new length scale L based on the energy E. When we upscale all these values of energy by a factor \(f^3 = (y_c S)^{-1}\), they all become unity. The reason that we keep that single-valued column, is to offer a clarifying reminder that it represents the only fixed scaling in Tables 2–4.

We have introduced a dimensionless upscaling factor f designed for rescaling length according to the new length scale \(L = (E/(\rho g))^{1/3}\). An upscaling of all lengths means to multiply each of them by the upscaling factor f defined by \(f = (y_c S)^{-1/3}\). The area must also be upscaled, by a factor \(f^2 = (y_c S)^{-2/3}\).

We may now interpret the results from the viewpoint that a given water wave with prescribed total energy is approaching a sloping beach. We want to investigate the highest possible elevated surface shape from this given incoming wave that has a fixed energy content. Table 4 shows how the geometric parameters for stagnant configurations vary with the slope angle when the total energy is fixed.

In Table 4, we note the rescaled vertical coordinates fy of the key geometric parameters. We observe from Table 4 that the rescaled waterline position \(f y_1\) gets its maximum for the slope angle \(\alpha = 52.5^{\circ }\), which is slightly below the threshold value \(\alpha _c = 54.7^{\circ }\). For a given total energy of the wave in the run-up, there will be no potential energy left to be converted into a further advancement of fluid along the slope. Table 4 indicates that the values for \(f y_1\) are the theoretically maximal heights of the waterline for steep slopes with \(\alpha > 52.5^{\circ }\), when the total energy is the fixed physical parameter. Fixed total energy means that the incoming solitary wave is given.

It is interesting to consider the dependency of the rescaled surface peak elevation \(f y_2\) as a function of the slope angle \(\alpha \). In Table 4 the maximum value of \(f y_2\) occurs at the slope angle \(\alpha = 37.5^{\circ }\). The fact that the maximal peak height \(f y_2\) occurs at a smaller slope than the maximal waterline height \(f y_1\) has to do with the fact that the distance from the peak to the bottom is shorter for a milder slope.

A set of results that can be extracted from Table 4, is the difference \(f (x_2 - x_1)\). It is the rescaled horizontal distance between the contact point on the slope and the peak. A notable result is that this rescaled distance has a minimum slightly above unity when \(\alpha = 60 ^{\circ }\). The chosen energy unit is thus accompanied by an approximate length unit.

Concerning the rescaled area \(f^2 A\), it is a trivial fact that this area will increase as \(\alpha \) decreases. It is linked to another trivial fact, that the rescaled centre of gravity height \(f y_c\) goes to zero as the slope angle \(\alpha \) decreases.

4 Discussion and conclusions

In the present paper, we have elaborated on the very simple idea that maximal run-up of a solitary wave along a sloping beach may correspond to zero kinetic energy at the moment where run-up is maximal. The mathematical problem is simplified by considering only 2D flow along a beach with a constant slope angle and assume infinite depth apart from the sloping wall.

The approach of a stagnant run-up was initially presented by Spielvogel [8]. He went further with his modeling than we do. He studied the problem by backward numerical simulation in time the incoming wave in its last stages before its final stagnant run-up with maximal elevation. His simulations were based on nonlinear shallow-water equations.

Even though his choice of the initial configuration is legal, Spielvogel [8] did not consider the initial acceleration field, which is our present focus. He did not solve Laplace’s equation for the highly deformed initial surface. Thereby he downplayed the dispersive nature of the initial flow near the shoreline where the fluid layer loses contact with the slope, and the shallow-water approximation collapses. His shallow-water theory is better near the highest narrow wedge tip of fluid has practically zero dynamic pressure when it moves close to its highest position. Just before it stops and during its early downward motion, it slides along the slope with the component of the gravitational acceleration, \(g \sin \alpha \), which is a greater acceleration than the bulk of fluid that supports this tip. Much higher dynamic pressure than a shallow-water type of model allows, is needed for catapulting out the narrow wedge tip during the final stage of run-up. Otherwise, it would not have the speed for overcoming the strong backward acceleration. Our approach indicates that a shallow-water simulation of the stagnant tip will become inconsistent, since the steepness of the downward moving wave will become too great. This is what Spielvogel [8] experienced in the simulations, displayed in his Figs. 5–7. The front of the backward sliding wave became too steep for his simulations.

Nevertheless, we find the approach by Spielvogel [8] fruitful in that he attempted a compact physical modeling with few parameters. We have followed up his ideas by presenting a single-parameter approach for high elevations of concentrated fluid mass along a sloping beach, characterized by only the slope angle. Our model may represent an oversimplification of the complicated nonlinear run-up phenomena, but it can be interpreted as a highest possible configuration where the entire energy is stored instantaneously as gravitational potential energy. Our solution applies the exact nonlinear dynamic boundary condition at a deformed free surface. We present a compact dimensionless description of flow parameters and geometric lengths based on the total energy as the basic dimensional unit.

Carrier et al. [17], followed up by Kanoglu and Synolakis [18], also made numerical simulations by releasing an initial surface deflection at a uniformly sloping beach. However, in contrast to Spielvogel [8] their initial states were not states of stagnant run-up, but shallow-water wave packets that would climb upward to develop run-up.

It is not easy to compare our work with existing papers on run-up. A suggestion may be to take an almost-highest wave close to our stagnant free-surface configurations as the initial state for a numerical model like the ones described in [19, 20]. From a backward modeling in time, a class of waves may emerge for underlying causation of the class of stagnant run-up shapes that we have considered.

The selected stagnant acceleration flow field with arbitrary slope angle consists of two oppositely directed dipoles, resulting in a quadrupole far field. The induced free surface and isobars are computed from the nonlinear dynamic free-surface condition. We pick the peaked surface shape as a one-parameter description of stagnant fluid shapes, dependent only on the slope angle of the beach. Our suggested one-parameter classification is a qualitative contribution to this very complicated field of research. We have identified a criterion for defining a steep slope, with a slope angle steeper than \(54.7^{\circ }\). The initial flow is purely downward along a steep slope, whereas all milder slopes have a dividing streamline above which there will be an initial wedge that will climb further along the slope while the bulk fluid starts sliding down.

Only the peaked surface represents a one-parameter family characterized by the slope angle alone. Isobars below the surface may represent a broader family of free-surfaces shapes, if their contour can be extended continuously to great distances from the slope where the pressure will be close to hydrostatic.

The established literature on tsunami waves and run-up on beaches has now reached an enormous size, and elementary causal approaches like that of Spielvogel [8] become rarer and rarer. The mathematical models in the field are both diversified and highly advanced. As such, they need to be complemented by compact dimensional analyses with few parameters, involving more explicit physical postulates of cause and effect.