Skip to main content
SpringerLink
Log in

Influence of initial geometric imperfection on static and free vibration analyses of porous FG nanoplate using an isogeometric approach

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

In this paper, the size-dependent analysis of geometrically imperfect porous functionally graded (FG) nanoplates is studied by an isogeometric approach based on a new refined plate theory. Simultaneous effects of initial geometric imperfection and porosity on the natural frequency and deflection of the FG nanoplates are investigated. The initial geometric imperfection is considered as an initial curvature and modeled by an analytical function in the governing equations of the nanoplate. Material properties of porous FG nanoplate are defined by a modified power-law function, and two types of distribution for porosity are used. A four-variable refined plate theory with a new polynomial shape function is proposed. Based on Hamilton’s principle, a weak form of static and free vibration problem for nonlocal plate is derived. The discrete system of equations is solved by an isogeometric approach based on NURBS basis functions, and the accuracy of the present study is verified by comparing the results with solutions given in published papers. Present results indicate the importance of porosity parameter, porosity distributions, nonlocal parameter, material index, plate geometrical parameters, and specially imperfection amplitude on the static and free vibration behavior of FG nanoplates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Availability of data and material

Not applicable.

Code availability

Not applicable.

Abbreviations

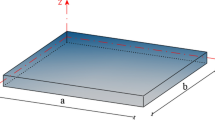
a, b, h :

Length, width, and thickness of the plate

\({C}_{ij}\) :

Elastic coefficients

\({D}^{b}\) , \({D}^{s}\) :

Material matrices

E :

Young’s modulus

F :

Global load vector

G e :

Effective shear modulus

I i :

Mass moments of inertia

K :

Global stiffness matrix

K e :

Effective Bulk modulus

M :

Global mass matrix

m :

Mass matrix

n :

Material index

p, q :

Order of NURBS function in two directions

\({P}_{I}\) :

Control point

\({R}_{I}\) :

NURBS basis function

\({u}_{I}\) :

Degrees of freedom vector of the control point I

u 0, v 0 :

Mid-plane displacements in x-, y-direction

\({V}_{c}, {V}_{m}\) :

Volume fraction of ceramic and metal

\({w}^{b}, {w}^{s}\) :

Transverse bending and shear displacements

\({w}^{i}\) :

Initial geometric imperfection

\(\stackrel{-}{w}\) :

Non-dimensional deflection

\(\alpha \) :

Porosity volume fraction

\(\gamma :\) :

Out of plane shear strain

\(\delta U, \delta V, \delta T\) :

The variation of strain energy, work done by external forces, and kinetic energy

\({\varepsilon }^{b}\) :

In-plane strain

\({\xi }^{*}\) :

Imperfection amplitude

\(\xi ,\eta \) :

Parametric spaces

\(\mu \) :

Nonlocal parameter

\(\upsilon \) :

Poisson’s ratio

\(\stackrel{-}{\omega }\) :

Non-dimensional frequency

\(\rho \) :

Density

References

  1. Natarajan S, Chakraborty S, Thangavel M, Bordas S, Rabczuk T (2012) Size-dependent free flexural vibration behavior of functionally graded nanoplates. Comput Mater Sci 65:74–80. https://doi.org/10.1016/j.commatsci.2012.06.031

    Article  Google Scholar 

  2. Daneshmehr A, Rajabpoor A, Hadi A (2015) Size-dependent free vibration analysis of nanoplates made of functionally graded materials based on nonlocal elasticity theory with high order theories. Int J Eng Sci 95:23–35. https://doi.org/10.1016/j.ijengsci.2015.05.011

    Article  MathSciNet  MATH  Google Scholar 

  3. Shahverdi H, Barati MR (2017) Vibration analysis of porous functionally graded nanoplates. Int J Eng Sci 120:82–99. https://doi.org/10.1016/j.ijengsci.2017.06.008

    Article  MathSciNet  MATH  Google Scholar 

  4. Wattanasakulpong N, Ungbhakorn V (2014) Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerosp Sci Technol 32:111–120. https://doi.org/10.1016/j.ast.2013.12.002

    Article  Google Scholar 

  5. Radwan AF (2019) Quasi-3D integral model for thermomechanical buckling and vibration of FG porous nanoplates embedded in an elastic medium. Int J Mech Sci 157–158:320–335. https://doi.org/10.1016/j.ijmecsci.2019.04.031

    Article  Google Scholar 

  6. Rezaei AS, Saidi AR (2015) Exact solution for free vibration of thick rectangular plates made of porous materials. Compos Struct 134:1051–1060. https://doi.org/10.1016/j.compstruct.2015.08.125

    Article  Google Scholar 

  7. Yang J, Chen D, Kitipornchai S (2018) Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos Struct 193:281–294. https://doi.org/10.1016/j.compstruct.2018.03.090

    Article  Google Scholar 

  8. Phung-Van P, Thai CH, Ferreira AJM, Rabczuk T (2020) Isogeometric nonlinear transient analysis of porous FGM plates subjected to hygro-thermo-mechanical loads. Thin-Walled Struct 148:106497. https://doi.org/10.1016/j.tws.2019.106497

    Article  Google Scholar 

  9. Mechab B, Mechab I, Benaissa S, Ameri M, Serier B (2016) Probabilistic analysis of effect of the porosities in functionally graded material nanoplate resting on Winkler-Pasternak elastic foundations. Appl Math Model 40(2):738–749. https://doi.org/10.1016/j.apm.2015.09.093

    Article  MathSciNet  MATH  Google Scholar 

  10. Fung CP, Chen CS (2006) Imperfection sensitivity in the nonlinear vibration of functionally graded plates. Eur J Mech A/Solids 25(3):425–436. https://doi.org/10.1016/j.euromechsol.2006.01.003

    Article  MATH  Google Scholar 

  11. Yamaki N, Chiba M (1983) Nonlinear vibrations of a clamped rectangular plate with initial deflection and initial edge displacement- part I: theory. Thin-Walled Struct 1(1):3–29. https://doi.org/10.1016/0263-8231(83)90003-4

    Article  Google Scholar 

  12. Kitipornchai S, Yang J, Liew KM (2004) Semi-analytical solution for nonlinear vibration of laminated FGM plates with geometric imperfections. Int J Solids Struct 41(9–10):2235–2257. https://doi.org/10.1016/j.ijsolstr.2003.12.019

    Article  MATH  Google Scholar 

  13. Chen CS, Hsu CY (2007) Imperfection sensitivity in the nonlinear vibration oscillations of initially stressed plates. Appl Math Comput 190(1):465–475. https://doi.org/10.1016/j.amc.2007.01.069

    Article  MathSciNet  MATH  Google Scholar 

  14. Gupta A, Talha M (2016) An assessment of a non-polynomial based higher order shear and normal deformation theory for vibration response of gradient plates with initial geometric imperfections. Compos B 107:141–161. https://doi.org/10.1016/j.compositesb.2016.09.071

    Article  Google Scholar 

  15. Gupta A, Talha M (2017) Nonlinear flexural and vibration response of geometrically imperfect gradient plates using hyperbolic higher-order shear and normal deformation theory. Compos B 123:241–261. https://doi.org/10.1016/j.compositesb.2017.05.010

    Article  Google Scholar 

  16. Jalali SK, Jomehzadeh E, Pugno NM (2016) Influence of out-of-plane defects on vibration analysis of graphene sheets: molecular and continuum approaches. Superlattices Microstruct 91:331–344. https://doi.org/10.1016/j.spmi.2016.01.023

    Article  Google Scholar 

  17. Chasiotis I, Knauss WG (2003) The mechanical strength of polysilicon films: part 2 size effects associated with elliptical and circular perforations. J Mech Phys Solids 51(8):1551–1572. https://doi.org/10.1016/S0022-5096(03)00050-4

    Article  Google Scholar 

  18. Eringen AC (2002) Nonlocal continuum field theories. Springer, NewYorkhttps://doi.org/10.1007/b97697

    MATH  Google Scholar 

  19. Sarrami-Foroushani S, Azhari M (2016) Nonlocal buckling and vibration analysis of thick rectangular nanoplates using finite strip method based on refined plate theory. Acta Mech 227:721–742. https://doi.org/10.1007/s00707-015-1482-4

    Article  MathSciNet  MATH  Google Scholar 

  20. Analooei HR, Azhari M, Sarrami-Foroushani S, Heidarpour A (2020) On the vibration and buckling analysis of quadrilateral and triangular nanoplates using nonlocal spline finite strip method. J Braz Soc Mech Sci Eng 42:149. https://doi.org/10.1007/s40430-020-2245-2

    Article  Google Scholar 

  21. Bakhshalizadeh H, Ghadiri M (2020) Size-dependent vibration behavior of graphene sheet with attached spring-mass and damper system based on the nonlocal Eringen theory. Mech Adv Mater Struct. https://doi.org/10.1080/15376494.2020.1780525

    Article  Google Scholar 

  22. Soleimani A, Naei MH, Mashhadi MM (2017) Nonlocal postbuckling analysis of graphene sheets with initial imperfection based on first order shear deformation theory. Results Phys 7:1299–1307. https://doi.org/10.1016/j.rinp.2017.03.003

    Article  Google Scholar 

  23. Bastami M, Behjat B (2018) Free vibration and buckling investigation of piezoelectric nano-plate in elastic medium considering nonlocal effects. J Braz Soc Mech Sci Eng 40:281

    Article  Google Scholar 

  24. Shahbaztabar A, Rahbar Ranji A (2019) Vibration analysis of functionally graded rectangular plates partially resting on elastic supports using the first-order shear deformation theory and differential quadrature element method. J Braz Soc Mech Sci Eng 41:102. https://doi.org/10.1007/s40430-019-1600-7

    Article  Google Scholar 

  25. Chai Y, Li F, Song Z (2019) Nonlinear vibrations, bifurcations and chaos of lattice sandwich composite panels on Winkler-Pasternak elastic foundations with thermal effects in supersonic airflow. Meccanica 54:919–944. https://doi.org/10.1007/s11012-019-00995-4

    Article  MathSciNet  Google Scholar 

  26. Nguyen TN, Ngo TD, Nguyen-Xuan H (2017) A novel three-variable shear deformation plate formulation: theory and Isogeometric implementation. Comput Methods Appl Mech Eng 326:376–401. https://doi.org/10.1016/j.cma.2017.07.024

    Article  MathSciNet  MATH  Google Scholar 

  27. Senthilnathan NR, Lim SP, Lee KH, Chow ST (1987) Buckling of shear-deformable plates. AIAA J 25:1268–1271. https://doi.org/10.2514/3.48742

    Article  Google Scholar 

  28. Zenkour AM (2013) A simple four-unknown refined theory for bending analysis of functionally graded plates. Appl Math Model 37(20–21):9041–9051. https://doi.org/10.1016/j.apm.2013.04.022

    Article  MathSciNet  MATH  Google Scholar 

  29. Barati MR, Shahverdi H (2018) Nonlinear thermal vibration analysis of refined shear deformable FG nanoplates: two semi-analytical solutions. J Braz Soc Mech Sci Eng 40:64. https://doi.org/10.1007/s40430-018-0968-0

    Article  Google Scholar 

  30. Xue Y, Jin G, Ding H, Chen M (2018) Free vibration analysis of in-plane functionally graded plates using a refined plate theory and isogeometric approach. Compos Struct 192:193–205. https://doi.org/10.1016/j.compstruct.2018.02.076

    Article  Google Scholar 

  31. Liu Z, Wang C, Duan G, Tan J (2019) A new refined plate theory with isogeometric approach for the static and buckling analysis of functionally graded plates. Int J Mech Sci 161–162:105036. https://doi.org/10.1016/j.ijmecsci.2019.105036

    Article  Google Scholar 

  32. Tran HQ, Vu VT, Tran MT, Nguyen-Tri P (2020) A new four-variable refined plate theory for static analysis of smart laminated functionally graded carbon nanotube reinforced composite plates. Mech Mater 142:103294. https://doi.org/10.1016/j.mechmat.2019.103294

    Article  Google Scholar 

  33. Belkorissat I, Houari MSA, Tounsi A, Bedia EAA, Mahmoud SR (2015) On vibration properties of functionally graded nano-plate using a new nonlocal refined four-variable model. Steel Compos Struct 18(4):1063–1081. https://doi.org/10.12989/scs.2015.18.4.1063

    Article  Google Scholar 

  34. Barati MR, Zenkour AM, Shahverdi H (2016) Thermo-mechanical buckling analysis of embedded nanosize FG plates in thermal environments via an inverse cotangential theory. Compos Struct 141:203–212. https://doi.org/10.1016/j.compstruct.2016.01.056

    Article  Google Scholar 

  35. Barati MR, Shahverdi H (2016) A four-variable plate theory for thermal vibration of embedded FG nanoplates under non-uniform temperature distributions with different boundary conditions. Struct Eng Mech 60(4):707–727. https://doi.org/10.12989/sem.2016.60.4.707

    Article  Google Scholar 

  36. Bouazza M, Becheri T, Boucheta A, Benseddiq N (2016) Thermal buckling analysis of nanoplates based on nonlocal elasticity theory with four-unknown shear deformation theory resting on Winkler-Pasternak elastic foundation. Int J Comput Methods Eng Sci Mech 17(5–6):362–373. https://doi.org/10.1080/15502287.2016.1231239

    Article  MathSciNet  Google Scholar 

  37. Bouazza M, Zenkour AM, Benseddiq N (2018) Closed-from solutions for thermal buckling analyses of advanced nanoplates according to a hyperbolic four-variable refined theory with small-scale effects. Acta Mech 229:2251–2265. https://doi.org/10.1007/s00707-017-2097-8

    Article  MathSciNet  MATH  Google Scholar 

  38. Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement. Comput Methods Appl Mech Eng 194(39–41):4135–4195. https://doi.org/10.1016/j.cma.2004.10.008

    Article  MathSciNet  MATH  Google Scholar 

  39. Yin S, Yu T, Bui TQ, Zheng X, Tanaka S (2016) In-plane material inhomogeneity of functionally graded plates: a higher-order shear deformation plate isogeometric analysis. Compos B 106:273–284. https://doi.org/10.1016/j.compositesb.2016.09.008

    Article  Google Scholar 

  40. Tornabene F, Fantuzzi N, Bacciocchi M (2017) A new doubly-curved shell element for the free vibrations of arbitrarily shaped laminated structures based on weak formulation isogeometric analysis. Compos Struct 171:429–461. https://doi.org/10.1016/j.compstruct.2017.03.055

    Article  Google Scholar 

  41. Tan P, Nguyen-Thanh N, Zhou K (2017) Extended isogeometric analysis based on Bézier extraction for an FGM plate by using the two-variable refined plate theory. Theor Appl Fract Mech 89:127–138. https://doi.org/10.1016/j.tafmec.2017.02.002

    Article  Google Scholar 

  42. Phung-Van P, Lieu QX, Nguyen-Xuan H, Abdel Wahab M (2017) Size-dependent isogeometric analysis of functionally graded carbon nanotube-reinforced composite nanoplates. Compos Struct 166:120–135. https://doi.org/10.1016/j.compstruct.2017.01.049

    Article  Google Scholar 

  43. Thai CH, Ferreira AJM, Tran TD, Phung-Van P (2019) A size-dependent quasi-3D isogeometric model for functionally graded graphene platelet-reinforced composite microplates based on the modified couple stress theory. Compos Struct. https://doi.org/10.1016/j.compstruct.2019.111695

    Article  Google Scholar 

  44. Thanh CL, Tran LV, Vu-Huu T et al (2019) The size-dependent thermal bending and buckling analyses of composite laminate microplate based on new modified couple stress theory and isogeometric analysis. Comput Methods Appl Mech Eng. https://doi.org/10.1016/j.cma.2019.02.028

    Article  MathSciNet  MATH  Google Scholar 

  45. Thanh CL, Ferreira AJM, Abdel Wahab M (2019) A refined size-dependent couple stress theory for laminated composite micro-plates using isogeometric analysis. Thin-Walled Struct 145:106427. https://doi.org/10.1016/j.tws.2019.106427

    Article  Google Scholar 

  46. Thai CH, Ferreira AJM, Phung-Van P (2020) Free vibration analysis of functionally graded anisotropic microplates using modified strain gradient theory. Eng Anal Bound Elem 117:284–298. https://doi.org/10.1016/j.enganabound.2020.05.003

    Article  MathSciNet  MATH  Google Scholar 

  47. Nguyen-Xuan H, Tran LV, Thai CH, Kulasegaram S, Bordas SPA (2014) Isogeometric analysis of functionally graded plates using a refined plate theory. Compos B 64:222–234. https://doi.org/10.1016/j.compositesb.2014.04.001

    Article  Google Scholar 

  48. Tran LV, Thai CH, Le HT, Gan BS, Lee J, Nguyen-Xuan H (2014) Isogeometric analysis of laminated composite plates based on a four-variable refined plate theory. Eng Anal Bound Elem 47:68–81. https://doi.org/10.1016/j.enganabound.2014.05.013

    Article  MathSciNet  MATH  Google Scholar 

  49. Thai CH, Zenkour AM, Abdel Wahab M, Nguyen-Xuan H (2016) A simple four-unknown shear and normal deformations theory for functionally graded isotropic and sandwich plates based on isogeometric analysis. Compos Struct 139:77–95. https://doi.org/10.1016/j.compstruct.2015.11.066

    Article  Google Scholar 

  50. Nguyen NT, Hui D, Lee J, Nguyen-Xuan H (2015) An efficient computational approach for size-dependent analysis of functionally graded nanoplates. Comput Methods Appl Mech Engrg 297:191–218. https://doi.org/10.1016/j.cma.2015.07.021

    Article  MathSciNet  MATH  Google Scholar 

  51. Nguyen HX, Nguyen TN, Abdel Wahab M, Bordas SPA, Nguyen- Xuan H, Thuc PV (2017) A refined quasi-3D isogeometric analysis for functionally graded microplates based on the modified couple stress theory. Comput Meth Appl Mech Eng 313:904–940. https://doi.org/10.1016/j.cma.2016.10.002

    Article  MathSciNet  MATH  Google Scholar 

  52. Phung-Van P, Ferreira AJM, Nguyen-Xuan H, Abdel-Wahab M (2017) An isogeometric approach for size-dependent geometrically nonlinear transient analysis of functionally graded nanoplates. Compos Part B Eng 118:125–134

    Article  Google Scholar 

  53. Norouzzadeh A, Ansari R (2018) Isogeometric vibration analysis of functionally graded nanoplates with the consideration of nonlocal and surface effects. Thin-Walled Struct 127:354–372. https://doi.org/10.1016/j.tws.2017.11.040

    Article  Google Scholar 

  54. Phung-Van P, Thai CH, Nguyen-Xuan H, Abdel-Wahab M (2019) Porosity-dependent nonlinear transient responses of functionally graded nanoplates using isogeometric analysis. Compos B 164:215–225. https://doi.org/10.1016/j.compositesb.2018.11.036

    Article  Google Scholar 

  55. Phung-Van P, Thai CH, Nguyen-Xuan H, Abdel-Wahab M (2019) An isogeometric approach of static and free vibration analyses for porous FG nanoplates. Eur J Mech/A Solids 78:103851. https://doi.org/10.1016/j.euromechsol.2019.103851

    Article  MathSciNet  MATH  Google Scholar 

  56. Phung-Van P, Thai CH, Abdel-Wahab M, Nguyen-Xuan H (2020) Optimal design of FG sandwich nanoplates using size-dependent isogeometric analysis. Mech Mater 142:103277. https://doi.org/10.1016/j.mechmat.2019.103277

    Article  Google Scholar 

  57. Nguyen TN, Thai CH, Nguyen-Xuan H (2016) On the general framework of high order shear deformation theories for laminated composite plate structures: a novel unified approach. Int J Mech Sci 110:242–255. https://doi.org/10.1016/j.ijmecsci.2016.01.012

    Article  Google Scholar 

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Central Tehran Branch, Islamic Azad University, Tehran, Iran

    Heidar Fazeli, Armen Adamian & Ahmad Hosseini-Sianaki

Authors
  1. Heidar Fazeli
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Armen Adamian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ahmad Hosseini-Sianaki
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Not applicable.

Corresponding author

Correspondence to Armen Adamian.

Ethics declarations

Conflict of interest

We wish to confirm that there are no known conflicts of interest associated with this publication, and there has been no financial support for this work that could have influenced its outcome.

Additional information

Technical Editor: Marcelo Areias Trindade.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

The governing equations for the local plate

$$ \begin{aligned} &\delta u_{0} : N_{xx,x} + N_{xy,y} = I_{1} \ddot{u}_{0} - I_{2} \ddot{w}^{{b}}{}_{,x} + I_{4} \ddot{w}^{s}{}_{,x}\\ &\delta v_{0} : N_{yy,y} + N_{xy,x} = I_{1} \ddot{v}_{0} - I_{2} \ddot{w}^{b}{}_{,y} + I_{4} \ddot{w}^{s}{}_{,y} \\ &\delta w^{b} : (N_{xx} w^{i}{}_{,x} ){}_{,x} + (N_{yy} w^{i}{}_{,y} ){}_{,y} + (N_{xy} w^{i}{}_{,y} ){}_{,x} + (N_{xy} w^{i}{}_{,x} ){}_{,y} + M^{b}{}_{xx,xx} + M^{b}{}_{yy,yy} - 2M^{b}{}_{xy,xy} \\&\qquad\qquad\qquad =- q + I_{2} \left( { \ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) - I_{3} \left( {\ddot{w}^{b}{}_{,xx} + \ddot{w}^{b}{}{}_{,yy} } \right) + I_{5} \left( {\ddot{w}^{s}{}{}_{,xx} + \ddot{w}^{s}{}_{,yy} } \right) + I_{1} \left( {\ddot{w}^{b} + \ddot{w}^{s} } \right)\\ &\delta w^{s} : -\,M^{s}{}_{xx,xx} - M^{s}{}_{yy,yy} - 2M^{s}{}_{xy,xy} + Q_{xz,x} + Q_{yz,y} + (M^{i}_{xx} w^{i}{}_{,x} ){}_{,x} + (M^{i}{}_{yy} w^{i}{}_{,y} ){}_{,y} + (M^{i}{}_{xy} w^{i}_{,x} ){}_{,y}+ (M^{i}{}_{xy} w^{i}{}_{,y} ){}_{,x}\\ &\qquad\qquad\qquad = - q - I_{4} \left( {\ddot{u}_{0,x} + \ddot{v}_{0,y} } \right) + I_{5} \left( {\ddot{w}^{b}{}_{,xx} + \ddot{w}^{b}{}_{,yy} } \right) - I_{6} \left( {\ddot{w}^{s}{}_{,xx} + \ddot{w}^{s}{}_{,yy} } \right) + I_{1} \left( {\ddot{w}^{b} + \ddot{w}^{s} } \right) \end{aligned} $$

The nonlocal governing equations in terms of displacement

$${\delta u}_{0}: {A}_{11}{({u}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,x})}_{,x}+{A}_{12} {({v}_{0,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,y})}_{,x}+{A}_{66}{({u}_{0,y}+{v}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,x})}_{,y}-{B}_{11}{{w}^{b}}_{,xxx}-{B}_{12}{{w}^{b}}_{,xyy}-2{B}_{66}{{w}^{b}}_{,xyy}+{E}_{11}{{w}^{s}}_{,xxx}+{E}_{12}{{w}^{s}}_{,xyy}+2{E}_{66}{{w}^{s}}_{,xyy}={\left(1-\mu {\nabla }^{2}\right)(I}_{1}{\ddot{u}}_{0}-{I}_{2}{{\ddot{w}}^{b}}_{,x}+{I}_{4}{{\ddot{w}}^{s}}_{,x})$$
$$\delta {v}_{0}: {A}_{21}{({u}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,x})}_{,y}+{A}_{22}{({v}_{0,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,y})}_{,y}+{A}_{66}{({u}_{0,y}+{v}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,x})}_{,x}-{B}_{21}{{w}^{b}}_{,xxy}-{B}_{22}{{w}^{b}}_{,yyy}-2{B}_{66}{{w}^{b}}_{,xxy}+{E}_{21}{{w}^{s}}_{,xxy}+{E}_{22}{{w}^{s}}_{,yyy}+2{E}_{66}{{w}^{s}}_{,xxy}={\left(1-\mu {\nabla }^{2}\right)(I}_{1}{\ddot{v}}_{0}-{I}_{2}{{\ddot{w}}^{b}}_{,y}+{I}_{4}{{\ddot{w}}^{s}}_{,y})$$
$${\delta {w}^{b}: A}_{11}{\left(({u}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,x}\right){{w}^{i}}_{,x})}_{,x}+{A}_{12}{\left(({v}_{0,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,y}\right){{w}^{i}}_{,x})}_{,x}+{A}_{21}{\left(({u}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,x}\right){{w}^{i}}_{,y})}_{,y}+{A}_{22}{\left(({v}_{0,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,y}\right){{w}^{i}}_{,y})}_{,y}+{A}_{66}\left[{\left(({u}_{0,y}+{v}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,x}\right){{w}^{i}}_{,y})}_{,x}+{\left(({u}_{0,y}+{v}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,x}\right){{w}^{i}}_{,x})}_{,y}\right]+{B}_{11}{({u}_{0,xx}+{{w}^{b}}_{,x}{{w}^{i}}_{,xx})}_{,x}+{B}_{12}{({v}_{0,xy}+{{w}^{b}}_{,xy}{{w}^{i}}_{,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,xy}-{{w}^{b}}_{,yy}{{w}^{i}}_{,x})}_{,x}+{B}_{21}{({u}_{0,xy}+{{w}^{b}}_{,xy}{{w}^{i}}_{,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,yy}-{{w}^{b}}_{,xx}{{w}^{i}}_{,y})}_{,y}+{B}_{22}{({v}_{0,yy}+{{w}^{b}}_{,y}{{w}^{i}}_{,yy})}_{,y}-2{B}_{66}\left[{u}_{0,xyy}+{v}_{0,xxy}+2{\left({{w}^{b}}_{,xy}{{w}^{i}}_{,y}\right)}_{,x}+2{\left({{w}^{b}}_{,xy}{{w}^{i}}_{,x}\right)}_{,y}+{\left({{w}^{b}}_{,x}{{w}^{i}}_{,yy}\right)}_{,x}{+\left({{w}^{b}}_{,y}{{w}^{i}}_{,xx}\right)}_{,y}\right]-{D}_{11}{{w}^{b}}_{,xxxx}-{D}_{12}{{w}^{b}}_{,xxyy}-{D}_{21}{{w}^{b}}_{,yyxx}-{D}_{22}{{w}^{b}}_{,yyyy}+4{D}_{66}{{w}^{b}}_{,xyxy}+{E}_{11}{\left({{w}^{s}}_{,xx}{{w}^{i}}_{,x}\right)}_{,x}+{E}_{12}{\left({{w}^{s}}_{,yy}{{w}^{i}}_{,x}\right)}_{,x}+{E}_{21}{\left({{w}^{s}}_{,xx}{{w}^{i}}_{,y}\right)}_{,y}+{E}_{22}{\left({{w}^{s}}_{,yy}{{w}^{i}}_{,y}\right)}_{,y}+2{E}_{66}\left[{\left({{w}^{s}}_{,xy}{{w}^{i}}_{,y}\right)}_{,x}+{\left({{w}^{s}}_{,xy}{{w}^{i}}_{,x}\right)}_{,y}\right]+{F}_{11}{{w}^{s}}_{,xxxx}+{F}_{12}{{w}^{s}}_{,xxyy}+{F}_{21}{{w}^{s}}_{,yyxx}+{F}_{22}{{w}^{s}}_{,yyyy}-4{F}_{66}{{w}^{s}}_{,xyxy}=\left(1-\mu {\nabla }^{2}\right)[-q+{I}_{2}\left({\ddot{u}}_{0,x}+{\ddot{v}}_{0,y}\right){-{I}_{3}\left({{\ddot{w}}^{b}}_{,xx}+{{\ddot{w}}^{b}}_{,yy}\right)+I}_{5}\left({{\ddot{w}}^{s}}_{,xx}+{{ \ddot{w}}^{s}}_{,yy}\right)+{I}_{1}\left({\ddot{w}}^{b}+{\ddot{w}}^{s}\right)]$$
$$\delta {w}^{s}: {-E}_{11}{({u}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,x})}_{,xx}{-E}_{12}{({v}_{0,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,y})}_{,xx}{-E}_{21}{({u}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,x})}_{,yy}{-E}_{22}{({v}_{0,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,y})}_{,yy}-2{E}_{66}{\left({u}_{0,y}+{v}_{0,x}+{{w}^{b}}_{,x}{{w}^{i}}_{,y}+{{w}^{b}}_{,y}{{w}^{i}}_{,x}\right)}_{,xy}+{F}_{11}{{w}^{b}}_{,xxxx}+{F}_{12}{{w}^{b}}_{,xxyy}+{F}_{21}{{w}^{b}}_{,yyxx}+{F}_{22}{{w}^{b}}_{,yyyy}+4{F}_{66}{{w}^{b}}_{,xyxy}-{H}_{11}{{w}^{s}}_{,xxxx}-{H}_{12}{{w}^{s}}_{,xxyy}-{H}_{21}{{w}^{s}}_{,yyxx}-{H}_{22}{{w}^{s}}_{,yyyy}-4{H}_{66}{{w}^{s}}_{,xyxy}-{Z}_{33}{w}^{s}+{{D}^{s}}_{44}{{w}^{s}}_{,yy}+{{D}^{s}}_{55}{{w}^{s}}_{,xx}=\left(1-\mu {\nabla }^{2}\right)[{-I}_{4}\left({\ddot{u}}_{0,x}+{\ddot{v}}_{0,y}\right){+{I}_{5}\left({{\ddot{w}}^{b}}_{,xx}+{{\ddot{w}}^{b}}_{,yy}\right)-I}_{6}\left({{\ddot{w}}^{s}}_{,xx}+{{ \ddot{w}}^{s}}_{,yy}\right)+{I}_{1}\left({\ddot{w}}^{b}+{\ddot{w}}^{s}\right)]$$

Appendix B

See (Fig. 

Fig. 12
figure 12

Flowchart of various steps involved in the solution process

Full size image

12).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fazeli, H., Adamian, A. & Hosseini-Sianaki, A. Influence of initial geometric imperfection on static and free vibration analyses of porous FG nanoplate using an isogeometric approach. J Braz. Soc. Mech. Sci. Eng. 43, 200 (2021). https://doi.org/10.1007/s40430-021-02847-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-021-02847-3

Keywords

Search

Navigation