Modeling the Effects of Latency Reversing Drugs During HIV-1 and SIV Brain Infection with Implications for the “Shock and Kill” Strategy

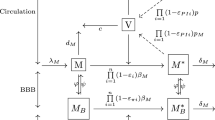
Abstract

Combination antiretroviral therapy (cART) has greatly increased life expectancy for human immunodeficiency virus-1 (HIV-1)-infected patients. Even given the remarkable success of cART, the virus persists in many different cells and tissues. The presence of viral reservoirs represents a major obstacle to HIV-1 eradication. These viral reservoirs contain latently infected long-lived cells. The “Shock and Kill” therapeutic strategy aims to reactivate latently infected cells by latency reversing agents (LRAs) and kill these reactivated cells by strategies involving the host immune system. The brain is a natural anatomical reservoir for HIV-1 infection. Brain macrophages, including microglia and perivascular macrophages, display productive HIV-1 infection. A mathematical model was used to analyze the dynamics of latently and productively infected brain macrophages during viral infection and this mathematical model enabled prediction of the effects of LRAs applied to the “Shock and Kill” strategy in the brain. The model was calibrated using reported data from simian immunodeficiency virus (SIV) studies. Our model produces the overarching observation that effective cART can suppress productively infected brain macrophages but leaves a residual latent viral reservoir in brain macrophages. In addition, our model demonstrates that there exists a parameter regime wherein the “Shock and Kill” strategy can be safe and effective for SIV infection in the brain. The results indicate that the “Shock and Kill” strategy can restrict brain viral RNA burden associated with severe neuroinflammation and can lead to the eradication of the latent reservoir of brain macrophages.

Appendices

Appendix A: Mathematical Results and Proofs

Using the theory of asymptotically autonomous differential equations (Thieme 1994; Castillo-Chavez and Thieme 1994), the asymptotic behaviors of system (1) are the same as the following two-dimensional system of differential equations in the bounded feasible region $D=\{ (x,y)\in {\mathbb {R}}^{2}_{+}: 0 \le x+y \le \frac{\lambda }{k} \}$:

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&= \lambda -kx-(1-\epsilon )\beta _{1}xy-\beta _{2}x\left( \frac{\lambda }{k}-x-y\right) = g(x, y),\\ \frac{\mathrm{d}y}{\mathrm{d}t}&= p(1-\epsilon )\beta _{1}xy -(k+\epsilon \gamma )y = h(x, y). \end{aligned} \end{aligned}$$

(8)

The Jacobian matrix of system (8) is

$$\begin{aligned} J = \begin{bmatrix} -k - (1 - \epsilon ) \beta _1 y + \beta _2 x - \beta _2 (\frac{\lambda }{k} - x - y) &{} - (1 - \epsilon ) \beta _1 x + \beta _2 x \\ p (1 - \epsilon ) \beta _1 y &{} p (1 - \epsilon ) \beta _1 x - k - \epsilon \gamma \end{bmatrix}. \end{aligned}$$

(9)

Theorem 1

• 1. If the control reproduction number $R_c < 1$, then the disease-free equilibrium $P_0$ is locally asymptotically stable. If $R_c > 1$, then $P_0$ is unstable.

• 2. If $R_c > 1$ and $R_{c1} > R_{c2}$, then the productive equilibrium $P_1$ is locally asymptotically stable.

• 3. If $R_c > 1$ and $R_{c1} < R_{c2}$, then the latent equilibrium $P_2$ is locally asymptotically stable.

Proof

The Jacobian matrix evaluated at $P_0$ is

$$\begin{aligned} J(P_0) = \begin{bmatrix} -k + \beta _2 \frac{\lambda }{k} &{} (\beta _2 - (1 - \epsilon \beta _1)) \frac{\lambda }{k} \\ 0 &{} p (1 - \epsilon ) \beta _1 \frac{\lambda }{k} - (k + \epsilon \gamma ) \end{bmatrix}. \end{aligned}$$

(10)

Since the matrix (10) is upper triangular, the eigenvalues of the matrix $J(P_0)$ are $\mu _1 = -k + \beta _2 \frac{\lambda }{k}$ and $\mu _2 = p (1 - \epsilon ) \beta _1 \frac{\lambda }{k} - (k + \epsilon \gamma )$. If $R_c < 1$, then $\mu _1, \mu _2 < 0$ and the disease-free equilibrium $P_0$ is locally asymptotically stable. If $R_c > 1$, then max$\{\mu _1, \mu _2 \} > 0$ and $P_0$ is unstable.

The Jacobian matrix evaluated at $P_1$ is

$$\begin{aligned} \begin{aligned} J(P_1)&= \begin{bmatrix} -k - (1 - \epsilon ) \beta _1 y_1 + \beta _2 x_1 - \beta _2 (\frac{\lambda }{k} - x_1 - y_1) &{} - (1 - \epsilon ) \beta _1 x_1 + \beta _2 x_1 \\ p (1 - \epsilon ) \beta _1 y_1 &{} p (1 - \epsilon ) \beta _1 x_1 - k - \epsilon \gamma \end{bmatrix} \\&= \begin{bmatrix} -k - (1 - \epsilon ) \beta _1 y_1 + \beta _2 x_1 - \beta _2 (\frac{\lambda }{k} - x_1 - y_1) &{} - (1 - \epsilon ) \beta _1 x_1 + \beta _2 x_1 \\ p (1 - \epsilon ) \beta _1 y_1 &{} 0 \end{bmatrix} \end{aligned} \end{aligned}$$

(11)

since $p (1 - \epsilon ) \beta _1 x_1 - k - \epsilon \gamma = \frac{(p(1 - \epsilon ) \beta _1)(k + \epsilon \gamma )}{p(1 - \epsilon ) \beta _1} - (k + \epsilon \gamma )$ = 0. If $R_c > 1$ and $R_{c1} > R_{c2}$, then $R_{c1}> 1 > \frac{R_{c2}}{R_{c1}}$ and by using the productive equilibrium $P_1$,

$$\begin{aligned} \begin{aligned} \text {tr}(\text {J}(P_1))&= -k - \frac{\lambda }{k} \beta _2 + 2 x_1 \beta _2 - ((1 - \epsilon ) \beta _1 - \beta _2) y_1 \\&= k (\frac{R_{c2}}{R_{c1}} - R_{c1}) \\&< 0 \end{aligned} \end{aligned}$$

(12)

and

$$\begin{aligned} \begin{aligned} \text {det}(\text {J}(P_1))&= ((1 - \epsilon ) \beta _1 - \beta _2) p (1 - \epsilon ) \beta _1 x_1 y_1\\&= (1 - \frac{1}{R_{c1}}) (1 - \frac{R_{c2}}{R_{c1}})\\&> 0. \end{aligned} \end{aligned}$$

(13)

By the Routh–Hurwitz condition, $P_1$ is locally asymptotically stable.

The Jacobian matrix evaluated at $P_2$ is

$$\begin{aligned} J(P_2) = \begin{bmatrix} k - \frac{\lambda }{k} \beta _2 &{} \frac{- (1 - \epsilon ) \beta _1 k}{\beta _2} + k\\ 0 &{} p (1 - \epsilon ) \beta _1 \frac{k}{\beta 2} - k - \epsilon \gamma \end{bmatrix}. \end{aligned}$$

(14)

Since the matrix (14) is upper triangular, the eigenvalues of the matrix 14 are $\mu _1 = k - \frac{\lambda }{k} \beta _2$ and $\mu _2 = p (1 - \epsilon ) \beta _1 \frac{k}{\beta 2} - k - \epsilon \gamma$. If $R_c > 1$ and $R_{c1} < R_{c2}$, then $\mu _1, \mu _2 < 0$ and the latent equilibrium $P_2$ is locally asymptotically stable.

$\square$

Theorem 2

If the control reproduction number $0 < R_c \le 1$, then the disease-free equilibrium $P_0$ is globally asymptotically stable in $\varGamma$.

Proof

When $0 < R_c \le 1$, $P_0$ is the only equilibrium.

Consider the Lyapunov function $L = y$. Then

$$\begin{aligned} {\dot{L}}&=y'=p(1-\epsilon )\beta _{1}xy- k y - \epsilon \gamma y \le (k + \epsilon \gamma ) y (R_{c1} - 1)\\&\le (k+\epsilon \gamma )y \big (R_c - 1\big ) \le 0. \end{aligned}$$

The maximal invariant set in $\{(x, y, l) \in \varGamma : {\dot{L}} = 0\}$ is the singleton $P_0$. By LaSalle’s invariance principle, all limit points of solutions belong to the largest invariant set in $\{(x, y, l) \in \varGamma : {\dot{L}} = 0\}$. Therefore, all solutions in $\varGamma$ converge to $P_0$ and $P_0$ is globally asymptotically stable in $\varGamma$.

$\square$

Theorem 3

If $R_c > 1$ and $R_{c1} > R_{c2}$, then the productive equilibrium $P_1$ is globally asymptotically stable in $\mathring{\varGamma }$. If $R_c > 1$ and $R_{c1} < R_{c2}$, then the latent equilibrium $P_2$ is globally asymptotically stable in $\varGamma$.

Proof

The asymptotic behaviors of system (1) in $\varGamma$ are the same as the asymptotic behaviors of system (8) in D. In system (8), let $\mathbf{f } (x, y) = (g(x, y), h(x, y))$.

Consider a scalar-valued function $\alpha (x, y) = \frac{1}{x y (\frac{\lambda }{k} - x - y)}$,

where $(x, y) \in \mathring{D} = \{(x, y): 0< x + y < \frac{\lambda }{k} \}$. For all $(x, y) \in \mathring{D}$,

$$\begin{aligned} div(\alpha \mathbf{f })&=\frac{\partial }{\partial x} (\alpha g) + \frac{\partial }{\partial y} (\alpha h)\\&= \frac{1}{x y (\frac{\lambda }{k} - x - y)} \left( \frac{- \lambda }{x} + \frac{\lambda - k x}{(\frac{\lambda }{k} - x - y)} - \frac{(1 - p) (1 - \epsilon ) \beta _1 x y}{(\frac{\lambda }{k} - x - y)} - \frac{(k + \epsilon \gamma ) y}{\frac{\lambda }{k} - x - y} \right) \\&< \frac{1}{x y (\frac{\lambda }{k} - x - y)} \left( \frac{- \lambda }{x} + k - \frac{(1 - p) (1 - \epsilon ) \beta _1 x y}{(\frac{\lambda }{k} - x - y)} - \frac{(k + \epsilon \gamma ) y}{\frac{\lambda }{k} - x - y} \right) \\&< \frac{1}{x y (\frac{\lambda }{k} - x - y)} \left( \frac{- \lambda }{x} + k \right) \\&= \frac{k}{x^2 y \left( \frac{\lambda }{k} - x - y\right) } (x - \frac{\lambda }{k})\\&< 0. \end{aligned}$$

Therefore, by Dulac’s criteria, system (8) has no closed orbit lying entirely in $\mathring{D}$. So, no periodic solutions can exist.

By the Poincare–Bendixson theorem, if $R_c > 1$ and $R_{c1} > R_{c2}$, all solutions with initial condition in $\mathring{D}$ must have $P_1$ as an $\omega$-limit point. Since $P_1$ is locally asymptotically stable, solutions that get close to $P_1$ must converge to $P_1$ and all $\omega$-limit sets in $\mathring{D}$ are equal to the singleton $\{ P_1 \}$. Therefore, $P_1$ is globally stable in $\mathring{D}$ when $R_c > 1$ and $R_{c1} > R_{c2}$.

Similarly, by using the Poincare–Bendixson theorem, if $R_c > 1$ and $R_{c1} < R_{c2}$, then $P_2$ is globally stable in $\mathring{D}$.

$\square$

Appendix B: Data Conversion

SIV brain viral DNA was measured in three different units (Clements et al. 2002; Zink et al. 2010; Graham et al. 2011; Clements et al. 2005): $\text {log}_{10}$ SIV DNA copy equivalents per 2 micrograms of total DNA, $\text {log}_{10}$ SIV DNA copy equivalents per 10,000 cells, and SIV DNA copy equivalents per microgram of total DNA.

The first and second SIV brain viral DNA units were converted to integrated SIV DNA per gram of brain tissue in the same fashion as described in the supplementary material of our previous modeling study (Roda et al. 2017). Since each SIV-infected brain macrophage is assumed to contain a single copy of integrated viral DNA, the integrated SIV DNA per gram of brain tissue is equal to the number of stably infected brain macrophages per gram of brain tissue.

For the third SIV brain viral DNA unit, these data were converted to integrated SIV DNA per gram of brain tissue in a similar way to the first SIV brain viral DNA unit. The SIV DNA copy equivalents per microgram of total DNA were converted to SIV DNA copy equivalents per gram of brain tissue by using the conversion that each gram of brain tissue contains 4 micrograms of total host genomic DNA. By using the ratio of integrated proviral DNA to total viral DNA (1:86) (Suspène and Meyerhans 2012) and our assumption that each SIV-infected brain macrophage is assumed to contain a single copy of integrated viral DNA, we obtain the number of stably infected brain macrophages per gram of brain tissue.

SIV brain viral RNA was measured in five different units (Avalos et al. 2016; Babas et al. 2003; Barber et al. 2006; Clements et al. 2002; Graham et al. 2011; Helke et al. 2005; Meulendyke et al. 2014; Witwer et al. 2009; Zink et al. 1999, 2005, 2010): SIV RNA copy equivalents per microgram of total RNA, $\text {log}_{10}$ SIV RNA copy equivalents per microgram of total RNA, SIV RNA copy equivalents per 2 micrograms of total RNA, $\text {log}_{10}$ SIV RNA copy equivalents per 2 micrograms of total RNA, and $10^6$ SIV RNA copy equivalents per microgram of total RNA. When the SIV brain viral RNA unit is not already in the form of SIV RNA copy equivalents per microgram of total RNA, they are converted to SIV RNA copy equivalents per microgram of total RNA by exponentiation. The SIV RNA copy equivalents per microgram of total RNA were converted to SIV RNA copy equivalents per gram of brain tissue by using the conversion that each gram of brain tissue contains 25 micrograms of total host genomic RNA.

Some SIV studies measured SIV brain viral DNA and RNA in multiple regions of the brain (Avalos et al. 2016; Clements et al. 2002; Graham et al. 2011; Helke et al. 2005; Witwer et al. 2009; Zink et al. 1999; Clements et al. 2005). For these SIV studies, the average SIV brain viral DNA and RNA across the brain regions was used. This was done so that the fitted system (1) and prediction using system (5) would be projecting the average viral dynamics per gram of brain tissue.

After these conversions are completed, the data for SIV RNA copies per gram of brain tissue and the estimated number of stably infected brain macrophages per gram of brain tissue are given in Table 5.

Table 5 SIV RNA copies per gram of brain tissue and estimated number of stably infected brain macrophages per gram of brain tissue at different times post-inoculation (p.i.)

Prior Distributions for Bayesian Inference

The prior distributions are listed in Table 6. The parameters $\beta _1$, $\beta _2$, k, and $x_0$ used the same uniform prior distributions as described in (Roda et al. 2017) and they are the following:

Table 6 Uniform prior distributions for parameters

$\beta _1 \sim U(1 \times 10^{-8}, 1 \times 10^{-4})$, $\beta _2 \sim U(1 \times 10^{-8}, 1 \times 10^{-4})$, $k \sim U(0.5, 10.22)$, and $x_0 \sim U(2.07 \times 10^{6}, 3.94 \times 10^{6})$. The constraint $\beta _2 < p \beta _1$ was used for the assumption that infection due to productively infected brain macrophages, $\beta _2$, is sufficiently larger than that due to latently infected brain macrophages, $\beta _1$. Since $x_0 = \frac{\lambda }{k}$, $\lambda$ is determined by $x_0$ and k. Simple linear regression is used to estimate, $\text {log}_{10} (y_0)$, by fitting the following linear model to the $\text {log}_{10}$ SIV DNA copies per gram data for untreated infection (row 1 in Table 2):

$$\begin{aligned} \text {log}_{10} (y) = \text {log}_{10} (y_0) + m_y t_y, \end{aligned}$$

(15)

where $\text {log}_{10} (y)$ is the $\text {log}_{10}$ SIV DNA copies per gram data for untreated infection, $\text {log}_{10} (y_0)$ is the intercept, $m_y$ is the slope, and $t_y$ is the independent variable time. The intercept of this regression model, $\text {log}_{10} (y_0)$, is estimated to be 1.045, and consequently, $y_0$ is estimated to be 11.1 and the chosen prior distribution is $y_0 \sim U(1, 11.1)$. It is assumed that $l_0 = 0$. The initial viral load is given by $v_0 = N y_0$ and consequently, $N = \frac{v_0}{y_0}$. Simple linear regression is used to estimate, $\text {log}_{10} (v_0)$, by fitting the following linear model to the $\text {log}_{10}$ SIV RNA copies per gram data for untreated infection (row 2 in Table 2):

$$\begin{aligned} \text {log}_{10} (v) = \text {log}_{10} (v_0) + m_v t_v, \end{aligned}$$

(16)

where $\text {log}_{10} (v)$ is the $\text {log}_{10}$ SIV RNA copies per gram data for untreated infection, $\text {log}_{10} (v_0)$ is the intercept, $m_v$ is the slope, and $t_v$ is the independent variable time. The intercept of this regression model, $\text {log}_{10} (v_0)$, is estimated to be 3.676 and hence $v_0$ is estimated to be $4.74 \times 10^3$. Since $v_0$ is estimated to be $4.74 \times 10^3$ and $y_0 \sim U(1, 11.1)$, $N \sim U(427, 4.74 \times 10^3)$. The cART effectiveness, $\epsilon$, varies between 0 and 1 and the prior distribution is $\epsilon \sim U(0.01, 1)$. The rate productively infected brain macrophages are deactivated once cART is applied, $\epsilon \gamma$, is unknown and a broad range is chosen for $\gamma \sim U(0.01, 200)$. The proportion of newly infected susceptible brain macrophages by productively infected brain macrophages that enter the productively infected population is assumed to be $p = 0.5$.

Model Fitting and Prediction Using Bayesian Inference

Bayesian inference is used to fit system (1) simultaneously to the SIV brain viral data for untreated and cART-exposed animals (data in the first eight rows of Table 2). Let $D_j = \{ d^{j}_1, \dots , d^{j}_{n_j} \}$ and $T_j = \{ t^{j}_1, \dots , t^{j}_{n_j} \}$ be the SIV brain viral data and times corresponding to the $j^{\text {th}}$ row of Table 2. Let $D = \{ D_1, \dots , D_8 \}$ and $T = \{ T_1, \dots , T_8 \}$.

System (1) was solved numerically by using the MATLAB function ode45 with the option setting odeset(“nonnegative,” 2) to ensure that numerically solved solutions have nonnegative values (Inc. 2019). The function ode45 is based on an explicit Runge–Kutta (4,5) formula.

There are four different scenarios being considered when system (1) is being fit simultaneously to the SIV brain viral data for untreated and cART-exposed animals: untreated SIV infection, SIV infection with cART initiated at 4 days p.i., SIV infection with cART initiated at 12 days p.i., and SIV infection with cART initiated at 42 days p.i. For untreated SIV infection, $\epsilon$ is set to zero in system (1). For the scenarios when cART is initiated at a certain time p.i., $\epsilon$ is time dependent in system (1):

$$\begin{aligned} \epsilon (t) = {\left\{ \begin{array}{ll} 0 &{} \text {before cART is initiated} \\ \epsilon &{} \text {when cART is initiated} \end{array}\right. } \end{aligned}$$

(17)

where the constant $\epsilon$ and is to be estimated. The parameter vector to be estimated in system (1) is $\varvec{\nu } = \langle \beta _1, \beta _2, k, x_0, y_0, N, \epsilon , \gamma \rangle$. For untreated infection, let the model solution vector over time for stably infected brain macrophages per gram of brain tissue and SIV RNA copy equivalents per gram of brain tissue be given by $s_u(\varvec{\nu }, t)$ and $v_u(\varvec{\nu }, t)$, respectively. The dataset $D_1$ will be described by the model solution vector over time $s_u(\varvec{\nu }, t)$. The dataset $D_2$ will be described by the model solution vector over time $v_u(\varvec{\nu }, t)$. Similarly, for the scenarios when cART is initiated at a certain time p.i., $D_3$ and $D_4$ will be described by $s_g(\varvec{\nu }, t)$ and $v_g(\varvec{\nu }, t)$, respectively, $D_5$ and $D_6$ will be described by $s_z(\varvec{\nu }, t)$ and $v_z(\varvec{\nu }, t)$, respectively, and $D_7$ and $D_8$ will be described by $s_c(\varvec{\nu }, t)$ and $v_c(\varvec{\nu }, t)$, respectively. The subscript letters g, z, and c are inspired by the last name of the first author on the SIV studies (Graham et al. 2011; Zink et al. 2010; Clements et al. 2005) in order to quickly keep track of the corresponding model solution vector for each of the datasets $D_3$ through $D_8$.

Since each of the observed SIV brain viral datasets $D_1$ and $D_3$ through $D_8$ is overdispersed count data (variance of the data is larger than the mean of the data), a negative binomial distribution is chosen to describe each of the datasets $D_1$ and $D_3$ through $D_8$. The observed SIV brain viral RNA dataset for untreated animals $D_2$ is also overdispersed count data. However, many of the counts in the dataset $D_2$ are very large positive numbers. For this reason, a normal distribution is used to describe the $\text {log}_{10}$ of the data $D_2$.

Hence, for $j = 1, 3, \dots , 8$, the probability of observing $d_i^j$ is given by the negative binomial distribution:

$$\begin{aligned} f(d_i^j) = \frac{\varGamma (d_i^j + r_i^j)}{d_i^j ! \varGamma (r_i^j)} (p^j)^{(r_i^j)} (1 - p^j)^{d_i^j}, \end{aligned}$$

(18)

where $r_i^j = \frac{(p^j) (\mu _i^j)}{1 - (p^j)} \iff \mu _i^j = \frac{(r_i^j) (1 - p^j)}{p^j}$ changes depending on the time $t_i^j$, and $0< p^j < 1$ is specific to the $j^{\text {th}}$ dataset $D_j$ and determines the most likely shape of the negative binomial distribution given the data $D_j$. Hence, the variance, $Var[ D_i^j ] = \frac{\mu _i^j}{p^j}$, also changes over time. Here $\mu _i^1 = s_u(\varvec{\nu }, t_i^1)$, $\mu _i^3 = s_g(\varvec{\nu }, t_i^1)$, $\mu _i^4 = v_g(\varvec{\nu }, t_i^1)$, $\mu _i^5 = s_z(\varvec{\nu }, t_i^1)$, $\mu _i^6 = v_z(\varvec{\nu }, t_i^1)$, $\mu _i^7 = s_c(\varvec{\nu }, t_i^1)$, and $\mu _i^8 = v_c(\varvec{\nu }, t_i^1)$.

Based on the datasets $D_1, D_3, \dots , D_8$, the following uniform prior distributions are chosen for $p^1, p^3, \dots , p^8$:

$p^1 \sim U(1 \times 10^{-3}, 1)$, $p^3 \sim U(1 \times 10^{-4}, 1)$, $p^4 \sim U(1 \times 10^{-4}, 1)$,

$p^5 \sim U(1 \times 10^{-2}, 1)$, $p^6 \sim U(1 \times 10^{-1}, 1)$, $p^7 \sim U(1 \times 10^{-1}, 1)$, and

$p^8 \sim U(1 \times 10^{-1}, 1)$.

For $j = 2$, the probability of observing $\text {log}_{10} (d_i^2)$ is given by the normal distribution:

$$\begin{aligned} g(d_i^2) = \sqrt{\frac{\tau }{2 \pi }} \text {exp} \left( - \frac{1}{2} \tau (\text {log}_{10} (d_i^2) - \mu _i^2)^2 \right) , \end{aligned}$$

(19)

where the mean $\mu _i^2$ changes depending on the time, $t_i^2$, and the variance $\frac{1}{\tau }$ is specific to the dataset $D_2$. Here $\mu _i^2 = \text {log}_{10} (v_u(\varvec{\nu }, t_i^2))$.

Based on the dataset $D_2$, the uniform prior distribution for $\tau$ is chosen to be $U(1 \times 10^{-2}, 100)$.

Let $\varvec{\phi } = \langle p^1, \tau , p^3, p^4, p^5, p^6, p^7, p^8 \rangle$. Given the extra parameters in vector $\varvec{\phi }$, we want to estimate the vector $\varvec{\theta } = \langle \varvec{\nu }, \varvec{\phi } \rangle$.

The probability model for datasets $D_1, D_3, \dots , D_8$ is

$$\begin{aligned} P_{1} (D | \varvec{\theta }) = \prod _{j = 1, 3, \dots , 8} \prod _{i = 1}^{n_j} f(d_i^j), \end{aligned}$$

(20)

and the probability model for dataset $D_2$ is

$$\begin{aligned} P_{2} (D_2 | \varvec{\theta }) = \prod _{i = 1}^{n_2} g(d_i^2). \end{aligned}$$

(21)

The likelihood function for $\varvec{\theta }$ is given by

$$\begin{aligned} L (\varvec{\theta }) = C P_{1} (D | \varvec{\theta }) P_{2} (D_2 | \varvec{\theta }), \end{aligned}$$

(22)

where C is any positive constant not depending on $\varvec{\theta }$ used to simplify the likelihood function. For more information about Bayesian inference for dynamical systems and combining probability models, we refer the reader to the recent lecture notes (Roda 2020).

The prior distribution for $\varvec{\theta }$ is equal to the product of the uniform distributions specified for the parameters in $\varvec{\theta }$.

The fitting was completed using an affine invariant ensemble Markov Chain Monte Carlo (MCMC) sampling program from the MATLAB Central File Exchange (Grinsted 2015). The MCMC program sampled from the following unnormalized posterior distribution, $\pi (\varvec{\theta } | D)$:

$$\begin{aligned} \pi (\varvec{\theta } | D) = L(\varvec{\theta }) P(\varvec{\theta }), \end{aligned}$$

(23)

where $\varvec{\theta }$ is the vector of unknown parameters, $D = \{ D_1, \dots , D_8 \}$ is the observed data, $L(\varvec{\theta })$ is the likelihood function, and $P(\varvec{\theta })$ is the prior distribution.

The parameters to be estimated in system (1) are $\varvec{\nu } = \langle \beta _1, \beta _2, k, x_0, y_0, N, \epsilon , \gamma \rangle$.

The affine invariant ensemble MCMC sampler was used with $T = 375,000$ iterations and $K = 32$ walkers making a total of $K T = 12,000,000$ samples. Every $10^{\text {th}}$ sample is thinned from each walker during the MCMC algorithm to decrease autocorrelation. After the iterations of the MCMC sampler are completed, a burn-in of 10,000 is used for each walker and the number of pooled samples after the burn-in is $H = 880,000$. Convergence of the MCMC sampling to the estimated posterior distribution for each parameter in $\varvec{\theta }$ was determined by using a general univariate comparison method (Gelman and Brooks 1998). The general univariate comparison method uses the distance of the empirical $100 (1 - \alpha )\%$ interval for the pooled samples, S, and divides this distance by the average of the distances of the empirical $100 (1 - \alpha )\%$ interval for each of the K walkers, $s_i$, to receive the potential scale reduction factor, r (Gelman and Brooks 1998). Here the empirical 95% interval ($\alpha = 0.05$) is used for the general univariate comparison method. Table 7 contains the estimated parameters in $\varvec{\theta }$ with the 95% credible intervals and the potential scale reduction factors, r, for each parameter. The potential scale reduction factors, r, are close to 1 and this indicates that the sampler converged to the posterior distribution.

Table 7 Fitted parameter estimates in $\varvec{\theta }$, with 95% credible intervals and potential scale reduction factors, r

The 95% prediction intervals for each dataset $D_j$, $j = 1, \dots , 8$, are determined by the posterior predictive distribution as described in (Roda 2020).

For the scenario when cART is initiated at a certain time p.i. and LRA drugs are initiated at a later time p.i., $\omega$ is set to zero in system (5) and $\epsilon$ and $\alpha$ are time dependent in system (5). The time-dependent $\epsilon$ is given by (17) and $\alpha (t)$ is given by

$$\begin{aligned} \alpha (t) = {\left\{ \begin{array}{ll} 0 &{} \text {before LRA drugs are initiated} \\ \alpha &{} \text {when LRA drugs are initiated} \\ 0 &{} \text {when LRA drugs are stopped} \end{array}\right. } \end{aligned}$$

(24)

where $\alpha$ is a constant.

For the model prediction of the LRA drug SIV experiment (data $D_9$), the vector $\varvec{\nu }$ in the pooled samples of $\varvec{\theta } = \langle \varvec{\nu }, \varvec{\phi } \rangle$ in H are used in system (5) with $\omega = 0$ and the reactivation rate, $\alpha$, in (24) is varied from 0.01 to 100 to determine which predicted solutions pass near the points in data $D_9$. The mean of these predicted solutions is displayed in Fig. 5.

Likewise, for the scenario when cART is initiated at a certain time p.i. and the “Shock and Kill” strategy is initiated at a later time p.i., $\epsilon$, $\alpha$, and $\omega$ are time dependent in system (5). The time-dependent $\epsilon$ is given by (17) and $\alpha (t)$ is given by

$$\begin{aligned} \alpha (t) = {\left\{ \begin{array}{ll} 0 &{} \text {before LRA drugs are initiated} \\ \alpha &{} \text {when LRA drugs are initiated}, \end{array}\right. } \end{aligned}$$

(25)

where $\alpha$ is a constant, and

$$\begin{aligned} \omega (t) = {\left\{ \begin{array}{ll} 0 &{} \text {before additional kill strategy is initiated} \\ \omega &{} \text {when additional kill strategy is initiated}, \end{array}\right. } \end{aligned}$$

(26)

where $\omega$ is a constant.

Similarly, for the prediction of the “Shock and Kill” strategy, the vector $\varvec{\nu }$ in the pooled samples of $\varvec{\theta } = \langle \varvec{\nu }, \varvec{\phi } \rangle$ in H are used. For each vector $\varvec{\nu }$, system (5) is solved and the control reproduction number, ${\overline{R}}_{c}$, is calculated as the reactivation rate, $\alpha$, in (25) and additional kill rate, $\omega$, in (26) are varied from 0 to 40. The mean control reproduction number, mean ${\overline{R}}_{c}$, is shown in Fig. 6 and the mean of the predicted model solutions within the safe and effective region (turquoise region in Fig. 6) are shown in Fig. 7.