Spatial movement with distributed memory

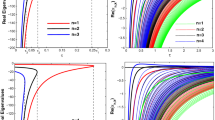
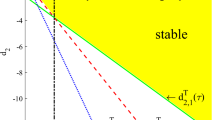
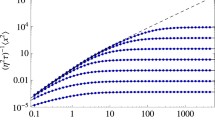
Abstract

Diffusion has been widely applied to model animal movement that follows Brownian motion. However, animals typically move in non-Brownian ways due to their perceptual judgment. Spatial memory and cognition recently have received much attention in characterizing complicated animal movement behaviours. Explicit spatial memory is modeled via a distributed delayed diffusion term in this paper. The distributed time represents the memory growth and decay over time, and the spatial nonlocality reflects the dependence of spatial memory on location. When the temporal delay kernel is weak under the assumption that animals can immediately acquire knowledge and memory decays over time, the equation is equivalent to a Keller–Segel chemotaxis model. For the strong kernel with learning and memory decay stages, rich spatiotemporal dynamics, such as Turing and checker-board patterns, appear via spatially non-homogeneous steady-state and Hopf bifurcations.

Appendix

Proof of Theorem 3

We apply Theorem 1.7 of Crandall and Rabinowitz (1971) for the local bifurcation. Fixing $d_1,\tau >0$, we define a nonlinear mapping $F:{\mathbb R}^+\times X^2\rightarrow Y^2$ by

$$\begin{aligned} F(d_2,u,v)=\left( \begin{array}{cccc} &{} d_1\Delta u+d_2div(u\nabla v)+f(u)\\ &{} d_1\Delta v+\frac{1}{\tau }(u-v)\\ \end{array}\right) . \end{aligned}$$

(7.1)

It is clear that $F(d_2,\theta ,\theta )=0$ for any $d_2>0$. The Fréchet derivative of F with respect to (u, v) is

$$\begin{aligned} \begin{aligned}&F_{(u,v)}\left( d_{2,n}^{w}, \theta ,\theta \right) [\varphi ,\psi ] =\left( \begin{array}{cc} &{}d_1\Delta \varphi +d_{2,n}^{w}\theta \Delta \psi +f'(\theta )\varphi \\ &{}d_1\Delta \psi +\frac{1}{\tau }(\varphi -\psi )\\ \end{array}\right) :=L[\varphi ,\psi ].\end{aligned} \end{aligned}$$

(7.2)

Step 1. First we determine the null space of L. From Lemma 4, we have $D_n(d_{2,s}^w)=0$ so $\mu =0$ is an eigenvalue of $J_n^w$ defined in (3.3) thus also an eigenvalue of (3.2) and there exists $q=(\varphi ,\psi )^T=(1,h_n)\phi _n\in \mathcal {N}(L)$. Moreover as $T_n(d_{2,s}^w)>0$, $\mu =0$ is a simple eigenvalue of $J_n^w$; and since $\lambda _n$ is a simple eigenvalue of (1.4), and $d_{2,n}^w\ne d_{2,k}^w$ for any $k\in {\mathbb N}$ and $k\ne n$, then $\mu =0$ is as simple eigenvalue of L and

$$\begin{aligned} \mathcal {N}(L)=\text {Span}\left\{ q=(1,h_n)\phi _n \right\} , \end{aligned}$$

with $h_n=1/(d_1\lambda _n\tau +1)$, thus $\dim \left( {\mathcal {N}(L)}\right) =1$.

Step 2. We next consider the range space $\mathcal {R}(L)$ of L. We can verify that $\mathcal {R}(L)$ is given by $\{(f_1,f_2)\in Y^2: \langle q^*, (f_1,f_2)\rangle =0\}$ where $q^*\in \mathcal {N}(L^*)$ and $L^*$ is the adjoint operator of L and defined by

$$\begin{aligned} \begin{aligned}&L^*\left[ \varphi ,\psi \right] =\left( \begin{array}{cc} &{}d_1\Delta \varphi +f'(\theta )\varphi +\frac{1}{\tau }\psi \\ &{}d_1\Delta \psi +d_{2,n}^{w}\theta \Delta \varphi -\frac{1}{\tau }\psi \\ \end{array}\right) .\end{aligned} \end{aligned}$$

(7.3)

Since $\mathcal {N}(L^*)=\text {Span}\left\{ q^*=\left( 1,r_n\right) ^T\phi _n\right\}$, where $r_n=\tau (d_1\lambda _n-f'(\theta ))$. We obtain

$$\begin{aligned} \mathcal {R}(L)=\left\{ (f_1,f_2)\in Y^2:\ \int _{\Omega }\left( f_1+r_nf_2\right) \phi _ndx=0\right\} , \end{aligned}$$

and $\text {codim}\left( \mathcal {R}(L)\right) =1$.

Step 3. We show that $F_{d_2(u,v)}(d_{2,n}^w,\theta ,\theta )[q]\not \in \mathcal {R}(L)$. From (7.1), we have

$$\begin{aligned} F_{d_2(u,v)}\left( d_{2,n}^w,\theta ,\theta \right) [q]=(\theta h_n\Delta \phi _n,0)^T=(-\theta \lambda _n h_n \phi _n,0)^T. \end{aligned}$$

(7.4)

Since

$$\begin{aligned} \int _{\Omega }\left( -\theta \lambda _nh_n\phi _n+0\right) \phi _ndx=-\theta \lambda _nh_n\int _{\Omega }\phi _n^2dx<0, \end{aligned}$$

thus $F_{d_2(u,v)}\left( d_{2,n}^w,\theta ,\theta \right) [q]\not \in \mathcal {R}(L)$ by the definition of $\mathcal {R}(L)$. From Step 1, 2 and 3, now we can apply Theorem 1.7 of Crandall and Rabinowitz (1971) to obtain part (i).

Step 4. Now we consider the bifurcation direction and stability of the bifurcating solutions in $\Gamma _n$. To obtain more detailed information of the bifurcation, we use one-dimensional domain $\Omega =(0,l\pi )$. In this case, it is known that $\phi _n=\cos (nx/l)$ and $\lambda _n=n^2/l^2$, so that $q=(1,h_n)^{T}\cos (nx/l)$. From Shi (1999), we have

$$\begin{aligned} d'_{2,n}(0)=-\dfrac{\langle l, F_{(u,v)(u,v)}(d_{2,n}^{w},\theta ,\theta )[q,q]\rangle }{2\langle l, F_{d_2(u,v)}(d_{2,n}^{w},\theta ,\theta )[q]\rangle }, \end{aligned}$$

where $l\in Y$ satisfies $\mathcal {N}(l)=\mathcal {R}(L)$ and can be calculated as

$$\begin{aligned} \langle l,(f_1,f_2)\rangle =\displaystyle \int _0^{l\pi }\left( f_1+r_nf_2\right) \cos \left( \frac{nx}{l}\right) dx. \end{aligned}$$

By (7.4) and the definition of l, we have

$$\begin{aligned} \left\langle l,\ F_{d_2(u,v)}\left( d_{2,n}^{w}, \theta ,\theta \right) [q]\right\rangle =-\lambda _nh_n\theta \int _{0}^{l\pi }\cos ^2\left( \frac{nx}{l}\right) dx=-\frac{\lambda _nh_n\theta l\pi }{2}. \end{aligned}$$

From (7.1), it can be obtained that

$$\begin{aligned} F_{(u,v)(u,v)}(d_2,u,v)[\varphi ,\psi ][\varphi ,\psi ]=\left( 2d_2\varphi '\psi '+2d_2\varphi \psi ''+f''(u)\varphi ^2,0\right) ^{T}. \end{aligned}$$

(7.5)

This implies that

$$\begin{aligned} \ F_{(u,v)(u,v)}\left( d_{2,n}^{w}, \theta ,\theta \right) [q,q]=\left( \frac{f''(\theta )}{2}+\left( \frac{f''(\theta )}{2}-2d_{2,n}^wh_n\lambda _n\right) \cos \left( \frac{2nx}{l}\right) ,0\right) ^{T}, \end{aligned}$$

(7.6)

and thus

$$\begin{aligned} \begin{aligned}&\left\langle l,\ F_{(u,v)(u,v)}\left( d_{2,n}^{w}, \theta ,\theta \right) [q,q]\right\rangle \\ =&\int _{0}^{l\pi }\left( \frac{f''(\theta )}{2}+\left( \frac{f''(\theta )}{2}-2d_{2,n}^w h_n\lambda _n\right) \cos \left( \frac{2nx}{l}\right) \right) \cos \left( \frac{nx}{l}\right) dx=0. \end{aligned} \end{aligned}$$

Therefore $d'_{2,n}(0)=0$.

Next we calculate $d''_{2,n}(0)$ to determine the bifurcation direction by modifying the calculation in Jin et al. (2013). From Shi (1999), $d''_{2,n}(0)$ takes the form:

$$\begin{aligned} d''_{2,n}(0)=-\dfrac{\left\langle l,\ F_{(u,v)(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [q,q,q]\right\rangle +3\left\langle l,\ F_{(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [q,\Theta ]\right\rangle }{3\left\langle l,\ F_{d_2(u,v)}(d_{2,n}^{w},\theta ,\theta )[q]\right\rangle }, \end{aligned}$$

where $\Theta =(\Theta _1,\Theta _2)$ is the unique solution of

$$\begin{aligned} F_{(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [q,q]+F_{(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [\Theta ]=0. \end{aligned}$$

(7.7)

From (7.5), we have

$$\begin{aligned} F_{(u,v)(u,v)(u,v)}\left( d_2,u,v\right) [\varphi ,\psi ][\varphi ,\psi ][\varphi ,\psi ]=(f'''(u)\varphi ^3,0)^{T}, \end{aligned}$$

thus

$$\begin{aligned} \langle l,F_{(u,v)(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [q,q,q]\rangle =\int ^{l\pi }_{0}f'''(\theta )\cos ^4\left( \frac{nx}{l}\right) dx=\frac{3l\pi }{8}f'''(\theta ). \end{aligned}$$

(7.8)

In the following, we show the calculation of $\left\langle l,\ F_{(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [q,\Theta ]\right\rangle$. By (7.6) and (7.7), we may assume $\Theta =(\Theta _1,\Theta _2)$ has the following form

$$\begin{aligned} \Theta _1=\Theta _1^0+\Theta _1^2\cos \left( \frac{2nx}{l}\right) ,~\Theta _2=\Theta _2^0+\Theta _2^2\cos \left( \frac{2nx}{l}\right) , \end{aligned}$$

(7.9)

since $F_{(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right)$ consists of only constant and $\cos \left( \frac{2nx}{l}\right)$ terms. Substituting (7.9) into (7.7), we obtain

$$\begin{aligned} \begin{aligned}&\left( \begin{array}{cc} &{}-4d_1\lambda _n\Theta _1^2\cos \left( \frac{2nx}{l}\right) -4d_{2,n}^{w}\theta \lambda _n\Theta _2^2\cos \left( \frac{2nx}{l}\right) +f'(\theta )\left( \Theta _1^0+\Theta _1^2\cos \left( \frac{2nx}{l}\right) \right) \\ &{}-4d_1\lambda _n\Theta _2^2\cos \left( \frac{2nx}{l}\right) +\frac{1}{\tau }[\Theta _1^0-\Theta _2^0+(\Theta _1^2-\Theta _2^2)\cos \left( \frac{2nx}{l}\right) ] \end{array}\right) \\&=-\left( \frac{f''(\theta )}{2}+\left( \frac{f''(\theta )}{2}-2d_{2,n}^{w}\lambda _nh_n\right) \cos \left( \frac{2nx}{l}\right) ,0\right) ^{T}. \end{aligned} \end{aligned}$$

(7.10)

Form Eq. (7.10), we can solve $\Theta$ as in (3.10). Thus, we obtain

$$\begin{aligned} \begin{aligned}&\left\langle l,\ F_{(u,v)(u,v)}\left( d_{2,n}^{w},\theta ,\theta \right) [q,\Theta ]\right\rangle \\ =&2d_{2,n}^{w}\lambda _n(\Theta _2^2+h_n\Theta _1^2)\int ^{l\pi }_0\sin \left( \frac{2nx}{l}\right) \sin \left( \frac{nx}{l}\right) \cos \left( \frac{nx}{l}\right) dx\\&+\left( f''(\theta )-d_{2,n}^{w}\lambda _nh_n\right) \Theta _1^0\int ^{l\pi }_0\cos ^2\left( \frac{nx}{l}\right) dx\\&+\left( f''(\theta )\Theta _1^2-d_{2,n}^{w}\lambda _nh_n\Theta _1^2-4d_{2,n}^w\lambda _n\Theta _2^2\right) \Theta _1^2\int ^{l\pi }_0\cos \left( \frac{2nx}{l}\right) \cos ^2\left( \frac{nx}{l}\right) dx\\ =&\frac{l\pi }{2}d_{2,n}^{w}(\Theta _2^2+h_n\Theta _1^2\lambda _n) +\frac{l\pi }{2}\left( f''(\theta )-d_{2,n}^{w}\lambda _nh_n\right) \Theta _1^0\\&+\frac{l\pi }{4}(f''(\theta )\Theta _1^2-4d_{2,n}^w\lambda _n\Theta _2^2-d_{2,n}^w\lambda _nh_n\Theta _1^2). \end{aligned} \end{aligned}$$

Using all above we obtain $d_{2,n}''(0)$ in Eq. (3.9).

Step 5. By applying Corollary 1.13 and Theorem 1.16 of Crandall and Rabinowitz (1973) or Theorem 5.4 of Liu and Shi (2018), the stability of the bifurcating non-constant steady states can be determined by the sign of $\mu (s)$ which satisfies

$$\begin{aligned} \lim _{s\rightarrow 0}\frac{-sd'_{2,n}(s)m'(d_{2,n}^{w})}{\mu (s)}=1, \end{aligned}$$

(7.11)

where $m(d_2)$ and $\mu (s)$ are the eigenvalues defined as

$$\begin{aligned} \begin{aligned} F_{(u,v)}(d_2,\theta ,\theta )[\varphi (d_2),\psi (d_2)]&=m(d_2)K[\varphi (d_2),\psi (d_2)],\;\;\\&\quad \text {for}~d_2\in (d_{2,n}^{w}-\epsilon ,d_{2,n}^{w}+\epsilon ),\\ F_{(u,v)}(d_{2,n}(s),U_n(s),V_n(s))[\Lambda (s),\Phi (s)]&=\mu (s)K[\Lambda (s),\Phi (s)],\;\;~\text {for}~s\in (-\delta ,\delta ), \end{aligned} \end{aligned}$$

with $K:X\rightarrow Y$ is the inclusion map $K(u)=u$, $m\left( d_{2,n}^{w}\right) =\mu (0)=0$ and $\left( \varphi \left( d_{2,n}^{w}\right) ,\psi \left( d_{2,n}^{w}\right) \right) =(\Lambda (0),\Phi (0))=(1,h_n)\cos \left( \frac{nx}{l}\right)$.

Now consider the bifurcation at $d_2=d_{2,N}^w=d_2^*$. From Lemma 4, $(\theta ,\theta )$ is stable and $m(d_2)<0$ when $d_2>d_{2,N}^{w}$, and it is unstable and $m(d_2)>0$ when $d_2<d_{2,N}^{w}$. One can calculate that

$$\begin{aligned} m(d_2)=\frac{-T_N+\sqrt{T_N^2-4D_N}}{2}, \end{aligned}$$

where $T_N,D_N$ are defined in (3.5), and this implies that $m'(d_{2,N}^{w})=-\theta \lambda _N/(T_N\tau )<0$. If $d''_{2,N}(0)<0$, then $d'_{2,N}(s)<0$ for $s\in (0,\delta )$ and $d'_{2,N}(s)>0$ for $s\in (-\delta ,0)$. Hence $-sd'_2(s)m'(d_{2,N}^{w})<0$ for $s\in (-\delta ,\delta )\backslash \{0\}$, and consequently $\mu (s)<0$ by(7.11) and the bifurcating solutions are locally asymptotically stable. Similarly when $d''_{2,N}(0)>0$, the bifurcating solutions are unstable. For any other bifurcation at $d_2=d_{2,n}^w<d_2^*$, the trivial solution $(\theta ,\theta )$ is already unstable at the bifurcation point, hence all bifurcating solutions are also unstable.