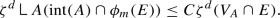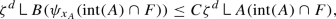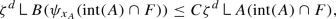Abstract
We show that the weak limit of a quasiminimizing sequence is a quasiminimal set. This generalizes the notion of weak limit of a minimizing sequences introduced by De Lellis, De Philippis, De Rosa, Ghiraldin, and Maggi. This result is also analogous to the limiting theorem of David in local Hausdorff convergence. The proof is based on the construction of suitable deformations and is not limited to the ambient space \({\mathbf {R}}^n \setminus \Gamma \), where \(\Gamma \) is the boundary. We deduce a direct method to solve various Plateau problems, even minimizing the intersection of competitors with the boundary. Furthermore, we propose a structure to build Federer–Fleming projections as well as a new estimate on the choice of the projection centers.








Similar content being viewed by others
Notes
A set \(E \subset X\) is coral in X if E is the support of
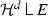 in X. Equivalently, E is closed in X and for all \(x \in E\) and for all \(r > 0\), \({\mathcal {H}}^d(E \cap B(x,r)) > 0\).
in X. Equivalently, E is closed in X and for all \(x \in E\) and for all \(r > 0\), \({\mathcal {H}}^d(E \cap B(x,r)) > 0\).In a topological space X, a family of sets \((A_i)\) is locally finite provided that for every \(x \in X\), there exists a neighborhood U of x such that \(\{i | A_i \cap U \ne \emptyset \}\) is finite. As a consequence, if the sets \(A_i\) are closed, their union \(\bigcup A_i\) is closed in X.
A set \(E \subset X\) is coral in X if E is the support of
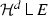 in X. Equivalently, E is closed in X and for all \(x \in E\) and for all \(r > 0\), \({\mathcal {H}}^d(E \cap B(x,r)) > 0\).
in X. Equivalently, E is closed in X and for all \(x \in E\) and for all \(r > 0\), \({\mathcal {H}}^d(E \cap B(x,r)) > 0\).
References
Almgren, F.J.: Existence and regularity almost everywhere of solutions to elliptic variational problems among surfaces of varying topological type and singularity structure. Ann. Math. (2) 87, 321–391 (1968)
Almgren, F.J.: Existence and regularity almost everywhere of solutions to elliptic variational problems with constraints. Mem. Am. Math. Soc. 4(165), viii+199 (1976)
David, G.: Limits of Almgren quasiminimal sets. In: Harmonic Analysis at Mount Holyoke (South Hadley, MA, 2001), Contemp. Math., vol. 320, pp. 119–145. Amer. Math. Soc., Providence, RI (2003)
David, G.: Hölder regularity of two-dimensional almost-minimal sets in \({\bf R}^n\). Ann. Fac. Sci. Toulouse Math. (6) 18(1), 65–246 (2009)
David, G.: \(C^{1+\alpha }\)-regularity for two-dimensional almost-minimal sets in \({\bf R}^n\). J. Geom. Anal. 20(4), 837–954 (2010)
David, G.: Regularity of minimal and almost minimal sets and cones: J. Taylor’s theorem for beginners. In: Analysis and Geometry of Metric Measure Spaces, CRM Proc. Lecture Notes, vol. 56, pp. 67–117. Amer. Math. Soc., Providence, RI (2013)
David, G.: Should we solve Plateau’s problem again? Advances in analysis: the legacy of Elias M. Stein, Princeton Math. Ser., vol. 50, pp 108–145. Princeton Univ. Press, Princeton, NJ (2014)
David, G.: Local regularity properties of almost- and quasiminimal sets with a sliding boundary condition. Astérisque No 411, ix+377 (2019)
De Lellis, C.: Rectifiable Sets, Densities and Tangent Measures. Zurich Lectures in Advanced Mathematics. European Mathematical Society (EMS), Zürich (2008)
De Rosa, A., Kolasiński, S.: Equivalence of the ellipticity conditions for geometric variational problems. Commun. Pure Appl. Math. (2020). https://doi.org/10.1002/cpa.21890. ArXiv:1810.07262
David, G., Semmes, S.: Uniform rectifiability and quasiminimizing sets of arbitrary codimension. Mem. Am. Math. Soc. 144(687), viii+132 (2000)
De Lellis, C., Ghiraldin, F., Maggi, F.: A direct approach to Plateau’s problem. J. Eur. Math. Soc. (JEMS) 19(8), 2219–2240 (2017)
De Philippis, G., De Rosa, A., Ghiraldin, F.: A direct approach to Plateau’s problem in any codimension. Adv. Math. 288, 59–80 (2016)
De Philippis, G., De Rosa, A., Ghiraldin, F.: Rectifiability of varifolds with locally bounded first variation with respect to anisotropic surface energies. Commun. Pure Appl. Math. 71(6), 1123–1148 (2018)
De Lellis, C., De Rosa, A., Ghiraldin, F.: A direct approach to the anisotropic Plateau problem. Adv. Calc. Var. 12(2), 211–223 (2019)
De Philippis, G., De Rosa, A., Ghiraldin, F.: Existence results for minimizers of parametric elliptic functionals. J. Geom. Anal. 30(2), 1450–1465 (2020)
Dal Maso, G., Morel, J.-M., Solimini, S.: A variational method in image segmentation: existence and approximation results. Acta Math. 168(1–2), 89–151 (1992)
Fang, Y.: Existence of minimizers for the Reifenberg plateau problem. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 16(3), 817–844 (2016)
Fang, Y.: A note on the convergence of almost minimal sets. (2017). arXiv:1705.04556
Fang, Y., Kolasiński, S.: Existence of solutions to a general geometric elliptic variational problem. Calc. Var. Partial Differ. Equ. 57(3), 71 (2018)
Feuvrier, V.: Un résultat d’existence pour les ensembles minimaux par optimisation sur des grilles polyédrales. PhD thesis, Université Paris Sud (Orsay)
Federer, H.: Geometric Measure Theory. Die Grundlehren der mathematischen Wissenschaften, Band, vol. 153. Springer, New York (1969)
Harrison, J., Pugh, H.: Existence and soap film regularity of solutions to Plateau’s problem. Adv. Calc. Var. 9(4), 357–394 (2016)
Mattila, P.: Geometry of sets and measures in Euclidean spaces. (English summary) Fractals and Rectifiability. Cambridge Studies in Advanced Mathematics, vol. 44. Cambridge University Press, Cambridge (1995)
Reifenberg, E.R.: Solution of the Plateau problem for \(m\)-dimensional surfaces of varying topological type. Acta Math. 104, 1–92 (1960)
Acknowledgements
I would like to thank Guy David for his warm and helpful discussions. I thank the anonymous reviewers who have improved this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Continuous and Lipschitz Extensions
1.1 Continuous Extensions
Lemma A.1
(Tietze extension) Let X be a metric space and A be a closed subset of X. Any continuous function \(f:A \rightarrow {\mathbf {R}}^n\) has a continuous extension \(g:X \rightarrow {\mathbf {R}}^n\).
Remark A.1
Note that we can postcompose g with the orthogonal projection onto the closed convex hull of f(A). Thus, we obtain another continuous extension whose image is included in the convex hull of f(A). For example, if \(\vert f\vert \le M\), we can assume \(\vert g\vert \le M\) as well.
1.2 Lipschitz Extensions
The McShane–Whitney formula is a simple technique to build Lipschitz extensions.
Lemma A.2
(McShane–Whitney extension) Let X be a metric space and \(A \subset X\). Any Lipschitz function \(f:A \rightarrow {\mathbf {R}}^n\) has a Lipschitz extension \(g:X \rightarrow {\mathbf {R}}^n\).
Proof
We cover the case \(n = 1\) because it suffices to extend each coordinate functions independently. Let L be the Lipschitz constant of f. Then the McShane–Whitney extension of f is given by the formula
One can check that g is real-valued, coincides with f in A and is L-Lipschitz. \(\square \)
Remark A.2
If \(\Vert f\Vert \) is the Lipschitz constant of f, the McShane–Whitney extension is \(C\Vert f\Vert \)-Lipschitz, where C is a positive constant that depends only on n. In the case \(X = {\mathbf {R}}^m\), the Kirzbraun theorem gives an extension g with the same Lipschitz constant as f. As before, we can postcompose g with the orthogonal projection onto the closed convex hull of f(A). We obtain another Lipschitz extension whose image is included in the closed convex hull of f(A). This operation does not increase the Lipschitz constant. For example, given \(\vert f\vert \le M\), we can assume \(\vert g\vert \le M\) as well without increasing the Lipschitz constant of g.
We also want to approximate continuous functions by Lipschitz functions.
Lemma A.3
Let X be a metric space. Let \(f:X \rightarrow {\mathbf {R}}^n\) be a bounded and uniformly continuous function. Then for all \(\varepsilon > 0\), there exists a Lipschitz function \(g:X \rightarrow {\mathbf {R}}^n\) such that \(\vert g - f\vert \le \varepsilon \).
Proof
We cover the case \(n=1\) because it suffices to approximate each coordinate functions independently. Let us fix \(\varepsilon > 0\); there exists \(\delta > 0\) such that for all \(x, y \in X\) with \(\vert x - y\vert \le \delta \), \(\vert f(x) - f(y)\vert \le \varepsilon \). We define \(M = \sup \vert f\vert \) and
One can check that g is real-valued, \(g \le f\) and g is \(2M \delta ^{-1}\)-Lipschitz. Next, we check that \(f \le g + \varepsilon \). For \(x, y \in X\), either \(\vert x - y\vert \ge \delta \) and then
or \(\vert x - y\vert \le \delta \) and then
In both cases, \(f(x) \le f(y) + 2M\delta ^{-1}\vert x - y\vert + \varepsilon \) and since \(y \in X\) is arbitrary, \(f(x) \le g(x) + \varepsilon \). \(\square \)
Corollary A.4
Let X be a metric space. Let \(f:X \rightarrow {\mathbf {R}}^n\) be a bounded uniformly continuous function which is Lipschitz on some subset \(A \subset X\). Then, for all \(\varepsilon > 0\), there exists a Lipschitz function \(g:X \rightarrow {\mathbf {R}}^n\) such that \(\vert g - f\vert < \varepsilon \) in X and \(g = f\) in A.
Proof
According to Lemma A.3, there exists a Lipschitz function \(g:X \rightarrow {\mathbf {R}}^n\) such that \(\vert g - f\vert \le \frac{\varepsilon }{2}\). The function \(u = f - g\) is Lipschitz on A and satisfies \(\vert u\vert \le \frac{\varepsilon }{2}\), so Lemma A.2 say that it admits a Lipschitz extension \(v:X \rightarrow {\mathbf {R}}^n\) with \(\vert v\vert \le \frac{\varepsilon }{2}\). We conclude that \(g + v\) is a solution to our problem. \(\square \)
Toolbox for Sliding Deformations
1.1 Local Retractions
We will often need to localize a retraction of the boundary in a given open set.
Lemma B.1
Let \(\Gamma \) be a Lipschitz neighborhood retract in X. For all open sets \(U \subset X\) and for all \(\varepsilon > 0\), there exists a Lipschitz map \(p:{\mathbf {R}}^n \rightarrow {\mathbf {R}}^n\) and an open subset \(O \subset X\) such that \(\Gamma \cap U \subset O \subset U\) and
Moreover, we can build p such that its Lipschitz constant depends only on n and \(\Gamma \) (but not U and \(\varepsilon \)).
Proof
Let r be a Lipschitz retraction from an open set \(O_0\) containing \(\Gamma \) onto \(\Gamma \). Let \(\varepsilon > 0\), we define the open set
In particular, \(\Gamma \cap U \subset O \subset U\) and \(r(O) \subset \Gamma \). Consider the partially defined map
Notice that \(\Gamma \subset O \cup (X \setminus U)\) so \(p = \mathrm {id}\) on \(\Gamma \). It is straightforward that \(\vert p - \mathrm {id}\vert \le \varepsilon \) because \(\vert r - \mathrm {id}\vert \le \varepsilon \) in O. Next, we estimate the Lipschitz constant of \(p - \mathrm {id}\). Let \(\Vert r\Vert \) be the Lipschitz constant of r. For \(x, y \in O\),
For \(x \in O\) and for \(y \in X \setminus U\),
We assume \(\varepsilon \le 1\) so that \(p-\mathrm {id}\) is \((1 + \Vert r\Vert )\)-Lipschitz on its domain. Finally, we apply Lemma A.2 in Appendix A to \(p-\mathrm {id}\). Thus, p extends as a Lipschitz map \(p:{\mathbf {R}}^n \rightarrow {\mathbf {R}}^n\) such that \((p-\mathrm {id})\) is \(C(1 + \Vert r\Vert )\)-Lipschitz (where C depends only on n) and \(\vert p-\mathrm {id}\vert \le \varepsilon \). \(\square \)
1.2 Stability of Sliding Deformations
Our working space in an open set X of \({\mathbf {R}}^n\). The next lemma says that a slight modification of a sliding deformation is still a sliding deformation.
Lemma B.2
Let \(\Gamma \) be a Lipschitz neighborhood retract in X. Let E be a closed subset of X. Let f be a sliding deformation of E in an open subset \(U \subset X\). Let W be an open set such that \(W \subset \subset E \cap U\). Then there exists \(\delta > 0\) such that all Lipschitz maps \(g:E \rightarrow {\mathbf {R}}^n\) satisfying
are sliding deformations of E in U.
Proof
Let F be a sliding homotopy associated to f. We define
and we underline that \(W_0 \subset \subset E \cap U\). Thus, there exists an open set \(U_0\) such that
We fix \(\delta _0 > 0\) such that \(\mathrm {d}(U_0,X \setminus U) \ge \delta _0\). We apply Lemma B.1 to obtain a Lipschitz function \(p:X \rightarrow {\mathbf {R}}^n\) and an open set \(O \subset X\) containing \(\Gamma \) such that
The map p will not be used in step 1 but the open set O will be needed.
Step 1. Let \(\delta > 0\) (to be precised momentarily) and let g be as the statement. We introduce the homotopy \(G_t = F_t + t(g - f)\). It is clear that \(G_0 = \mathrm {id}\), \(G_1 = g\) and for all \(t \in I\), \(G_t = \mathrm {id}\) in \(E \setminus W_0\). The condition \(\vert g - f\vert \le \delta \) also implies that for all \(t \in I\), \(\vert G_t - F_t\vert \le \delta \). We are going to see that if \(\delta \) is sufficiently small, then for all \(t \in I\),
Since \(I \times \overline{W_0}\) is compact and \(F(I \times \overline{W_0}) \subset U_0\), we can take \(\delta > 0\) small enough so that for all \(t \in I\), for all \(x \in \overline{W_0}\),
Thus, for all \(t \in I\), \(x \in W_0\),
We deduce that for all \(t \in I\), \(G_t(E \cap U_0) \subset U_0\) as \(G_t = \mathrm {id}\) in \(E \cap U_0 \setminus W_0\). Similarly, \(I \times (\Gamma \cap \overline{W_0})\) is compact and \(F(I \times (\Gamma \cap \overline{W_0})) \subset O\) because \(F(I \times (\Gamma \cap E)) \subset \Gamma \subset O\). We take \(\delta > 0\) small enough so for all \(t \in I\), for all \(x \in \Gamma \cap \overline{W_0}\),
and we deduce that for all \(t \in I\), \(G_t(E \cap \Gamma ) \subset O\).
Step 2. We would like to retract \(G_t(\Gamma )\) onto \(\Gamma \) so we define
This map is continuous as a pasting of continuous maps in closed domains (relative to \(I \times E\)). As \(G_t(E \cap \Gamma ) \subset O\), we have \(H_t(E \cap \Gamma ) \subset \Gamma \). Since \(\vert p - \mathrm {id}\vert \le \delta _0\), H also satisfies the inequality \(\vert H_t - G_t\vert \le \delta _0\). We apply the Tietze Extension Theorem (Lemma A.1, Appendix A) in the working space \(I \times E\) to \(H - G\). Thus, we extend H into a continuous function \(H:E \rightarrow {\mathbf {R}}^n\) such that \(\vert H_t - G_t\vert \le \delta _0\) in E. Combining \(\vert H_t - G_t\vert \le \delta _0\) and \(G_t(E \cap U_0) \subset U_0\), we deduce that \(H_t(E \cap U_0) \subset U\) by definition of \(\delta _0\). Moreover, \(H_t = \mathrm {id}\) on \(E \setminus U_0\) so we have in fact \(H_t(U) \subset U\). We conclude that H is a sliding homotopy. \(\square \)
1.3 Global Sliding Deformations
Our working space is an open set X of \({\mathbf {R}}^n\). We recall that a global sliding deformation in an open set \(U \subset X\) is a sliding deformation of X in U (the set E is replaced by X in Definition 1.4). Our goal is to show that global sliding deformations induce the same quasiminimal sets. First, we present a necessary and sufficient condition for a sliding deformations on E to extend as a global deformation.
Lemma B.3
(Sliding Deformation Extension) Let \(\Gamma \) be a Lipschitz neighborhood retract in X. Let E be a closed subset of X. Let f be a sliding deformation of E in an open set \(U \subset X\). Then f extends as a global sliding deformation in U if and only if there exists a constant \(C \ge 1\) such that for all \(x \in E\),
Proof
Let us justify that the condition is necessary. Assume that there exists a global sliding deformation g in U which coincides with f on E. For all \(x \in E\), for all \(y \in \Gamma \), we have \(g(y) \in \Gamma \) so
where \(\Vert g\Vert \) is the Lipschitz constant of g. Since \(y \in \Gamma \) is arbitrary, it follows that \(\mathrm {d}(f(x), \Gamma ) \le \Vert g\Vert \mathrm {d}(x,\Gamma )\). From now on, we assume (601) and we build an extension of f.
This paragraph is devoted to introducing a few objects and notation. Let F be a sliding homotopy associated to f. Our extension of F risks overstepping U so we are going to work in a smaller open set \(U_0\) which is relatively compact in U. Let \(K \subset E \cap U\) be a compact set such that for all t, \(F_t = \mathrm {id}\) in \(E \setminus K\). As \(F(I \times K)\) is a compact subset of U, there exists an open set \(U_0 \subset \subset U\) such that \(F(I \times K) \subset U_0\). In particular \(K \subset U_0\) because \(F_0 = \mathrm {id}\). Let W be an open set such that \(K \subset W \subset \subset U_0\). The point of such set W is that there exists a constant \(M > 0\) such that for all \(x \in E \cap K\),
Of course, the inequality still holds for all \(x \in E\) since \(f = \mathrm {id}\) outside K. This inequality will allow to extend f in a Lipschitz way by \(f = \mathrm {id}\) in \(X \setminus W\). Finally, we want a Lipschitz retraction onto \(\Gamma \). We apply Lemma B.1 to obtain a Lipschitz map \(p:X \rightarrow {\mathbf {R}}^n\) and an open subset \(O \subset X\) containing \(\Gamma \) such that
where \(\varepsilon \) is a small positive constant that we will specify later.
Step 1. The first part of the proof consists in building a continuous function \(G:I \times X \rightarrow {\mathbf {R}}^n\) which is an extension of F and such that
The partially defined function
is continuous because it is obtained by pasting continuous functions in closed domains. We apply the Tietze Theorem to obtain a continuous extension \(G:I \times X \rightarrow {\mathbf {R}}^n\). In order to obtain the conditions (607), we will re-parametrize \(G_t\). By compactness, the inclusion \(I \times K \subset G^{-1}(U_0)\) implies the existence of an open set \(V \subset X\) such that \(K \subset V\) and
We apply the same argument in \(I \times \Gamma \) where the inclusion \(I \times (\Gamma \cap K) \subset G^{-1}(\Gamma ) \subset G^{-1}(O)\) implies the existence of a relative open set \(V_\Gamma \subset \Gamma \) such that \(\Gamma \cap K \subset V_\Gamma \) and
Let \(\varphi :X \rightarrow [0,1]\) be a continuous function such that \(\varphi = 1\) in K and \(\varphi = 0\) in \(X \setminus V\) and \(\Gamma \setminus V_\Gamma \). We define
Hence \(G'\) is a continuous function which satisfies
In addition, \(G'\) coincides with F on \(I \times E\). Combining \(G'_t(V) \subset U_0\) and \(G'_t = \mathrm {id}\) in \(X \setminus V\), one deduces that \(G'_t(U_0) \subset U_0\). Similarly, \(G'_t(\Gamma ) \subset O\). Nex, we replace \(G'_1\) with a Lipschitz approximation. As \(W \subset \subset U_0\), \(G(I \times {\overline{W}})\) is a compact subset of \(U_0\) and there exists \(\delta > 0\) such that for all \(t \in I\), for all \(x \in {\overline{W}}\),
The set \(G(I \times (\Gamma \cap {\overline{W}}))\) is also a compact subset of O so we can assume that for all \(t \in I\), for all \(x \in \Gamma \cap {\overline{W}}\),
We are going to replace \(G'_1\) with a Lipschitz function \(g:X \rightarrow {\mathbf {R}}^n\) such that \(g = G'_1\) in \(E \cup (X \setminus W)\) and \(\vert g - G'_1\vert \le \delta \) in X. We start by checking that \(G'_1\) is Lipschitz in \(E \cup (X \setminus W)\). Indeed \(G_1 = f\) in E, \(G_1 = \mathrm {id}\) in \(X \setminus W\) and for \(x \in E\) and \(y \in X \setminus W\), (605) yields
We can apply Lemma A.4 to \(G'_1 - \mathrm {id}\) as it is continuous with compact support. Hence we obtain a Lipschitz function \(v:X \rightarrow {\mathbf {R}}^n\) such that \(v = G'_1 - \mathrm {id}\) in \(E \cup (X \setminus W)\) and \(\vert G'_1 - \mathrm {id} - v\vert < \delta \). Then we define \(g = v + \mathrm {id}\) and we replace \(G'\) with
Combining (613), (614), and the facts that \(\vert g - G'_1\vert < \delta \) and \(g = \mathrm {id}\) in \(X \setminus W\), one can see that \(G''_t(\Gamma ) \subset O\) and \(G''_t(U_0) \subset U_0\). We conclude that \(G''\) solves step 1. It will be denoted G in the next step.
Step 2. We would like to retract \(G_t(\Gamma )\) onto \(\Gamma \) so we define
This function is continuous as a pasting of continuous functions in closed domains. As \(G_t(\Gamma ) \subset O\), we have \(H_t(\Gamma ) \subset \Gamma \). It satisfies the inequality \(\vert H_t - G_t\vert \le \varepsilon \) because \(\vert p - \mathrm {id}\vert \le \varepsilon \). Let us check that \(H_1\) is Lipschitz on its domain. The Lipschitz constants of p, \(p - \mathrm {id}\), and g are denoted by \(\Vert p\Vert \), \(\Vert p - \mathrm {id}\Vert \), and \(\Vert g\Vert \), respectively. Note that for all \(x \in {\mathbf {R}}^n\), for all \(y \in \Gamma \),
whence for all \(x \in X\),
Using the Lemma assumption (601), we deduce that for \(x \in E\) and \(y \in \Gamma \), we have
We also have for \(x \in X \setminus W\) and \(y \in \Gamma \),
We apply the extension Lemma A.2 to extend \(H_1\) as a Lipschitz function \(H_1:X \rightarrow {\mathbf {R}}^n\) such that \(\vert H_1 - g\vert \le \varepsilon \). Then, we use the Tietze Extension Lemma (Lemma A.1, Appendix A) to extend H as a continuous function \(H:I \times X \rightarrow {\mathbf {R}}^n\) such that \(\vert H_t - G_t\vert \le \varepsilon \). We assume that \(\varepsilon \) is small enough so that for all \(x \in U_0\), \({\overline{B}}(x, \varepsilon ) \subset U\). Thus, the conditions \(G_t(U_0) \subset U_0\) and \(\vert H_t - G_t\vert \le \varepsilon \) ensure that \(H_t(U_0) \subset U\). Moreover, \(H_t = \mathrm {id}\) in \(X \setminus U_0\), so we have in fact \(H_t(U) \subset U\). We conclude that H solves the lemma. \(\square \)
Combining the previous lemmas, we prove that every sliding deformation can be replaced by an equivalent global sliding deformation.
Lemma B.4
(Sliding Deformation Alternative) Let \(\Gamma \) be a Lipschitz neighborhood retract in X. Let E be a closed subset of X which is \({\mathcal {H}}^d\) locally finite in X. Let f be a sliding deformation of E in an open subset \(U \subset X\). Then for all \(\varepsilon > 0\), there exists a global sliding deformation g in U such that \(\vert g - f\vert \le \varepsilon \), \(E \cap W_g \subset \subset W_f\), and
where
Proof
Given Lemmas B.3 and B.2, it suffices to build a Lipschitz function \(g:E \rightarrow {\mathbf {R}}^n\) which satisfies the following conditions: \(\vert g - f\vert \le \varepsilon \), \(g(E \cap \Gamma ) \subset \Gamma \), \(W_g \subset \subset W_f\), there exists \(C \ge 1\) such that for all \(x \in E\),
and finally,
We fix \(\varepsilon _0 > 0\). The construction will brings into play an intermediate variable \(\varepsilon > 0\). First, we want to build a Lipschitz function \(p:X \rightarrow {\mathbf {R}}^n\) (whose Lipschitz constant depends only on \(\Gamma \)) such that \(\vert p - \mathrm {id}\vert \le \varepsilon _0\), \(p = \mathrm {id}\) on \(\Gamma \) and such that there exists an open set O with \(\Gamma \subset O \subset X\) and \(p(O) \subset \Gamma \). Moreover, we want that
and
where \(W_p = \{x \in X | p(x) \ne x\}\). Let us proceed to build p. Since \(\overline{W_f}\) is a compact subset of E, we have \({\mathcal {H}}^d(W_f) < \infty \) so we can find an open set V such that \(\Gamma \subset V \subset X\) and
and
Then we apply Lemma B.1 in the open set V: there exists a Lipschitz function \(p:X \rightarrow {\mathbf {R}}^n\) (whose Lipschitz constant depends only on \(\Gamma \)) and an open set O such that \(\Gamma \cap V \subset O \subset V\) and
As \(W_p \subset V \setminus \Gamma \), we deduce
and
Next, we truncate f in view of obtaining the property \(W_g \subset \subset W_f\). We introduce the set
and since \(W_f\) is a relative an open subset of E, we can assume \(\varepsilon \) small enough so that
Let \(f'\) be partially defined by
We are going to estimate \(\vert f - f'\vert \) and the Lipschitz constant of \(f - f'\). The Lipschitz constant of \(f - \mathrm {id}\) plays a special role in these estimates and is denoted by L. We start by proving that for \(x \in E \setminus W_\varepsilon \),
Indeed, for \(x \in E \setminus W_\varepsilon \), there exists \(y \in E \setminus W_f\) such that \(\vert x - y\vert \le \varepsilon \) whence
Now, it is straightforward that \(\vert f' - f\vert \le L \varepsilon \) on the domain of \(f'\). We are going to see that \(f' - f\) is L-Lipschitz on the domain of \(f'\). It is clear that \(f - f'\) is L-Lipschitz on \(W_{2\varepsilon }\) and \(E \setminus W_\varepsilon \), respectively. For \(x \in W_{2\varepsilon }\) and \(y \in X \setminus W_\varepsilon \), we have \(\vert x - y\vert \ge \varepsilon \) so
We apply Lemma A.2 to \(f' - f\) so as to extend \(f'\) as a Lipschitz map \(f':E \rightarrow {\mathbf {R}}^n\) such that \(\vert f' - f\vert \le L \varepsilon \) with a Lipschitz depending only on n and f. Before moving to the next paragraph, we require \(f'(E) \subset X\). As \(f(E) \subset X\) and \(\overline{W_f}\) is a compact subset of E, we can assume \(\varepsilon \) small enough so that for all \(x \in \overline{W_f}\),
This implies \(f'(E) \subset X\) as \(f' = f\) in \(E \setminus W_f\) and \(\vert f' - f\vert \le L \varepsilon \).
We finally define the map g on E by
We have \(\vert p - \mathrm {id}\vert \le \varepsilon _0\) and \(\vert f' - f\vert \le L\varepsilon \) so \(\vert g - f\vert \le 2\varepsilon _0 + L \varepsilon \). We assume \(\varepsilon \) small enough so that \(\vert g - f\vert \le 3\varepsilon _0\). Observe that \(g = \mathrm {id}\) in \(E \setminus W_\varepsilon \) so \(W_g \subset \subset W_f\). Next, we prove that there exists a constant \(C \ge 1\) such that for all \(x \in E\),
This inequality is clearly true for \(x \in E \setminus W_f\) so we focus on \(W_f\). As \(\Gamma \) is relatively closed in X and \(\overline{W_f}\) is compact subset of X, \(\Gamma \cap \overline{W_f}\) is compact. Its image \(f(\Gamma \cap \overline{W_f})\) is a compact subset of \(\Gamma \subset O\) so there exists \(\delta > 0\) such that for all \(y \in f(\Gamma \cap \overline{W_f})\),
We introduce
so the set \(f^{-1}(O_\delta )\) is a relative open set of E containing \(\Gamma \cap \overline{W_f}\). By compactness, we can assume \(\varepsilon \) small enough so that
Then for \(x \in \overline{W_f}\) such that \(\mathrm {d}(x,\Gamma ) \le \varepsilon \), we have \(f(x) \in O_\delta \) and thus \(f'(x) \in O\) assuming \(\varepsilon \) small enough so that \(\vert f' - f\vert \le \delta \). We are also going to need the fact that for \(x \in E\),
where \(\Vert p - \mathrm {id}\Vert \) is the Lipschitz constant of \(p - \mathrm {id}\). Indeed for all \(x \in E\) and all \(y \in \Gamma \),
and since y is arbitrary in \(\Gamma \), \(\vert p(x) - x\vert \le \Vert p - \mathrm {id}\Vert \mathrm {d}(x,\Gamma )\). We are ready to prove (657). For \(x \in W_f\), we have either \(\mathrm {d}(x, \Gamma ) \le \varepsilon \), either \(\mathrm {d}(x,\Gamma ) \ge \varepsilon \). In the first case, \(f'(x) \in O\) so \(p \circ f(x) \in \Gamma \) and then
In the second case,
In both cases, we have \(\mathrm {d}(g(x),\Gamma ) \le C \mathrm {d}(x,\Gamma )\), where \(C \ge 1\) is a constant that does not depends on x. To finish the proof, we show that
where \(\Vert g\Vert \) is the Lipschitz constant of g (it depends only on n, f, and \(\Gamma \)). Observe that \(g = f\) on \(W_{2\varepsilon } \setminus (W_p \cup f^{-1}(W_p))\). Moreover, by (646),
The result follows. \(\square \)
Grassmannian Space
Let E be an Euclidean vector space of dimension n and \(0 \le d \le n\) be an integer. The Grassmannian G(d, E) is the set of all d-linear planes of E. Given a linear map \(u:E \rightarrow E\), the symbol \(\Vert u\Vert \) denotes the operator norm
Other authors use the Hilbert–Schmidt norm \(\Vert u\Vert _{HS} = \sqrt{\mathrm {trace}(u^* u)}\). Each linear plane \(V \in G(d,E)\) is uniquely identified by the orthogonal projection \(p_V\) onto V. This correspondence induces a distance on G(d, E):
The action of the orthogonal group O(E) on G(d, E), \((g,V) \mapsto gV\), is distance-preserving because \(p_{gV} = g \circ p_V \circ g^{-1}\). The application \(G(d,E) \rightarrow G(n-d,E)\), \(V \rightarrow V^\perp \) is an isometry. In the case \(E = {\mathbf {R}}^n\), the Grassmannian G(d, E) is simply denoted by G(d, n).
1.1 Metric Structure
Given a subspace V of \({\mathbf {R}}^n\) and a linear map \(u :{\mathbf {R}}^n \rightarrow {\mathbf {R}}^n\), we define
We are going to see that it suffices to compute the norm \(\Vert p_V - p_W\Vert \) on V, \(V^\perp \) or V, W. This is helpful because the expression \(p_V - p_W\) can be simplified on these subspaces.
Lemma C.1
For \(V, W \in G(d,n)\),
Proof
For \(x \in {\mathbf {R}}^n\), we denote \(x_V = p_V(x)\) and \(x_{V^\perp } = p_{V^\perp }(x)\). Observe that \((p_V - p_W)(x_V) \in W^\perp \) and \((p_V - p_W)(x_{V^\perp }) \in W\) so
We deduce that
Since the maps \((p_V - p_W):V^\perp \rightarrow W\) and \((p_V - p_W):W \rightarrow V^\perp \) are adjoints of one another, we have \(\Vert p_V - p_W\Vert _{V^\perp } = \Vert p_V - p_W\Vert _W\). Finally, it is clear that
\(\square \)
The next lemma describes the local structure of G(d, n).
Lemma C.2
-
(i)
For all \(V, W \in G(d,n)\), \(\mathrm {d}(V,W) \le 1\) and there is equality if and only if \(V \cap W^\perp \ne 0\) or \(V^\perp \cap W \ne 0\).
-
(ii)
Let \(V, W \in G(d,n)\) be such that \(\mathrm {d}(V,W) < 1\), then for all \(x \in W\),
$$\begin{aligned} \vert x\vert \le \frac{1}{\sqrt{1 - \mathrm {d}(V,W)^2}} \vert p_V(x)\vert \end{aligned}$$(680)Thus, \(p_V\) induces a linear isomorphism \(p_* :W \rightarrow V\). In particular, \(W = \left\{ x + \varphi (x) | x \in V\right\} \), where \(\varphi :V \rightarrow V^\perp \), \(x \rightarrow p_*^{-1}(x) - x\).
-
(iii)
Let V and \(W \in G(d,n)\) for which there exists a linear application \(\varphi :V \rightarrow V^\perp \) such that \(W = \left\{ x + \varphi (x) | x \in V\right\} \), then
$$\begin{aligned} \mathrm {d}(V,W) = \frac{\Vert \varphi \Vert }{\sqrt{1 + \Vert \varphi \Vert ^2}}. \end{aligned}$$(681)
Proof
1) Let \(V, W \in G(d,n)\). For \(x \in {\mathbf {R}}^n\), the orthogonal projection \(p_V(x)\) satisfies the equation \(p_V(x) \cdot (x - p_V(x)) = 0\) because \(x - p_V(x) \in V^\perp \). Observe that this is equivalent to \(\vert p_V(x) - \frac{x}{2}\vert = \frac{\vert x\vert }{2}\) (we have a similar property for \(p_W(x)\)). According to the triangular inequality,
so \(\Vert p_V - p_W\Vert \le 1\). Assume that \(\vert p_V(x) - p_W(x)\vert = \vert x\vert \) for some \(x \in {\mathbf {R}}^n \setminus 0\). The previous inequalities become equalities so
We deduce that \(p_V(x)\) and \(p_W(x)\) are antipodals on the sphere \(S(\frac{x}{2}, \frac{\vert x\vert }{2})\), whence
or equivalently
As \(x \ne 0\), we have either \(p_V(x) \ne 0\) or \(p_{V^\perp }(x) \ne 0\). In the first case,
and in the second case
The converse is straightforward.
2) For all \(x \in W\),
so
3) We show first that
where \(\varphi ^*:V^\perp \rightarrow V\) is the adjoint of \(\varphi \). For \(x \in V\) and \(y \in V^\perp \), we have
As \(W = \{x + \varphi (x) | x \in V\}\), we have shown that
The map \(x \mapsto x - \varphi ^*(x)\) is injective on \(V^\perp \) because x and \(\varphi ^*(x)\) are orthogonals. We conclude that this inclusion is an equality by a dimension argument.
Next we prove that \(\mathrm {d}(V,W) \le \frac{\Vert \varphi \Vert }{\sqrt{1 + \Vert \varphi \Vert ^2}}\). According to Lemma C.1,
If we show that
the same proof will yield
Therefore, we only prove (699). Let us fix \(x \in V \setminus 0\). As \(\vert x - p_W(x)\vert = \mathrm {d}(x,W)\), we see that for all \(t \in {\mathbf {R}}\), \(\vert x - p_W(x)\vert \le \vert x - t(x + \varphi (x))\vert \). The right-hand side attains its minimum for
and one can compute
We conclude that \(\mathrm {d}(V,W) \le \frac{\Vert \varphi \Vert }{\sqrt{1 + \Vert \varphi \Vert ^2}}\). It is left to prove the reverse inequality. For all \(x \in V\),
By (680), we have
We deduce that \(\Vert \varphi \Vert \le \frac{\mathrm {d}(V,W)}{\sqrt{1 - \mathrm {d}(V,W)^2}}\) or equivalently,
\(\square \)
Finally, we estimate the Lipschitz constant of a linear isomorphism acting on G(d, n).
Lemma C.3
Let \(u:{\mathbf {R}}^n \rightarrow {\mathbf {R}}^n\) be a linear isomorphism. Then for all \(V, W \in G(d,n)\),
If \(\Vert u - \mathrm {id}\Vert < 1\), then for all \(V \in G(d,n)\),
Proof
According to Lemma C.1,
By symmetry, we only need to show that
and this amounts to say that for all \(y \in u(V)\),
Indeed, there exists \(x \in V\) such that \(y = u(x)\) so
This proves the first assertion. We are going to prove the second assertion similarly. For \(x \in V\),
and for \(y \in u(V)\), there exists \(x \in V\) such that \(y = u(x)\) so
Note that if \(\Vert u - \mathrm {id}\Vert < 1\), then
\(\square \)
1.2 Haar Measure
Let E be an Euclidean vector space of dimension n and \(0 \le d \le n\) be an integer. The Haar measure \(\gamma _{d,E}\) is the unique Radon measure on G(d, E) whose total mass is 1 and which is invariant under the action of O(E) (see [24, Chapter 3] for existence and unicity). In the case \(E = {\mathbf {R}}^n\), the Haar measure is simply denoted by \(\gamma _{d,n}\).
It is usually not defined that way but \(\gamma _{d,n}\) coincides with the Hausdorff measure of dimension \(m=d(n-d)\), up to a multiplicative constant. Indeed, G(d, n) is non-empty compact manifold of dimension m so \(\sigma = {\mathcal {H}}^m(G(d,n))\) is finite and positive. Then \(\sigma ^{-1} {\mathcal {H}}^m\) is a Radon measure on G(d, n) whose total mass is 1 and which is invariant under the isometries of G(d, n). In particular, it is invariant under the action of O(n). One can justify similarly that for all \(A \subset G(1,n+1)\)
where \(\sigma _n = {\mathcal {H}}^n({\mathbf {S}}^n)\).
Lemma C.4
(Disintegration Formula) Let p, q, n be non-negative integers with \(p + q \le n\). For all Borel set \(A \subset G(n,p + q)\),
We omitted to write \(W \in G(q,V^\perp )\) to ease the notation.
Proof
We introduce some notation so as to interpret the right-hand side as a pushforward measure. Let us define the space
This space is closed in \(G(p,n) \times G(q,n)\) because it can be written
In particular, X is a compact space. We equip X with the Radon measure \(\gamma _{p \perp q,n}\) defined for all Borel set \(A \subset X\) by
Finally, we define the map \(f:X \rightarrow G(p+q,n)\), \((V,W) \rightarrow V + W\). The map f is Lipschitz because \(V \perp W\) implies \(p_{V + W} = p_V + p_W\).
Now, the lemma reduces to showing that
According to [24, Theorem 1.18] \(f_{\#} \gamma _{n,p \perp q}\) is a Radon measure on \(G(p+q,n)\). It is easy to see that it is invariant under the action of O(n) and that its total mass is 1. By uniqueness of uniformly distributed measures on \(G(p+q,n)\), it coincides with \(\gamma _{p+q,n}\). \(\square \)
Lemma C.5
Let H be an affine hyperplane in \({\mathbf {R}}^{n+1}\) which does not pass through 0, let \(r_0 = \mathrm {d}(0,H)\). Then for all bounded subset \(A \subset H\),
where \(r = \sup \limits _{x \in A}\vert x\vert \) and \(\sigma _n = {\mathcal {H}}^n({\mathbf {S}}^n)\). Moreover, for all \(L \in G(1,n+1)\) such that L meets A, we have
where \(L_0\) is the vector line orthogonal to H.
Proof
Let \(x_0\) be the orthogonal projection of 0 onto H (in particular \(L_0\) is the line generated by \(x_0\)). The application
is bijective from H onto \({\mathbf {S}}^n_+ =\{y \in {\mathbf {S}}^n | y \cdot x_0 > 0\}\). We want to compute the local Lipschitz constant of \(f^{-1}\). One idea is to compute the differential of \(f^{-1}\) but we propose a geometric approach. The idea is to show that for all \(x, y \in {\mathbf {R}}^n \setminus 0\) such that \(x \ne y\),
where (xy) is the line passing through x and y. Let z be the orthogonal projection of 0 onto the line (xy). We write \(x = z + u\) and \(y = z + v\) where u, v are orthogonal to z and collinear to see that
Then
It is clear that for all \(x, y \in H\), we have \(\mathrm {d}(0,(xy)) \ge r_0\) so (736) gives
We deduce that the Lipschitz constant of \(f^{-1}\) on f(A) is \(\le \frac{r^2}{r_0}\). By the action of Lipschitz functions on Hausdorff measures,
Next, we show that for all \(L \in G(1,n+1)\) which meets A, we have
First of all, L cannot be orthogonal to \(L_0\) so \(\mathrm {d}(L,L_0) < 1\). There exists a linear application \(\varphi _L:L_0 \rightarrow L_0^\perp \) such that
and the point of intersection between L and H is \(x_L = x_0 + \varphi _L(x_0)\). According to (681), we have
Since \(\varphi _L\) is defined on a line, it is easy to compute \(\Vert \varphi \Vert \):
and the result follows. \(\square \)
Construction of the Federer–Fleming Projection
We recall a few notions. Let K be a n-complex. For any integer d, the set \(\{A \in K | \mathrm {dim}(A) = d\}\) is denoted by \(K^d\). For any subcomplex L of K, we define
According the properties of n-complexes, this is an open set of \({\mathbf {R}}^n\). We define the gauge \(\zeta ^d\) on Borel subsets of \({\mathbf {R}}^n\) by
For a cell A, we define the restriction of this gauge to A

where \(\mathrm {aff}(A)\) is the affine span of A and \(G(\mathrm {aff}(A),d)\) is the set of all d-linear planes of \(\mathrm {aff}(A)\) centered at an arbitrary point.
We recall what we want to do. Let us say K as the set of dyadic cells of sidelength \(2^{-k}\) which are included in \(Q = [-1,1]^n\) but not in \(\partial Q\). Let us say that E is a 1-dimensional subset of Q. We perform a radial projection in each cell \(A \in L^n\), then in each cell \(A \in L^{n-1}, \ldots \) until the cells \(A \in L^2\). This operation sends E to
Throughout the construction, we choose the centers of projections so that \({\mathcal {H}}^d(\phi (E)) \le C {\mathcal {H}}^d(E)\) and \(\zeta ^d(\phi (E)) \le C \zeta ^d(E)\). However, at the end we will only evaluate \(\zeta ^d\) on restriction to cells \(A \in K^d\) so that \(\zeta ^d\) reduces to \({\mathcal {H}}^d\).
We prove the construction in two steps. In the first Lemma, we forget about the set E and we just show that making radial projections in the cells of a subcomplex L of K yields a Lipschitz retraction onto \(\vert K\vert \setminus U(L)\). In the second Lemma, we focus about the choice of projection centers.
Lemma D.1
Let K be a n-complex, let L be a subcomplex of K which does not contain 0-dimensional cells. There exists a Lipschitz function \(\phi :\vert K\vert \rightarrow \vert K\vert \) satisfying the following properties:
-
(i)
for all \(A \in K\), \(\phi (A) \subset A\);
-
(ii)
\(\phi = \mathrm {id}\) in \(\vert K\vert \setminus U(L)\);
-
(iii)
there exists a relative open set \(O \subset \vert K\vert \) containing \(\vert K\vert \setminus U(L)\) such that
$$\begin{aligned} \phi (O) \subset \vert K\vert \setminus U(L). \end{aligned}$$(752)
Proof
The letter C plays the role of a constant \(\ge 1\) that depends on n, \(\kappa \), \(\Gamma \). Its value can increase from one line to another (but a finite number of times). We build by induction a family of locally Lipschitz functions
indexed by a decreasing integer \(m = n+1, \ldots , 1\). The application \(\phi _m\) is obtained by composing \(\phi _{m+1}\) with radial projections in the cells \(A \in L\) of dimension m. We define
and we require that
-
(i)
for all \(A \in K\), \(\phi _m(A) \subset A\),
-
(ii)
\(\phi _m = \mathrm {id}\) in \(\vert K\vert \setminus U_m(L)\),
-
(iii)
there exists a relative open set \(O \subset \vert K\vert \) containing \(\vert K\vert \setminus U_m(L)\) such that
$$\begin{aligned} \phi (O) \subset \vert K\vert \setminus U_m(L). \end{aligned}$$(755)
The induction starts with \(\phi _{n+1} = \mathrm {id}\). Assume that \(\phi _{m+1}\) is well defined for some \(m \le n\). We are going to post-compose \(\phi _{m+1}\) with a function \(\psi _m\). We define first \(\psi _m\) on \(\vert K\vert \setminus U_{m+1}(L)\). We observe that
but according to Lemma 2.2, \(\vert L^m\vert \) is disjoint from \(U_{m+1}(L)\) so
We set
and we set \(\psi _m\) in each cell \(A \in L^m\) to be a radial projection. For \(A \in L^m\), let \(x_A\) be the center of A and let \(\delta _A > 0\) be such that
We define \(\psi _m\) in \(A \setminus B(x_A, \delta _A)\) to be the radial projection centered in \(x_A\) onto \(\partial A\). As A is a face of cube, \(\psi _m\) is Lipschitz with a controlled constant: for all \(x, y \in A \setminus B(x_A, \delta _A)\),
We extend \(\psi _m\) as a \(C \mathrm {diam}(A) \delta _A^{-1}\)-Lipschitz function \(\psi _m :A \rightarrow A\). The function \(\psi _m\) is now well defined on \(\vert K\vert \setminus U_{m+1}(L)\). By construction, \(\psi _m\) is Lipschitz in each cell \(A \in L^m\) and it is the identity map on \(\vert K\vert \setminus U_m(L)\). We are going to deduce that \(\psi _m\) is Lipschitz on \(\vert K\vert \setminus U_{m+1}(L)\). Consider \(A, B \in L^m\) such that \(A \ne B\) and let \(x \in A\) and \(y \in B\). According to Lemma 2.2, we have \(V_A \cap B = \emptyset \). And by the properties of n-complexes, there exists a constant \(\kappa \ge 1\) (depending on n) such that \(V_A(\kappa ) \subset V_A\). We deduce that \(y \notin V_A(\kappa )\), i.e., \(\mathrm {d}(y, \partial A) \le \kappa \mathrm {d}(y,A)\). Let \(z \in \partial A\) be such that \(\vert y - z\vert = \mathrm {d}(y, \partial A)\), in particular
Similarly, one can find \(z' \in \partial B\) such that
Using the triangular inequality, we see that
Thus
Next consider \(A \in L^m\), \(x \in A\) and \(y \in \vert K\vert \setminus U_m(L)\). We have \(V_A(\kappa ) \subset V_A \subset U_m(L)\) so \(\mathrm {d}(y, \partial A) \le \kappa \mathrm {d}(y,A)\). Let \(z \in \partial A\) be such that \(\vert y - z\vert = \mathrm {d}(y, \partial A)\), in particular
Using the triangular inequality, we see that \(\vert x - z\vert \le C\kappa \vert x - y\vert \). It follows that
As \(x_A\) is the center of A, it is possible to choose \(\delta _A\) in such a way that \(\mathrm {diam}(A) \delta _A^{-1} \le C\). This concludes the proof that \(\psi _m\) is well defined and C-Lipschitz on \(\vert K\vert \setminus U_{m+1}(L)\). In a future lemma, we will copy the proof but in a situation where we cannot choose \(x_A\) to be the center of A. Thus we will not be able to control the ratio \(\mathrm {diam}(A) \delta _A^{-1}\).
In this paragraph, we extend \(\psi _m\) over \(\vert K\vert \) in such way that for each \(A \in K\), \(\psi _m(A) \subset A\). We present the extension procedure and we will check afterward that \(\psi _m\) preserves every face. If \(m = n\), we have
so \(\psi _m\) is already defined over \(\vert K\vert \). Assume that \(m < n\). For \(A \in L^{m+1}\), Lemma 2.2 says that
so \(\psi _m\) is defined and C-Lipschitz on \(\partial A\) and we can extend it as a C-Lipschitz function \(\psi _m :A \rightarrow A\). We recall that
so the function \(\psi _m\) is now well defined on \(\vert K\vert \setminus U_{m+2}(L)\). It is Lipschitz in each cell \(A \in L^{m+1}\) and it is Lipschitz on \(\vert K\vert \setminus U_{m+1}(L)\). We can deduce that it is Lipschitz on \(\vert K\vert \setminus U_{m+2}(L)\) using the same proof than in the previous paragraph. We continue the process until \(\psi _m\) is defined on \(\vert K\vert \). Let us prove that \(\psi _m\) preserves every face \(A \in K\). There are two cases to distinguish. If \(A \subset \vert K\vert \setminus U_m(L)\), then \(\psi _m = \mathrm {id}\) on A by (758). If \(A \cap U_m(L) \ne \emptyset \), there exists \(B \in L\) such that \(\mathrm {dim} \, B \ge m\) and \(A \cap \mathrm {int}(B) \ne \emptyset \). By the first point of Lemma 2.2, \(B \subset A\) so \(\mathrm {dim} \, A \ge m\) and, by the properties of subcomplexes, \(A \in L\). We conclude that \(\psi _m\) preserves A by construction.
We finally define \(\phi _m = \psi _m \circ \phi _{m+1}\). By construction, \(\phi _m\) is C-Lipschitz and satisfies the first and second requirement of the induction. Let us check that it satisfies the third requirement. By assumption, there exists a relative open set O of \(\vert K\vert \) which contains \(\vert K\vert \setminus U_{m+1}(L)\) and such that
We will solve the induction with the set
We justify that \(O'\) contains \(\vert K\vert \setminus U_m(L)\). First, we have trivially
In addition \(\phi _{m+1} = \mathrm {id}\) on \(\vert K\vert \setminus U_m(L)\) and this set is disjoint from
We justify that \(O'\) is open. The family \((A \cap {\overline{B}}(x_A, \delta _A))_A\) is a locally finite family of closed sets in \(\vert K\vert \) so its union is relatively closed. Then \(O'\) is relatively open in \(\vert K\vert \) by continuity of \(\psi _{m+1}\). Finally, we justify that \(\psi _m(O') \subset \vert K\vert \setminus U_m(L)\). We have \(\phi _{m+1}(O) \subset \vert K\vert \setminus U_{m+1}(L)\) and
so
by construction of \(\psi _m\). \(\square \)
Lemma D.2
(Federer–Fleming projection) Let K be n-complex. Let \(0 \le d < n\) be an integer and let E be Borel subset of \(\vert K\vert \) such that \({\mathcal {H}}^{d+1}(\vert K\vert \cap {\overline{E}}) = 0\). Then there exists a locally Lipschitz function \(\phi :\vert K\vert \rightarrow \vert K\vert \) satisfying the following properties:
-
(i)
for all \(A \in K\), \(\phi (A) \subset A\);
-
(ii)
\(\phi = \mathrm {id}\) in \(\vert K\vert \setminus \bigcup \{\mathrm {int}(A) | \mathrm {dim} \, A > d\}\);
-
(iii)
there exists a relative open set \(O \subset \vert K\vert \) such that \(E \subset O\) and
$$\begin{aligned} \phi (O) \subset \vert K\vert \setminus \bigcup \{\mathrm {int}(A) | \mathrm {dim} \, A > d\}; \end{aligned}$$(782) -
(iv)
for all \(A \in K\),
$$\begin{aligned} {\mathcal {H}}^d(\phi (A \cap E)) \le C {\mathcal {H}}^d(A \cap E); \end{aligned}$$(783) -
(v)
for all \(A \in K^d\),
$$\begin{aligned} {\mathcal {H}}^d(A \cap \phi (E)) \le C \int _{G(d,n)} {\mathcal {H}}^d(p_V(V_A \cap E)) \, \mathrm {d}V, \end{aligned}$$(784)
where \(C \ge 1\) is a constant that depends only on n.
Remark D.1
We do not say that for all \(A \in K^n\),
because \(\phi (A \cap E)\) may not be included in the d-skeleton of K. Thus \(\zeta ^d\) may not reduce to \({\mathcal {H}}^d\) on \(\phi (E \cap A)\).
Proof
The letter C plays the role of a constant \(\ge 1\) that depends on n. Its value can increase from one line to another (but a finite number of times). The principle of the proof is to build by induction a family of locally Lipschitz functions
indexed by a decreasing integer \(m = n+1, \ldots , d+1\). The application \(\phi _m\) is obtained by composing \(\phi _{m+1}\) with radial projections in the cells \(A \in L\) of dimension m. We define
and require that
-
(i)
for all \(A \in K\), \(\phi _m(A) \subset A\);
-
(ii)
\(\phi _m = \mathrm {id}\) in \(\vert K\vert \setminus U_m(K)\);
-
(iii)
there exists a relative open set \(O \subset \vert K\vert \) containing \(\vert K\vert \setminus U_m(K)\) such that
$$\begin{aligned} \phi (O) \subset \vert K\vert \setminus U_m(K); \end{aligned}$$(788) -
(iv)
for all \(A \in K\),
$$\begin{aligned} {\mathcal {H}}^d(\phi _m(A \cap E)) \le C {\mathcal {H}}^d(A \cap E); \end{aligned}$$(789) -
(v)
for all \(A \in K\),
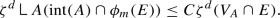 (790)
(790)
The proof follows the same scheme as Lemma D.1 (where the subcomplex L is the set of cells \(A \in K\) of dimension \(\ge d+1\)) but we choose the center of projection wisely. The induction starts with \(\phi _{n+1} = \mathrm {id}\). Assume that \(\phi _{m+1}\) is well defined for some \(d < m \le n\). We post-compose \(\phi _{m+1}\) with a function \(\psi _m\) made of radial projections in the cells of K of dimension m. Fix \(A \in K^m\). For \(x \in \mathrm {int}(A)\), let \(\psi _x\) be the radial projection onto \(\partial A\) centered at x. We want a center of projection \(x_A \in \frac{1}{2} A\) such that
-
1.
\(x_A \notin \overline{\phi _{m+1}(E)}\);
-
2.
for all \(B \in K\) containing A,
$$\begin{aligned} {\mathcal {H}}^d(\psi _{x_A}(\mathrm {int}(A) \cap F_B)) \le C {\mathcal {H}}^d(\mathrm {int}(A) \cap F_B) \end{aligned}$$(791)where \(F_B = \phi _{m+1}(B \cap E)\);
-
3.
for all \(B \in K\) included in \(\partial A\),
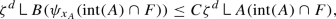 (792)
(792)where \(F = \phi _{m+1}(E)\).
We are going to show that such centers \(x_A\) exists. First, we have
because \(\phi _{m+1}\) is locally Lipschitz. This means that the first requirement is satisfied for \({\mathcal {H}}^m\)-almost every \(x_A \in \mathrm {int}(A)\). Now we deal with the second and the third requirements. Let \(F_1, \ldots , F_N\) be a Borel subset of A such that \({\mathcal {H}}^{d+1}(\overline{F_i}) = 0\). We fix an index i and we apply Lemma 2.9 to \(F_i\) in combination with the Markov inequality. We estimate that for \(\lambda > 0\),
and thus
We deduce that for \(\lambda \) big enough (depending on n, N) there exists \(x \in \tfrac{1}{2} A \setminus \bigcup \overline{F_i}\) such that for all i,
We apply this reasoning to the sets \(F_B\) and F. Note that \(N \le 3^n + 1\) because there are at most \(3^n\) cells B that contain A. The center of projection \(x_A\) is chosen. We let \(\delta _A > 0\) be such that
and we define \(\psi _m\) in \(A \setminus B(x_A, \delta _A)\) to be the radial projection centered in \(x_A\) onto \(\partial A\). In particular \(\psi _m\) is \(C\mathrm {diam}(A) \delta _A^{-1}\) Lipschitz and we extend \(\psi _m\) as a \(C \mathrm {diam}(A) \delta _A^{-1}\)-Lipschitz function \(\psi _m :A \rightarrow A\). The construction of \(\psi _m\) continues just as in the proof of Lemma D.1 and \(\phi _m\) is finally defined as \(\phi _m = \psi _m \circ \phi _{m+1}\).
It is left to show that for all \(B \in K\),
and for all \(A \in K\),

The other requiremements are practically proved in D.1. We fix \(B \in K\) and we prove that
We have
We observe that \(\phi _{m+1}(B \cap E) \subset B\) so for \(A \in L^m\) such that \(\mathrm {int}(A) \cap B \ne \emptyset \), we have \(A \subset B\). The union in (802) is in fact indexed by \(A \in L^m\) such that \(A \subset B\). By construction, we have \(\psi _m = \mathrm {id}\) on \(\vert K\vert \setminus U_{m+1}\) and for all \(A \in L^m\) such that \(A \subset B\),
As \({\mathcal {H}}^d\) is \(\sigma \)-additive on Borel sets and the cells \(A \in K^m\) have disjoint interiors, we conclude that
We fix \(A \in K\) and we prove that

If \(\mathrm {dim}(A) > m\) this is trivial because \(\phi _m(E) \subset \vert K\vert \setminus U_m\). If \(\mathrm {dim}(A) < m-1\), this is trivial because \(\phi _m = \mathrm {id}\) on \(\vert K\vert \setminus U_m\) (and we use (114)). We assume that \(\mathrm {dim}(A) = m-1\). Here again,
For \(B \in K^m\) such that \(\psi _m^{-1}(\mathrm {int}(A)) \cap \mathrm {int}(B) \ne \emptyset \), we have \(\mathrm {int}(A) \cap B \ne \emptyset \), because \(\psi _m(B) \subset B\). As a consequence \(A \subset B\) but since \(\mathrm {dim} \, A < \mathrm {dim} \, B\), we also have \(\mathrm {int}(B) \cap A = \emptyset \). This proves that the union in (808) is indexed by \(B \in K^m\) such that \(A \subset \partial B\). By construction, we have \(\psi _m = \mathrm {id}\) on \(\vert K\vert \setminus U_{m+1}\) and for all \(B \in K^m\) such that \(A \subset \partial B\),



As there are at most \(3^n\) cells \(B \in K^m\) such that \(A \subset \partial B\), we conclude that
\(\square \)
In the next Lemma, we provide two conditions to control the Lipschitz constant of \(\phi \). The second condition is a weak form of Ahlfors-regularity (see Remark D.2 below the proof)
Lemma D.3
We keep the notations of the Lemma D.2. Let us assume that there exists a constant \(\lambda \ge 1\) such that
-
(i)
for all \(A, B \in K\) which are not 0-cells and such that \(A \subset B\), we have \(\mathrm {diam}(B) \le \lambda \mathrm {diam}(A)\);
-
(ii)
for all bounded subset \(S \subset E\), for all radius \(\rho > 0\), the set S can be covered by at most \(\lambda \rho ^{-d} \mathrm {diam}(S)^d\) balls of radius r.
Then \(\phi \) can be taken C-Lipschitz where C depends on n, \(\lambda \).
Proof
The letter C plays the role of constant \(\ge 1\) that depends on on n and \(\lambda \). Given a C-Lipschitz \(\phi _{m+1}\), we want to build a C-Lipschitz \(\psi _m\). According to the proof of Lemma D.1, it suffices that for all \(A \in K^m\),
We prove the existence of \(x_A \in \frac{1}{2}\) such that
-
1.
\(\mathrm {diam}(A) \mathrm {d}(x, \phi _{m+1}(E))^{-1} \le C\);
-
2.
for all \(B \in K\) containing A,
$$\begin{aligned} {\mathcal {H}}^d(\psi _{x_A}(\mathrm {int}(A) \cap F_B)) \le C {\mathcal {H}}^d(\mathrm {int}(A) \cap F_B) \end{aligned}$$(814)where \(F_B = \phi _{m+1}(B \cap E)\);
-
3.
for all \(B \in K\) included in \(\partial A\),
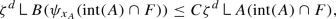 (815)
(815)where \(F = \phi _{m+1}(E)\).
Remember that to obtain the second requirement on \(x_A\), we have chosen C big enough (depending on n) so that for \(B \in K\) containing A,
is sufficiently small (depending on n). We have obtained the third requirement on \(x_A\) similarly. Now, we also want C big enough (depending on n, \(\lambda \)) so that
is sufficiently small (depending on n). Thus, the points \(x \in \mathrm {int}(A)\) that do not satisfy all our criteria will have a small \({\mathcal {H}}^m\)-measure compare to \({\mathcal {H}}^m(A)\). Fix \(0 < \delta \le 1\). We recall that
where \(\bigcup _B\) is indexed by the cells \(B \in K\) containing A. For such B, we can cover \(E \cap B\) by at most \(C \delta ^{-d}\) balls of radius \(\delta \mathrm {diam}(A)\). Since \(\phi _{m+1}\) is C-Lipschitz and since, by Definition 2.6, there are at most \(3^n\) cells \(B \in K\) containing A, the set \(\mathrm {int}(A) \cap \phi _{m+1}(E)\) is covered by at most \(C\delta ^{-d}\) balls of radius \(C\delta \mathrm {diam}(A)\). We deduce that
As \(m > d\) and \(\delta \) is arbitrary small, we can find C big enough so that
is sufficiently small. \(\square \)
Remark D.2
Let \(E \subset {\mathbf {R}}^n\) be a Borel set and B be a ball of radius \(R > 0\). We assume that there exists a constant \(\lambda \ge 1\) such that for all \(x \in E \cap B\), for all \(0 \le r \le 2R\),
Then there exists a constant \(C \ge 1\) (depending on \(\lambda \), d) such that for all subset \(S \subset E \cap B\), for all radius \(r > 0\), the set S can be covered by at most \(C r^{-d} \mathrm {diam}(S)^d\) balls of radius r. Here is the proof.
We assume that S contains at least one point, denoted by \(x_S\). The property is trivial for \(r > \mathrm {diam}(S)\) because S is covered by by \(B(x_S,r)\). Now we work with \(r \le \mathrm {diam}(S)\). Let \((x_i)\) be a maximal sequence of points in S such that \(\vert x_i - x_j\vert \ge r\). By maximality, S is covered by the balls \(B(x_i,r)\). Then, we estimate the cardinal N of such family. The balls \(E \cap B(x_i,\tfrac{1}{2}r)\) are disjoints and included in \(E \cap B(x_S, 2\mathrm {diam}(S))\). It follows that
We apply (821) and obtain
About this article
Cite this article
Labourie, C. Weak Limits of Quasiminimizing Sequences. J Geom Anal 31, 10024–10135 (2021). https://doi.org/10.1007/s12220-021-00637-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-021-00637-w



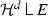 in X. Equivalently, E is closed in X and for all
in X. Equivalently, E is closed in X and for all 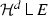 in X. Equivalently, E is closed in X and for all
in X. Equivalently, E is closed in X and for all