Expected returns with leverage constraints and target returns

Abstract

Classic mean–variance optimization is very sensitive to expected returns. An alternative and more robust approach is to calculate the implied returns given the current portfolio allocation and risk profile. Portfolio managers can then do a reality check on the implied returns and find opportunities for better allocations. The most common implied return calculation assumes normal distribution and unlimited leverage, and use volatility as risk measure and covariance matrix as model input. However, practitioners usually have leverage constraints, often use non-parametric risk models, and care about portfolio tail risk. This paper presents a new approach to calculate expected returns with leverage constraints. This approach is flexible enough to alleviate normal distribution assumption, connect with non-parametric risk models, and use tail risk measures, such as conditional VaR.

Appendices

Appendix 1: Proofs of Propositions

Proof of Proposition 1

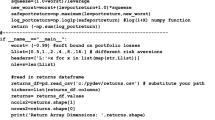
Under the definition (7), the utility function (1) becomes

$$\begin{aligned} U & = r_{p} - \frac{\lambda }{2}\sigma_{p}^{2} \\ & = W^{\prime}R - W^{{\prime }} 1_{N} r_{f} + r_{f} - \frac{\varvec{\lambda}}{2}W^{\prime } \varSigma W \end{aligned}$$

(17)

To maximize (17), consider

$$\frac{\partial U}{\partial W} = R - 1_{N} r_{f} - \lambda \varSigma W = 0.$$

Then, we have

$$R = 1_{N} r_{f} + \lambda \varSigma W.$$

(18)

Since $\frac{{\partial \sigma_{p} }}{\partial W} = \frac{\varSigma W}{{\varsigma_{p} }},$ then $\varSigma W = \sigma_{p} \left( {\frac{{IVol_{1} }}{{w_{1} }},\frac{{IVol_{2} }}{{w_{2} }}, \ldots ,\frac{{IVol_{N} }}{{w_{N} }}} \right)^{'} ,$ and thus $\left( {r_{1} - r_{f} , \ldots , r_{N} - r_{f} } \right)^{'} = \lambda \sigma_{p} \left( {\frac{{IVol_{1} }}{{w_{1} }}, \ldots ,\frac{{IVol_{N} }}{{w_{N} }}} \right)^{'}$. Correspondingly,

$$r_{i} - r_{f} = \lambda \sigma_{p} (IVol_{i} /w_{i} ),$$

(19)

for any $i \in \left[ {1,2, \ldots , N} \right]$. Now from (18), it is easy to see that $W^{\prime}R - W^{\prime}1_{N} r_{f}$ = $r_{p} - r_{f} = \lambda \sigma_{p}^{2}$ and thus $\frac{{r_{p} - r_{f} }}{{\sigma_{p} }} = \lambda \sigma_{p} .$ Consequently, $r_{i} - r_{f} = \frac{{r_{p} - r_{f} }}{{\sigma_{p} }}\left( {IVol_{i} /w_{i} } \right),$ for any $i \in \left[ {1,2, \ldots , N} \right].$ This completes the proof. From the proof, we see that $\lambda =$ $\frac{{r_{p} - r_{f} }}{{\sigma_{p}^{2} }}$.

Proof of Proposition 2

When the leverage constraint ($\mathop \sum \nolimits_{i = 1}^{N} w_{i} = 1)$ exists for portfolios, we have $r_{p} = \mathop \sum \nolimits_{i} w_{i} r_{i} = W^{\prime}R$ with $\mathop \sum \nolimits_{i = 1}^{N} w_{i} = 1,$ according to (7). To maximize the utility function (1) under the leverage constraint, we consider the utility function incorporating the constraint as:

$$U_{1} = r_{p} - \frac{\lambda }{2}\sigma_{p}^{2} + \theta (W^{{\prime }} 1_{N} - 1) = W^{{\prime }} R - \frac{\lambda }{2}W^{{\prime }} \varSigma W + \theta W^{{\prime }} 1_{N} - \theta .$$

(20)

By setting$\frac{{\partial U_{1} }}{\partial W} = R + 1_{N} \theta - \lambda\varSigma W = 0$, we have $R = - 1_{N} \theta + \lambda \varSigma W$. Then, following the proof of Proposition 1 with $r_{f}$ replaced by $- \theta$, we can obtain

$$r_{j} + \theta = \frac{{r_{p} + \theta }}{{\sigma_{p} }}\left( {IVol_{j} /w_{j} } \right),$$

(21)

for any $j \in \left[ {1,2, \ldots , N} \right]$.

Let $\varphi = \frac{{r_{p} + \theta }}{{\sigma_{p} }} .$ Then, we have $(r_{j} + \theta )w_{j} = \varphi IVol_{j}$, for $j \in \left[ {1,2, \ldots , N} \right]$, and $r_{p} + \theta = \varphi \sigma_{p}$. Therefore, $r_{p} + \theta - (r_{j} + \theta )w_{j} = \varphi (\sigma_{p} - IVol_{j} )$. Correspondingly, $r_{p} - w_{j} r_{j} + \theta \left( {1 - w_{j} } \right) = \varphi (\sigma_{p} - IVol_{j} )$. Under the leverage constraint $\mathop \sum \nolimits_{i = 1}^{N} w_{i} = 1$, it follows that $\mathop \sum \nolimits_{i}^{i \ne j} w_{i} r_{i} + \theta \left( {1 - w_{j} } \right) = \varphi (\sigma_{p} - IVol_{j} )$, and thus

$$\frac{{\mathop \sum \nolimits_{i}^{i \ne j} w_{i} r_{i} }}{{1 - w_{j} }} + \theta = \varphi \left( {\frac{{\sigma_{p} - IVol_{j} }}{{1 - w_{j} }}} \right).$$

(22)

Subtracting (22) from (21), we have

$r_{j} - \frac{{\mathop \sum \nolimits_{i}^{i \ne j} w_{i} *r_{i} }}{{1 - w_{j} }} = \varphi \left( {\frac{{IVol_{j} }}{{w_{j} }} - \frac{{\sigma_{p} - IVol_{j} }}{{1 - w_{j} }}} \right)$, for any $j \in \left[ {1,2, \ldots , N} \right]$. This completes the proof. From the proof, we see the relationship $\theta = \varphi \sigma_{p} - r_{p}$. With this new ratio $\varphi ,$ the proposed model has more economic meanings and is more interpretable.

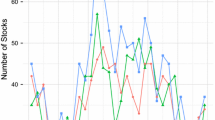
Appendix 2: Statistics for the sample portfolio

For the risk calculation of the sample portfolio, we use the daily returns from January 1st, 2011 to September 30th, 2016. Following are some statistics of the sample portfolio (Exhibits 5, 6).

Exhibit 5 Statistics on sample portfolio

Exhibit 6 Correlation matrix of sample portfolio