Common dynamic factors for cryptocurrencies and multiple pair-trading statistical arbitrages

Abstract

In this paper, we apply dynamic factor analysis to model the joint behaviour of Bitcoin, Ethereum, Litecoin and Monero, as a representative basket of the cryptocurrencies asset class. The empirical results suggest that the basket price is suitably described by a model with two dynamic factors. More precisely, we detect one integrated and one stationary factor until the end of August 2019 and two integrated factors afterwards. Based on this evidence, we define a multiple long-short trading strategy which proves profitable when the second factor is stationary.

1 Introduction

Since their initial creation, most cryptocurrencies, in particular Bitcoin, proved to be highly volatile investment assets. For example, at the beginning of 2 January 2013, Bitcoin had a value of about 13 USD, reached a value of more than 19,000 USD in December 2017 and fell down to 7000 USD by the end of 2019.

Statistical analysis of cryptocurrencies has revealed a number of stylized facts, i.e. statistical findings that appear regularly in the time series under analysis; a non-exhaustive list of empirical studies is represented by Zhang et al. (2018, 2019), Bariviera et al. (2017), Hu et al. (2019) and Giudici and Pagnottoni (2020) which mainly focus on individual behaviour of cryptocurrencies. Findings similar to those of traditional financial assets include the non-stationarity of prices, which display an integrated I(1) behaviour and, as a consequence, the stationarity of price differences; besides, returns show weak autocorrelation, while their absolute values are strongly autocorrelated.

The abnormal and unexpected returns of Bitcoin after 2016 have produced a surge in scientific research on the economics of cryptocurrencies. Several studies investigate the relationship between cryptocurrencies and other financial assets, such as commodities, currencies and market indexes, e.g. Dyhrberg (2016), Ciaian et al. (2016), Kang et al. (2019); besides, hedging and safe-haven properties of cryptocurrencies against the risk of stock markets has been investigated by Tiwari et al. (2019), Shahzad et al. (2019) and Bouri et al. (2017).

Many empirical papers also address the dependence on other candidate factors; Kristoufek (2015) elaborates on the relationship of Bitcoin prices with the number of transactions as well as with several crypto-related factors, such as the mining difficulty and the hashrate. Ciaian et al. (2016), Figá-Talamanca and Patacca (2019, 2020), Cretarola et al. (2020), Ahn and Kim (2019) and Eom et al. (2019) investigate whether Bitcoin returns and volatility are associated with investor attention, sentiment or by specific measures of market attractiveness.

Structural breaks and/or bubbles in the dynamics have been evidenced, among others, in Garcia et al. (2014), Cheah and Fry (2015), Fry and Cheah (2016), Corbet et al. (2018), Bouri et al. (2019), Cretarola and Figà-Talamanca (2019, 2020), Chaim and Laurini (2019) and Agosto and Cafferata (2019).

Most of the above contributions focus on Bitcoin either because of data availability or as a benchmark for the whole sector. Indeed, the price dynamics of several cryptocurrencies display common movements to that of Bitcoin, e.g. Ciaian and Rajcaniova (2018), Blau et al. (2020). Notably, in Yaya et al. (2019), the dependence between the price dynamics of Bitcoin and other cryptocurrencies is identified within the theory of fractional cointegration. Furthermore, Figà-Talamanca et al. (2020) evidence common regimes in the dynamics of several cryptocurrencies, by applying the theory of Hidden Markov models.

By taking advantage of the mutual dependence across several cryptocurrencies, it is reasonable to explore the possibility of forming market neutral strategies, where gains and losses depend only on the relative behaviour of assets. Market neutral strategies are well known to investors in stocks and other conventional assets. They are based on the principle that although the behaviour of each individual asset might not be forecastable, the relative behaviour of assets can be forecasted. Several statistical techniques help in forming market neutral strategies. Most strategies are based on some variant of cointegration or factor models. See Pole (2011) and Avellaneda and Lee (2010) for an introduction to market neutral strategies.

An attempt in this direction is given in Leung and Nguyen (2019): the authors, after evidencing the presence of statistical cointegration among several cryptocurrencies, detect the linear relationship between the cryptocurrencies under analysis and investigate the output of a spread statistical arbitrage which takes advantage of this specific association. Cointegration-based and other arbitrage strategies are analysed in Lintilhac and Tourin (2017), Bistarelli et al. (2018, 2019) by exploiting Bitcoin price differences across online trading exchanges, rather than considering multiple cryptocurrencies.

In this paper, we also build on statistical cointegration in order to create a market neutral strategy by investing in a basket of cryptocurrencies. However, our trading investment is based on the assumption that the multivariate price dynamics of the assets is suitably modelled by a dynamic factor model and proves profitable when the dynamics is described by one integrated and one stationary factor.

Precisely, we estimate the model on moving windows which include three years of previous daily observations starting on January 2019, of Bitcoin, Ethereum, Litecoin and Monero prices. Building on the above result, we suggest a trading strategy on multiple pair spreads, and we provide an empirical investigation of the final value of the strategy as well as of its time changes over the period from January 2019 to November 2019. Our findings suggest that the strategy is particularly profitable when the second factor is stationary, i.e. until the end of August 2019. The paper is organized as follows: in Sect. 2 we perform the preliminary statistical analysis to confirm stylized facts, in particular cointegration, for the basket under investigation; in Sect. 3, we introduce dynamic factor models as a general framework while in Sect. 4 we suggest and estimate a specific price dynamics. In Sect. 5, we define the proposed marked neutral strategy, detail its theoretical properties and provide empirical results. Finally, in Sect. 6 we give some concluding remarks.

2 Preliminary analysis

We consider, among the 20 cryptocurrencies with the highest market caps according to https://coinmarketcap.com/ on December 2019, those which existed and traded by January 2016: we end up with a sample for the price of four cryptocurrencies: Bitcoin (BTC), Ethereum (ETH), Litecoin (LTC) and Monero (XMR), observed from January 2016 to the end of November 2019. The first three years of data are considered for estimation purposes only, while observations from January to November, 2019 serve as test-dates in order to evaluate the profitability of the market neutral strategy to be defined thereafter.

Table 1 summarizes descriptive statistics, and Figure 1 represents the prices behaviour of the four cryptocurrencies for the whole dataset.

Table 1 Summary Statistics of Cryptocurrencies prices from January 1, 2016 to November 30, 2019

Fig. 1

Price behaviour for Bitcoin (top-left), Ethereum (top-right), Litecoin (bottom-left) and Monero (bottom-right) from January 1, 2016 to November 30, 2019

In line with the study of stylized empirical facts for general financial markets (Cont 2001; Cont and Tankov 2004), we perform the Augmented Dickey Fuller (ADF) and the Kwiatkowsky–Phillips–Schmidt–Shin (KPSS) tests on prices and price differences: the former tests the null hypothesis of unit root while the latter tests the null of trend stationarity against the alternative of a unit root. We then apply the Ljung-Box autocorrelation test to the whole basket of returns. Results, summed up in Table 2, show that all cryptocurrencies are integrated of order one (I(1)) while their differences are stationary (I(0)). Besides, the weak autocorrelation of returns and the strong autocorrelation of their absolute values are confirmed by the Ljung-Box test.¹

Table 2 ADF and KPSS tests of cryptocurrencies daily prices (Panel a) and price differences (Panel b) from January 1, 2016 to November 30, 2019

As a preliminary check on whether a dynamic factor model may be suitable to describe the price dynamics of the basket, we also perform a cointegration analysis on the four cryptocurrencies; Table 3 displays the outcomes of the Johansen cointegration test², see Johansen (1991).

Table 3 Johansen cointegration test between Bitcoin, Ethereum, Litecoin and Monero prices: data are from January 1, 2016 to November 30, 2019

It is clear that the four cryptocurrencies are cointegrated with three cointegrating vectors and consequently, they share one common integrated I(1) factor.

3 Dynamic factor models

Classical factor models have a long history which goes back to the formalization of psychometric models. Spearman (1904) introduced a one-factor model of mental abilities, Thurstone (1938, 1947) introduced the first multi-factor model, and Hotelling (1933) described principal components analysis. Classical factor models as described, for example, in Anderson (2003), are strict factor models with a finite number of variables. In a strict factor model, residuals are mutually uncorrelated and uncorrelated with factors. This implies that all correlations are due to factors.

In order to identify a strict factor model, additional assumptions are needed. The setting of classical strict static factor models is one of independent samples extracted from a population with a multivariate Gaussian distribution and observations are i.i.d. vectors. Time-varying behaviour is not accounted for when samples are taken at different points in time. Dynamic factor models generalize the above setting by allowing to specify dynamics for the factors and for the processes themselves.

While modern static multi-factor models were initially proposed in the early 30s by Hotelling (1933), the first dynamic factor models were introduced in econometrics, by Geweke (1977) and by Sargent and Sims (1977), more than forty years later. The subsequent development of dynamic factor models followed two lines:

• dynamic factor models of stationary processes;

• dynamic factor models of integrated processes.

3.1 Dynamic factor models of stationary processes

Sargent and Sims (1977) and Geweke (1977) proposed dynamic factor models to describe the behaviour of I stationary variables, when observed up to time T, by means of K factors. The authors assume that I is finite, $K<<I$ and T very large. In addition, factors and residuals are uncorrelated and that residuals are mutually uncorrelated though possibly autocorrelated.

The above assumptions were relaxed in Engle and Watson (1981), Sargent (1989) and Stock and Watson (1989) by allowing for a small number of variables; parameter estimates are obtained by maximizing the likelihood and factors are recovered through the Kalman filter. An alternative estimation procedure, when a small number of variables is considered together with a large number of observations, is to consider dynamic factor models as instances of state-space models (see Lütkepohl and Poskitt 1991).

In general, we can specify a dynamic factor model as follows:

$$\begin{aligned} \begin{aligned}&r_t =\beta f_{t} + \epsilon _t \\&\Phi (L) f_t = \Theta (L)\eta _t \\&\Phi (L) = 1-\Phi _1 L-\dots -\Phi _pL^p \\&\Theta (L) = 1-\Theta _1 L-\dots -\Theta _qL^q \\ \end{aligned} \end{aligned}$$

(1)

where $r=\lbrace {r_t\rbrace }_{t=1,2,\ldots ,T}$ is a vector processes with I components, the $\beta _i$ are $I \times K$ matrices, $f=\lbrace {f_t\rbrace }_{t=1,2,\ldots ,T}$ is the vector of K stationary process (the factors) and L is the lag operator. The error process $\epsilon =\lbrace {\epsilon _t\rbrace }_{t=1,2,\ldots ,T}$ is a white noise with a full covariance matrix, $\eta =\lbrace {\eta _t\rbrace }_{t=1,2,\ldots ,T}$ has a full-rank covariance matrix and is serially uncorrelated and $\epsilon$ and $\eta$ are mutually uncorrelated at all lags. That is, the common dynamic structure comes only from the factors while the idiosyncratic components can be correlated but no autocorrelation is allowed.

3.2 Dynamic factor models of integrated processes

The model specification for dynamic factor models of integrated factors does not differ from (1) but allows for the possibility of considering non-stationary, i.e. integrated, factors. The estimation of such models introduced in Peña and Poncela (2006) generalizes the estimation methodology for the case of stationary factors put forward in Peña and Box (1987). The paper proposes a test for the number of common factors based on the analysis of the eigenvalues of the generalized covariance matrices and factors are estimated with maximum likelihood. Further, Peña and Poncela (2004) analyse the forecasting performance of such models.

The notion of a factor model of integrated processes is rooted in the concept of cointegration. There is a vast literature on cointegration and on determining the number of cointegrating relationships. Following Engle and Granger (1987), who were jointly awarded the 2003 Nobel Memorial Prize in Economic Sciences for the discovery of cointegration and autoregressive conditional heteroskedasticity (ARCH) behaviour, two or more integrated time series are cointegrated if there is a linear combination $\sum _{i=1}^{I} \alpha _i x_{it}$ of the series that is stationary. The linear combinations $\sum _{i=1}^{I} \alpha _i x_{it}$ that are stationary are called cointegrating relationships. As observed in Galeano and Peña (2000), the idea that two or more time series can be individually integrated but that a linear combination of the series is stationary had already been put forward by Box and Tiao (1977) in introducing canonical correlation analysis. The state-of-the-art cointegration test is the Johansen test (Johansen 2000). A concise yet exhaustive presentation of cointegration is given in Hendry and Juselius (2000) and Hendry and Juselius (2001).

The first link between cointegration and dynamic factor models appeared in Stock and Watson (1988). This landmark paper demonstrates that if a set of I time series is cointegrated with K cointegrating relationships, then there are $Q=I-K$ integrated common trends and the I series can be described as regressions on the common trends. Later, Escribano and Peña (1994) established that common trends are equivalent to common dynamic factors in the sense that the existence of K cointegrating relationships is equivalent to the existence of $I-K$ dynamic integrated factors.

The outcomes of the cointegration analysis performed for the analysed cryptocurrencies together with the above remarks motivate the following section where a dynamic factor model with one integrated factor is suggested for modelling the basket price dynamics.

4 A dynamic factor model for cryptocurrencies

As already remarked, many cryptocurrencies are currently available for trading on online exchange platforms. It has been claimed in Ciaian and Rajcaniova (2018) and Blau et al. (2020) that the whole sector is possibly driven by the dynamics of Bitcoin (in particular in the short-run) or, alternatively, by a single common factor. Indeed, the price dynamics of several cryptocurrencies show a similar path, as evidenced in Fig. 1.

We build on these findings by assuming that the prices of a basket of cryptocurrencies may be described through a dynamic factor model. If this is the case, it would be reasonable to explore the possibility of forming market neutral strategies, where gains and losses depend only on the relative behaviour of the assets.

The dataset is split into two subsamples with the first three years of data (January 1, 2016–December 31, 2018) used only for model estimation and the remainder (January 1, 2019–November 30, 2019) as test dates for the performance of the market neutral strategy suggested in Sect. 5.

4.1 Model specification and fitting

Assume we are given with I different cryptocurrencies; based on our preliminary analysis, we model their mutual relationship through a dynamic factor model.

More precisely, we assume that, for $i=1,2,\ldots ,I$ and $t=1,2,\ldots ,T$:

$$\begin{aligned} \begin{aligned} p_{i,t}&=\alpha _i+\sum _{k=1}^K\beta _{ik} f_{k,t} + \epsilon _{i,t},\\ f_{k,t}&=\lambda _k f_{k,t-1}+\eta _{k,t},\,\, k=1,2,\ldots ,K\\ \epsilon _{i,t}&=\phi _{i,1}\epsilon _{i,t-1}+\phi _{i,2}\epsilon _{i,t-2}+\ldots +\phi _{i,p_i}\epsilon _{i,t-p_i}+u_{i,t}.\\ \end{aligned} \end{aligned}$$

(2)

where $p_{i,t}$ is the price at time t of the cryptocurrency i and $f_{k,t}$, for $k=1,2,\ldots ,K$ are the common factors. For each cryptocurrency i, $\epsilon _{i,t}$ is a centered process, representing the error term at time t, which may be autocorrelated and is suitably described by an autoregressive $AR(p_i)$ process; the error terms $u_{i,t}$ and $\eta _{k,t}, k=1,2,\ldots ,K$ are normally distributed i.i.d processes. We further assume, in line with Koop and Korobilis (2010), the independence between the factors and the error processes $u_i,\eta _k,\eta _h$, for $i=1,2,\ldots ,I$ and $k,h=1,2,\ldots K$, with $k\ne h$, and between the error process $u_i$ and $u_j$, for $i,j=1,2,\ldots ,I$, with $i\ne j$.

Factors can be confidently estimated by means of principal components analysis in the limit case of an infinite market, in practice a very large market. When a limited number I of assets is given, dynamic factor models are usually estimated as state space models (Lütkepohl and Poskitt 1991). We used the $\hbox {Matlab}^{{{\textregistered }}}$ software for Bayesian models provided by Koop and Korobilis (2009), which adopts the latter methodology, since in the empirical application we have $I=4$.

When focusing on the first three years of our specific sample ($T=$ December 31, 2018), the Johansen cointegration test confirms the existence of a common non-stationary factor, hence we expect one common factor, say $f_1$, to be integrated I(1), see Escribano and Peña (1994). In order to detect the correct number of common factors, we estimate, as a first step, the model in (2) with just one factor $f_1$; then we compute the covariance matrix of residuals $\epsilon _{i,t}, i=1,2,\ldots , 4$ and corresponding eigenvalues, given by (1184763.89, 6946.14, 185.03, 14.32), which suggest the presence of a second relevant factor.

Therefore, we will assume $k=2$ throughout our empirical investigation; the considered model specification is finally given by:

$$\begin{aligned} \begin{aligned} p_{i,t}&=\alpha _i+\beta _{i1} f_{1,t} +\beta _{i2}f_{2,t}+ \epsilon _{i,t},\\ f_{1,t}&= \lambda _1 f_{1,t-1}+\eta _{1,t},\\ f_{2,t}&=\lambda _2 f_{2,t-1}+\eta _{2,t},\\ \epsilon _{i,t}&=\phi _{i,1}\epsilon _{i,t-1}+\phi _{i,2} \epsilon _{i,t-2}+\ldots +\phi _{i,p_i}\epsilon _{i,t-p_i}+u_{i,t}.\\ \end{aligned} \end{aligned}$$

(3)

Stationarity or non-stationarity for the factors is established by the estimated values of the autoregressive parameters $\lambda _1, \lambda _2$. As already noticed, the cointegration analysis suggests that $f_1$ is integrated I(1), hence we expect $\lambda _1=1$ and $f_{1,t} = f_{1,t-1}+\eta _{1,t}$.

By iteration, we get ${\mathbb {E}}\left[ f_{1,t}\right] =f_{1,0}{:}{=}\mu$, which may be different from 0, and $Var(f_{1,t})=t\sigma _{\eta _1}^2$ where $\sigma _{\eta _1}^2=Var(\eta _{1,t})$. As a consequence ${\mathbb {E}}\left[ p_{i,t}\right] =\alpha _i+\beta _{i1}\mu$.

Summing up, model (3) is fitted by applying the following estimation procedure:

• The model in (3) is estimated on demeaned prices to get parameters³$\beta _{ij}$, and the time series for the two hidden factors.

• $\mu$ is estimated as the sample mean of the first factor and $\alpha _i, i=1,2,\ldots ,I$ are obtained by solving $\alpha _i={\bar{p}}_{i,t}-\beta _{i1}\mu$ where ${\bar{p}}_{i}$ is the sample mean of the process $p_i$.

The estimated hidden factors $f_1,f_2$ are plotted in Fig. 2: the first factor is an I(1) process as suggested by our model specification, since the Augmented Dickey fuller test confirms that the estimated value of $\lambda _1$ is not significantly different from the unit ($\lambda _1$=0.9962, ADF p value=0.2712⁴) while the second factor is a stationary process ($\lambda _2=0.9823$, ADF p value=0.0056⁴), independent of $f_1$. Corresponding parameter estimates $\alpha _i,\beta _{ij},i=1,2,3,4$ and $j=1,2$ are reported in Table 4; the estimated value for $\mu$ is negligible.

Fig. 2

Factors $f_1$ and $f_2$ from January, 2016 to December, 2018

Table 4 Parameter estimates from January, 2016 to December, 2018

It is clear from both the estimates and the plots that the first factor essentially emulates the dynamics of Bitcoin: indeed $\beta _{11}=0.9911$ is the largest coefficient and it is very close to one. Figure 3, where the first factor and Bitcoin are overlaid, confirms this evidence. Besides, the second factor is strongly related to Ethereum ($\beta _{22}=5.2255)$ though its scale is larger.

Fig. 3

First factor $f_1$ and Bitcoin price from January, 2016 to December, 2018

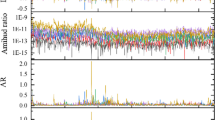
In order to check whether the model in (3) is consistent with observed data we also perform usual diagnostics on factors and residuals $u_i, i=1,2,3,4$, detailed results are reported in Appendix 1 (Tables 7, 8). Specifically the correlations between two factors do not significantly differ from zero ($\rho _{f_1,f_2}=0.005$) as well as the correlation among residuals. Besides, the Ljung-Box autocorrelation test, for different values of maximum lag H⁵, of the four residual processes is quite satisfactory, with the exception of Ethereum for which the process $u_2$ still shows some residual autocorrelation.

For completeness we also sum-up in Appendix 1 (Table 9) the estimates of the AR($p_i$) model for the error terms $\epsilon _i$ where the autoregression order $p_i$ has been selected by minimizing the Bayesian Information Criteria, according to Rachev et al. (2007). It is worth noticing that above estimates are not necessary in order to build a market neutral strategy to exploit the relationship between the analysed cryptocurrencies, as it will be clear in the next section.

Since we are interested in building an investment strategy to take advantage of the dynamic model defined in (3), we can, without loss of generality, scale the price equations with the corresponding $\beta _{i1}$ coefficients. Hence, we get:

$$\begin{aligned} p^*_{i,t} = \frac{p_{i,t}}{\beta _{i1}} = \frac{\alpha _i}{\beta _{i1}}+f_{1,t}+\frac{\beta _{i2}}{\beta _{i1}}f_{2,t}+ \epsilon _{i,t} \end{aligned}$$

(4)

Notably, the scaled prices are equal to the integrated factor $f_{1,t}$ plus a stationary process $f_{2,t}$ and a constant term, which are the same for all rescaled prices; in this way, the gain from a simple long-short strategy with any pair of assets is only driven by the stationary factor $f_2$. Specifically, the difference (spread) between the prices of cryptocurrencies $i,k\in \lbrace {1,2,\dots ,I\rbrace }$ is given by the following equation:

$$\begin{aligned} d_{ik,t}=\frac{ p_{i,t}}{\beta _{i1}}-\frac{ p_{k,t}}{\beta _{k1}}= \left( \frac{\alpha _{i}}{\beta _{i1}}-\frac{\alpha _{k}}{\beta _{k1}}\right) +\left( \frac{\beta _{i2}}{\beta _{i1}} -\frac{\beta _{k2}}{\beta _{k1}}\right) f_{2,t}+ \epsilon _{ik,t} . \end{aligned}$$

(5)

The above difference process will be crucial in defining a market neutral strategy on the available basket of cryptocurrencies.

5 Market neutral strategy

Let us assume that we are at time $\tau$ and that the price of our basket of cryptocurrencies is described by the model in (3). Once model parameters have been estimated on a time series of prices observed up to a varying time $T=\tau$, we obtain one-day ahead forecasted prices as:

$$\begin{aligned} {\hat{p}}_{i,\tau +1} = {\mathbb {E}}_{\tau }\left( p_{i,\tau +1}\right) =\hat{\alpha _i}+{\hat{\beta }}_{i1}{\mathbb {E}}_{\tau }\left( f_{1,\tau +1}\right) +{\hat{\beta }}_{i2}{\mathbb {E}}_{\tau }\left( f_{2,\tau +1}\right) \end{aligned}$$

(6)

where

$$\begin{aligned} {\mathbb {E}}_{\tau }\left( f_{1,\tau +1}\right) ={\hat{\lambda }}_1 f_{1,\tau } \quad , \quad {\mathbb {E}}_{\tau }\left( f_{2,\tau +1}\right) ={\hat{\lambda }}_2 f_{2,\tau }. \end{aligned}$$

(7)

Hence, the one-day-ahead forecasted difference in $\tau +1$ for any pair $i,k\in \lbrace {1,2,\dots ,I\rbrace }$ of cryptocurrencies is given by

$$\begin{aligned} {\hat{d}}_{ik,\tau +1}= & {} \left( \frac{{\hat{\alpha }}_{i}}{{\hat{\beta }}_{i1}} -\frac{{\hat{\alpha }}_{k}}{{\hat{\beta }}_{k1}}\right) + \left( \frac{{\hat{\beta }}_{i2}}{{\hat{\beta }}_{i1}}-\frac{{\hat{\beta }}_{k2}}{\hat{\beta _{k1}}}\right) {\mathbb {E}}_{\tau }\left( f_{2,\tau +1}\right) \nonumber \\= & {} \left( \frac{{\hat{\alpha }}_{i}}{{\hat{\beta }}_{i1}} -\frac{{\hat{\alpha }}_{k}}{{\hat{\beta }}_{k1}}\right) + \left( \frac{{\hat{\beta }}_{i2}}{{\hat{\beta }}_{i1}} -\frac{{\hat{\beta }}_{k2}}{\hat{\beta _{k1}}}\right) {\hat{\lambda }}_2 f_{2,\tau } \end{aligned}$$

(8)

If the above difference is strictly positive, a future revenue can be obtained by applying a long-short investment in the pair i, k. The forecasted difference only depends on the second factor at time $\tau$. As the first factor may be interpreted as the market factor, the above pair trading strategy is market neutral. In order to maximize the revenue in $\tau +1$, a multiple pair trading strategy is obtained by investing on several pairs $i,k\in \lbrace {1,2,\dots ,I\rbrace }$ which display a non-negative forecasted difference. More precisely, if we denote with ${\hat{p}}_{\tau +1}^{(i)}, i=1,2\ldots ,I$ the ordinal statistics (in decreasing order) of the scaled forecasted prices for time $\tau +1$, the multiple pair trading consists essentially of short positions on the first half of cryptocurrencies (with higher forecasted prices) and long positions in the second half of cryptocurrencies (with lower forecasted prices). Denote with $v_\tau$ the value at time $\tau$ of the above investment portfolio. The one-day-ahead expected value of the strategy, computed at time $\tau$, is given by

$$\begin{aligned} g_{\tau +1}={\mathbb {E}}_{\tau } \left[ v_{\tau +1}\right] =\sum _{i=1}^{\lfloor I/2\rfloor } {\hat{p}}_{\tau +1}^{(i)} -\sum _{i=\lceil I/2\rceil +1}^{I} {\hat{p}}_{\tau +1}^{(i)} \end{aligned}$$

(9)

where $\lfloor I/2\rfloor , \lceil I/2 \rceil$ are, respectively, the floor and ceil rounding of I/2.

In general, we will adopt the above pair trading strategy (go long with the multiple pair trading) whether $g_{\tau +1} > v_{\tau }$ or the opposite strategy (going short in the pair trading) in case $g_{\tau +1} < v_{\tau }$. In addition, in order to avoid huge transaction costs, the above multiple pairs strategy can be optimized by trading only when the difference between the forecasted and current value of the investment is above a fixed threshold.

Specifically, we suggest the following strategy:

• if $g_{\tau +1}>v_{\tau }+c\sigma ^v_{\tau }$, go long with the multiple pair trading,

• if $g_{\tau +1}<v_{\tau }-c\sigma ^v_{\tau }$, go short with the multiple pair trading,

• if $v_{\tau }-c\sigma ^v_{\tau }\le g_{\tau +1} \ge v_{\tau }+c\sigma ^v_{\tau }$, hold the current positions (no trade),

where c is an arbitrary chosen constant and $\sigma ^v_{\tau }$ is the standard deviation of the trading position value corresponding to the basket price time series observed up to time $\tau$. If $c=0$ the trading strategy reduces to the multiple pair trading defined above.

Example 1

Assume we are in time $\tau$, we have estimated the model in (3) up to time $\tau$ and we have the data reported in Table 5 where all prices are given in USD.

Table 5 Observed and forecasted data available at time $\tau$

Recall that, for $i=1,2,3,4$, $\beta _{i1}$ is the coefficient of the first factor in (3); ${\bar{p}}_{i,\tau }$ is the mean price up to time $\tau$, $p_{i,\tau }$ is the observed price at time $\tau$ while ${\hat{p}}_{i, \tau +1}$ is the one-day ahead price forecast (computed at time $\tau$). Finally, ${\hat{p}}_{i, \tau }^*$ is the scaled price defined in (4).

After computation of the ordinal statistics ${\hat{p}}_{\tau +1}^{(i)}, i=1,2\ldots ,I$, the suggested multiple pair trading strategy is based on selling the highest two ranked cryptocurrencies (BTC, ETH) and buying the lowest two (LTC, XMR). The forecasted one-day ahead gain $g_{\tau +1}$ of above positions is given by:

$$\begin{aligned} g_{\tau +1}={\mathbb {E}}_{\tau } \left[ v_{\tau +1}\right] = (8950.00 + 295.00 - 45.00 - 78.00) \$ = 9122.00 \$ \end{aligned}$$

(10)

The decision on whether to trade the above strategy and its direction (long or short) depends on the comparison between $g_{\tau +1}$ and $v_{\tau }\pm c\sigma ^v_{\tau }$ where $v_\tau =(9000.00+ 300.00- 40.00 - 75.00)$ $=9185.00$ . If we have $c=0.1$, $\sigma ^v_{\tau }=500.00$, we get $g_{\tau +1}=9122.00$ $< v_{\tau }-c\sigma ^v_{\tau }=9135.00$; hence, we short the suggested multiple pair trading and collect 9185.00. If we further assume that future prices at time $\tau +1$ are given by $p_{1,\tau +1}=8900$, $p_{2,\tau +1}=290$, and $p_{4,\tau +1}=80.00$, we get and we are allowed to close the strategy with a net gain .

The suggested investment selection can be generalized to a dynamical setting where the model in (3) is estimated on moving windows and every long-short portfolio is liquidated on the following date. The above strategy provides a non-negative payoff, for each date $s\in \lbrace {\tau +1,\tau +2, \ldots \tau +M\rbrace }$, on the condition that the basket prices are properly described by model (3) in the corresponding moving window. Hence, usual diagnosis tests should be repeated for each moving window.

If the above trading strategy is repeated for m consecutive days $\left\{ \tau +1,\right.$ $\left. \tau +2, \ldots \tau +m\right\}$ then the expected cumulative gain in $\tau +m$ is given by

$$\begin{aligned} G_{\tau +m}=\sum _{l=\tau }^{\tau +m-1} \left[ g_{l+1} - v_{l} \right] \mathbb {1}_{trade(l)} \;, \end{aligned}$$

(11)

where the indicator function $\mathbb {1}_{trade(l)}$ is defined by

$$\begin{aligned} \mathbb {1}_{trade(l)}= {\left\{ \begin{array}{ll} 1 \; \hbox { if there is trade at time } l \\ 0 \; \text{ if } \text{ there } \text{ is } \text{ no } \text{ trade } \text{ at } \text{ time } l. \end{array}\right. } \end{aligned}$$

(12)

5.1 Empirical results

In this subsection, we provide the empirical results obtained by applying the market neutral strategy proposed above to the daily prices of Bitcoin, Ethereum, Litecoin and Monero, from January 1, 2019–November 30, 2019, i.e. a total of $M=334$ days. Each day the dynamic factor model is estimated on a moving window of daily observations available for the previous three years ($T=1096$ observations). Precisely, the first window starts in January 2016 and ends in December 2018, then the window moves one-day-ahead so that the last one runs from November 30, 2016 to November 29, 2019.

Once parameters are estimated on each moving window, the forecasted prices for the four cryptocurrencies in the basket are computed using the rule in (6). Since our strategy depends on the forecasted differences in (5), Fig. 4 displays these values for all pairs in the basket.

Fig. 4

Forecasted value of differences ${\hat{d}}_{ik,\tau +m}$ from $\tau +1$=January 1, 2019 to $\tau +M$=November 30, 2019

The suggested trading strategy is repeated each day from January 1, 2019 to November 30, 2019, after fitting the model in (3) on a three years long moving window; the suggested trading strategy has been shown to be (theoretically) profitable under specific assumptions: the existence of a non-stationary and a stationary factor and their mutual independence (or, at least, weak correlation). In order to consider a dynamic generalization of the strategy, the above hypothesis should be verified on each moving window and the actual trading should be conditioned on their validity. Hence, we avoid trading when both factors $f_1$ and $f_2$ are integrated and/or highly correlated. In the empirical application, the suggested market neutral strategy is applied only when the mutual correlation between factors is below 0.18⁶. Figure 5 shows the value of correlation between factors $f_1$, $f_2$ for all moving windows ($m=1,2,\ldots , M$) and the threshold level.

Fig. 5

Correlation between factors $f_1$, $f_2$ for all moving windows ($m=1,2,\ldots , M$). The threshold level 0.18 for no trade is also plotted as an horizontal line

In order to appreciate the influence of the arbitrary constant c on the cumulative gain of our strategy, Table 6, Panel a, shows the summary statistics of the cumulative gain at time $\tau +M$, $G_{\tau +M}$, corresponding to several choices of c. In addition, to evaluate the performance of the suggested trading strategy in a real market, where transaction cost is associated to each trade, the net cumulative gain $G_{\tau + M}^{*}$ is also reported in Table 6, Panel b. The net gain is computed under the assumption that transaction fees are given by the $0.10\%$ of the investment, which corresponds to the maker fee of Coinbase⁷ for the pricing tier from $100k to $1m of USD trading volume over the trailing 30-day period.

As expected, the number of trades decreases when c increases and the cumulative gain is maximized when $c=0$ (Panel a); a wise selection appears to be $c=0.20$, which maximizes the net cumulative gain, once transactions fees are accounted for (Panel b).

Table 6 Summary statistics of cumulative gain $G_{\tau +M}$ and net cumulative gain $G_{\tau +M}^{*}$

The time-varying dynamics of the cumulative gain $G_{\tau +m}$, $m=1,2,\ldots ,M$ when $c=0.00$ and $c=0.20$ is illustrated in the top-picture of Fig. 6. Notably, no transactions appear after September 2019; indeed, the outcomes from the Johansen cointegration test, applied within the time frame of each moving window, suggest the existence of two common integrated factors (rather than one), starting from August 20, 2019; moreover, the correlation between the two estimated factors is above the fixed threshold (see Fig. 5). These two evidences are in contrast with the basic assumptions underlying the proposed strategy and suggest no trading. Finally, it is worth noticing that the strategy is as much profitable as higher is the forecasted value of $f_2$, plotted in Fig. 6 (bottom picture).

Fig. 6

Cumulative gain $G_{\tau +m}$ with parameter $c=0.00$ and $c=0.20$ (top) and forecasted value of factor $f_{2,\tau +m}$ (bottom) from $\tau +1$=January 1, 2019 to $\tau +M$=November 30, 2019

Similarly, in Fig. 7 we plot the time-varying net cumulative gain $G_{\tau + m}^{*}$, $m=1,2,\ldots ,M$ when $c=0.00$ and $c=0.20$. It is evident that, in both cases, the proposed strategy provides a net positive gain even when taking into account transaction costs.

Fig. 7

Net cumulative gain $G_{\tau +m}^*$ with parameter $c=0.00$ and $c=0.20$ from $\tau +1$=January 1, 2019 to $\tau +M$=November 30, 2019.

6 Concluding remarks

In this paper, we suggest a dynamic factor model to describe the price dynamics of a basket of cryptocurrencies including Bitcoin, Ethereum, Litecoin and Monero, observed daily from January 1, 2016–November 30, 2019. These were selected among the 20 cryptocurrencies with highest market cap, according to https://coinmarketcap.com/ on December 2019, which existed and traded for at least three years. The outcomes of our analysis confirm the presence of cointegration as already evidenced in Ciaian and Rajcaniova (2018) and Blau et al. (2020) and show the appropriateness of dynamic factor models to describe the price process of the whole basket. Indeed, it is evidenced that the basket is driven by two common, dynamic factors, the first of which is a non-stationary I(1) process. In order to check the consistency over time of the suggested model specification, the estimation is repeated on three-year long moving windows. By applying usual diagnostic checks, it is proven that dynamic factor models provide a satisfactory fit throughout the analysed period. It is worth noticing that the second factor displays a stationary behaviour on moving windows series observed until the end of August 2019 while it is integrated I(1) afterwards. Besides, the correlation between the two factors increases within the same period. We stress that our analysis is limited to a basket of four cryptocurrencies since dynamic factor models rely on a large set of parameters which need to be estimated on a sufficiently long time series. Nevertheless, we conjecture that analogous results would be obtained on a larger basket if longer time series were available.

The common factor dynamics depicted in the first part of the paper is exploited in order to define a market neutral strategy consisting of suitably scaled long short investments on suitably selected cryptocurrency pairs. Theoretical properties of the suggested strategies are analysed: in particular the time-varying value for the cumulative gain is computed daily from January to November, 2019. Our findings suggest that the proposed trading strategy is particularly profitable until the second factor remains stationary. By taking into account transaction fees, according to the trading rules imposed by the Coinbase exchange, we also prove that the net cumulative gain remains positive throughout the considered period. A yet more profitable trading strategy might be defined by investing in multiple (rather than two) pairs, once a larger basket is available.

Appendix

See Tables 7, 8 and 9.

Table 7 Correlation matrix between the two factors and residuals u from January, 2016 to December, 2018

Table 8 Ljung-Box p values for u residuals from January, 2016 to December, 2018

Table 9 Parameter estimates of $\phi$ coefficients from January, 2016 to December, 2018