Valley Orientation of Electrons and Excitons in Atomically Thin Transition Metal Dichalcogenide Monolayers (Brief Review)

The main aspects of physical phenomena associated with the optical orientation of the spin and valley degrees of freedom in transition metal dichalcogenide monolayers and in van der Waals heterostructures based on them have been briefly reviewed. Owing to features of the band structure and spin–orbit coupling in such systems, circularly polarized light induces optical transitions in different valleys K₊ and K_– of the Brillouin zone; consequently, the optical orientation of charge carriers and excitons is accompanied by their valley polarization. The main features of the band structure of transition metal dichalcogenide monolayers, excitonic effects, and results of theoretical studies of the valley orientation of excitons and electrons at one-photon absorption have been reported. The linear–circular dichroism and valley orientation of free charge carriers and excitons at multiphoton absorption have been studied. Effects associated with the trigonal symmetry of monolayers, including the inversion of valley polarization at two-photon transitions and the second harmonic generation, have been discussed. The considered theoretical models have been illustrated by experimental data.

1 INTRODUCTION

The investigation of processes of optical orientation of spins of charge carriers, spin dynamics, and manifestation of spin polarization in the optical response of semiconductors and semiconductor nanosystems has become an actively developing field of modern physics [1–4]. The appearance of novel material systems with unusual crystal and band structures stimulates theoretical and experimental studies in this field.

Structures with “extreme” two-dimensionality such as graphene, transition metal dichalcogenide (TMDC) monolayers, hexagonal boron nitride monolayers, and van der Waals heterostructures based on them have become of particular interest in the last several years in the physics of semiconductor nanosystems [5, 6]. In TMDC monolayers [7–10], among which MoS₂, MoSe₂, WS₂, and WSe₂ are the most studied and which are considered in this brief review, a direct band gap is formed at the points K₊ and K_– at the edges of the hexagonal Brillouin zone because of the strong spin–orbit coupling and a specific symmetry of the crystal lattice. Light with a given circular polarization ${{\sigma }^{ + }}$ or ${{\sigma }^{ - }}$ in the dipole approximation is absorbed in the ${{{\mathbf{K}}}_{ + }}$ or ${{{\mathbf{K}}}_{ - }}$ valley, respectively, and the spin orientation of charge carriers is accompanied by their valley orientation [9, 11–16]. Another feature of TMDC monolayers is a strong Coulomb interaction, which is responsible for the connection of the optical response of such structure with Wannier–Mott excitons having a significant binding energy of 100–500 meV [17–20]. The fine structure of the energy spectrum, as well as the dynamics of spin and valley degrees of freedom of excitons, in such extremely two-dimensional systems is actively studied both experimentally and theoretically [21–30].

The aim of this work is to briefly review features of the valley orientation of charge carriers and excitons in TMDC monolayers with the focus on effects associated with features of the symmetry of the system, energy spectrum, and Coulomb interaction. The basic information on the crystal and electronic structures of TMDC monolayers, as well as the specificity of exciton states, is presented in Section 2. Section 3 is devoted to the optical orientation of electrons and excitons at single-photon transitions, аs well as to features of the valley dynamics of excitons caused by the long-range electron–hole exchange interaction. The specificity of multiphoton transitions in TMDC monolayers is considered in Section 4. Section 5 describes the manifestations of the specific trigonal symmetry and the absence of the inversion center in the linear and nonlinear optical response of TMDC monolayers.

2 MAIN FEATURES OF TMDC MONOLAYERS

Figures 1a and 1b schematically show the crystal structure and positions of atoms in TMDC monolayers. The monomolecular layer is described by the point group ${{D}_{{3h}}}$, and the horizontal plane of reflection passes through the layer of metal atoms. The unit cell contains a metal atom and two chalcogenide atoms located in planes above and below the metal plane. The Brillouin zone is a regular hexagon (see Fig. 1c); the direct band gap is formed at the points K₊ and K_– related by the time reversal operation. The point group of the wave vector at the points K₊ and K_– is ${{C}_{{3h}}}$. The dispersion relation of electrons in the valence and conduction bands near the points K₊ and K_– is parabolic (see Fig. 1d). We note that spin degeneracy of bands is completely lifted at the points K₊ and K_–, and the time reversal symmetry relates states with the opposite spins in different valleys.

Fig. 1.

(Color online) (a) Schematic of the crystal structure of the monomolecular TMDC layer described by the chemical formula MX₂. The black and yellow balls are metal (M) and chalcogenide (X) atoms, respectively. (b) Projections of atoms on the plane. (с) Two-dimensional Brillouin zone. (d) Scheme of energy bands near the points K₊ and K_– and the selection rules at normal incidence of radiation. Light with a given circular polarization induces transitions with the conservation of the electron spin and change in the component of the angular momentum of the orbital Bloch function by ±1.

Within the minimal model, the effective 2 × 2 Hamiltonian describing the states of the conduction and valence bands with the parallel spins $s = + 1{\text{/}}2$ near the point ${{{\mathbf{K}}}_{ + }}$ has the form [9, 19, 31]

$${{\mathcal{H}}_{ + }} = \left( {\begin{array}{*{20}{c}} {{{E}_{{\text{g}}}}{\text{/}}2}&{\gamma ({{k}_{x}} - i{{k}_{y}})} \\ {\gamma ({{k}_{x}} + i{{k}_{y}})}&{ - {{E}_{{\text{g}}}}{\text{/}}2} \end{array}} \right).$$

(1)

Here, ${\mathbf{k}} = ({{k}_{x}},{{k}_{y}})$ is the two-dimensional wave vector of the electron measured from the point ${{{\mathbf{K}}}_{ + }}$, γ is the parameter proportional to the interband matrix element of the momentum operator, and E_g is the width of the band gap. The Hamiltonian for a pair of spin sublevels with $s = - 1{\text{/}}2$ in the same valley has the form (1) with the substitution ${{E}_{{\text{g}}}} \to {{E}_{{\text{g}}}} + \Delta$, where Δ is the sum of the spin–orbit splittings of the conduction and valence bands. It is noteworthy that the order of spin conduction subbands is different in molybdenum- and tungsten-based structures [19, 31]. The effective Hamiltonian in the ${{{\mathbf{K}}}_{ - }}$ valley is obtained from Eq. (1) by the substitution ${{k}_{x}} \pm i{{k}_{y}} \to {{k}_{x}} \mp i{{k}_{y}}$. We note that the characteristic E_g values are about 2 eV and the effective masses of electrons and holes are $\sim {\kern 1pt} 0.5{{m}_{0}}$, where ${{m}_{0}}$ is the mass of the free electron [19, 31–35]. The energy spectrum of the electron with the Hamiltonian (1) has the Dirac form

$${{\varepsilon }_{{\lambda ,k}}} = \lambda {{\varepsilon }_{k}},\quad {{\varepsilon }_{k}} = \sqrt {{{{({{E}_{{\text{g}}}}{\text{/}}2)}}^{2}} + {{\gamma }^{2}}{{k}^{2}}} ,$$

(2)

where $\lambda = +$ and – correspond to the conduction and valence bands, respectively.

We now describe the exciton states in TMDC monolayers. A feature of such structures is their significant dielectric contrast, which leads to the difference of the potential energy of attraction between the electron and hole from the Coulomb law $V(\rho ) \propto - 1{\text{/}}\rho$, where ρ is the distance between the electron and hole in the monolayer plane. The Rytova–Keldysh model [36, 37] is usually used to take into account the dielectric screening (see [38, 39], where the applicability and generalizations of this model for structures with extreme two-dimensionality were discussed), in which the Fourier transform of the potential energy has the compact form

$$V(q) = - \frac{{2\pi {{e}^{2}}}}{{\varkappa q(1 + q{{r}_{0}})}}.$$

(3)

Here, q is the wave vector, ϰ is the relative permittivity of the medium surrounding the monolayer, and ${{r}_{0}}$ is the effective screening radius, which is determined by the polarizability of the monolayer. The Fourier image of the potential at low q values (distances $\rho \sim {{q}^{{ - 1}}}$ large compared to ${{r}_{0}}$) behaves as 1/q; i.e., the two-dimensional Coulomb law is valid in real space, whereas the potential at high q values (small distances $\rho \sim {{q}^{{ - 1}}}$) behaves as $- 1{\text{/}}{{q}^{2}}$ or, in the coordinate space, as $\ln(\rho {\text{/}}{{r}_{0}})$. This leads to the deviation of the binding energy of exciton states from a hydrogen-like series [18], to the lifting of “accidental” Coulomb degeneracy [39], and to the relative increase in the oscillator strength of excited states of the exciton [40]. Another reason for the deviation of the exciton series in TMDC monolayers from the hydrogen-like series is the nonparabolicity of the energy spectrum of charge carriers [41–44]. The dispersion relation (2) at low k values can be approximated by the parabola

$${{\varepsilon }_{k}} \approx \frac{{{{E}_{{\text{g}}}}}}{2} + \frac{{{{\hbar }^{2}}{{k}^{2}}}}{{2m{\text{*}}}},$$

where $m\text{*} = {{E}_{{\text{g}}}}{\text{/}}(2v_{0}^{2})$ is the effective mass and ${{{v}}_{0}} = \gamma {\text{/}}\hbar$ is the velocity. With increasing k, the dispersion relation changes from parabolic to linear. If the binding energy of the exciton is not too low compared to the width of the band gap E_g, nonparabolicity changes the structure of the exciton wavefunction: it becomes four-component and includes the electron–hole excitations with electron and hole states having both signs of the energy ${{\lambda }_{e}} = \pm$ and ${{\lambda }_{h}} = \pm$, respectively (see Eq. (2)). In TMDC monolayers, nonparabolicity results not only in the renormalization of the binding energy of the exciton but also in a noticeable change in the oscillator strength [44].

In single-photon processes within the axial approximation, to describe the energy spectrum of charge carriers, s-excitons with the zero component of the angular momentum of the envelope function are optically active. The analysis shows that the experimentally observed positions of exciton resonances are satisfactorily described within the method of the eff-ective mass taking into account the screened potential (3) [18, 40]. To compare the calculated and measured oscillator strengths, it is necessary to take into account that multiple reflection of light from the boundaries of dielectric layers of the sample surrounding TMDC monolayers in experimentally studied van der Waals heterostructures like that presented in Figs. 2a and 2b. As a result, depending on the thicknesses of these layers, resonances in the reflection spectra associated with excited exciton states can have an intensity comparable to the intensity of the ground state, despite an order of magnitude difference in the oscillator strengths. The calculations within the transfer-matrix method make it possible to adequately describe the reflection spectra of such structures; the fitted thicknesses of the layers correspond to those measured by atomic force microscopy [40].

Fig. 2.

(Color online) (a) Optical microscopy image of the structure with the MoS₂ monolayer. (b) Scheme of the structure. (с) Differential reflection coefficient $DR{\text{/}}R$, where $DR$ is the difference of the light reflection coefficients from the structure with and without the monolayer: (points 1) experimental data; (lines 2–5) model calculations with different thicknesses of the layers: (green line 2) ${{L}_{{{\text{hBN}}}}} = 155$ nm, ${{L}_{{{\text{Si}}{{{\text{O}}}_{2}}}}} = 83$ nm; (blue line 3) ${{L}_{{{\text{hBN}}}}} = 90$ nm, ${{L}_{{{\text{Si}}{{{\text{O}}}_{2}}}}} = 83$ nm; (violet line 4) ${{L}_{{{\text{hBN}}}}} = 135$ nm, ${{L}_{{{\text{Si}}{{{\text{O}}}_{2}}}}} = 114$ nm; and (red line 5) ${{L}_{{{\text{hBN}}}}} = 7$ nm, ${{L}_{{{\text{Si}}{{{\text{O}}}_{2}}}}}$ = 83 nm. The best agreement is reached with the last pair of layer thicknesses according to the atomic force microscopy (AFM) data. The thickness of the covering layer was ${{L}_{{{\text{cap}}}}} = 10$ nm. The figure is taken from [40].

The possibility of controlled modification of the radiative lifetime of the exciton in TMDC monolayers owing to the variation of the dielectric environment was demonstrated in [45] (see also [46–48]). It can be shown [45] that the radiative decay rate of the exciton in the structure with the TMDC monolayer placed on the substrate with the amplitude reflection coefficient r can be written as

$$\Gamma _{0}^{{{\text{eff}}}} = {{\Gamma }_{0}}(1 + \Re {\text{\{ }}r{\text{\} }}),$$

(4)

where ${{\Gamma }_{0}}$ is the radiative decay rate of the exciton in the monolayer without the substrate. Figure 3 shows the dependence of the radiative lifetime of the exciton ${{\tau }_{X}} = {{(2\Gamma _{0}^{{{\text{eff}}}})}^{{ - 1}}}$, measured by the time-resolved photoluminescence method, on the thickness d of the hexagonal boron nitride (hBN) layer (see the inset). Experimental data are quantitatively described by the theory developed in [45] taking into account the Purcell effect in the van der Waals heterostructure. Oscillatory dependence ${{\tau }_{X}}(d)$ is due to the interference of electromagnetic wave in the hBN layer, which leads to oscillations of r in Eq. (4) as a function of the thickness of the layer. Fitting the experimental data, we found that the radiative decay time of the exciton for the monolayer in vacuum is 2.7 ps in agreement with theoretical estimates [21].

Fig. 3.

(Color online) Radiative lifetime of the exciton in the MoSe₂ monolayer versus the thickness of the hBN layer: the experimental points in comparison with the theoretical solid line. The dashed line is the relative intensity of the electromagnetic field on the monolayer. The inset shows the scheme of the structure. The figure is taken from [45].

3 VALLEY ORIENTATION OF ELECTRONS AND EXCITONS AT SINGLE-PHOTON TRANSITIONS

Important features of TMDC monolayers are the so-called chiral selection rules for optical transitions: light with the polarization ${{\sigma }^{ + }}$ (${{\sigma }^{ - }}$) at normal incidence is absorbed in the valley ${{{\mathbf{K}}}_{ + }}$ (${{{\mathbf{K}}}_{ - }}$) and the optical transition occurs with the conservation of the spin of the electron (see Eq. (1) and Fig. 1d). This allows optically selective excitation and detection of charge carriers and excitons in the valleys K₊ and K_– [12–16]. We note that spin-flip transitions in the polarization orthogonal to the monolayer are possible at oblique incidence of radiation [21, 49]. The situation is richer in structures with TMDC bilayers [50, 51]. Below, we consider only structures with monolayers.

As in structures with quantum wells [52, 53], the main mechanism of depolarization of excitons is the long-range exchange interaction between an electron and a hole. The theory of long-range exchange interaction for TMDC monolayers was developed in [21] (see also [23, 24] and [54], where features of van der Waals heterostructures with TMDCs were analyzed). It can be shown that the effective Hamiltonian describing the radiative doublet of the exciton in the basis of circularly polarized states has the form

$$\mathcal{H}({\mathbf{K}}) = \frac{\hbar }{2}({\mathbf{\Omega }_{{{\kern 1pt} {\kern 1pt} {\mathbf{K}}}}}\boldsymbol{\sigma} ).$$

(5)

Here, K is the wave vector of the exciton as a whole, σ is the vector composed of the Pauli matrices describing the pseudospin operator of the exciton, and

$${\mathbf{\Omega }_{{{\kern 1pt} {\mathbf{K}}}}} = \frac{{\Delta {{E}_{{{\text{LT}}}}}(K)}}{\hbar }[\cos(2{{\varphi }_{{\mathbf{K}}}}),\sin(2{{\varphi }_{{\mathbf{K}}}}),0]$$

(6)

is the effective spin precession frequency, where ${{\varphi }_{{\mathbf{K}}}}$ is the angle of the wave vector in the monolayer plane and $\Delta {{E}_{{{\text{LT}}}}}(K)$ is the longitudinal–transverse splitting, which can be represented at $K \gg {{\omega }_{0}}{\text{/}}c$ in the form [54]

$$\Delta {{E}_{{{\text{LT}}}}} = \frac{{\hbar {{\Gamma }_{0}}}}{{{{\varkappa }_{{{\text{eff}}}}}}}\frac{{cK}}{{{{\omega }_{0}}}}.$$

(7)

Here, ${{\omega }_{0}}$ is the exciton excitation frequency, and the effective permittivity ϰ_eff depends on the structure and thicknesses of the layers and depends very weakly on K.

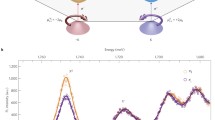
Figure 4a shows the experimental data from [55] on the valley dynamics of excitons obtained by the pump–probe method, where the circularly polarized pump pulse creates excitons with the corresponding pseudospin component and the linearly polarized pulse is used to detect the polarization from the spin Kerr effect. As the temperature increases, the depolarization of excitons becomes faster: the effect is qualitatively due to an increase in the splitting $\propto {\kern 1pt} K$ (see Eq. (7)) with an increase in the temperature of the exciton gas. The kinetic theory of the effect developed in [55] within the density matrix method reproduces the experiment (see Fig. 4b); the comparison of the theory and experiment makes it possible to estimate the time of scattering of excitons.

Fig. 4.

(Color online) (a) Kerr rotation signal induced by the polarization of excitons in the WSe₂ monolayer versus the time delay between pump and probe pulses. (b) Time of valley depolarization of excitons. The circles are the experimental data and the red solid and black dashed lines are the calculations with excitation scattering times τ = 0.066 and 0.25 ps, respectively. The figure is taken from [55].

The excitation of doped structures by circularly polarized light results in the polarization of resident charge carriers [3, 4, 56]. The optical valley orientation of electrons and holes was observed in TMDC monolayers (see, e.g., [57, 58]). Figure 5 shows the results from [57], where the time resolved Kerr rotation method was used to study the spin dynamics of electrons and holes in doped structures with the WSe₂ monolayer. It is seen that the relaxation times of resident electrons are significantly longer than the relaxation times of excitons (cf. Fig. 4b and Figs. 5d, 5e) because the mechanism associated with long-range exchange interaction between electrons and holes is suppressed and the relaxation of spin/valley degrees of freedom of free charge carriers is due to processes of spin-flip scattering and/or intervalley scattering [24, 59]. The depolarization times of charge carriers in the n- and p-type structures are about 0.1 and 1 µs, respectively. The relaxation times of electrons and holes are strongly different apparently because spin splitting in the valence band is much larger than that in the conduction band and only the intervalley spin-flip transitions occur for holes under the condition of the experiment reported in [57], whereas the depolarization of electrons can be due both to intravalley spin-flip transitions and to intervalley transitions with the conservation of the spin (cf. Figs. 5g and 5f).

Fig. 5.

(Color online) (a) Layout of the time-resolved Kerr rotation experiment on the structure with the WSe₂ monolayer and the electrostatic gate. (b, c) Normalized reflection spectra of the n- and p-type structures. (d, e) Kerr rotation versus the time delay at (d) gate voltage ${{V}_{{\text{G}}}} = + 100$ V, electron density ${{n}_{e}} = 7.2 \times {{10}^{{12}}}$ cm^–2, and magnetic field B_y = (red line) 0, (orange line) 20, (blue line) 40, and (black line) 190 mT and (e) ${{V}_{{\text{G}}}} = - 40$ V, ${{n}_{h}} = 3 \times {{10}^{{12}}}$ cm^–2, and B_y = (red line) 0 and (black line) 360 mT. (f, g) Scheme of scattering of charge carriers in doped structures; K and $K{\kern 1pt} '$ denote the ${{{\mathbf{K}}}_{ + }}$ and ${{{\mathbf{K}}}_{ - }}$ valleys, respectively; and RCP and LCP mean the ${{\sigma }^{ + }}$ and ${{\sigma }^{ - }}$ polarizations, respectively. The figure is taken from [57].

4 LINEAR–CIRCULAR DICHROISM AND VALLEY ORIENTATION AT MULTIPHOTON TRANSITIONS

The investigation of nonlinear optical processes in semiconductors, including processes of higher harmonic generation and multiphoton absorption, opens access to the symmetry of a system, features of the energy spectrum, and selection rules at optical transitions [2, 60]. In particular, cubic crystals having isotropic linear optical properties demonstrate a significant polarization dependence of the nonlinear response, including linear–circular dichroism and the anisotropy of absorption of linearly polarized light [61–68]. In this section, we discuss the valley orientation of charge carriers and excitons in TMDC monolayers, as well as linear–circular dichroism in the case of two- and three-photon absorption, within the two-band model (1). Additional effects occurring in real crystals, which are beyond this minimal model, are described in the next section.

We first analyze effects of nonlinear absorption of light, neglecting the Coulomb interaction between an electron and a hole. The rate of the n-photon transition between states of the valence and conduction bands in the ${{{\mathbf{K}}}_{\tau }}$ ($\tau = \pm$) valley, which are described by the Hamiltonian (1), can be represented in the form

$$W_{{cv,\tau }}^{{(n)}}({\mathbf{e}}) = \frac{{2\pi }}{\hbar }\mathop {\left( {\frac{{e{{A}_{0}}}}{c}} \right)}\nolimits^{2n} \sum\limits_{\mathbf{k}} {\kern 1pt} {\text{|}}M_{{cv,\tau }}^{{(n)}}({\mathbf{e}}){{{\text{|}}}^{2}}\delta (n\hbar \omega - 2{{\varepsilon }_{k}}).$$

(8)

Here, ${{A}_{0}}$ is the amplitude of the vector potential of the incident field; ω is the radiation frequency; e is the complex polarization vector of radiation; ${{\varepsilon }_{k}}$ is the energy given by Eq. (2), so that $2{{\varepsilon }_{k}}$ is the energy of the photoexcited electron–hole pair; $M_{{cv,\tau }}^{{(n)}}({\mathbf{e}})$ is the matrix element of n-photon absorption in the ${{{\mathbf{K}}}_{\tau }}$ valley; and the normalization area is taken as unity. We consider the normal incidence of light on the monolayer plane, at which the polarization vector e = (e_x, e_y) is parallel to this plane.

To characterize n-photon absorption, we introduce the linear–circular dichroism

$${{\mathcal{L}}^{{(n)}}} = \frac{{W_{{cv, + }}^{{(n)}}({\text{circ}}) + W_{{cv, - }}^{{(n)}}({\text{circ}})}}{{W_{{cv, + }}^{{(n)}}({\text{lin}}) + W_{{cv, - }}^{{(n)}}({\text{lin}})}},$$

(9)

where circ and lin mean circular polarization (${{\sigma }^{ + }}$ or ${{\sigma }^{ - }}$) and linear polarization, e.g., ${\mathbf{e}}\parallel x$, respectively, and the degree of the valley polarization of photoelectrons at the excitation of circularly polarized light ${{\sigma }^{ + }}$

$${{\mathcal{P}}^{{(n)}}} = \frac{{W_{{cv, + }}^{{(n)}}({{\sigma }^{ + }}) - W_{{cv, - }}^{{(n)}}({{\sigma }^{ + }})}}{{W_{{cv, + }}^{{(n)}}({{\sigma }^{ + }}) + W_{{cv, - }}^{{(n)}}({{\sigma }^{ + }})}}.$$

(10)

Because of the axial symmetry of the Hamiltonian (1) and the time reversal symmetry of the structure, the total absorption of light in the two valleys is independent of the sign of the circular polarization and of the direction of the vector ${\mathbf{e}}$ of linear polarization. In addition, the probabilities of absorption in different valleys are related as $W_{{cv, + }}^{{(n)}}({{\sigma }^{ \pm }}) = W_{{cv, - }}^{{(n)}}({{\sigma }^{ \mp }})$ and $W_{{cv, + }}^{{(n)}}({\text{lin}}) = W_{{cv, - }}^{{(n)}}({\text{lin}})$. Consequently, the numerator and denominator in Eq. (9) can be replaced by $W_{{cv, + }}^{{(n)}}({{\sigma }^{ + }}) + W_{{cv, + }}^{{(n)}}({{\sigma }^{ - }})$ and $2W_{{cv, + }}^{{(n)}}({\text{lin}})$, respectively.

The matrix element of the optical transition at the single-photon absorption is the scalar product of the interband matrix element of the velocity operator ${{{\mathbf{v}}}_{{cv, + }}}$ and the vector e:

$$M_{{cv, + }}^{{(1)}}({\mathbf{e}}) = {{v}_{0}}\left( {T_{ + }^{2}{{e}_{ - }} - T_{ - }^{2}\frac{{k_{ - }^{2}}}{{{{k}^{2}}}}{{e}_{ + }}} \right),$$

where ${{e}_{ \pm }} = {{e}_{x}} \pm {\text{i}}{{e}_{y}}$ and

$${{T}_{ \pm }} = \sqrt {\frac{1}{2}\left( {1 \pm \frac{{{{E}_{{\text{g}}}}}}{{2{{\epsilon }_{k}}}}} \right)} .$$

(11)

Two-photon absorption includes one interband and one intraband virtual transition and the composite matrix element has the form

$$M_{{cv, + }}^{{(2)}} = \frac{{{{v}_{{cc}}} - {{v}_{{vv}}}}}{{\hbar \omega }}{{v}_{{cv}}} = \frac{{2{{v}_{{cc}}}{{v}_{{cv}}}}}{{\hbar \omega }},$$

(12)

where ${{v}_{{n'n}}} = {\mathbf{e}}{{{\mathbf{v}}}_{{n'n, + }}}$, ${{{\mathbf{v}}}_{{cc, + }}} = - {{{\mathbf{v}}}_{{vv, + }}} = (\hbar v_{0}^{2}{\text{/}}{{\varepsilon }_{k}}){\mathbf{k}}$, and it is taken into account that ${{\varepsilon }_{k}} = \hbar \omega$. The contribution to three-photon absorption comes not only from the $v \to c \to v \to c$ processes but also from the processes with $v \to v \to v \to c$, $v \to v \to c \to c$, and $v \to c \to c \to c$ intraband transitions. Taking into account the equality $2{{\varepsilon }_{k}} = 3\hbar \omega$, the total contribution of these processes to the composite matrix element is transformed to the form

$$M_{{cv, + }}^{{(3)}} = \left( { - \frac{{{{v}_{{cv}}}{{v}_{{vc}}}}}{4} + v_{{c,c}}^{2}} \right)\frac{{{{v}_{{cv}}}}}{{{{{(\hbar \omega )}}^{2}}}},$$

(13)

where

$${{v}_{{vc}}} = {{v}_{0}}\left( {T_{ + }^{2}{{e}_{ + }} - T_{ - }^{2}\frac{{k_{ + }^{2}}}{{{{k}^{2}}}}{{e}_{ - }}} \right).$$

Figure 6a shows the calculated absorption dichroism ${{\mathcal{L}}^{{(n)}}}$ at $n = 1,2,3$. Linear–circular dichroism is absent in the case of single-photon absorption. Dichroism in the case of two-photon absorption is absent at small detunings from the absorption edge. In the case of three-photon absorption, circularly polarized light is not absorbed at $3\hbar \omega \approx {{E}_{{\text{g}}}}$ because the projection of the total angular momentum of three circularly polarized photons is +3 or –3, whereas the component of the angular momentum in transitions between the conduction and valence band within the minimal model (1) changes by unity (cf. [63, 64]). Three-photon transitions in the case of circular polarization are possible taking into account intraband processes, their contribution increases sharply with the frequency of light, and dichroism ${{\mathcal{L}}^{{(3)}}}$ is larger than unity already at a small detuning $3\hbar \omega - {{E}_{{\text{g}}}}$. At $n = 2$, the excess angular momentum ±2 of circularly polarized photons is transferred to free charge carriers owing to the intraband transitions and the dichroism ${{\mathcal{L}}^{{(2)}}}$, which is 1 at $2\hbar \omega = {{E}_{{\text{g}}}}$, increases monotonically with the frequency.

Fig. 6.

(Color online) (a) Linear–circular dichroism of n-photon absorption calculated by Eqs. (8) and (9) versus the relative detuning ($n\hbar \omega - {{E}_{{\text{g}}}}$)/E_g. (b) Degree of valley polarization calculated by Eq. (14).

Figure 6b shows the degree of valley polarization of photoelectrons at excitation by ${{\sigma }^{ + }}$ polarized light. It can be shown that the degree of valley polarization ${{\mathcal{P}}^{{(n)}}}$ is independent of n (at the same energy of the photoelectron) and has the form

$$\mathcal{P} = \frac{{\sqrt {1 + 4{{{(\gamma k{\text{/}}{{E}_{{\text{g}}}})}}^{2}}} }}{{1 + 2{{{(\gamma k{\text{/}}{{E}_{{\text{g}}}})}}^{2}}}},$$

(14)

where k is the wave vector of the photoexcited electron determined by the condition $2{{\varepsilon }_{k}} = n\hbar \omega$. A reason for the independence from n is the possibility of representing $M_{{c{v}, + }}^{{(n)}}$ in the form ${{U}^{{(n)}}}{{v}_{{cv}}}$, where the absolute value of the factor ${{U}^{{(n)}}}$ is independent of the sign of the circular polarization ${{\sigma }^{ + }}$ or ${{\sigma }^{ - }}$. The degree of valley polarization at the absorption edge reaches 100% (see Fig. 1d), because ${{{\mathbf{e}}}_{ - }} \cdot {{{\mathbf{v}}}_{{cv, + }}} \to 0$ at $k \to 0$ according to the selection rules. This scalar product increases (from zero) with the detuning $n\hbar \omega - {{E}_{{\text{g}}}}$, and the degree of valley polarization decreases. The parameter ${{\mathcal{L}}^{{(2)}}}$ is related to $\mathcal{P}$ as

$${{\mathcal{L}}^{{(2)}}} = \mathop {\left( {1 - \frac{1}{2}\sqrt {1 - {{\mathcal{P}}^{2}}} } \right)}\nolimits^{ - 1} .$$

We now briefly discuss excitonic effects under the assumption that the binding energy of the exciton is low compared to $\hbar \omega$. This means that the Coulomb interaction can be taken into account only in the final state. The analysis in [69, 70] shows that $M_{{cv}}^{{(2)}} \propto ({\mathbf{e}} \cdot {\mathbf{k}})$ in the considered model and light produces p-excitons (component of the angular momentum of the envelope is $m = \pm 1$). Three-photon transitions in the case of linear polarization can excite s- and d-excitons (cf. [71]) and only d-excitons in the case of circular polarization.

Figure 7 shows the spectra of two- and one-photon absorption of the WSe₂ monolayer measured in experiments on the excitation of the luminescence of the 1s‑exciton. The two- and one-photon absorption spectra clearly demonstrate p and s states of the exciton, respectively, in agreement with the above model. A significant circular polarization is also observed in the case of two-photon absorption in the spectral range of 2p- and 3p-excitons.

Fig. 7.

(Color online) Excitation spectra of (a) two- and (b) one-photon photoluminescence of the WSe₂ monolayer detected on the 1s-exciton. The right axis shows the degree of circular polarization of luminescence. The figure is taken from [72].

5 EFFECTS OF TRIGONAL SYMMETRY

Features of the symmetry of monolayers—the absence of the center of space inversion and the presence of a three-fold rotation axis perpendicular to the monolayer—result in the important specificity of multiphoton absorption [70, 73, 74] and differences from the simplest model described in Section 4. In particular, at normal incidence of radiation, the component of the angular momentum is conserved only modulo 3; therefore, s-excitons can also be excited in two-photon transitions and the selection rules have the form

$$2{{\sigma }^{ + }} \to ns,\;{{{\mathbf{K}}}_{ - }},$$

(15a)

$$2{{\sigma }^{ - }} \to ns,\;{{{\mathbf{K}}}_{ + }}.$$

(15b)

Here, K_– and K₊ indicate valleys in which the electron is excited in the exciton. The description of such transitions cannot be carried out within the minimal model (1) and requires the inclusion of intermediate states in remote bands. The microscopic theory of this effect was developed in [70], where it was shown that excitons with different parities, in particular, s- and p‑excitons, are also mixed.

According to the selection rules (15a) and (15b), at the resonant or quasi-resonant two-photon excitation of the 1s-exciton, the circular polarization of luminescence should be inverted compared to the circular polarization of excitation. This effect is illustrated by experimental data in Fig. 8, which shows the photoluminescence spectra at two-photon excitation of the structure with a microcavity containing the MoSe₂ monolayer [75]. The experiment clearly demonstrates the inversion of the circular polarization in agreement with predictions of the theory.

Fig. 8.

(Color online) Photoluminescence spectrum of the structure with the quantum microcavity containing the MoSe₂ monolayer at the two-photon excitation of the (a) ${{\sigma }^{ + }}$ and (b) ${{\sigma }^{ - }}$ polarizations. The right axes show the degree of circular polarization. The orange vertical band indicates the doubled excitation energy. The figure is taken from [75].

For the same reasons, TMDC monolayers demonstrate the effective second optical harmonic generation [70, 72, 76, 77], which is phenomenologically described by the relation

$${{P}_{{2\omega ,x}}} = 2\chi {{E}_{{\omega ,x}}}{{E}_{{\omega ,y}}},\quad {{P}_{{2\omega ,y}}} = \chi (E_{{\omega ,x}}^{2} - E_{{\omega ,y}}^{2}).$$

(16)

Here, ${{{\mathbf{E}}}_{\omega }}$ is the electric field vector of the fundamental harmonic (at the frequency ω), ${{{\mathbf{P}}}_{{2\omega }}}$ is the induced polarization vector at the doubled frequency, χ is the nonlinear susceptibility, and the x and y axes are chosen according to Fig. 1b. The comparison of the microscopic theory of the effect developed in [70] (see also [78]) with the experimental data [70, 72] indicates that the leading contribution to χ comes from transitions with intermediate states in far bands; for this reason, the second harmonic generation is the most efficient on the 1s-exciton.

6 CONCLUSIONS

There are currently well-developed theoretical concepts of the processes of optical orientation of spin and valley degrees of freedom of charge carriers and Coulomb complexes in atomically thin transition metal dichalcogenide layers. Numerous optical experiments demonstrate the effective control of the valley polarization. However, this field of physics is far from complete development. In our opinion, one of the interesting open problems is the experimental observation and study of linear–circular dichroism of multiphoton absorption in the transition metal dichalcogenide monolayers both in the region of exciton transitions and for transitions to the electron–hole excitation continuum. In particular, such studies will allow establishing the ranges of application of the simplest Dirac model to describe the energy spectrum of charge carriers in these systems.