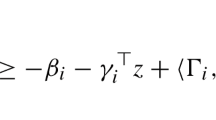Transversals of Total Strict Linear Orders

Abstract

Given a set M, let ${\mathcal O}(M)$ be the set of all the total strict linear orders on M and, given an integer 2 ≤ k ≤|M|, let ${\mathcal O}_{k}(M) = \{{\mathbf R} \in {\mathcal O}(N) : \text {\textit {N} is a \textit {k}-subset of \textit {M}}\}$, that is, let ${\mathcal O}_{k}(M)$ be the family of all the total strict linear orders on each of all the k-subsets of M. A subset ${\mathcal T}\subseteq {\mathcal O}_{k}(M)$ will be called congruent if given any pair $\{a,b\}\subseteq M$, if for some ${\mathbf R} \in {\mathcal T}$ we have (a,b) ∈R, then for every ${\mathbf Q}\in {\mathcal T}$ we have (b,a)∉Q. A subset ${\mathcal T}\subseteq {\mathcal O}_{k}(M)$ will be called a k-transversal of ${\mathcal O}(M)$ if for every ${\mathbf R} \in {\mathcal O}(M)$ there is ${\mathbf Q} \in {\mathcal T}$ such that either ${\mathbf Q} \subseteq {\mathbf R}$ or ${\mathbf Q}^{-}\subseteq {\mathbf R}$ (where Q⁻ = {(b,a) : (a,b) ∈Q} is the inverse order of Q). A subset ${\mathcal T}\subseteq {\mathcal O}_{k}(M)$ will be called a congruent k-transversal of ${\mathcal O}(M)$ if ${\mathcal T}$ is congruent and is a k-transversal of ${\mathcal O}(M)$. In this note we characterize, in terms of 2-arc-colourings of digraphs, the sets of congruent k-transversals of a given set ${\mathcal O}(M)$. Also we show some relations between these structures with the diagonal Ramsey numbers and with the chromatic number.