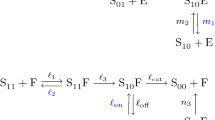Abstract
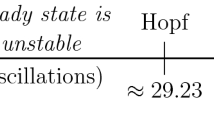
We consider a model of extracellular signal-regulated kinase regulation by dual-site phosphorylation and dephosphorylation, which exhibits bistability and oscillations, but loses these properties in the limit in which the mechanisms underlying phosphorylation and dephosphorylation become processive. Our results suggest that anywhere along the way to becoming processive, the model remains bistable and oscillatory. More precisely, in simplified versions of the model, precursors to bistability and oscillations (specifically, multistationarity and Hopf bifurcations, respectively) exist at all “processivity levels”. Finally, we investigate whether bistability and oscillations can exist together.






Similar content being viewed by others
Notes
The map \(\phi \) is a steady-state parametrization (Obatake et al. 2019).
Dissipative means that there is a compact subset of \({\mathcal {S}}_c\) that every trajectory eventually enters; being dissipative is automatic when the network is conservative (Conradi et al. 2017).
The reduced ERK network is not in this list, as it does not admit bistability (Obatake et al. 2019).
References
Banaji M (2018) Inheritance of oscillation in chemical reaction networks. Appl Math Comput 325:191–209
Banaji M, Pantea C (2018) The inheritance of nondegenerate multistationarity in chemical reaction networks. SIAM J Appl Math 78(2):1105–1130
Breiding P, Timme S (2018) Homotopycontinuation.jl: a package for homotopy continuation in Julia. In: Davenport JH, Kauers M, Labahn G, Urban J (eds) Mathematical Software ICMS 2018
Cappelletti D, Feliu E, Wiuf C (2020) Addition of flow reactions preserving multistationarity and bistability. Math Biosci 320:108295
Conradi C, Shiu A (2015) A global convergence result for processive multisite phosphorylation systems. Bull Math Biol 77(1):126–155. ISSN 1522-9602. http://dx.doi.org/10.1007/s11538-014-0054-4
Conradi C, Feliu E, Mincheva M, Wiuf C (2017) Identifying parameter regions for multistationarity. PLoS Comput Biol 13(10):e1005751
Conradi C, Mincheva M, Shiu A (2019) Emergence of oscillations in a mixed-mechanism phosphorylation system. Bull Math Biol 81(6):1829–1852
Conradi C, Feliu E, Mincheva M (2020) On the existence of Hopf bifurcations in the sequential and distributive double phosphorylation cycle. Math Biosci Eng 17(1):494–513
Cox DA, Little J, O’Shea D (2007) Ideals, varieties, and algorithms: an introduction to computational algebraic geometry and commutative algebra, 3/e (Undergraduate Texts in Mathematics). Springer, Berlin, 0387356509
Dickenstein A, Millan MP, Shiu A, Tang X (2019) Multistationarity in structured reaction networks. Bull Math Biol 81(5):1527–1581
DiStefano III J (2013) Dynamic Systems Biology Modeling and Simulation. Academic Press, London
Feliu E, Wiuf C (2013) Simplifying biochemical models with intermediate species. J R Soc Interface 10(87). ISSN 1742-5662. https://doi.org/10.1098/rsif.2013.0484
Feliu E, Lax C, Walcher S, Wiuf C (2019) Quasi-steady state and singular perturbation reduction for reaction networks with non-interacting species. Preprint, available from arXiv:1908.11270
Futran AS, Link AJ, Seger R, Shvartsman SY (2013) ERK as a model for systems biology of enzyme kinetics in cells. Curr Biol 23(21):R972–R979. ISSN 0960-9822. https://doi.org/10.1016/j.cub.2013.09.033
Giaroli M, Rischter R, Pérez Millán M, Dickenstein A (2019) Parameter regions that give rise to \(2[n/2] +1\) positive steady states in the n-site phosphorylation system. Math Biosci Eng. 16(6):7589–7615. https://doi.org/10.3934/mbe.2019381
Hell J, Rendall AD (2016) Sustained oscillations in the map kinase cascade. Math Biosci 282:162–173
Joshi B, Shiu A (2013) Atoms of multistationarity in chemical reaction networks. J Math Chem 51(1):153–178. ISSN 1572-8897. https://doi.org/10.1007/s10910-012-0072-0
Kuznetsov YA (1995) Elements of Applied Bifurcation Theory, vol 112. Springer, Berlin
Obatake N, Shiu A, Tang X, Torres A (2019) Oscillations and bistability in a model of ERK regulation. J Math.Biol 79(4):1515–1549
Plotnikov A, Zehorai E, Procaccia S, Seger R (2011) The MAPK cascades: signaling components, nuclear roles and mechanisms of nuclear translocation. BBA-Mol Cell Res 1813(9):1619–1633
Rubinstein BY, Mattingly HH, Berezhkovskii AM, Shvartsman SY (2016) Long-term dynamics of multisite phosphorylation. Mol Biol Cell 27(14):2331–2340. https://doi.org/10.1091/mbc.E16-03-0137
Sadeghimanesh AH, Feliu E (2019) The multistationarity structure of networks with intermediates and a binomial core network. Bull Math Biol 81(7):2428–2462
Salazar C, Höfer T (2009) Multisite protein phosphorylation—from molecular mechanisms to kinetic models. FEBS J, 276(12):3177–3198, ISSN 1742-4658. https://doi.org/10.1111/j.1742-4658.2009.07027.x
Sontag ED (2001) Structure and stability of certain chemical networks and applications to the kinetic proofreading model of T-cell receptor signal transduction. IEEE Trans Autom Control 46(7):1028–1047
Sun J, Yi M, Yang L, Wei W, Ding Y, Jia Y (2014) Enhancement of tunability of MAPK cascade due to coexistence of processive and distributive phosphorylation mechanisms. Biophys J 106(5):1215–1226
Tang X, Wang J (2019) Bistability of sequestration networks. Preprint arXiv: 1906.00162
Torres A, Feliu E (2019) Detecting parameter regions for bistability in reaction networks. Preprint, arXiv: 1909.13608
Tyson JJ, Albert R, Goldbeter A, Ruoff P, Sible J (2008) Biological switches and clocks. J R Soc Interface 5:S1–S8
Wang L, Sontag E (2008) On the number of steady states in a multiple futile cycle. J Math Biol 57(1):29–52
Wiuf C, Feliu E (2013) Power-law kinetics and determinant criteria for the preclusion of multistationarity in networks of interacting species. SIAM J Appl Dyn Syst 12(4): 1685–1721. ISSN 1536-0040. https://doi.org/10.1137/120873388
Yang X (2002) Generalized form of Hurwitz-Routh criterion and Hopf bifurcation of higher order. Appl Math Lett 15(5):615–621. ISSN 0893-9659. https://doi.org/10.1016/S0893-9659(02)80014-3
Acknowledgements
Part of this research was initiated at the Madison Workshop on Mathematics of Reaction Networks at the University of Wisconsin in 2018. NO, AS, and XT were partially supported by the NSF (DMS-1752672). XT was partially supported by the NSFC 12001029. CC was partially supported by the Deutsche Forschungsgemeinschaft, 284057449. The authors thank Elisenda Feliu, Henry Mattingly, Stanislav Shvartsman, Sascha Timme, Angélica Torres, and Emanuele Ventura for helpful discussions. The authors acknowledge three referees whose insightful comments helped strengthen this work. In particular, Remark 4.7 is inspired by the very detailed comments of one reviewer who suggested the limiting process described there. Ideas in Remark 5.3 are also due to this reviewer.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A files in the supporting information
Table 5 lists the files in the Supporting Information, and the result or section each file supports. All files can be found at the online repository: https://github.com/neeedz/COST
B Procedure to study multistationarity numerically
Here we describe the procedure we used in Sect. 4.3 for numerically studying multistationarity in the minimally bistable ERK network at various processivity levels \(p_k\) and \(p_{\ell }\).
We begin by mirroring the analysis of Sect. 4.2. Specifically, we use the parameters given in (14) to study the critical function \(C(\kappa ,{{\hat{x}}})\) for \(x_1=x_2=T\) and \(x_3=1\). Due to this choice of \(\kappa \) and \({{\hat{c}}}\), the critical function is a (rational) function of \(p_k\), \(p_\ell \), and T only, i.e., \(C(\kappa ,{{\hat{x}}}) \equiv C(p_k,p_\ell ,T)\). The numerator is the following polynomial:
As \(0< p_k, p_\ell < 1\), the leading coefficient of \(q(p_k,p_\ell ,T)\) as a polynomial in T is positive. Next, the steady-state parametrization \(\phi \) from Proposition 3.1 is as follows (cf. eq. (6)):
To numerically study multistationarity for \(p_k\), \(p_\ell \rightarrow 1\), we proceed as follows:
-
(i)
Pick values of \(0< {{\tilde{p}}}_k, {{\tilde{p}}}_\ell < 1\) and \({{\tilde{T}}}>0\) such that \(q({{\tilde{p}}}_k, {{\tilde{p}}}_\ell , {{\tilde{T}}})>0\) (recall eq. (25)).
-
(ii)
Substitute into (26) the values of \({{\tilde{p}}}_k\), \({{\tilde{p}}}_\ell \), and \({{\tilde{T}}}\) from the previous step to obtain a steady state \({{\tilde{x}}}\).
-
(iii)
Compute, using (5), the total amounts \(\tilde{c}_1\), \({{\tilde{c}}}_2\), and \({{\tilde{c}}}_3\) at \({{\tilde{x}}}\).
-
(iv)
Use Matcont with initial condition near \({{\tilde{x}}}\) and bifurcation parameter \(c_2\), to obtain a bifurcation curve.
-
(v)
To compare curves corresponding to distinct \({{\tilde{p}}}_k\) and \({{\tilde{p}}}_\ell \), compute relative concentrations \(\frac{x_i}{{{\tilde{c}}}_1}\) and \(\frac{c_2}{{{\tilde{c}}}_2}\) that relate \(x_i\) and \(c_2\) to the \({{\tilde{x}}}\) and \({{\tilde{c}}}_2\) computed in steps (ii) and (iii) .
Step (v) is crucial for interpreting the numerical results obtained by the above procedure, because certain total amounts differ by orders of magnitude as \(p_k\), \(p_\ell \rightarrow 1\), and so it is more meaningful to compare values relative to the reference point \({{\tilde{x}}}\) obtained in step (ii) Figs. 6 and 7.
Rights and permissions
About this article
Cite this article
Conradi, C., Obatake, N., Shiu, A. et al. Dynamics of ERK regulation in the processive limit. J. Math. Biol. 82, 32 (2021). https://doi.org/10.1007/s00285-021-01574-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00285-021-01574-6
Keywords
- Chemical reaction network
- Extracellular signal-regulated kinase
- Bistability
- Oscillation
- Hopf bifurcation