Explicit parallel co-simulation approach: analysis and improved coupling method based on H-infinity synthesis

Abstract

Co-simulation is widely used in the industry for the simulation of multidomain systems. Because the coupling variables cannot be communicated continuously, the co-simulation results can be unstable and inaccurate, especially when an explicit parallel approach is applied. To address this issue, new coupling methods to improve the stability and accuracy have been developed in recent years. However, the assessment of their performance is sometimes not straightforward or is even impossible owing to the case-dependent effect. The selection of the coupling method and its tuning cannot be performed before running the co-simulation, especially with a time-varying system.

In this work, the co-simulation system is analyzed in the frequency domain as a sampled-data interconnection. Then a new coupling method based on the H-infinity synthesis is developed. The method intends to reconstruct the coupling variable by adding a compensator and smoother at the interface and to minimize the error from the sample-hold process. A convergence analysis in the frequency domain shows that the coupling error can be reduced in a wide frequency range, which implies good robustness. The new method is verified using two co-simulation cases. The first case is a dual mass–spring–damper system with random parameters and the second case is a co-simulation of a multibody dynamic (MBD) vehicle model and an electric power-assisted steering (EPAS) system model. Experimental results show that the method can improve the stability and accuracy, which enables a larger communication step to speed up the explicit parallel co-simulation.

1 Introduction

Co-simulation is widely used in the virtual development of multidomain systems. It brings about new opportunities and challenges in the simulation of a multibody dynamic (MBD) system interacting with other systems, e.g., the pantograph–catenary interaction [21], or the vehicle–track interaction [2, 22]. Especially in automotive engineering, an MBD vehicle system always needs to interact with hydraulic, and electronic subsystems. The subsystem models from each domain are usually built in domain-specific software tools, shared as black boxes from suppliers and integrated using co-simulation for holistic system development. To integrate the different models in a unified format, a functional mock-up interface standard has been introduced in the academia and industry [8]. According to this standard, each model can be calculated as a single functional mock-up unit (FMU) and its input–output variables (i.e., coupling variables) are synchronized and communicated by a co-simulation master. As each local solver can adapt to the subsystem model, co-simulation is a computationally time efficient solution. A multicore distributed simulation of a combustion engine has been presented by Khaled [4]. The simulation is accelerated by partitioning different cylinder models involving discrete events. Andersson partitioned a race car model to achieve an accelerated parallel co-simulation [1]. Gallrein used a co-simulation of high-fidelity tyre models and an MBD vehicle model for real-time driver-in-the-loop application [15].

In a mono-simulation where the dynamic equations are solved together by a single solver, the simulation accuracy and stability depend on the time-stepping method. However, the co-simulation accuracy and stability are also related to the discrete communication between each subsystem, and this issue has been an active topic of research in the last decade [1, 3, 9, 29, 30]. An extensive state-of-the-art survey on the co-simulation of continuous, discrete, and hybrid systems was conducted by Gomes [16]. First, a co-simulation can be distinguished by the time-stepping method of the master, namely the explicit (non-iterative), semi-explicit, and implicit (iterative) co-simulation. In addition, the slave subsystems can be calculated in parallel (Jacobi scheme), sequential (Gauss–Seidel scheme), and iterative schemes. For a co-simulated mechanical system, the coupling configuration can be further distinguished by the algebraic constraint [29] and applied force [30] approaches. The applied force approach, in which the coupling variables are force–displacement (FD coupling) or displacement–displacement (DD coupling), is the preferred one because an algebraic loop can be avoided [9].

The explicit parallel co-simulation, i.e., where each subsystem model is simulated on its own in parallel and exchanges the coupling variables only at specified communication instants, can be easily implemented and is more common than the alternatives. In this approach, the master is not required to control an iterative process or a calculation sequence of the slaves. Besides, the slave model is not required to be controllable for rollback or observable for the internal states. This feature can be supported by most commercial software tools and black-box models for intellectual property protection. In general, the explicit parallel co-simulation has a reduced computational burden and a shorter elapsed time, which is more suitable for optimization and real-time applications, e.g., the hardware-in-loop simulation. However, it is well known that the explicit parallel co-simulation has drawbacks in accuracy and stability, because the input to each subsystem is unknown during the communication interval $\Delta t$ (i.e., the macro-step) and needs to be approximated by some extrapolation methods. The simplest method is to keep the latest exchanged value during the macro-step, i.e., the zeroth-order hold (ZOH) method. The resulting approximation error, i.e., the coupling error, can be significant regarding the accuracy and stability. Unlike iterative approaches [29], explicit co-simulation cannot undo the step and recalculate the input. Therefore, to improve its result by coupling methods is challenging but highly needed in engineering.

Busch [9] systematically analyzed extrapolation methods with Lagrange and Hermite polynomials containing first-order derivatives. It shows that higher-order extrapolation polynomials increase the error order, may stabilize or destabilize the system, and the performance varies with the system parameters. To predict the coupling variable, usually additional information about the system is needed. Andersson [1] used the partial derivatives with respect to the coupling variables for a linear correction. Another interesting concept is the energy-based coupling method. The rationale is that the inconsistent energy from the discrete communication can yield instability of the system, and thus, should be avoided. Benedikt [7] used the generalized energy in a macro-step to correct the coupling variables. Drenth [13] proposed a new sample-hold design to preserve the energy in a power bond. In these approaches, the coupling variables are actually corrected separately to preserve their product, i.e., the energy. However, if only the energy is conserved, the result might be still incorrect, as shown by González [17] and Wu [32]. González [18] developed an energy-leak monitoring framework, in which the dissipated energy inside the system is needed to correct the coupling variables. Rahikainen [25] took the residual energy as an indicator, using its linearity with the macro-step to verify the co-simulation accuracy and stability. In the aforementioned methods, the energy reference is usually calculated from the available results in a previous macro-step, which causes an inherent macro-step delay. Furthermore, some adaptive coupling methods are developed for complex systems. Sadjina [28] considered the residual energy as an error estimator to control a variable macro-step. Stettinger [31] developed a model-based coupling approach using extended Kalman filter and recursive least square algorithms, which are commonly used control techniques. Khaled [5] developed a context-based heuristic method to adapt the extrapolation polynomial. Peiret [23] used an adaptive reduced-order interface model to represent complex systems and generate approximated variables during the communication interval.

From the point of view of the authors, some challenges still remain in the state-of-the-art methods. First, the parameters of the aforementioned methods do not always have a straightforward or physical interpretation, which makes their tuning work less transparent. Second, the parameter values are not optimized due to the lack of an objective function and a reference system. Several parameters can be dependent and difficult to tune together to improve the performance. Third, the performance of the coupling method can be strongly case-dependent. The combination effect of different system dynamics and coupling configurations (e.g., DD and FD couplings) makes the performance assessment less intuitive and its generalization to a more complex engineering system even impossible [17, 30].

In this work, we see the explicit parallel co-simulation in the frequency domain as a sampled-data interconnection. The objective is to focus on the coupling interface itself, which releases the complexity of subsystems. Some well-established control theorems are adopted to interpret the co-simulation problems. Furthermore, we design a new coupling method similarly as a signal reconstruction work, which relies on the $\mathcal{H}_{\infty }$ synthesis. This method intends to reduce the coupling error directly by minimizing its $\mathcal{L}_{2}$ norm.

This paper is organized as follows: a co-simulated system is formulated as a closed-loop interconnection in Sect. 2. The stability is analyzed by the Nyquist stability criterion. Then the coupling method design is formulated as a $\mathcal{H}_{\infty }$ synthesis problem in Sect. 3 and solved by an optimization routine, followed by a convergence analysis and a parameter study. In Sect. 4, the new method is verified with a dual mass–spring–damper system and a real engineering case, which is a co-simulation of an MBD vehicle model and an electric power-assisted steering (EPAS) system model. The work is further discussed and concluded in Sect. 5.

2 Analysis of co-simulated system

In the first step, we present a basic co-simulated system as a sample-data system because of the common nature of discrete communication. Then we show how the co-simulation degrades in terms of error and stability.

2.1 Closed-loop interconnection formulation

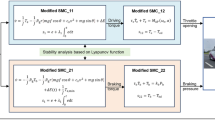
A basic parallel co-simulated system can be simplified as two weakly coupled subsystems. For ease of analysis, we assume that 1. the subsystems are linear time-invariant (LTI) with zero initial condition; 2. the subsystems are coupled by a single input and a single output; 3. each subsystem can be accurately solved by an appropriate solver, so the integration error is minor compared to the coupling error [14, 26]. Then we use transfer functions $Q_{1}(s)$ and $Q_{2}(s)$ to represent two subsystems, $s$ denoting the Laplace domain. A non-feed-through subsystem [20] yields a strictly proper transfer function (i.e., the degree of the numerator polynomial is less than that of the denominator). A feed-through subsystem yields a proper transfer function.

In parallel co-simulation, the input–output variables are communicated every macro-step $\Delta t$. This is similar to adding sample and hold devices to the continuous reference system. Thus, the system becomes a sampled-data closed-loop interconnection (Fig. 1(a)), which introduces error and stability issues [24]. The sampled input $u^{*}(t)$ is a product of the continuous input $u(t)$ and a periodic impulse train and its Laplace transform is known as

$$ u^{*}(t)=\sum _{n=-\infty }^{\infty } u(t)\delta (t-n\Delta t), \qquad u^{*}(s)= \frac{1}{\Delta t}\sum _{n=-\infty }^{\infty } u(s-jn\omega _{s}), $$

(1)

where $\omega _{s}=2 \pi / \Delta t$. The continuous approximation $\tilde{u}(s)$ during $\Delta t$ is obtained from holding $u^{*}(s)$ with an extrapolation operator $H(s)$, e.g., the ZOH method.

$$ \tilde{u}(s)=H(s)u^{*}(s). $$

(2)

Actually, $H(s)$ can differ in each subsystem, but we assume that the same $H(s)$ is applied in the interconnection. Afterwards, two important characters of co-simulation are concerned: 1. the accuracy of the coupling method; 2. the stability and robustness of co-simulation.

Fig. 1

(a) Co-simulated system is formulated as a closed-loop interconnection. (b) A truncated subsystem on one side and coupling error $\xi _{u}$ is an input multiplicative disturbance

2.2 Analysis of the coupling error

The coupling error $\xi _{u}(s)$ is the difference of the continuous input and its approximation

$$ \begin{aligned} \xi _{u}(s)&=\tilde{u}(s)-u(s) \\ &=\underbrace{\Big(\frac{H(s)}{\Delta t}-1\Big)u(s)}_{\text{low-frequency component}}+ \underbrace{\frac{H(s)}{\Delta t}\sum _{n=1}^{\infty }u(s\pm jn\omega _{s})}_{\text{high-frequency component}} \end{aligned} ,$$

(3)

which can be modeled as an input multiplicative disturbance (Fig. 1(b)). When the sampling frequency $\omega _{s}=2 \pi / \Delta t$ is not typically higher than the signal frequency $\omega$, the high-frequency components can be mirror into the low-frequency part, i.e., an aliasing effect occurs in the co-simulation [6]. In this circumstance, a severe low-frequency error is introduced and should be avoided in the first place. Engineers can select $\Delta t$ according to the subsystem bandwidth or an estimation of frequency components from its standalone simulation. However, this requirement cannot guarantee the accuracy and stability of the co-simulation.

The hold operator $H(s)$ varies with the extrapolation degree $k$. For simplicity, we consider the zeroth-order hold $H_{zoh}(s)$, first-order hold $H_{foh}(s)$, and second-order hold $H_{soh}(s)$ methods ($k=0,1,2$, respectively):

$$ \begin{aligned} H_{zoh}(s)&=\frac{1-e^{-s\Delta t}}{s}, \\ H_{foh}(s)&=\frac{1+s\Delta t}{\Delta t}(\frac{1-e^{-s\Delta t}}{s})^{2}, \\ H_{soh}(s)&=( \frac{2+3s\Delta t + 2 s^{2} \Delta t^{2}}{2\Delta t^{2}} ) ( \frac{1- e^{-s\Delta t}}{s})^{3}. \end{aligned} $$

(4)

$\xi _{u}(s)$ in combination with different $H(s)$ can be expanded with the Taylor series

$$ \begin{aligned} \xi _{u,zoh}(s)&=\big[-\frac{1}{2}s\Delta t + s^{2}\mathcal{O}( \Delta t^{2}) \big]u(s)+\big[1+s \mathcal{O}(\Delta t) \big] \Sigma (s), \\ \xi _{u,foh}(s)&=\big[ -\frac{5}{12}(s\Delta t)^{2} + s^{3} \mathcal{O}(\Delta t^{3})\big] u(s)+\big[1+s^{2} \mathcal{O}(\Delta t^{2}) \big]\Sigma (s), \\ \xi _{u,soh}(s)&=\big[ -\frac{3}{8}(s\Delta t)^{3} + s^{4} \mathcal{O}(\Delta t^{4}) \big]u(s)+\big[1+s^{3} \mathcal{O}(\Delta t^{3}) \big] \Sigma (s), \\ \text{where }& \quad \Sigma (s) = \sum _{n=1}^{\infty }u(s\pm jn\omega _{s}). \end{aligned} $$

(5)

When $\Delta t$ is sufficiently small $\xi _{u}(s)$ can be approximated adequately by its low-frequency component [24]. Then a $k$-degree extrapolation method yields an error with an order of $\mathcal{O}(\Delta t^{k+1}$). This might not be true if the high-frequency component $\Sigma (s)$ is non-negligible. For LTI subsystems, the output error is a result of linear mapping from the input error

$$ \begin{aligned} \xi _{y}(s)=\xi _{u}(s)Q(s) \end{aligned} ,$$

(6)

which has a same error order of $\mathcal{O}(\Delta t^{k+1}$), and the convergence property is preserved. This is consistent with a time-domain analysis based on a LTI system [9]. Similarly, the state error $\xi _{x}(s)$ is mapped from $\xi _{u}(s)$ with a transfer function $Q_{x}(s)$, and thus, it has the same order.

When the subsystem $Q(s)$ and $Q_{x}(s)$ are underdamped and have fast dynamics, they become less robust to the disturbance $\xi _{u}(s)$. The corresponding output $y$ and state $x$ can be more easily excited by its high-frequency component, and consequently, ripples may occur in co-simulation.

2.3 Analysis of stability and robustness

In a stable co-simulation, the error $\xi _{y}(s)$ is convergent. In other words, it will not propagate incrementally in the closed-loop interconnection. To derive $\xi _{y}(s)$, an exogenous input vector $u_{e}$ should be added to excite both subsystems in the interconnection (Fig. 1(a)). The output of the two subsystems becomes

$$ \begin{aligned} \tilde{y}=\frac{1}{1-(1+\phi )^{2}Q_{1}Q_{2}} \begin{bmatrix} (1+\phi )Q_{1} & (1+\phi )^{2}Q_{1}Q_{2} \\ (1+\phi )^{2}Q_{1}Q_{2}& (1+\phi )Q_{2}\end{bmatrix} u_{e} \end{aligned} $$

(7)

where the notation $s$ is dropped for clarity and $\phi$ is the operator for the multiplicative disturbance. In the continuous nominal system, the error-free output is

$$ y=\frac{1}{1-Q_{1}Q_{2}} \begin{bmatrix} Q_{1} & Q_{1}Q_{2} \\ Q_{1}Q_{2}& Q_{2}\end{bmatrix} u_{e} $$

(8)

then $\xi _{y}$ can be derived from the difference

$$ \begin{aligned} \xi _{y}= \frac{1}{1-(1+\phi )^{2}Q_{1}Q_{2}} \frac{1}{1-Q_{1}Q_{2}} \begin{bmatrix} \phi Q_{1}+ \phi (1+\phi )Q_{1}^{2}Q_{2} & \phi (2+\phi )Q_{1}Q_{2} \\ \phi (2+\phi )Q_{1}Q_{2}& \phi Q_{2}+ \phi (1+\phi )Q_{1}Q_{2}^{2} \end{bmatrix} u_{e}. \end{aligned} $$

(9)

Subsystems $Q_{1}$, $Q_{2}$, and the terms cascaded with $\phi$ are always stable. In addition, the nominal closed-loop system is stable. Therefore, the convergence of $\xi _{y}$ is determined by $-(1+\phi )^{2}Q_{1}Q_{2}$, i.e., the loop transfer function of the system. For a stable system, its loop transfer function should not encircle the point $-1+ j0$ in the complex plane as $s \in (-j\infty , +j\infty )$ according to the Nyquist stability criterion. Besides this geometrical approach, two well-established control theorems can be used in co-simulation problem.

Remark 1

Small-gain theorem

The closed-loop interconnection (Fig. 1(a)) is stable if it fulfills $||(1+\phi )^{2}Q_{1}Q_{2}||_{\infty }<1$ (it can be generalized to a nonlinear multi-input and multi-output system) [19].

$||(1+\phi )^{2}Q_{1}Q_{2}||_{\infty }$ is the maximum gain of a single-input single-output system or the maximum singular value of a multi-input and multi-output system. It means that the system is stable if $-(1+\phi )^{2}Q_{1}Q_{2}$ is bounded within a unit circle. Since the ZOH method does not amplify the system gain, it guarantees a stable co-simulation if the nominal system fulfills $||Q_{1} Q_{2}||_{\infty }<1$ and no aliasing occurs.

Furthermore, the system with a smaller loop gain $-(1+\phi )^{2}Q_{1}Q_{2}$ has a better rejection to the disturbance (i.e., the coupling error). This can be achieved by selecting a more robust coupling configuration [27]. In an FD coupling, applying the force variable to the stiffer side can also reduce the loop gain and make the co-simulation more stable and accurate. Examples can be seen in the vehicle–steering interaction [10] and the vehicle–track interaction [22]. Scaling down the coupling variables can also reduce the loop gain and enhance the stability. It gives incorrect simulation results but can be useful to obtain a stable initial setup.

Remark 2

Passivity theorem

The closed-loop interconnection (Fig. 1(a)) is stable if its subsystems $(1+\phi ) Q_{1}$, $-(1+\phi ) Q_{2}$ are either strictly passive or output strictly passive and zero-state observable (it can be generalized to a nonlinear system) [19].

It means that the system is stable if $-(1+\phi )^{2}Q_{1}Q_{2}$ has a phase angle in $(-180^{o}, 180^{o})$. However, extrapolation method (4) always shows an ever-increasing phase delay in high frequency. This destroys the passivity of subsystem $Q_{1}$, $Q_{2}$. Physically, an additional energy flows into the interconnection, and if it is not sufficiently dissipated or stored, the system might get unstable. This brings an intuitive explanation on the physics of a co-simulated system. Herein, we can conclude that to improve the stability, the phase delay should be compensated or the loop gain should be reduced.

3 Improved coupling method by $\mathcal{H}_{\infty }$ synthesis

From the foregoing analysis, the sample-hold process is the error source of co-simulation. To reduce this error, a new coupling method is given next. It adds a compensator and a smoother at the coupling interface.

3.1 Formulation of the error system

The concept can be illustrated using an error system (Fig. 2) inspired by the modern signal reconstruction work [33]. $u(s)$ is a coupling variable from subsystem 1 to subsystem 2. An appropriate coupling method should minimize $\xi _{u}(s)$ in the entire frequency range or at least in the bandwidth of interest. A compensator $K_{1}(s)$ and a smoother $K_{2}(s)$ are added, respectively, to the output and input of the two subsystems. They can be calculated by different solvers and should be invariant with the integration step. Therefore, a continuous expression is taken. In addition, the sample-hold process $H^{*}(s)\approx H(s)/\Delta t$ is simplified using a second-order Padé approximation. The problem is to find the best pair of $K_{1}(s)$, $K_{2}(s)$ to reduce $\xi _{u}(s)$.

Fig. 2

Formulation of an error system for one coupling variable

In this method, we focus on the interface itself and exclude the subsystem dynamics, which can be quite complex or difficult to know. On the contrary, the sample-hold process is determined (2), and it is invariant with a fixed macro-step $\Delta t$. The subsystem dynamics is implicitly incorporated by $u(s)$.

In practice, the exact input $u(s)$ is unspecified and not accessible, and consequently $\xi _{u}(s)$ is unknown. However, it is apparent that $\xi _{u}(s)=0$ if $K_{1}(s)K_{2}(s)=H^{*}(s)^{-1}$. Unfortunately, this solution is not valid because it is unstable and improper, and thus not implementable. Instead, the design objective can be formulated as a minimization of the $\mathcal{L}_{2}$ norm of error $||\xi _{u}||_{2}$. We denote the transfer function of the error system as $T_{ue}$, then $||\xi _{u}||_{2}$ fulfills

$$ ||\xi _{u}||_{2}=||T_{ue}u||_{2}\le ||T_{ue}||_{\infty }|| u||_{2} $$

(10)

which means that $||\xi _{u}||_{2}$ is upper-bounded by $||T_{ue}||_{\infty }|| u||_{2}$. Therefore, the well-designed terms $K_{1}(s)$, $K_{2}(s)$ should give a minimal $||T_{ue}||_{\infty }$. $||T_{ue}||_{\infty }$ by definition is the worst-case energy gain. This implies that the concept intends to minimize the energy of the coupling error, which is similar to the energy-based concept. At this stage, the coupling design problem can be solved by the $\mathcal{H}_{\infty }$ synthesis framework.

3.2 $\mathcal{H}_{\infty }$ synthesis for the coupling design

To apply the $\mathcal{H}_{\infty }$ synthesis, the error system (Fig. 2) needs to be reformulated into a generalized plant $G$ connected with a controller $K$ (Fig. 3). $W_{f}$ is a weighting function added to the error system and will be explained later. The problem can be stated as follows.

Fig. 3

A generalized plant $G$ and an undetermined controller $K$ as an equivalence to the error system

$\mathcal{H}_{\infty }$ synthesis problem: Given a LTI system $G$, find a feedback controller $K$ such that the closed-loop system is stable and the following objective is satisfied:

$$ ||\xi _{u}||_{2}< \gamma || u||_{2}, \quad ||T_{ue}||_{\infty }:=\sup _{Re\{s\}>0} ||T_{ue}(s)||< \gamma $$

(11)

where the scalar $\gamma$ is the $\mathcal{L}_{2}$ gain performance to be minimized. The solution of control law $K$ is the correction term $K_{1}(s)$, which is always proper, and therefore implementable.

In the aforementioned assumption, $H^{*}(s)$ is simplified using Padé approximation. However, its high-frequency component (3) still exists in reality, which yields a large piecewise constant input after $H^{*}(s)$. To address this issue, $K_{2}(s)$ is designed as a low-pass filter to smooth the input signal to the subsystem. The weighting function $W_{f}(s)$ cascaded to the output $\xi _{u}$ is another low-pass filter, and its purpose is to reduce more the error in low frequency. The introduction of $W_{f}(s)$ is also necessary for a feasible solution. Because the worst-case $\xi _{u}$ occurs in high frequency, a minimization of $||\xi _{u}||_{2}$ in all frequency range would largely distort the low-frequency component.

The problem (11) can be readily solved using the Matlab Robust Control Toolbox. For the scope of this journal, we provide the detailed procedure of the solution in Appendix A. In the optimization, a pole-placement constraint is given to bound the poles of $T_{ue}(s)$, and consequently, the poles of $K_{1}(s)$ [12]. The constraint is for the purpose of implementation:

• 1. $K_{1}$(s) can be guaranteed to be stable with a specified solver. If its poles $\lambda$ are in a disc-shaped region $\{ \lambda \in \mathbb{C}, |1+h\lambda |<1 \}$, a forward Euler method with step $h$, and other methods, can be applied.

• 2. The fast mode of $K_{1}(s)$ can be removed to avoid a small integration step and a longer computation time.

The pole-placement constraint mainly affects the fast modes, and thus it is more relevant to computation than to the accuracy. In summary, $K_{1}(s)$ is optimized according to the base terms $K_{2}(s)$, $W_{f}(s)$, and sample-hold process $H^{*}(s)$ (Table 1). Therefore, their selection and effects are studied in the next section.

Table 1 Three base terms of $\mathcal{H}_{\infty }$ method and their parameters

3.3 Convergence analysis and parameter study

The accuracy of the coupling method can be verified by the transfer behavior of $T_{ue}(s)$. In this analysis, the error $\xi _{u}$ with different coupling methods is approximated by the low-frequency component (3). To show the convergence property with $\Delta t$, the error magnitudes are plotted versus a normalized frequency $f_{n}=\omega \Delta t / 2\pi$ similarly to [6], in both decibel and absolute scales (Fig. 4).

Fig. 4

Magnitude of $\xi _{u}$ with different coupling methods. A $k$-degree extrapolation introduces an error of order $s^{k+1} \mathcal{O}(\Delta t ^{k+1})$. The $\mathcal{H}_{\infty }$ method with a higher-order $W_{f}$ yields an error that converges faster, and a lower limit occurs below $f_{W_{f}}$

In the decibel scale, the error order can be clearly observed from the slope of the error magnitude, and a higher-order $\xi _{u}$ converges faster by reducing $\Delta t$. In the absolute scale, it is apparent that a higher-degree extrapolation is more accurate with a low $f_{n}$ and a small $\Delta t$. However, $\xi _{u}$ is minor in this circumstance and the co-simulation problem might be less crucial. Meanwhile, a higher-degree extrapolation introduces a larger $\xi _{u}$ with a high $f_{n}$ and a big $\Delta t$, and the co-simulation problem becomes more critical. Therefore, a high-degree extrapolation is rarely employed for coupling in practice.

A parameter study is taken to investigate how $K_{2}(s)$, $W_{f}(s)$, and $H^{*}(s)$ in $\mathcal{H}_{\infty }$ method influence its convergence property. First, the ZOH, FOH, and SOH methods are selected for $H^{*}(s)$. Actually, $K_{1}(s)$ is optimized accordingly to compensate $H^{*}(s)$, the resulting $T_{ue}(s)$ is very similar. This means that $H^{*}(s)$ is less important to $\xi _{u}$, and the result is shown in Appendix B. Moreover, a general $\mathcal{H_{\infty }}$ synthesis gives a $K_{1}(s)$ with a same order as the generalized plant, so that a higher-degree $H^{*}(s)$ adds to the computation and implementation difficulty. As a consequence, $H^{*}(s)$ can be simply fixed with the ZOH method without a loss of accuracy improvement, and its only parameter is $\Delta t$. Similarly, a low-order smoother $K_{2}(s)$ is preferred. Thus, a second-order low-pass filter is taken to mitigate the sharp edges of the input signal, which can be incurred with a first-order filter. The key parameter is the cut-off frequency $f_{K_{2}}$. The tuning of $f_{K_{2}}$ is very intuitive and it defines how smooth the input signal is desired. In a general setup, $f_{K_{2}}$ can be specified with the Nyquist frequency $0.5/\Delta t$, because the main component of the signal should have a frequency lower than $0.5/\Delta t$ to be sufficiently sampled.

$W_{f}(s)$, which can have various orders and cut-off frequencies $f_{W_{f}}$, is important to the accuracy because it is the weighting of the optimization target. In the study, $W_{f}(s)$ are specified as first-order, second-order, and third-order Butterworth filters, and the corresponding error magnitudes are compared in Fig. 4. It can be seen that $W_{f}(s)$ introduces an error with a same order. In this regard, the $\mathcal{H}_{\infty }$ method with a higher-order $W_{f}(s)$ behaves as a higher-degree extrapolation. Moreover, $\xi _{u}$ does not drop monolithically and it reaches a lower limit below $f_{W_{f}}$. From the point of view of the authors, this saturation is not a weakness of the method because the lower limit can be substantially small. In addition, $\Delta t$ is lower-bounded by the solver integration step and cannot be arbitrarily small in reality.

By lowering $f_{W_{f}}$, the lower limit can be reduced, but $\xi _{u}$ is amplified in high frequency (see Fig. 4, and when $W_{f}(s)$ is of third order, $f_{w_{f}}$ reduces from $0.06/\Delta t$ to $0.01/\Delta t$). This implies a compromise between low-frequency and high-frequency accuracy. The low-frequency accuracy weights more with a higher-order $W_{f}(s)$ and a smaller $f_{W_{f}}$. To achieve a good compromise, $f_{W_{f}}$ can be specified, by trial and error, as $0.01/ \Delta t$, $0.03/ \Delta t$, $0.06/ \Delta t$ for the first-order, second-order, third-order $W_{f}(s)$, respectively. With the proposed specification, $\xi _{u}$ is reduced compared with other basic methods (Fig. 4). The reduction occurs in a wider frequency range, which implies that the method is robust and can well approximate an input with diverse frequency components. This feature is achieved by the worst-case minimization nature of the $\mathcal{H}_{\infty }$ synthesis method.

In summary, the three base terms $H^{*}(s)$, $K_{2}(s)$, and $W_{f}(s)$ can be simplified without a loss of accuracy improvement. Only three key parameters need to be tuned and their effects are independent. $f_{K_{2}}$ defines the input signal smoothness. $W_{f}(s)$ is relevant to the convergence property, and $f_{W_{f}}$ defines the weights of the frequency components.

3.4 Approximation by $\mathcal{H}_{\infty }$ method

The $\mathcal{H}_{\infty }$ method is further experimented in the time domain to demonstrate how it works. We assume a sweep signal (e.g., a force/velocity variable) ranging from 0.001 to 30 Hz is communicated with a $\Delta t$ of 10 ms. The performance of the method can be assessed by how well it reconstructs the reference input. According to the parameter study, $K_{2}(s)$ is a second-order filter with $f_{K_{2}}=0.5/\Delta t=50$ Hz and $W_{f}(s)$ is a first-order filter with $f_{W_{f}}=0.01/\Delta t=1$ Hz, and the base terms are specified as follows:

$$ \begin{aligned} H_{zoh}(s) &= \frac{1-e^{-0.01 s}}{s} , \\ H^{*}(s) &\approx \frac{120000}{ s^{2} + 600 s + 1.2e05} \quad \text{(by second-order Pad\'{e} approximation)}, \\ W_{f}(s) &= \frac{1}{\frac{s}{2 \pi f_{W_{f}}}+1}= \frac{6.283}{ s + 6.283}, \\ K_{2}(s) & = \frac{1}{(\frac{s}{2 \pi f_{K_{2}}})^{2}+1.4142 \frac{s}{2 \pi f_{K_{2}}}+1}= \frac{9.87e04}{s^{2} + 444.3 s + 9.87e04}. \end{aligned} $$

(12)

The pole-placement constraint is defined as $\{ \lambda \in \mathbb{C}, |1+0.001 \lambda |<1 \}$. The optimization takes 55 iterations and an elapsed time of 1.628 s to determine $K_{1}(s)$:

$$ \begin{aligned} K_{1}(s) &= \frac{(s+1942.9)(s+6.2789)(s^{2} + 599.9 s + 1.2e05)(s^{2} + 444.3 s + 9.87e04)}{(s+1924.0)(s+6.2837)(s^{2} + 2240 s + 1.392e06)(s^{2} + 774.8 s + 7.154e05)}, \end{aligned} $$

(13)

which can be seen as a combination of terms with different orders and optimal weights. Alternatively, the smoother $K_{2}(s)$ can be specified with $f_{K_{2}}=30$ Hz, which is the input bandwidth. A different $K_{1}(s)$ is synthesized accordingly:

$$ \begin{aligned} K_{1}(s) &= \frac{(s+1682.9)(s+6.2825)(s^{2} + 600 s + 1.2e05)(s^{2} + 266.6 s + 3.553e04)}{(s+1470.1)(s+6.2833)(s^{2} + 1870 s + 9.674e05)(s^{2} + 617.6 s + 5.111e05)}. \end{aligned} $$

(14)

The approximation results by the ZOH and $\mathcal{H}_{\infty }$ methods are shown in Fig. 5. The rebuilt signal is fairly close to the reference. In addition, the large piecewise constant signal is smoothed, which introduces a phase delay. Actually, this phase delay is already compensated by $K_{1}(s)$. In this experiment, a quite large $\Delta t$ is taken to make the deviation more visible. $K_{2}(s)$ with a lower $f_{K_{2}}=30$ Hz makes the input signal smoother, and the compensator $K_{1}(s)$ increases more the input magnitude and adds more phase-lead in advance.

Fig. 5

Comparison of input approximation. $h_{\infty }$ unsmoothed is the compensated signal sent every $\Delta t$ and $h_{\infty }$ smoothed is the signal sent to the model after the smoother. With a stronger smoother (b), $K_{1}(s)$ amplifies more the input magnitude for compensation

In another aspect, the $\mathcal{H}_{\infty }$ method works similarly to a correction–interpolation approach given that a corrected value, instead of the exact value (as in the ZOH method), is communicated.

4 Case study

In this section, the $\mathcal{H}_{\infty }$ method is implemented in two co-simulation cases, where the subsystems are involved. The first case is a dual mass–spring–damper system, which is a classic benchmark problem in co-simulation. The second case, is a co-simulation of multibody vehicle system with a steering mechatronic system.

4.1 Co-simulation of a dual mass-spring-damper system

The dual mass–spring–damper system can be partitioned into two models with a single mass (Fig. 6). Both models are solved by a forward Euler method with a step of 1 ms. The coupling variables are the force $F_{c}=k_{c}(x_{1}-x_{2})+d_{c}(\dot{x}_{1}-\dot{x}_{2})$ and the velocity $\dot{x}_{2}$, which is the same as FD coupling and velocity being used to avoid a derivation error.

Fig. 6

The dual mass–spring–damper system is coupled by force and velocity. The state vectors of the two models are $[\dot{x}_{1}, x_{1}]^{T}$, $[\dot{x}_{2}, x_{2}]^{T}$

For comparison, a mono-simulation reference and co-simulation with other coupling methods (ZOH, FOH, and SOH) are implemented. The macro-step is defined as $\Delta t = 50$ ms, and the $\mathcal{H_{\infty }}$ method is designed following a general setup: $W_{f}(s)$ is of first order with $f_{W_{f}}=0.01/ \Delta t =0.2$ Hz and $K_{2}(s)$ is of second order with $f_{K_{2}}=0.5/\Delta t=10$ Hz.

A coupling method might perform well in a specific case but much worse in other cases. To avoid this case-dependent effect, the parameters are specified in a stochastic way as the uniform distributed random variables in Table 2. The damping coefficients $d_{1}$ and $d_{2}$ are calculated to maintain the damping ratio $\zeta _{1}= d_{1}/ \sqrt{m_{1} k_{1}}$, $\zeta _{2}= d_{2}/ \sqrt{m_{2} k_{2}}$ in the target range. Thus, it is possible to cover various cases such as stiff and non-stiff systems, overdamped and underdamped systems, and highly asymmetric systems.

Table 2 Parameters of the dual mass–spring–damper system

An external input at a given frequency may excite the system in a certain frequency range that makes a coupling method always win (see [25]). To avoid this, the system dynamics is examined by its impulse response. During a simulation of 5 s, two external force impulses of 1 N are applied on $m_{2}$ at the first and the fourth second. In total, 2000 random cases are simulated, and the coupling methods are fixed. Some cases, where the solver is unable to calculate the model owing to an extremely small mass or large stiffness, are excluded. The accuracy of the results is evaluated by a normalized root mean square (NRMS) error of the coupling variable:

$$ \varepsilon _{nrms,x}= \frac{\sqrt{\sum _{t=0}^{T}\Big((x(t)-x_{ref}(t)\Big)^{2}/T}}{x_{ref,max}-x_{ref,min}} $$

(15)

where $x$ is the coupling variable, $T$ is the simulation time, and $x_{ref,max}$ and $x_{ref,min}$ are the maximum and minimum values of the reference. The NRMS errors of both coupling variables, i.e., $\varepsilon _{nrms, F_{c}}$ and $\varepsilon _{nrms, \dot{x}_{2}}$, can reflect the simulation accuracy. If they exceed a threshold value $\eta$

$$ \begin{aligned} \varepsilon _{nrms, F_{c}} > \eta \quad \text{or} \quad \varepsilon _{nrms, \dot{x}_{2}} > \eta \end{aligned} $$

(16)

then an inaccurate case can be counted. The numbers of inaccurate cases with different threshold values $\eta$ are presented in Table 3. The $\mathcal{H}_{\infty }$ method is more accurate in more possible cases, showing its advantages of accuracy and robustness. The other coupling methods have more unreliable cases, which might be due to the imprecision of a low-order approximation (ZOH) or the lack of robustness of a high-order method (SOH).

Table 3 Number of inaccurate cases exceeding the threshold value (16)

The stability is examined by the simulation traces of $\dot{x}_{2}$, $F_{c}$. The impulse response of a stable LTI system should either converge monotonically (overdamped) or oscillate with a decay (underdamped). Otherwise, the system is unstable. The statistical results of the unstable case are presented in Table 4. In general, the stability deteriorates with the increase in extrapolation degree, and it is enhanced with the $\mathcal{H_{\infty }}$ method.

Table 4 Number of unstable cases by examining the simulation traces

Furthermore, four representative cases are shown in Fig. 7–Fig. 10. The system is highly underdamped in the first case (Fig. 7). Two masses oscillate after the impulse excitation. The SOH method is better than the lower-order coupling method. The second case is an overdamped system (Fig. 8), in which the SOH method introduces an oscillatory result. The $\mathcal{H}_{\infty }$ method yields a small $\varepsilon _{nrms, \dot{x}_{2}}$ and a minimum $\varepsilon _{nrms, F_{c}}$. In the third case (Fig. 9), the system is numerically stiff with small masses and large stiffness, and the mass ratio $m_{1}/m_{2}$ is very small. The result is similar to the previous case in that the $\mathcal{H}_{\infty }$ method can approximate the coupling variable fairly well. The fourth case is also a stiff system (Fig. 10), but the mass ratio $m_{1}/m_{2}$ is very large. This can introduce a severe instability problem, because the system loop gain is enlarged [10]. In this case, the co-simulation is stable only with the $\mathcal{H}_{\infty }$ method, and the error grows with the extrapolation degree.

Fig. 7

Time response of $\dot{x}_{2}, F_{c}$ and $\varepsilon _{nrms, \dot{x}_{2}}, \varepsilon _{nrms, F_{c}}$. In this case, the system is highly underdamped with $\zeta _{1}=0.0934, \zeta _{2}=0.1053$. $m_{1}, m_{2}$ are $8.6856, 6.7863$ kg, $k_{1}, k_{2}, k_{c}$ are $176.6611, 895.8553, 171.7$ N/m, $d_{1}, d_{2}, d_{c}$ are $3.6585, 16.4162, 0.0857$ Ns/m, respectively

Fig. 8

Time response of $\dot{x}_{2}, F_{c}$ and $\varepsilon _{nrms, \dot{x}_{2}}, \varepsilon _{nrms, F_{c}}$. In this case, the system is overdamped with $\zeta _{1}=1.0236, \zeta _{2}=1.2271$. $m_{1}, m_{2}$ are $3.2365, 8.9549$ kg, $k_{1}, k_{2}, k_{c}$ are $120.5520, 995.0490, 701.9907$ N/m, $d_{1}, d_{2}, d_{c}$ are $20.2187, 231.6654, 12.5715$ Ns/m, respectively

Fig. 9

Time response of $\dot{x}_{2}, F_{c}$ and $\varepsilon _{nrms, \dot{x}_{2}}, \varepsilon _{nrms, F_{c}}$. In this case, the system is stiff with small masses and large stiffness. $m_{1}, m_{2}$ are $0.0901, 2.8877$ kg, $k_{1}, k_{2}, k_{c}$ are $871.8076, 712.9230, 654.9675$ N/m, $d_{1}, d_{2}, d_{c}$ are $8.6864, 86.5947, 0.5438$ Ns/m, respectively

Fig. 10

Time response of $\dot{x}_{2}, F_{c}$ and $\varepsilon _{nrms, \dot{x}_{2}}, \varepsilon _{nrms, F_{c}}$. In this case, the system is stiff with small masses and large stiffness. $m_{1}, m_{2}$ are $9.9049, 0.3935$ kg, $k_{1}, k_{2}, k_{c}$ are $586.9352, 956.6108, 741.3214$ N/m, $d_{1}, d_{2}, d_{c}$ are $50.9125, 20.1711, 40.3909$ Ns/m, respectively

Even in a specific case, for one coupling method it is difficult to be the optimum for both coupling variables. Therefore, it is difficult to assess their performance with a complex system. To adapt the coupling method to the model might be a solution. However, this can be challenging in implementation and computation. Alternatively, the $\mathcal{H}_{\infty }$ method may address this issue with a fixed solution owing to its robustness, which has been verified in the convergence analysis and the statistic experiment. This is similar to the $\mathcal{H}_{\infty }$ control technique, which can control a complex, nonlinear, or even uncertain system with a robust linear control law.

4.2 Co-simulation of an MBD vehicle model and an EPAS system model

The second application case is a co-simulation of an MBD vehicle model and an EPAS system model. The vehicle model is composed of a vehicle body, four suspensions and wheels. One of the front suspension is presented in Fig. 11. The knuckle is constrained by five linkages so it moves up and down, and steers by the moving tie rods. The wheel rotation and forces are transmitted to the steering rack through the linkages, which are modeled as rigid bodies. The vehicle model is created using the multibody system library in Dymola and it has 36487 equations. It is computationally heavy owing to the calculation of large-size matrices and a DASSL solver is used. In a high-frequency maneuver, the maximum integration step is around 18 ms. In a low-frequency maneuver it can be 100 ms with much less Jacobian evaluations.

Fig. 11

Layout of a co-simulation of an MBD vehicle model and an EPAS system model. The models are in functional mock-up units (FMU) and the discrete ECU software model is in s-function as a black box

The EPAS system model has 3 degrees of freedom (Fig. 11): the rotation of steering column $\delta _{s}$, EPAS motor $\delta _{m}$ and the rack displacement ${x}_{r}$:

$$ \begin{aligned} J_{col} \ddot{\delta }_{s}= & T_{s}-T_{\mathit{pinion}}-T_{c_{\mathit{friction}}} , \\ J_{m} \ddot{\delta }_{m}=& T_{m}-T_{\mathit{belt}} , \\ m_{r} \ddot{x}_{r}= &F_{\mathit{pinion}}+F_{\mathit{assist}}-F_{r}-F_{r_{\mathit{friction}}}, \end{aligned} $$

(17)

the forces $F_{\mathit{pinion}}$ and $F_{\mathit{assist}}$ can be calculated from the transmission ratios: $F_{\mathit{pinion}} = T_{\mathit{pinion}}/i_{\mathit{pinion}}, F_{\mathit{assist}} = T_{\mathit{belt}}/( i_{\mathit{belt}} i_{bs})$. The belt drive and the ball screw mechanism generate a large inertia ratio and highly underdamped dynamics, which makes the model numerically stiff. The friction force $F_{r_{\mathit{friction}}}$ (similarly to friction torque $T_{c_{\mathit{friction}}}$) are represented by the LuGre friction model:

$$ \begin{aligned} \dot{z}&= v-\sigma _{0} z/{g(v)}|v|, \\ g(v) &= F_{c}+(F_{s}-F_{c})e^{-(v/v_{s})^{2}} , \\ F_{\mathit{friction}}&= \sigma _{0} z+\sigma _{1} \dot{z}+\sigma _{2} v, \end{aligned} $$

(18)

to capture the stick–slip effect, which further adds to the stiffness. $v$ is the sliding velocity, $z$ is the internal state. The bristle stiffness $\sigma _{0}$ and micro-damping $\sigma _{1}$ produce a spring-like behavior in small displacements. $\sigma _{2}$ is the viscous friction coefficient. $g(v)$ is a velocity-dependent term based on the Coulomb friction $F_{c}$, the static friction $F_{s}$ and the Stribeck velocity $v_{s}$ ($g(v)$ has been simplified in this case). The parameter values are summarized in Table 5. To solve the EPAS system model, a fourth-order Runge–Kutta method with a step of 0.25 ms is employed in the FMU.

Table 5 Parameters of the EPAS system model

The EPAS system model is further coupled with an electric control unit (ECU) model which is discrete with a step of 1 ms (Fig. 11). It is a black box from the supplier and comprises the control code to generate $T_{m}$. More information of the model is provided in the work of the authors [11].

An explicit parallel co-simulation is applied in this complex engineering case. The vehicle model and the EPAS model are coupled using the rack force $F_{r}$ and rack speed $\dot{x}_{r}$ with $\Delta t_{1}=1$ ms and $\Delta t_{2} = 20$ ms. Here, the $\mathcal{H_{\infty }}$ method with a general setup is implemented inside the FMUs.

Two steering tests are simulated, in which a steering torque $T_{s}$ with a magnitude of 2.5 Nm is applied. A low-frequency $T_{s}$ growing from 0 to 1 Hz is applied in the first test, and a high-frequency $T_{s}$ from 0 to 3 Hz is applied in the second test. The system states, i.e., the steering angle $\delta _{s}$, rack speed $\dot{x}_{r}$, vehicle yaw rate, and vehicle lateral velocity are shown in Fig. 13 and Fig. 14. The vehicle states show less discrepancies due to their slow dynamics.

The SOH method gives unstable results with large deviations. According to the NRMS error (Fig. 12), the $\mathcal{H}_{\infty }$ method is more accurate than the ZOH and FOH methods in both the low-frequency and the high-frequency cases. In the low-frequency case (Fig. 13), no significant error is incurred with all the methods, and the accuracy improvement is a bit saturated due to the inherent error from the discrete communication. In the high-frequency case (Fig. 14), the FOH method gives an oscillatory rack speed. However, the $\mathcal{H}_{\infty }$ method shows both an oscillation depression and accuracy improvement.

Fig. 12

NRMS error of the simulation results with a low-frequency (left) and a high-frequency (right) steering torque input (the results of the SOH method are not plotted owing to the large deviation)

Fig. 13

Simulation results with a low-frequency steering torque input

Fig. 14

Simulation results with a high-frequency steering torque input (unstable results with the SOH method are not plotted for a better visibility)

Furthermore, the elapsed time has been reduced drastically in the co-simulation (Table 6), comparing it to the mono-simulation. The $\mathcal{H}_{\infty }$ method shows an elapsed time close to that of the basic coupling methods, because the additional workload is only the computation of the fixed compensator and smoother.

Table 6 Elapsed time of the simulation with different coupling methods

5 Conclusion

In this work, we reviewed the explicit parallel co-simulation approach in a new framework. Its analysis has been conducted in the frequency domain and we have the following observations:

• The coupling method has a frequency-domain characteristic. Therefore, its performance depends on the system dynamics and also the system input, which was discussed previously in the literature.

• Co-simulation stability is a closed-loop property, which is highly dependent on the input–output transfer behavior of each subsystem.

• There is no optimal coupling method in general. One should specify the possible frequency range of the coupling variable. Otherwise, it is expected that the coupling method can reduce the error in a wider frequency range.

Based on the new framework, a coupling method relying on the $\mathcal{H}_{\infty }$ synthesis is developed, which can fulfill the aforementioned needs. Despite its theoretical complexity, the implementation is not challenging as the $\mathcal{H}_{\infty }$ synthesis problem can be solved by Matlab functions. The limitation and unmet challenges are:

• To add a compensator and a smoother at the interface can be easy for the engineers who prepare the subsystem models, but it might be challenging when the subsystems are unchangeable black boxes by the current standard.

• The aliasing effect should be taken into account, but has been simplified in the current step.

Nonetheless, the $\mathcal{H}_{\infty }$ method has shown a potential in accuracy improvement and robustness, which is much desired for complex systems but has not been addressed explicitly before. The approach might be also useful to optimize other existing coupling methods, if they can be formulated as a fixed-structure $\mathcal{H}_{\infty }$ synthesis problem.

Appendices

Appendix A: Procedure to solve the $\mathcal{H}_{\infty }$ synthesis problem

The base terms inside $G$ can be expressed by state-space realizations

$$ H^{*}(s):=\left [ \textstyle\begin{array}{c@{\ }|@{\ }c} A_{h} & B_{h} \\ \hline C_{h} & D_{h}\end{array}\displaystyle \right ],\quad W_{f}(s):=\left [ \textstyle\begin{array}{c@{\ }|@{\ }c} A_{w} & B_{w} \\ \hline C_{w} & D_{w} \end{array}\displaystyle \right ], \quad K_{2}(s):=\left [ \textstyle\begin{array}{c@{\ }|@{\ }c} A_{k2} & B_{k2} \\ \hline C_{k2} & D_{k2} \end{array}\displaystyle \right ] $$

(19)

then the generalized plant $G$ added with $W_{f}(s)$ can be derived as

$$ \begin{aligned} G:=\left [ \textstyle\begin{array}{c@{\ }|@{\ }c@{\quad }c} A & B_{1} & B_{2} \\ \hline C_{1} & D_{11} & D_{12} \\ C_{2} & D_{21} & D_{22} \\ \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\ }|@{\ }c@{\quad }c} A_{h}& 0 & 0&0 &B_{h} &0 \\ B_{k2}C_{h}& A_{k2} & 0&0 &B_{k2}D_{h}&0 \\ B_{w} C_{h} D_{k2}& B_{w} C_{k2} & A_{w}&0 &B_{w} D_{h} D_{k2}&0 \\ 0 & 0 & 0&A_{w} &0 &B_{w} \\ \hline -C_{h} D_{k2} D_{w}& -C_{k2}D_{w} & -C_{w}&C_{w} & -D_{h} D_{k2} D_{w}& D_{w} \\ 0 & 0 & 0 & 0&I& 0 \end{array}\displaystyle \right ] \end{aligned} $$

(20)

Closing the loop with the undetermined controller

$$ K_{1}(s) \equiv K(s):=\left [ \textstyle\begin{array}{c@{\ }|@{\ }c} A_{k} & B_{k} \\ \hline C_{k} & D_{k} \end{array}\displaystyle \right ] $$

(21)

the error system becomes $T_{ue}(s)=C_{cl}(sI -A_{cl})^{-1}B_{cl}+D_{cl}$, where

$$ \begin{aligned} A_{cl} &= \begin{bmatrix} A + B_{2} D_{k} C_{2} & B_{2} C_{k} \\ B_{k} C_{2} & A_{k} \end{bmatrix} , \quad B_{cl} = \begin{bmatrix} B_{1}+B_{2} D_{k} D_{2} \\ B_{k} D_{21} \end{bmatrix} , \\ C_{cl} &= \begin{bmatrix} C_{1}+D_{12} D_{k} C_{2} & D_{12}C_{k} \end{bmatrix} , \quad D_{cl} = \begin{bmatrix} D_{11}+D_{12} D_{k} D_{21} \end{bmatrix} . \end{aligned} $$

(22)

According to the bounded real lemma [12], problem (11) is equivalent to the existence of a positive definite matrix $P\succ 0$ fulfilling the linear matrix inequality (LMI) condition:

$$ \begin{aligned} \text{min} \quad &\gamma \\ \text{subject to} &\begin{bmatrix} A^{T}_{cl}P +P A_{cl}+C^{T}_{cl} C_{cl} \quad & C_{cl}^{T} D_{cl}+ P B_{cl} \\ B_{cl}^{T} P + D^{T}_{cl} C_{cl} \quad & D^{T}_{cl}D_{cl}-\gamma I \end{bmatrix} \prec 0 \end{aligned} $$

(23)

and $K_{1}(s)$ can be determined with a feasible $\gamma$.

Appendix B: Parameter study of $H^{*}(s)$

ZOH, FOH, and SOH methods can be applied in $H^{*}(s)$, and different $K_{1}(s)$ are synthesized accordingly. It can be seen that no significant change of $\xi _{u}$ occurs (Fig. 15), and only the high-frequency component increases with a higher-order approximation.

Fig. 15

Comparison of error magnitude when the ZOH, FOH, and SOH methods are applied in the $\mathcal{H}_{\infty }$ method. The other base terms, $K_{2}(s)$ and $W_{f}(s)$, are the same

In addition, the approximated $H^{*}(s)$ has an order of two with the ZOH method, four with the FOH method, and six with the SOH method. This results in a $K_{1}(s)$ with an order of five, seven, and nine, respectively, which needs an unnecessary effort in implementation and computation.