Block boundary value methods for linear weakly singular Volterra integro-differential equations

Abstract

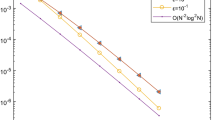
A class of block boundary value methods (BBVMs) is constructed for linear weakly singular Volterra integro-differential equations (VIDEs). The convergence and stability of these methods is analysed. It is shown that optimal convergence rates can be obtained by using special graded meshes. Numerical examples are given to illustrate the sharpness of our theoretical results and the computational effectiveness of the methods. Moreover, a numerical comparison with piecewise polynomial collocation methods for VIDEs is given, which shows that the BBVMs are comparable in numerical precision.

Piecewise polynomial collocation methods

We give a brief review of piecewise polynomial collocation methods in this appendix. Introducing a new unknown function $x=y'$, the VIDE (1.1) can be rewritten as

$$\begin{aligned} x(t)&= b(t) + y_0 a(t) + y_0 \int _0^t K(t,v)dv + a(t) \int _0^t x(v)dv \\&\quad + \int _0^t K(t,v) \int _0^v x(\tau ) d\tau dv,~~t \in [0,T]. \end{aligned}$$

Using the same mesh as before, with the same notation, we write $x_{n,i}$ for the computed approximation of $x(t_{n,i})$ for $0 \le i \le m$ and $1\le n \le N$. This is defined by

$$\begin{aligned} x_{n,i}&= b(t_{n,i}) + y_0 a(t_{n,i}) + y_0 \int _0^{t_{n,i}} K(t_{n,i},v)dv \\&\qquad + a(t_{n,i}) \sum _{j=1}^{n-1} \int _{t_{j-1}}^{t_{j}} \hat{P}_{m,j}(v)dv + a(t_{n,i}) \int _{t_{n-1}}^{t_{n,i}} \hat{P}_{m,n}(v)dv \\&\qquad + \sum _{j=1}^{n-1} h_j \int _{0}^{m} K(t_{n,i},t_{j,\theta }) \left[ \sum _{q=1}^{j-1} \int _{t_{q-1}}^{t_{q}} \hat{P}_{m,q}(\tau )d\tau + \int _{t_{j-1}}^{t_{j,\theta }} \hat{P}_{m,j}(\tau ) d\tau \right] d\theta \\&\qquad + h_n \int _{0}^{i} K(t_{n,i},t_{n,\theta }) \left[ \sum _{q=1}^{n-1} \int _{t_{q-1}}^{t_{q}} \hat{P}_{m,q}(\tau )d\tau + \int _{t_{n-1}}^{t_{n,\theta }} \hat{P}_{m,n}(\tau ) d\tau \right] d\theta \\&= b(t_{n,i}) + y_0 a(t_{n,i}) + y_0 \int _0^{t_{n,i}} K(t_{n,i},v)dv \\&\qquad + a(t_{n,i}) \sum _{j=1}^{n-1} \sum _{s=0}^m \int _{t_{j-1}}^{t_{j}} L_{m,j,s}(v) x_{j,s} dv + a(t_{n,i}) \sum _{s=0}^m \int _{t_{n-1}}^{t_{n,i}} L_{m,n,s}(v) x_{n,s}dv \\&\qquad + \sum _{j=1}^{n-1} h_j \int _{0}^{m} K(t_{n,i},t_{j,\theta }) \left[ \sum _{q=1}^{j-1} \sum _{s=0}^m \int _{t_{q-1}}^{t_{q}} L_{m,q,s}(\tau ) x_{q,s} d\tau + \sum _{s=0}^m \int _{t_{j-1}}^{t_{j,\theta }} L_{m,j,s}(\tau ) x_{j,s} d\tau \right] d\theta \\&\qquad + h_n \int _{0}^{i} K(t_{n,i},t_{n,\theta }) \left[ \sum _{q=1}^{n-1} \sum _{s=0}^m \int _{t_{q-1}}^{t_{q}} L_{m,q,s}(\tau ) x_{q,s} d\tau + \sum _{s=0}^m \int _{t_{n-1}}^{t_{n,\theta }} L_{m,n,s}(\tau ) x_{n,s} d\tau \right] d\theta . \end{aligned}$$

In the above formulas,

$$\begin{aligned} \hat{P}_{m,j}(t) = \sum _{s=0}^m L_{m,j,s}(t)x_{j,s},~~~\text{ where }~L_{m,j,s}(t) = \prod _{l=0,l \ne s}^m \frac{t-t_{j,l}}{t_{j,s}-t_{j,l}}. \end{aligned}$$

From the above equation, for each $n\ge 1$ one can obtain the unknown vector $X_n = \left( x_{n,1}^T,x_{n,2}^T,\ldots ,x_{n,m}^T\right) ^T$. Then the approximation y is computed iteratively by

$$\begin{aligned} y(t_{n,i}) = y_0 + \int _0^{t_{n,i}} x(v) dv = \sum _{j=1}^{n-1} \sum _{s=0}^m \int _{t_{j-1}}^{t_j} L_{m,j,s}(v)x_{j,s} dv + \sum _{s=0}^m \int _{t_{n-1}}^{t_{n,i}} L_{m,n,s}(v)x_{n,s} dv. \end{aligned}$$