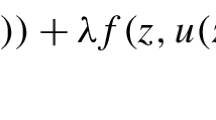1 Introduction

Let \(\Omega \subseteq {\mathbb {R}}^N\) be a bounded domain with a \(C^2\)-boundary \(\partial \Omega \). In this paper, we study the following nonlinear, nonhomogeneous Robin problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _p u(z)-\Delta _q u(z)+\xi (z)|u(z)|^{p-2}u(z)=f(z,u(z)) &{} \text{ in } \Omega \\ \displaystyle \frac{\partial u}{\partial n_{pq}}+\beta (z)|u|^{p-2}u=0 &{}\text{ on } \partial \Omega \end{array}\right. }, \end{aligned}$$
(1.1)

with \(1<q<p\). For every \(r\in (1,\infty )\), by \(\Delta _r\) we denote the r-Laplace differential operator defined by

$$\begin{aligned} \Delta _r u = \mathrm{div}\, \left( |Du|^{r-2}Du\right) \qquad \text{ for } \text{ all } u\in W^{1,r}(\Omega ). \end{aligned}$$

In problem (1.1) we have the sum of two such operators. So, the differential operator in (1.1) is not homogeneous and so many of the techniques used in p-Laplacian equations, can not be employed here. Equations driven by the sum of two operators of different nature, arise often in the mathematical models of various physical processes. We mention the works of Bahrouni-Rădulescu-Repovš [3] (transonic flow problems), Benci-D’Avenia-Fortunato-Pisani [5] (quantum physics), Cherfils-Il’yasov [7] (reaction-diffusion systems), Zhikov [34] (nonlinear elasticity theory).

In problem (1.1), in addition to the (p, q)-differential operator there is also a potential term \(\xi (z) |u|^{p-2}u\), with the potential function \(\xi \in L^\infty (\Omega )\) being in general indefinite (that is, sign-changing). This means that the left-hand side of (1.1) is not coercive, an additional difficulty in dealing with problem (1.1).

In the reaction (right-hand side of (1.1)), the function f(z, x) is a Carathéodory function (that is, \(z\mapsto f(z,x)\) is measurable for all \(x\in {\mathbb {R}}\) and \(x\mapsto f(z,x)\) is continuous for a.a. \(z\in \Omega \)). We consider two different cases concerning the growth of \(f(z,\cdot )\) as \(x\rightarrow \pm \infty \). First we assume that \(f(z,\cdot )\) exhibits \((p-1)\)-linear growth as \(x\rightarrow \pm \infty \) (that is, \(f(z,\cdot )\) is asymptotically \((p-1)\)-homogeneous). In this case we permit resonance with respect to the principal eigenvalue of \(u\mapsto -\Delta _p u + \xi (z)|u|^{p-2}u\) with Robin boundary condition. The resonance occurs from the right of the principal eigenvalue \({\widehat{\lambda }}_1(p)\), in the sense that

$$\begin{aligned} p F(z,x)-{\widehat{\lambda }}_1(p) |x|^p\rightarrow +\infty \end{aligned}$$

uniformly for a.a. \(z\in \Omega \), as \(x\rightarrow \pm \infty \), with \(F(z,x)=\int _0^x f(z,s)\,\mathrm{d}s\).

This makes the energy (Euler) functional of the problem unbounded from below (hence noncoercive) and so we can not use the direct method of the calculus of variations. In the second case we assume that \(f(z,\cdot )\) is \((p-1)\)-superlinear as \(x\rightarrow \pm \infty \) but without satisfying the usual in such cases Ambrosetti-Rabinowitz condition (the “AR-condition” for short). In both cases we assume that \(f(z,\cdot )\) is concave near the origin and also has an oscillatory behavior.

In the boundary condition \(\frac{\partial u}{\partial n_{pq}}\) denotes the conormal derivative corresponding to the (p, q)-Laplacian. This directional derivative is interpreted using the nonlinear Green’s identity (see Papageorgiou-Rădulescu-Repovš [21], Corollary 1.5.16, p. 34) and if \(u\in C^1({\overline{\Omega }})\), then

$$\begin{aligned} \frac{\partial u}{\partial n_{pq}}=\left[ |Du|^{p-2}+|Du|^{q-2}\right] \frac{\partial u}{\partial n},\end{aligned}$$

with \(n(\cdot )\) being the outward unit normal on \(\partial \Omega \).

Using variational tools based on the critical point theory together with truncation and comparison techniques, we show that in both cases problem (1.1) has at least five nontrivial smooth solutions which are ordered and we provide sign information for all of them.

The starting point of our work here is the recent paper of Papageorgiou-Scapellato [24] where the authors deal with a generalized version of the classical concave-convex problem, for equations driven only by the p-Laplacian. The reaction there is parametric and nonnegative and they prove a bifurcation-type theorem describing the changes in the set of positive solutions as the parameter \(\lambda >0\) varies. Here there is no parameter and for this reason we require that \(f(z,\cdot )\) changes sign. Moreover, in the present work in addition to constant sign solutions, we also produce nodal (that is, sign-changing) solutions.

Multiplicity results for (p, q)-equations with resonant or superlinear reaction, can be found in Candito-Gasiński-Livrea [6], Filippakis-Papageorgiou [8], Gasiński-Papageorgiou [10], Gasiński-Winkert [12], Li-Rong-Liang [16], Papageorgiou-Rădulescu [17, 18], Papageorgiou-Scapellato [25], Papageorgiou-Vetro-Vetro [26], Pei-Zhang [29], Sun [31]. Also our work here extends that of Gasiński-Papageorgiou [11], where the authors permit only nonuniform nonresonance for equations driven by the Dirichlet p-Laplacian with no potential term. We also mention the very recent work of Vetro [32], where the author examines perturbations (both sublinear and superlinear) of the eigenvalue problem for the operator \(u\mapsto -\Delta _p u+\xi (z)|u|^{p-2}u\) with Robin boundary condition. Finally we should also mention the works of Amster [2], Papageorgiou-Rădulescu-Repovš [22, 23] and Papageorgiou-Zhang [28], where the authors deal with problems involving concave terms.

2 Mathematical background-hypotheses

In the analysis of problem (1.1), the main spaces are the Sobolev space \(W^{1,p}(\Omega )\) and the Banach space \(C^1({\overline{\Omega }})\). By \(\Vert \cdot \Vert \) we denote the norm of \(W^{1,p}(\Omega )\) defined by

$$\begin{aligned} \Vert u\Vert =\left[ \Vert u\Vert _p^p + \Vert Du\Vert _p^p\right] ^{\frac{1}{p}}\quad \text {for all}\, u\in W^{1,p}(\Omega ). \end{aligned}$$

The space \(C^1({\overline{\Omega }})\) is an ordered Banach space with positive (order) cone \(C_+=\{u\in C^1(\overline{\Omega }): u(z)\ge 0 \; \text {for all}\, z\in \overline{\Omega }\}\). This cone has a nonempty interior given by

$$\begin{aligned} \mathrm{int}\, C_+ = \{u\in C_+: u(z)>0\; \text {for all}\, z\in {\overline{\Omega }}\}. \end{aligned}$$

Let \(r\in (1,\infty )\). By \(A_r: W^{1,r}(\Omega )\rightarrow W^{1,r}(\Omega )^*\) we denote the nonlinear operator defined by

$$\begin{aligned} \langle A_r(u), h\rangle =\int _\Omega |Du|^{r-2}(Du,Dh)_{{\mathbb {R}}^N}\mathrm{d}z\quad \text {for all}\, u,h\in W^{1,r}(\Omega ). \end{aligned}$$

The next proposition summarizes the main properties of this map (see Gasiński-Papageorgiou [12], p. 279).

Proposition 2.1

The operator \(A_r: W^{1,r}(\Omega )\rightarrow W^{1,r}(\Omega )^*\) is bounded (that is, it maps bounded sets to bounded sets), continuous, monotone (hence maximal monotone too) and of type \((S)_+\), that is, it has the following property

“If \(u_n \xrightarrow {w}{u}\) in \(W^{1,r}(\Omega )\) and \(\displaystyle \lim _{n\rightarrow \infty }\langle A_r(u_n), u_n-u\rangle \le 0\), then \(u_n \rightarrow u\) in \(W^{1,r}(\Omega )\)”.

For \(x\in {\mathbb {R}}\), we set \(x^\pm =\max \{\pm x,0\}\). Then, for \(u\in W^{1,p}(\Omega )\), we define \(u^\pm (z)=u(z)^\pm \) for all \(z\in \Omega \). We know that

$$\begin{aligned} u^\pm \in W^{1,p}(\Omega ),\quad |u|=u^++u^-,\quad u=u^+-u^-.\end{aligned}$$

If \(h_1,h_2:\Omega \rightarrow {\mathbb {R}}\) are two measurable functions such that \(h_1(z)\le h_2(z)\) for a.a. \(z\in \Omega \), then we define the order interval \([h_1,h_2]\) in \(W^{1,p}(\Omega )\) by

$$\begin{aligned}{}[h_1,h_2]=\{u\in W^{1,p}(\Omega ): h_1(z)\le u(z)\le h_2(z)\; \text {for a.a.}\, z\in \Omega \}. \end{aligned}$$

Also, we define

$$\begin{aligned}&[h_1)=\{u\in W^{1,p}(\Omega ): h_1(z)\le u(z)\; \text {for a.a.}\, z\in \Omega \},\\&(h_2]=\{v\in W^{1,p}(\Omega ): v(z)\le h_2(z)\; \text {for a.a.}\, z\in \Omega \}. \end{aligned}$$

Given a set \(S\subseteq W^{1,p}(\Omega )\), we say that S is downward (resp. upward) directed, if for every \(u_1,u_2\in S\) we can find \(u\in S\) such that \(u\le u_1\), \(u\le u_2\) (resp. \(u_1\le u\), \(u_2\le u\)).

Let X be a Banach space and \(\varphi \in C^1(X)\). By \(K_\varphi \) we denote the critical set of \(\varphi \), that is,

$$\begin{aligned} K_\varphi = \{u\in X: \varphi '(u)=0\}.\end{aligned}$$

We say that \(\varphi (\cdot )\) satisfies the C-condition, if it has the following property

“Every sequence \(\{u_n\}_{n\in {\mathbb {N}}}\subseteq X\) such that

$$\begin{aligned}&\{\varphi (u_n)\}_{n\in {\mathbb {N}}}\subseteq {\mathbb {R}}\; \text {is bounded},\\&(1+\Vert u_n\Vert _X)\varphi '(u_n)\rightarrow 0\; \text {in}\, X^{*} \,\text {as}\, n\rightarrow \infty , \end{aligned}$$

admits a strongly convergent subsequence”.

For \(c\in {\mathbb {R}}\), let \(\varphi ^c=\{u\in X: \varphi (u)\le c\}\). Let \(Y_2\subseteq Y_1\subseteq X\). For every \(k\in {\mathbb {N}}_0={\mathbb {N}}\cup \{0\}\), by \(H_k(Y_1,Y_2)\) we denote the \(k^{\mathrm{th}}\) relative singular homology group with integer coefficients for the pair \((Y_1,Y_2)\). Suppose that \(u\in K_\varphi \) is isolated and let \(c=\varphi (u)\). Then, the critical groups of \(\varphi (\cdot )\) at u, are defined by

$$\begin{aligned} C_k(\varphi ,u)=H_k(\varphi ^c\cap {\mathcal {U}}, \varphi ^c\cap {\mathcal {U}}{\setminus } \{u\})\; \text {for all}\, k\in {\mathbb {N}}_0, \end{aligned}$$

where \({\mathcal {U}}\) is an open neighborhood of u such that \(K_\varphi \cap \varphi ^c \cap {\mathcal {U}}=\{u\}\).

The excision property of singular homology, implies that this definition is independent of the choice of the isolating neighborhood \({\mathcal {U}}\).

In the resonant case we will use the spectrum of the operator \(u\mapsto -\Delta _p u +\xi (z)|u|^{p-2}u\) with the Robin boundary condition. So, for \(\xi \in L^\infty (\Omega )\) and \(\beta \in C^{0,\alpha }(\partial \Omega )\) (\(0< \alpha <1\)), \(\beta \ge 0\), we consider the following nonlinear eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _p u(z)+\xi (z)|u(z)|^{p-2}u(z)={\widehat{\lambda }} |u(z)|^{p-2}u(z) &{} \text {in}\,\Omega \\ \frac{\partial u}{\partial n_p}+\beta (z)|u|^{p-2}u=0 &{} \text {on}\, \partial \Omega \end{array}\right. }. \end{aligned}$$
(2.1)

We say that \({\widehat{\lambda }}\in {\mathbb {R}}\) is an eigenvalue, if problem (2.1) admits a nontrivial solution \({\widehat{u}}\in W^{1,p}(\Omega )\), known as an eigenfunction corresponding to the eigenvalue \({\widehat{\lambda }}\in {\mathbb {R}}\). The nonlinear regularity theory (see Lieberman [15]) implies that \({\widehat{u}}\in C^1({\overline{\Omega }})\). The eigenvalue problem (2.1) was studied by Fragnelli-Mugnai-Papageorgiou [9], who established the existence of a smallest eigenvalue \({\widehat{\lambda }}_1(p)\in {\mathbb {R}}\), which is simple, isolated and admits the following variational characterization

$$\begin{aligned} {\widehat{\lambda }}_1(p)=\inf \left[ \frac{\gamma _p (u)}{\Vert u\Vert _p^p}: u\in W^{1,p}(\Omega ),\; u\ne 0\right] . \end{aligned}$$
(2.2)

Here \(\gamma _p: W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) is the \(C^1\)-functional defined by

$$\begin{aligned} \gamma _p(u)=\Vert Du\Vert _p^p+\int _\Omega \xi (z)|u|^p\,\mathrm{d}z+\int _{\partial \Omega }\beta (z)|u|^p\,\mathrm{d}\sigma \quad \text {for all}\, u\in W^{1,p}(\Omega ), \end{aligned}$$

with \(\sigma (\cdot )\) denoting the \((N-1)\)-dimensional Hausdorff (surface) measure on \(\partial \Omega \). The infimum in (2.2) is realized on the corresponding one-dimensional eigenspace, the elements of which have fixed sign. By \({\widehat{u}}_1(p)\) we denote the positive, \(L^p\)-normalized (that is, \(\Vert {\widehat{u}}_1(p)\Vert _p=1\)) eigenfunction for \({\widehat{\lambda }}_1(p)\). The nonlinear regularity theory and the nonlinear maximum principle, imply that \({\widehat{u}}_1(p)\in \mathrm{int}\, C_+\). Note that if \(\xi \ge 0\) and \(\xi \not \equiv 0\) or \(\beta \not \equiv 0\), then \({\widehat{\lambda }}_1(p)>0\) (see [9]).

We mention that \({\widehat{\lambda }}_1(p)\) is the only eigenvalue with eigenfunctions of fixed sign. All other eigenvalues have nodal (that is, sign-changing) eigenfunctions.

Now we can introduce our hypotheses on the data of problem (1.1).

  • \(\mathrm{H}_0\): \(\xi \in L^\infty (\Omega )\), \(\beta \in C^{0,\alpha }(\partial \Omega )\), \(\beta (z)\ge 0\) for all \(z\in \partial \Omega \).

Remarks

We stress thay \(\xi (\cdot )\) is in general sign changing. If \(\beta \equiv 0\), then we have a Neumann problem.

For the resonant case, the hypotheses on the reaction f(z, x) are the following (recall that \(F(z,x)=\int _0^x f(z,s)\,\mathrm{d}s\)).

  • \({\mathrm{H}}_1\): \(f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a Carathéodory function such that \(f(z,0)=0\) for a.a. \(z\in \Omega \) and

    • (i) \(|f(z,x)|\le a(z)[1+|x|^{p-1}]\) for a.a. \(z\in \Omega \), all \(x\in {\mathbb {R}}\), with \(a\in L^\infty (\Omega )\);

    • (ii) \(\displaystyle \lim _{x\rightarrow \pm \infty }\frac{p F(z,x)}{|x|^p}={\widehat{\lambda }}_1 (p)\) uniformly for a.a. \(z\in \Omega \);

    • (iii) there exists \(\tau \in (q,p)\) such that

      $$\begin{aligned} \limsup _{x\rightarrow \pm \infty }\frac{f(z,x)x-pF(z,x)}{|x|^\tau }\le -\gamma _0<0\quad \text {uniformly for a.a.}\, z\in \Omega ; \end{aligned}$$

    • (iv) there exist \(\mu \in (1,q)\) and \(\delta >0\) such that

      $$\begin{aligned} c_0 |x|^\mu \le f(z,x)x\le \mu F(z,x)\quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, |x|\le \delta ; \end{aligned}$$

    • (v) there exist \(\vartheta _-<0<\vartheta _+\) such that for a.a. \(z\in \Omega \) we have

      $$\begin{aligned} f(z,\vartheta _+)-\xi (z)\vartheta _+^{p-1}\le -{\widehat{c}}_+<0<{\widehat{c}}_-\le f(z,\vartheta _-)+\xi (z)|\vartheta _-|^{p-1};\end{aligned}$$

    • (vi) for every \(\rho >0\), there exists \({\widehat{\xi }}_\rho >0\) such that for a.a. \(z\in \Omega \), the function \(x\mapsto f(z,x)+{\widehat{\xi }}_\rho |x|^{p-2}x\) is nondecreasing on \([-\rho ,\rho ]\).

Remarks

If \(\lim _{x\rightarrow \pm \infty }\frac{f(z,x)}{|x|^{p-2}x}={\widehat{\lambda }}_1(p)\) uniformly for a.a. \(z\in \Omega \), then hypothesis \(\mathrm{H}_1\)(ii) is satisfied. Therefore we see thay hypothesis \(\mathrm{H}_1\)(ii) covers the case of problems which are resonant as \(x\rightarrow \pm \infty \) with respect to the principal eigenvalue \({\widehat{\lambda }}_1 (p)\). In the process of the proof, we will show that

$$\begin{aligned} \liminf _{x\rightarrow \pm \infty } \frac{p F(z,x) - {\widehat{\lambda }}_1 (p) |x|^p}{|x|^\tau }\ge \gamma _1>0\end{aligned}$$

uniformly for a.a. \(z\in \Omega \). This means that the resonance occurs from the right of \({\widehat{\lambda }}_1 (p)\) and this makes the energy functional of the problem noncoercive, hence we can not employ the direct method of the calculus of variations. Hypothesis \(\mathrm{H}_1\)(iv) implies the presence of a concave term near zero. When there is no potential term (that is, \(\xi \equiv 0\)), then hypotheses \(\mathrm{H}_1\)(iv), (v) dictate an oscillatory behavior for \(f(z,\cdot )\) near zero. In the general case the oscillatory behavior concerns the function \(x\mapsto f(z,x)-\xi (z)|x|^{p-2}x\). Hypothesis \(\mathrm{H}_1\)(vi) is essentially a one-sided Hölder condition. It is satisfied if \(f(z,\cdot )\) is differentiable for a.a. \(z\in \Omega \) and for every \(\rho >0\), we can find \({\widehat{\xi }}_\rho >0\) such that \(f_x' (z,x)x^2\ge -{\widehat{\xi }}_\rho |x|^p\) for a.a. \(z\in \Omega \), all \(|x|\le \rho \).

3 Constant sign solutions

In this section we produce multiple constant sign solutions.

We start by producing two nontrivial smooth solutions, one positive and the other negative, using only the conditions on \(f(z,\cdot )\) near zero.

Proposition 3.1

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) (iv), (v), (vi) hold, then problem (1.1) has two constant sign solutions \(u_0\in \mathrm{int}\, C_+\), \(v_0\in -\mathrm{int}\, C_+\) and \(\vartheta _-< v_0(z)<0<u_0(z)<\vartheta _+\) for all \(z\in {\overline{\Omega }}\).

Proof

First we produce the positive solution.

Let \(\eta >\Vert \xi \Vert _\infty \) (see hypotheses \(\mathrm{H}_0\)) and consider the Carathéodory function \(k_+:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned} k_+ (z,x)={\left\{ \begin{array}{ll} f(z,x^+)+\eta (x^+)^{p-1} &{} \text {if}\, x\le \vartheta _+\\ f(z,\vartheta _+)+\eta \vartheta _+^{p-1} &{} \text {if}\, \vartheta _+<x \end{array}\right. }. \end{aligned}$$
(3.1)

We set \(K_+(z,x)=\int _0^x k_+(z,s)\,\mathrm{d}s\) and consider the \(C^1\)-functional \(w_+: W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned} w_+(u)=\frac{1}{p} \gamma _p (u)+\frac{\eta }{p}\Vert u\Vert _p^p+\frac{1}{q} \Vert Du\Vert _q^q - \int _\Omega K_+(z,u)\,\mathrm{d}z\quad \text {for all}\, u\in W^{1,p}(\Omega ). \end{aligned}$$

From (3.1) and since \(\eta >\Vert \xi \Vert _\infty \) and \(\beta \ge 0\) (see hypotheses \(\mathrm{H}_0\)), we see that \(w_+(\cdot )\) is coercive. Also, using the Sobolev embedding theorem, we show that \(w_+(\cdot )\) is sequentially weakly lower semicontinuous. So, by the Weierstrass-Tonelli theorem, we can find \(u_0\in W^{1,p}(\Omega )\) such that

$$\begin{aligned} w_+(u_0)=\min \left[ w_+(u): u\in W^{1,p}(\Omega )\right] . \end{aligned}$$
(3.2)

Let \(u\in \mathrm{int}\, C_+\) and choose \(t\in (0,1)\) small such that

$$\begin{aligned} 0<tu(z)\le \min \{\vartheta _+,\delta \}\quad \text {for all}\, z\in {\overline{\Omega }}, \end{aligned}$$
(3.3)

with \(\delta >0\) as in hypothesis \(\mathrm{H}_1\)(iv). We have

Since \(\mu <q\) (see \(\mathrm{H}_1\)(iv)), choosing \(t\in (0,1)\) even smaller if necessary, we have

From (3.2) we have

$$\begin{aligned} w_+'(u_0)=0, \end{aligned}$$
$$\begin{aligned}&\Rightarrow \quad \langle \gamma _p'(u_0), h\rangle +\int _\Omega \eta |u_0|^{p-2}u_0h \,\mathrm{d}z+\langle A_q(u_0),h\rangle \nonumber \\&\quad = \int _\Omega k_+(z,u_0)h\,\mathrm{d}z \quad \text {for all}\, h\in W^{1,p}(\Omega ). \end{aligned}$$
(3.4)

Evidently

$$\begin{aligned} \langle \gamma _p'(u_0), h\rangle&= \langle A_p(u_0),h\rangle +\int _\Omega \xi (z)|u_0|^{p-2}u_0 h\,\mathrm{d}z + \int _{\partial \Omega } \beta (z) |u_0|^{p-2}u_0 h\,\mathrm{d}z\\&\quad \text {for all}\, h\in W^{1,p}(\Omega ). \end{aligned}$$

Choosing \(h=-u_0^-\in W^{1,p}(\Omega )\) in (3.4), we obtain

$$\begin{aligned}&\gamma _p (u_0^-)+\eta \Vert u_0^-\Vert _p^p+\Vert Du_0^-\Vert _q^q = 0 \quad \text {(see (3.1))},\\&\quad \Rightarrow \quad c_3 \Vert u_0^-\Vert ^p\le 0 \quad \text {for some}\, c_3>0\, (\text {since}\, \eta >\Vert \xi \Vert _\infty ),\\&\quad \Rightarrow \quad u_0\ge 0,\; u_0\ne 0. \end{aligned}$$

Next in (3.4) we choose \(h=[u_0-\vartheta _+]^+\in W^{1,p}(\Omega )\). We have

$$\begin{aligned}&\langle \gamma _p' (u_0), (u_0-\vartheta _+)^+\rangle + \int _\Omega \eta |u_0|^{p-2} u_0(u_0-\vartheta _+)^+\,\mathrm{d}z+\langle A_q(u_0), (u_0-\vartheta _+)^+\rangle \\&\quad = \int _\Omega \left[ f(z,\vartheta _+)+\eta \vartheta _+^{p-1}\right] (u_0-\vartheta _+)^+\,\mathrm{d}z\quad \text {(see} (3.1))\\&\quad \le \quad \int _\Omega [\xi (z)+\eta ] \vartheta _+^{p-1} (u_0-\vartheta _+)^+\,\mathrm{d}z \quad \text {(see hypothesis}\, {\mathrm{H}}_{1}(\mathrm{v}))\\&\quad \le \quad \langle \gamma _p'(\vartheta _+), (u_0-\vartheta _+)^+\rangle \\&\qquad + \int _\Omega \eta \vartheta _+^{p-1}(u_0-\vartheta _+)^+\,\mathrm{d}z+\langle A_q(\vartheta _+), (u_0-\vartheta _+)^+\rangle \quad \text {(since}\, \beta \ge 0)\\&\quad \Rightarrow \quad u_0\le \vartheta _+. \end{aligned}$$

So, we have proved that

$$\begin{aligned} u_0\in [0,\vartheta _+],\; u_0\ne 0. \end{aligned}$$
(3.5)

From (3.5), (3.1) and (3.4) it follows that

$$\begin{aligned} u_0\in W^{1,p}(\Omega ) \text {is a positive solution of}\, (1.1). \end{aligned}$$

From Proposition 2.10 of Papageorgiou-Rădulescu [18] we have that \(u_0\in L^\infty (\Omega )\). So, we can apply the nonlinear regularity theory of Lieberman [15] and infer that \(u_0\in C_+{\setminus } \{0\}\). For \(\rho =\Vert u_0\Vert _\infty \), let \({\widehat{\xi }}_\rho >0\) be as postulated by hypothesis \(\mathrm H_1\)(vi). We have

$$\begin{aligned}&\Delta _p u_0+\Delta _q u_0 \le \left[ \Vert \xi \Vert _\infty + {\widehat{\xi }}_\rho \right] u_0^{p-1}\quad \text {in}\, \Omega \, (\text {see hypothesis}\, {\mathrm{H}}_1(\mathrm{vi})),\\&\quad \Rightarrow \quad u_0\in \mathrm{int}\, C_+ \quad \text {(see Pucci-Serrin}\, [30], \mathrm{pp}.~111,120). \end{aligned}$$

Clearly we can always assume that \({\widehat{\xi }}_\rho >\Vert \xi \Vert _\infty \). We have

$$\begin{aligned}&-\Delta _p u_0-\Delta _q u_0+\left[ \xi (z)+{\widehat{\xi }}_\rho \right] u_0^{p-1} \nonumber \\&\quad =\quad f(z,u_0)+{\widehat{\xi }}_\rho u_0^{p-1} \nonumber \\&\quad \le \quad f(x,\vartheta _+)+{\widehat{\xi }}_\rho \vartheta _+^{p-1}\quad \text {(see}\, (3.5)\, \text {and hypothesis}\, \mathrm H_1(vi)) \nonumber \\&\quad \le \quad -\Delta _p \vartheta _+ -\Delta _q \vartheta _+ +\left[ \xi (z)+{\widehat{\xi }}_\rho \right] \vartheta _+^{p-1} \quad \text {(see hypothesis}\, \mathrm H_1(v)). \end{aligned}$$
(3.6)

On account of hypothesis \(\mathrm H_1\)(v) and using Proposition 2.10 of Papageorgiou-Rădulescu-Repovš [20], from (3.6) we infer that

$$\begin{aligned} u_0(z)<\vartheta _+\quad \hbox { for all}\ z\in \Omega . \end{aligned}$$

Suppose that for some \(z_0\in \partial \Omega \) we have \(u_0(z_0)=\vartheta _+\). Then, from [20] we have \(\frac{\partial u_0}{\partial n}(z_0)>0\). On the other hand from the Robin boundary condition, we have

$$\begin{aligned} \frac{\partial u_0}{\partial n}(z_0)=-\beta (z_0)u_0(z_0)^{p-1}\le 0,\end{aligned}$$

a contradiction. Therefore, we conclude that

$$\begin{aligned} 0<u_0(z)<\vartheta _+\quad \hbox { for all}\ z\in {\overline{\Omega }}.\end{aligned}$$

For the negative solution, we introduce the Carathéodory function \(k_-(z,x)\) defined by

$$\begin{aligned} k_-(z,x)={\left\{ \begin{array}{ll} f(z,\vartheta _-)-\eta |\vartheta _-|^{p-1} &{} \hbox { if}\ x<\vartheta _-\\ f(z,-x^-)-\eta (x^-)^{p-1} &{} \hbox { if}\ \vartheta _-\le x \end{array}\right. }. \end{aligned}$$
(3.7)

We set \(K_-(z,x)=\int _0^x k_-(z,s)\,\mathrm{d}s\) and consider the \(C^1\)-functional \(w_-: W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned}w_-(u)=\frac{1}{p} \gamma _p(u)+\frac{\eta }{p}\Vert u\Vert _p^p+\frac{1}{q} \Vert Du\Vert _q^q-\int _\Omega K_-(z,u)\,\mathrm{d}z\quad \hbox { for all}\ u\in W^{1,p}(\Omega ).\end{aligned}$$

Using \(w_-(\cdot )\), (3.7) and the direct method of the calculus of variations, as before, we produce a negative solution \(v_0\in W^{1,p}(\Omega )\) for problem (1.1) such that

$$\begin{aligned}v_0\in - \mathrm{int}\, C_+,\quad \vartheta _-<v_0(z)<0\quad \hbox { for all}\ z\in {\overline{\Omega }}.\end{aligned}$$

\(\square \)

Using these two constant sign solutions and activating the asymptotic hypotheses as \(x\rightarrow \pm \infty \) (see \(\mathrm H_1\)(ii), (iii)), we can produce two more constant sign smooth solutions localized with respect to \(u_0\) and \(v_0\) respectively.

So, let \(u_0\in \mathrm{int}\,C_+\) and \(v_0\in -\mathrm{int}\, C_+\) be the two solutions from Proposition 3.1. As before, let \(\eta >\Vert \xi \Vert _\infty \) and consider the Carathéodory functions \({\widehat{g}}_+,{\widehat{g}}_-:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned}&{\widehat{g}}_+(z,x)={\left\{ \begin{array}{ll} f(z,u_0(z))+\eta u_0(z)^{p-1} &{} \hbox { if}\ x\le u_0(z)\\ f(z,x) + \eta x^{p-1} &{} \hbox { if}\ u_0(z)<x \end{array}\right. }, \end{aligned}$$
(3.8)
$$\begin{aligned}&{\widehat{g}}_-(z,x)={\left\{ \begin{array}{ll} f(z,x)+\eta |x|^{p-2}x &{} \hbox { if}\ x< v_0(z)\\ f(z,v_0(z)) + \eta |v_0(z)|^{p-2}v_0(z) &{} \hbox { if}\ v_0(z)\le x \end{array}\right. }. \end{aligned}$$
(3.9)

We set \({\widehat{G}}_+(z,x)=\int _0^x {\widehat{g}}_+(z,s)\,\mathrm{d}s\) and \({\widehat{G}}_-(z,x)=\int _0^x {\widehat{g}}_-(z,s)\,\mathrm{d}s\) and consider the \(C^1\)-functionals \({\widehat{\varphi }}_+, {\widehat{\varphi }}_-: W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned}&{\widehat{\varphi }}_+(u)=\frac{1}{p} \gamma _p(u)+\frac{\eta }{p}\Vert u\Vert _p^p+\frac{1}{p} \Vert Du\Vert _q^q-\int _\Omega {\widehat{G}}_+(z,u)\,\mathrm{d}z\\&{\widehat{\varphi }}_-(u)=\frac{1}{p} \gamma _p(u)+\frac{\eta }{p}\Vert u\Vert _p^p+\frac{1}{p} \Vert Du\Vert _q^q-\int _\Omega {\widehat{G}}_-(z,u)\,\mathrm{d}z \end{aligned}$$

for all \(u\in W^{1,p}(\Omega )\).

Since \(u_0(z)<\vartheta _+\) and \(\vartheta _-<v_0(z)\) for all \(z\in {\overline{\Omega }}\) (see Proposition 3.1), we can also introduce the following truncations of \({\widehat{g}}_\pm (z,\cdot )\)

$$\begin{aligned}&{\widehat{g}}_+^* (z,x)={\left\{ \begin{array}{ll} {\widehat{g}}_+(z,x) &{} \hbox { if}\ x\le \vartheta _+\\ {\widehat{g}}_+(z,\vartheta _+) &{} \hbox { if}\ \vartheta _+<x \end{array}\right. }, \end{aligned}$$
(3.10)
$$\begin{aligned}&{\widehat{g}}_-^* (z,x)={\left\{ \begin{array}{ll} {\widehat{g}}_-(z,\vartheta _-) &{} \hbox { if}\ x< \vartheta _-\\ {\widehat{g}}_-(z,x) &{} \hbox { if}\ \vartheta _-\le x \end{array}\right. }. \end{aligned}$$
(3.11)

Both are Carathéodory functions. We set \({\widehat{G}}_+^*(z,x)=\int _0^x {\widehat{g}}_+^* (z,s)\,\mathrm{d}s\) and \({\widehat{G}}_-^*(z,x)=\int _0^x {\widehat{g}}_-^* (z,s)\,\mathrm{d}s\) and consider the \(C^1\)-functionals \({\widehat{\varphi }}_+^*, {\widehat{\varphi }}_+^*:W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned}&{\widehat{\varphi }}_+^*(u)=\frac{1}{p} \gamma _p(u)+\frac{\eta }{p}\Vert u\Vert _p^p+\frac{1}{p} \Vert Du\Vert _q^q-\int _\Omega {\widehat{G}}_+^*(z,u)\,\mathrm{d}z\\&{\widehat{\varphi }}_-^*(u)=\frac{1}{p} \gamma _p(u)+\frac{\eta }{p}\Vert u\Vert _p^p+\frac{1}{p} \Vert Du\Vert _q^q-\int _\Omega {\widehat{G}}_-^*(z,u)\,\mathrm{d}z \end{aligned}$$

for all \(u\in W^{1,p}(\Omega )\).

From (3.10) and (3.11) and since \(\eta >\Vert \xi \Vert _\infty \), we see that the functionals \({\widehat{\varphi }}_+^*, {\widehat{\varphi }}_+^*\) are coercive. Moreover, from (3.8), (3.9), (3.10), (3.11), we have that

$$\begin{aligned} {\widehat{\varphi }}_+\Big |_{[0,\vartheta _+]}={\widehat{\varphi }}_+^*\Big |_{[0,\vartheta _+]} \quad \text {and}\quad {\widehat{\varphi }}_+'\Big |_{[0,\vartheta _+]}=\left( {\widehat{\varphi }}_+^*\right) '\Big |_{[0,\vartheta _+]}. \end{aligned}$$
(3.12)

Similarly for \({\widehat{\varphi }}_-\) and \({\widehat{\varphi }}_-^*\) on \([\vartheta _-,0]\).

Proposition 3.2

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) hold, then the functionals \({\widehat{\varphi }}_+, {\widehat{\varphi }}_+\) satisfy the C-condition.

Proof

We do the proof for \({\widehat{\varphi }}_+(\cdot )\), the proof for \({\widehat{\varphi }}_-(\cdot )\) being similar.

So, we consider a sequence \(\{u_n\}_{n\in {\mathbb {N}}}\subseteq W^{1,p}(\Omega )\) such that

$$\begin{aligned}&|{\widehat{\varphi }}_+ (u_n)|\le c_4 \quad \text {for some}\,\, c_4>0,\, \text {all}\, n\in {\mathbb {N}}, \end{aligned}$$
(3.13)
$$\begin{aligned}&(1+\Vert u_n\Vert ){\widehat{\varphi }}_+'(u_n)\rightarrow 0 \quad \text {in }\,W^{1,p}(\Omega )^*\, \text {as}\, n\rightarrow \infty . \end{aligned}$$
(3.14)

From (3.14) we have

$$\begin{aligned}&\left| \langle \gamma _p'(u_n), h \rangle + \int _\Omega \eta |u_n|^{p-2}u_n h \,\mathrm{d}z+\langle A_q(u_n),h\rangle -\int _\Omega {\widehat{g}}_+(z,u_n)h\,\mathrm{d}z\right| \le \frac{\epsilon _n \Vert h\Vert }{1+\Vert u_n\Vert }\nonumber \\&\quad \text {for all}\, h\in W^{1,p}(\Omega ),\, \text {with}\, \epsilon _n\rightarrow 0^+. \end{aligned}$$
(3.15)

In (3.15) we choose \(h=-u_n^-\in W^{1,p}(\Omega )\). Then, from (3.8) we have

$$\begin{aligned}&\gamma _p(u_n^-)+\eta \Vert u_n^-\Vert _p^p\le c_5 \quad \text {for some}\, c_5>0,\, \text {all}\, n\in {\mathbb {N}}, \nonumber \\&\quad \Rightarrow \quad \Vert u_n^-\Vert ^p\le c_6 \quad \text {for some}\, c_6>0,\, \text {all}\, n\in {\mathbb {N}}\, (\text {since}\, \eta >\Vert \xi \Vert _\infty ),\nonumber \\&\quad \Rightarrow \quad \{u_n^-\}_{n\in {\mathbb {N}}}\subseteq W^{1,p}(\Omega ) \; \text {is bounded.} \end{aligned}$$
(3.16)

Next we show that \(\{u_n^+\}\subseteq W^{1,p}(\Omega )\) is bounded too. We argue by contradiction. So, by passing to a subsequence if necessary, we may assume that

$$\begin{aligned} \Vert u_n^+\Vert \rightarrow +\infty \; \text {as}\, n\rightarrow \infty . \end{aligned}$$
(3.17)

We set \(y_n=\frac{u_n^+}{\Vert u_n^+\Vert }\), \(n\in {\mathbb {N}}\). Then \(\Vert y_n\Vert =1\), \(y_n\ge 0\) for all \(n\in {\mathbb {N}}\). We may assume that

$$\begin{aligned} y_n\xrightarrow {w} y\;\; \hbox { in}\ W^{1,p}(\Omega )\quad \text {and}\quad y_n\rightarrow y\;\; \text {in}\, L^p(\Omega )\, \text { and in}\, L^p(\partial \Omega ), y\ge 0. \end{aligned}$$
(3.18)

From (3.13) and (3.16), we have

$$\begin{aligned}&\frac{{\widehat{\varphi }}_+ (u_n^+)}{\Vert u_n^+\Vert }\le \frac{c_7}{\Vert u_n^+\Vert ^p}\quad \text {for some } c_7>0 \hbox {, all} n\in {\mathbb {N}}, \nonumber \\&\quad \Rightarrow \quad \frac{1}{p} \gamma _p (y_n)+\frac{1}{q}\frac{1}{\Vert u_n^+\Vert ^{p-q}}\Vert Dy_n\Vert _q-\int _\Omega \frac{F(z,u_n^+)}{\Vert u_n^+\Vert ^p}\,\mathrm{d}z\nonumber \\&\quad \le \frac{c_7}{\Vert u_n^+\Vert ^p} \quad \text {for all}\, n\in {\mathbb {N}}\; (\text {see}\,(3.8)). \end{aligned}$$
(3.19)

Hypotheses \(\mathrm{H}_1\)(ii), (iii) imply that given \(\epsilon >0\), we can find \(c_8>0\) such that

$$\begin{aligned} F(z,x)\le \frac{1}{p} \left[ {\widehat{\lambda }}_1 (p)+\epsilon \right] x^p+c_8\quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, x\ge 0. \end{aligned}$$
(3.20)

We return to (3.19) and (3.20). We obtain

$$\begin{aligned}\frac{1}{p} \gamma _p(y_n)\le \frac{1}{p} \int _\Omega \left[ {\widehat{\lambda }}_1 (p)+\epsilon \right] y_n^p\,\mathrm{d}z+\epsilon _n'\quad \hbox { with}\ \epsilon _n'\rightarrow 0^+.\end{aligned}$$

We pass to the limit as \(n\rightarrow \infty \) and use (3.18) and the weak lower semicontinuity of \(\gamma _p(\cdot )\) (since \(\gamma _p(\cdot )\) is continuous, convex). We obtain

$$\begin{aligned}\frac{1}{p} \gamma _p(y)\le \frac{1}{p} \int _\Omega \left[ {\widehat{\lambda }}_1 (p)+\epsilon \right] y^p\,\mathrm{d}z.\end{aligned}$$

Since \(\epsilon >0\) is arbitrary, we let \(\epsilon \rightarrow 0^+\) and we have

$$\begin{aligned}&\gamma _p(y)\le {\widehat{\lambda }}_1(p)\Vert y\Vert _p^p, \nonumber \\&\quad \Rightarrow \quad \gamma _p(y)={\widehat{\lambda }}_1(p)\Vert y\Vert _p^p \quad \text {(see}\, (2.2)). \end{aligned}$$
(3.21)

From (3.14), (3.16) and (3.8), we have

$$\begin{aligned}&\left| \langle \gamma _p'(u_n^+), h\rangle + \langle A_q(u_n^+), h\rangle - \int _\Omega f(z,u_n^+)h\,\mathrm{d}z\right| \le c_9 \Vert h\Vert \quad \hbox {for some}\,\, c_9>0 \text {, all } n\in {\mathbb {N}}, \nonumber \\&\quad \Rightarrow \quad \left| \langle \gamma _p'(u_n^+), h\rangle + \frac{1}{\Vert u_n^+\Vert ^{p-q}}\langle A_q(y_n),h\rangle - \int _\Omega \frac{f(z,u_n^+)}{\Vert u_n^+\Vert ^{p-1}}h\,\mathrm{d}z\right| \nonumber \\&\quad \le \frac{c_9 \Vert h\Vert }{\Vert u_n^+\Vert ^{p-1}}\quad \hbox { for all} \ n\in {\mathbb {N}}. \end{aligned}$$
(3.22)

Hypothesis \(\mathrm{H}_1\)(i) implies that

$$\begin{aligned} \left\{ \frac{f(\cdot , u_n^+(\cdot ))}{\Vert u_n^+\Vert ^{p-1}}\right\} _{n\in {\mathbb {N}}}\subseteq L^{p'}(\Omega ) \;\; \text {is bounded}\, \left( p'=\frac{p}{p-1}\right) . \end{aligned}$$
(3.23)

So, if in (3.22) we choose \(h=y_n-y\in W^{1,p}(\Omega )\), pass to the limit as \(n\rightarrow +\infty \) and use (3.17), (3.18) and (3.23), we obtain

$$\begin{aligned}&\lim _{n\rightarrow \infty } \langle A_p(y_n), y_n-y\rangle = 0, \nonumber \\&\quad \Rightarrow \quad y_n\rightarrow y\;\; \hbox { in}\ W^{1,p}(\Omega ) \quad \text {and so}\quad \Vert y\Vert =1,\; y\ge 0. \end{aligned}$$
(3.24)

From (3.21) and (3.24), we infer that

$$\begin{aligned} y=c{\widehat{u}}_1(p)\in \mathrm{int}\, C_+\quad \hbox { with}\ c>0.\end{aligned}$$

Then it follows that

$$\begin{aligned}&u_n^+(z)\rightarrow +\infty \;\; \hbox { for a.a.}\ z\in \Omega , \nonumber \\ \Rightarrow \quad&\limsup _{n\rightarrow \infty }\frac{f(z,u_n^+(z))u_n^+(z)-pF(z,u_n^+(z))}{u_n^+(z)^\tau }\le -\gamma _0<0\nonumber \\&\quad \text {for a.a.}\, z\in \Omega \, (\text {see hypothesis}\, \mathrm{H}_1(\mathrm{iii})),\nonumber \\ \Rightarrow \quad&\liminf _{n\rightarrow \infty }\int _\Omega \frac{pF(z,u_n^+)-f(z,u_n^+)u_n^+}{\Vert u_n^+\Vert ^\tau }\ge \gamma _1>0\nonumber \\&\quad \text {(using Fatou's lemma and}\, (3.24)). \end{aligned}$$
(3.25)

From (3.13), (3.16), (3.8) and (3.17), we have

$$\begin{aligned}&-\gamma _p(y_n)-\frac{p}{q}\frac{1}{\Vert u_n^+\Vert ^{p-q}}\Vert Dy_n\Vert _q^q+\int _\Omega \frac{pF(z,u_n^+)}{\Vert u_n^+\Vert ^p}\,\mathrm{d}z\le \frac{c_{10}}{\Vert u_n^+\Vert ^p}\nonumber \\&\quad \text {for some}\, c_{10}>0,\, \text {all}\, n\in {\mathbb {N}}. \end{aligned}$$
(3.26)

On the other hand, from (3.15) with \(h=u_n^+\in W^{1,p}(\Omega )\), (3.16) and (3.8), we have

$$\begin{aligned}&\gamma _p(y_n)+\frac{1}{\Vert u_n^+\Vert ^{p-q}}\Vert Dy_n\Vert _q^q-\int _\Omega \frac{f(z,u_n^+)u_n^+}{\Vert u_n^+\Vert ^p}\,\mathrm{d}z\le \frac{c_{11}}{\Vert u_n^+\Vert ^p}\nonumber \\&\quad \text {for some}\, c_{11}>0,\, \text {all}\, n\in {\mathbb {N}}. \end{aligned}$$
(3.27)

We add (3.26) and (3.27). Then we have

$$\begin{aligned}&\frac{1}{\Vert u_n^+\Vert ^{p-\tau }}\int _\Omega \frac{pF(z,u_n^+)-f(z,u_n^+)u_n^+}{\Vert u_n^+\Vert ^\tau }\,\mathrm{d}z\le \left( \frac{p}{q}-1\right) \frac{1}{\Vert u_n^+\Vert ^{p-q}}\Vert Dy_n\Vert _q^q+\frac{c_{12}}{\Vert u_n^+\Vert ^p} \nonumber \\&\quad \text {for some}\, c_{12}>0, \text {all}\, n\in {\mathbb {N}},\nonumber \\&\quad \Rightarrow \quad \int _\Omega \frac{pF(z,u_n^+)-f(z,u_n^+)u_n^+}{\Vert u_n^+\Vert ^\tau }\,\mathrm{d}z\le \left( \frac{p}{q}-1\right) \frac{1}{\Vert u_n^+\Vert ^{\tau -q}}\Vert Dy_n\Vert _q^q+\epsilon _n^* \nonumber \\&\quad \text {for all}\, n\in {\mathbb {N}},\, \text {with}\, \epsilon _n^*\rightarrow 0^+,\nonumber \\&\quad \Rightarrow \quad \limsup _{n\rightarrow \infty }\int _\Omega \frac{pF(z,u_n^+)-f(z,u_n^+)u_n^+}{\Vert u_n^+\Vert ^\tau }\,\mathrm{d}z\le 0\nonumber \\&\quad \text {(recall that}\, q<\tau \, \text {and see}\, (3.17)). \end{aligned}$$
(3.28)

Comparing (3.28) and (3.25), we have a contradiction. Hence

$$\begin{aligned}&\{u_n^+\}_{n\in {\mathbb {N}}}\subseteq W^{1,p}(\Omega )\;\; \text {is bounded,}\\&\quad \Rightarrow \quad \{u_n\}_{n\in {\mathbb {N}}}\subseteq W^{1,p}(\Omega )\;\; \text {is bounded (see}\, (3.16)). \end{aligned}$$

We may assume that

$$\begin{aligned} u_n\xrightarrow {w} u\;\; \hbox { in}\ W^{1,p}(\Omega )\quad \text {and}\quad u_n\rightarrow u\;\; \text {in}\, L^p(\Omega )\, \text {and in}\, L^p(\partial \Omega ). \end{aligned}$$
(3.29)

In (3.15) we choose \(h=u_n-u\in W^{1,p}(\Omega )\), pass to the limit as \(n\rightarrow \infty \) and use (3.29). Then

$$\begin{aligned}&\lim _{n\rightarrow \infty }\left[ \langle A_p(u_n), u_n-u\rangle + \langle A_q(u_n), u_n-u\rangle \right] =0,\\&\quad \Rightarrow \quad \limsup _{n\rightarrow \infty }\left[ \langle A_p(u_n), u_n-u\rangle + \langle A_q(u), u_n-u\rangle \right] \le 0 \quad \text {(since}\, A_q(\cdot )\, \text { is monotone)},\\&\quad \Rightarrow \quad \limsup _{n\rightarrow \infty }\langle A_p(u_n), u_n-u\rangle \le 0 \quad \text {(see}\, (3.30),\\&\quad \Rightarrow \quad u_n\rightarrow u \;\; \text {in}\, W^{1,p}(\Omega )\,\, \text {(see Proposition}~2.1). \end{aligned}$$

This proves that \({\widehat{\varphi }}_+(\cdot )\) satisfies the C-condition.

In a similar fashion, we show that \({\widehat{\varphi }}_-(\cdot )\) satisfies the C-condition. \(\square \)

Proposition 3.3

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) hold, the \({\widehat{\varphi }}_\pm (t{\widehat{u}}_1(p))\rightarrow -\infty \) as \(t\rightarrow \pm \infty \).

Proof

For a.a. \(z\in \Omega \) and all \(x>0\), we have

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{F(z,x)}{x^p}\right)= & {} \frac{f(z,x)x^p-pF(z,x)x^{p-1}}{x^{2p}}\nonumber \\= & {} \frac{f(z,x)x-pF(z,x)}{x^{p+1}}. \end{aligned}$$
(3.30)

On account of hypothesis \(\mathrm{H}_1\)(iii), we can find \(\gamma _2\in (0,\gamma _0)\) and \(M>0\) such that

$$\begin{aligned} f(z,x)x-pF(z,x)\le -\gamma _2 x^\tau \quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, x\ge M. \end{aligned}$$
(3.31)

We return to (3.30) and use (3.31). Then

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{F(z,x)}{x^p}\right) \le -\frac{\gamma _2 x^\tau }{x^{p+1}}=-\frac{\gamma _2}{x^{p-\tau +1}}\quad \hbox {for a.a.}\,\, z\in \Omega \text {, all } x\ge M,\\&\quad \Rightarrow \quad \frac{F(z,x)}{x^p}-\frac{F(z,y)}{y^p}\le \frac{\gamma _2}{p-\tau }\left( \frac{1}{x^{p-\tau }}-\frac{1}{y^{p-\tau }}\right) \quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, x\ge y\ge M. \end{aligned}$$

We pass to the limit as \(x\rightarrow +\infty \) and use hypothesis \(\mathrm{H}_1\)(ii). Then

$$\begin{aligned}&\frac{{\widehat{\lambda }}_1 (p)}{p}-\frac{F(z,y)}{y^p}\le -\frac{\gamma _2}{p-\tau }\frac{1}{y^{p-\tau }}\quad \hbox {for a.a.} z\in \Omega \hbox {, all} y\ge M,\\&\quad \Rightarrow \quad \frac{pF(z,y)-{\widehat{\lambda }}_1(p)y^p}{y^\tau }\ge \frac{\gamma _2}{p-\tau }\quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, y\ge M. \end{aligned}$$

We infer that

$$\begin{aligned} \liminf _{x\rightarrow +\infty }\frac{pF(z,x)-{\widehat{\lambda }}_1(p)x^p}{x^\tau }\ge \gamma _3>0\;\; \text {uniformly for a.a.}\, z\in \Omega . \end{aligned}$$
(3.32)

Then we have

$$\begin{aligned}&{\widehat{\varphi }}_+(t{\widehat{u}}_1(p))=\frac{{\widehat{\lambda }}_1(p)}{p}\Vert t{\widehat{u}}_1(p)\Vert _p^p+\frac{t^q}{q}\Vert D{\widehat{u}}_1\Vert _q^q-\int _\Omega F(z,t{\widehat{u}}_1 (p))\,\mathrm{d}z\\&\quad \Rightarrow \quad p {\widehat{\varphi }}_+(t{\widehat{u}}_1(p)) =\int _\Omega \frac{{\widehat{\lambda }}_1(p)(t{\widehat{u}}_1 (p))-pF(z, t{\widehat{u}}_1 (p))}{t^\tau } t^\tau \,\mathrm{d}z+\frac{t^q}{q}\Vert D{\widehat{u}}_1\Vert _q^q. \end{aligned}$$

Using (3.32) and the fact that \(\tau >q\) (see hypothesis \(\mathrm{H}_1\)(iii)), we infer that

$$\begin{aligned} {\widehat{\varphi }}_+(t{\widehat{u}}_1(p)) \rightarrow -\infty \;\; \hbox { as}\ t\rightarrow +\infty .\end{aligned}$$

In a similar fashion we show that

$$\begin{aligned} {\widehat{\varphi }}_-(t{\widehat{u}}_1(p)) \rightarrow -\infty \;\; \hbox { as}\ t\rightarrow -\infty . \end{aligned}$$

\(\square \)

Using (3.8) and (3.9), we can easily check that

$$\begin{aligned} K_{{\widehat{\varphi }}_+}\subseteq [u_0)\cap \mathrm{int}\, C_+\quad \text {and} \quad K_{{\widehat{\varphi }}_-}\subseteq (v_0]\cap (-\mathrm{int}\, C_+). \end{aligned}$$
(3.33)

We may assume that

$$\begin{aligned} K_{{\widehat{\varphi }}_+}\cap [0,\vartheta _+]=\{u_0\} \quad \text {and} \quad K_{{\widehat{\varphi }}_-}\cap [\vartheta _-,0]=\{v_0\}. \end{aligned}$$
(3.34)

Otherwise we already have two more constant sign solutions, one positive different from \(u_0\) in \([u_0,\vartheta _+]\cap \mathrm{int}\, C_+\) and the other negative different from \(v_0\) in \([\vartheta _-,v_0]\cap (-\mathrm{int}\, C_+)\). So, we are done.

Clearly the functionals \({\widehat{\varphi }}_+^*\) and \({\widehat{\varphi }}_-^*\) are coercive (see (3.10) and (3.11)) and sequentially weakly lower semicontinuous. Moreover, we can easily check that

$$\begin{aligned} K_{{\widehat{\varphi }}_+^*}\subseteq [u_0,\vartheta _+]\cap \mathrm{int}\, C_+\quad \text {and} \quad K_{{\widehat{\varphi }}_-^*}\subseteq [\vartheta _-,v_0]\cap (-\mathrm{int}\, C_+). \end{aligned}$$
(3.35)

The Weierstrass-Tonelli theorem, together with (3.34), (3.35) and (3.12) and the fact that \(u_0\in \mathrm{int}\,_{C^1({\overline{\Omega }})}[0,\vartheta _+]\) (that is, the interior in \(C^1({\overline{\Omega }})\) of \([0,\vartheta _+]\cap C^1({\overline{\Omega }})\)), \(v_0\in \mathrm{int}\,_{C^1({\overline{\Omega }})}[-\vartheta _-,0]\) (that is, the interior in \(C^1({\overline{\Omega }})\) of \([\vartheta _-,0]\cap C^1({\overline{\Omega }})\)), imply that

$$\begin{aligned} \hbox {} u_0\,\, \hbox {is a local}\,\, C^1({\overline{\Omega }})-\text {minimizer of}\,\, {\widehat{\varphi }}_+, \end{aligned}$$

and

$$\begin{aligned}v_0\, \text {is a local}\, C^1({\overline{\Omega }})-\text {minimizer of}\,\, {\widehat{\varphi }}_-. \end{aligned}$$

From Papageorgiou-Rădulescu [18] (see also Bai-Gasiński-Winkert-Zeng [4] for a nonsmooth version), we have

$$\begin{aligned} u_0\, \text {is a local}\, W^{1,p}(\Omega )-\text {minimizer of}\,\, {\widehat{\varphi }}_+, \end{aligned}$$
(3.36)

and

$$\begin{aligned} {v_0}\, \text {is a local}\, W^{1,p}(\Omega )-\text {minimizer of}\,\, {\widehat{\varphi }}_-. \end{aligned}$$
(3.37)

Note that we may say that the sets

$$\begin{aligned} K_{{\widehat{\varphi }}_+}\, \text {and}\, K_{{\widehat{\varphi }}_-}\, \text {are finite} \end{aligned}$$
(3.38)

otherwise on account of (3.35), (3.8), (3.9) we already have a sequence of distinct positive solutions bigger than \(u_0\) and a sequence of distinct negative solutions smaller than \(v_0\) and so we are done. From (3.36), (3.37), (3.38) and Theorem 5.7.6, p. 449, of Papageorgiou-Rădulescu-Repovš, we see that we can find \(\rho \in (0,1)\) small such that

$$\begin{aligned}&{\widehat{\varphi }}_+(u_0)<\inf \left[ {\widehat{\varphi }}_+(u): \Vert u-u_0\Vert =\rho \right] ={\widehat{m}}_+, \end{aligned}$$
(3.39)
$$\begin{aligned}&{\widehat{\varphi }}_-(v_0)<\inf \left[ {\widehat{\varphi }}_-(v): \Vert v-v_0\Vert =\rho \right] ={\widehat{m}}_-. \end{aligned}$$
(3.40)

Now we are ready to produce two more constant sign solutions for problem (1.1).

Proposition 3.4

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) hold, then problem (1.1) has two more constant sign solutions \({\widehat{u}}\in \mathrm{int}\, C_+\), \(u_0\le {\widehat{u}}\), \(u_0\ne {\widehat{u}}\), \({\widehat{v}}\in - \mathrm{int}\, C_+\), \({\widehat{v}}\le v_0\), \({\widehat{v}}\ne v_0\).

Proof

Propositions 3.2 and 3.3 and (3.39), (3.40) permit the use of the mountain pass theorem on the functionals \({\widehat{\varphi }}_+\), \({\widehat{\varphi }}_-\). Hence we can find \({\widehat{u}}\in K_{{\widehat{\varphi }}_+}\subseteq [u_0)\cap \mathrm{int}\, C_+\), \({\widehat{v}}\in K_{{\widehat{\varphi }}_-}\subseteq (v_0]\cap (-\mathrm{int}\, C_+)\) (see (3.33)) such that

$$\begin{aligned} {\widehat{m}}_+ \le {\widehat{\varphi }}_+({\widehat{u}})\quad \text {and}\quad {\widehat{m}}_-\le {\widehat{\varphi }}_-({\widehat{v}}). \end{aligned}$$
(3.41)

From (3.39), (3.40), (3.41) we infer that

$$\begin{aligned}&u_0\le {\widehat{u}},\; u_0\ne {\widehat{u}},\\&\quad {\widehat{v}}\le v_0,\; {\widehat{v}}\ne v_0. \end{aligned}$$

\(\square \)

4 Extremal constant sign solutions

In this section we show that problem (1.1) has extremal constant sign solutions, that is, there exist a smallest positive solution and a biggest negative solution. Using these extremal solutions, in the next section, we will be able to produce a nodal (sign-changing) solution.

Let \(S_+\) (resp. \(S_-\)) be the set of positive (resp. negative) solutions of (1.1). In Sect. 3, we saw that

$$\begin{aligned}\varnothing \ne S_+\subseteq \mathrm{int}\, C_+\quad \text {and}\quad \varnothing \ne S_-\subseteq -\mathrm{int}\, C_+.\end{aligned}$$

Proposition 4.1

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) hold, then problem (1.1) admits a smallest positive solution \(u_*\in \mathrm{int}\, C_+\) and a biggest negative solution.

Proof

From Papageorgiou-Rădulescu-Repovš [19] (see the proof of Proposition 7), we know that \(S_+\) is downward directed. So, using Lemma 3.10, p. 178, of Hu-Papageorgiou [14], we can find a decreasing sequence \(\{u_n\}_{n\in {\mathbb {N}}}\subseteq S_+\) such that

$$\begin{aligned}\inf _{n\ge 1} u_n=\inf S_+.\end{aligned}$$

We have

$$\begin{aligned}&\langle \gamma _p'(u_n),h\rangle + \langle A_q(u_n), h\rangle =\int _\Omega f(z,u_n)h\,\mathrm{d}z\quad \text {for all}\, h\in W^{1,p}(\Omega ),\, \text {all}\, n\in {\mathbb {N}}, \end{aligned}$$
(4.1)
$$\begin{aligned}&0\le u_n\le u_1\quad \text {for all}\, n\in {\mathbb {N}}. \end{aligned}$$
(4.2)

From (4.1) (with \(h=u_n\in W^{1,p}(\Omega )\)), (4.2) and hypothesis \(\mathrm{H}_1\)(i) it follows that \(\{u_n\}_{n\ge 1}\subseteq W^{1,p}(\Omega )\) is bounded. So, we may assume that

$$\begin{aligned} u_n\xrightarrow {w} u_*\;\; \text {in}\, W^{1,p}(\Omega )\quad \text {and}\quad u_n\rightarrow u_*\;\; \text {in}\, L^p(\Omega )\, \text {and in}\, L^p(\partial \Omega ). \end{aligned}$$
(4.3)

In (4.1) we choose \(h=u_n-u_*\in W^{1,p}(\Omega )\), pass to the limit as \(n\rightarrow \infty \) and use (4.3). Then, as in the proof of Proposition 3.2, we obtain

$$\begin{aligned}&\limsup _{n\rightarrow \infty }\langle A_p(u_n),u_n-u_*\rangle \le 0,\nonumber \\&\quad \Rightarrow \quad u_n\rightarrow u_*\; \text {in}\, W^{1,p}(\Omega )\,\, (\text {see Proposition}~(2.1)). \end{aligned}$$
(4.4)

So, passing to the limit as \(n\rightarrow \infty \) in (4.1) and using (4.4), we have that

$$\begin{aligned} \langle \gamma _p'(u_*),h\rangle + \langle A_q(u_*), h\rangle =\int _\Omega f(z,u_*)h\,\mathrm{d}z\quad \text {for all}\, h\in W^{1,p}(\Omega ).\end{aligned}$$

If we show that \(u_*\ne 0\), then \(u_*\in S_+\) and so \(u_*=\inf S_+\).

On account of hypotheses \(\mathrm{H}_1\)(i), (iv), we have

$$\begin{aligned} f(z,x)\ge c_0 |x|^\mu -c_{13}|x|^r\quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, x\in {\mathbb {R}},\, \text {with}\, c_{13}>0, r\in (p,p^*).\nonumber \\ \end{aligned}$$
(4.5)

The unilateral growth restriction on \(f(z,\cdot )\) leads to the following auxiliary Robin problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _p u-\Delta _q u+|\xi (z)||u|^{p-2}u=c_0 |u|^{\mu -2}u-c_{13}|u|^{r-2}u &{} \text {in}\, \Omega \\ \frac{\partial u}{\partial n_{pq}}+\beta (z)|u|^{p-2}u=0 &{} \text {on}\, \partial \Omega \end{array}\right. }. \end{aligned}$$
(4.6)

From Proposition 12 of Papageorgiou-Vetro-Vetro [27], we know that this problem has a unique positive solution \({\widetilde{u}}\in \mathrm{int}\, C_+\) and since the equation is odd, \({\widetilde{v}}=-{\widetilde{u}}\in -\mathrm{int}\, C_+\) is the unique negative solution of (4.6).

Claim. \({\widetilde{u}}\le u\) for all \(u\in S_+\) and \(v\le {\widetilde{v}}\) for all \(v\in S_-\).

Let \(u\in S_+\) and consider the Carathéodory function \(k_+:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned} k_+(z,x)={\left\{ \begin{array}{ll} c_0(x^+)^{\mu -1}-c_{13}(x^+)^{r-1} &{} \text {if}\, x\le u(z)\\ c_0 u(z)^{\mu -1}-c_{13}u(z)^{r-1} &{} \text {if}\, u(z)<x \end{array}\right. }. \end{aligned}$$
(4.7)

We set \(K_+(z,x)=\int _0^x k_+(z,s)\,\mathrm{d}s\) and consider the \(C^1\)-functional \(\psi _+: W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned} \psi _+(u)=\frac{1}{p} {\widehat{\gamma }}_p(u) +\frac{1}{q} \Vert Du\Vert _q^q-\int _\Omega K_+(z,u)\,\mathrm{d}z\quad \text {for all}\, u\in W^{1,p}(\Omega ) \end{aligned}$$

with \({\widehat{\gamma }}_p\in C^1(W^{1,p}(\Omega ))\) being defined by

$$\begin{aligned} {\widehat{\gamma }}_p(u)=\Vert Du\Vert _p^p+\int _\Omega |\xi (z)||u|^p\,\mathrm{d}z+\int _{\partial \Omega }\beta (z)|u|^p\,\mathrm{d}\sigma \quad \text {for all}\, u\in W^{1,p}(\Omega ). \end{aligned}$$

Note that \(\psi _+(\cdot )\) is coercive (see (4.7)). Indeed, for every \(v\in W^{1,p}(\Omega )\) we have that

$$\begin{aligned} \int _\Omega K_+ (z,v)\,\mathrm{d}z= & {} \int _{\{v\le u\}}\left[ \frac{c_0}{\mu }(v^+)^{\mu }-\frac{c_{13}}{r}(v^+)^r\right] \,\mathrm{d}z + \int _{\{u<v\}}[c_0 u^{\mu -1}-c_{13}u^{r-1}](v-u)\,\mathrm{d}z\\\le & {} {\widehat{c}}_1 \left[ 1+\Vert v\Vert \right] \quad \text {for some}\,\,\, {\widehat{c}}_1>0, \\\Rightarrow & {} -\int _\Omega K_+(z,v)\,\mathrm{d}z\ge -{\widehat{c}}_1 \left[ 1+\Vert v\Vert \right] .\end{aligned}$$

From this we infer the coercivity of \(\psi _+ (\cdot )\) since \(p>1\).

Also \(\psi _+(\cdot )\) is sequentially weakly lower semicontinuous. So, we can find \({\widetilde{u}}_0\in W^{1,p}(\Omega )\) such that

$$\begin{aligned} \psi _+({\widetilde{u}}_0)=\inf \left[ \psi _+(u): u\in W^{1,p}(\Omega )\right] . \end{aligned}$$
(4.8)

Since \(\mu<q<p\), it follows that

$$\begin{aligned}&\psi _+({\widetilde{u}}_0)<0=\psi _+(0),\\&\quad \Rightarrow \quad {\widetilde{u}}_0\ne 0. \end{aligned}$$

Using (4.7) and the nonlinear regularity theory (see [15]), we obtain

$$\begin{aligned} K_{\psi _+}\subseteq [0,u]\cap C_+. \end{aligned}$$
(4.9)

From (4.8), (4.9) it follows that

$$\begin{aligned}&{\widetilde{u}}_0\in [0,u],\; {\widetilde{u}}_0\ne 0,\\&\quad \Rightarrow \quad {\widetilde{u}}_0={\widetilde{u}}\in \mathrm{int}\, C_+\;\; \text {(see}\, (4.7)),\\&\quad \Rightarrow \quad {\widetilde{u}}\le u \;\; \text {for all}\, u\in S_+ (\text {see}\, (4.9)). \end{aligned}$$

Similarly we show that \(v\le {\widetilde{v}}\) for all \(v\in S_-\). This proves the Claim.

From (4.4) and the Claim, we have \({\widetilde{u}}\le u_*\). Hence \(u_*\ne 0\) and so \(u_*\in S_+\), \(u_*=\inf S_+\).

Similarly, we prove the existence of \(v_*\in S_-\) and \(v\le v_*\) for all \(v\in S_-\). We point out that now \(S_-\) is upward directed. \(\square \)

5 Nodal solutions

In this section, using the extremal constant sign solutions \(u_*\in \mathrm{int}\,C_+\) and \(v_*\in - \mathrm{int}\,C_+\) produced in Proposition 4.1, we show the existence of a nodal (sign-changing) solution. The idea is simple. We focus on the order interval \([v_*,u_*]\) and using a combination of tools and techniques we show that the problem has a solution in \([v_*,u_*]\) distinct from 0, \(u_*\), \(v_*\). Then, on account of the extremality of \(u_*\), \(v_*\), such a solution will be nodal.

To this end, let \(\eta >\Vert \xi \Vert _\infty \) and consider the Carathéodory function \(l:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned} l(z,x)={\left\{ \begin{array}{ll} f(z,v_*(z))+\eta |v_*(z)|^{p-2}v_*(z) &{} \text {if}\, x<v_*(z)\\ f(z,x)+\eta |x|^{p-2}x &{} \text {if}\, v_*(z)\le x\le u_*(z)\\ f(z,u_*(z))+\eta u_*(z)^{p-1} &{} \text {if}\, u_*(z)<x \end{array}\right. }. \end{aligned}$$
(5.1)

Also, we consider the positive and negative truncations of \(l(z,\cdot )\), namely the Carathéodory functions \(l_\pm : \Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned} l_\pm (z,x)=l(z,\pm x^\pm ). \end{aligned}$$
(5.2)

We set \(L(z,x)=\int _0^x l(z,s)\,\mathrm{d}s\), \(L_\pm (z,s)=\int _0^x l_\pm (z,s)\,\mathrm{d}s\) and consider the \(C^1\)-functionals \(\lambda ,\lambda _\pm : W^{1,p}(\Omega )\rightarrow {\mathbb {R}}\) defined by

$$\begin{aligned}&\lambda (u)=\frac{1}{p} \left[ \gamma _p(u)+\eta \Vert u\Vert _p^p\right] +\frac{1}{q} \Vert Du\Vert _q^q-\int _\Omega L(z,u)\,\mathrm{d}z,\\&\quad \lambda _\pm (u)=\frac{1}{p} \left[ \gamma _p(u)+\eta \Vert u\Vert _p^p\right] +\frac{1}{q} \Vert Du\Vert _q^q-\int _\Omega L_\pm (z,u)\,\mathrm{d}z, \end{aligned}$$

for all \(u\in W^{1,p}(\Omega )\).

Using (5.1), (5.2) and the nonlinear regularity theory (see [15]), we show that

$$\begin{aligned}&K_\lambda \subseteq [v_*,u_*]\cap C^1({\overline{\Omega }}), \end{aligned}$$
(5.3)
$$\begin{aligned}&K_{\lambda _+}\subseteq [0,u_*]\cap C_+,\quad K_{\lambda _-}\subseteq [v_*,0]\cap (-C_+). \end{aligned}$$
(5.4)

From (5.4) and the extremality of \(u_*\) and \(v_*\), we conclude that

$$\begin{aligned} K_{\lambda _+}=\{0,u_*\},\quad K_{\lambda _-}=\{0,v_*\}. \end{aligned}$$
(5.5)

Proposition 5.1

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) hold, then problem (1.1) admits a nodal solution \(y_0\in C^1({\overline{\Omega }})\) such that \(v_*\le y_0\le u_*.\)

Proof

Clearly \(\lambda _+\) is coercive (see (5.1), (5.2)). Also it is sequentially weakly lower semicontinuous. So, we can find \({\widetilde{u}}_*\in W^{1,p}(\Omega )\) such that

$$\begin{aligned} \lambda _+({\widetilde{u}}_*)=\min \left[ \lambda _+(u): u\in W^{1,p}(\Omega )\right] . \end{aligned}$$
(5.6)

On account of hypothesis \(\mathrm{H}_1\) (iv), we have

$$\begin{aligned}&\lambda _+({\widetilde{u}}_*)<0=\lambda _+(0),\\&\quad \Rightarrow \quad {\widetilde{u}}_*\ne 0,\\&\quad \Rightarrow \quad {\widetilde{u}}_*=u_* \;\; \text {(see}\, (5.6) \,\,\text {and}\,\, (5.5)). \end{aligned}$$

Since \(\lambda \Big |_{C_+}=\lambda _+\Big |_{C_+}\) and \(u_*\in \mathrm{int}\, C_+\), it follows that

$$\begin{aligned}&u_*\,\, \text {is a local}\, C^1({\overline{\Omega }})-\text {minimizer of}\, \lambda (\cdot ),\nonumber \\&\quad \Rightarrow \quad u_* \,\, \text {is a local}\, W^{1,p}(\Omega )-\text {minimizer of}\, \lambda (\cdot )\,\, \text {(see [18], [4])}. \end{aligned}$$
(5.7)

Similarly, using this time \(\lambda _-(\cdot )\) we obtain that

$$\begin{aligned} v_*\, \text {is a local}\, W^{1,p}(\Omega )-\text {minimizer of}\, \lambda (\cdot ). \end{aligned}$$
(5.8)

We may assume that \(\lambda (v_*)\le \lambda (u_*)\), the analysis is similar if the opposite inequality holds, using (5.8) instead of (5.7). From (5.1) and (5.3) we see that we may assume that \(K_\lambda \) is finite (otherwise, we already have a whole sequence of distinct smooth nodal solutions in \([v_*,u_*]\)).

Then from (5.7) and using Theorem 5.7.6, p. 449, of Papageorgiou-Rădulescu-Repovš [21], we can find \(\rho \in (0,1)\) small such that

$$\begin{aligned} \lambda (v_*)\le \lambda (u_*)<\inf \left[ \lambda (u): \Vert u-u_*\Vert =\rho \right] =m_\rho . \end{aligned}$$
(5.9)

Since \(\lambda (\cdot )\) is coercive (see (5.1)), it satisfies the C-condition. This fact and (5.9), permit the use of the mountain pass theorem. So, we can find \(y_0\in W^{1,p}(\Omega )\) such that

$$\begin{aligned} y_0\in K_\lambda \subseteq [v_*, u_*]\cap C^1({\overline{\Omega }})\;\; \text {(see}\, (5.3)),\quad m_\rho \le \lambda (y_0)\;\; \text {(see}\, (5.9)). \end{aligned}$$
(5.10)

Evidently \(y_0\notin \{v_*, u_*\}\) (see (5.9), (5.10)). Also from Theorem 6.5.8, p. 527, of Papageorgiou-Rădulescu-Repovš [21], we have

$$\begin{aligned} C_1(\lambda ,y_0)\ne 0. \end{aligned}$$
(5.11)

On the other hand, from hypothesis \(\mathrm{H}_1\)(iv) and Proposition 3.7 of Papageorgiou-Rădulescu [17], we have that

$$\begin{aligned} C_k(\lambda ,0)=0\;\; \text {for all}\, k\in {\mathbb {N}}_0. \end{aligned}$$
(5.12)

Comparing (5.11) and (5.12), we see that \(y_0\ne 0\) and so \(y_0\in C^1({\overline{\Omega }})\) is a nodal solution of (1.1) and \(v_*\le y_0\le u_*\). \(\square \)

So, summarizing the situation for the resonant case, we can state the following multiplicity theorem for problem (1.1).

Theorem 5.2

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) hold, then problem (1.1) has at least five nontrivial solutions \(u_0,{\widehat{u}}\in \mathrm{int}\, C_+\), \(u_0\le {\widehat{u}}\),\(u_0\ne {\widehat{u}}\), \( v_0,{\widehat{v}}\in - \mathrm{int}\, C_+\), \({\widehat{v}}\le v_0\), \(v_0\ne {\widehat{v}}\), \(y_0\in C^1({\overline{\Omega }})\) nodal, \(v_0\le y_0\le u_0\).

6 Superlinear problem

In this section we examine what happens when the reaction \(f(z,\cdot )\) is \((p-1)\)-superlinear as \(x\rightarrow \pm \infty \). The precise hypotheses on the reaction f(z, x) are the following:

  • \({\mathrm{H}}_1'\): \(f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}\) is a Carathéodory function such that \(f(z,0)=0\) for a.a. \(z\in \Omega \) and

    • (i) \(|f(z,x)|\le a(z)[1+|x|^{r-1}]\) for a.a. \(z\in \Omega \), all \(x\in {\mathbb {R}}\), with \(a\in L^\infty (\Omega )\), \(p<r<p^*\);

    • (ii) \(\displaystyle \lim _{x\rightarrow \pm \infty }\frac{F(z,x)}{|x|^p}=+\infty \) uniformly for a.a. \(z\in \Omega \);

    • (iii) there exists \(\tau \in \left( \max \left\{ 1,\frac{N}{p}\right\} (r-p), p^*\right) \), \(\tau >q\), such that

      $$\begin{aligned} 0<{\widehat{\gamma }}_0\le \liminf _{x\rightarrow \pm \infty }\frac{f(z,x)x-pF(z,x)}{|x|^\tau } \quad \text {uniformly for a.a.}\, z\in \Omega ; \end{aligned}$$

    • (iv) there exist \(\mu \in (1,q)\) and \(\delta >0\) such that

      $$\begin{aligned} c_0 |x|^\mu \le f(z,x)x\le \mu F(z,x)\quad \text {for a.a.}\, z\in \Omega ,\, \text {all}\, |x|\le \delta ; \end{aligned}$$

    • (v) there exist \(\vartheta _-<0<\vartheta _+\) such that for a.a. \(z\in \Omega \) we have

      $$\begin{aligned}f(z,\vartheta _+)-\xi (z)\vartheta _+^{p-1}\le -{\widehat{c}}_+<0<{\widehat{c}}_-\le f(z,\vartheta _-)+\xi (z)|\vartheta _-|^{p-1};\end{aligned}$$

    • (vi) for every \(\rho >0\), there exists \({\widehat{\xi }}_\rho >0\) such that for a.a. \(z\in \Omega \), the function \(x\mapsto f(z,x)+{\widehat{\xi }}_\rho |x|^{p-2}x\) is nondecreasing on \([-\rho ,\rho ]\).

Remarks

So now compared with hypotheses \(\mathrm{H}_1\), the conditions determining the behavior of \(f(z,\cdot )\) near zero remain the same (see hypotheses \(\mathrm{H}_1'\)(iv), (v), (vi)) and change the asymptotic conditions as \(x\rightarrow \pm \infty \) (see hypotheses \(\mathrm{H}_1'\)(ii), (iii)). Hypotheses \(\mathrm{H}_1'\)(ii), (iii) imply that for a.a. \(z\in \Omega \), \(f(z,\cdot )\) is \((p-1)-\)superlinear, but need not satisfy the usual in superlinear problems Ambrosetti-Rabinowitz condition (the AR-condition for short). Our framework incorporates also superlinear nonlinearities with “slower” growth as \(x\rightarrow \pm \infty \). For example, if \(\xi \equiv 0\) (no potential term), then the function

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} |x|^{\mu -2}x-2|x|^{\vartheta -2}x &{} \text {if}\, |x|\le 1\\ |x|^{p-2}x[\ln |x|-1] &{} \text {if}\,1<|x| \end{array}\right. } \end{aligned}$$

wth \(\mu<q<p\), \(\vartheta >\mu \), satisfies hypotheses \(\mathrm{H}_1'\) but fails to satisfy the AR-condition.

We argue as in the resonant case. In this case, Proposition 3.2 (the C-condition for the functionals \({\widehat{\varphi }}_+\), \({\widehat{\varphi }}_-\)), is proved as in the Claim in the proof of Proposition 2 in Papageorgiou-Scapellato [24]. Moreover, in this case Proposition 3.3, is an immediate consequence of hypothesis \(\mathrm{H}_1'\)(ii). Since the conditions near zero are the same, the rest of the results (Proposition 3.4 and those in Sect. 4), remain valid and so finally we can state the following multiplicity theorem for the superlinear problem.

Theorem 6.1

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1'\) hold, then problem (1.1) has at least five nontrivial solutions \(u_0,{\widehat{u}}\in \mathrm{int}\, C_+\), \(u_0\le {\widehat{u}}\), \(u_0\ne {\widehat{u}}\), \(v_0,{\widehat{v}}\in - \mathrm{int}\, C_+\), \({\widehat{v}}\le v_0\), \(v_0\ne {\widehat{v}}\), \(y_0\in C^1({\overline{\Omega }})\) nodal, \(v_0\le y_0\le u_0\).

Remark

We stress that in both Theorems 5.2 and 6.1 the solutions are ordered.

7 The (p, 2)-equation

In this section we show that when \(q=2\), we can slightly improve the two multiplicity theorems (Theorem 5.2 and Theorem 6.1). Our work in this section is also related to the recent paper of Vetro [33] on semilinear equations driven by the Robin Laplacian plus an indefinite potential. The author proves a multiplicity result using the reduction technique of Amann [1].

So, now the problem under consideration is the following

$$\begin{aligned} {\left\{ \begin{array}{ll} -\Delta _p u(z)-\Delta u(z)+\xi (z)|u(z)|^{p-2}u(z)=f(z,u(z)) &{} \text{ in } \Omega \\ \displaystyle \frac{\partial u}{\partial n_{p2}}+\beta (z)|u|^{p-2}u=0 &{}\text{ on } \partial \Omega \end{array}\right. }, \end{aligned}$$
(7.1)

with \(2<p\).

Let \(a:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^N\) be defined by

$$\begin{aligned}a(y)=|y|^{p-2}y+y.\end{aligned}$$

Evidently

$$\begin{aligned}\mathrm{div}\, a(Du)=\Delta _p u+\Delta u\quad \text {for all}\, u\in W^{1,p}(\Omega ).\end{aligned}$$

Note that \(a\in C^1({\mathbb {R}}^N,{\mathbb {R}}^N)\) and we have

$$\begin{aligned} \nabla a(y)=|y|^{p-2}\left[ \mathrm {id}+(p-2)\frac{y \otimes y}{|y|^2}\right] +\mathrm {id}\quad \text {for all}\, y\in {\mathbb {R}}^N. \end{aligned}$$
(7.2)

We have

$$\begin{aligned}(\nabla a(y)\vartheta , \vartheta )_{{\mathbb {R}}^N}\ge |\vartheta |^2\quad \text {for all}\, y,\vartheta \in {\mathbb {R}}^N.\end{aligned}$$

So, invoking the tangency principle of Pucci-Serrin [30] (Theorem 2.5.2, p. 35) and using Proposition 2.10 of [20], we obtain

$$\begin{aligned} u_0(z)< {\widehat{u}}(z)\quad \text {for all}\, z\in {\overline{\Omega }}. \end{aligned}$$

In a similar fashion we also have

$$\begin{aligned}&{\widehat{v}}(z)<v_0(z)\quad \text {for all}\, z\in {\overline{\Omega }}, \\&\quad v_0(z)<y_0(z)<u_0(z) \quad \text {for all}\, z\in {\overline{\Omega }}. \end{aligned}$$

Therefore for problem (7.1) we can have the following slightly improved version of Theorems 5.2 and 6.1.

Theorem 7.1

If hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1\) (with \(q=2\)) or hypotheses \(\mathrm{H}_0\), \(\mathrm{H}_1'\) (with \(q=2\)) hold, then problem (7.1) has at least five nontrivial solutions \( u_0,{\widehat{u}}\in \mathrm{int}\, C_+\), \({\widehat{u}}-u_0\in \mathrm{int}\,C_+\), \( v_0,{\widehat{v}}\in - \mathrm{int}\, C_+\), \(v_0-{\widehat{v}}\in \mathrm{int}\, C_+\), \(y_0\in C^1({\overline{\Omega }})\) nodal, \(y_0\in \mathrm{int}_{C^1({\overline{\Omega }})}[v_0,u_0]\).