Skip to main content
SpringerLink
Log in

Fully dispersive Boussinesq models with uneven bathymetry

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

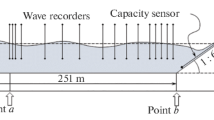
Three weakly nonlinear but fully dispersive Whitham–Boussinesq systems for uneven bathymetry are studied. The derivation and discretization of one system is presented. The numerical solutions of all three are compared with wave gauge measurements from a series of laboratory experiments conducted by Dingemans (Comparison of computations with Boussinesq-like models and laboratory measurements. Delft Hydraulics memo H168412, 1994). The results show that although the models are mathematically similar, their accuracy varies dramatically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Dingemans M (1994) Comparison of computations with Boussinesq-like models and laboratory measurements. Delft Hydraulics memo H168412

  2. Madsen P, Fuhrman D, Sørensen O (1991) A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast Eng 15:371–388

    Article  Google Scholar 

  3. Witting J (1984) A unified model for the evolution of nonlinear water waves. J Comput Phys 56:203–236

    Article  Google Scholar 

  4. Madsen P, Sørensen O (1992) A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast Eng 18:183–204

    Article  Google Scholar 

  5. Nwogu O (1993) Alternative form of Boussinesq equations for nearshore wave propagation. J Waterway Port Coast Ocean Eng 119:618–638

    Article  Google Scholar 

  6. Brocchini M (2013) A reasoned overview on Boussinesq-type models: the interplay between physics. Proc R Soc Lond Ser A 469:1–27

    MathSciNet  MATH  Google Scholar 

  7. Madsen P, Fuhrman D, Wang B (2006) A Boussinesq-type method for fully nonlinear waves interacting with rapidly varying bathymetry. Coast Eng 53:487–504

    Article  Google Scholar 

  8. Roeber V, Cheung K, Kobayashi M (2010) Shock-capturing Boussinesq-type model for nearshore wave processes. Coast Eng 57:407–433

    Article  Google Scholar 

  9. Whitham G (1974) Linear and nonlinear waves. Wiley, New York

    MATH  Google Scholar 

  10. Moldabayev D, Kalisch H, Dutykh D (2015) The Whitham equation as a model for surface water waves. Physica D 309:99–107

    Article  MathSciNet  Google Scholar 

  11. Carter J (2018) Bidirectional Whitham equations as models of waves on shallow water. Wave Motion 82:51–61

    Article  MathSciNet  Google Scholar 

  12. Aceves-Sánchez P, Minzoni A, Panayotaros P (2013) Numerical study of a nonlocal model for water-waves with variable depth. Wave Motion 50:80–93

    Article  MathSciNet  Google Scholar 

  13. Dinvay E (2019) On well-posedness of a dispersive system of the Whitham–Boussinesq type. Appl Math Lett 88:13–20

    Article  MathSciNet  Google Scholar 

  14. Hur V, Pandey A (2019) Modulational instability in a full-dispersion shallow water model. Stud Appl Math 142:3–47

    Article  MathSciNet  Google Scholar 

  15. Craig W, Guyenne P, Nicholls D, Sulem C (2005) Hamiltonian long-wave expansions for water waves over a rough bottom. Proc R Soc Lond Ser A 461:839–873

    MathSciNet  MATH  Google Scholar 

  16. Pei L, Wang Y (2019) A note on well-posedness of bidirectional Whitham equation. Appl Math Lett 98:215–223

    Article  MathSciNet  Google Scholar 

  17. Claassen K, Johnson M (2018) Numerical bifurcation and spectral stability of wavetrains in bidirectional Whitham models. Stud Appl Math 141:205–246

    Article  MathSciNet  Google Scholar 

  18. Dinvay E, Dutykh D, Kalisch H (2019) A comparative study of bi-directional Whitham systems. Appl Numer Math 141:248–262

    Article  MathSciNet  Google Scholar 

  19. Lannes D (2013) The water waves problem. American Mathematical Society, Providence

    Book  Google Scholar 

  20. Dinvay E, Selberg S, Tesfahun A (2020) Well-posedness for a dispersive system of the Whitham–Boussinesq type. SIAM J Math Anal 52:2353–2382

    Article  MathSciNet  Google Scholar 

  21. Dinvay E, Nilsson D (2021) Solitary wave solutions of a Whitham–Boussinesq system. Nonlinear Anal Real World Appl 60:103280

  22. Craig W, Groves M (1994) Hamiltonian long-wave approximations to the water-wave problem. Wave Motion 19:367–389

    Article  MathSciNet  Google Scholar 

  23. Alazard T, Burq N, Zuily C (2011) On the water-wave equations with surface tension. Duke Math J 158:413–499

    Article  MathSciNet  Google Scholar 

  24. Zakharov V (1998) Weakly nonlinear waves on the surface of an ideal finite depth fluid. Am Math Soc Transl 182:167–197

    MathSciNet  MATH  Google Scholar 

  25. Papoutsellis CE (2015) Numerical simulation of non-linear water waves over variable bathymetry. Procedia Comput Sci 66:174–183

    Article  Google Scholar 

  26. Andrade D, Nachbin A (2018) A three-dimensional Dirichlet-to-Neumann operator for water waves over topography. J Fluid Mech 845:321–345

    Article  MathSciNet  Google Scholar 

  27. Gobbi M, Kirby J (1999) Wave evolution over submerged sills: tests of a high-order Boussinesq model. Coast Eng 37:57–96

    Article  Google Scholar 

  28. Chazel F, Lannes D, Marche F (2011) Numerical simulations of strongly nonlinear and dispersive waves using a Green–Naghdi model. J Sci Comput 48:105–116

    Article  MathSciNet  Google Scholar 

  29. Aston P (1991) Local and global aspects of the (1, \(n\)) mode interaction for capillary-gravity waves. Physica D 52:415–428

    Article  MathSciNet  Google Scholar 

  30. Remonato F, Kalisch H (2017) Numerical bifurcation for the capillary Whitham equation. Physica D 343:51–62

    Article  MathSciNet  Google Scholar 

  31. Madsen P, Fuhrman D (2020) Trough instabilities in Boussinesq formulations for water waves. J Fluid Mech 889:A38

    Article  MathSciNet  Google Scholar 

  32. Lannes D, Bonneton P (2009) Derivation of asymptotic two-dimensional time-dependent equations for surface water wave propagation. Phys Fluids 21:016601

    Article  Google Scholar 

  33. Wei G, Kirby J, Grilli S, Subramanya R (1995) A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J Fluid Mech 294:71–92

    Article  MathSciNet  Google Scholar 

  34. Bacigaluppi P, Ricchiuto M, Bonneton P (2020) Implementation and evaluation of breaking detection criteria for a hybrid Boussinesq model. Water Waves 2:207–241

    Article  MathSciNet  Google Scholar 

  35. Bjørkavåg M, Kalisch H (2011) Wave breaking in Boussinesq models for undular bores. Phys Lett A 375:1570–1578

    Article  Google Scholar 

  36. Kazolea M, Delis A, Synolakis C (2014) Numerical treatment of wave breaking on unstructured finite volume approximations for extended Boussinesq-type equations. J Comput Phys 271:281–305

    Article  MathSciNet  Google Scholar 

  37. Tonelli M, Petti M (2011) Simulation of wave breaking over complex bathymetries by a Boussinesq model. J Hydraul Res 49:473–486

    Article  Google Scholar 

  38. Tissier M, Bonneton P, Marche F, Chazel F, Lannes D (2012) A new approach to handle wave breaking in fully non-linear Boussinesq models. Coast Eng 67:54–66

    Article  Google Scholar 

Download references

Acknowledgements

This research was supported by the U.S. National Science Foundation under grant number DMS-1716120 (JDC), the Research Council of Norway under grant no. 239033/F20 (ED & HK), and the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 763959 (HK). Additionally, a Fulbright Core Scholar Award allowed JDC to spend a semester visiting HK and ED at the University of Bergen.

Author information

Authors and Affiliations

  1. Mathematics Department, Seattle University, Seattle, USA

    John D. Carter

  2. Inria Rennes, Bretagne Atlantique Campus, universitaire de Beaulieu Avenue du, Général Leclerc, 35042 Rennes Cedex, France

    Evgueni Dinvay

  3. Department of Mathematics, University of Bergen, Bergen, Norway

    Henrik Kalisch

Authors
  1. John D. Carter
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Evgueni Dinvay
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Henrik Kalisch
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to John D. Carter.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Carter, J.D., Dinvay, E. & Kalisch, H. Fully dispersive Boussinesq models with uneven bathymetry. J Eng Math 127, 10 (2021). https://doi.org/10.1007/s10665-021-10099-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-021-10099-2

Keywords

Search

Navigation