A harmonically weighted filter for cyclical long memory processes

Abstract

The estimation of the long memory parameter d is a widely discussed issue in the literature. The harmonically weighted (HW) process was recently introduced for long memory time series with an unbounded spectral density at the origin. In contrast to the most famous fractionally integrated process, the HW approach does not require the estimation of the d parameter, but it may be just as able to capture long memory as the fractionally integrated model, if the sample size is not too large. Our contribution is a generalization of the HW model, denominated the Generalized harmonically weighted (GHW) process, which allows for an unbounded spectral density at $k \ge 1$ frequencies away from the origin. The convergence in probability of the Whittle estimator is provided for the GHW process, along with a discussion on simulation methods. Fit and forecast performances are evaluated via an empirical application on paleoclimatic data. Our main conclusion is that the above generalization is able to model long memory, as well as its classical competitor, the fractionally differenced Gegenbauer process, does. In addition, the GHW process does not require the estimation of the memory parameter, simplifying the issue of how to disentangle long memory from a (moderately persistent) short memory component. This leads to a clear advantage of our formulation over the fractional long memory approach.

1 Introduction

Many environmental and financial time series show dependence between distant observations, denoting a phenomenon that is known in the literature as long memory. Adopting a common definition (see Beran (1994) and Hassler (2019)), a stochastic process exhibits long memory if the autocovariance function is not absolutely summable or, equivalently, if the spectral density is unbounded. When the singularity in the spectrum is located at a frequency away from the origin, then the process exhibits cyclical long memory, denoting some periodicity.

In the last decades, cyclical long memory processes have been proposed in the literature to model time series characterized by a strong quasi-periodic behaviour. In particular, the well-known Gegenbauer autoregressive moving average (GARMA) process was introduced in the pioneer work of Hosking (1981) and then formalized in Andel (1986) and Gray et al. (1989). It generalizes the fractionally integrated ARMA (FARIMA) model by Hosking (1981) allowing for an unbounded spectral density also at a frequency away from zero. Woodward et al. (1998) extended this result to the k-factor GARMA process, where the spectral density is unbounded at $k \ge 1$ frequencies. The following equation describes the latter:

$$\begin{aligned} \prod _{j=1}^{k}(1-2\cos (\lambda _{g,j})L+L^2)^{d_j}(y_t-\mu )=x_t \end{aligned}$$

(1)

where k is a positive integer and $d_j \in (0,1)$, while $x_t$ is assumed to be an ARMA(p, q) process, such that $x_t=\frac{\psi (L)}{\phi (L)} \varepsilon _t =c(L)\varepsilon _t$ with $\sum _{j=0}^\infty | c_j|<\infty$ and $\varepsilon _t$ is a white noise (WN) sequence. The process in (1) displays cyclical long memory, and the contribution of each pole to the periodicity of the process is controlled by the $d_j$ parameters. According to the literature (see Woodward et al. (1998) and also Dissanayake et al. (2018) for a review), the k-factor GARMA process is covariance stationary and exhibits long memory if $d_j \in (0,\frac{1}{2})$ and $|\cos (\lambda _{g,j})|<1$ for $j =1, \cdots , k$ (or if $d_j \in (0,\frac{1}{4})$ whenever $|\cos (\lambda _{g,j})|=1$).

The estimation of the memory parameter d is a widely discussed issue in the literature, and plenty of methods were developed to address it (see Hassler (2019) for a review). For instance, in the case of a singularity in the spectrum at the zero frequency, Geweke and Porter-Hudak (1983) and Robinson (1995b) proposed log-periodogram regression methods. On the other hand, a full Whittle likelihood approach (c.f. Whittle (1953)) can be found in Beran (1994), while a semiparametric local Whittle method has been formalized in Robinson (1995a). Pseudo-Whittle estimates have been proposed in Velasco and Robinson (2000) for the no-stationary case. Regarding cyclical long memory processes, Chung (1996a, b) proposed the conditional sum of squares method for the parameters estimation of the GARMA model, while Arteche and Robinson (2000) generalized the local Whittle and log-periodogram methods allowing for a singularity in the spectrum away from the origin. A full Whittle likelihood approach is discussed in Ferrara and Guegan (1999). See also Palma and Chan (2005) and Reisen et al. (2006) for further study.

In practice, when it comes to estimating d, the issue is to separate long memory from a (moderately persistent) short memory component. This is complicated by the difficulty of estimating d correctly. For instance, it often happened that different researchers estimated different values of the memory parameter analysing the same data set. Recently, Hassler and Hosseinkouchack (2020) introduced the harmonically weighted (HW) process that theoretically displays less persistence and weaker memory than the fractionally integrated model of order d. Although the two processes have different qualities asymptotically, in terms of persistence and memory, they are hard to distinguish given realistic sample sizes. The HW process is characterized by an unbounded spectral density at the origin and does not require the estimation of the memory parameter, even though the HW approach may be just as able to capture long memory as the fractionally integrated model, if the sample size is not too large. In this case, the long memory could be captured just by filtering the data.

Our purpose is to extend the contribution of Hassler and Hosseinkouchack (2020) considering also cyclical long memory time series characterized by a strong quasi-periodic behavior. The novel approach, denominated the generalized harmonically weighted (GHW) process, generalizes the HW filter allowing for an unbounded spectral density at $k \ge 1$ frequencies away from zero. We provide analytical expressions for the spectrum and the autocovariance function of the GHW process, along with simulation and estimation methodologies and the convergence in probability of the Whittle estimator. Finally, an empirical application on paleoclimatic temperature reconstructions is discussed, comparing the results performed both via the GHW and the k-factor GARMA models. Our main conclusion is that the GHW model is able to capture the long memory, as well as the standard GARMA does. In addition, the GHW process does not require the estimation of the d parameter, simplifying the issue of how to disentangle long memory from a short memory component. This leads to a clear advantage of our formulation over the GARMA approach; for instance, the estimation by exact maximum likelihood can be easily implemented if the frequency parameters are supposed to be known.

We organize the rest of the paper as follows. In sect. 2, we recall the main characteristics of the HW process. In sect. 3, we introduce the GHW process, providing analytical formulas for the autocovariance function and the spectral density. Multiple periodicity and simulation methods are also considered in this section. Section 4 discusses estimation methodologies, providing the convergence in probability of the Whittle estimator. In sect. 5, an empirical application on the EPICA Dome C series of paleoclimatic temperature reconstructions is examined. The last section concludes the paper. Mathematical proofs are relegated to the appendix.

2 Review of the harmonically weighted process

Let us start with a definition of long memory that is very common in the literature (see for istance Beran (1994), Palma (2006) and, more recently, Hassler (2019)).

Definition 1

A stationary process $\lbrace y_t \rbrace$ is said to display long memory if its autocovariance function is not absolutely summable or, equivalently, if its spectral density is unbounded at one or more frequencies. Otherwise, it is said to have short memory.

Definition 1 meets the FARIMA and GARMA processes introduced by Hosking (1981). Both of them depend on a fractional parameter d and can capture the long memory from the data via the estimation of a fractional filter, depending on d. Hassler and Hosseinkouchack (2020) introduced an alternative way to model long memory in time series, which does not require the estimation of d. They defined the harmonically weighted filter h(L) by the formal expansion of $\ln (1-L)$:

$$\begin{aligned} h(L)=-\frac{\ln (1-L)}{L}=\sum _{j=0}^{\infty } \frac{L^j}{j+1} \end{aligned}$$

(2)

Basically, the filter inputs result to be harmonically weighted. Let us assume $x_t=\sum _{j=0}^{\infty } c_j \varepsilon _{t-j}$ as a general short memory process with $\varepsilon _{t} \sim WN(0,\sigma ^2)$. This assumption meets all stationary and invertible ARMA processes, since $c_j$ is geometrically bounded in the ARMA case.

The harmonically weighted (HW) process is described by:

$$\begin{aligned} y_t=\mu +h(L)x_t=\mu +\sum _{j=0}^{\infty }\frac{1}{j+1}x_{t-j} \end{aligned}$$

where $y_t$ is a second-order stationary harmonically weighted process with mean $\mu$ and moving average representation:

$$\begin{aligned} h(L)c(L)\varepsilon _t=\sum _{j=0}^{\infty }b_j\varepsilon _{t-j}=b(L)\varepsilon _t \end{aligned}$$

with

$$\begin{aligned} b_j=\sum _{k=0}^{j}\frac{c_k}{j+1-k} \end{aligned}$$

The autoregressive representation is given by:

$$\begin{aligned} c(L)^{-1}g(L)(y_t-\mu )=c(L)^{-1} \left( 1-\sum _{j=1}^{\infty }g_jL^j \right) (y_t-\mu )= a(L)(y_t-\mu ) \end{aligned}$$

with

$$\begin{aligned} g_j=\frac{1}{j+1}-\sum _{i=1}^{j-1}\frac{g_i}{j-i+1}\>\>\>;\>\>\> j \ge 1 \>\>\>;\>\>\> g_0=1 \end{aligned}$$

where $g(L)=h(L)^{-1}$ is defined as the harmonic inverse transformation (HIT) function. For $\lambda >0$, the spectral density is given by:

$$\begin{aligned} f(\lambda )=\left[ \ln ^2 \left( 2 \sin \frac{\lambda }{2} \right) + \left( \frac{\pi -\lambda }{2} \right) ^2 \right] f_x(\lambda ) \end{aligned}$$

where

$$\begin{aligned} f(\lambda ) \sim \ln ^2(\lambda )f_x(0)\>\>\> \text{ as }\>\>\> \lambda \rightarrow 0 \end{aligned}$$

As $k \rightarrow \infty$, the autocovariance function behaves like:

$$\begin{aligned} \gamma (k) \sim 2\pi f_x(0) \frac{\ln k}{k} \end{aligned}$$

The above process displays standard long memory with an unbounded spectral density at the zero frequency and not absolutely summable autocovariance function, which decays to zero slowly (see Hassler and Hosseinkouchack (2020) for further details).

3 The generalized harmonically weighted process

In this section, we introduce a novel process that generalizes the HW filter to admit cyclical long memory. In substance, it consists in allowing for an unbounded spectral density also at a frequency away from the origin. Let $\lambda _g \in [0, \pi ] \backslash \lbrace \frac{\pi }{2} , \frac{\pi }{3} \rbrace$ be the Gegenbauer frequency (see Gray et al. (1989)), the following filter generalizes the Hassler and Hosseinkouchack (2020) filter allowing for a singularity in the spectrum away from zero:

$$\begin{aligned} \begin{array}{cccc} h(L) &{}= &{} -\frac{\ln (1-2 \eta L+L^2)}{2 L} &{} \\ &{} &{} &{} \\ &{} = &{} {\mathop {\sum }\limits _{j=0}^{\infty }} \frac{\cos (\lambda _g(j+1))}{j+1} L^j &{} \end{array} \end{aligned}$$

(3)

where $\eta = \cos (\lambda _g)$. Let us observe that if $\lambda _g=0$ (which implies $\eta =1$) the expression in (3) is reduced to the HW filter in (2).

Proposition 1

Let $x_t$ be an ARMA(p, q) process such that $x_t = \frac{\psi (L)}{\phi (L)}\varepsilon _t = c(L) \varepsilon _t$ with $\sum _{j=0}^{\infty }|c_j|<\infty$, $\phi _0=\psi _0=1$ and $\varepsilon _t \sim WN(0, \sigma ^2)$. Let $\eta =\cos (\lambda _g)$ with $\lambda _g \in \left[ 0,\pi \right] \backslash \lbrace \frac{\pi }{2}, \frac{\pi }{3} \rbrace$, then the process:

$$\begin{aligned} \begin{array}{cccccc} y_t &{}=&{} \mu +h(L)x_t &{}= &{} \mu -{\frac{\ln (1-2 \eta L+L^2)}{2 L} x_t }&{} \\ &{} &{} &{} &{} &{} \\ &{} &{} &{}=&{} \mu + {\mathop {\sum }\limits _{j=0}^{\infty }}\frac{\cos (\lambda _g(j+1))}{j+1}x_{t-j} &{} \end{array} \end{aligned}$$

is a second-order stationary generalized harmonically weighted (GHW) process with mean $\mu$ and moving average representation:

$$\begin{aligned} h(L)c(L)\varepsilon _t=\sum _{j=0}^{\infty }b_j\varepsilon _{t-j} =b(L)\varepsilon _t \end{aligned}$$

with

$$\begin{aligned} b_j=\sum _{k=0}^{j}c_{j-k}\frac{\cos (\lambda _g(k+1))}{(k+1)} \end{aligned}$$

The autoregressive representation is given by:

$$\begin{aligned} c(L)^{-1}g(L)(y_t-\mu )=c(L)^{-1}\sum _{j=0}^{\infty }g_j(y_{t-j}-\mu )=a(L)(y_t-\mu ) \end{aligned}$$

with

$$\begin{aligned} g_j=-\sum _{k=1}^{j}\frac{\cos (\lambda _g(k+1))}{\eta (k+1)}g_{j-k} \>\>\>\> \text{ and } \>\>\>\> g_0=\eta ^{-1} \end{aligned}$$

where $g(z)=h(z)^{-1}$ is defined as the generalized harmonic inverse transform (GHIT) function.

The spectral density of $\lbrace y_t \rbrace$ is:

$$\begin{aligned} f(\lambda )= \frac{1}{4} \left( \ln ^2(2|\cos (\lambda )-\eta |) +(\alpha \pi -\lambda )^2 \right) f_x(\lambda ) \>\>\> with \>\>\> \lambda \in [-\pi ,\pi ] \backslash \lbrace \lambda _{g} \rbrace \end{aligned}$$

where $f_x(\lambda )$ is the spectral density of the short memory component $x_t$ and

$$\begin{aligned} \alpha = {\left\{ \begin{array}{ll} \> 1, &{} if\ \lambda>\lambda _g\\ \> 0, &{} if\ -\lambda _g<\lambda< \lambda _g \\ -1, &{} if\ \lambda < -\lambda _g \end{array}\right. } \end{aligned}$$

As $\lambda \rightarrow \lambda _g$, the spectral density behaves like:

$$\begin{aligned} f(\lambda ) \sim {\left\{ \begin{array}{ll} \frac{1}{4} \ln ^2|\lambda -\lambda _g| f_x(\lambda _g), &{} if\ \lambda _g \notin \lbrace 0, \pi \rbrace \\ \\ \ln ^2(\lambda ) f_x(0), &{} if\ \lambda _g = 0 \\ \\ \ln ^2(\lambda -\pi ) f_x(\pi ), &{} if\ \lambda _g = \pi \end{array}\right. } \end{aligned}$$

The autocovariance function admits the Wold representation:

$$\begin{aligned} \gamma (k) = \sum _{j=0}^{\infty }b_jb_{j+k}\sigma ^2 \>\>\> with \>\>\> k \in \mathbb {Z} \end{aligned}$$

Proof

The proof of Proposition 1 is given in the Appendix. $\square$

It is immediately clear that the spectrum of the process in Proposition 1 is unbounded at $\lambda _g$. According to Definition 1, both the HW and the GHW processes exhibit long memory, but let us say that the latter exhibits cyclical long memory if $\lambda _g>0$. This implies a singularity in the spectrum away from the origin, denoting some periodicity in the process.

We also point out that the GHIT function is not defined if $\lambda _g=\frac{\pi }{2}$. Moreover, the infinite sum of the $g_j$ coefficients converges only if $\lambda _g \ne \frac{\pi }{3}$, because of:

$$\begin{aligned} g(1)= -\frac{2}{\ln (2(1-\cos (\lambda _g)))} \end{aligned}$$

Therefore, if we have a time series that shows a fundamental frequency or a harmonic close to $\frac{\pi }{2}$ or to $\frac{\pi }{3}$, then the $\lbrace g_j \rbrace$ sequence diverges as j increases, prejudicing a good filtering. In this case, we cannot compute the short memory component by filtering the data.

3.1 Multiple periodicity with the GHW process

In this section, a multiplicative model that generalizes the process in Proposition 1 is introduced. It allows for an unbounded spectral density at $k \ge 1$ frequencies, and its main properties are summarized by the following proposition.

Proposition 2

Let $x_t$ be an $\hbox {ARMA}(p,q)$ process such that $x_t = \frac{\psi (L)}{\phi (L)}\varepsilon _t = c(L) \varepsilon _t$ with $\sum _{j=0}^{\infty }|c_j|<\infty$, $\phi _0=\psi _0=1$ and $\varepsilon _t \sim WN(0, \sigma ^2)$. Consider the set of frequencies $\lbrace \lambda _{g,j}\rbrace _{j=1}^k \in [0,\pi ]\backslash \lbrace \frac{\pi }{2}, \frac{\pi }{3} \rbrace$, then the process:

$$\begin{aligned} y_t=\mu +\left[ \prod _{j=1}^{k} h_j(L) \right] x_t \end{aligned}$$

with

$$\begin{aligned} h_j(L)= \sum _{i=0}^{\infty }\frac{\cos (\lambda _{g,j}(i+1))}{(i+1)}L^i \end{aligned}$$

is a second-order stationary k-factor generalized harmonically weighted (k-GHW) process with mean $\mu$ and spectral density :

$$\begin{aligned} f(\lambda )= \prod _{j=1}^{k} \left( \frac{1}{4} \left( \ln ^2(2|\cos (\lambda )-\cos (\lambda _{g,j})|) +(\alpha _j \pi -\lambda )^2 \right) \right) f_x(\lambda ) \>\>\>\>\> \>\> \>\>\> \lambda \in [-\pi ,\pi ] \backslash \lbrace \lambda _{g,j} \rbrace _{j=1}^{k} \end{aligned}$$

where $f_x(\lambda )$ is the spectral density of the process $x_t$ and

$$\begin{aligned} \alpha _j= {\left\{ \begin{array}{ll} \> 1, &{} if\ \lambda>\lambda _{g,j}\\ \> 0, &{} if\ -\lambda _{g,j}<\lambda< \lambda _{g,j} \\ -1, &{} if\ \lambda < -\lambda _{g,j} \end{array}\right. } \end{aligned}$$

The autocovariance function admits the Wold representation:

$$\begin{aligned} \gamma (h) = \sum _{j=0}^{\infty }b_j b_{j+h}\sigma ^2 \>\>\> with \>\>\> h \in \mathbb {Z} \end{aligned}$$

where the polynomial b(L) is given by the convolution of c(L) and $\prod _{j=1}^{k} h_j(L)$ such that:

$$\begin{aligned} c(L)\prod _{j=1}^{k} h_j(L)=b(L) \end{aligned}.$$

Proof

It follows directly from the proof of Proposition 1. $\square$

Basically, we generalized the GHW process similarly as Woodward et al. (1998) generalized the Gegenbauer process via the k-factor GARMA model. The process in Proposition 2 exhibits cyclical long memory with an unbounded spectral density in the set of frequencies $\lbrace \lambda _{g,j}\rbrace _{j=1}^k$. We collect these latter into a vector defined as the frequency parameters vector: $\lambda _g = [\lambda _{g,1} , \cdots , \lambda _{g,k} ]^{\top }$.

The determination of the length k of the frequency parameters vector is an issue that requires further discussion. In the case of a k-factor GARMA process, Leschinski and Sibbertsen (2019) proposed a novel procedure based on sequential tests of the maximum of the periodogram and semiparametric estimators of the model parameters. A similar approach could be implemented also in the k-GHW framework. A preliminary analysis on the residuals periodogram is suggested here as a starting point. If k is chosen too low, then the residuals should display poles in the periodogram. In contrast, if k is chosen too high, the residual process should exhibit antipersistence. At the end, we should try to balance between these two possible scenarios. In sect. 3.2, we will see as the frequency parameters can affect persistence in the k-GHW process.

3.2 Comparison with respect to the GARMA process

Fig. 1

Comparison between the spectra of a fractionally differenced Gegenbauer noise and of a GHW noise with $\lambda _g=0.6$ and $\sigma =1$

Before proceeding further, we need to introduce the concept of “persistence” in time series analysis. According to Hassler (2019), it is related but not equivalent to the concept of “memory” given in Definition 1. Indeed, while the definition of “memory” focuses on the absolute summability of the autocovariance function, the concept of “persistence” considers just its sum.

Definition 2

Let $\lbrace y_t \rbrace$ be a second-order stationary process and let us define $\omega ^2=\sum _{k=-\infty }^{\infty }\gamma (k) = 2 \pi f(0)$ as the long-run variance, where f(0) is the spectral density of $y_t$ evaluated at the zero frequency. Considering $\omega ^2 \ge 0$ (as implied by Theorem 1.5.1 in Brockwell and Davis (1986)), we have that the process $y_t$ is:

• (i) moderately persistent if $\omega ^2<\infty$ ,

• (ii) anti-persistent if $\omega ^2=0$,

• (iii) strongly persistent if $\omega ^2= \infty$.

Now, let us compare the behaviour at the origin between the spectra of a GHW noise (defined by assuming $f_x(\lambda ) = \sigma ^2/2 \pi$ in Proposition 1) and of a fractionally differenced Gegenbauer noise (that is the GARMA process in (1) with $k=1$ and $x_t=\varepsilon _t \sim WN(0,\sigma ^2)$). The spectrum of the fractionally differenced Gegenbauer noise is given by the following equation (see Andel (1986)):

$$\begin{aligned} f(\lambda )=\frac{\sigma ^2}{2 \pi } \left( 4\sin \left( \frac{\lambda -\lambda _g}{2}\right) \sin \left( \frac{\lambda +\lambda _g}{2}\right) \right) ^{-2d} \end{aligned}$$

(4)

The function in (4) is proportional to $\left( 4 \sin ^2(\frac{\lambda _g}{2}) \right) ^{-2d}$ as $\lambda$ approaches to zero. On the other hand, the spectrum of the GHW noise behaves at the origin as a square logarithmic function with $f_{GHWn}(0) \propto \ln ^2(2 \sin (\frac{\lambda _g}{2}))$. In Fig. 1, we compare the two spectra for the true values of $\sigma =1$, $\lambda _g=0.6$ and for different values of the d parameter. According to Definition 2, the GHW noise seems to be the least persistent with respect to the others. For any $d \in (0, 1)$ and unit variance parameter for both processes, we can state that the GHW noise is the least persistent if the following inequality holds:

$$\begin{aligned} \ln ^2 \left( 2 \sin \left( \frac{\lambda _g}{2}\right) \right) < \left( 4 \sin ^2 \left( \frac{\lambda _g}{2}\right) \right) ^{-2d} \end{aligned}$$

(5)

Fig. 2

Considering the inequality in (5), we plot the LHS versus the RHS for different values of d

Obviously, we know that both the left-hand side (LHS) and the right-hand side (RHS) of (5) diverge to $+\infty$ as $\lambda _g \rightarrow 0$, leading to an indeterminate form of the limit ratio. However, applying the Hopital’s rule the RHS dominates the other one as $\lambda _g$ approaches to zero. In Fig. 2, we plot both sides of (5) as a function of $\lambda _g$ for different values of d in the RHS. Observe that the GHW noise is the least persistent for low values of the frequency parameter $\lambda _g$; however, as $\lambda _g$ becomes larger, the RHS and the LHS of (5) seem to be closer. In this case, the GHW and Gegenbauer noise display similar persistence (notice that if $d>0.5$, we refer to the pseudo-spectrum of the fractionally differenced Gegenbauer noise, see Velasco and Robinson (2000) for further details).

In conclusion, similar arguments can be generalized to include also multiple periodicity, pointing out that the persistence of the GHW process is affected by the frequency parameters. This is in contrast to the GARMA model, where the d parameters allow for a better control on the contribution of each pole to the memory and persistence of the process.

3.3 Simulation of the GHW process

A simple way to simulate T realizations from a Gaussian GHW process is to truncate its MA representation according to:

$$\begin{aligned} y_t = \sum _{j=0}^{t}b_j\varepsilon _{t-j} \end{aligned}$$

(6)

for $t=1,\cdots ,T$ and $\varepsilon _{t} \sim N(0,\sigma ^2)$. The $b_j$ coefficients are defined in Proposition 1. Following Hassler and Hosseinkouchack (2020), we can simulate a sample size of length T from a (type I) GHW process generating $5000+T$ realizations from the (type II) GHW process in (6), and then discarding the first 5000 observations. However, this simulation approach may be computationally expensive if the $b_j$ coefficients are given by the convolution of many polynomials.

An alternative way to simulate T realizations from the Gaussian GHW process is to use approximate methods, like for instance, the spectral method described in Dieker and Mandjes (2003). The latter is particularly useful in the GHW case because we have a closed form of the spectral density but not of the autocovariance function. According to the spectral analysis of a stationary discrete-time Gaussian process, see Dieker and Mandjes (2003), we can represent $y_t$ in terms of its spectral density $f(\lambda )$ as:

$$\begin{aligned} y_t = \int _0^\pi \sqrt{2f(\lambda )} \cos (t \lambda ) dB_1(\lambda ) - \int _0^\pi \sqrt{2f(\lambda )} \sin (t \lambda ) dB_2(\lambda ) \end{aligned}$$

(7)

where $B_1(\lambda )$ and $B_2(\lambda )$ are mutually independent Brownian motions.

Notice that the two integrand functions $r_1(\lambda )= \sqrt{2 f(\lambda )} \cos (t \lambda )$ and $r_2(\lambda )= \sqrt{2 f(\lambda )} \sin (t \lambda )$ in (7) are simple functions in the sense that, given a positive integer $l$ and a strictly increasing sequence of real numbers $\lbrace u_j \rbrace _{j=0}^{ l -1}$ with $u_0 = 0$ and $u_ l ` = \pi$, as well as given two bounded sequences of real numbers $\lbrace r_{1,j} \rbrace _{j=0}^{ l -1}$ and $\lbrace r_{2,j} \rbrace _{j=0}^{ l -1}$, we can write $r_1(z) = r_{1,j}$ and $r_2(z) = r_{2,j}$ for $z \in (u_j, u_{j+1} ]$. As a consequence, the stochastic integrals in (7) have the following definitions:

$$\begin{aligned} \begin{array}{lcl} \int _0^\pi r_1(\lambda ) dB_1(\lambda ) &{} := &{} {\sum }_{j=0}^{ l -1} r_{1,j} (B_1(u_{j+1}) - B_1(u_{j})) \\ \\ \int _0^\pi r_2(\lambda ) dB_2(\lambda ) &{} := &{} {\sum }_{j=0}^{ l -1} r_{2,j} (B_2(u_{j+1}) - B_2(u_{j})) \end{array} \end{aligned}$$

(8)

Fig. 3

Simulation of $10^3$ realizations from a GHW Gaussian process with an ARMA(1, 1) as short memory component. The true values of the parameters are $\lambda _g=0.6$, $\phi =0.8$, $\psi =-0.4$ and $\sigma =1$ ($\phi$ and $\psi$ are the AR and MA coefficients, respectively). On the bottom, we show a comparison between the theoretical spectral density and the periodogram of the simulated series

Using (8) and the properties of the standard Brownian motion, we can approximate (7) as:

$$\begin{aligned} y_t \simeq \sum _{j=0}^{ l -1} \sqrt{2 \pi f(u_{j+1}) / l } \left( \cos (t u_{j+1}) \epsilon _j - \sin (t u_{j+1}) \epsilon ^*_j \right) \end{aligned}$$

(9)

where $u_j= \pi j / l$ and $\epsilon _j , \epsilon ^*_j$ are i.i.d. standard normal random variables.

Obviously, by simulating a GHW process through (9) we have to consider that $f(\lambda )$ is not defined in its poles. To address this issue, we approximate $f(\lambda _g) \simeq \left( \tilde{\gamma }(0) + 2 \sum _{k=1}^{T-1} \tilde{\gamma }(k) \cos (k \lambda _g) \right) f_x(\lambda _g)$ where $\tilde{\gamma }(k)$ is computed by truncating at T the Wold representation of the autocovariance function of the standardized GHW noise, while $f_x(\lambda _g)$ is defined in Proposition 1.

All the previous relations can be generalized to simulate the k-GHW process.

Let us consider again the GHW process in Proposition 1, assume $\mu =0$ and an ARMA(1, 1) as short memory component. Figure 3 shows a simulation of this process obtained through the spectral method in (9) with $l= \lfloor \frac{T}{2}\rfloor$ and a comparison between the periodogram and the spectral density along with a comparison between the log-periodogram and the log-spectrum.

In the following, we compare the two simulation methods involving (6) and (9) for the above process by computing the square of the Euclidean distance between the theoretical log spectral density and the log expected value of the periodogram, such that:

$$\begin{aligned} \mathcal {D}_n= 2 \sum _{\begin{array}{c} j=1 \\ \lambda _j \ne \lambda _g \end{array}}^{\lfloor \frac{T}{2}\rfloor } \left( \ln f(\lambda _j) - \ln E [ I(\lambda _j) ] \right) ^2 \end{aligned}$$

(10)

where $\biggr \lbrace \lambda _j \biggr \rbrace _{j=1}^{\frac{T}{2}}= \biggr \lbrace \frac{2 \pi j}{T} \biggr \rbrace _{t=1}^{\frac{T}{2}}$ is the grid of Fourier frequencies and $I(\lambda _j)$ is the periodogram defined as:

$$\begin{aligned} I(\lambda _j) = \frac{1}{2 \pi T} \biggr | \sum _{t=0}^{T-1} y_{t+1} e^{\imath t \lambda _j} \biggr |^2 \end{aligned}$$

For obvious reason, we do not consider the Gegenbauer frequency when we are computing (10). To get an estimate of $E [ I(\lambda _j) ]$, we simulate the process with each method for $n= \lbrace 250, 500, 1000 \rbrace$ reps, then we take the expectation of the periodogram. As is known, see Percival and Walden (1993), the expected value of the periodogram is an asymptotically unbiased estimator of the spectral density. Table 1 shows the ratio between the $\mathcal {D}_n$ measure computed through the spectral method in (9) over the same measure computed via the method involving (6). Let us observe that we do not see a huge difference between the two methods, therefore the spectral approximation approach can be used as a valid alternative.

Table 1 Ratio between the $\mathcal {D}_n$ measure defined in (10) computed through the spectral simulation method in (9) over the same measure computed via the truncation method involving (6)

4 Estimation of the GHW parameters

According to Quinn and Hannan (2001), the periodogram is a visual powerful tool for locating a frequency pole in the theoretical spectral density. However, spurious peaks could mistakenly indicate the presence of a periodicity in the process. This section discusses the estimation in the frequency domain of the GHW model via the maximization of the standard Whittle likelihood (see Whittle (1953)), where we set the local maximizers of the periodogram as initial guess of the frequency parameters vector in the optimization algorithm.

Let $y = \begin{bmatrix}y_1,&\cdots&, y_T \end{bmatrix} ^\top$ be T realizations of a random variable $Y \sim N(0, \varSigma _\theta )$ where $\varSigma _\theta$ is the covariance matrix. According to Dzhaparidze and Yaglom (1983), the exact log-likelihood function can be written as:

$$\begin{aligned} LL(\theta ) = -\frac{T}{2} \ln (2\pi ) -\frac{1}{2} y^{\top } \varSigma _\theta ^{-1} y - \frac{1}{2} \ln |\varSigma _\theta | \end{aligned}$$

(11)

where $\theta$ is the parameters vector.

The Whittle likelihood is an approximation of (11) where the covariance terms in the time domain are substituted by spectral terms in the frequency domain. It is given from the following function:

$$\begin{aligned} L_W(\theta )=- \frac{T}{4\pi } \int _{-\pi }^{\pi } \ln f(\lambda ;\theta ) d\lambda - \frac{T}{4\pi } \int _{-\pi }^{\pi } \frac{I(\lambda )}{f(\lambda ;\theta )} d\lambda \end{aligned}$$

(12)

where $f(\lambda ;\theta )$ is the spectral density evaluated at the $\theta$ parameters and T is the sample size. The integral terms in (12) can be approximated via Riemann sums (c.f. Beran (1994)), such that:

$$\begin{aligned} \tilde{L}_W(\theta )=- \sum _{t=1}^{\lfloor \frac{T}{2}\rfloor } \ln f(\lambda _{t};\theta )- \sum _{t=1}^{\lfloor \frac{T}{2}\rfloor } \frac{I(\lambda _{t})}{f(\lambda _{t};\theta )} \end{aligned}$$

Relatively to maximum exact likelihood estimation, the Whittle approach simplifies considerably computations (from $O(T^2)$ to $O(T \ln (T))$). Furthermore, difficulties encountered with a non-zero mean, which is hard to estimate under long memory, can be avoided by performing Whittle estimation, since the periodogram is invariant with respect to an additive constant like the mean (see Hassler (2019) for further details).

Consider now the k-GHW process in Proposition 2 and let $f_x(\lambda _t)=\frac{\sigma ^2}{2 \pi }$ be the spectral density of the short memory component. We can estimate the model parameters $\theta = [ \lambda _{g,1}, \cdots , \lambda _{g,k}, \sigma ^2 ]^\top$ via the maximization of (12), with $\theta \in \varTheta \subset S$ where $\varTheta$ is assumed to be a compact set and S follows from Proposition 2. Defining the k-GHW spectral density as $f(\lambda _t)=\sigma ^2 h(\lambda _t)$, it is easy to verify that $\frac{\partial \tilde{L}_W(\theta )}{\partial \sigma ^2} = 0$ implies $\hat{\sigma }^2 = \frac{2}{T} \sum _{j=0}^{\lfloor \frac{T}{2} \rfloor } \frac{I(\lambda _t)}{h(\lambda _t)}$. Therefore, the parameter $\sigma ^2$ can be concentrated outside the likelihood.

In the following equations, we provide the gradient and the Hessian of the Whittle likelihood function for a k-GHW noise. The gradient is given by:

$$\begin{aligned} \frac{\partial L_W(\theta )}{\partial \theta _{i}} = \frac{T}{4\pi } \int _{-\pi }^{\pi } \left( \frac{ I(\lambda )}{f(\lambda )} - 1 \right) \frac{\partial \ln f(\lambda )}{\partial \theta _i} d\lambda \end{aligned}$$

(13)

The ij-element of the $(k+1) \times (k+1)$ Hessian matrix can be computed as:

$$\begin{aligned} H_{i,j} (\theta )= - \frac{T}{4 \pi } \int _{-\pi }^{\pi } \frac{\partial \ln f(\lambda )}{\partial \theta _i} \frac{\partial \ln f(\lambda ) }{\partial \theta _j} \left( \frac{ I(\lambda )}{f(\lambda )} \right) d\lambda \end{aligned}$$

(14)

for $i,j \in \lbrace 1,2,\cdots , k + 1 \rbrace$. The terms in (13) and (14) can be obtained as follows:

$$\begin{aligned} \frac{\partial \ln f(\lambda ) }{\partial \lambda _{g,i}}= \frac{2 \ln \left( 2 |\cos (\lambda )-\cos (\lambda _{g,i})| \right) \sin (\lambda _{g,i})}{\cos (\lambda )-\cos (\lambda _{g,i})} \left( \ln ^2(2|\cos (\lambda )-\cos (\lambda _{g,i})|) +(\alpha _i \pi -\lambda )^2 \right) ^{-1}; \end{aligned}$$

for $i,j=1,2,\cdots ,k$ and ${ \frac{\partial \ln f(\lambda ) }{\partial \sigma ^2}= \frac{1}{\sigma ^2} }$.

Notice that if $\lambda _{g,i}$ approaches to zero, then the Hessian in (14) becomes singular because of the sine function. According to Dzhaparidze and Yaglom (1983), defining $\varGamma ^{-1}(\theta )$ as the asymptotic covariance matrix for the Whittle estimator $\hat{\theta }_T = \text{ argmax}_{\theta \in \varTheta } L_W(\theta )$, we can obtain the ij-element of $\varGamma (\theta )$ in the usual way as:

$$\begin{aligned} \lim _{T \rightarrow \infty } - \frac{1}{T} E(H_{i,j} (\theta ) ) = \frac{1}{4 \pi } \int _{-\pi }^{\pi } \frac{\partial \ln f(\lambda )}{\partial \theta _i} \frac{\partial \ln f(\lambda ) }{\partial \theta _j} d\lambda = \varGamma _{i,j} (\theta ) \end{aligned}$$

where the first equality is implied by Theorem 3.4 in Zygmund and Fefferman (2003).

4.1 Consistency of the parameters

In this subsection, we will see that, under some regularity conditions, the Whittle estimator is a consistent estimator of the k-GHW process with an ARMA(p, q) as short memory component. Following the asymptotic theory in Hannan (1973), Giraitis and Leipus (1995) and Giraitis et al. (2001) provided the consistency of the Whittle estimator for a k-factor GARMA process with unknown poles in the spectrum.

Consider the k-GHW process in Proposition 2 and let $f_x(\lambda )=\frac{\sigma ^2}{2 \pi } \biggr | \frac{\psi (e^{-\imath \lambda })}{\phi (e^{-i\lambda })} \biggr |^2$ be the spectral density of the short memory ARMA(p, q) component. Let $\theta = [\sigma ^2, \lambda _{g,1}, \cdots , \lambda _{g,k}, \phi _1, \cdots , \phi _p, \psi _1, \cdots , \psi _q]^\top$ be the parameters vector such that $\theta \in \varTheta \subset S$ where $\varTheta$ is assumed to be a compact set and S follows from Proposition 2. The next theorem establishes the consistency of the Whittle estimator $\hat{\theta }_T$.

Theorem 1

Let $y_t$ be a k-factor GHW process such that:

$$\begin{aligned} y_t = \sum _{i=0}^{\infty } b_i \varepsilon _t = \left( \prod _{j=1}^k h_j(L) \right) \frac{\psi (L)}{\phi (L)} \varepsilon _t \end{aligned}$$

where $h_j(L) = \sum ^{\infty }_{i=0} \frac{\cos (\lambda _{g,j}(i+1))}{i+1} L^i$ and $\varepsilon _t \sim WN(0,\sigma ^2)$.

Let $\theta = [\sigma ^2, \lambda _{g,1}, \cdots , \lambda _{g,k}, \phi _1, \cdots , \phi _p, \psi _1, \cdots , \psi _q]^\top$ be the vector of the parameters such that $\theta \in \varTheta \subset S$ where $\varTheta$ is assumed to be a compact set and $S = (0,\infty ) \times \varLambda ^k \times \mathrm{I\!R}^{p+q}$ with $\varLambda = [0,\pi ]$. Under the following conditions

• (i) $\sum _{i=0}^{\infty } b_i^2 < \infty$,

• (ii) $\phi (0) = \psi (0) =1$,

• (iii) The polynomials $\phi (\cdot )$ and $\psi (\cdot )$ have no common zeros such that $\phi (z) \ne 0$ and $\phi (0) \ne 0$ for $|z|<1$,

• (iv) The spectral density $f(\lambda ; \theta )$ of the process $y_t$ is uniquely determined by the parameters in $\theta$,

the Whittle estimator $\hat{\theta }_T$ converges in probability to the true value of the parameters:

$$\begin{aligned} \hat{\theta }_T \overset{p}{\rightarrow } \theta _0 \>\>\>\>\>\> as \>\>\>\>\>\> T \rightarrow \infty \end{aligned}$$

Proof

The proof of Theorem 1 is given in the Appendix. $\square$

Table 2 Bias and MSEs of the Whittle estimator for $10^3$ simulated series generated by a GHW process with an ARMA(1, 1) as short memory component

4.2 A simulation experiment

In the following, we implement a Monte Carlo experiment simulating $10^3$ times a sample size of $T =\lbrace 100, 200, 600, 1000 \rbrace$ realizations generated by the GHW process in Proposition 1, with $\mu =0$ be known and an ARMA(1, 1) as short memory component. At the end, the model is estimated via the standard concentrated Whittle likelihood.

Process simulations have been carried out via the spectral method in (9), considering different values of $\lambda _g$ and setting the short memory parameters as $\sigma =1$, $\phi =0.8$ and $\psi =-0.4$, where $\phi$ and $\psi$ are the AR and MA coefficients, respectively. Initial guesses in the optimization algorithm are set equal to the maximizer of the periodogram for $\lambda _g$, while they are obtained through a grid search procedure for the $\phi$ and $\psi$ parameters under the restrictions in Proposition 1. Table 2 shows the parameters bias and mean square error (MSE). Let us observe that they becomes smaller for each parameter as the sample size increases, matching the statement in Theorem 1.

Table 3 Squared Euclidean distance between the log theoretical spectral density of the Gegenbauer DGP and the log estimated spectral density of the $\hbox {GHW}(p,q)$ model

4.3 How the GHW model fits the Gegenbauer process

In this subsection, we investigate the issue of how the GHW model fits data generated from a Gegenbauer process. Let us start by considering a fractionally differenced Gegenbauer noise as the data generating process (DGP), whose theoretical spectral density is defined in (4). Data are simulated considering a type I and type II processes as in Sect. 3.3 for different values of the d parameter, while the Gegenbauer frequency is set to $\pi /4$ and $\sigma ^2=1$. Then, the GHW filter in (3) is applied to the simulated series assuming $\mu =0$ and $\lambda _g=\pi /4$ be known.

In the following, a Monte Carlo experiment has been carried out considering $10^3$ reps, where the Gegenbauer fractional noise is simulated at each repetition and then filtered via (3). Finally, an ARMA(p, q) component is estimated from the filter output via the exact likelihood method.

Table 3 shows the squared Euclidean distance between the log theoretical spectral density of the Gegenbauer DGP and the log estimated spectral density of the GHW(p, q) model, where p and q refer to the order of the ARMA short memory component. The squared Euclidean distance is computed via the numerical approximation of the following integral:

$$\begin{aligned} \mathcal {D}_T = 2 \int _0^\pi \left( \ln f_{\rm{GARMA}}(\lambda ) - \ln \hat{f}_{\rm{GHW}} (\lambda ) \right) ^2 d\lambda \end{aligned}$$

where $f_{\rm{GARMA}}(\lambda )$ and $f_{\rm{GHW}}(\lambda )$ are the spectral densities of the Gegenbauer and GHW processes, respectively. Let us observe that $\mathcal {D}_T$ is lower when the d parameter is larger and an AR(1) component is assumed (see columns GHW(1,0) and GHW(1,1)). Therefore, it should be feasible to state that the weaker persistence characterizing the GHW process with respect to the Gegenbauer may be compensated by assuming an autoregressive component. This is also confirmed by the visual examination of Fig. 4, where it is clear that the GHW log estimated spectrum fits the theoretical Gegenbauer log spectral density almost ideally if an AR component is considered along with an high value of the memory parameter. On the other hand, it is also evident that the GHW model fails in fitting the generated data when d assumes small values, even if an AR coefficient is estimated. In this case, we observe that the outcomes may be improved by estimating an ARMA(1,1) component.

Fig. 4

Comparison between the log theoretical spectral density of the Gegenbauer DGP and the log estimated spectral density of the GHW(p, q) model, considering $T=250$ (left column) and $T=1000$ (right column) as sample sizes

Fig. 5

On the top: transformed series of the EPICA Dome C temperature reconstructions. It consists on 801 observations with time interval length of 1000 years. The zero on the x-axis corresponds to the present age (1950). On the bottom: periodogram of the above series

5 Empirical application on EPICA dome C temperature reconstructions

The European Project for Ice Coring in Antarctica (EPICA) is a multinational European activity for deep ice core drilling. Its main objective is to report full documentation of the atmospheric record archived in Antarctic ice. Evaluation of these results provides information about the natural climate variability and mechanisms of climatic changes.

Figure 5 shows the transformed series of the paleoclimatic temperature reconstructions since $\sim 800,000$ years ago. The series is obtained by interpolating the data set provided by Jouzel and Masson-Delmotte (2007), who elaborated the EPICA Dome C ice cores records, considering a fix time interval of 1,000 years. Then, data have been transformed according to Davidson et al. (2016) such that $y_t = \ln (z_t + 16)$, where $z_t$ is the original series of length $T=801$ observations obtained from the interpolation. Previous analysis on this data set can be found in Davidson et al. (2016) and Castle and Hendry (2020).

By visual inspection of the periodogram on the bottom of Figure 5, we easily identify two main periodicities of 100 and 41 thousands of years (kyrs). This result is coherent with respect to the paleoclimatic literature (see Petit et al. (1999)). Although others shorter cycles could be considered for this series, a preliminary analysis on residuals suggests the choice of $k=2$ and $\lambda _g=\begin{bmatrix} 0.06&0.16 \end{bmatrix}^\top$ as optimal. In particular, the possibility to include a further cycle (for instance the one related to the tiny peak on the periodogram at frequency $\lambda =0.27$) is excluded after the residuals analysis of the 3-GHW(p, q) estimation (here, the notation (p, q) refers to the order of the ARMA short memory component). In this case, the square sum of the sample autocorrelations $\sum ^{T-1}_{k=1} \hat{\rho }^2(k)$ results to be higher for the 3-GHW(1,0), 3-GHW(0,1) and 3-GHW(1,1) models with respect to the 2-GHW counterparts. At the end, the choice $k=2$ is hence preferred. Moreover, we assume the frequency parameters vector to be known such that $\lambda _g=\begin{bmatrix} 0.06&0.16 \end{bmatrix}^\top$ and it will not be considered again in the estimation.

Table 4 Estimation results of the 2-factor GHW and GARMA models with an ARMA(p, q) as short memory components for the EPICA Dome C paleoclimatic temperature reconstructions

Let us proceed by estimating both a 2-factor GHW and GARMA models for these data. The 2-GARMA model is estimated through the Whittle approach in a one-step procedure. On the other hand, the 2-GHW model is estimated in a 2-step procedure. First, we filter the series via the GHIT function in order to obtain the short memory component $x_t$. Then, we fit an ARMA(p, q) process for $x_t$ through the maximization of the exact likelihood. We do not consider p and q orders larger than one since the choice of a higher-order ARMA component does not change significantly our final remarks.

Table 4 shows the estimation results. Let us observe that the memory parameters estimates belong to the stationary region in the GARMA case. The short memory component is obtained via:

$$\begin{aligned} x_t = F(L)y_t-F(1)\hat{\mu }, \>\>\>\> t=1,\cdots ,T \end{aligned}$$

(15)

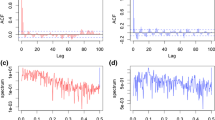
where $F(L)=\prod _{j=1}^{2} g_j(L)$ if the 2-factor GHIT filter is considered, while $F(L)=\prod _{j=1}^{2}(1-2\cos (\lambda _{g,j})L+L^2)^{d_j}$ in the 2-GARMA case. $\hat{\mu }$ is the sample mean estimator computed as $\hat{\mu }=\frac{1}{T}\sum _{t=1}^{T}y_t$. Figure 6 shows the sample autocorrelation function (ACF), the sample partial ACF and the periodogram of the short memory components for the 2-GHW and 2-GARMA models obtained through (15), given the parameters estimates of the first and fifth rows in Table 4. It should be clear that both approaches are able to reduce the main peaks in the EPICA Dome C periodogram, although the GARMA filter performs slightly better in removing the 100 kyrs periodicity. On the other hand, the two models perform almost equal if we compare the correlogram and the periodogram in Fig. 7 obtained from the 2-GHW(1,0) and 2-GARMA(1,0) estimates in Table 4, where an AR(1) component is considered. In the last column of Table 4, we also show the sum of square of autocorrelations. Notice that the two models are very close in controlling for the long-memory features if an AR coefficient is estimated.

In the following, we perform a rolling forecast experiment with a moving window of length $W=300$ observations such that we compute predictions of the EPICA Dome C temperature reconstructions according to a 2-GHW and 2-GARMA models with an ARMA(1, 1) as short memory component. The h-step-ahead predictor $\hat{y}_{t+h|t}$ is obtained in the standard way with the support of the Durbin-Levinson (DL) recursion (see Brockwell and Davis (1986)). We set the truncation parameter $\tilde{n}$ in the DL recursion by finding the lower Mean Square Forecast Error (MSFE) for each model. At the end, we set $\tilde{n}=290$.

Fig. 6

Sample ACF, sample partial ACF and periodogram of the short memory components obtained via (15) considering the 2-GHW(0,0) and 2-GARMA(0,0) models in Table 4

Fig. 7

Sample ACF, sample partial ACF and periodogram of the residuals obtained by estimating an AR(1) as short memory component for the 2-GHW(1,0) and 2-GARMA(1,0) models in Table 4

Fig. 8

Residuals obtained from the one-step-ahead forecasts computed via the DL recursion considering the 2-GHW(1,1) model

Fig. 9

Residuals obtained from the one-step-ahead forecasts computed via the DL recursion considering the 2-GARMA(1,1) model

Fig. 10

Five-step-ahead forecasts and predictability for the EPICA Dome C temperature reconstructions

Figures 8 and 9 show the correlogram and the periodogram relatively to the residuals obtained from the one-step-ahead linear predictor. Notice that both models are able to capture the cyclical long memory removing the main peaks in the EPICA Dome C periodogram. On the other hand, the correlograms show very weak autocorrelation. On the top of Fig. 10, an illustration of the five-step-ahead forecasts for the two models is provided for example purposes. On the bottom of Fig. 10, the two models are compared in terms of predictability, referring to the following measure:

$$\begin{aligned} \mathcal {P}(h)= (T-W) \left( \sum _{t=W+h}^{T}(y_t - \hat{y}_{t|t-h})^2 \right) ^{-1} \end{aligned}$$

which is basically the reciprocal of the MSFE as a function of the prediction horizon h. Notice that it is almost impossible to distinguish between the two approaches in terms of forecasting performance.

All these results lead to the conclusion that the GHW model behaves more or less similar to its classical competitor, the GARMA process, in controlling for long memory in quasi-periodic time series.

6 Conclusions

The estimation of the d parameter is a widely discussed issue in the long memory literature (see for instance Geweke and Porter-Hudak (1983), Beran (1994), Robinson (1995a, 1995b), Ferrara and Guegan (1999), Arteche and Robinson (2000) and Hassler (2019) for a review). Recently, Hassler and Hosseinkouchack (2020) introduced a new way to model long memory without estimate d. In this paper, a generalization of their contribution is proposed through the introduction of a novel process for cyclical long memory time series. Our main conclusion is that the GHW process is able to model long memory, as well as the GARMA does. In addition, the GHW process does not require the estimation of the memory parameters, simplifying the issue of how to disentangle long memory from a (moderately persistent) short memory component. This leads to a clear advantage of our formulation over its classical competitor, the Gegenbauer process. However, the k-GHW model does not allow for a good control on the single contribution of each pole in the spectrum to the periodicity of the process. This is in contrast to the GARMA model, where the contribution of each singularity is regulated by the d parameters. On the other hand, although the 1-factor GHW model displays less persistence with respect to the fractionally integrated Gegenbauer process, this weaker persistence may be compensated by estimating a further ARMA(p, q) short memory component. In particular, we observed that the AR coefficient plays a significant role. Furthermore, the GHW model is more parsimonious and allows to consider more frequency parameters in the GHIT filter without estimate further d parameters. Moreover, if we consider the frequency parameters vector to be known (for instance, by estimating it through the periodogram in a preliminary estimation step), we can obtain the short memory component just by filtering the data. Even so, we must be careful when we add frequency parameters to the GHIT filter, in order to prevent overfitting and antipersistence. The selection of the length k of the frequency parameters vector is a crucial step. In fact, if k is too large, it would lead to an antipersistent output and to overfitting. On the other hand, if k is too small, we will not be able to “remove” completely the periodicity from the data. Therefore, a preliminary analysis on filter residuals and on the periodogram of the short memory component is recommended.

Finally, we provide analytical expressions for the spectral density and the autocovariance function of the GHW process along with the consistency of the Whittle estimator. These mathematical tools could be useful in further researches to get worthy results in empirical applications.

Appendix

1.1 Proof of Proposition 1

Using $\ln (1- z) = - \sum _{j=1}^\infty \frac{z^j}{j}$ we can write (with $\imath = \sqrt{-1}$):

$$\begin{aligned} \begin{array}{lll} \ln (1 - 2 \cos ( \lambda _g)z + z^2) &{} =&{} \ln (1-z e^{\imath \lambda _g}) + \ln (1-z e^{-\imath \lambda _g}) \\ &{} = &{} - {\sum }_{j=1}^\infty \left( \frac{z^j e^{-\imath j \lambda _g}}{j} + \frac{z^j e^{\imath j \lambda _g}}{j} \right) \\ &{} = &{} - 2 {\sum }_{j=1}^\infty \frac{z^j \cos (\lambda _g j)}{j} \end{array} \end{aligned}$$

Therefore, the following equations hold:

$$\begin{aligned} h(L)=-\frac{\ln (1-2 \eta L+L^2)}{2 L}=\sum _{j=0}^{\infty }\frac{\cos (\lambda _g(j+1))}{(j+1)}L^{j} \end{aligned}$$

We get the coefficients of g(z) and b(z) by equalling the following polynomials:

$$\begin{aligned} 1 = h(L)g(L) = \left( \tilde{b}_0 + \frac{\tilde{b}_1}{2} z + \frac{\tilde{b}_2}{3} z^2 + \cdots \right) \left( g_0 + g_1 z + g_2 z^2 + \cdots \right) \end{aligned}$$

and

$$\begin{aligned} h(L)c(L)= & {} \left( \tilde{b}_0 + \frac{\tilde{b}_1}{2} z + \frac{\tilde{b}_2}{3} z^2 + \cdots \right) \left( c_0 + c_1 z + c_2 z^2 + \cdots \right) \\= & {} \left( b_0 + b_1 z + b_2 z^2 + \cdots \right) = b(L) \end{aligned}$$

Finally, we prove the equation for the spectral density by considering:

$$\begin{aligned} f(\lambda )=\biggr |\frac{\ln (1-2 \eta e^{-\imath \lambda }+e^{-\imath 2 \lambda })}{2 e^{-\imath \lambda }} \biggr |^2 f_x(\lambda )=\frac{|\ln (r(\lambda )e^{\imath \varphi (\lambda )})|^2}{4 }f_x(\lambda ) \end{aligned}$$

We proceed by computing the modulus and the argument of the complex number inside the logarithm. The first one is given by:

$$\begin{aligned} r(\lambda )= & {} |1-2 \cos (\lambda _g) \cos (\lambda ) + \cos (2 \lambda ) + \imath (2 \cos (\lambda _g) \sin (\lambda ) \\&- \sin (2 \lambda )) |^2 = 2 |\cos (\lambda )-\cos (\lambda _g) | \end{aligned}$$

On the other hand, we get the argument $\varphi (\lambda )$ considering the ratio:

$$\begin{aligned}&\frac{2 \cos (\lambda _g) \sin (\lambda ) - \sin (2 \lambda )}{1-2 \cos (\lambda _g) \cos (\lambda ) + \cos (2 \lambda ) } \\&\quad = \frac{\sin (\lambda ) \left( \cos (\lambda _g) - \cos (\lambda ) \right) }{-\cos (\lambda ) \left( \cos (\lambda _g) - \cos (\lambda ) \right) } = \frac{v(\lambda )}{u(\lambda )} \end{aligned}$$

where $u(\lambda )$ and $v(\lambda )$ are, respectively, defined as the real and imaginary parts of the complex number inside the logarithm, such that:

$$\begin{aligned} \varphi (\lambda )= {\left\{ \begin{array}{ll} \arctan \left( \frac{v(\lambda )}{u(\lambda )} \right) , &{} \text {if}\ u(\lambda )> 0 \\ \arctan \left( \frac{v(\lambda )}{u(\lambda )} \right) + \pi , &{} \text {if}\ u(\lambda )< 0 \>\>\text{ and }\>\> v(\lambda ) \ge 0\\ \arctan \left( \frac{v(\lambda )}{u(\lambda )} \right) - \pi , &{} \text {if}\ u(\lambda )< 0 \>\>\text{ and }\>\> v(\lambda ) < 0 \end{array}\right. } \end{aligned}$$

with $\varphi (\lambda ) \in (-\pi ,\pi ]$.

Let us consider $\lambda \in (- \pi , \pi )$ and recall that the tangent function is not defined in $\frac{\pi }{2}$ while the identity $\arctan (\tan (x)) = x$ holds only if $x \in (-\frac{\pi }{2},\frac{\pi }{2})$. Therefore, considering $\tan (\lambda )=\tan (\lambda - \pi )$ if $\lambda > \frac{\pi }{2}$ and $\tan (\lambda )=\tan (\lambda + \pi )$ if $\lambda < -\frac{\pi }{2}$, we get:

• if $\cos (\lambda _g) - \cos (\lambda ) > 0$ (which implies $\lambda \notin (-\lambda _g,\lambda _g)$):

  $$\begin{aligned} \varphi (\lambda )= {\left\{ \begin{array}{ll} \arctan \left( -\tan (\lambda +\pi ) \right) = -\lambda - \pi , &{} \text {if}\ - \pi< \lambda< -\frac{\pi }{2} \\ \arctan \left( -\tan (\lambda ) \right) -\pi = -\lambda - \pi , &{} \text {if}\ -\frac{\pi }{2}< \lambda< 0\\ \arctan \left( -\tan (\lambda ) \right) +\pi = -\lambda + \pi , &{} \text {if}\ 0<\lambda< \frac{\pi }{2} \\ \arctan \left( -\tan (\lambda -\pi ) \right) = -\lambda + \pi , &{} \text {if}\ \frac{\pi }{2}< \lambda < \pi \end{array}\right. } \end{aligned}$$

• if $\cos (\lambda _g) - \cos (\lambda ) < 0$ (which implies $\lambda \in (-\lambda _g,\lambda _g)$):

  $$\begin{aligned} \varphi (\lambda )= {\left\{ \begin{array}{ll} \arctan \left( -\tan (\lambda +\pi ) \right) + \pi = -\lambda , &{} \text {if}\ - \pi< \lambda< -\frac{\pi }{2} \\ \arctan \left( -\tan (\lambda ) \right) = -\lambda , &{} \text {if}\ -\frac{\pi }{2}< \lambda< 0\\ \arctan \left( -\tan (\lambda ) \right) = -\lambda , &{} \text {if}\ 0<\lambda< \frac{\pi }{2} \\ \arctan \left( -\tan (\lambda -\pi ) \right) -\pi = -\lambda , &{} \text {if}\ \frac{\pi }{2}< \lambda < \pi \end{array}\right. } \end{aligned}$$

Finally, we end the proof by solving:

$$\begin{aligned} f(\lambda ) = \frac{\ln ^2 \left( r(\lambda ) \right) + \varphi ^2}{4}f_x(\lambda ) \end{aligned}$$

Notice that if $\lambda _g=0$ (which implies $\eta =1$), the spectral density in Proposition 1 coincides with the one of the HW process.

We get the asymptotic behaviour of the spectrum as $\lambda \rightarrow \lambda _g$ by taking the Taylor expansion of $\cos (\lambda )$ as $\lambda \rightarrow \lambda _g$. If $\lambda _g \notin \lbrace 0 , \pi \rbrace$, we consider the first order expansion $\cos (\lambda ) \sim \eta - \sin (\lambda _g)(\lambda -\lambda _g)$. If $\lambda _g \in \lbrace 0 , \pi \rbrace$, we need the second-order expansion $\cos (\lambda ) \sim 1 - \frac{(\lambda -\lambda _g)^2}{2}$. $\square$

1.2 Proof of Theorem 1

Let us define the spectral density of the process $y_t$ as $f(\lambda , \theta )=\frac{\sigma ^2}{2 \pi } h(\lambda ,\theta )$. Notice that the stationarity condition (i) in Theorem 1 always holds for the k-GHW process in Proposition 2 because $\sum _{i=1}^\infty \frac{\cos (i \lambda _{g,j})^2}{i^2} < \infty$ for each $\lbrace \lambda _{g,j} \rbrace _{j=1}^k \in \varLambda$ and $x_t = \frac{\psi (L)}{\phi (L)}\varepsilon _t$ is defined as an ARMA(p, q) process. Moreover, the square summability in i) implies that $\int _{-\pi }^{\pi } \ln h(\lambda ,\theta ) d \lambda = 0$ holds (see Theorem 5.8.1 in Brockwell and Davis (1986)). Conditions (ii) and (iii) follow directly from the definition of $x_t$ as an ARMA(p, q) process, while condition (iv) holds since the spectral density of the k-GHW process is determined uniquely by $\theta$.

Finally, if conditions (i), (ii), (iii) and (iv) are satisfied, then Theorem 3 in Giraitis and Leipus (1995) holds and the Whittle estimator converges in probability to the true value of the parameters.