Abstract
We study how and to what extent the existence of non-local diffusion affects the transport of chemical species in a composite medium. For our purposes, we prescribe the mass flux to obey a two-scale, non-local constitutive law featuring derivatives of fractional order, and we employ the asymptotic homogenisation technique to obtain an overall description of the species’ evolution. As a result, the non-local effects at the micro-scale are ciphered in the effective diffusivity, while at the macro-scale the homogenised problem features an integro-differential equation of fractional type. In particular, we prove that in the limit case in which the non-local interactions are neglected, classical results of asymptotic homogenisation theory are re-obtained. Finally, we perform numerical simulations to show the impact of the fractional approach on the overall diffusion of species in a composite medium. To this end, we consider two simplified benchmark problems, and report some details of the numerical schemes based on finite element methods.
Similar content being viewed by others
1 Introduction
The main purpose of the theory of homogenisation is to predict the overall properties of heterogeneous media in connection with the intrinsic features of their internal structure [20]. In the modelling of multi-scale composites, homogenisation methods permit to decouple the structural characteristic length scales [2, 10, 40, 42, 55, 57], and, in particular, the asymptotic homogenisation technique [15, 17, 27, 74] makes use of multiple scale expansions of the unknown fields to acquire an effective description of the medium at its coarser scales.
Usually, local constitutive laws are adopted in the description of the constituents of composite materials or heterogeneous media, thereby leading, in the majority of cases, to a homogenised local response of the composite. However, in certain circumstances, this has conducted to discrepancies with the experimental studies on heterogeneous media whose macro-scale properties could be more appropriately modelled by constitutive laws of non-local type. For instance, according to the experiments performed in [18, 36, 45, 48], a medium with an involved structure may develop spontaneous restrictions on the way in which the transport processes occurring inside it are to take place. In turn, these restrictions, dictated by the medium’s internal geometry, apply to the various length scales characteristing the transport processes and may result into non-local diffusion, thereby yielding non-Fickian diffusion [18, 21, 29, 48]. Furthermore, it is worth noticing that, although the response of the constituents of a composite is often taken to be of local type at the lowest scale, in some cases, non-locality in time or space may arise as a result of homogenisation processes [9, 26, 37], or even by the adoption of standard concepts of solid mechanics [78], without having recourse to homogenisation techniques. For instance, as shown in [19], viscoelasticity can be obtained from suitable upscaling of a fluid–structure interaction problem between an elastic medium and a Newtonian fluid.
1.1 Scopes and novelties
To the best of our knowledge, there exist few works in which the constitutive laws of the constituents of composite media are assumed to be non-local already at the lower scales [20, 79]. For instance, in [20], the homogenised properties of thermoelastic composites are studied by considering non-local integral operators for the characterisation of the stress–strain constitutive laws. In [20], the Author motivates the need for this constitutive choice by relating it to the complex geometrical and physical connections among the spatial length-scale of real materials, as is the case of hierarchical composite media [46].
In this work, motivated by the interest towards diffusion in highly heterogeneous biological media, we study a problem in which the mass flux of a chemical species in each constituent is related to the species’ concentration gradient by means of a spatially non-local constitutive law. We do this by admitting that, in principle, two types of non-locality coexist: one pertains to the micro-scale and is thus associated with each constituent of the composite medium, while the other one is introduced a priori to allow for a non-local behaviour at the macro-scale. Note that these two types of non-locality are, in general, independent of each other. In the following, we will address each of these two non-localities through dedicated benchmark problems (see Sect. 5).
Several types of non-locality can be accounted for. For instance, as mentioned in [67], one can introduce higher-order gradients or integro-differential relations in the constitutive laws [4, 8, 14, 31, 34, 38, 47]. In the present work, continuing the research lines initiated in [67], we exploit Fractional Calculus [7, 23, 64] to describe diffusion processes that may deviate from Fick’s law because of possible non-local behaviours in space. This modelling choice is motivated by the “success” of Fractional Calculus in addressing such phenomena [24, 25, 52, 54]. In doing this, we have taken inspiration from the works [22, 67, 75].
In an attempt to realise how and to what extent non-local diffusion may affect the overall evolution of a given chemical substance in a composite medium, we prescribe a two-scale, non-local constitutive law for the mass flux of the considered substance. With this aim, we consider the asymptotic homogenisation technique to determine the effective diffusivity and the macroscopic evolution of the species. In doing this, we end up with an effective characterisation of the composite that is subjected to the existence of non-local interactions at both the micro- and the macro-scale. This is one of the novelties of this work.
As remarked in [67], the numerics of fractional diffusion in bounded domains requires special care because of the way in which the integro-differential operators featuring in the constitutive laws are to be handled, e.g. within FE methods. These difficulties increase if the medium in which fractional diffusion takes place is heterogeneous, as is the case in this work. A standard way of addressing numerically fractional differential equations in bounded domains is to have recourse to finite differences, specifically in the form of Grünwald–Letnikov schemes (see, e.g. [50, 53]), although we are aware of works in which FE procedures are adopted [35, 43, 67, 71]. However, this is not done for fractional differential equations in a multi-scale context, at least to our knowledge.
Another novelty of our work is that we address the FE discretisation of benchmark problems that include the non-local nature of the mass flux and the role of the heterogeneous structure of the medium under study. In this respect, we report the most important aspects of the FE discretisation and discuss some of the properties of the stiffness matrix and nodal force vector that feature in the resulting algebraic equations.
In summary, the main novelties of this work are:
-
(i)
The establishment of a combined framework in which some constitutive laws involving fractional derivatives are studied in conjunction with asymptotic homogenisation, in order to solve problems characterised by non-local diffusion at different scales.
-
(ii)
The realisation of a numerical scheme capable of putting together FE techniques with the integro-differential operators from Fractional Calculus.
Our main result is the quantification of the impact of the spatially non-local diffusion of fractional type of chemical substances, resolved at the macro- and at the micro-scale of a strongly heterogeneous composite medium, on the transport of such substances within the medium. By employing asymptotic homogenisation to determine the effective diffusivity coefficient of the considered medium, our computations predict that, at the macro-scale, the attainment of the stationary state of the diffusion process is appreciably hindered by the non-local interactions accounted for by the operators of fractional differentiation that define the diffusion fluxes. This retardation manifests itself for decreasing values of a real parameter (the fractional order of differentiation) that defines the strength of such non-local interactions, at the micro- and at the macro-scale.
Finally, we mention that, in this work, we adopt a formalism that can be easily adapted to a two- or three-dimensional context. However, since it can be challenging to study non-local phenomena in composite media via asymptotic homogenisation, we prefer, for the time being, to contextualise our mathematical model in a one-dimensional framework. Moreover, we remark that the results presented hereafter can be adapted in a straightforward manner to the study of thermal diffusion. Still, in the sequel, we shall only discuss diffusion of chemical species because the main problems that we have in mind come from the transport of chemical species in biological tissues.
1.2 Organisation of our work
The manuscript is organised as follows: in Sect. 2, some aspects of the topology of the composite are discussed, and we introduce the multi-scale governing equations describing the non-local diffusion of the chemical species. In Sect. 3, we consider the separation of scales between the macro- and the micro-scale, we illustrate the topology of the micro-structure, and discuss some aspects regarding periodicity in a two-scale context. Additionally, we reformulate the original governing equations to account for the two-scale nature of the non-local phenomena. In Sect. 4, the main mathematical tools of the asymptotic homogenisation technique are introduced, and we derive the effective properties and the homogenised equations for the composite under study. Furthermore, in Sect. 5, we specialise the general theory by presenting two different benchmark problems and discuss the results produced by numerical simulations. Moreover, we provide some details on the numerical schemes based on FE methods. Finally, in Sect. 6, we highlight the main results and outline some future developments.
2 Formulation of the problem
2.1 Topology of the composite
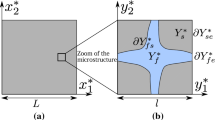
Let \({\mathscr {B}}=]0,L[\), with \(L>0\), be an open and bounded set of the one-dimensional Euclidean space, taken as the representation of a heterogeneous cylinder with periodic structure at the micro-scale, in which the heterogeneity is only along the axis of the cylinder. In particular, the open subsets \({\mathscr {B}}_{1}=\cup _{i=0}^{N}]X_{2i},X_{2i+1}[\subset {\mathscr {B}}\) and \({\mathscr {B}}_{2}=\cup _{i=0}^{N}]X_{2i+1},X_{2i+2}[\subset {\mathscr {B}}\) form the periodic structure of \({\mathscr {B}}\) and, for every i, each pair of intervals \(]X_{2i},X_{2i+1}[\) and \(]X_{2i+1},X_{2i+2}[\) represents two different constituents of the composite \({\mathscr {B}}\). Moreover, it holds that \({\overline{{\mathscr {B}}}} = {\overline{{\mathscr {B}}}}_{1}\cup {\overline{{\mathscr {B}}}}_{2}\) and \({\overline{{\mathscr {B}}}}_{1}\cap {\mathscr {B}}_{2} = {\mathscr {B}}_{1}\cap {\overline{{\mathscr {B}}}}_{2} = \emptyset \), where the bar symbol indicates the closure of the set. In addition, we use the notation \({\mathscr {I}}\) to specify the interface separating the constituents \({\mathscr {B}}_{1}\) and \({\mathscr {B}}_{2}\), namely \({\mathscr {I}}={\overline{{\mathscr {B}}}}_{1}\cap {\overline{{\mathscr {B}}}}_{2}=\cup _{i=0}^{N}\{X_{2i+1}\}\) (see Fig. 1).
2.2 Diffusion of chemical species
The diffusion of a chemical species in the composite \({\mathscr {B}}\) is described by
with \(\{X_{j}=X_{2i+1}\}_{i=0}^{N}\subset {\mathscr {I}}\), together with suitable initial and boundary conditions. Note that for ease of exposition these conditions will be specified later, when the benchmark problems are presented.
Equations (1b) and (1c) describe the contact on \({\mathscr {I}}\), which in this case is assumed to be ideal, and the operator  denotes the jump of \(\varPhi \) across the interface \({\mathscr {I}}\), i.e.
denotes the jump of \(\varPhi \) across the interface \({\mathscr {I}}\), i.e.
Moreover, Q denotes the mass flux of the chemical species and, as done in [67], we propose to express it in terms of the following non-local constitutive law,
where \(D(X,{\tilde{X}})\) is referred to as non-local diffusivity, and is written as the product of the scalar quantity \({\mathfrak {F}}(X-{\tilde{X}})\) and the fractional diffusivity \({\mathfrak {D}}(X,{\tilde{X}})\), both taken to be strictly positive. We emphasise that \({\mathfrak {F}}\) is defined for \(X\ne {\tilde{X}}\), and that both D and \({\mathfrak {D}}\) have, in general, physical dimensions different from those of standard diffusivity, depending on the prescription on \({\mathfrak {F}}\). Additionally, C and Q are continuous in \({\mathscr {B}}\), which means that they are prolonged at the interfaces.
It is worth noticing that further generalisations to the study of transport processes, involving for instance Darcy’s law, can be found, e.g. in [1]. This work, however, pursues goals different from ours, since it considers constitutive laws that relate the time fractional derivative of the mass flux with the time fractional derivative of the classical pressure gradient. On the other hand, a one-dimensional diffusion problem in a bounded homogeneous medium is studied in [76], wherein Darcy’s equation is generalised with a fractional integral in space. Furthermore, in the context of hierarchical materials, such as bones and ligaments, a generalised viscoelastic approach has been proposed to describe their rheological properties by using fractional derivatives and integrals [3, 30], while numerical methods have been developed for the case of hereditary-ageing materials in [16]. Additionally, we notice that in [81] the analytical and numerical solution of a generalised heat conduction equation was studied by considering a fractional time derivative instead of the first-order partial time derivative of the temperature. Moreover, in [5], the authors considered a model in which, in addition to the fractional derivative in time, the heat conduction equation in a homogeneous material is extended by replacing the classical gradient of the temperature with its symmetrised Caputo fractional derivative. Finally, we point out that, in the context of viscoelastic composites, the Rabotnov exponential kernel [66], which is employed to construct a type of fractional derivative, has been considered in [70].
3 Multi-scale formulation of the problem
3.1 Separation of scales
In the characterisation of the two-scale nature of the composite, we assume the existence of two characteristic length scales, associated with the composite as a whole and its internal structure. Specifically, for our purposes, we denote by \(L_{\mathrm {c}}\) and \(\ell \) the characteristic length scales of the composite medium and of its internal structure, respectively. Moreover, we require that the considered length scales are well separated by enforcing that \(\ell /L_{\mathrm {c}}\ll 1\). Therefore, we introduce the dimensionless, smallness parameter \(\varepsilon \), referred to as the scaling parameter, which is defined as the ratio
We notice that \(\varepsilon \) characterises the heterogeneity of the composite, and permits to explicitly specify the two-scale nature of a given physical quantity \(\varPhi :{\mathscr {B}}\times [0,t_{\mathrm {f}}[\rightarrow {\mathbb {R}}\). In fact, following the discussion given in [32, 63], one can take into account the multi-scale character of \(\varPhi (X,t)\) by rewriting it as \(\varPhi (X,t)={\check{\varPhi }}(X,t;\ell ,L_{\mathrm {c}})\). As a particular case of this writing, we can impose that \({\check{\varPhi }}(X,t;\ell ,L_{\mathrm {c}})={\hat{\varPhi }}(X/L_{\mathrm {c}},X/\ell ,t)\), so that the dependence on the characteristic length scales is explicit. In this way, we have that
where the dimensionless variables \(x:=X/L_{\mathrm {c}}\) and \(y := x/\varepsilon \) are referred to as the macroscopic, or slow, variable, and the microscopic, or fast, variable, respectively. Note that, within this non-dimensional setting, \({\mathscr {B}}\) becomes \({\mathscr {X}}:=\,]0,L/L_{\mathrm {c}}[\) and, accordingly, the non-dimensional variables x and y vary in \({\mathscr {X}}\) and in \({\mathscr {X}}/\varepsilon =\,]0,L/\ell [=]0,\tfrac{1}{\varepsilon }L/L_{\mathrm {c}}[\), respectively.
As stated in Eq. (5), one is able to express \(\varPhi \) as a function of two formally independent variables, thereby distinguishing the two scales characterising its nature. This means that, for every time t, the newly introduced function \(\phi \) is defined, in general, as \(\phi (\cdot ,\cdot ,t):{\mathscr {D}}_{x}\times {\mathscr {D}}_{y}\rightarrow {\mathbb {R}}\), where \({\mathscr {D}}_{x}\subseteq {\mathscr {X}}\) and \({\mathscr {D}}_{y}\subseteq {\mathscr {X}}/\varepsilon \).
Finally, we note that, by using the representation (5) and employing the chain rule, we can write
3.2 Topology of the micro-structure
At the micro-scale, the reference or elementary cell is the open interval \(]0,\ell [\), which in a non-dimensional formalism becomes \({\mathscr {Y}}\!=\,]0,1[\,\subset {\mathscr {X}}/\varepsilon \). Specifically, we assume \({\mathscr {Y}}\) to consist of two non-empty, open subsets \({\mathscr {Y}}_{1}=\,]0,y_{\mathrm {I}}[\) and \({\mathscr {Y}}_{2}=\,]y_{\mathrm {I}},1[\), where \(y_{\mathrm {I}}\in \,]0,1[\) denotes the interface between the intervals \({\mathscr {Y}}_{1}\) and \({\mathscr {Y}}_{2}\) (see Fig. 1). Furthermore, we consider that
Here, for the sake of simplicity, we adopt the assumption of macroscopic uniformity [41, 60, 61]. This choice allows to choose the elementary cell, \({\mathscr {Y}}\), independently of the macroscopic variable x, so that \({\mathscr {Y}}\) is representative of the composite’s micro-structure (see Fig. 1). Moreover, for the type of functions \(\phi (\cdot ,\cdot ,t):{\mathscr {D}}_{x}\times {\mathscr {D}}_{y}\rightarrow {\mathbb {R}}\) used in the forthcoming calculations, we assume \({\mathscr {Y}}\setminus \{y_{\mathrm {I}}\}\subset {\mathscr {D}}_{y}\) and the existence of the lateral limits \(\lim _{y\rightarrow 1^{\pm }}\phi (x,y,t)\) and \(\lim _{y\rightarrow 0^{+}}\phi (x,y,t)\). In the sequel, this property will be used to formalise the periodicity of \(\phi \) with respect to its microscopic variable (this will be referred to as \({\mathscr {Y}}\)-periodicity), especially in the case in which \({\mathscr {D}}_{y}\) has the form
where N is a sufficiently large natural number. These considerations imply that it is sufficient to reformulate the problem at hand in the reference cell \({\mathscr {Y}}=\,]0,1[\), along with the lateral limits outlined above, although for some physical quantities \(y_{\mathrm {I}}\) does not belong to the set in which they can be evaluated.
In addition, since \({\mathscr {Y}}\) is chosen independently of the macroscopic variable x, also the following relation holds
In general, however, if the hypothesis of macroscopic uniformity is not valid, the topology and geometry of the reference cell, \({\mathscr {Y}}\), could vary with respect to the macroscopic spatial variable x and, thus, the reference cell should be regarded as a function of x, \({\mathscr {Y}}(x)\). In this case, Reynolds’ transport theorem prescribes to rewrite the derivative of the left-hand side of Eq. (9) as
where \(w_{n}(x,y)\) is the normal “velocity” with which the boundary of the cell varies (see, e.g. [33, 63] and the references therein for more details).
3.3 Periodicity
From the point of view of the small characteristic length scale \(\ell \), the body \({\mathscr {B}}\) can be approximated as unbounded, so that one can assume \({\mathscr {B}}={\mathbb {R}}\). Within this approximation, a function \(\varPhi \) is said to be \(\ell \)-periodic in the sense that \(\varPhi (X,t)=\varPhi (X+p\ell ,t)\), for all \(p\in {\mathbb {Z}}\), provided X and \(X+p\ell \) are points in which the function can be evaluated [27].
Within the context of asymptotic homogenisation, one rephrases the periodicity of \(\varPhi \) in terms of the periodicity of the corresponding function \(\phi \) with respect to the microscopic variable y. To this end, and to account for the fact that \(\phi \) may be undefined for some values of y, it is necessary to express the periodicity of \(\phi \) in the weaker sense supplied by
with \(\phi (x,y_{*}^{\pm },t)=\lim _{y\rightarrow y_{*}^{\pm }}\phi (x,y,t)\), for all \(y_{*}\) for which both lateral limits exist. This picture is consistent with the case in which \(\phi (x,\cdot ,t)\) is defined in a set \({\mathscr {D}}_{y}\) of the type specified in (8) and \(y_{*}\) is either p or \(p+y_{\mathrm {I}}\), with \(p=1,\ldots ,N-2\). In particular, the case \(y_{*}=p+y_{\mathrm {I}}\) is important for performing the continuous prolongation at the interface of those physical quantities that have to be continuous at this point (for instance, the fluxes).
As anticipated above, the macroscopic uniformity, along with the \({\mathscr {Y}}\)-periodicity of the functions of interest for the problem at hand, enable us to restrict a given physical quantity to a single cell. For this purpose, one may choose the reference cell \({\mathscr {Y}}=\,]0,1[\,\), and take the restriction \(\phi (x,\,\cdot \,,t)_{|{\mathscr {Y}}}\). Furthermore, to account for the presence of the interface, which splits the cell in the disjoint union of two materials with different properties, we define \(\phi (x,\,\cdot \,,t)_{|{\mathscr {Y}}}\) as the piecewise function
In particular, to describe the periodicity at \(y_{*}=0\), we invoke Eq. (11), so that,
Granted this result, we notice that, if \(\phi \) is a function for which the continuity condition at the boundary of the periodic cell must be respected (for example, a concentration or mass flux), we also find
and, thus, because of periodicity,
3.4 Multi-scale non-local diffusion
Upon adopting the above considerations, and recalling the identities (5) and (6), we rephrase the original problem (1a)–(1c) as follows (see Remark 1 for further details),
with \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\), and where the index \(k\in \{1,2\}\) indicates in which sub-cell Eq. (16a) and the quantities \(c_{k}\) and \(q_{\alpha ,\beta _{k}}\) are defined. Particularly, the two-scale, non-local flux \(q_{\alpha ,\beta _{k}}\) is given by
where \(d_{\alpha ,\beta _{k}}(x,{\tilde{x}},y,{\tilde{y}})\) represents a two-scale “version” of the non-local diffusivity coefficient \(D(X,{\tilde{X}})\). More precisely, by using Eq. (5), we have that \(D(X,{\tilde{X}})\) is replaced by \(d_{\alpha ,\beta _{k}}(x,{\tilde{x}},y,{\tilde{y}})\), which means that the parameters \(\alpha \) and \(\beta _{k}\) (see below) are already present in \(D(X,{\tilde{X}})\). Analogously, \({\mathfrak {f}}_{\alpha ,\beta _{k}}(x-{\tilde{x}},y-{\tilde{y}})\) and \({\mathfrak {d}}_{\alpha ,\beta _{k}}(x,{\tilde{x}},y,{\tilde{y}})\) replace \({\mathfrak {F}}(X-{\tilde{X}})\) and \({\mathfrak {D}}(X,{\tilde{X}})\) in the decomposition (3b), but describe the non-locality and the fractional diffusivity resolved on the two different scales accounted for in this work. Particularly, \(\alpha \in {\mathbb {R}}^{+}\) is referred to as the macro-scale non-locality parameter and characterises the non-local interactions in the region \({\mathscr {X}}\). On the other hand, \(\beta _{k}\in {\mathbb {R}}^{+}\), with \(k=1,2\), is the micro-scale non-locality parameter describing the non-locality within the sub-cell \({\mathscr {Y}}_{k}\). Note that \(q_{\alpha ,\beta _{k}}\) absorbs the factor \(1/L_{\mathrm {c}}\) that stems from the chain rule (6) when one switches to the two-scale representation of the flux.
Remark 1
The representation of the two-scale, non-local mass flux in Eqs. (17a) and (17b) does not follow directly from (3a). This is because the double integral over \({\mathscr {X}}\times {\mathscr {Y}}_{k}\) defining \(q_{\alpha ,\beta _{k}}\) cannot be obtained by only applying the two-scale representation prescribed by (5) and (6) to the integrand of (3a). Rather, to account for the two-scale resolution of the flux, a further step is needed, which requires to pass from a single integration in the variable \({\tilde{X}}\) to a double integration in the two auxiliary variables \({\tilde{x}}\) and \({\tilde{y}}\). In this respect, it must be clearly stated that the flux \(q_{\alpha ,\beta _{k}}\) is not equal to Q, and it is introduced ad hoc as a mathematical tool with the purpose of resolving the two-scale dependence of the original flux. Hence, the definition of \(q_{\alpha ,\beta _{k}}\) must be regarded as a conjecture, which in the limit \(\varepsilon \rightarrow 0\), and within the asymptotic homogenisation approach, converges to an effective flux that represents the limit of Q [refer to Eq. (45b)]. Proving this rigorously is part of our current investigations, which involve, among others, the concept of two-scale convergence [27, 58, 80].
We remark that the introduction of the non-local parameters \(\alpha \) and \(\beta _{k}\) follows from the fact that we interpret non-local effects by using the notions of Fractional Calculus [7], in which derivatives and integrals of fractional order are considered. The parameter \(\alpha \) accounts for the intensity of non-locality at the macro-scale, whereas we have intentionally introduced two different non-locality parameters, \(\beta _{1}\) and \(\beta _{2}\), at the microscopic level to describe the existence of “long-range” interactions even at the scale of each sub-cell \({\mathscr {Y}}_{k}\). This is indeed the essence of the micro-scale non-locality.
We further notice that, if the concentration \(c_{k}\) is dimensionless, the flux \(q_{\alpha ,\beta _{k}}\) must have the physical dimensions of the reciprocal of time, and it follows from Eq. (17b) that the same must be true for the dimensions of \(d_{\alpha ,\beta _{k}}\). To guarantee the latter condition, and keeping in mind that \({\mathfrak {d}}_{\alpha ,\beta _{k}}\) is a (fractional) diffusivity, we take the dimensions of \({\mathfrak {d}}_{\alpha ,\beta _{k}}\) to be \([{\mathfrak {d}}_{\alpha ,\beta _{k}}]=\mathrm {length}^{\xi (\alpha ,\beta _{k})}/\mathrm {time}\), where \(\xi (\alpha ,\beta _{k})\) is a real number expressed as a function of \(\alpha \) and \(\beta _{k}\), and, consequently, we take \([{\mathfrak {f}}_{\alpha ,\beta _{k}}]=\mathrm {length}^{-\xi (\alpha ,\beta _{k})}\). In the local case, the non-locality function may be taken dimensionless, which means that \(\xi (\alpha ,\beta _{k})\) must tend towards zero, and the fractional diffusivity becomes a pure rate, that is \([{\mathfrak {d}}_{\alpha ,\beta _{k}}]=\mathrm {time}^{-1}\).
In the sequel, we assume that every field is periodic with respect to the micro-scale variable y. Moreover, the spatial fractional diffusivity \({\mathfrak {d}}_{\alpha ,\beta _{k}}\) is considered to be independent of x, \({\tilde{x}}\) and y, and with a slight abuse of notation, we simply write \({\mathfrak {d}}_{\alpha ,\beta _{k}}({\tilde{y}})\). This simplification, however, has not major repercussions in the results of the following sections.
4 Two-scale asymptotic homogenisation approach
In this work, we adopt the asymptotic homogenisation technique and prescribe a formal two-scale expansion for \(c_{k}\) in power series of the smallness parameter \(\varepsilon >0\), namely
where each \(c_{k}^{(n)}(x,\cdot ,t)\), \(n=0,1,2,\ldots \), is assumed to be periodic with respect to y (said more rigorously: periodic with respect to its second argument).
Before substituting the formal expansion (18) into (16a)–(16c), we find it convenient to rewrite Eqs. (16a)–(16c) as follows
where the following notation has been adopted
Specifically, in (20a) and (20b), the uppercase and lowercase symbols \({\mathcal {Q}}_{\alpha ,\beta _{k}}\) and \({\mathcal {q}}_{\alpha ,\beta _{k}}\) indicate the partial differentiation of \(c_{k}\) inside the integral with respect to \({\tilde{x}}\) and \({\tilde{y}}\), respectively. Moreover, it holds that \(q_{\alpha ,\beta _{k}} = {\mathcal {Q}}_{\alpha ,\beta _{k}} +\varepsilon ^{-1}{\mathcal {q}}_{\alpha ,\beta _{k}}\).
After substituting (18), truncated to the order \(\varepsilon ^{2}\), into (19a)–(19c), (20a) and (20b), the problem reduces to finding the leading order coefficients \(c_{k}^{(n)}\) of the power series (18), which solve the boundary problems resulting from equating all the terms in the same powers of \(\varepsilon \). To this end, it is useful to write explicitly the generic coefficients of the expansion of the fluxes \({\mathcal {q}}_{\alpha ,\beta _{k}}\) and \({\mathcal {Q}}_{\alpha ,\beta _{k}}\), i.e.
for \(n=0,1,2,\ldots \), so that, in the limit \(\varepsilon \rightarrow 0\), \({\mathcal {q}}_{\alpha ,\beta _{k}}\) and \({\mathcal {Q}}_{\alpha ,\beta _{k}}\) can be approximated by
Next, the problem (16a)–(16c), truncated to the order \(\varepsilon ^{2}\), splits into three sub-problems, one for each of the considered orders of \(\varepsilon \).
In the sequel, to avoid the proliferation of indices, we simplify the notation as follows
Analogously, we set \({\mathfrak {f}}_{\alpha ,\beta _{k}}\equiv {\mathfrak {f}}_{k}\) and \({\mathfrak {d}}_{\alpha ,\beta _{k}}\equiv {\mathfrak {d}}_{k}\).
(i) To the order \(\varepsilon ^{0}\),
Equation (24a) implies that \({\mathcal {q}}_{k}^{(0)}\) is independent of the microscopic variable, since its partial derivative with respect to y is zero. One possible way of ensuring this condition could be to drop the dependence of \({\mathfrak {f}}_{k}\) on the micro-scale variables. However, this assumption would eliminate the possibility of keeping track of the non-locality at the micro-scale, which is clearly in contrast with our purposes. Instead, to guarantee the fulfilment of Eq. (24a) and to make sure we remain within a non-local setting, we require \(c_{k}^{(0)}\) to be independent of y. Hence, with a slight abuse of notation, we set
thereby satisfying Eqs. (24a)–(24c), since \({\mathcal {q}}_{k}^{(0)}=0\), without having to rebut the dependence of \({\mathfrak {f}}_{k}\) on the micro-scale. The above consideration is a standard result of linear asymptotic homogenisation, whereas it is often assumed for nonlinear problems (see, e.g. [28, 65, 68]). A direct consequence of (25) is that \(c^{(0)}_{1}\) and \(c^{(0)}_{2}\) coincide with each other, so that we can write
(ii) To the order \(\varepsilon ^{1}\) By taking into consideration Eq. (25), we have that
with \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\). The structure of (27a) implies that, in general, this equation must be solved in the spatial domain \({\mathscr {X}}\times {\mathscr {Y}}_{k}\), which in the context of asymptotic homogenisation means that one needs to consider a problem defined in \({\mathscr {Y}}_{k}\) for each \(x\in {\mathscr {X}}\).
Remark 2
(A comment on the solution to (27a)–(27c)) The local counterpart of the problem (27a)–(27c) (see [15, 27]) can be obtained by choosing the non-locality function
where \(\delta \) is Dirac’s delta. Specifically,
with \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\). In Eqs. (29b) and (29c) the evaluation in \(y_{\mathrm {I}}\) of \({\mathfrak {d}}_{k}\) and \(\partial _{y}c_{k}^{(1)}\) are to be understood in the sense of lateral limits \(y\rightarrow y_{\mathrm {I}}^{\pm }\). In this particular case, the problem (29a)–(29c) admits a unique solution, which is defined up to a function depending solely on time, t, and on the slow variable, x [15, 27]. This unique solution is usually expressed through the ansatz
where \(\vartheta _{k}\) is the new unknown of the problem (29a)–(29c) and \(\varphi \) is a function of x and t that spans the family of all the solutions [11, 63]. To the best of our knowledge, in the non-local case there is no theorem that guarantees the existence and uniqueness (even in the sense explained above) of the solution. Still, in the absence of a supporting theory, we guess that, similarly to the local case, the solution should have the form (30), with \(\vartheta _{k}\) suitably parametrised by \(\alpha \) and \(\beta _{k}\). \(\square \)
By substituting (30) into (27a)–(27b), we require the auxiliary functions \(\vartheta _{k}\) to satisfy the non-local cell problem,
with \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\) and
We notice that the structure of the non-local problem (31a)–(31c) does not permit, in general, to factorise the macroscopic term \(\partial _{{\tilde{x}}}c^{(0)}({\tilde{x}},t)\). This implies that one should account for the macroscopic contributions at the micro-structural level and, thus, for the interchange of information between the two length scales.
(iii) To the order \(\varepsilon ^{2}\),
with \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\).
Before going further in our analysis, we introduce, for a given field \(\phi \), defined in the cell \({\mathscr {Y}}\) or in a subset of it having the same measure, the operators
such that the sum \(\langle \phi \rangle _{1}+\langle \phi \rangle _{2}=\langle \phi \rangle \) is the average of \(\phi \) over the cell \({\mathscr {Y}}\). Then, by applying these operators to (33a), we have
Because of Eq. (26), \(c^{(0)}\) depends only on x and t and then,
Moreover, the assumption of macroscopic uniformity (see Sect. 3.2) implies that the differential operator \(\partial _{x}\) and the integral operator \(\langle \cdot \rangle _{k}\) commute, so that, the second term of (35) rewrites as,
Therefore, summing up Eq. (35) over k and taking into account the relations (36) and (37), we obtain
We notice that the third term of (38) can be computed as
where we have employed Gauss’ theorem and the continuity of the fluxes at the interface and at the boundaries of the cell. Specifically, because of the continuity of the fluxes at the interface \(y_{\mathrm {I}}\), it holds true that
which eliminates the first and the fourth summand on the far right-hand side of Eq. (39). Moreover, the flux computed at the right boundary of the cell, i.e. \({\mathcal {q}}_{2}^{(2)}(x,1^{-},t)+{\mathcal {Q}}_{2}^{(1)}(x,1^{-},t)\), must be equal to the flux entering or leaving the neighbouring cell, which can be written as \({\mathcal {q}}_{1}^{(2)}(x,1^{+},t)+{\mathcal {Q}}_{1}^{(1)}(x,1^{+},t)\). Therefore, by invoking the \({\mathscr {Y}}\)-periodicity of the flux, we can conclude that the second and the third term of Eq. (39) also cancel themselves, i.e.
Equations (40) and (41) explain in detail the reason why Eq. (39) holds true. Before going further, we emphasise that the considerations done so far hold true also for all the other orders of the asymptotic expansion of the flux, like, for instance, \({\mathcal {q}}_{k}^{(1)}+{\mathcal {Q}}_{k}^{(0)}\).
Then, the substitution of (39) into (38) yields the homogenised problem for the leading order term \(c^{(0)}\), i.e.
where
is referred to as the non-local effective mass flux, while \(d^{\,\mathrm {eff}}\) is defined through the expression
and represents the non-local effective diffusivity. We notice that the homogenised equation (42) has the same structure as (1a), but, in this case, the contributions of the micro-structure are resolved by means of the non-local effective coefficient \(d^{\,\mathrm {eff}}\).
Finally, according to [63, 68] we introduce the notation \({\mathscr {X}}_{\mathrm {h}}\) to denote the homogenised version of the composite medium, and we reformulate the homogenised problem (42) and (43) as follows
which has to be supplemented with appropriate initial and boundary conditions for the unknown \(c^{(0)}\).
Remark 3
Note that, since \({\mathfrak {f}}_{k}\) and \({\mathfrak {d}}_{k}\) are short-hand notations for \({\mathfrak {f}}_{\alpha ,\beta _{k}}\) and \({\mathfrak {d}}_{\alpha ,\beta _{k}}\), both the non-local effective diffusivity, \(d^{\,\mathrm {eff}}\), and the non-local effective flux, \(q^{\,\mathrm {eff}}\), depend on the collection of all the parameters that describe the non-locality of the problem, i.e. \(\alpha \), \(\beta _{1}\) and \(\beta _{2}\). Hence, the effective quantities \(d^{\,\mathrm {eff}}\) and \(q^{\,\mathrm {eff}}\) keep track simultaneously of the non-locality occurring both at the scale of the sub-cells, through \(\beta _{1}\) and \(\beta _{2}\), and at the scale of the medium, through \(\alpha \). In the following, with the purpose of leaving the notation at a minimum level of complexity, we shall keep the symbols \(d^{\,\mathrm {eff}}\) and \(q^{\,\mathrm {eff}}\), although we mean \(d^{\,\mathrm {eff}}_{\alpha ,\beta _{1},\beta _{2}}\) and \(q^{\,\mathrm {eff}}_{\alpha ,\beta _{1},\beta _{2}}\), respectively.
\(\square \)
Remark 4
In summary, the equations to be solved are (31a) for \(\vartheta _{k}\) and (45a) for \(c^{(0)}\). We notice that, in general, these equations are coupled in contrast to the local case of the standard asymptotic homogenisation in which the cell and the homogenised problems are uncoupled. As anticipated above, this is due to the fact that \(\partial _{x}c^{(0)}(x,t)\) cannot be factorised out the integral in Eq. (32a). \(\square \)
Remark 5
It is worth noticing that if the non-locality function is \({\mathfrak {f}}_{k}(x-{\tilde{x}},y-{\tilde{y}})=\delta (x-{\tilde{x}})\delta (y-{\tilde{y}})\), we end up with classical results of homogenisation theory [15, 27, 63, 69]. That is, by substituting this expression for \({\mathfrak {f}}_{k}\) into Eq. (31a), the cell problem reads
where \(\mathrm {d}_{y}\vartheta _{k}(y)\) denotes the total derivative of \(\vartheta _{k}\). Furthermore, the non-local effective diffusivity, \(d^{\,\mathrm {eff}}\), is
with \({\hat{d}}^{\,\mathrm {eff}}_{\mathrm {s}\mathrm {t}}\) being entirely defined by the sum over k in (47). In this case, \({\hat{d}}^{\,\mathrm {eff}}_{\mathrm {s}\mathrm {t}}\) is a constant coefficient that coincides with the effective diffusivity of a standard diffusion problem in a composite medium [15, 51, 56]. Furthermore, after substitution of (47) into (45a), we obtain the standard homogenised equations
where standard Fick’s law is re-obtained for the flux. \(\square \)
Remark 6
We notice that in the present framework, we do not take into account the timescales associated with the problems (24a), (27a) and (33a), since we intend to focus on the spatial connections between heterogeneity and non-locality. Nevertheless, one can notice that the characteristic length scales \(L_{\mathrm {c}}\) and \(\ell \) associated with the composite medium and with its internal structure, respectively, induce different timescales (see, e.g. [49]). In fact, by virtue of a reference diffusivity \( {\mathfrak {d}}_{\mathrm {R}}\), these can be expressed as
Since in the sequel we specialise Eq. (49) to the case of media with different diffusivities inside the sub-cells \({\mathscr {Y}}_{1}\) and \({\mathscr {Y}}_{2}\), we can prescribe \({\mathfrak {d}}_{\mathrm {R}}:=\min \{{\mathfrak {d}}_{1\mathrm {R}},{\mathfrak {d}}_{2\mathrm {R}}\}\).
By employing (49), we deduce the following relationship between the characteristic time scales,
Now, before proceeding further, we mention that in this multi-scale framework, a given physical quantity \(\varPhi (X,t)\) can be rewritten as
with \(\zeta :=t/\zeta _{\mathrm {c}}\) and \(\eta :=\zeta /\varepsilon ^{2}\) (compare Eq. (51) with Eq. (5) in which time was not rescaled). Therefore, Eq. (16a) rewrites
which, after substituting the two-scale expansion (18) and equating in the same powers of \(\varepsilon \), up to the order \(\varepsilon ^{2}\), yields
As Eqs. (53a)–(53c) prescribe, this approach calls for the solution of diffusion problems at each order of \(\varepsilon \). Moreover, the consideration of the separation of the time scales conduces to leading-order problems that are characterised by the presence of the rapid time variable \(\eta \). The analysis of these equations is part of our current research.
5 Description of the benchmark problems
In this section, we present two simplified models in which the non-local effects are only present at the macro-scale or at the micro-scale, and we report some details of the numerical schemes based on FE methods.
It is worth mentioning that the cell and the homogenised problems obtained in this work feature integro-differential equations of fractional type in bounded domains and, therefore, the classical solution techniques, such as Laplace and Fourier transforms, used in Fractional Calculus are not suitable. Consequently, either do we need to develop dedicated numerical algorithms or we resort to well-established numerical methods, and we adapt them to take into account the presence of fractional differential operators in the considered problems. Here, we follow the second path and, indeed, we write a numerical scheme based on a finite element (FE) discretisation of the original integro-differential problems. In doing this, we need to emphasise that, partly because of the very easy geometry of the problems (we deal, in fact, with one-dimensional benchmark studies), and partly because the focus of our work is not on the numerics, the presentation of the FE scheme is very elementary. Indeed, it can be obtained by appropriately rephrasing the one-dimensional formulation of the FE method as presented, e.g. in [44]. Moreover, we do not fuss over some technical aspects of the finite element procedures, such as the “element point of view” [44] et similia, since our scope is solely meant to highlight how the symmetrised Caputo fractional derivatives affect the stiffness matrix and the nodal force of the discretisation. Clearly, a more detailed numerical study is required, and this is part of our current investigations. We highlight that previous works in this direction are [35, 43, 71]. In particular, the work we took major inspiration from is [43].
In the remainder of this work, the following considerations are adopted.
(i) Fractional diffusivity. We prescribe \({\mathfrak {d}}_{1}\) and \({\mathfrak {d}}_{2}\) to be constant in \({\mathscr {Y}}_{1}\) and \({\mathscr {Y}}_{2}\), respectively. Then, by recalling the discussion made in Sect. 3.4, we express each \({\mathfrak {d}}_{k}\) as
where \({\mathfrak {d}}_{k\mathrm {R}}\) is the constant reference diffusivity of \({\mathscr {Y}}_{k}\) and it has the dimensions of a standard diffusivity, i.e. length squared over time [67].
(ii) Initial and boundary conditions for the homogenised equation. We enforce an initial spatial distribution for \(c^{(0)}\) of the form
where k, r and \(x_{0}\) are model parameters.
To contextualise our work, we mention that the initial condition \(c_{\mathrm {in}}(x)\) in (55) is sometimes employed to simulate the initial concentration of molecules after photobleaching in a Fluorescence recovery after photobleaching (FRAP) experiment [13]. In this way, following [39], the model is prepared to describe the fluorescence recovery pattern of molecules surrounding a certain region of a tissue (in particular, articular cartilage) after being photobleached, by using a high-intensity laser beam. Here, we do not go into the technical details pertaining to a FRAP experiment, since this is not the focus of our work, and the benchmark proposed hereafter is also markedly different from the one developed in [39]. Thus, we do not claim that our results are meant to simulate a FRAP experiment. Still, since the setting presented in [39] refers to a tissue with hierarchical internal structure, as is the case of articular cartilage, our work might bring some new insight into the interpretation of the experimental results. To this end, we adapt the framework described in [39] to the setting of the homogenised problem (45a)–(45b) and, specifically, we identify k, r and \(x_{0}\) with the bleaching depth parameter, the dimension of the bleached area, and the centre of the bleached region, respectively.
We notice that, since this work is framed in a one-dimensional setting, r characterises the measure of a line-segment of \({\mathscr {X}}_{\mathrm {h}}\), and we choose \(x_{0}\) as the centre of the macroscopic domain \({\mathscr {X}}_{\mathrm {h}}\), namely \(x_{0}=\tfrac{1}{2}(L/L_{\mathrm {c}})\). In addition, we adapt the boundary conditions given in [39] to the geometry of our problem, and impose Dirichlet boundary conditions for \(c^{(0)}\) at \(x=0\) and \(x=L/L_{\mathrm {c}}\). Specifically, we set
which implies
(iii) Parameters. In Table 1, we provide the values of the parameters used in our numerical simulations. We notice that the value of r is meant to “cover” 100 reference cells.
5.1 Benchmark problem I: micro-scale non-locality
Let us consider the case in which the non-locality is accounted for only at the micro-scale. This can be achieved by prescribing
that is, we accept the existence of “long-range” interactions in each sub-cell \({\mathscr {Y}}_{k}\). Note that we use quotation marks because the concept of long-range interactions has to be understood with respect to each sub-cell, which is microscopic, and, in this context, as a synonym of non-locality. We also notice that the index k in \({\mathfrak {g}}_{k}\) allows to characterise two different non-local frameworks occurring in each sub-cell \({\mathscr {Y}}_{k}\). For instance, as discussed above, we could enforce that the non-local interactions exist only in one of the two sub-cells, although here we consider non-locality acting in both sub-cells.
Clearly, different forms for \({\mathfrak {g}}_{k}\) can be considered, each of which leading to diverse non-local models of diffusion. In this work, we adopt the decaying power-law [6, 22, 59, 67, 76]
where \(\varGamma (\cdot )\) denotes the Euler Gamma function and \(\beta _{k}\in \,]0,1[\). From here on, we set \(\beta _{1}=\beta _{2}=\beta \), thereby obtaining \({\mathfrak {g}}_{1}={\mathfrak {g}}_{2}={\mathfrak {g}}\) and \({\mathfrak {f}}_{1}={\mathfrak {f}}_{2}={\mathfrak {f}}\). We notice that \({\mathfrak {g}}\) scales multiplicatively with \(L_{\mathrm {c}}^{1-\beta }\) because it is expressed as a function of dimensionless variables. Accordingly, the physical dimensions of the fractional diffusivities \({\mathfrak {d}}_{k}\) are given by \([{\mathfrak {d}}_{k}]=L_{\mathrm {c}}^{-1+\beta }t_{\mathrm {c}}^{-1}\) for each \(k=1,2\). Hence, Eq. (54) yields
5.1.1 The non-local cell problem
By considering Eqs. (58) and (59), the non-local cell problem is given by
where \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\) and
As shown in (62a) and (62b), the assumption of non-locality only at the micro-scale permits to factorise \(\partial _{x}c^{(0)}\) from the integrals expressing \({\mathcal {q}}^{(1)}_{k}\) and \({\mathcal {Q}}^{(0)}_{k}\). Consequently, the auxiliary unknowns \(\vartheta _{1}\) and \(\vartheta _{2}\) can be reformulated as functions of y only, and for further use, the following notation is introduced
We notice that the quantities \({\mathcal {q}}_{k}(y)\) and \({\mathcal {Q}}_{k}(y)\) defined in (63a) and (63b) represent, up to the sign, “dressed” diffusivities rather than fluxes. In fact, we may write
We further mention that, in the proper limit, \({\mathcal {q}}_{k}(y)\) and \({\mathcal {Q}}_{k}(y)\) return the negative of the standard diffusivities (see Remark 7). Particularly, in Eqs. (63a) and (63b), we recognise the symmetrised Caputo fractional derivative of order \(\beta \in \,]0,1[\) [7]. Then, it holds true that
where \(\kappa (y)=y\), and
denotes the symmetrised Caputo fractional derivative of order \(\beta \) of a generic differentiable function \(\phi \). Furthermore, we notice that \({\mathcal {Q}}_{k}(y)\) can be computed explicitly for each \(k=1,2\), and reads
where the functions \({\mathcal {A}}_{1}\) and \({\mathcal {A}}_{2}\) are given by
Because of these results, the flux (64b) admits the explicit expression
while, for the time being, no explicit expression can be given to \({\mathcal {q}}_{k}\), since the functions \(\vartheta _{k}\) are still unknown. Upon recalling the definition (12), in which a given function restricted to the elementary cell is assigned in a piecewise manner, the fluxes \({\mathcal {Q}}_{1}^{(0)}\) and \({\mathcal {Q}}_{2}^{(0)}\) in (65) can be rejoined in a unique flux, whose restriction to \({\mathscr {Y}}\) is given by
Now, for the function \({\mathcal {Q}}^{(0)}\) given in (70), we can employ the definition of periodicity specified in (13), so that it holds
It follows from this result that \({\mathcal {Q}}^{(0)}\) is \({\mathscr {Y}}\)-periodic and that such periodicity does not depend on the point \(y_{\mathrm {I}}\) in which the interface is placed within the elementary cell.
By using the above results, the non-local cell problem (61a)–(61c) can be rewritten as
where the right-hand side of (72c) is the result of the difference \({\mathcal {Q}}_{2}(y_{\mathrm {I}})-{\mathcal {Q}}_{1}(y_{\mathrm {I}})\). We recall that all the expressions at the interface are to be understood for the values of the limits of the corresponding physical quantities for \(y\rightarrow y_{\mathrm {I}}^{\pm }\). Indeed, for instance, \({\mathcal {Q}}_{1}(y_{\mathrm {I}})\) means, with a slight abuse of notation, \({\mathcal {Q}}_{1}(y_{\mathrm {I}})=\lim _{y\rightarrow y_{\mathrm {I}}^{-}}{\mathcal {Q}}_{1}(y)\).
Remark 7
We notice that for \(y\in {\mathscr {Y}}_{k}\), it holds
while
Then, it follows from Eqs. (73)–(74b) that the convergence of \({\mathcal {Q}}_{k}\) for \(\beta \rightarrow 1^{-}\) is not uniform in \({\overline{{\mathscr {Y}}}}_{k}\).
By comparing with classical results of the asymptotic homogenisation technique, the above computations suggest that, for \(\beta \rightarrow 1^{-}\), the solution of the non-local cell problem must approach the solution of the classical, local cell problem. We notice that the 2 in the denominator of (74b) does not appear in the formulation of the standard cell problem. Nevertheless, it compensates with the 2 in the denominator of the left-hand side of (72c), hidden in the fractional derivatives defining \({\mathcal {q}}_{k}\), which can be determined after finding \(\vartheta _{k}\). \(\square \)
5.1.2 The homogenised equation
By taking into account Eqs. (58) and (59), the non-local effective coefficient can be rewritten as
and, therefore, according to Eq. (43), the effective flux is given by
where we have set
Hence, the effective fractional diffusivity, \({\hat{d}}^{\,\mathrm {eff}}(\beta )\), can be expressed in terms of the symmetrised Caputo fractional derivative of \(\vartheta _{k}\). We notice that, in this particular case, \({\hat{d}}^{\,\mathrm {eff}}(\beta )\) does not depend on space and time, while it is parametrised by \(\beta \). Furthermore, from its mathematical expression it is clear that it ciphers the information on the non-local interactions at the micro-scale.
Remark 8
The form of the effective fractional diffusivity (77) recalls the relation obtained in the standard case by means of asymptotic homogenisation [12, 15, 69]. Particularly, by Fubini’s theorem and Eq. (67), \({\hat{d}}^{\,\mathrm {eff}}(\beta )\) can be equivalently rewritten as
Therefore, taking into account Eq. (73), we obtain that
which coincides with the effective diffusivity of a standard diffusion problem with unitary reference cell (see, e.g. [27]).
Furthermore, since Eqs. (77) and (78) provide equivalent writings for \({\hat{d}}^{\,\mathrm {eff}}(\beta )\), from (79) it follows that, in the limit \(\beta \rightarrow 1^{-}\), the symmetrised Caputo fractional derivative of \(\vartheta _{k}\) converges to the first derivative of \(\vartheta _{k}\), namely,
and therefore, we can conclude that \({\mathcal {q}}_{k}^{(1)}\) (see Eq. (64a)) recovers Fick’s law in bounded domains. \(\square \)
Finally, taking into account Eq. (77) and the initial and boundary conditions (55)–(57), the homogenised problem reads
We notice that, in this simplified case, the non-local cell problem (72a)–(72c) and the homogenised problem (81a)–(81c) are not coupled.
5.1.3 Numerical solution
In this section, we solve numerically the mathematical model given by the non-local cell problem (72a)–(72c) and the homogenised problem (81a)–(81c). In particular, the homogenised problem is characterised by a partial differential equation, while the non-local cell problem features an integro-differential equation of fractional type.
For solving Eqs. (72a)–(72c) in a bounded domain, the techniques based on Fourier and Laplace transforms are of little help and, consequently, we implement a numerical algorithm. Specifically, we solve the non-local cell problem by means of a FE scheme which accounts for fractional derivatives and interface conditions. Since the homogenised problem (81a)–(81c) involves classical FE techniques, in what follows we report only on the numerical scheme to be used for solving the non-local cell problem (72a)–(72c), and for the computation of the non-local effective diffusivity (77).
Before going further, we notice that, in the classical homogenisation literature, the uniqueness of the solution of the cell problem is guaranteed by imposing that \(\langle \vartheta _{k}\rangle _{k}\) is equal to zero. However, from a computational point of view, a more feasible condition is to fix the value of the auxiliary variables \(\vartheta _{k}\) at one point in the cell [62]. Accordingly, here, we impose that \(\vartheta _{1}\) is zero at \(y=0\), and by periodicity \(\vartheta _{2}\) is also zero at \(y=1\).
Now, let us introduce the following spaces of test functions
where \({\mathscr {H}}^{1}({\mathscr {Y}}_{k})\) is the Sobolev space of functions of \(L^{2}({\mathscr {Y}}_{k})\) with finite \(L^{2}({\mathscr {Y}}_{k})\)-norm of their distributional derivatives up to order one [73]. Then, by multiplying Eq. (72a) by \(v_{k}\), integrating over \({\mathscr {Y}}_{k}\), and adding over \(k=1,2\), we obtain
Hence, due to the continuity condition at the interface (72c), and the restrictions made for \(v_{k}\), Eq. (83) reads
Equation (84) represents the weak formulation of the non-local cell problem (72a)–(72c), and is discretised by employing the FE technique. Therefore, we introduce for \({\mathscr {Y}}_{1}\) and \({\mathscr {Y}}_{2}\), \(N_{1}+1\) and \((N_{2}+1)-N_{1}\) discretisation points, respectively, and the function bases \(\{\psi ^{1}_{i}\}_{i=0}^{N_{1}}\) and \(\{\psi ^{2}_{i}\}_{i=N_{1}}^{N_{2}}\), with \(N_{1}>1\) and \(N_{2}>N_{1}+1\) and, for each \(k=1,2\),
with \(y_{N_{1}}=y_{\mathrm {I}}\). Then, the test functions \(v_{k}\) are approximated by
where \(\upsilon ^{k}_{j}\), \(k=1,2\), are nonzero, arbitrary constants. Analogously, the approximated trial functions \({\check{\vartheta }}_{k}(y)\) are written as
where \(\omega ^{k}_{i}\) are unknown constant coefficients representing the nodal values of \({\check{\vartheta }}_{k}\). We notice that, in this particular case, the coefficients \(\omega ^{k}_{i}\) do not depend on time, whereas in a more general setting they should be defined as functions of time.
Next, by substituting expressions (87) and (86) into (84), we obtain the following system of equations for \(\omega ^{k}_{i}\),
where
represent, for each \(k=1,2\), the components of the fractional stiffness matrix of the FE discretisation of the sub-cell \({\mathscr {Y}}_{k}\), and of the nodal fractional force associated with the j-th node of \({\mathscr {Y}}_{k}\), respectively.
Remark 9
(Density and limit of \({\mathsf {L}}^{k}(\beta )\) and \({\mathsf {F}}^{k}(\beta )\)) It is worth noting that, whereas in the standard cell problem the stiffness matrix is tridiagonal for each \(k=1,2\), in the present framework it is dense because the cross integrations between the derivatives of the basis functions lead to nonzero components of
for each pair of j and i. This is due to the non-locality introduced by the fractional derivatives \({\mathcal {D}}_{k}^{\beta }[\psi _{i}^{k}]\), as reported in the far right-hand side of Eq. (90). Specifically, even though two discretisation nodes are far away from each other, the entries of the matrix corresponding to those nodes are nonzero. This results in a dense stiffness matrix and, the stronger the non-locality, the denser the matrix will be. Nevertheless, the fractional stiffness matrix will converge to a tridiagonal matrix when \(\beta \rightarrow 1^{-}\). Indeed, as discussed in Remark 8, when \(\beta \rightarrow 1^{-}\) we obtain
Analogously, from the definition of \({\mathsf {F}}_{j}^{k}(\beta )\), i.e.
we infer that the existence of the non-locality function implies that the entries of \({\mathsf {F}}^{k}_{j}(\beta )\) are nonzero. Furthermore, recalling that \(\lim _{\beta \rightarrow 1^{-}}[{\mathcal {A}}_{k}(y;\beta )/2\varGamma (1-\beta )]=1\), for \(y\in {\mathscr {Y}}_{k}\), we have that
Equation (93) returns 0 for all \(j\ne N_{1}\) and \({\mathfrak {d}}_{k\mathrm {R}}L_{\mathrm {c}}^{-2}\) if \(j=N_{1}\).
To exemplify the limit of the symmetrised Caputo fractional derivative of the bases functions, we report in Fig. 2 a comparison of the symmetrised Caputo fractional derivative of order \(\beta \in \,]0,1[\) of the function
which recalls a Lagrange polynomial of the first order, with the classical first derivative of the same function. \(\square \)
Next, to obtain the algebraic form of the FE procedure, we introduce the notation
where \(\upsilon ^{\mathrm {I}}_{N_{1}} = \upsilon ^{1}_{N_{1}} = \upsilon ^{2}_{N_{1}}\) and \(\omega ^{\mathrm {I}}_{N_{1}} = \omega ^{1}_{N_{1}} = \omega ^{2}_{N_{1}}\) are the nodal values of the virtual concentration and of the unknown concentration at the interface, and we write the final forms of the fractional stiffness matrix and of the fractional nodal force as follows
Note that in (96a) and (96b), we have omitted the dependence on \(\beta \) , although this dependence is understood.
Then, by using the notation introduced in Eqs. (95a)–(96b), Eq. (88) can be rewritten as
which leads to the algebraic equation
On the other hand, by using the expression for \({\check{\vartheta }}_{k}\) given in (87), the approximation of the effective fractional diffusivity (77) can be numerically calculated as
which we call numerical effective fractional diffusivity. We provide details about the explicit form of Eqs. (98) and (99) in “Appendix A”.
5.1.4 Results and discussion
In this section, we show the numerical results for the benchmark problem described above, and we discuss the influence of the micro-scale non-local interactions on the homogenised behaviour of the concentration.
To begin with, in Fig. 3, we report the profile of the solution of the non-local cell problem (72a)–(72c), i.e. \({\check{\vartheta }}_{k}\), and compare it with the solution of the standard, local cell problem. Specifically, the solid lines distinguish the solutions of the non-local cell problem for different values of the non-locality parameter \(\beta \in \,]0,1[\), and the dashed line represents the solution of the standard, local cell problem. In particular, the space discretisation of the computational domain was done by fixing the grid size to \(h:=y_{i}-y_{i-1}=1.3\times 10^{-3}\) uniformly with respect to i. We notice that the results of the finite element analysis are not affected appreciably by subsequent mesh refinements.
In Fig. 3, we observe that the spatial distribution of \({\check{\vartheta }}_{k}\) varies with \(\beta \) and it converges to the solution of the local cell problem as \(\beta \rightarrow 1^{-}\) (dashed line in Fig. 3). This outcome is coherent with the theoretical results previously obtained in this section. Furthermore, we notice that the non-local solutions fluctuate around the local one, and they intersect each other and the local solution in symmetric points. Nevertheless, the non-local solutions are not symmetric with respect to the line \(y=y_{\mathrm {I}}\).
Before going further, few words should be spent about the issue of symmetry. To this end, let us assume just for this discussion that the interface between the sub-cells, \(y_{\mathrm {I}}\), is not the midpoint of the cell \({\mathscr {Y}}\!=\,]0,1[\), and let us start with the local case (recovered for \(\beta \rightarrow 1^{-}\)). In the local case, the solution of the cell problem, here denoted by \(\vartheta ^{\mathrm {local}}\) and defined as \(\vartheta ^{\mathrm {local}}(y)=\vartheta _{1}^{\mathrm {local}}(y)\) for \(y\in \,[0,y_{\mathrm {I}}]\) and \(\vartheta ^{\mathrm {local}}(y)=\vartheta _{2}^{\mathrm {local}}(y)\) for \(y\in \,]y_{\mathrm {I}},1]\), is in general not symmetric because the diffusivity coefficients are distributed within the cell in a non-symmetric way (clearly, this asymmetry would disappear if the diffusivities were equal to each other). Within the framework studied here, the solution will have, indeed, the shape of a non-symmetric “roof”, with an increasing straight line on \([0,y_{\mathrm {I}}]\) and a decreasing straight line on \(]y_{\mathrm {I}},1]\), whose slopes have different signs and different absolute values. In other words, the inequality \({\mathfrak {d}}_{1\mathrm {R}}\ne {\mathfrak {d}}_{2\mathrm {R}}\) and the position of the interface break the symmetry that the solution would have in the homogeneous case (the solution of the problem at hand would trivially boil down to a constant in the homogeneous case). Symmetry, however, can be partially restored if the interface is assumed to be placed at the midpoint, as is the case in our simulations. This condition, indeed, places a geometric constraint that forces the solution to be symmetric, thereby acquiring the shape of a symmetric “roof”, with the slope of the straight line on \([0,y_{\mathrm {I}}]\) being the opposite of the slope of the straight line on \(]y_{\mathrm {I}},1]\). This means that we have passed from the continuous symmetry of the homogeneous solution to the discrete symmetry of the heterogeneous solution with interface in the midpoint of the cell.
The picture just described changes considerably when the non-local case is studied. Indeed, for \(\beta \in \,]0,1[\), the fractional derivatives featuring in the non-local cell problem are an additional source of symmetry breaking that, together with the heterogeneity of the diffusivity, make the solution even more non-symmetric. This remains true even though \(y_{\mathrm {I}}\) is the midpoint of the cell. More importantly, since the local solution is symmetric for \(y_{\mathrm {I}}=1/2\) in spite of the heterogeneity of the diffusivity, this setting singles out the contribution of the fractional derivatives to the symmetry breaking of the problem. We believe that the asymmetry of the non-local solution, which decreases with \(\beta \), may be ascribable to an interplay between non-locality and heterogeneity: in the sub-cell in which the medium is more diffusive, the solution is “stiffer” which results into moderate deviations from the standard solution; on the other hand, in the sub-cell in which the diffusivity is smaller, the solution is more “compliant”, thereby producing large deviations from the local solution.
Now, once \({\check{\vartheta }}_{k}\) is known, we can compute the effective fractional diffusivity \({\hat{d}}^{\,\mathrm {eff}}_{\mathrm {num}}\) as prescribed by formula (99). Particularly, in Fig. 4, we plot the values of this homogenised coefficient for varying \(\beta \in \,[0,1]\) and compare them with the classical effective diffusivity, i.e. the one resulting from the local case. Specifically, a closer look at the data reported in Fig. 4 reveals that, for increasing \(\beta \), the value of the effective fractional diffusivity resulting from a non-local setting is higher. In particular, as discussed in Remark 8, as \(\beta \) tends to 1 from below, the approximated effective fractional diffusivity converges to the standard effective one given by the local case.
We notice that for \(\beta =0\) the auxiliary problem is ill-posed and, thus, \({\check{\vartheta }}_{k}\) cannot be determined. This is also reflected by the fact that the stiffness matrix of the problem, \({\mathsf {L}}(0)\), becomes singular for \(\beta =0\), and \({\check{\vartheta }}_{k}\) becomes non-differentiable at \(y=y_{\mathrm {I}}\) and at the boundaries of the cell. On the other hand, for \(\beta >0\), the gradients of \({\check{\vartheta }}_{k}\) exist at these points but their magnitude increases for \(\beta \rightarrow 0^{+}\). Nevertheless, it is worth remarking that, for very small values of \(\beta \), the numerical solution almost does not change. Particularly, the \(L^{\infty }\)-norm of the error between the numerical solutions for \(\beta =10^{-8}\) and \(\beta =10^{-3}\) is of the order of \(10^{-4}\). In addition to these considerations, we would like to point out that neither \({\check{\vartheta }}_{k}\) nor its gradient are observable physical quantities. Rather, \({\check{\vartheta }}_{k}(y)\) is just an auxiliary quantity for determining the observables \({\mathcal {q}}_{k}^{(1)}(x,y,t)\), \({\mathcal {q}}_{k}(y)\), and, more importantly, the effective fractional diffusivity and the homogenised solution. To this end, we notice that, in fact, \({\hat{d}}^{\,\mathrm {eff}}(\beta )\) and \(c^{(0)}\) are well behaved for all values of \(\beta \in \,]0,1[\) as shown in Figs. 4 and 5, and also for \(\beta =0\). Specifically, in spite of the technical difficulty for \(\beta =0\), which makes the employment of the FE method impossible, it is still possible to determine the variations
which return the value of \(\vartheta _{k}\) at the interface. This calculation allows us to compute, even in this limit case, the effective diffusivity coefficient \({\hat{d}}^{\,\mathrm {eff}}(\beta )\), which, as shown in Eq. (77), we rephrase as a function of \(\beta \) and, for \(\beta = 0\), reads
Since, as per Fig. 4, which is the plot of Eq. (77), \({\hat{d}}^{\,\mathrm {eff}}(\beta )\) is a continuous and monotonically increasing function of \(\beta \in [0,1]\), it occurs that the value \({\hat{d}}^{\,\mathrm {eff}}_{0}\) represents the absolute minimum of the effective diffusivity coefficient, i.e. \({\hat{d}}^{\,\mathrm {eff}}_{0}=\min _{\beta \in [0,1]}\{{\hat{d}}^{\mathrm {eff}}(\beta )\}\), and the absolute maximum is \({\hat{d}}^{\,\mathrm {eff}}(1)=\max _{\beta \in [0,1]}\{{\hat{d}}^{\,\mathrm {eff}}(\beta )\}\).
The above result describes, for each \(\beta \in [0,1]\), the influence of the micro-scale non-locality on the macroscopic distribution of the concentration \(c^{(0)}\) (see Fig. 5). In particular, for \(\beta \) tending towards zero, i.e. for increasing “strength” of the micro-scale non-locality, the macro-scale diffusion of the considered substance is hindered, and \(c^{(0)}(x,t)\) consistently tends to vary rather slowly in time. On the contrary, in the limit case \(\beta \rightarrow 1^{-}\), \(c^{(0)}(x,t)\) varies more rapidly in time, since the diffusion tends to acquire the “classical” behaviour predicted by Fick’s law (see Fig. 5). In this respect, the consideration of non-local interactions at the micro-scale influences the way in which diffusion takes place in the composite medium. Returning to the FRAP experiment in the context of the benchmark problem, this theoretical behaviour implies that the recovery pattern of chemical species after being photobleached is slower for \(\beta \) near 0, whereas it is faster for \(\beta \) close to 1, thereby simulating a standard diffusion process.
5.2 Benchmark problem II: macro-scale non-locality
In this section, we assume that the non-local interactions are present at the macro-scale only. Thus, by specialising \({\mathfrak {f}}_{\alpha ,\beta _{k}}\) in (17b) to the limit case \(\beta _{k}\rightarrow 1^{-}\), we consider the following form for the non-locality function
Hence, since \({\mathfrak {h}}_{\alpha }\) depends only on the difference \(x-{\tilde{x}}\), the non-local character of the diffusion process is accounted for at the macroscopic level only, and similarly to what was done in the previous section, we write
In this particular case, the physical dimensions of the fractional diffusivities \({\mathfrak {d}}_{k}\) are \([{\mathfrak {d}}_{k}]=L_{\mathrm {c}}^{-1+\alpha }t_{\mathrm {c}}^{-1}\) and hence, from (54), we have that
5.2.1 The cell problem
By considering the expressions (102)–(104), the non-local cell problem (31a)–(31c) rewrites
where \((x,y,t)\in {\mathscr {X}}\times {\mathscr {Y}}_{k}\times ]0,t_{\mathrm {f}}[\) and
In (106b), \({\mathcal {D}}^{\alpha }[c^{(0)}]\) represents the symmetrised Caputo fractional derivative of order \(\alpha \in \,]0,1[\) of \(c^{(0)}\).
Particularly, the computational complexity of the above cell problem is significantly reduced if the solution \(\vartheta _{k}\) is x-constant (which in the present framework also implies that it is constant in time). Then, with a slight abuse of notation we write \(\vartheta _{k}(x,y,t)=\vartheta _{k}(y)\), and \({\mathcal {q}}_{k}^{(1)}\) in (106a) becomes
while Eq. (105a) rewrites
We notice that \(c^{(0)}(x,t)\equiv c^{(0)}(t)\) is the only solution of the equation \({\mathcal {D}}^{\alpha }[c^{(0)}](x,t)=0\) [6]. Therefore, by excluding this case, the cell problem can be written in the more standard form
In this specific case, the analytical solution of the cell problem (109a)–(109c) can be found by using standard techniques for differential equations. However, since our scope is to find the effective coefficient, this is not necessary. Indeed, from (109a) we can deduce that
where \(a_{k}\), with \(k=1,2\), are two constants to be determined. In particular, substituting (110) in (109c) yields \(a_{1}=a_{2}\equiv a\), and the constant a can be computed by invoking periodicity and (109b). In fact, from (110), it follows that
and, by applying the operators defined in (34) to the last equation, we have
which implies that
Therefore, after substitution of (102) and (103) into Eq. (44), and using (110) and (113), the non-local effective coefficient can be computed as
It is worth mentioning that, even though, in this particular formulation, the cell and the homogenised problems have been decoupled, the non-local effective diffusivity (114) is still influenced by the non-local interactions occurring at the macroscopic level through the scalar function \(\vert x-{\tilde{x}}\vert ^{-\alpha }\). Note also that the last two factors of \(d^{\,\mathrm {eff}}(x,{\tilde{x}})\) in (114) are the kernel of the operator defined in (103).
5.2.2 The homogenised equation
By using the previous results, the effective non-local mass flux can be recast in the form
which is thus entirely determined by the symmetrised Caputo fractional derivative of order \(\alpha \) of the leading order concentration \(c^{(0)}\) and by the effective diffusivity coefficient
We notice that definition (116) coincides (not surprisingly) with the constant a defined in Eq. (113), and with the standard effective diffusivity [15, 27, 63]. Besides, the physical dimensions of \({\hat{d}}^{\,\mathrm {eff}}_{\mathrm {s}\mathrm {t}}\) are those of the reciprocal of time.
Finally, the homogenised equation (45a), with the boundary and initial conditions given in (55) and (57), reduces to
5.2.3 Numerical solution
In this section, we find the numerical solution of the non-local, homogenised problem (117a)–(117c) by means of FE methods. As we previously mentioned, in this context, the effective diffusivity can be found without recurring to solve the cell problem (compare Eqs. (116) and (113)).
To start with, we discretise the time interval \([0,t_{\mathrm {f}}]\) in M subintervals, which we assume of equal amplitude \(\tau \). Then, for simplicity of notation, we set \(c^{(0)}(x,t_{m})=u^{m}(x)\) and we adopt an implicit Euler scheme for Eq. (117a), which is thus approximated as
Next, by introducing the space of test functions [73]
where \({\mathscr {H}}^{1}({\mathscr {X}}_{\mathrm {h}})\) is defined analogously to \({\mathscr {H}}^{1}({\mathscr {Y}}_{k})\), we put Eq. (118) in weak form. To this end, we multiply Eq. (118) by the test function \(v\in {\mathscr {V}}\), and after integrating over \({\mathscr {X}}_{\mathrm {h}}\), we find
Next, we discretise the spatial domain \({\mathscr {X}}_{\mathrm {h}}\) in N finite elements, and introduce the function basis \(\{\psi _{i}\}_{i=0}^{N}\), with \(\psi _{i}(x_{j})=\delta _{ij}\) and \(i,j=0,\ldots ,N\). Then, we approximate v(x), the initial condition \(u^{0}(x)\), and \(u^{m}(x)\), for all m, as
where \(\omega _{i}^{m}\), with \(m=1,\ldots ,M+1\), are constant coefficients to be determined and \(t_{M+1}=t_{\mathrm {f}}\). Thus, by substituting (121a) and (121c) into (120), and adopting a standard procedure in FE, we find
where
It is worth to remark that both the stiffness matrix \({\mathsf {L}}_{ji}(\alpha )\) and the nodal force \({\mathsf {F}}_{j}(\alpha )\) depend on the parameter \(\alpha \in \,]0,1[\).
Then, Eq. (122) can be rewritten as
which, by factorising \(\{\upsilon \}^{\mathrm {T}}\), leads to the linear system
Details about the explicit form of Eq. (125) are provided in “Appendix B”.
5.2.4 Results and discussion
We notice that, in the present framework, to find the numerical solution of the homogenised problem, we only need to know \({\hat{d}}^{\,\mathrm {eff}}_{\mathrm {s}\mathrm {t}}\) as prescribed by Eq. (116). Particularly, by using the values reported in Table 1, we obtain
Then, in Fig. 6, we show the distribution of \(c^{(0)}\) for different values of \(\alpha \in \,]0,1[\) and for different instants of time. According to the plots, and similarly to the previous benchmark problem, the variation of the non-locality parameter influences the way in which diffusion takes place, and in which the stationary state is attained. That is, the progression of the solution towards the stationary states for \(\alpha =0.1\) is much slower than in the case determined by \(\alpha =0.9\). In particular, when \(\alpha \) approaches 1 from below, the standard diffusion is recovered. We remark that, although we have imposed an initial concentration with very small spatial derivative at the boundary, once time initiates to increase, the tails of the concentration profile tend to raise. This behaviour can be explained by the production of concentration gradients that are needed for the chemical species to diffuse, in this case, towards the centre of the specimen. However, such gradients tend to “turn off” themselves in the course of time since the concentration has to move towards its stationary value.
It is worth noticing that the way in which the non-local interactions are introduced influences the diffusion profile of the chemical species (see Fig. 7). Indeed, when considering the existence of non-local interactions at the micro-scale, these are ciphered into the effective coefficient \({\hat{d}}^{\,\mathrm {eff}}(\beta )\), which is parametrised by \(\beta \), while the effective mass flux has the classical form given by Fick’s law. On the other hand, the consideration of long-range interactions at the macro-scale leads, as prescribed by (114), to a non-local effective diffusivity that depends on the spatial points, and thus to a homogenised equation of fractional type for the leading order of concentration. In this case, as shown in Fig. 7, there is a strong memory of the initial concentration, that is, the fractional operators appearing in Eq. (117a) help to preserve the information of the initial distribution of chemical species as time passes. This phenomenon is less pronounced when the non-locality is considered only at the micro-scale, and indeed, for \(t\le 6\,\mathrm {h}\) the diffusion near the boundary of the composite is slower. We further notice that, by comparing the curves resulting from the benchmark problem I with the ones from the standard, local framework, the assumption of the non-locality at the micro-scale produces a slower diffusion of the species. Thus, we can conclude that the consideration of non-local effects at the micro-structure impacts the evolution of the concentration at the macro-scale.
Finally, we remark that for \(\alpha \rightarrow 1^{-}\) and \(\beta \rightarrow 1^{-}\) both benchmark tests restore the standard diffusion given by Fick’s law and, thus, they become indistinguishable in the limit. For this reason, in Fig. 7, we report only the cases in which there is a strong non-locality, that is when \(\alpha \) and \(\beta \) are near zero.
6 Conclusions
In this work, we study the two-scale, non-local diffusion of a chemical species in a composite medium. This is addressed by prescribing a two-scale constitutive law of fractional type for the mass flux of the chemical species and, with the aid of the asymptotic homogenisation technique, by solving the homogenised version of the original problem. Specifically, we obtain an effective characterisation of the composite, which is subjected to the existence of non-local interactions at both length scales. In fact, we prove that if non-locality is neglected, we recover the classical results of homogenisation theory.
To quantify the effects of the non-locality in our model, we present two simplified benchmark tests in which long-range interactions are considered at the micro-scale or at the macro-scale only. In both cases, we prove that in the limit in which the non-locality parameters \(\beta \) (in the benchmark test I) and \(\alpha \) (in the benchmark test II) tend to 1 from below, the fractional cell and homogenised problems lead to the standard ones given in the classical homogenisation literature.
Furthermore, we perform numerical simulations and report the most important steps leading to the finite element discretisation. We remark that the formulation of the FE scheme is very basic and was adapted from the one developed in [44] for one-dimensional problems. Nevertheless, the simplicity of the numerics allows us to discuss some of the specific properties of the algebraic equations resulting from the discretisation process. In particular, in the benchmark problems, the presence of the symmetrised Caputo fractional derivative results in fractional stiffness matrices and fractional nodal forces. More specifically, we prove that the fractional stiffness matrices are symmetric and, although they are dense because of the presence of the fractional derivatives, in the limits \(\alpha \rightarrow 1^{-}\) and \(\beta \rightarrow 1^{-}\) they become the standard stiffness matrices of tridiagonal form. The numerical simulations are in harmony with these theoretical predictions.
It is important to emphasise that the way in which the non-local interactions influence the macroscopic behaviour of the system depends on the scale at which these interactions are introduced. When the non-local interactions are considered at the micro-scale, they emerge also at the macro-scale through the effective fractional diffusivity \({\hat{d}}^{\,\mathrm {eff}}(\beta )\) and by slowing down the diffusion. However, the effect of the non-local interactions is more evident when those are accounted for at the macro-scale, and occurs through a deceleration of the diffusion process that is stronger than in the previous case. Hence, the information enclosed in the initial distribution of the concentration is kept for a “longer” time.
As a first step in our investigations, we conceived a model in one dimension. Clearly, this model can be generalised to higher dimensions. However, there are some issues that must be tackled. One of them is that the non-locality function and the normalisation factors should be conceived in a symmetry- and dimension-dependent way. Moreover, a more detailed numerical study would be required. These issues are part of our current research.
Change history
18 May 2021
Funding note has been updated in the article.
References
Alaimo, G., Piccolo, V., Cutolo, A., Deseri, L., Fraldi, M., Zingales, M.: A fractional order theory of poroelasticity. Mech. Res. Commun. 100, 103395 (2019). https://doi.org/10.1016/j.mechrescom.2019.103395
Allaire, G., Briane, M.: Multiscale convergence and reiterated homogenisation. Proc. R. Soc. Edinb. Sect. A Math. 126(02), 297–342 (1996). https://doi.org/10.1017/s0308210500022757
Alotta, G., Bologna, E., Zingales, M.: Exact mechanical hierarchy of non-linear fractional-order hereditariness. Symmetry 12(4), 673 (2020). https://doi.org/10.3390/sym12040673
Askes, H., Aifantis, E.C.: Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 48(13), 1962–1990 (2011). https://doi.org/10.1016/j.ijsolstr.2011.03.006
Atanacković, T., Konjik, S., Oparnica, L., Zorica, D.: The Cattaneo type space-time fractional heat conduction equation. Continuum Mech. Thermodyn. 24(4–6), 293–311 (2011). https://doi.org/10.1007/s00161-011-0199-4
Atanackovic, T., Stankovic, B.: Generalized wave equation in nonlocal elasticity. Acta Mech. 208(1–2), 1–10 (2008). https://doi.org/10.1007/s00707-008-0120-9
Atanacković, T.M., Pilipović, S., Stanković, B., Zorica, D.: Fractional Calculus with Applications in Mechanics: Vibrations and Diffusion Processes. ISTE Ltd., London (2014)
Atanackovic, T.M., Pilipovic, S., Zorica, D.: A diffusion wave equation with two fractional derivatives of different order. J. Phys. A: Math. Theor. 40(20), 5319–5333 (2007). https://doi.org/10.1088/1751-8113/40/20/006
Auriault, J.: Effective macroscopic description for heat conduction in periodic composites. Int. J. Heat Mass Transf. 26(6), 861–869 (1983). https://doi.org/10.1016/s0017-9310(83)80110-0
Auriault, J.L., Boutin, C., Geindreau, C. (eds.): Homogenization of Coupled Phenomena in Heterogenous Media. ISTE, London (2009). https://doi.org/10.1002/9780470612033
Auriault, J.L., Geindreau, C., Boutin, C.: Filtration law in porous media with poor separation of scales. Transp. Porous Media 60(1), 89–108 (2005). https://doi.org/10.1007/s11242-004-3649-7
Auriault, J.L., Lewandoska, J.: Effective diffusion coefficient: from homogenization to experiment. Transp. Porous Media 27(2), 205–223 (1997). https://doi.org/10.1023/a:1006599410942
Axelrod, D., Koppel, D., Schlessinger, J., Elson, E., Webb, W.: Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16(9), 1055–1069 (1976). https://doi.org/10.1016/s0006-3495(76)85755-4
Baglieri, O., Santagata, E., Sapora, A., Cornetti, P., Carpinteri, A.: Fractional viscoelastic modeling of antirutting response of bituminous binders. J. Eng. Mech. 143(5), D4016002 (2017). https://doi.org/10.1061/(asce)em.1943-7889.0001081
Bakhvalov, N., Panasenko, G.: Homogenisation: Averaging Processes in Periodic Media. Springer, Netherlands (1989)
Beltempo, A., Bonelli, A., Bursi, O.S., Zingales, M.: A numerical integration approach for fractional-order viscoelastic analysis of hereditary-aging structures. Int. J. Numer. Methods Eng. 121(6), 1120–1146 (2019). https://doi.org/10.1002/nme.6259
Bensoussan, A., Lions, J.L., Papanicolau, G.: Asymptotic Analysis for Periodic Structures. Elsevier Science, Amsterdam (1978)
Bueno-Orovio, A., Kay, D., Grau, V., Rodriguez, B., Burrage, K.: Fractional diffusion models of cardiac electrical propagation: role of structural heterogeneity in dispersion of repolarization. J. R. Soc. Interface 11, 20140352 (2014). https://doi.org/10.1098/rsif.2014.0352
Burridge, R., Keller, J.B.: Poroelasticity equations derived from microstructure. J. Acoust. Soc. Am. 70(4), 1140–1146 (1981). https://doi.org/10.1121/1.386945
Buryachenko, V.: On thermoelastostatics of composites with nonlocal properties of constituents I General representations for effective material and field parameters. Int. J. Solids Struct. 48(13), 1818–1828 (2011). https://doi.org/10.1016/j.ijsolstr.2011.02.023
Capuani, S., Palombo, M., Gabrielli, A., Orlandi, A., Maraviglia, B., Pastore, F.S.: Spatio-temporal anomalous diffusion imaging: results in controlled phantoms and in excised human meningiomas. Magn. Reson. Imaging 31(3), 359–365 (2013). https://doi.org/10.1016/j.mri.2012.08.012
Carpinteri, A., Cornetti, P., Sapora, A.: A fractional calculus approach to nonlocal elasticity. Eur. Phys. J. Spec. Top. 193(1), 193–204 (2011). https://doi.org/10.1140/epjst/e2011-01391-5
Carpinteri, A., Mainardi, F. (eds.): Fractals and Fractional Calculus in Continuum Mechanics. Springer, Vienna (1997)
del Castillo-Negrete, D.: Fractional diffusion models of nonlocal transport. Phys. Plasmas 13(8), 082308 (2006). https://doi.org/10.1063/1.2336114
Chaves, A.: A fractional diffusion equation to describe lévy flights. Phys. Lett. A 239(1–2), 13–16 (1998). https://doi.org/10.1016/s0375-9601(97)00947-x
Cherednichenko, K.D., Smyshlyaev, V.P., Zhikov, V.V.: Non-local homogenized limits for composite media with highly anisotropic periodic fibres. Proc. R. Soc. Edinb. Sect. A Math. 136(1), 87–114 (2006). https://doi.org/10.1017/s0308210500004455
Cioranescu, D.: An Introduction to Homogenization. Oxford University Press, Oxford (1999)
Collis, J., Brown, D.L., Hubbard, M.E., O’Dea, R.D.: Effective equations governing an active poroelastic medium. Proc. R. Soc. A Math. Phys. Eng. Sci. 473(2198), 20160755 (2017). https://doi.org/10.1098/rspa.2016.0755
Danyuo, Y., Ani, C.J., Salifu, A.A., Obayemi, J.D., Dozie-Nwachukwu, S., Obanawu, V.O., Akpan, U.M., Odusanya, O.S., Abade-Abugre, M., McBagonluri, F., Soboyejo, W.O.: Anomalous release kinetics of prodigiosin from poly-n-isopropyl-acrylamid based hydrogels for the treatment of triple negative breast cancer. Sci. Rep. 9(1), 1–14 (2019). https://doi.org/10.1038/s41598-019-39578-4
Deseri, L., Paola, M.D., Zingales, M., Pollaci, P.: Power-law hereditariness of hierarchical fractal bones. Int. J. Numer. Methods Biomed. Eng. 29(12), 1338–1360 (2013). https://doi.org/10.1002/cnm.2572
Di Paola, M., Zingales, M.: Long-range cohesive interactions of non-local continuum faced by fractional calculus. Int. J. Solids Struct. 45(21), 5642–5659 (2008). https://doi.org/10.1016/j.ijsolstr.2008.06.004
Di Stefano, S., Miller, L., Grillo, A., Penta, R.: Effective balance equations for electrostrictive composites. Zeitschrift für angewandte Mathematik und Physik 71(5), 1–36 (2020). https://doi.org/10.1007/s00033-020-01365-x
Dormieux, L., Djimédo, K., Franz-Josef, U.: Microporomechanics. Wiley, Chichester (2006)
Eringen, A.C.: Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 10(5), 425–435 (1972). https://doi.org/10.1016/0020-7225(72)90050-x
Estrada-Rodriguez, G., Gimperlein, H., Painter, K.J., Stocek, J.: Space-time fractional diffusion in cell movement models with delay. Math. Models Methods Appl. Sci. 29(01), 65–88 (2019). https://doi.org/10.1142/s0218202519500039
Filipovitch, N., Hill, K.M., Longjas, A., Voller, V.R.: Infiltration experiments demonstrate an explicit connection between heterogeneity and anomalous diffusion behavior. Water Resour. Res. 52(7), 5167–5178 (2016). https://doi.org/10.1002/2016wr018667
Geers, M., de Borst, R., Peijs, T.: Mixed numerical-experimental identification of non-local characteristics of random-fibre-reinforced composites. Compos. Sci. Technol. 59(10), 1569–1578 (1999). https://doi.org/10.1016/s0266-3538(99)00017-2
Gurtin, M., Fried, E., Anand, L.: The Mechanics and Thermodynamics of Continua. Cambridge University Press, Cambridge (2010)
Hashlamoun, K., Abusara, Z., Ramírez-Torres, A., Grillo, A., Herzog, W., Federico, S.: Fluorescence recovery after photobleaching: direct measurement of diffusion anisotropy. Biomech. Model. Mechanobiol. (2020). https://doi.org/10.1007/s10237-020-01346-z
Hill, R.: Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 11(5), 357–372 (1963). https://doi.org/10.1016/0022-5096(63)90036-x
Holmes, M.H.: Introduction to Perturbation Methods. Springer, New York (2013). https://doi.org/10.1007/978-1-4614-5477-9
Hori, M., Nemat-Nasser, S.: On two micromechanics theories for determining micro-macro relations in heterogeneous solids. Mech. Mater. 31(10), 667–682 (1999). https://doi.org/10.1016/s0167-6636(99)00020-4
Huang, Q., Huang, G., Zhan, H.: A finite element solution for the fractional advection–dispersion equation. Adv. Water Resour. 31(12), 1578–1589 (2008). https://doi.org/10.1016/j.advwatres.2008.07.002
Hughes, T.J.R.: The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Dover Publications, Mineola (2000)
Jiang, C., Cui, C., Li, L., Shao, Y.: The anomalous diffusion of a tumor invading with different surrounding tissues. PLoS ONE 9(10), e109784 (2014). https://doi.org/10.1371/journal.pone.0109784
Kim, C.S., Randow, C., Sano, T. (eds.): Hybrid and Hierarchical Composite Materials. Springer International Publishing, Berlin (2015). https://doi.org/10.1007/978-3-319-12868-9
Kröner, E.: Elasticity theory of materials with long range cohesive forces. Int. J. Solids Struct. 3(5), 731–742 (1967). https://doi.org/10.1016/0020-7683(67)90049-2
Lacks, D.J.: Tortuosity and anomalous diffusion in the neuromuscular junction. Phys. Rev. E 77(4), 041912 (2008). https://doi.org/10.1103/physreve.77.041912
Lunati, I., Attinger, S., Kinzelbach, W.: Macrodispersivity for transport in arbitrary nonuniform flow fields: asymptotic and preasymptotic results. Water Resour. Res. 38(10), 5-1 (2002). https://doi.org/10.1029/2001wr001203
Lynch, V., Carreras, B., del Castillo-Negrete, D., Ferreira-Mejias, K., Hicks, H.: Numerical methods for the solution of partial differential equations of fractional order. J. Comput. Phys. 192(2), 406–421 (2003). https://doi.org/10.1016/j.jcp.2003.07.008
Marchena-Menéndez, J., Ramírez-Torres, A., Penta, R., Rodríguez-Ramos, R., Merodio, J.: Macroscopic thermal profile of heterogeneous cancerous breasts. A three-dimensional multiscale analysis. Int. J. Eng. Sci. 144, 103135 (2019). https://doi.org/10.1016/j.ijengsci.2019.103135
Meerschaert, M.M., Mortensen, J., Wheatcraft, S.W.: Fractional vector calculus for fractional advection–dispersion. Phys. A 367, 181–190 (2006). https://doi.org/10.1016/j.physa.2005.11.015
Meerschaert, M.M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56(1), 80–90 (2006). https://doi.org/10.1016/j.apnum.2005.02.008
Metzler, R., Klafter, J.: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339(1), 1–77 (2000). https://doi.org/10.1016/s0370-1573(00)00070-3
Milton, G.W.: The Theory of Composites. Cambridge University Press, Cambridge (2002). https://doi.org/10.1017/cbo9780511613357
Muha, I., Naegel, A., Stichel, S., Grillo, A., Heisig, M., Wittum, G.: Effective diffusivity in membranes with tetrakaidekahedral cells and implications for the permeability of human stratum corneum. J. Membr. Sci. 368(1–2), 18–25 (2011). https://doi.org/10.1016/j.memsci.2010.10.020
Mura, T.: Micromechanics of Defects in Solids. Springer, Dordrecht (1987). https://doi.org/10.1007/978-94-009-3489-4
Nguetseng, G.: A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20(3), 608–623 (1989). https://doi.org/10.1137/0520043
Paradisi, P., Cesari, R., Mainardi, F., Maurizi, A., Tampieri, F.: A generalized Fick’s law to describe non-local transport effects. Phys. Chem. Earth Part B 26(4), 275–279 (2001). https://doi.org/10.1016/s1464-1909(01)00006-5
Penta, R., Ambrosi, D., Quarteroni, A.: Multiscale homogenization for fluid and drug transport in vascularized malignant tissues. Math. Models Methods Appl. Sci. 25(01), 79–108 (2014). https://doi.org/10.1142/s0218202515500037
Penta, R., Ambrosi, D., Shipley, R.J.: Effective governing equations for poroelastic growing media. Q. J. Mech. Appl. Math. 67(1), 69–91 (2014). https://doi.org/10.1093/qjmam/hbt024
Penta, R., Gerisch, A.: Investigation of the potential of asymptotic homogenization for elastic composites via a three-dimensional computational study. Comput. Vis. Sci. 17(4), 185–201 (2015). https://doi.org/10.1007/s00791-015-0257-8
Penta, R., Gerisch, A.: An introduction to asymptotic homogenization. In: Gerisch, A., Penta, R., Lang, J. (eds.) Lecture notes in computational science and engineering, pp. 1–26. Springer, Berlin (2017)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications (ISSN Book 198). Academic Press, Cambridge (1998)
Pruchnicki, E.: Hyperelastic homogenized law for reinforced elastomer at finite strain with edge effects. Acta Mech. 129(3–4), 139–162 (1998). https://doi.org/10.1007/bf01176742
Rabotnov, Y.: Elements of Hereditary Solid Mechanics. Mir, Moscow (1977)
Ramírez-Torres, A., Di Stefano, S., Grillo, A.: Influence of non-local diffusion in avascular tumour growth. Mech. Math. Solids (2020). https://doi.org/10.1177/1081286520975086. First Published online: January 4, 2021.
Ramírez-Torres, A., Di Stefano, S., Grillo, A., Rodríguez-Ramos, R., Merodio, J., Penta, R.: An asymptotic homogenization approach to the microstructural evolution of heterogeneous media. Int. J. Non-Linear Mech. 106, 245–257 (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.06.012
Ramírez-Torres, A., Rodríguez-Ramos, R., Sabina, F.J., García-Reimbert, C., Penta, R., Merodio, J., Guinovart-Díaz, R., Bravo-Castillero, J., Conci, A., Preziosi, L.: The role of malignant tissue on the thermal distribution of cancerous breast. J. Theor. Biol. 426, 152–161 (2017). https://doi.org/10.1016/j.jtbi.2017.05.031
Rodríguez-Ramos, R., Otero, J.A., Cruz-González, O.L., Guinovart-Díaz, R., Bravo-Castillero, J., Sabina, F.J., Padilla, P., Lebon, F., Sevostianov, I.: Computation of the relaxation effective moduli for fibrous viscoelastic composites using the asymptotic homogenization method. Int. J. Solids Struct. 190, 281–290 (2020). https://doi.org/10.1016/j.ijsolstr.2019.11.014
Roop, J.P.: Computational aspects of FEM approximation of fractional advection dispersion equations on bounded domains in \({\mathbb{R}}^2\). J. Comput. Appl. Math. 193(1), 243–268 (2006). https://doi.org/10.1016/j.cam.2005.06.005
Di Stefano, S., Ramírez-Torres, A., Penta, R., Grillo, A.: Self-influenced growth through evolving material inhomogeneities. Int. J. Non-Linear Mech. 106, 174–187 (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.08.003
Salsa, S.: Partial Differential Equations in Action: From Modelling to Theory. Springer, New York (2008)
Sanchez-Palencia, E.: Non-Homogeneous Media and Vibration Theory. Springer, Berlin (1980). https://doi.org/10.1007/3-540-10000-8
Sapora, A., Cornetti, P., Carpinteri, A.: Diffusion problems on fractional nonlocal media. Open Phys. 11(10), 1255–1261 (2013). https://doi.org/10.2478/s11534-013-0323-0
Sapora, A., Cornetti, P., Chiaia, B., Lenzi, E.K., Evangelista, L.R.: Nonlocal diffusion in porous media: a spatial fractional approach. J. Eng. Mech. 143(5), D4016007 (2017). https://doi.org/10.1061/(asce)em.1943-7889.0001105
Sciumè, G., Shelton, S., Gray, W.G., Miller, C.T., Hussain, F., Ferrari, M., Decuzzi, P., Schrefler, B.A.: A multiphase model for three-dimensional tumor growth. New J. Phys. 15(1), 015005 (2013). https://doi.org/10.1088/1367-2630/15/1/015005
Silling, S.A.: Origin and effect of nonlocality in a composite. J. Mech. Mater. Struct. 9(2), 245–258 (2014). https://doi.org/10.2140/jomms.2014.9.245
Svanstedt, N., Wyller, J., Malyutina, E.: A one-population Amari model with periodic microstructure. Nonlinearity 27(6), 1391–1417 (2014). https://doi.org/10.1088/0951-7715/27/6/1391
Visintin, A.: Towards a two-scale calculus. Control Optim. Calc. Var. 12(3), 371–397 (2006). https://doi.org/10.1051/cocv:2006012
Želi, V., Zorica, D.: Analytical and numerical treatment of the heat conduction equation obtained via time-fractional distributed-order heat conduction law. Phys. A 492, 2316–2335 (2018). https://doi.org/10.1016/j.physa.2017.11.150
Acknowledgements
ART and AG acknowledge the Dipartimento di Scienze Matematiche (DISMA) “G.L. Lagrange” of the Politecnico di Torino, “Dipartimento di Eccellenza 2018-2022” (“Department of Excellence 2018-2022”), Project No. E11G18000350001. RP is partially supported by EPSRC grants EP/S030875/1 and EP/T017899/1.
Funding
Open access funding provided by Politecnico di Torino within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Funding note has been updated in the article.
Appendices
FE discretisation of the non-local cell problem. Benchmark problem I
Here, we calculate the matrices appearing in Eq. (98) and the non-local effective diffusivity (99). Firstly, we recall that the system (98) reads
with
For the sake of simplicity, let us consider that the basis functions are Lagrange polynomials of the first order,
for \(i=1,\ldots ,N_{1}-1\) if \(k=1\), and \(i=N_{1}+1,\ldots ,N_{2}-1\) for \(k=2\), and at the interface \(y_{N_{1}}=y_{\mathrm {I}}\), we prescribe
Then, from the above expressions, the fractional stiffness matrices \({\mathsf {L}}^{k}_{ji}(\beta )\) are computed in two steps. First, we calculate the symmetrised Caputo fractional derivatives of (129)–(130b) and then, we substitute the results into (128a) and (128b). However, before doing this, we find it convenient to compute the following integrals,
From here on, for the sake of a lighter notation, we omit the dependence of \({\mathcal {H}}_{k,l}^{p,q}\) on \(\beta \). Moreover, we notice that
Therefore, by using the definitions for the basis functions \(\psi _{i}^{k}\) and (131a), the symmetrised Caputo fractional derivative of \(\psi _{i}^{k}\) is given by
where \(i=1,\ldots ,N_{1}-1\), if \(k=1\), and \(i=N_{1}+1,\ldots ,N_{2}-1\), if \(k=2\). Besides,
We remark that, by taking the limit in expressions (133)–(134b) for \(\beta \rightarrow 1^{-}\), we obtain
for \(y\ne y_{i}\), \(i=1,\ldots ,N_{1}-1,N_{1}+1,\ldots ,N_{2}\). Moreover, for \(y\ne y_{N_{1}}\),
Therefore, the results (135)–(136b), as previously proved, imply that the symmetrised Caputo fractional derivative of \(\psi _{i}^{k}\) tends to the first derivative of \(\psi _{i}^{k}\) for \(\beta \rightarrow 1^{-}\).
1.1 Computation of \({\mathsf {L}}^{k}\)
From (131b), we have that for \(j,i=1,\ldots ,N_{1}-1\), if \(k=1\), and \(j,i=N_{1}+1,\ldots ,N_{2}-1\), if \(k=2\), the components of the fractional stiffness matrix are
Furthermore,
-
if \(j=1,\ldots ,N_{1}-1\) and \(i=N_{1}\)
$$\begin{aligned} {\mathsf {L}}^{1}_{j\,N_{1}}(\beta )&= \frac{{\mathfrak {d}}_{1\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )}\frac{1}{y_{N_{1}}-y_{N_{1}-1}}\left( \frac{{\mathcal {H}}^{j-1,j}_{N_{1}-1,N_{1}}}{y_{j}-y_{j-1}}-\frac{{\mathcal {H}}^{j,j+1}_{N_{1}-1,N_{1}}}{y_{j+1}-y_{j}}\right) , \end{aligned}$$(138) -
if \(j=N_{1}\) and \(i=1,\ldots ,N_{1}-1\)
$$\begin{aligned} {\mathsf {L}}^{1}_{N_{1}i}(\beta )&= \frac{{\mathfrak {d}}_{1\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{1}{y_{N_{1}}-y_{N_{1}-1}}\left( \frac{{\mathcal {H}}^{N_{1}-1,N_{1}}_{i-1,i}}{y_{i}-y_{i-1}}-\frac{{\mathcal {H}}^{N_{1}-1,N_{1}}_{i,i+1}}{y_{i+1}-y_{i}}\right) , \end{aligned}$$(139) -
if \(i,j=N_{1}\)
$$\begin{aligned} {\mathsf {L}}^{1}_{N_{1}N_{1}}(\beta )&= \frac{{\mathfrak {d}}_{1\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{1}{(y_{N_{1}}-y_{N_{1}-1})^2}{\mathcal {H}}_{N_{1}-1,N_{1}}^{N_{1}-1,N_{1}}, \end{aligned}$$(140a)$$\begin{aligned} {\mathsf {L}}^{2}_{N_{1}N_{1}}(\beta )&= \frac{{\mathfrak {d}}_{2\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{1}{(y_{N_{1}+1}-y_{N_{1}})^2}{\mathcal {H}}_{N_{1},N_{1}+1}^{N_{1},N_{1}+1}, \end{aligned}$$(140b) -
if \(j=N_{1}\) and \(i=N_{1}+1,\ldots ,N_{2}-1\)
$$\begin{aligned} {\mathsf {L}}^{2}_{N_{1}i}(\beta )&= -\frac{{\mathfrak {d}}_{2\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{1}{y_{N_{1}+1}-y_{N_{1}}}\left( \frac{{\mathcal {H}}^{N_{1},N_{1}+1}_{i-1,i}}{y_{i}-y_{i-1}}-\frac{{\mathcal {H}}^{N_{1},N_{1}+1}_{i,i+1}}{y_{i+1}-y_{i}}\right) , \end{aligned}$$(141) -
if \(j=N_{1}+1,\ldots ,N_{2}-1\) and \(i=N_{1}\)
$$\begin{aligned} {\mathsf {L}}^{2}_{j\,N_{1}}(\beta )&= -\frac{{\mathfrak {d}}_{2\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{1}{y_{N_{1}+1}-y_{N_{1}}}\left( \frac{{\mathcal {H}}^{j-1,j}_{N_{1},N_{1}+1}}{y_{j} -y_{j-1}}-\frac{{\mathcal {H}}^{j,j+1}_{N_{1},N_{1}+1}}{y_{j+1}-y_{j}}\right) . \end{aligned}$$(142)
By looking at the above expressions, and exploiting the symmetry of \({\mathcal {H}}^{p,q}_{k,l}\) (here, symmetry means that the subscripts can be exchanged with the superscripts), namely
it can be proven that the non-local stiffness matrices (one for each sub-cell) are symmetric as in the standard case, i.e.
1.2 Computation of \({\mathsf {F}}^{k}\)
By recalling the definition of \({\mathsf {F}}^{k}(\beta )\) given in (128b), and using the expressions (132a)–(134b), the components of the nodal fractional force are given by
-
if \(j=1,\ldots ,N_{1}-1\)
$$\begin{aligned} {\mathsf {F}}^{1}_{j}(\beta )&= \frac{{\mathfrak {d}}_{1\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \left( \frac{{\mathcal {H}}_{j-1,j}^{0,N_{1}}}{y_{j}-y_{j-1}} - \frac{{\mathcal {H}}_{j,j+1}^{0,N_{1}}}{y_{j+1}-y_{j}}\right) , \end{aligned}$$(145) -
if \(j=N_{1}\)
$$\begin{aligned} {\mathsf {F}}^{1}_{N_{1}}(\beta )&= \frac{{\mathfrak {d}}_{1\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{{\mathcal {H}}_{N_{1}-1,N_{1}}^{0,N_{1}}}{y_{N_{1}}-y_{N_{1}-1}}, \end{aligned}$$(146a)$$\begin{aligned} {\mathsf {F}}^{2}_{N_{1}}(\beta )&= -\frac{{\mathfrak {d}}_{2\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \frac{{\mathcal {H}}_{N_{1},N_{1}+1}^{N_{1},N_{2}}}{y_{N_{1}+1}-y_{N_{1}}}, \end{aligned}$$(146b) -
if \(j=N_{1}+1,\ldots ,N_{2}-1\)
$$\begin{aligned} {\mathsf {F}}^{2}_{j}(\beta )&= \frac{{\mathfrak {d}}_{2\mathrm {R}}L_{\mathrm {c}}^{-2}}{2\varGamma (3-\beta )} \left( \frac{{\mathcal {H}}_{j-1,j}^{N_{1},N_{2}}}{y_{j}-y_{j-1}} - \frac{{\mathcal {H}}_{j,j+1}^{N_{1},N_{2}}}{y_{j+1}-y_{j}}\right) . \end{aligned}$$(147)
1.3 Numerical approximation of the effective coefficient
By using the definitions introduced in the previous sections, the numerical effective diffusivity \({\hat{d}}^{\,\mathrm {eff}}_{\mathrm {num}}\) in Eq. (99) can be computed as
We notice that in Eq. (148), the coefficients \(\omega _{i}^{k}\) are the solutions of the algebraic equation (98) and represent the nodal concentrations. Therefore, the effective coefficient can be computed after the non-local cell problem has been solved.
FE discretisation of the non-local homogenised problem. Benchmark problem II
Analogously to what has been done above, we consider the basis functions to be defined by Lagrange polynomials of the first order, i.e.
Then, by using (149b), the mass matrix is given by
Now, by recalling the expressions (131a) and (131b), with a slight abuse of notation, we have that
where x replaces y, and the parameter \(\alpha \) replaces \(\beta \). In the following discussion, we omit the dependence of \({\mathcal {H}}_{k,l}^{p,q}\) on \(\alpha \).
Thus, by using expressions (151a) and (151b), and the symmetrised Caputo derivative of order \(\alpha \) of \(\psi _{i}\), \(i=1,\ldots ,N\), i.e.
the fractional stiffness matrix \({\mathsf {L}}(\alpha )\) can be computed as follows
Moreover, by taking into account that
the elements of the fractional nodal force \({\mathsf {F}}(\alpha )\) are given by
As previously discussed, also in this case both the fractional stiffness matrix and the fractional nodal force tend to their classical counterparts when \(\alpha \rightarrow 1^{-}\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ramírez-Torres, A., Penta, R. & Grillo, A. Two-scale, non-local diffusion in homogenised heterogeneous media. Arch Appl Mech 92, 559–595 (2022). https://doi.org/10.1007/s00419-020-01880-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00419-020-01880-3