Self-similar generalized Riemann problems for the 1-D isothermal Euler system

Abstract

We consider self-similar solutions to the 1-dimensional isothermal Euler system for compressible gas dynamics. For each$\beta \in {\mathbb {R}}$, the system admits solutions of the form

$$\begin{aligned} \rho (t,x)=t^\beta \Omega (\xi )\qquad u(t,x)=U(\xi )\qquad \qquad \textstyle \xi =\frac{x}{t}, \end{aligned}$$

where $\rho$ and u denote the density and velocity fields. The ODEs for $\Omega$ and U can be solved implicitly and yield the solution to generalized Riemann problems with initial data

$$\begin{aligned} \rho (0,x)=\left\{ \begin{array}{ll} R_l |x|^\beta &{} x<0\\ R_rx^\beta &{} x>0 \end{array}\right. \qquad u(0,x)=\left\{ \begin{array}{ll} U_l &{} x<0\\ U_r &{} x>0, \end{array}\right. \end{aligned}$$

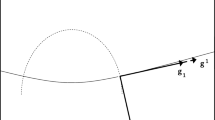
where $R_l,\, R_r>0$ and $U_l,\ U_r$ are arbitrary constants. For $\beta \in (-1,0)$, the data are locally integrable but unbounded at $x=0$, while for $\beta \in (0,1)$, the data are locally bounded and continuous but with unbounded gradients at $x=0$. Any (finite) degree of smoothness of the data is possible by choosing $\beta >1$ sufficiently large and $U_l=U_r$. (The case $\beta \le -1$ is unphysical as the initial density is not locally integrable and is not treated in this work.) The case $\beta =0$ corresponds to standard Riemann problems whose solutions are combinations of backward and forward shocks and rarefaction waves. In contrast, for $\beta \in (-1,\infty )\smallsetminus \{0\}$, we construct the self-similar solution and show that it always contains exactly two shock waves. These are necessarily generated at time $0+$ and move apart along straight lines. We provide a physical interpretation of the solution structure and describe the behavior of the solution in the emerging wedge between the shock waves.