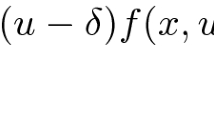Abstract
In this paper we are concerned with existence and behavior of positive solutions to the following class of linearly coupled elliptic systems with discontinuous nonlinearities
where \(\beta \ge 0\), \(N \ge 3\), \(V_{1},V_{2},\) \(a:{\mathbb {R}}^{N}\rightarrow {\mathbb {R}}\) are positive potentials, which can vanish at infinity, \(f_{1},f_{2}:{\mathbb {R}}\rightarrow {\mathbb {R}}\) are continuous functions and H is the Heaviside function, i.e, \(H(t)=0\) if \(t\le 0,\) \(H(t)=1\) if \(t>0\). We use a suitable nonsmooth truncation, for systems, to apply a version of the penalization method of Del Pino and Felmer (Calc Var Partial Differ Equ 4:121–137, 1996) combined with the Mountain Pass Theorem for locally Lipschitz functional to obtain a positive solution \((u_{\beta },v_{\beta })\) of \((S)_{\beta }\) in multivalued sense. In addition, we show that \((u_{\beta },v_{\beta })\rightarrow (u,v)\) in \(D^{1,2}({\mathbb {R}}^{N})\times D^{1,2}({\mathbb {R}}^{N})\) as \(\beta \rightarrow 0^{+}\), where (u, v) is a positive solution of the continuous system \((S)_{0}\) in strong sense.
Similar content being viewed by others
References
Akhmediev, N., Ankiewicz, A.: Novel soliton states and bifurcation phenomena in nonlinear fiber couplers. Phys. Rev. Lett. 70, 2395–2398 (1993)
Alves, C.O.: Existence of standing waves solutions for a Nonlinear Schrödinger equations in \({\mathbb{R}}^{N}\). J. Elliptic Parabol. Equ. 1, 231–241 (2015)
Alves, C.O., Figueiredo, G.M., Nascimento, R.G.: On existence and concentration of solutions for an elliptic problem with discontinuous nonlinearity via penalization method. Z. Angew Math. Phys. 65, 19–40 (2014)
Alves, C.O., Nascimento, R.G.: Existence and concentration of solutions for a class of elliptic problems with discontinuous nonlinearity in \({\mathbb{R}}^{N}\). Math. Scand. 112(1), 129–146 (2013)
Alves, C.O., Souto, M.A.S.: Existence of solution for a class of elliptic equations in \({\mathbb{R}}^{N}\) with vanishing potentials. J. Differ. Equ. 252, 5555–5568 (2012)
Ambrosetti, A., Badiale, M.: The dual variational problem and elliptic problems with discontinuous nonlinearities. J. Math. Anal. Appl. 140, 363–373 (1989)
Ambrosetti, A., Cerami, G., Ruiz, D.: Solitons of linearly coupled systems of semilinear non-autonomous equations on \({\mathbb{R}}^N\). J. Funct. Anal. 254, 2816–2845 (2008)
Ambrosetti, A., Turner, R.: Some discontinuous variational problems. Differ. Integral Equ. 1(3), 341–349 (1998)
Ambrosetti, A., Wang, Z.Q.: Nonlinear Schrödinger equations with vanishing and decaying potentials. Differ. Integral Equ. 18, 1321–1332 (2005)
Ambrosetti, A., Felli, V., Malchiodi, A.: Ground states of nonlinear Schrödinger equations with potentials vanishing at infinity. J. Eur. Math. Soc. 7, 117–144 (2005)
Arcoya, D., Calahorrano, M.: Some discontinuous variational problems with a quasilinear operator. J. Math. Anal. Appl. 187, 1059–1072 (1994)
Bartsch, T., Wang, Z.Q.: Existence and multiplicity results for some superlinear elliptic problems on \({\mathbb{R}}^{N}\). Comm. Partial Differ. Equ. 20, 1725–1741 (1995)
Berestycki, H., Lions, P.-L.: Nonlinear scalar field equations, I. Existence of a ground state. Arch. Rational Mech. Anal. 82, 313–346 (2020)
Berestycki, H., Lions, P.L.: Nonlinear scalar field equations, II. Existence of infinitely many solutions. Arch. Rat. Mech. Anal. 82, 347–375 (1983)
Brezis, H., Kato, T.: Remarks on the Schrödinger operator with singular complex potentials. J. Math. Pures Appl. 58, 137–151 (1979)
Brezis, H., Lieb, E.H.: Minimum action solutions of some vector field equations. Comm. Math. Phys. 96, 97–113 (1984)
Chang, K.C.: The obstacle problem and partial differential equations with discontinuous nonlinearities. Comm. Pure Appl. Math. 33, 139–158 (1978)
Chang, K.C.: Variational methods for nondifferentiable functionals and their applications to partial differential equations. J. Math. Anal. Appl. 80, 102–129 (1981)
Chen, Z., Zou, W.: Ground states for a system of Schrödinger equations with critical exponent. J. Funct. Anal. 262, 3091–3107 (2012)
Chen, Z., Zou, W.: On coupled systems of Schrödinger equations. Adv. Differ. Equ. 16, 775–800 (2011)
Clarke, F.H.: Optimization and nonsmooth analysis. Wiley, New York (1983)
Clarke, F.H.: Generalized gradients and applications. Trans. Am. Math. Soc. 265, 247–262 (1975)
del Pino, M., Felmer, P.L.: Local Mountain Pass for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differ. Equ. 4, 121–137 (1996)
Dinu, T.-L.: Entire solutions of Schrödinger elliptic systems with discontinuous nonlinearity and sign-changing potential. Math. Model. Anal. 11(3), 229–242 (2006)
Floer, A., Weinstein, A.: Nonspreading wave packets for the cubic Schrödinger equations with bounded potential. J. Funct. Anal. 69, 397–408 (1986)
Gilbarg, D., Trudinger, N.S.: Elliptic partial differential equations of second order. Springer, Berlin (1983)
Grossinho, M.R., Tersian, S.A.: An introduction to minimax theorems and their applications to differential equations. Nonconvex Optim. Appl. 52, (2001)
Kristály, A.: Existence of nonzero weak solutions for a class of elliptic variational inclusions systems in \({\mathbb{R}}^{N}\). Nonlinear Anal. 65, 1578–1594 (2006)
dos Santos, G.C.G., Figueiredo, G.M.: Existence of solutions for a NSE with discontinuous nonlinearity. J. Fixed Point Theory Appl. 19, 917–937 (2017)
dos Santos, G.G., Figueiredo, G.M., Nascimento, R.G.: Existence and behavior of positive solution for a problem with discontinuous nonlinearity in \({\mathbb{R}}^N\) via a nonsmooth penalization. Z. Angew. Math. Phys. 71, 71 (2020). https://doi.org/10.1007/s00033-020-01296-7
Oh, Y.G.: Existence of semi\(-\)classical bound states of nonlinear Schrödinger equations with potentials on the class \((V)\). Comm. Partial Differ. Equ. 13, 1499–1519 (1988)
Rabinowitz, P.H.: On a class of nonlinear Schrödinger equations. Z. Angew Math. Phys. 43, 270–291 (1992)
Strauss, W.A.: Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55, 149–162 (1977)
Struwe, M.: Applications to nonlinear partial differential equations and hamiltonian systems, 4th edn. Springer (2007)
Teng, K.: Existence and multiplicity results for some elliptic systems with discontinuous nonlinearities. Nonlinear Anal. 75, 2975–2987 (2012)
Zhang, G.Q., Liu, S.Y.: Multiplicity result for a class of elliptic problems with non-differentiable terms in \({\mathbb{R}}^{N}\). Nonlinear Anal. 71(5–6), 1611–1619 (2009)
Zhang, G.Q., Wang, Y.K.: On a class of Schrödinger systems with discontinuous nonlinearities. J. Math. Anal. Appl. 331, 1415–1424 (2007)
Acknowledgements
Research supported by CNPq. The authors would like to express their sincere gratitude to the referees for carefully reading the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
de Albuquerque, J.C., Santos, G.G.d. & Figueiredo, G.M. Existence and behavior of positive solutions for a class of linearly coupled systems with discontinuous nonlinearities in \({\mathbb {R}}^N\). J. Fixed Point Theory Appl. 23, 19 (2021). https://doi.org/10.1007/s11784-021-00858-0
Accepted:
Published:
DOI: https://doi.org/10.1007/s11784-021-00858-0
Keywords
- Linearly coupled systems
- variational methods
- nondifferentiable functionals
- discontinuous nonlinearity
- Lipschitz functional