Abstract
Due to the broadband response characteristics at low levels of excitations, nonlinear multistable systems have garnered a great deal of attention in the area of energy harvesting. Moreover, various performance enhancement strategies of multistable harvesters have been proposed and discussed extensively for systems with perfectly symmetric potentials. However, it is very difficult or even impossible in practice to modulate a nonlinear system with completely symmetric potentials. Therefore, this paper investigates the stochastic response characteristics of asymmetric potential multistable harvesters excited by Gaussian white noise. Approximate Fokker–Planck–Kolmogorov equation for multistable harvester is provided, and solved by the method of detailed balance. Numerical simulations are carried out to characterize the probability distribution and power output of the response of the harvesters. Results indicate that the theoretical method could well predict the response probability distribution of the systems under white noise excitations. To be more specific, the probability distribution of velocity response at a given excitation level is not affected by the asymmetry of potentials, while the probability density function of displacement is very dependent on the shape of potentials. In terms of the power output, the numerical results agree well with the theoretical results. However, the error between numerical and theoretical results increases with the increase in the number of the steady states and the degree of asymmetry of the harvesters.
Export citation and abstract BibTeX RIS
1. Introduction
The rapid development of wireless sensors and portable electronics over the last decades has put forward an urgent requirement in small-scale energy supply technologies [1]. Harvesting energy from surroundings through different mechanisms, such as piezoelectric [2–4], electromagnetic [5], pyroelectric [6], has been viewed as a feasible method to address this issue. Particularly, piezoelectric energy harvesters attracted the most attention due to the advantages of high-energy-density and easy fabrication in miniaturization. Before, linear energy harvesters (LEHs) [7–9] with various structures based on different vibration mechanisms have been proposed and investigated extensively. However, the narrowband issues of LEHs near the resonance frequency limited their wide application for the reason that the energy distributed in the environment is always in a wide frequency range [10]. Although array structures were proposed in different ways to enhance the performance, another issue was raised considering the efficient use of space.
Nonlinear multistable systems with different types of potential functions have been widely studied by numerical and experimental strategies for the reason that they possess the virtues of high sensitivity and wideband response [11–14]. Especially, monostable, bistable, and tristable harvesters were more remarkable due to the ease of modulation. For instance, Stanton et al [15] proposed the model of a monostable energy harvester (MEH) with bidirectional hysteresis, and experiments demonstrated the hardening and softening wideband response. Masana and Daqaq [16] obtained a MEH by a clamped-clamped piezoelectric beam and proved the wideband characteristic by the multiscale method. Besides, MEH was also proposed and optimized in different ways such as smart sand [17] and stoppers [18, 19]. Due to the snap-through characteristics, bistable energy harvesters (BEHs) with double potential wells were realized by various structures. The typical bistable system, induced by a cantilever coupled with external magnets, has been proposed and modeled by Erturk [20, 21], Stanton [22–24], Zhou [25], and Qin et al [26]. The nonlinear dynamic behaviors and broadband energy harvesting performance on high-energy branches [21, 27] were demonstrated by numerical and experimental methods. Further, the enhanced output characteristics obtained by impact [27, 28], impulse [29], and rotational [30] excitations have been indicated. The clamped-clamped bistable piezoelectric beam proposed by Masana and Daqaq [16] is another part that attracted lots of attention. The relative advantages over the MEH were illustrated by modulating the proper potential function [31], and super-harmonic resonances [32] were more preferable under a small base acceleration. Through skillfully applying the internal stress, bistable composite plates with piezoelectric layers were designed by Arrieta et al [33–36]. Theoretical modeling and experimental validation of the system were carried out, and some researchers focus on the response identification [37, 38] of the system. Moreover, some bistable harvesters were also realized by the structures of the inverted pendulum [39] and the flexure hinge mechanism [40]. In order to further enhance the performance under low levels excitations, the piezoelectric cantilever beam was designed with tristable [41–43], quad-stable [44, 45], and penta-stable [46] structures.
For the reason that the frequency of environmental vibrations always distributes in a wide range, investigations of multistable harvesters under random excitation garnered a great deal of attention. Numerically, Litak et al [47] simulated the response of a BEH driven by Gaussian white noise and demonstrated that the appearance of stochastic coherence resonance could enhance the performance. Zhao and Erturk [48] numerically and experimentally considered the performance of the MEH and BEH under broadband stochastic excitation, revealing that the BEH can be preferred only if it is designed under a known excitation. Moreover, Masana and Daqaq [49] experimentally investigated the influence of potential's shape on MEH and BEH excited under band-limited noise, in which the levels of excitations, bandwidths, and center frequencies were all considered. Recently, Jiang et al [50] applied the path integration method to calculate the probability density function from the Fokker–Planck–Kolmogorov (FPK) equation, results indicated that the numerical outcomes were in good agreement with the Monte Carlo simulation. Besides, various theoretical methods were applied to evaluate the performance of different harvesters under random excitations. Ali et al [51] investigated the output performance of a piezoelectric BEH under white noise by the method of equivalent linearization. Similarly, Jiang et al applied the same method to consider the output characteristics of a MEH [52]. By applied the moment equation, Jiang et al [53] analyzed the stochastic dynamics of the intra-well oscillation of a BEH. As a general method, stochastic averaging of energy envelope was applied by Xu et al [54] to derive the performance of MEH and BEH under white noise, by which the influence of parameters on performance was demonstrated. Jiang et al [55, 56] employed the stochastic averaging method to study the output of duffing systems with three types of potentials, and Monte Carlo simulation demonstrated the effectiveness of the method. Zhang et al [57] investigated the random bifurcation phenomenon and output performance of tristable electromagnetic harvesters under colored noise excitation by the stochastic average method. By solving the FPK equations theoretically, Daqaq [58–60] initially analyzed the response of MEH and BEH under different excitations such as the white, colored, and Ornstein–Uhlenbeck noise. Following, the FPK equations were considered by Green [61], Martens [62], Dasgupta [63] and Yang et al [64] to evaluate the performance of harvesters under random excitations.
Although much effort has been devoted to investigating the performance of multistable harvesters under harmonic and random excitations, the considered potential energy functions always possess symmetric potential functions. In practical conditions, it is impossible to modulate a perfectly symmetric potential function. Before, He and Daqaq [65] considered the performance of MEH and BEHs with asymmetric quadratic nonlinearity similar to that characterized by Halvorsen [66], results demonstrated the output power greatly depended on the asymmetry. Zhou et al [67] numerically and theoretically considered the response of a tristable harvester under harmonic excitation, indicating that the shape of potential functions influenced the performance. More recently, Wang et al [68] reported that the asymmetric potentials in BEH decrease the performance, while inclining the system with a certain bias angle [68] or oscillating the harvester from the shallower potential well [69] could improve the output power of the BEHs. Although the asymmetry in energy harvesters was studied, the influence of asymmetric potentials on the power output and probability distribution of multistable harvesters is still an open issue.
Therefore, investigations into the stochastic characteristics of asymmetric potential multistable harvesters under Gaussian white noise are carried out in this paper. The method of detailed balance is applied to solve the approximate FPK equation of multistable harvesters under white noise excitations. Numerical simulations for monostable, bistable, and tristable harvester are undertaken to demonstrate the effectiveness of the method, and results indicate that the probability density function of displacement mainly depends on the shape of potential functions. The remainder of the paper is organized as follows. In section 2, the electromechanical model of multistable harvesters is presented and the detailed balance method is applied to solve the approximate FPK equation. Numerical and theoretical analysis is undertaken in section 3 to investigate the performance and the probability distribution of the multistable harvester. Further, the influence of asymmetric potentials is studied here. In the final section 4, the conclusion is given.
2. Approximate FPK equation analysis of multistable harvesters
2.1. Dynamic model of multistable harvesters
The typical structure for multistable piezoelectric energy harvesters is illustrated in figure 1. It consists of a cantilever beam, two piezoelectric layers pasted at the root, and tip magnets coupled with two rotational external magnets. The multistable energy harvesters can be achieved by appropriately adjusting the parameters d, h, and ϑ, as well as the polarity of magnets. Due to the difficulties in modulation, it is impossible to attain a multistable harvester with a completely symmetric potential function.
Figure 1. Schematic diagram of the multistable energy harvester.
Download figure:
Standard image High-resolution imageBy applying the Hamilton principle and Euler–Bernoulli beam theory, the dynamic model of the multistable energy harvesters is expressed as follows:
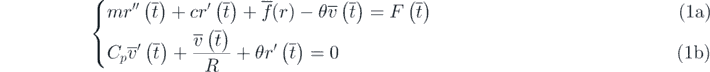
in which m, c, 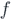 , θ, Cp
and R are the equivalent mass, equivalent damping, nonlinear restoring force, equivalent electromechanical coupling coefficient, equivalent capacitance, and the load resistance respectively. Also, r,
, θ, Cp
and R are the equivalent mass, equivalent damping, nonlinear restoring force, equivalent electromechanical coupling coefficient, equivalent capacitance, and the load resistance respectively. Also, r,  and F are the tip displacement of the cantilever, the voltage output, and the external excitation respectively. Further,
and F are the tip displacement of the cantilever, the voltage output, and the external excitation respectively. Further, 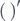 represents the derivate with respect to time
represents the derivate with respect to time 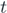 . By introducing the variables expressed by
. By introducing the variables expressed by  ,
, 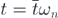 and
and  , the nondimensional model of the system is
, the nondimensional model of the system is
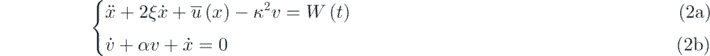
where l0 is a length scale, and ωn
is the resonance frequency. In this equation, x, v, and W respectively represent the dimensionless displacement, voltage, and the Gaussian white noise excitation, ξ is the damping ratio, α is the time constant ratio, κ2 is dimensionless electromechanical coupling coefficient, and 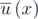 is the dimensionless nonlinear restoring force. Also, the upper dot is the derivate to dimensionless time t. Furthermore, W(t) is the Gaussian white noise.
is the dimensionless nonlinear restoring force. Also, the upper dot is the derivate to dimensionless time t. Furthermore, W(t) is the Gaussian white noise.
2.2. Approximate FPK equation analysis based on detailed balance
To characterize the dynamic behavior of multistable harvester under Gaussian white noise, the FPK equation governing equation (2) will be approximately solved by the method of detailed balance. Based on equation (2), the solution in global could be assumed as [55, 70]
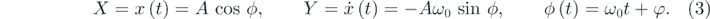
By combining the assumed solution with equation (2b), the response of voltage in global can be expressed by
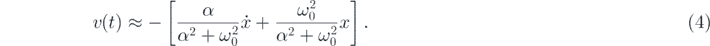
Substituting equation (4) to equation (2a), one can get the following approximate equation characterizing the model:

where 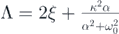 and
and 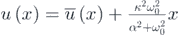 . For equation (5), it can be converted into the following Ito stochastic differential equation
. For equation (5), it can be converted into the following Ito stochastic differential equation
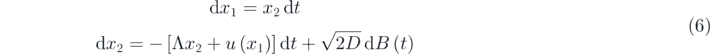
where 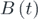 is a Brownian motion process and D is the noise intensity. The corresponding FPK equation of equation (6) is expressed as
is a Brownian motion process and D is the noise intensity. The corresponding FPK equation of equation (6) is expressed as
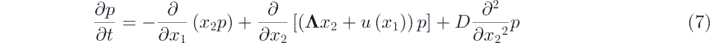
where p is the stationary probability density function with the boundary conditions 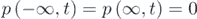 . The stationary solution of equation (7) can be supposed as
. The stationary solution of equation (7) can be supposed as

Based on the principle of detailed balance, the first and second-order derivative moment of equation (6) are
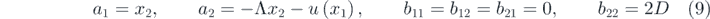
in which the reversible and irreversible part of the first-order derivative moment are respectively
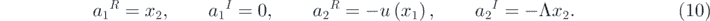
On account of detailed balance, the following equations explaining  are obtained
are obtained


By solving equations (11)–(12), the expression of 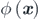 is
is
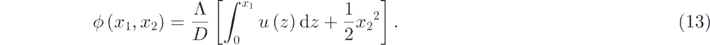
Thus, the stationary probability density function is achieved as
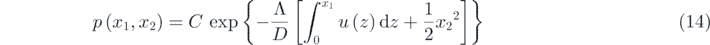
where ![${C}^{-1}={\int }_{-\infty }^{\infty }\mathrm{exp}\left\{-\frac{{\Lambda}}{D}\left[{\int }_{0}^{{x}_{1}}u\left(z\right)\mathrm{d}z+\frac{1}{2}{{x}_{2}}^{2}\right]\right\}\mathrm{d}{x}_{1}\enspace \mathrm{d}{x}_{2}$](https://content.cld.iop.org/journals/1742-5468/2021/2/023407/revision2/jstatabdd17ieqn15.gif) . Particularly, equation (14) could be expressed as follows
. Particularly, equation (14) could be expressed as follows
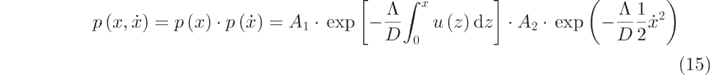
where ![${{A}_{1}}^{-1}={\int }_{-\infty }^{\infty }\mathrm{exp}\left[-\frac{{\Lambda}}{D}{\int }_{0}^{x}u\left(z\right)\mathrm{d}z\right]\mathrm{d}x$](https://content.cld.iop.org/journals/1742-5468/2021/2/023407/revision2/jstatabdd17ieqn16.gif) and
and 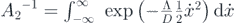 .
.
Although the voltage response has a relationship with the displacement response, it depends on the displacement in local potential wells. In order to characterize the power output of the system, the voltage response in local can be expressed as
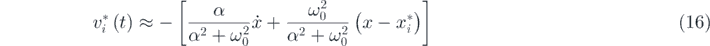
where i represents the ith response condition and  is the mean value of displacement response in the ith condition. For monostable harvesters, i equals to 1. While i is 3 for the bistable system representing two conditions of intrawell motion and one condition for inter-well oscillation. In a similar fashion, i is 4 for tristable energy harvesting systems. Then the mean square value of voltage is characterized by the following expression:
is the mean value of displacement response in the ith condition. For monostable harvesters, i equals to 1. While i is 3 for the bistable system representing two conditions of intrawell motion and one condition for inter-well oscillation. In a similar fashion, i is 4 for tristable energy harvesting systems. Then the mean square value of voltage is characterized by the following expression:
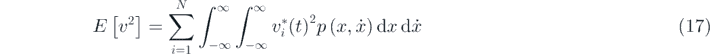
3. Theoretical and numerical analysis
In this section, numerical simulation and theoretical analysis are undertaken to demonstrate the effectiveness of the method of detailed balance. Marginal and joint probability density functions (PDF) are employed to illustrate the probability distribution of multistable harvesters, such as linear, monostable, bistable, and tristable harvesters. To explain the influence of the asymmetric potentials, asymmetries with different degrees are considered in the investigation. All the numerical simulations are carried out by applying the four-order Runge–Kutta method. Furthermore, parameters in equation (2) are set as D = 0.04, ξ = 0.1, κ2 = 0.002 and α = 0.4 unless other values are assigned specially.
3.1. Linear system analysis
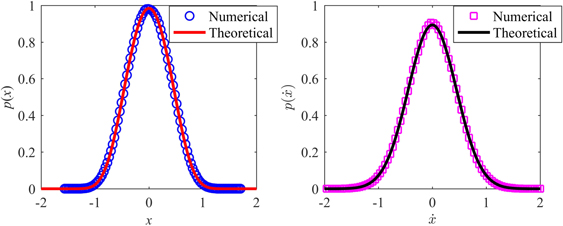
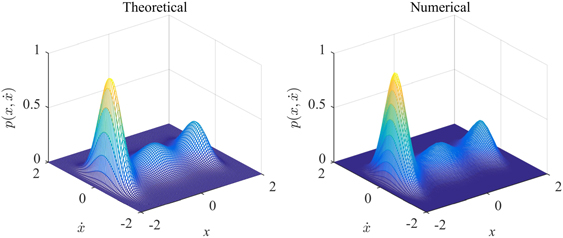
In the investigation into the probability distribution of linear harvester, the dimensionless nonlinear restoring force is 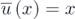 . For the numerical simulation, the sampling frequency is set to be 5 Hz and the data length is 2 × 106. Figures 2(a) and (b) illustrate the numerical and theoretical marginal PDF of displacement and velocity response of the linear harvester under white noise. Besides, the comparison of numerical and theoretical joint PDF of displacement and velocity is shown in figure 3. Results indicate that the response of the linear harvester mainly distributes around the original point, and numerical simulations are in good agreement with the theoretical calculation.
. For the numerical simulation, the sampling frequency is set to be 5 Hz and the data length is 2 × 106. Figures 2(a) and (b) illustrate the numerical and theoretical marginal PDF of displacement and velocity response of the linear harvester under white noise. Besides, the comparison of numerical and theoretical joint PDF of displacement and velocity is shown in figure 3. Results indicate that the response of the linear harvester mainly distributes around the original point, and numerical simulations are in good agreement with the theoretical calculation.
Figure 2. Marginal PDF of displacement and velocity of LEH under white noise (D = 0.04).
Download figure:
Standard image High-resolution imageFigure 3. Joint PDF of displacement and velocity of LEH under white noise (D = 0.04).
Download figure:
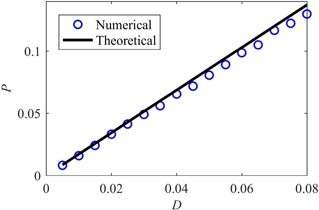
Standard image High-resolution imageTo study the average output power of the linear harvester under white noise, figure 4 compares the numerical and theoretical power under excitations with various intensities. It is seen that the power increase with an increase in the noise intensity of the excitation. Furthermore, figure 5 illustrates the variation of output power with other parameters such as dimensionless electromechanical coupling coefficient, time constant ratio, and damping ratio. Results demonstrate that the power decreases with an increase in the values of electromechanical coupling coefficient and damping ratio. While the power firstly increases and then decreases after a certain value of the time constant ratio, indicating that there is an optimum time constant ratio to maximize the output performance.
Figure 4. Relationship between average power and noise intensity for LEH.
Download figure:
Standard image High-resolution imageFigure 5. Influence of related parameters on average power P for LEH.
Download figure:
Standard image High-resolution image3.2. Monostable system analysis
In the investigation into monostable harvesters, the potential function expressed by 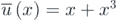 is firstly considered for the symmetric harvester. Under excitation with an intensity of 0.04, the marginal and joint PDF of displacement and velocity are depicted in figures 6 and 7. It is viewed that numerical results match well with the theoretical calculation. Compared with the linear harvester, there is a larger probability for the monostable one to oscillate near the stable point and this is due to the change in the potential energy function. While for the response probability distribution of velocity, it is not affected by the shape of potential energy functions. For the average output power shown in figure 10(a), numerical simulation agrees well with the theoretical analysis and the variation trend is similar to that of the linear harvester. The only point to be noted is that the introduction of cubic coefficients to the system decreases the output performance.
is firstly considered for the symmetric harvester. Under excitation with an intensity of 0.04, the marginal and joint PDF of displacement and velocity are depicted in figures 6 and 7. It is viewed that numerical results match well with the theoretical calculation. Compared with the linear harvester, there is a larger probability for the monostable one to oscillate near the stable point and this is due to the change in the potential energy function. While for the response probability distribution of velocity, it is not affected by the shape of potential energy functions. For the average output power shown in figure 10(a), numerical simulation agrees well with the theoretical analysis and the variation trend is similar to that of the linear harvester. The only point to be noted is that the introduction of cubic coefficients to the system decreases the output performance.
Figure 6. Marginal PDF of displacement and velocity of MEH under white noise (D = 0.04) for the symmetric potential.
Download figure:
Standard image High-resolution imageFigure 7. Joint PDF of displacement and velocity of MEH under white noise (D = 0.04) for the symmetric potential.
Download figure:
Standard image High-resolution imageFor an asymmetric monostable harvester, a quadratic coefficient in the nonlinear restoring force is considered with a value of 1.9. In this condition, the marginal PDF of displacement and velocity are shown in figure 8, while the joint distribution is figured in figure 9. Numerical and theoretical results all demonstrate that the probability distribution of velocity is the same as before discussed, that is to say, the potential function does not affect the probability distribution of velocity. While for the probability distribution of displacement, it indicates that the system has a larger probability to oscillate on the side with a smaller nonlinear restoring force. In figure 10(b), the relationship between average power and noise intensity for the asymmetric MEH is presented. With the appearance of asymmetry in a monostable system, the power output increases and the error between numerical and theoretical results shows an increasing tendency.
Figure 8. Marginal PDF of displacement and velocity of asymmetric MEH under white noise (D = 0.04, β = 1.9).
Download figure:
Standard image High-resolution imageFigure 9. Joint PDF of displacement and velocity of asymmetric MEH under white noise (D = 0.04, β = 1.9).
Download figure:
Standard image High-resolution imageFigure 10. Relationship between average power and noise intensity for MEH: (a) β = 0(symmetric potential); (b) β = 1.9 (asymmetric potential).
Download figure:
Standard image High-resolution image3.3. Bistable system analysis
In terms of nonlinear bistable harvesters, the nonlinear restoring force is considered with the expression of  . For symmetric bistable harvester with β = 0, the comparison between numerical and theoretical marginal and joint PDF of displacement and velocity are explained in figures 11 and 12. From the results, it is seen that the distribution of displacement exhibits obvious bimodal characteristics because of the two potential wells in the bistable system and the oscillator has a larger probability to vibrate in the two potential wells. While for the distribution of velocity, it is not affected by the bistable potential.
. For symmetric bistable harvester with β = 0, the comparison between numerical and theoretical marginal and joint PDF of displacement and velocity are explained in figures 11 and 12. From the results, it is seen that the distribution of displacement exhibits obvious bimodal characteristics because of the two potential wells in the bistable system and the oscillator has a larger probability to vibrate in the two potential wells. While for the distribution of velocity, it is not affected by the bistable potential.
Figure 11. Marginal PDF of displacement and velocity of BEH under white noise (D = 0.04) for the symmetric potential.
Download figure:
Standard image High-resolution imageFigure 12. Joint PDF of displacement and velocity of BEH under white noise (D = 0.04) for the symmetric potential.
Download figure:
Standard image High-resolution imageWhen an asymmetric potential is introduced with β = 0.15, the potential energy function has a deeper potential well on the left and a shallower on the right. In this case, the probability distribution is illustrated in figures 13 and 14. Again, the characteristic of velocity response is the same as before discussed and not influenced by potential shape. For the response of displacement, the distribution has the characteristic of asymmetric bimodal and a larger probability is obtained in the deeper well. As the quadratic coefficient further increases to 0.25 and 0.35, the theoretical joint PDF are shown in figure 15. Results demonstrate that the increase in the asymmetric degree increases the probability to oscillate in the deeper potential well, while decrease that in the shallower one. In figures 16(a) and (b), the relationship between average power and noise intensity for the symmetric and asymmetric (β = 0.35) BEH are respectively presented. The output power increases with an increase in the noise intensity and numerical results are in good agreement with the theoretical ones. By careful observation, it is viewed that the power output of the asymmetric (β = 0.35) BEH is a little lower than the symmetric BEH, and less interwell motion results in a small error between numerical and theoretical results.
Figure 13. Marginal PDF of displacement and velocity of asymmetric BEH under white noise (D = 0.04, β = 0.15).
Download figure:
Standard image High-resolution imageFigure 14. Joint PDF of displacement and velocity of asymmetric BEH under white noise (D = 0.04, β = 0.15).
Download figure:
Standard image High-resolution imageFigure 15. Influence of asymmetric degree on joint PDF (theoretical results) of displacement and velocity of BEH (D = 0.04).
Download figure:
Standard image High-resolution imageFigure 16. Relationship between average power and noise intensity for BEH: (a) β = 0; (b) β = 0.35.
Download figure:
Standard image High-resolution image3.4. Tristable system analysis
Regarding the tristable harvester, the nonlinear restoring force is expressed by the polynomial form of 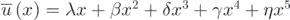 . For the reason that the dynamic behavior of the tristable system is very complex, the sampling frequency here is set to be 5 Hz and the data length is 2 × 107. When λ = 1, β = 0, δ = −2.5, γ = 0 and η = 1 for symmetric harvester, the potential energy function is shown in figure 17 with a blue line. Under Gaussian white noise excitation, the PDFs are shown in figures 18 and 19 for marginal and joint ones. Similar to the results before, the probability distribution of velocity is not affected. For the displacement response characteristics, the probability density function is symmetric with respect to x = 0, and a smaller probability is indicated in the shallower potential well in the middle.
. For the reason that the dynamic behavior of the tristable system is very complex, the sampling frequency here is set to be 5 Hz and the data length is 2 × 107. When λ = 1, β = 0, δ = −2.5, γ = 0 and η = 1 for symmetric harvester, the potential energy function is shown in figure 17 with a blue line. Under Gaussian white noise excitation, the PDFs are shown in figures 18 and 19 for marginal and joint ones. Similar to the results before, the probability distribution of velocity is not affected. For the displacement response characteristics, the probability density function is symmetric with respect to x = 0, and a smaller probability is indicated in the shallower potential well in the middle.
Figure 17. Nonlinear restoring force and potential energy function of tristable energy harvesters.
Download figure:
Standard image High-resolution imageFigure 18. Marginal PDF of displacement and velocity of TEH under white noise (D = 0.04) for the symmetric potential.
Download figure:
Standard image High-resolution imageFigure 19. Joint PDF of displacement and velocity of TEH under white noise (D = 0.04) for the symmetric potential.
Download figure:
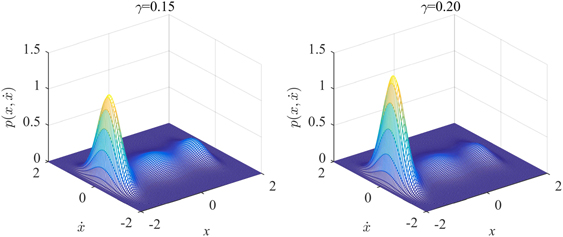
Standard image High-resolution imageWhen the quartic coefficient in nonlinear restoring force equals 0.10, 0.15, and 0.20, the potential energy functions are shown in figure 17(b). With an increase in the value of the quartic coefficient, the potential well on the left becomes much deeper while the right one becomes much shallower, and the potential well depth in the middle is not affected. Under white noise excitation with an intensity of 0.04, the marginal and joint probability distribution of the tristable system with γ = 0.10 is demonstrated in figures 20 and 21. The system has a larger probability to oscillate in the deeper potential well and a smaller one in the shallower potential well. This phenomenon is further illustrated by the joint probability distribution of the tristable system with γ equaling to 0.15 and 0.20 shown in figure 22. Figure 23 shows the variation of power output with noise intensity for the symmetric and asymmetric (γ = 0.20) TEH. Although the theoretical result predicts the numerical simulation in a certain degree, the error between numerical and theoretical results is larger than that for the monostable and bistable systems. The reason for the phenomenon is that equations (16) and (17) approximately viewed the interwell motion as periodic oscillation. While under random excitations, the interwell motion is always chaotic oscillation. Therefore, approximately viewing the interwell motion as periodic oscillation increases the error between numerical and theoretical results especially for tristable harvesters that possess large-amplitude periodic oscillation crossing the potential wells.
Figure 20. Marginal PDF of displacement and velocity of asymmetric TEH under white noise (D = 0.04, γ = 0.10).
Download figure:
Standard image High-resolution imageFigure 21. Joint PDF of displacement and velocity of asymmetric TEH under white noise (D = 0.04, γ = 0.10).
Download figure:
Standard image High-resolution imageFigure 22. Influence of asymmetric degree on joint PDF (theoretical results) of displacement and velocity of TEH.
Download figure:
Standard image High-resolution imageFigure 23. Relationship between average power and noise intensity for TEH: (a) γ = 0; (b) γ = 0.2.
Download figure:
Standard image High-resolution image4. Conclusion
This paper presents theoretical and numerical investigations into the stochastic characteristics of asymmetric potential multistable energy harvesters. The approximate FPK equation for multistable harvester is provided by applying the approximate solution of the dynamic model. The method of detailed balance is employed to solve the FPK equation under the excitation of Gaussian white noise, and numerical simulations are carried out for comparison. Results demonstrate that the average output power increases with an increase in the noise intensity and the introduction of nonlinearity into the system influences the performance greatly.
When an asymmetric potential appears in monostable harvesters, it promotes the oscillator to vibrate with a larger probability in the side with a smaller restoring force. For multistable energy harvesters, numerical and theoretical results all demonstrate that the probability of displacement response mainly depends on the shape of potential energy function. A larger probability is indicated for the system to oscillate in the potential well with deeper depth and an increase in the asymmetric degree will exacerbate this effect. For the probability distribution of velocity response at a certain noise intensity, it is not influenced by the shape of potential functions for monostable, bistable, and tristable harvesters. Regarding the output power, it increases with the appearance of asymmetry in monostable harvesters due to the smaller nonlinear restoring force on one side induced by asymmetric potentials. While for bistable and tristable systems, the asymmetry has a negative effect on the power for the reason that the asymmetric potentials cause a smaller probability for interwell motion as illustrated by the corresponding PDF.
Acknowledgments
This study was supported by the Project funded by China Postdoctoral Science Foundation (2020M682336), Science and Technology Project of Henan Province (212102310248), National Natural Science Foundation of China (Grant No. 51575426, 51611530547, 51811530321); this research was partly supported by China Scholarship Council. G L was supported by the program of the Polish Ministry of Science and Higher Education under the project DIALOG 0019/DLG/2019/10 in the years 2019–2021.