Abstract
The outbreak of coronavirus COVID-19 is spreading at an unprecedented rate to the human populations and taking several thousands of life all over the world. Scientists are trying to map the pattern of the transmission of coronavirus (SARS-CoV-2). Many countries are in the phase of lockdown in the globe. In this paper we predict about the effect of coronavirus COVID-19 and give a sneak peak when it will reduce the transmission rate in the world via mathematical modelling. In this research work our study is based on extensions of the well-known susceptible-exposed-infected-recovered (SEIR) family of compartmental models and later we observe the new model changes into (SEIR) without changing its physical meanings. The stability analysis of the coronavirus depends on changing of its basic reproductive ratio. The progress rate of the virus in the critically infected cases and the recovery rate have major roles to control this epidemic. The impact of social distancing, lockdown of the country, self-isolation, home quarantine and the wariness of global public health system have significant influence on the parameters of the model system that can alter the effect of recovery rates, mortality rates and active contaminated cases with the progression of time in the real world. The prognostic ability of mathematical model is circumscribed as of the accuracy of the available data and its application to the problem.
Similar content being viewed by others
Introduction
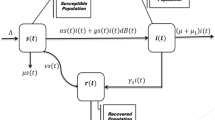
Susceptible (S) individuals are those who have never been infected with and thus have no immunity against COVID-19. Susceptible individuals become exposed once they are infected with the disease. The next stage is exposed (E) individuals in which those who have been infected with COVID-19 but are not yet infectious to others. An individual remains exposed for the length of the incubation period, after which they become infectious and experience non-critical clinical symptoms \((I_1)\). Infected \((I_1)\) individuals with a non-critical infection experience symptoms like fever and cough and may even have mild pneumonia but do not require hospitalization. These individuals may either recover or progress to the critical stage of the disease. One step further when the infected \((I_2)\) individuals with a critical infection experience respiratory failure, septic shock and/or multiple organ dysfunction or failure and require treatment in an ICU (Xiaobo et al. 2020; Fei et al. 2020; Rocklov et al. 2020). These individuals may either recover or die from the disease. Recovered (R) individuals are those who have recovered and are assumed to be immune to future infection with COVID-19 and lastly dead (D) individuals are those who have died in COVID-19. The flow chart diagram is given in Fig. 1. Previously, many studies have been done on the natural clinical progression of COVID-19 infection (Zunyou and McGoogan 2020). Infected individuals do not immediately develop severe symptoms, but instead pass through milder phases of infection first. In some studies, what we call mild infections are grouped into two different categories, mild and moderate, where individuals with moderate infection show radiographic signs of mild pneumonia. These mild and moderate cases occur at roughly equal proportions (Penghui et al. 2020). There is some debate about the role of pre-symptomatic transmission (occurring from exposed cases) and asymptomatic infected cases for coronavirus, which are not included in the present model (Biswas et al. 2014; Yi et al. 2009). We use a compartmental epidemiological model, followed by the traditional SEIR model, to illustrate the spread and clinical progression of COVID-19 (Safi and Garba 2012; Upadhyay et al. 2019). It is important to track the different clinical outcomes of infection, since they require different level of healthcare resources to care for and may be tested and isolated at different rates (Wu et al. 2020; Liu et al. 2020; Li et al. 2020; Kucharski et al. 2020). Susceptible (S) individuals who become infected start out in an exposed class (E), where they are asymptomatic and do not transmit infection. The rate of progressing from the exposed stage to the infected stage (I), where the individual is symptomatic and infectious, occurs at rate a. Infected individuals begin with non-critical infection \((I_1)\), with a recovery rate \(\gamma _1\), and progress to critical infection \((I_2)\), at rate of \(\alpha\). Individuals with critical infection recover at rate \(\gamma _2\) and death with rate of \(\mu\). Recovered individuals are tracked by class (R) and are assumed to be protected from re-infection for life. Individuals may transmit the infection at any stage with the transmission rates \(\beta _1\) and \(\beta _2\), respectively (David et al. 2020; Qifang et al. 2020; Zhanwei et al. 2020; Tapiwa et al. 2020). This model is formulated as a system of differential equations and the output therefore represents the expected values of each quantity. It does not take into account stochastic events, and so the epidemic cannot go extinct even when it gets to very low values (except when an intervention is stopped, at which case the number of individuals in each state is rounded to the nearest integer). The model does not report the expected variance in the variables, which can sometimes be large. Individuals must pass through a non-critical stage before reaching the critical stage. Only individuals in a critical stage die and all the individuals have equal transmission rates and equal susceptibility to infection. We introduce the COVID-19 model system as follows:
The initial conditions of (1) are given as \(S(0)\ge 0, E(0)\ge 0, I_1(0)\ge 0, I_2(0)\ge 0, R(0)\ge 0, D(0)\ge 0\). The dynamical behaviour of the model system is calculated by a set of rate parameters which include the transmission rates \(\beta _1\) and \(\beta _2\), the progression rates a and \(\alpha\), the recovery rates \(\gamma _1\) and \(\gamma _2\) and the death rate \(\mu\). In general, the parameter values are not measured directly in studies, other measurable quantities could be supported to back out these parameters. The time spent in the exposed class is called the incubation period and is generally assumed to be equal to the time between exposure to an infected source and the development of symptoms. In the model the average incubation period is \(\frac{1}{a}\). The infectious period is the time during which an individual can transmit to others (Qun et al. 2020; Steven et al. 2020; Lauren et al. 2020). In this paper we study about there are potentially two different infectious periods, occurring during each clinical stage of infection \(I_1\) and \(I_2\). We observe the duration of each of these stages. The study shows that an individual is most infectious during the stage of non-critical infection period. At this period population would still be in the community and feeling well enough to interact with others. However, there is also a chance to transmit the disease into the further stage such as critical stage (Wei-jie et al. 2020; Chaolin et al. 2020; Stephen et al. 2020; Natalie et al. 2020; Jingyuan et al. 2020; Yang et al. 2020). We exemplify this phenomena such as the transmission from hospitalized patients to their healthcare providers. At a population level, we expect most transmission to occur from these individuals with non-critical stage of infection, since most of the patients do not progress past this stage. For COVID-19 we can estimate the duration of the first stage from the duration of non-critical symptoms, the time from symptom onset to hospitalization (e.g. progress to critical stage), or the duration of viral shedding via sputum or throat swabs, the serial interval between symptom onset in an index case and a secondary case they infect. The probability of progressing to the critical stage is equal to the proportion of all infections that end up to critical. Individuals with critical infection \((I_2)\) need hospitalization. The duration of critical infections could be reported as the time from hospital admission to recovery for individuals or the time from hospital admission to ICU admission (since critical cases require ICU-level care). Since there are not direct estimates of this duration, we instead use estimates of the total time from symptom onset to ICU-admission (e.g. the length of critical infection). At the critical infection stage \((I_2)\) ICU care, generally with mechanical ventilation, is required. The duration of this stage of infection is the time from ICU admission to recovery or death. Study report shows that the total time from hospital admission to death, which can approximate the duration of the critical stage. The case fatality ratio (CFR) describes the fraction of all symptomatic infected individuals who eventually die. Since individuals must progress to critical infection to die, the conditional probability of someone in the critical stage dying vs recovering is given by the CFR divided by the fraction of all critical infections.
In this study, we investigate the scenario on population dynamics for coronavirus across the globe. The manuscript is organized as follows: mathematical simulations of epidemiological model and its properties are discussed in Sect. 2. Boundedness and stability analysis are elaborately discussed in Sects. 3 and 4. Impact of population density along with time is the mathematical key findings. Conditions of bifurcation analysis are studied in Sect. 5. Persistence of the model system and extinction properties are discussed in Sects. 6 and 7, respectively. Numerical simulation is described in Sect. 8. Finally in Sect. 9 we elaborately present our conclusions.
Mathematical simulations
We are interested in knowing how the number of active cases is going to change in the near term. We assume that active cases \((A_t)\) follow an exponential growth model such that \(E(A_t)=A_0e^{r_t}\). In reality, the growth dynamics are much more complex than this, but for short time periods the exponential model may provide a reasonable approximation. To fit this model, we take the natural logarithm of both sides, yielding \(lnA_t=r_t+lnA_0\) showing us that we can fit a simple linear regression of \(lnA_t\) against t. The slope of this fit is an estimate of the intrinsic growth rate, r. The doubling time \((t_d)\) is an intuitive measure of how fast a population is growing. It reports the number of days for the population to double in size and is calculated by setting \(A_t/A_0=2\), yielding \(t_d=\dfrac{ln2}{r}\). Public health interventions are firmly aimed at the reduction of virus transmission and also in the lightening the growth of the number of active cases. The earliest indications of intervention success will manifest in lowered growth rates.
Basic reproductive ratio
Basic reproductive ratio is termed as \(R_0\). The basic idea is that \(R_0\) is the sum of the average number of secondary infections generated from an individual in stage \(I_1\) and the probability that an infected individual progresses to \(I_2\) multiplied by the average number of secondary infections generated from an individual in stage \(I_2\). The value of \(R_0\) is as follows:
where \(N=S+E+I_1+I_2+R+D=\)Total population size (constant).
Epidemic growth rate
Early in the epidemic, before susceptible are depleted, the epidemic grows at an exponential rate r, which can also be described with doubling time \(T_2=ln(2)/r\). During this phase all infected classes grow at the same rate as each other and as the deaths and recovered individuals. The cumulative number of infections that have happened since the outbreak started also grows at the same rate. This rate can be calculated from the dominant eigenvalue of the linearized system of equations in the limit that \(S=N\). During this early exponential growth phase, there will be a fixed ratio of individuals between any pair of compartments. This expected ratio could be used to estimate the amount of under reporting in data. For example, we might think that all deaths are reported, but that some mild infections might not be reported, since these patients might not seek healthcare or might not be prioritized for testing. These ratios have expected values under the model for a fixed set of parameters. They can be calculated by finding the eigenvector corresponding to the dominant eigenvalue (r) for the linearized system described above. Ratios that deviate from these values suggest either (i) under reporting of cases relative to deaths, or (ii) local differences in the clinical parameters of disease progression. The expected ratios are as follows:
Updated model formulation
Now we validate our introduced extended SEIR model system (1) with the classic SEIR model (Trawicki 2017; Li and Muldowney 1995; He et al. 2020; Li and Muldowney 1995; Carcione et al. 2020). We will investigate in the development of lifetime immunity from this infectious disease and observe the dynamical changes over the progress of time for the both of the model systems (1) and the classic SEIR model system, respectively, via numerical simulations, which could be a similar case of the 1918 Spanish flu. Therefore, its significance in the real-world problem is much more important and we will show that this comparison can give the impactful results in the controlling of the pandemic by synthesizing the parameter data. Here, we consider the non-critical \((I_1)\) and critical \((I_2)\) infected individuals as a total number of infected individuals, i.e. \(I_1+I_2=I\) and assume that vital dynamics (births and deaths) can sustain an epidemic or allow new introductions to spread because new births provide more susceptible individuals. In a realistic population like this, disease dynamics will reach a steady state, where \(\Lambda\) and \(\mu\) represent the birth and death rates, respectively, and are assumed to be equal to maintain a constant population (Kermack and McKendrick 1927; Menon et al. 2020). \(\beta\), \(\gamma\) and a represent transmission rate, recovery rate and progression rate, respectively, and the variables are carried the same meaning as above. Then, system (1) becomes:
The initial conditions of (2) are given as \(S(0)\ge 0, E(0)\ge 0, I(0)\ge 0, R(0)\ge 0\). We know from the fundamental theory of functional differential equations, there is a unique solution (S(t), E(t), I(t), R(t)) to system (2) with above initial conditions.
Well-posed system
Feasible solution set of the system (2)
Here \(\mathbb {R}^4_+\) denotes the non-negative cone of \(\mathbb {R}^4\) with its lower-dimensional faces. If \(N>\frac{\Lambda }{\mu }\), we have \(\frac{dN}{dt}\le 0\), suggests that the host population decreases asymptotically to the carrying capacity. However, if \(N\le \frac{\Lambda }{\mu }\), each solution with initial conditions belongs to \(\mathbb {R}^4_+\) and the solution of (2) is positive for all values of \(t>0\). So, the region \(\Omega\) is positively invariant and the system (2) is well-posed.
Basic reproductive ratio
Basic reproductive ratio is termed as \(R_0\). The basic idea is that \(R_0\) is the probability that an exposed individual progresses to I multiplied by the average number of infections generated from an individual in stage I. The value of \(R_0\) is as follows:
where \(N=S+E+I+R=\)Total population size (constant).
The endemic equilibrium point is termed as
Theorem 1
For \(R_0>1\), there exists an unique endemic equilibrium \(E_*\).
Proof
When disease becomes endemic, mathematically we represent \(\frac{dE}{dt}>0\) and \(\frac{dI}{dt}>0\). The following inequalities are obtained from the system (2):
.
Now we are using the fact \(\frac{S}{N}<1\), we obtain the following inequality:
which follows \(R_0>1\).
This proves the theorem. \(\square\)
Boundedness of the system
Here we establish the condition of uniform boundedness of the model system (2). As per estimation, population level may generate with an exponential rate. The uniform boundedness suggests that the global solution of the model system exists. For the sake of our calculation, here we assume N(t) as variable otherwise rest of cases we consider N as constant.
Theorem 2
All the solutions of the system (2) which initiated in \(\mathbb {R}^4\) are uniformly bounded.
Proof
Let (S(t), E(t), I(t), R(t)) be any solution of the system (2) with positive initial condition.
Let us consider that, \(N(t)=S(t)+E(t)+I(t)+R(t)\), where we treat N(t) as variable and initial value is termed as N(0). Now we have,
Applying the theory of differential inequality we obtain \(N(t)= N(0)e^{-t}+\Lambda\).
Therefore, \(N(t) = \Lambda [\text{ as } t\rightarrow \infty ]\).
Hence, all the solutions of (2) that initiated in \(\mathbb {R}^4\) are uniformly bounded. \(\square\)
Stability analysis of the system
Our primary focus lies in examining the possible solution set of a dynamical system in a particular environment. Ecological stability rules resilience, persistence, elasticity, amplitude and constancy. The proper definition belongs to the context of the ecosystem. The concept of neighbourhood in stability and the domain of attraction in the ecosystem are introduced by dynamical system. A system is said to be locally stable if it is stable over small perturbations and globally stable if the system has a unique equilibrium point in the entire domain of attraction. We construct a mathematical model with respect to a given environment and then investigate the stability of that model by linearizing it. The Lyapunov stability method is also widely used for establishing the global stability in any mathematical model.
Properties of local stability
Model systems have three possible non-negative equilibria, namely \(E_0(0,0,0,0)\), \(E_1(N,0,0,0)\) and \(E_{*}(S^*,E^*,I^*,R^*)\). Now we show the feasibility and stability properties of the first two equilibria of the system in Table 1 along with the corresponding feasibility and stability properties for endemic equilibrium point \(E_*\). The Jacobian Matrix of the system (2) is as follows,
Theorem 3
Endemic equilibrium \(E_*\) of system (2) is locally asymptotically stable in \(\Omega\) when \(R_0>1\).
Proof
We evaluate the Jacobian matrix (3) at the endemic equilibrium to obtain
Now our aim is to determine the stability condition of the endemic equilibrium point \(E_{*}(S^*,E^*,I^*,R^*)\) for systems (2). We obtain a characteristic equation,
Thus, the characteristic equation becomes
where
Thus, from Routh–Hurwitz criterion (Gantmacher 1960) we have the matrix
According to the Routh–Hurwitz criterion when \(R_0>1\), the endemic equilibrium \(E_{*}(S^*,E^*,I^*,R^*)\) is locally asymptotically stable if
\(\square\)
Properties of global stability
A system is said to be globally stable if it can return to the equilibrium point from any possible starting point. Global stability conveys that a system possesses a unique equilibrium point in the entire domain of attraction that is the attracting basin of trajectories of a dynamical system is either the state space or a particular region in the state space, which is the identifying region of the state variables of the system. Global stability is a kind of asymptotic stability. Here, we describe the global stability of the endemic equilibrium point, \(E_{*}(S^*,E^*,I^*,R^*)\). The global stability of the endemic equilibrium is analysed using the following constructed Lyapunov function.
Theorem 4
When \(R_0>1\), endemic equilibrium point \(E_{*}(S^*,E^*,I^*,R^*)\) is globally asymptotically stable if \(A < B\) where
and
Proof
Let \(E_{*}(S^*,E^*,I^*,R^*)\) be the co-existing equilibrium point. The proof can be reached by constructing a Lyapunov function. Now, we consider a positive definite function as
Therefore,
Thus, collecting positive terms together and negative terms together from the above
where
and
Thus if \(A < B\), then we obtain that \(\frac{dV}{dt}\le 0\), noting that \(\frac{dV}{dt}= 0\) if and only if \(S=S^*\), \(E=E^*\), \(I=I^*\) and \(R=R^*\). Therefore, the largest compact invariant set in \(\{(S^*,E^*,I^*,R^*) \in \Omega : \frac{dV}{dt}=0\}\) is the singleton \(\{E_*\}\), where \({E_*}\) is the endemic equilibrium of system (2).
Thus, by LaSalle’s invariance principle (Hale 1969), it implies that \({E_*}\) is globally asymptotically stable in \(\Omega\) if \(A < B\). Therefore, the function V in the interior of the positive octant is a Lyapunov function. Hence, the equilibrium point \(E_{*}\) is globally asymptotically stable in the positive octant. \(\square\)
Analysis of bifurcation
For the qualitative behaviour of model system (2), we analyse the bifurcation of the equilibrium points and explain the results. In the bifurcation, endemic equilibrium point \(E_*\) exchanges stability, limit points of cycles in which a stable and an unstable cycles collide. In this section, we have mainly used Sotomayer’s theorem (Perko 2001) and the Hopf bifurcation theorem (Murray 1993) to discuss the bifurcation analysis of our system.
Theorem 5
(Sotomayer’s theorem) (Perko 2001) Consider the system
where \(\mu \in \mathbb {R}\), a parameter \(\mu _0\) with being the bifurcation threshold. Suppose that \(f\left( x_0,\mu _0\right) =0\) and that the \(n\times n\) matrix \(A=Df\left( x_0,\mu _0\right)\) has a simple eigenvalue \(\lambda =0\) with eigenvector \(\mathbf{v}\) and that \(A^T\) has an eigen vector \(\mathbf{w}\) corresponding to the eigenvalue \(\lambda =0\). Furthermore, suppose that A has k eigenvalues with negative real part and \((n-k-1)\) eigenvalues with positive real part and that the following conditions are satisfied
Then, there is a smooth curve of equilibrium points of (5) in \(\mathbb {R}^n \times \mathbb {R}\) passing through \(\left( x_0,\mu _0\right)\) and tangent to the hyperplane \(\mathbb {R}^n \times \{\mu _0\}\). Depending on the signs of the expressions in (6), there are no equilibrium points of (5) near \(x_0\) when \(\mu <\mu _0\) \(\left( \text{ or } \text{ when } ~\mu >\mu _0\right)\) and there are two equilibrium points of (5) near \(x_0\) when \(\mu >\mu _0\) \(\left( \text{ or } \text{ when }~ \mu <\mu _0\right)\). The two equilibrium points of (5) near \(x_0\) are hyperbolic and have stable manifolds of dimensions k and \(k + 1\) , respectively, i.e. the system (5) experiences a saddle-node bifurcation at the equilibrium point \(x_0\) as the parameter \(\mu\) passes through the bifurcation value \(\mu =\mu _0\).
Saddle-node bifurcation
Theorem 6
The system (2) exhibits a saddle-node bifurcation around the equilibrium point \(E_1(N,0,0,0)\) when the bifurcation parameter \((\mu )\) tends to zero.
Proof
The Jacobian matrix J of the system (2) around the disease free equilibrium point \(E_1=(N,0,0,0)\) is given by
Clearly, two of the eigenvalues of \(J_{E_1}\) are negative and the other two eigenvalues will tend to zero. If V and W denote the eigenvectors corresponding to the eigenvalue zero of the matrices \(J_{E_1}\) and \(J_{E_1}^T\), respectively, then we obtain V = \((\beta -\gamma , \beta , \beta , 0)^T\) and W = \((1, 0, 0, 1)^T\).
Now,
By Sotomayer’s theorem (5), system (2) undergoes a saddle-node bifurcation around the equilibrium point \(E_1(N,0,0,0)\). \(\square\)
Hopf bifurcation
On the basis of Poincaré–Bendixson theorem, in this section we analyse the existence of limit cycle.
Theorem 7
(Poincaré–Bendixson theorem) (Meiss 2007) Let D be a simply connected subset of \(\mathbb {R}^4\) and \(\omega\) is a flow on D. Suppose that the forward orbit of some \(z\in D\) is contained in a compact set and \(\omega (z)\) contains no equilibrium points. Then, \(\omega (z)\) is a periodic orbit.
Let us consider \(\alpha\) as bifurcation parameter of a system where the characteristic equation corresponding to an equilibrium point \(E_{*}(S^*,E^*,I^*,R^*)\) of the system is
then the statement of the Hopf bifurcation theorem is as follows:
Theorem 8
(Hopf bifurcation theorem) (Murray 1993) If \(C_i(\alpha ); i=1,2,3,4\) are continuous functions of \(\alpha\) in \(N_\epsilon (\alpha _0), (\epsilon > 0), \alpha _0 \in R\) such that the characteristic equation has
(i) a pair of complex eigenvalues \(H = k(\alpha ) + il(\alpha ) (with~ k(\alpha ), l(\alpha ) \in R)\) so that they become purely imaginary at \(\alpha = \alpha _0 ~and ~(\frac{dk}{d\alpha })_{\alpha =\alpha _0}= 0\),
(ii) the other eigenvalue is negative at \(\alpha = \alpha _0\), then a Hopf bifurcation occurs around \(E_{*}(S^*,E^*,I^*,R^*)\) at \(\alpha = \alpha _0\).
Remark 1
From Poincaré–Bendixson theorem (7) and (4), there exists an unique limit cycle.
Remark 2
The above similar process follows for the bifurcation parameter \(\gamma _2\).
Analysis of persistence of the system
Persistence is an important dynamical characteristic of any system in the sense that it describes long-term behaviour of the system. Suppose \(P(t)>0\) for \(t\ge 0\), then P(t) is persistent if \(\lim _{t\rightarrow \infty } \inf P(t) >0\). A differential equation shows persistence provided all the solutions with positive initial conditions are persistent (i.e. if there is a fixed bounded region then all the trajectories lie in the region for sufficiently large time t) (Butler et al. 1986). In accordance with population biology, differential equations among interactive populations illustrate the persistence of the system associated with the survival of all interacting populations. The most significant part is the peak times of infected population and its repeated nature (Feng 2007). The peaks are related to local or global extremums of I(t). From system (2), we have \(I(t) = \frac{aE(t)}{\gamma +\mu }\). This can be solved by the solution variables \((S,E,I,R)^T\). It has been observed that there are many more local peaks of the infected population over the time along with repeated behaviours, which has been noticed in the earlier pandemics such as Spanish flu (1918 pandemic influenza), which had three pandemic waves of infection within quick interval of few months (Goncalves et al. 2011).
Definition 1
If there exist positive constants m and M, which are independent of the solution of system (2) such that solution I(t) of system (2) satisfies
then system (2) is persistent.
Lemma 1
(Chen 2005) If \(a>0, b>0\) and \(\frac{dX}{dt} \ge (b-ax)\) when \(t \ge 0\) and \(x(0)>0\), we have
If \(a>0, b>0\) and \(\frac{dX}{dt} \le (b-ax)\) when \(t \ge 0\) and \(x(0)>0\), we have
Theorem 9
Let I(t) be any solution of system (2), then
then system (2) is persistent.
Proof
Let I(t) be a solution of system (2). From system (2), we have
Applying Lemma (1) to (8), it immediately follows that
Again we have,
Applying Lemma (1) to (10), it immediately follows that
\(\square\)
Now we conclude that from Definition (1), Lemma (1) and Theorem (9), we have that the system (2) is persistent.
Remark 3
Over the progression of time, the fatal disease can be repeated pseudo-periodically, i.e. coronavirus can return once again in the later seasons of the year or over the years in the worldwide and it becomes into a persistent disease in the long term of period. The amplitude and time gap of the infection peaks totally rely on the parameters of the system (2).
Extinction properties
The termination of an individual is termed as extinction. When the death of the last individual of any population occurs, then the extinction of that individual is confirmed, although the capacity to breed and recover may have been lost before this point. The absence of any surviving individuals (that can reproduce and create a new generation) of that particular individual confirms the extinction of that populations. However, an individual may become functionally extinct when only a few number of that individuals survive. This section shall give us the conditions for which exposed and infected populations wash out from the system in long run of the time. Let us consider the notation: \(\lim _{t\rightarrow \infty } \sup I(t) = \bar{I}\). Here, we assume the following fact: \(I < \bar{I}+ \epsilon\), where \(\lim _{t\rightarrow \infty } \sup I(t) \le \bar{I}\).
Theorem 10
If \(\frac{\mu +a}{\beta }>{\bar{I}}\), then \(\lim _{t\rightarrow \infty } E(t) = 0\).
Proof
Choose \(0< \epsilon < \frac{\mu +a}{\beta } - I\) Then \(\exists\) \(t_1 >0\), s.t. \(I(t)<{\bar{I}}+\epsilon , \forall t>t_1\). Also we know that, \(N=S+E+I+R\). Then from the model system (2), we have
Hence, \(\lim _{t\rightarrow \infty } E(t) = 0\). \(\square\)
Remark 4
The progression rate is enough to extinct the exposed populations.
Theorem 11
If \((1+\frac{\gamma + \mu }{a})>N\), then \(\lim _{t\rightarrow \infty } I(t) = 0\).
Proof
Here we know that \(N=S+E+I+R\). Then from the model system (2), we have
Hence, \(\lim _{t\rightarrow \infty } I(t) = 0\). \(\square\)
Remark 5
The higher recovery rate helps to extinct the infected populations.
Numerical simulation
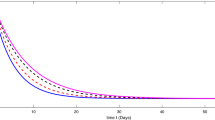
We validate the analytical results of our model systems (1) and (2) which are obtained by the numerical simulation (Sameni 2020; Prem et al. 2017; Mossong et al. 2008; Tapiwa et al. 2020; Kissler et al. 2020; Pan et al. 2020). The transmission rates are generally impossible to directly observe or estimate. Instead, these values can be backed out by looking at the early exponential growth rate (r) of an epidemic and choosing transmission rates that recreate these observations. The growth of COVID-19 outbreaks has varied a lot between settings and over time. Some values reported in the literature are in Tables 2, 3 and 4. We consider that the dominant source of transmission is from individuals with having non-critical infections who are likely to still be in the community, as opposed to isolate in the hospital. In the first column of Fig. 2, we distinguish the outbreak of corona virus between model systems (1) and (2), respectively, and it is noticed that the lifetime immunity has been developed from this viral disease, so there is no sign of returning cases recovered to susceptible compartment. In second and third columns of Fig. 2, the interesting fact is noticed that the peaks are decaying over the progress of the time for the both of the model systems (1) and (2), respectively, which has been similar situation to the 1918 Spanish flu. So from above we conclude that our parameter selection for both of the model systems (1) and (2) is very much significant and it gives us satisfactory result indeed. In Figure 3(i), we illustrate the effect of lockdown, applied by the government to determine the exposed and infected cases and it gives us a proper idea about the effect of quarantine period and also suggests that the population ratio of infected and exposed peaks have decreased after the lockdown period. However, 3(ii) indicates the mortality rate does not significantly fluctuate after the six months period of lockdown. The main reason of this because of after the lockdown period is over, a fraction of the exposed population can again restart the corona virus spread. In Fig. 3(iii), it is observed that the recovery rate has been increased after the lockdown period and the significance of this phenomenon pays a major role to fight against COVID-19. In Fig. 3(iv), we investigate that the effect of healthcare system capacity reaches to its threshold point for the model system (1) during the lockdown period. In Fig. 4, we show the Hopf bifurcation phenomenon in the three-dimensional space with respect to the bifurcation parameters \(\gamma _2\) and \(\alpha\), respectively, whilst portraying the stability analysis of model system (1) at the endemic equilibrium point \(E_*\). Other parameter values are given as following: \(\beta _1=0.6, \beta _2=0.002, a=0.056, \gamma _1=0.0025, \mu =0.02\).
Compare the simulation between the model systems (1) and (2), respectively. In the first column we illustrate the simulation of around six–seven months and in the second and third columns we consider the time about ten years. Here violet represents susceptible (S), green indicates exposed (E), orange illustrates infected (I), brown stands for recovered (R) and sky-blue is for dead (D) populations. Parameter values of system (1): \(\beta _1=0.6, \beta _2=0.002, a=0.056, \alpha =0.85, \gamma _1=0.0025,\gamma _2=0.1, \mu =0.02\) and parameter values of system (2): \(\Lambda =0.1, \beta =0.015, a=0.017, \gamma =0.15, N=1, \mu =0.001\) (colour figure online)
(i) Simulation of the model system (1) with a lockdown period correspond to the effect of before and after the lockdown. (ii) The effect of mortality rate before and after the lockdown. (iii) The effect of recovered rate before and after the lockdown. (iv) Healthcare capacity system reaches its threshold point at \(I=0.1\). Parameter values of system (1): \(\beta _1=0.6, \beta _2=0.002, a=0.056, \alpha =0.085, \gamma _1=0.0025,\gamma _2=0.1, \mu =0.02\). During the lockdown period \(\beta _1\) and \(\beta _2\) are decreased to 0.1 and 0.001, respectively, whilst other parameters are fixed. When the lockdown period is over, the value of \(\beta _1\) is increased to 0.4 (more than lockdown period); however, \(\beta _2\) remains unchanged as 0.001 which implies that after the lockdown is lifted people remain keep social distance with the infected populations
a Hopf bifurcation diagram of system (1) with respect to the bifurcation parameter \(\gamma _2\) is drawn in the three-dimensional space \((\gamma _2, I_2, E)\). This figure shows that the coexistence equilibrium \(E_*\) is unstable focus for \(\gamma _2>0.16\), now system converges to stable limit cycle (depicted by different colour cycles different values of \(\gamma _2\)), stable focus for \(\gamma _2<0.16\) (depicted by dotted line) and a Hopf bifurcation occurs at \(\gamma _2=0.16\). b Hopf bifurcation diagram of system (1) with respect to the bifurcation parameter \(\alpha\) is drawn in the three-dimensional space \((\alpha , I_1, E)\). This figure shows that the coexistence equilibrium \(E_*\) is unstable focus for \(\alpha <0.5\), now system converges to stable limit cycle (depicted by different colour cycles different values of \(\alpha\)), stable focus for \(\alpha <0.5\) (depicted by dotted line) and a Hopf-bifurcation occurs at \(\alpha =0.5\). Other parameters are in the text
Conclusions and discussion
Some recent reports have suggested that healthcare workers are disproportionally infected with COVID-19, suggesting that there is some role to hospital-based transmission (e.g. from individuals in states \(I_1\) and \(I_2\), or individuals who are hospitalized with only mild infection). In China, approximately 5% of all infections were in healthcare workers (Jiancong et al. 2020), and in Italy the number is currently around 10% (Jiancong et al. 2020). One of the biggest dangers of a widespread COVID-19 epidemic is the strain it could place on hospital resources, since individuals with critical infection require hospital care. The critical stage of infection requires mechanical ventilation, which is ICU-level care. Individuals with non-critical infection do not require hospitalization and could recover at home on their own or can be treated in a regular hospital ward. However, in many countries these individuals have also been hospitalized, likely as a way to isolate them and decrease the transmission rate, as well as to observe them for progression to more aggressive disease stages. In recent studies on COVID-19, it has been noticed that nearly all individuals included had symptoms, since the presence of symptoms was used to determine whether someone would be admitted for a test of COVID-19. However, it is possible that some individuals may be infected and be able to transmit to others without developing symptoms. Recent studies show that asymptomatic individuals were also screened for infection and tested positive. The model also suggests the possibility of pre-symptomatic transmission. In general compartmental epidemiological models assume that the onset of symptoms and the onset of infectiousness coincide, but recent evidence indicates that symptoms may be delayed relative to when an individual is infectious. Viral loads are measured over time in symptomatic individuals, studies show that they are at a peak on the first day of symptoms, suggesting that they were already high before symptoms started (Roman et al. 2020). Detailed contact tracing studies that have tracked transmission chains where the infector and the infectee are both known have found the serial interval, which is the time between symptom onset in the infector and infectee, is sometimes less than the incubation period. This means there must be pre-symptomatic transmission. A wide range of values for the proportion of all transmission that is pre-symptomatic have been estimated (12–62%), so we choose an intermediate value of 25%, consistent with (Yang et al. 2020). A related line of evidence for the presence of pre symptomatic infection is that the average length of the serial interval is quite close to the average length of the incubation period in a few studies. This suggests either a very short symptomatic and infectious period, or, significant pre-symptomatic transmission. The main uncertainty thing in this pandemic has been undetected cases. COVID-19 has been quite a sneaky pathogen, and observation has often not been adequate, often resulting in a large number of infections in a country before it is noticed. Practically all cases are not detected and so the reported number of active cases is almost always lower than the true number of cases. Non-detected cases are such as undiagnosed, those that will be diagnosed soon. Individuals who are infected but yet to notice the symptoms and undetected, those that will never be diagnosed. Individuals that present with mild symptoms, or are missed by surveillance. In the first case, there is shown a lateness between infection and diagnosis. However, if we know something about the length of this delay then we can use this information to inflate the observed case numbers to produce estimates of the number of undiagnosed cases. The most important determinant of the delay is the incubation period of the infection. This is known to be highly variable but can be modelled using a probability distribution, which is called the incubation distribution. Information about the incubation distribution exists from external sources. It is known that the average incubation period is 5–6 days and that 95 per cent of infections have reported with an incubation period of time not more than 12–13 days. The daily diagnosis counts reflect a larger and unknown number of COVID-19 infections in the population, aggregated with the incubation distribution. The undetected cases are completely missed by surveillance. To estimate these, we use a heuristic that assumes deaths do not go undetected, that there is community transmission (and a closed population), that there is a case fatality rate for symptomatic cases (here assumed to be quite high 3.3 per cent and lower numbers will cause our detection estimate to be lower), that detection is constant, and that there is a fixed time between onset and death. In countries with many undetected cases, there are many more deaths than there should be given reported case numbers. One obvious source of bias in both estimates is imported cases. When there is movement between countries and large differences in case-load, countries with small numbers of cases will have a large proportion of imported cases. These will cause us to estimate a larger number of non-detections than there are. To control this epidemic, government has to impose lockdown situation so that the effectiveness of the virus spreading is delaying over the time and the peaks of the infected population becomes minimize. However, this process is insufficient for a long term of period. Social distancing, effectiveness of quarantine and less crowd gathering are most feasible conditions to become the zero contaminated zone for a longer period of time. In many countries it has been noticed that with limited test kits, medication, hospitalization, excessive fatigue or mortality of the healthcare personnel, economic breakdowns, etc. cause healthcare system to reach its threshold capacity. This situation looked as worst-case scenario for pandemic strategies. Now the situation becomes more worried as there are observed instability in the community since the outbreak of such pandemic is spreading rapidly. Mathematically we investigate the whole situation in this paper. We offer some proposals to control this fatal epidemic disease followings:
-
Embed maximum lockdown of the entire population in the country, send to quarantine of the infected cases, impose home isolation of the asymptomatic cases (rest of the people who are not infected) and look after in the application of these above mentioned cases as soon as possible.
-
Figure out the number of exposed cases and distinguish the level of their infectiousness.
-
Maximal lockdown remains until as many of all the number of estimated exposed cases are calculated.
-
Lift the lockdown and apply strict social distancing upon economical conditions.
-
Back to normal life if there is no new cases have been registered for a long period of time.
-
Select a state as a model state and apply all the above regulations and observe the effectiveness if results will fruitful then apply the regulations in whole country.
The condition of human lives are such metastable so that we all need to think as united against the deadly coronavirus and make a way through this such fatal phase. Unless the parametric conditions, nothing is specified about the coronavirus. Here we present both theoretical and analytical studies and compare them to real-world problem by fitting our model over real data and predict the infected and mortality rates with all possible patterns of the epidemic disease over the progression of time.
References
Abbott S (2020) Temporal Variation in Transmission During the COVID-19 Outbreak, CMMID
Biswas MHA, Paiva LT, Pinho M (2014) A seir model for control of infectious diseases with constraints. Math Biosci Eng 11:761
Butler G, Freedman HI, Walyman P (1986) Uniformly persistent systems. Proceedings of the American Mathematical Society 96(3):425–430
Carcione JM, Santos JE, Bagaini C, Ba J (2020) A simulation of a COVID-19 epidemic based on a deterministic SEIR model. Front Public Health 8
Chaolin H, Wang Y, Li X, Ren L, Zhao J, Hu Y, Zhang L et al (2020) Clinical features of patients infected with 2019 Novel Coronavirus in Wuhan, China. Lancet 395(10223):497–506
Chen FD (2005) On a nonlinear non-autonomous predator-prey model with diffusion and distributed delay. J Comput Appl Math 180(1):33–49
David B, Qi X, Nielsen-Saines K, Musso D, Pomar L, Favre G (2020) Real estimates of mortality following COVID-19 infection. Lancet Infect Dis
Fei Z, Yu T, Du R, Fan G, Liu Y, Liu Z, Xiang J et al (2020) Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan. A Retrospective Cohort Study, The Lancet, China
Feng Z (2007) Final and peak epidemic sizes for seir models with quarantine and isolation. Math Biosci Eng 4:675
Gantmacher FR (1960) The theory of matrices. Chelsea Publishing, New York
Goncalves S, Abramson G, Gomes MF (2011) Oscillations in sirs model with distributed delays. Eur Phys J B 81:363–371
Hale JK (1969) Ordinary differential equations. Wiley, New York
He S, Peng Y, Sun K (2020) SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn 101:1667–1680
Hiroshi N, Kobayashi T, Miyama T, Suzuki A, Jung S, Hayashi K, Kinoshita R et al (2020) Estimation of the asymptomatic ratio of Novel Coronavirus infections (COVID-19), medRxiv
Jiancong W, Zhou M, Liu F (2020) Exploring the reasons for healthcare workers infected with Novel Coronavirus Disease 2019 (COVID-19) in China. J Hosp Infect
Jingyuan L, Liu Y, Xiang P, Pu L, Xiong H, Li C, Zhang M et al (2020) Neutrophil-to-lymphocyte ratio predicts severe illness patients with 2019 Novel Coronavirus in the early stage, medRxiv
Joseph W, Leung K, Bushman M, Kishore N, Niehus R, Salazar PM, Cowling BJ, Lipsitch M, Leung GM (2020) Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat Med 1–5
Julien R, Hauser A, Counotte MJ, Althaus CL (2020) Adjusted age-specific case fatality ratio during the COVID-19 Epidemic in Hubei, China, January and February 2020, medRxiv
Kenji M, Kagaya K, Zarebski A, Chowell G (2020) Estimating the asymptomatic ratio of 2019 Novel Coronavirus onboard the princess cruises ship, medRxiv
Kermack WO, McKendrick AG (1927) A contribution to the mathematical theory of epidemics. Proc R. Soc A 115(772):700–721
Kissler SM, Tedijanto C, Goldstein E, Grad YH, Lipsitch M (2020) Projecting the transmission dynamics of SARS-CoV-2 through the post-pandemic period, MedRxiv
Kucharski AJ, Russell TW, Diamond C, Liu Y, Edmunds WJ, Funk S, Eggo RM (2020) Early dynamics of transmission and control of COVID-19 in Wuhan. Lancet Infect Dis 20:553–558
Lauren T, Coombe M, Stockdale JE, Garlock E, Lau WYV, Saraswat M, Lee YB et al (2020) Transmission interval estimates suggest pre-symptomatic spread of COVID-19, medRxiv
Li MY, Muldowney JS (1995) Global stability for the SEIR model in epidemiology. Math Biosci 125:155–164
Li M, Muldowney J (1995) Global stability for the SEIR model in epidemiology. Math Biosci 125:155–164
Li Q, Guan X, Wu P et al (2020) Early transmission dynamics in Wuhan, China, of Novel Coronavirus-infected pneumonia. N Engl J Med 382:1199–1207
Liu T, Hu J, Xiao J et al (2020) Time-varying transmission dynamics of Novel Coronavirus Pneumonia in China, Biorxiv
Meiss JD (2007) Differential dynamical systems. Society for Industrial and Applied Mathematics, Philadelphia
Menon A, Rajendran NK, Chandrachud A, Setlur G (2020) Modelling and simulation of COVID-19 propagation in a large population with specific reference to India, medRxiv
Mossong J, Hens N, Jit M, Beutels P, Auranen K et al (2008) Social contacts and mixing patterns relevant to the spread of infectious diseases. PLOS Med 5(3):e74
Murray JD (1993) Mathematical biology. Springer, New York
Natalie L, Kobayashi T, Yang Y, Hayashi K, Akhmetzhanov AR, Jung S, Yuan B, Kinoshita R, Nishiura H (2020) Incubation period and other epidemiological characteristics of 2019 Novel Coronavirus infections with right truncation: a statistical analysis of publicly available case data. J Clin Med 9(2):538
Pan A, Liu L, Wang C et al (2020) Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA 323:1915–1923
Penghui Y, Ding Y, Xu Z, Pu R, Li P, Yan J, Liu J et al (2020) Epidemiological and clinical features of COVID-19 patients with and without pneumonia in Beijing, China, medRxiv
Perko L (2001) Differential equations and dynamical systems. Springer, New York
Prem K, Cook AR, Jit M (2017) Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput Biol 13(9):e1005697
Qifang B, Wu Y, Mei S, Ye C, Zou X, Zhang Z, Liu X et al (2020) Epidemiology and transmission of COVID-19 in Shenzhen China: analysis of 391 Cases and 1,286 of Their Close Contacts, medRxiv
Qun L, Guan X, Wu P, Wang X, Zhou L, Tong Y, Ren R et al (2020) Early transmission dynamics in Wuhan, China, of Novel Coronavirus-infected pneumonia. N Engl J Med
Robert V, Okell LC, Dorigatti I, Winskill P, Whittaker C, Imai N, Cuomo-Dannenburg G et al (2020) Estimates of the severity of COVID-19 disease, medRxiv
Rocklov J, Sjodin H, Wilder-Smith A (2020) COVID-19 outbreak on the Diamond Princess cruise ship: estimating the epidemic potential and effectiveness of public health countermeasures. J Travel Med
Roman W, Corman VM, Guggemos W, Seilmaier M, Zange S, Mueller MA, Niemeyer D et al (2020) Clinical presentation and virological assessment of hospitalized cases of Coronavirus disease 2019 in a travel-associated transmission cluster, medRxiv
Safi MA, Garba SM (2012) Global stability analysis of SEIR model with Holling Type II incidence function. Comput Math Methods Med
Sameni R (2020) Mathematical modeling of epidemic diseases
Stephen L, Grantz KH, Bi Q, Jones FK, Zheng Q, Meredith H, Azman AS, Reich NG, Lessler J (2020) The incubation period of 2019-nCoV from publicly reported confirmed cases: estimation and application, medRxiv
Steven S, Lin YT, Xu C, Romero-Severson E, Hengartner N, Ke R (2020) The Novel Coronavirus, 2019-nCoV, is highly contagious and more infectious than initially estimated, medRxiv
Tapiwa G, Kremer C, Chen D, Torneri A, Faes C, Wallinga J, Hens N (2020) Estimating the generation interval for COVID-19 based on symptom onset data, medRxiv
Timothy R (2020) Estimating the infection and case fatality ratio for COVID-19 using age-adjusted data from the outbreak on the diamond princess cruise ship, CMMID
Trawicki MB (2017) Deterministic seirs epidemic model for modeling vital dynamics, vaccinations, and temporary immunity. J Bioinform Comput Biol 5:7
Upadhyay RK, Pal AK, Kumari S et al (2019) Dynamics of an SEIR epidemic model with nonlinear incidence and treatment rates. Nonlinear Dyn 96:2351–2368
Wei-jie G, Ni Z, Hu Y, Liang W, Ou C, He J, Liu L et al (2020) Clinical characteristics of coronavirus disease 2019 in China. N Engl J Med
Wu JT, Leung K, Leung GM (2020) Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet 395:689–697
Xiaobo Y, Yu Y, Xu J, Shu H, Xia J, Liu H, Wu Y et al (2020) Clinical course and outcomes of critically ill patients with SARS-CoV-2 pneumonia in Wuhan, China: a single-centered. Retrospective, Observational Study. Lancet Respir Med
Yang L, Funk S, Flasche S (2020) The Contribution of pre-symptomatic transmission to the COVID-19 Outbreak, CMMID
Yi N, Zhang Q, Mao K, Yang D, Li Q (2009) Analysis and control of an SEIR epidemic system with nonlinear transmission rate. Math Comput Model 50:1498–1513
Zhanwei D, Xu X, Wu Y, Wang L, Cowling BJ, Meyers LA (2020) The serial interval of COVID-19 from publicly reported confirmed cases, medRxiv
Zunyou W, McGoogan JM (2020) Characteristics of and important lessons from the Coronavirus Disease 2019 (COVID-19) outbreak in China: summary of a report of 72314 cases from the Chinese center for disease control and prevention. JAMA 323:1239–1242
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Batabyal, S., Batabyal, A. Mathematical computations on epidemiology: a case study of the novel coronavirus (SARS-CoV-2). Theory Biosci. 140, 123–138 (2021). https://doi.org/10.1007/s12064-021-00339-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12064-021-00339-5