Abstract
Thermal concentrators and cloaks with ellipsoidal shapes are designed by utilizing the transformation thermotics method and finite element simulations. The thermal conductivities for the concentrator and cloak are directly derive in Cartesian coordinates. The simulation results show that the ellipsoidal thermal concentrator can focus heat flux into a central region and that the ellipsoidal thermal cloak can guide heat flux around the cloaked region smoothly without disturbing the external temperature distribution and heat flux. The present method can be extended to design arbitrarily shaped thermal metadevices with novel properties.
Export citation and abstract BibTeX RIS
In recent years, the developed technique of transformation optics (TO)[1–6] has become a powerful means to control electromagnetic waves in almost arbitrary ways. The TO method is based on the form invariant of Maxwell's equations under coordinate transformations.[1,7] However, this approach is not limited only to electromagnetic waves. For example, the TO method has been extended to other fields including acoustics,[8] thermotics,[9–27] elastic waves,[28] matter waves,[29] fluid flow,[30] etc. The fundamental reason for such an extension is that the governing equations describing these systems are form invariant under coordinate transformations.
Over the last few decades, increasing attention has been paid to renewable energy. In addition to solar energy, another important energy source is thermal energy, which can be collected from environment. Therefore, it is particularly important to manipulate heat transfer at will. To date, studies on thermal concentrators have been limited to cylinders[12,13] and spheres.[31] In the present work, we investigate an ellipsoidal thermal concentrator and cloak for heat flux using the transformation thermotics method. For convenience, we directly derive the thermal conductivity tensors for the concentrator and cloak in Cartesian coordinates. With the derived material parameters, the finite element simulation results are analyzed to display the corresponding functions. For the designed ellipsoidal thermal concentrator, the heat flux can be concentrated in the central region. However, for the ellipsoidal thermal cloak, the heat flux can be excluded from an object without perturbing the exterior heat flux. For the designed devices, the heat flux can be guided back to its original path. Based on the transformation thermotics method and thermal metamaterials, we can design thermal concentrator and cloak with different shapes, and furthermore, develop various thermal devices with novel functionalities, such as thermal diodes.[21] The extension of the TO method to the thermal field could open a new field of study since it promises unprecedented manipulation of the heat flux, which may lead to new phenomena and applications.
Let us start by investigating the heat conduction equation. At the equilibrium, the stationary heat conduction equation in the absence of sources is given by

where T is the temperature state variable, and κ is the material thermal conductivity. Because the heat conduction equation is invariant in its form under the transformation from an original coordinate to a transformed coordinate,[7] in the new coordinate system, we must use the renormalized value of the thermal conductivity:
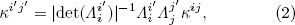
where the Roman indices extend from 1 to 3 for the three spatial coordinates, and  is the transformation operator. The bases denoted by the indices i and i' are coordinate bases. The transformation operator is derived as
is the transformation operator. The bases denoted by the indices i and i' are coordinate bases. The transformation operator is derived as

The coordinate transformation method is valid for any complicated transformation. As an example, we investigate an ellipsoidal concentrator. The coordinate transformation used in the studies of spherical cloaks[1,3] can be readily generalized to ellipsoids. For an ellipsoid with its semi-axes lying along the x, y, and z directions with lengths α1 c, α2 c, and α3 c, respectively, the ellipsoidal equation can be expressed as
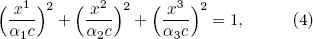
where α1, α2, and α3 are positive numbers describing the aspect ratio of the ellipsoid and do not transform as a vector. For a prolate sphere, we choose α1 = α2 < α3. For an oblate sphere, we choose α1 < α2 = α3. For the design, we obtain three ellipsoidal equations by substituting c = R1, c = R2 and c = R3 into Eq. (4). We redefine r as a scaled distance:[32]
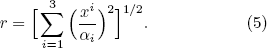
For the ellipsoidal thermal concentrator, we adopt the following linear transformations:
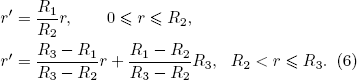
Now, since our transformation is radially symmetric, the unit vectors in the transformed space and in the original space must be equal to each other:[3]

The position vector in the transformed space in terms of only the components in the original space for the region of the ellipsoid with semi-axes α1 R2, α2 R2, and α3 R2 can be written as

Thus, we can obtain the transformation matrix

For the ellipsoidal shell with lengths of outer semi-axes α1 R3, α2 R3, and α3 R3, and lengths of inner semi-axes α1 R2,α2 R2, and α3 R2, the position vector can be written as
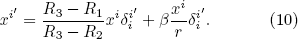
Then, we can obtain the transformation matrix
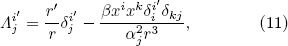
where β can be written as
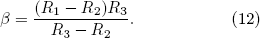
The transformation in Eq. (8) maps the field in the region of the ellipsoid with the semi-axes α1 R2, α2 R2, and α3 R2 onto the region of the ellipsoid with the semi-axes α1 R1, α2 R1, and α3 R1. Equation (10) transforms an ellipsoidal shell with lengths of outer semi-axes α1 R3, α2 R3, and α3 R3 and lengths of inner semi-axes α1 R2, α2 R2, and α3 R2 into an ellipsoidal shell with the same lengths of outer semi-axes and lengths of inner semi-axes α1 R1, α2 R1 and α3 R1. Using Eq. {2}, we can obtain the material parameters in the region of the ellipsoid with the semi-axes α1 R1, α2 R1, and α3 R1:
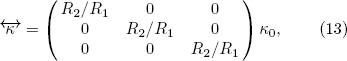
where κ0 is the thermal conductivity in the original coordinates. The material parameters in an ellipsoidal shell with lengths of outer semi-axes α1 R3, α2 R3, and α3 R3 and lengths of inner semi-axes α1 R1, α2 R1, and α3 R1 can be expressed as
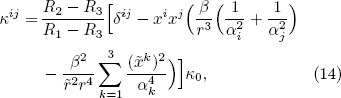
where  and
and  read
read
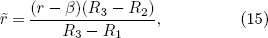
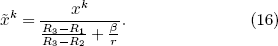
Next, we investigate the ellipsoidal thermal cloak. For the design, we adopt the linear transformation
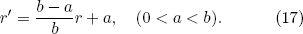
Based on Eqs. (7) and (17), we can obtain the components of the position vector in the transformed space in terms of only the components in the original space:
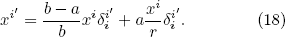
Therefore, the coordinate transformation given by Eqs. (17) and (18) transforms a closed ellipsoid with α1 b, α2 b, and α3 b into an ellipsoidal shell with the same lengths of outer semi-axes and lengths of inner semi-axes α1 a, α2 a, and α3 a. By using the same method discussed above, the material property in the ellipsoidal shell is then given by
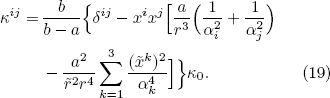
Here,  and
and  are given by
are given by


We have obtained the thermal conductivity tensor of an ellipsoidal thermal cloak. In the special case of spheres, αi = 1, the coefficient of Eq. (19) reduces to the simple result, which is exactly the same form as Eq. (20) in Ref. [3].
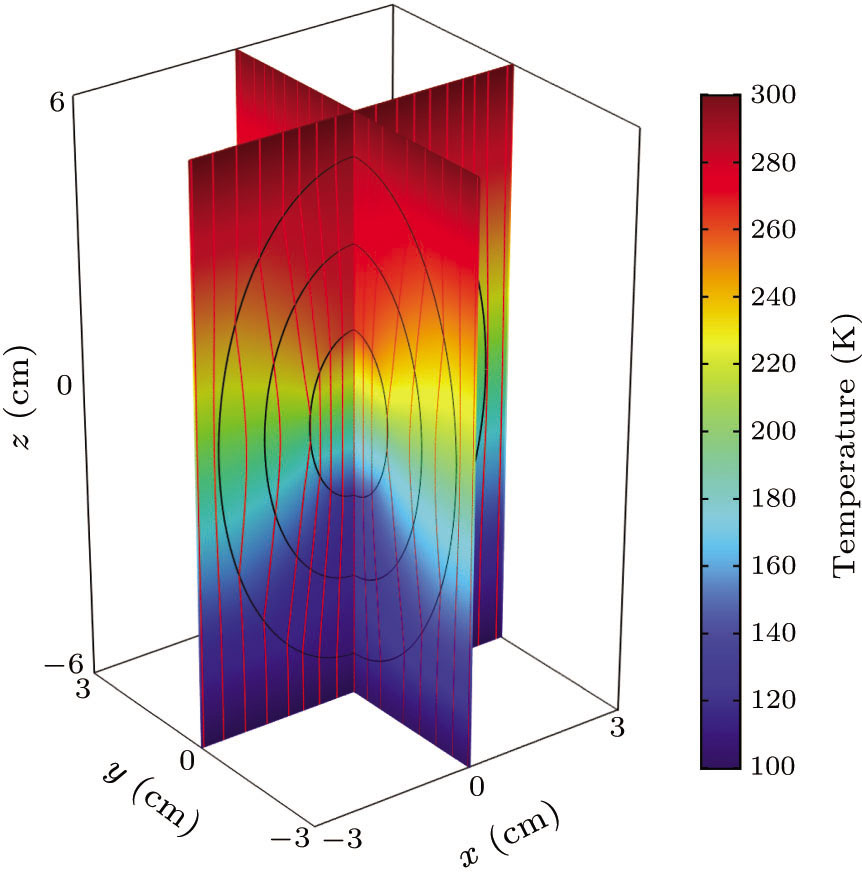
We are now in a position to perform 3D finite element simulations based on the commercial software COMSOL Multiphysics.[33] In the simulations, the boundary conditions are set to be 100 K and 300 K on the lower and upper boundaries of the cuboid simulation area, respectively, with thermal insulation for the other boundaries. The thermal conductivity of the background is set to be 1 W/mK. The color represents the temperature distribution, and the red lines denote the pathway of heat flux. For the ellipsoidal concentrator, we choose the parameters κ0 = 1 W/mK, α1 = 1, α2 = 1, α3 = 2, R1 = 1 cm, R2 = 2 cm, and R3 = 3 cm. Figure 1 shows the results of the 3D simulation of a prolate spheroidal concentrator. It is proven to be well suited for the confinement of thermal energy from outside, which may be used for thermally enhanced sensing.
Fig. 1. Three-dimensional finite element simulation of a prolate spheroidal concentrator with parameters κ0 = 1 W/mK, α1 = 1, α2 = 1, α3 = 2, R1 = 1 cm, R2 = 2 cm, and R3 = 3 cm.
Download figure:
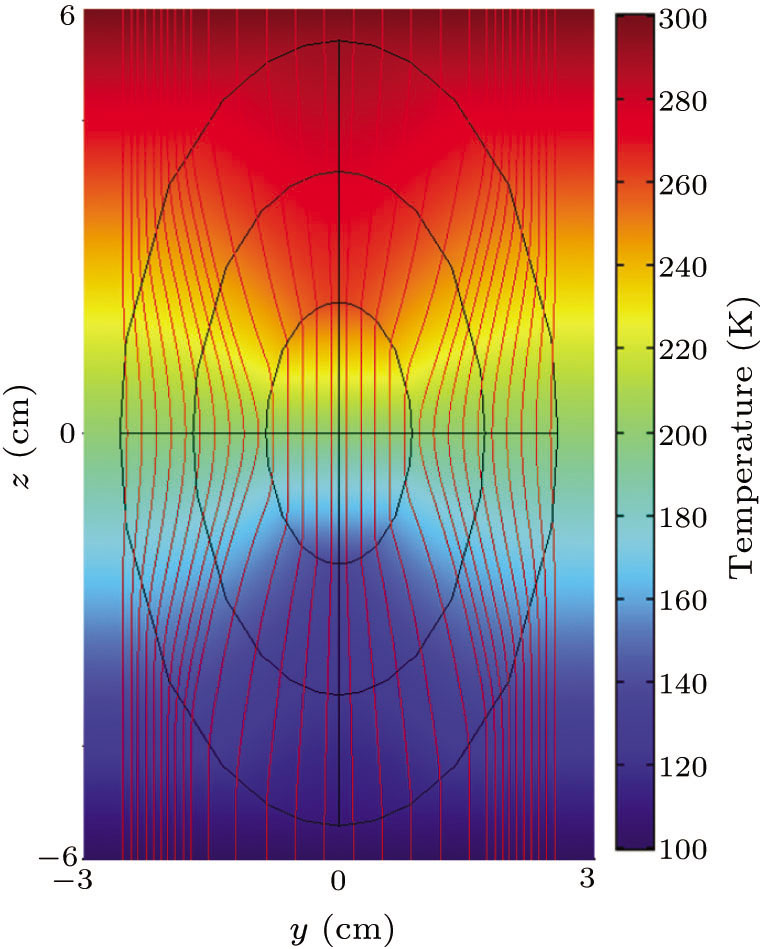
Standard imageFigure 2 illustrates the results of the 3D simulation of a prolate spheroidal concentrator with α1 = 1, α2 = 1, and α3 = 2. The slice is in the zy plane.
Fig. 2. The same as Fig. 1 but the slice in the zy plane.
Download figure:
Standard imageFigure 3 illustrates the results of the 3D simulation of an oblate spheroidal concentrator with α1 = 1, α2 = 2, and α3 = 2. The slice is in the zy plane. The proposed ellipsoidal thermal concentrator is proven to be well suited for the confinement of thermal energy from outside.
Fig. 3. The same as Fig. 1 but for oblate spheroidal concentrator with parameters α1 = 1, α2 = 2, and α3 = 2, and the slice is in the zy plane.
Download figure:
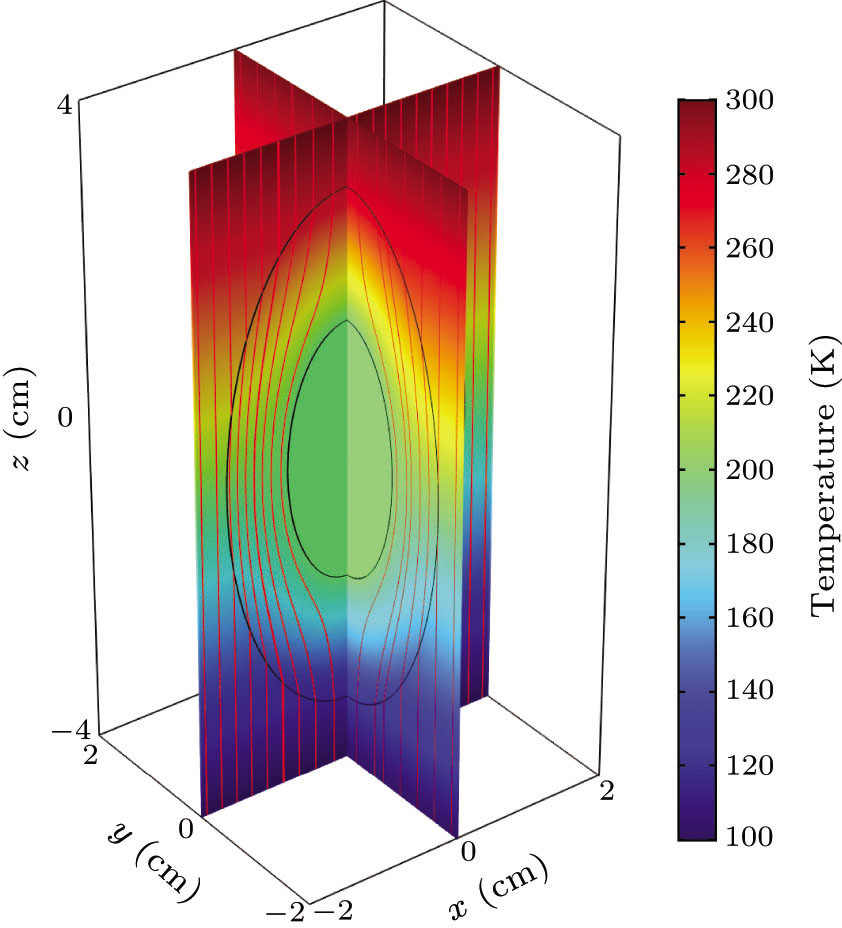
Standard imageFigure 4 illustrates the results of the 3D simulation of a prolate spheroidal cloak with α1} = 1, α2 = 1, and α3 = 2. The heat flux is smoothly bent around the center of the ellipsoidal cloak. Outside the cloak, the heat flux returns to the original direction as if nothing happens.
Fig. 4. Three-dimensional simulation of a prolate spherical cloak with α1 = 1, α2 = 1, α3 = 2, a = 1 cm, and b = 2 cm.
Download figure:
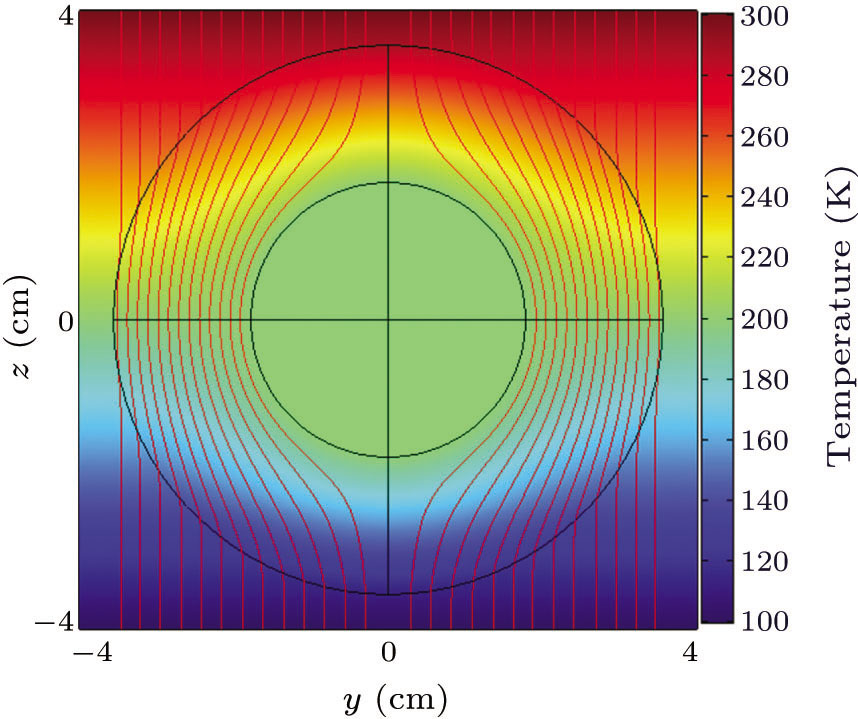
Standard imageFigure 5 illustrates the results of the 3D simulation of a prolate spherical cloak with α1} = 1, α2 = 1, and α3 = 2. The slice is in the zy plane.
Fig. 5. The same as Fig. 4 but the slice in the zy plane.
Download figure:
Standard imageFigure 6 illustrates the results of the 3D simulation of an oblate spherical cloak with α1 = 1, α2 = 2, and α3 = 2. The slice is in the zy plane. The heat flux is smoothly bent around the center of the ellipsoidal cloak.
Fig. 6. The same as Fig. 4 but for oblate spherical cloak with parameters: α1 = 1, α2 = 2, and α3 = 2, and for the slice in the zy plane.
Download figure:
Standard imageIn summary, we have theoretically and numerically demonstrated transformation media based devices for controlling heat flux. An ellipsoidal thermal concentrator and cloak are designed, and the corresponding thermal conductivities are derived explicitly using the transformation thermotics method. With the derived material parameters, 3D finite element simulations have been performed to confirm the theoretical predictions. The numerical results show that the ellipsoidal concentrator can concentrate heat flux in a small region, which can be used to collect thermal energy from the environment. The ellipsoidal cloak can mold the dynamic flow of heat around an object as if no object is there. Such thermal cloaks can temporarily protect sensitive regions from excessive heating. Our theory can be extended to investigate irregularly shaped concentrators and cloaks, such as rounded cuboids and rounded cylinders. In principle, we can design thermal concentrator and cloak with arbitrary geometries and can also suggest some thermal devices with novel properties. Based on thermal metamaterials, the developed technique of transformation thermotics provides a powerful means to precisely control the heat flux in almost arbitrary ways. The devices suggested in our work may have potential applications in devices such as solar thermal panels and thermal-electric devices. The devices could be probably achieved using composite materials or a layered structure with the designed material parameters. These kinds of artificially engineered thermal metamaterials can yield characteristics that far exceed those available with natural materials, and such thermal metamaterials should lead to unprecedented heat flux control and intriguing energy-related applications.
Footnotes
Supported by the Gaoyuan Discipline of Shanghai-Environmental Science and Engineering (Resource Recycling Science and Engineering).