Abstract
A direct, explicit derivation of the recently discovered time–information uncertainty relation in thermodynamics [S. B. Nicholson et al (2020), Nat. Phys. 16, 1211] is presented.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
The evolution of entropy and related uncertainty relations are of great importance in nonequilibrium thermodynamics and statistical mechanics [1–3]. Nicholson et al have recently discovered a time–information uncertainty relation in thermodynamics [4]:
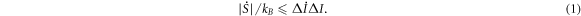
S is the Shannon entropy:
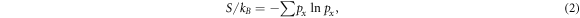
where kB is the Boltzmann constant, px is the probability of the state x (= 1, 2, ... , N), and the simplified symbol of summation in this note denotes:
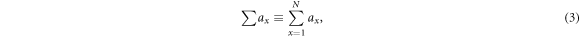
where ax
is a general variable.  is the evolution rate or time derivative of the entropy:
is the evolution rate or time derivative of the entropy:

ΔI is the standard deviation of the surprisal or information content Ix :

and  is the standard deviation of the evolution rate of the surprisal [5–7]. Because px
is a stochastic variable, other statistical variables such as S, Ix
, and their derivatives are also stochastic. The relation of equation (1) provides an upper bound of the entropy evolution rate in a system, and thus is positioned as a milestone in multiple fields including informatics, nonequilibrium thermodynamics, and energy science and engineering. The time–information uncertainty relation and the associated speed limit for flows of heat and entropy were validated with a number of examples [4]. This uncertainty applies to various systems ranging from energy transducers [8–10] to consciousness neuroinformatics [11–13]. In this short note, we present a more explicit derivation of the time–information uncertainty relation of equation (1), solely using the most primitive variable, px
, as a supplement of the original article by Nicholson et al [4], for the convenience of the community.
is the standard deviation of the evolution rate of the surprisal [5–7]. Because px
is a stochastic variable, other statistical variables such as S, Ix
, and their derivatives are also stochastic. The relation of equation (1) provides an upper bound of the entropy evolution rate in a system, and thus is positioned as a milestone in multiple fields including informatics, nonequilibrium thermodynamics, and energy science and engineering. The time–information uncertainty relation and the associated speed limit for flows of heat and entropy were validated with a number of examples [4]. This uncertainty applies to various systems ranging from energy transducers [8–10] to consciousness neuroinformatics [11–13]. In this short note, we present a more explicit derivation of the time–information uncertainty relation of equation (1), solely using the most primitive variable, px
, as a supplement of the original article by Nicholson et al [4], for the convenience of the community.
Let us start with the formulation of the standard deviation of the surprisal and of the surprisal evolution rate. From equation (5),
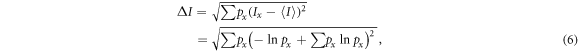
where the symbol of expectation denotes:
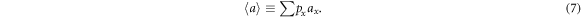

since
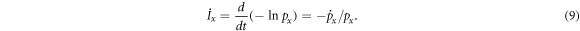
Next, let us move onto the entropy evolution rate. From equation (2),
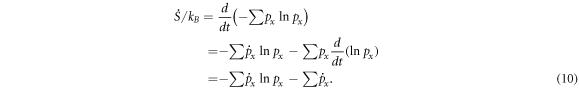
Because 
 This fact allows for a trick to multiply the second term of equation (10) by
This fact allows for a trick to multiply the second term of equation (10) by  (=
(= ):
):
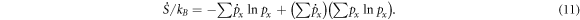
From equation (11), by further tricky transformations,
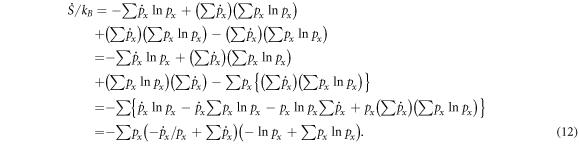
For the transformation across the second equality sign in equation (12), a general property  where A is a constant, was used. Using the Cauchy–Schwarz inequality
where A is a constant, was used. Using the Cauchy–Schwarz inequality  where bx
is a general variable, from equation (12),
where bx
is a general variable, from equation (12),
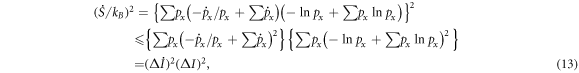
via equations (6) and (8). Hence,  (equation (1)).
(equation (1)).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).


