Informal versus formal judgment of statistical models: The case of normality assumptions

Abstract

Researchers sometimes use informal judgment for statistical model diagnostics and assumption checking. Informal judgment might seem more desirable than formal judgment because of a paradox: Formal hypothesis tests of assumptions appear to become less useful as sample size increases. We suggest that this paradox can be resolved by evaluating both formal and informal statistical judgment via a simplified signal detection framework. In 4 studies, we used this approach to compare informal judgments of normality diagnostic graphs (histograms, Q–Q plots, and P–P plots) to the performance of several formal tests (Shapiro–Wilk test, Kolmogorov–Smirnov test, etc.). Participants judged whether or not graphs of sample data came from a normal population (Experiments 1–2) or whether or not from a population close enough to normal for a parametric test to be more powerful than a nonparametric one (Experiments 3–4). Across all experiments, participants’ informal judgments showed lower discriminability than did formal hypothesis tests. This pattern occurred even after participants were given 400 training trials with feedback, a financial incentive, and ecologically valid distribution shapes. The discriminability advantage of formal normality tests led to slightly more powerful follow-up tests (parametric vs. nonparametric). Overall, the framework used here suggests that formal model diagnostics may be more desirable than informal ones.

Statistical models are sometimes judged informally. For example, distributional assumptions might be judged by considering a histogram; homoscedasticity might be judged by examining a plot of the residuals across a regression line; two variations of a model might be judged holistically by comparing several pieces of information, such as measures of complexity-corrected fit, out-of-sample prediction error, and/or other graphical or numerical information. Such judgments matter, as different statistical models of the same data set could lead to substantially different conclusions (e.g., Silberzahn et al., 2018). The primary goal of this paper is to compare the effectiveness of informal and formal judgments of statistical models, and specifically judgments that are often referred to as model diagnostics, misspecification tests, or assumption checking.

For several reasons, we focus primarily on the judgments of normality. Normality assumptions are common, as they appear in the general linear model, and by extension, in all models of this type (e.g., ANOVAs, t tests). Various normality assumptions also underlie other commonly used statistical procedures, ranging from simple bivariate correlations to structural equation models. When normality assumptions are violated, the general linear model and other commonly used tests can produce inflated Type I and Type II errors, as well as other undesirable properties (Bishara & Hittner, 2012; Kelley, 2005; Levine & Dunlap, 1982; Sawilowsky & Blair, 1992; West, Finch, & Curran, 1995). Such violations may be common because nonnormality is common in psychological and educational data sets (Blanca, Arnau, López-Montiel, Bono, & Bendayan, 2013; Cain, Zhang, & Yuan, 2017; Micceri, 1989).

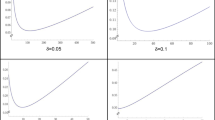
Incorrect normality assumptions can cause problems even in large samples. For instance, when a confidence interval is constructed using a method that incorrectly assumes normality, as sample size increases, confidence interval coverage can actually decrease (e.g., Bishara, Li, & Nash, 2018). Furthermore, as n increases, even though parametric models sometimes become robust in terms of Type I error, other models may still be preferable (see Sawilowsky & Blair, 1992). For example, consider the power of an independent-samples t test as compared with its nonparametric analog, the Mann–Whitney–Wilcoxon (MWW) test, also known as the ranked-sums test. As shown in Fig. 1, as n increases from 5 to 200, the power of an independent-samples t test will sometimes increase at a slower rate than that of the MWW test. In other words, a large sample size does not guarantee that a model which assumes normality will be preferable to one that does not.

Fig. 1

As n increases, the power of nonparametric tests (e.g., Mann–Whitney–Wilcoxon test [MWW]) sometimes increases at a faster rate than that of parametric ones (independent-samples t test). As one example, this figure shows power to detect a difference between two means in an independent-groups design,with both groups drawn from skewed populations (χ² with df = 1, and population effect size d = .5). In other situations (not shown here) where populations are approximately normal, the t test generally has higher power than MWW. In still other situations, the t test has higher power with small ns, but MWW has higher power with large ns. Power was estimated through 10,000 Monte Carlo simulations at ns ranging from 5 to 200. The 95% CI of each plotted point is less than ±.010. Though not shown here, neither test exceeded a Type I error rate of .060 (which would be significantly greater than .050). The equal-variance t test is shown, but Welch’s unequal-variance t test had similar power, also below that of MWW

Unfortunately, though, there is no single agreed-upon method for judging normality; there are numerous methods belonging to one of two families. One family involves informal judgment, often using histograms, Q–Q plots, or P–P plots. A second family involves formal statistical methods, such as the Kolmogorov–Smirnov test, the Shapiro–Wilk test, and many others. How well do these methods distinguish between nonnormal and normal? Relatedly, how well do they distinguish between nonnormal and approximately normal—that is, normal enough for a parametric model to have higher power to detect a true nonzero effect without increasing the Type I error rate?

FormalPara Informal versus formal diagnostic decisions

The two families of normality judgment can be viewed as belonging to two more general strategies for diagnostic decisions. One general strategy is to rely on informal intuitive judgment, perhaps of an expert. A second strategy is to rely on a formal, mechanical decision rule, often involving a formula with numeric cutoff values that determine the decision. A large body of empirical work has shown that the second strategy can often outperform the first—that is, formal decision rules can often match or beat informal judgments, even those of experts (Dawes, Faust, & Meehl, 1989; Meehl, 1954; Swets, Dawes, & Monahan, 2000). In one meta-analysis, informal judgments of medical and psychological experts were, on average, outperformed by formal decision rules when making predictions about diagnoses, prognoses, and personalities (Grove, Zald, Lebow, Snitz, & Nelson, 2000). Additionally, experts’ informal judgments are sometimes outperformed by relatively simple decision rules—even rules created to mimic those same experts in their use of cues—partly because such decision rules are more consistent than are informal human judgments (Camerer, 1981; Dawes, 1971; Karelaia & Hogarth, 2008). The superiority of formal decisions rules often occurs in situations where experts do not receive immediate or clear feedback about their decisions (Kahneman & Klein, 2009; Shanteau, 1992), although it sometimes occurs even despite such feedback (e.g., Goldberg, 1968). In short, the broader literature on diagnostic decision-making suggests that formal judgments often do as well as or better than informal ones.

Much of the above-described research pertains to diagnostic decisions about human behavior or disease, but what of decisions about data patterns? Researchers commonly make decisions about data by informally judging a graph, and it is customary to do so in single-case experimental designs (Skinner, 1956). For such designs, empirical studies have shown that expert judgments of graphs sometimes have high interrater reliability (Kahng et al., 2010), but not always (Parker & Brossart, 2003). Unfortunately, expert judgments sometimes lead to excessive Type I and Type II errors (Matyas & Greenwood, 1990). Perhaps because of these findings, in single-subject designs, the focus has been shifting toward more formal statistical analyses (Fisch, 2001; Manolov, Gast, Perdices, & Evans, 2014; Smith, 2012), or at the very least toward formal quantifications of visual depictions (Lane & Gast, 2014).

Especially pertinent to normality judgment is the informal judgment of scatterplots. With scatterplots, a pattern of dots close to a positively sloped line indicates a strong positive correlation. Many visual depictions of normality involve a similar principle. For example, with Q–Q plots and P–P plots (see Fig. 2), dots close to the positively sloped reference line indicate an approximately normal distribution. Empirical research on judgments of scatterplots has shown that human judges are sensitive to correlations depicted in them, albeit not perfectly (Rensink, 2017). For instance, human judges tend to overemphasize the distance between the dots and the reference line, and underemphasize other cues, such as slope and scale (Lane, Anderson, & Kellam, 1985). Additionally, there is error in informal human estimates, and the error tends to increase as r approaches zero (Doherty, Anderson, Angott, & Klopfer, 2007).

Fig. 2

Examples of graphs used in experiments here. In each case, the green reference curve/line shows what is expected if the sample is perfectly normal, whereas bars/dots show the actual sample. Q–Q (quantile–quantile) plots show the observed scores on the y-axis and the theoretically expected quantiles derived from a normal distribution on the x-axis. The first Q–Q plot row has the reference line drawn through the first and third quartiles of the data (the default in the software R). The stable Q–Q plot involves a fixed scale and a reference line along the diagonal, so that the reference line remains stable across different data sets. P–P (percent–percent) plots show the observed versus theoretically expected scores on the scale of percentiles. Q–Q plots tend to magnify the deviations from the normal distribution in the tails, whereas P–P plots tend to magnify the deviations in the center

Unfortunately, the existing literature offers no empirical studies of informal judgments of normality. That is, there is no direct empirical evidence to indicate the superiority of some informal methods over others, or to compare informal judgments to formal hypothesis tests. In the absence of direct empirical evidence, researchers might instead rely on the advice of authorities.

Review of popular statistics textbooks

To gauge the current advice about normality judgments, we reviewed 20 of the most popular statistics textbooks, operationally defined here as the Top 10 Amazon Best Sellers in the Statistics category and by the Top 10 library holdings as indicated by the WorldCat database (see references with † or ‡, respectively; for details, see Supplement 1). Unsurprisingly, most textbooks included basic definitions of normal distributions, as well as curve and/or histogram depictions of them. However, only 8 textbooks offered specific recommendations for judging whether normality had been adequately satisfied or not.

Of these eight books, all recommended at least one visual inspection method, most commonly Q–Q plots (6), followed by histograms (4), and P–P plots (3), with some textbooks recommending more than one type of graph. Q–Q plots, in addition to being mentioned by several books, were treated as essential in some. For example, the most popular book from the Amazon Best Seller set (Triola, 2012) suggested that bell-shaped histograms alone could not assure normality, and so Q–Q plots must also be used. Additionally, a text with especially comprehensive coverage of normality (Field, 2013) suggested that Q–Q plots would be easier to interpret than P–P plots, at least in large samples. Thus, among visual inspection methods, popular textbooks showed a preference for Q–Q plots.

Regarding formal statistical tests to evaluate normality, only five books described at least one statistical test, most commonly the Kolmogorov–Smirnov test (3), followed by the Shapiro–Wilk, Anderson–Darling, Pearson χ², and Ryan–Joiner test, and also tests of skewness and kurtosis values (one book each). Additionally, one book encouraged comparing the correlation of Q–Q plot coordinates to critical correlation values (Sullivan, 2017; see Looney & Gulledge, 1985), a method similar to the Shapiro–Francia test. Although the most commonly mentioned test was the Kolmogorov–Smirnov test, the books did not specifically endorse this test as preferred. Indeed, one book noted that it was less powerful than the Shapiro–Wilk test (online supplement of Field, 2013; for evidence, see Shapiro, Wilk, & Chen, 1968; Thode, 2002). Table 1 provides a summary of the major normality tests examined in the present research. These tests were chosen because they were well-known (Kolmogorov–Smirnov), well-supported in the simulation literature (Shapiro–Wilk, Shapiro–Francia, Anderson–Darling), somehow analogous to informal graph judgments (Pearson χ², Shapiro–Francia), or because of some combination of these reasons.

Table 1 Summary of formal hypothesis tests of normality examined here

A paradox of formal assumption tests

Interestingly, some popular textbooks expressed concerns about formal normality tests (Field, 2013; McClave, Benson, & Sincich, 2014). Formal tests may produce significant results (“nonnormal” decisions) too easily, and so they may be too sensitive to tiny deviations from normality in the data. The problem becomes worse with larger samples, where formal tests reject the null of normality for vanishingly small deviations from it as n increases. That is, in large samples, a formal normality test may lead a researcher to adopt a nonparametric test even when a parametric test would be more powerful. This concern is paradoxical because large samples are thought to be more problematic than small ones, a pattern opposite that of most other statistical situations.

This paradox matters, as it often leads to the encouragement of informal judgment and discouragement of formal tests. This paradox appears not only in popular texts but also in websites that offer statistical advice.¹ Furthermore, this paradox generalizes beyond normality assumption tests to other model diagnostics. For example, many models rely on equal variance assumptions (homoscedasticity, and relatedly, homogeneity of variance). Formal tests of these assumptions have equal variance as the null hypothesis. Therefore, large samples cause equal variance to be rejected for even trivial variance differences. The paradox can even arise with Bayesian models. For instance, if n is large, posterior predictive checks can produce small p values for trivial differences between empirical and posterior predictive distributions.

We suggest that this paradox can be resolved via signal detection theory, and even via a simplified version of it that only makes use of receiver operating characteristics (ROCs; Peterson & Birdsall, 1953). The paradox reflects a problem not with formal judgments per se, but rather with the criterion used in them. The typical criterion is determined by setting alpha to some fixed value (.05), which may lead to too many decisions in one direction rather than another. Of course, the criterion can be easily adjusted simply by changing the alpha level. To examine all possible criterion settings, it is useful to plot ROCs, which illustrate trade-offs between true positives (y-axis) and false positives (x-axis; for a review, see Macmillan & Creelman, 2004). ROCs have proven useful for a diverse array of problems in psychological research (McFall & Treat, 1999; Swets et al., 2000; Wixted & Mickes, 2014; for a history see Wixted, 2020), but ROCs can be especially useful for assessing statistical hypothesis tests, where the true positive rate is equivalent to power, and the false positive rate is equivalent to the Type I error rate.

Consider, for example, a hypothetical formal test of normality (perhaps the Shapiro–Wilk test in a particular situation) that produces power of .70 with a Type I error rate of .05. That is, it has a 70% chance to correctly label a sample “nonnormal” when it truly came from a nonnormal population, and a 5% chance to incorrectly label it “nonnormal” when it truly came from a normal population. This situation is illustrated by Point A in Fig. 3.

Fig. 3

The hypothetical receiver operating characteristics (ROCs) indicate that Method B is better able to discriminate between two types of stimuli (e.g., normal versus nonnormal) than Method A. Methods A and B could be formal hypothesis tests or informal human judgments. The curves indicate all possible combinations of power and Type I error rate that could be achieved for each method by adjusting the criterion (alpha for formal tests, confidence threshold for informal judgments)

Other methods for assessing normality might produce different combinations of power and Type I error rate. Point B illustrates a different method that yields higher power (.90), with the same Type I error rate as Point A. The curves show how the two methods that produced Points A and B would perform at all possible criterion settings—that is, alpha settings. These curves illustrate a clear advantage for Method B over Method A. At any given criterion, Method B results in higher power, lower Type I error rate, or both. In signal detection terms, Method B has higher discriminability. That is, Method B is better able to distinguish between normal and nonnormal distributions. Generally, higher discriminability is more desirable, and is represented by a curve closer to the upper left corner of the ROC plot. Discriminability is often measured as the proportion of the graph area under the curve (AUC). An AUC of 1.0 would indicate perfect discriminability. In Fig. 3, Method B has a higher AUC (.97) than Method A (.89). AUC can be interpreted as the probability that stimuli from two different populations will be correctly ranked. For example, the AUC of the Shapiro–Wilk test represents the probability that a randomly chosen sample from a nonnormal population has a smaller p value on the Shapiro–Wilk test than does a randomly chosen sample from a normal population.

Although the above-discussed Methods A and B could represent formal hypothesis tests, they could also represent informal judgments. Informal judgments of normality produce power and Type I error rates that may be better or worse than those of formal tests. Additionally, informal judgments can also be made at different criterion levels, or thresholds of confidence. For example, Point A might represent an extreme level of confidence: “definitely not normal.” In contrast, Point “a” might represent a different threshold, the sum of “definitely not normal” and “probably not normal” judgments. The more relaxed criterion in “a” yields higher power, but also a higher Type I error rate.

Using ROCs to examine all possible criterion settings, do formal judgments still appear to be problematic, as the paradox suggests they are? Or, as suggested by the literature on diagnostic decision-making, could formal judgments perform as well as informal ones, or perhaps even better? In Experiments 1–2, the primary goal was to identify the most discriminating informal judgment type by comparing performance across different types of graphs (histograms, Q–Q plots, and P–P plots). Additionally, even in these early experiments, informal graph judgments were compared with formal hypothesis tests on the same data sets. Experiments 3–4 relied on the most discriminating graph type identified in earlier experiments, using this graph type to compare informal and formal judgments in more ecologically valid contexts. Experiments 3–4 also examined whether informal or formal judgments would lead to higher statistical power of follow-up tests, tests chosen based on these normality judgments.

Experiment 1: Histograms and Q–Q plots

In the absence of existing data on informal judgments of normality, a reasonable starting point would be to test the common textbook advice that Q–Q plots are easier to judge than other graphs. So, participants were randomly assigned to make judgments of either Q–Q plots or of the second most commonly mentioned graph: histograms. On each trial, a sample of 60 values was simulated from either a normal or nonnormal population. A graph of this sample was presented on a computer screen, and participants judged it on a 6-point scale ranging from “Definitely Normal” to “Definitely NOT Normal.” To explore the potential for learning in this task, participants judged 80 graphs without feedback, then 320 with feedback, and finally 80 without. Feedback consisted of an indication of the correct answer (“Normal” or “NOT normal”) after each response.

Method

Participants

A total of 46 participants were recruited through an introductory psychology course participant pool, and they participated individually in private laboratory rooms. Three participants did not complete the study due to a program or scheduling error. Based on preliminary analyses (all blind to graph condition to avoid bias), we decided to exclude any participant with a median response time of less than 500 milliseconds or accuracy less than .40 during any stage of the experiment (pretraining, training, or posttraining). These restrictions excluded only one participant. The final data set had 42 participants (31 females). Participants were compensated with course credit.

Design and materials

The experiment had a 2 (graph type: histogram vs. Q–Q plot) × 6 (trial block) factorial design, with graph type between subjects and trial block within subjects. Each participant was randomly assigned to view histograms (n = 24) or Q–Q plots (n = 18). There was one pretraining block, followed by four training blocks, and then one posttraining block. Only the training blocks provided feedback.

All graphs were generated in the programming language R (R Core Team, 2016). Histograms were generated using the default “hist()” function (for binning details, see Sturges, 1926). For reference, a green normal bell curve appeared on each histogram. Q–Q plots were generated using the “qqnorm()” function and a reference line (also in green) created by the “qqline()” function. By default, this line passed through the 1st and 3rd quartiles of the data. All graphs omitted axis labels so that participants could focus on data shapes and feedback while learning. See the first two rows of Fig. 2 for examples.

Each graph had a sample size of 60 drawn from either a normal or nonnormal population. There were four different types of nonnormal populations: (a) no skewness and negative kurtosis, (b) no skewness and positive kurtosis, (c) positive skewness and positive kurtosis, and (d) negative skewness and positive kurtosis. To define these, let the kth central population moment be:

$$ {\mu}_k=E\left[{\left(x-\mu \right)}^k\right], $$

(1)

where μ with no subscript is the population mean. Population skewness and kurtosis are then defined, respectively, as:

$$ {\gamma}_1=\frac{\mu_3}{\sigma^3}, $$

(2)

$$ {\gamma}_2=\frac{\mu_4}{\sigma^4}-3, $$

(3)

where σ is the population standard deviation. In a normal population, γ₁ = γ₂ = 0. There were four nonnormal populations used here: (a) γ₁ = 0, γ₂ = −1, (b) γ₁ = 0, γ₂ = 10, (c) γ₁ = 2, γ₂ = 8, and (d) γ₁ = −2, γ₂ = 8. These values were chosen in an attempt to make the nonnormal situations equally difficult, at least for visual inspection methods. Nonnormal distributions were generated using the fifth-order polynomial family (Headrick, 2002), with approximate densities shown in Fig. 4.

Fig. 4

Approximate densities of populations used in Experiment 1. n = normal; a = no skewness and negative kurtosis; b = no skewness and positive kurtosis; c = positive skewness and positive kurtosis; and d = negative skewness and positive kurtosis (see Design and Materials for details)

There were 64 samples generated from each the 4 types of nonnormal population, and 256 normal samples, for a total of 512. Of these 512 samples, the first 480 were used as critical stimuli (counted in the analyses) and the last 32 were reserved. From this reserve set, 3 relatively average stimuli were chosen as instruction examples by selecting the median Shapiro–Wilk test p-values from “normal” and “not normal” categories. The 480 critical stimuli were assigned to the 6 blocks (80 stimuli per block). Assignment was random for each participant with the constraint that each block contained half normal and half nonnormal stimuli. Presentation order within blocks was random with the constraint that each 8-trial sub-block contained 4 normal and 4 nonnormal stimuli (with 1 of each of the types of nonnormal). The experiment was programmed in E-Prime. Technical details of graphs and normality tests can be found in Supplement 2, and all materials and code to generate them can be found at https://osf.io/msv72.

Procedure

Participants first answered demographic questions. Next, the researcher read aloud instructions adapted from Triola (2012, pp. 57, 297). In the histogram condition, participants were told that the graph was not normal if it had “rectangles that depart dramatically from the bell-shaped curve.” In the Q–Q plot condition, they were told that the graph was not normal if the “circles do not lie reasonably close to a straight line, or the circles may show some systematic pattern that is not a straight-line pattern.”

Next, participants placed their middle three fingers of each hand on the six keys from “c” to “,” on the computer keyboard. The six keys had colored stickers corresponded to a color-coded, 6-point Likert scale that was visible on the screen. The colors from left to right were light green, green, dark green, dark red, red, light red. The Likert scale from left to right was “Definitely Normal,” “Probably Normal,” “Guess Normal,” “Guess NOT Normal,” “Probably NOT Normal,” “Definitely NOT Normal” (see Supplement 3). Participants were encouraged to use the whole range of this scale and were informed that they would have 10 seconds to decide for each graph. They were also informed that each graph would have an equal chance of being normal or not.

The pretraining block consisted of 80 trials without feedback, where each button press led to the next stimulus being presented. Next, there were four training blocks with 80 trials each. During these blocks, after either a button was pressed or 10 seconds had elapsed, the screen indicated that the correct answer was either “normal” or “NOT normal,” in light green or light red font, respectively. This feedback remained on the screen for 3.5 seconds before the next trial. Finally, there was a posttraining block of 80 trials without feedback. At the end of the experiment, participants were asked to estimate their percentage of accurate decisions for the experiment as a whole (all six blocks), and for the posttraining block in particular (see Supplement 4 for details).

Data analysis

The experiments here were intended to inform decisions about which statistical models to use. However, we must choose which statistical models to use to analyze data from these experiments. To avoid circularity, we decided ahead of time to use procedures that are usually robust to nonnormality and other typical assumption violations. First, all reported confidence intervals were constructed using bootstrapping with bias correction and acceleration (BCa; via Kirby & Gerlanc, 2013). Second, the measure of discriminability was computed without making distributional assumptions for signal and noise. In other words, discriminability was computed by the empirical ROCs rather than by curve-fitted ROCs. Third, in all analyses of variance (ANOVAs), df with decimals indicates that a significant violation of sphericity occurred and the Greenhouse–Geisser correction was applied. Fourth, for two-sample t tests, df always have decimals because Welch’s unequal variance version was routinely applied without a precursor assumption test (see Moser & Stevens, 1992; Zimmerman, 2004).

Results and discussion

As shown in Fig. 5, accuracy increased across blocks, and was higher for Q–Q plots than for histograms. Accuracy was calculated by collapsing across confidence level. For example, if the graph showed a sample from a normal population, any of the “normal” confidence responses (“definitely,” “probably,” or “guess”) was considered accurate; any of the “nonnormal” confidence levels was considered inaccurate. A 2 (graph type) × 6 (trial block) ANOVA showed that accuracy was significantly higher for Q–Q plots than for histograms, F(1, 40) = 7.36, p = .01, η_p² = .16, a medium effect. There was also a significant effect of trial block, F(3.87, 154.7) = 10.5, p < .001, η_p² = .21, a medium effect. Finally, the interaction between trial block and graph type was not significant, F(3.87, 154.7) = .45, p = .77, η_p² = .01. Of most importance, though, is performance posttraining, when feedback was no longer available, just as in realistic situations. Posttraining accuracy was significantly higher for Q–Q plots (.80) than for histograms (.73), and with a large effect, t(32.7) = 2.74, p = .010, d = .878, 95% CI [.114, 1.619]. However, most formal hypothesis tests were more accurate (range: .78–.93) than informal judgments, except for the Pearson χ² test, which was similar to judgments of Q–Q plots, especially in later blocks.

Fig. 5

Proportion of decisions that were accurate in Experiment 1. Black lines (Q and H) indicate accuracy of informal human judgments, where any “normal” response (“definitely,” “probably,” or “guess”) was considered accurate for normal trials, and any “NOT normal” response was considered accurate for nonnormal trials. Colored lines indicate accuracy of formal hypothesis tests using α = .05 as the criterion. Because the same samples were used to generate stimuli for all participants, and a formal test is consistent each time it is used on the same sample, the formal tests are shown as constants. Random assignment of samples to blocks created a trivial amount variability in formal test accuracy (e.g., Shapiro–Wilk test accuracy ranged from .925 to .935 across blocks). Kolm.-Smir. (L) = Kolmogorov–Smirnov (Lilliefors version), Pears. = Pearson

Accuracy scores neglect differences among confidence levels in informal judgments, and likewise, different possible alpha levels that could be used in formal tests. To consider the whole range of confidence levels and alpha levels, Fig. 6 shows the ROCs of formal tests and mean informal judgments (for pretraining and posttraining blocks). As shown in Fig. 6, for a given Type I error rate, the Shapiro–Wilk test typically had higher power than any other method, whether formal test or informal judgment of a graph. One can also see that Q–Q plot performance tended to be better than histograms performance, but worse than formal tests.

Fig. 6

In Experiment 1, power of hypothesis tests across all possible alpha levels, and power of human decisions across all possible confidence thresholds. Kolm.-Smir. (L.) = Kolmogorov–Smirnov (Lilliefors version)

To confirm previously established accuracy patterns, but with the ROCs, we examined area under the curve (AUC), which is simply the area between the curve and the bottom and right borders of the graph expressed as a proportion of the total graph area (A_g in Macmillan & Creelman, 2004). Confirming the accuracy analyses, posttraining Q–Q plot judgments had significantly higher AUC (.826) than posttraining histogram judgments (.749), again with a large effect, t(30.1) = 2.86, p = .008, d = .931, 95% CI [.181, 1.715]. Nevertheless, posttraining Q–Q plot AUC was still significantly lower than the AUC of all formal tests, as is shown in Table 2.

Table 2 Posttraining discriminability as measured by area under the curve (AUC) for all experiments (1–4)

Overall, for informal judgments, discrimination between normal and nonnormal populations was better with Q–Q plots than with histograms, and this performance improved across blocks of the experiment. However, formal tests performed better than informal judgments, and this was especially true for the Anderson–Darling, Shapiro–Francia, and Shapiro–Wilk tests.

Experiment 2: Q–Q plot variants

It is possible that the Q–Q plot used in the previous experiment might be improved upon, especially considering research on the closely related issue of scatterplot judgments. Such research has shown that scatterplot interpretation can be improved by making constant the shape and size of the plot (Doherty & Anderson, 2009). Such research also suggests that graph judgments could be improved by making the reference line constant, as is the default in some software packages (e.g., SPSS, Minitab). To examine this possibility, participants were randomly assigned to judge one of three types of graphs: Q–Q plots used in the previous study, stable Q–Q plots, or P–P plots (see Fig. 2). Both stable Q–Q plots and P–P plots have reference lines that are consistently on the diagonal, as well as fixed ranges of the x-axis and y-axis. These properties could make stable Q–Q plots and P–P plots easier to judge.

Method

Only differences relative to the previous experiment are reported here and in subsequent Method sections.

Before conducting the experiment, to estimate a target sample size, a power analysis was conducted using the effect size for the accuracy difference between histograms and Q–Q plots posttraining (d = .88). To achieve .95 power to detect a comparable difference between two independent sample means would require approximately 35 participants per condition (using R’s “pwr” package, pwr::pwr.t.test(d=.88, power=.95, type=“two.sample”, alt=“two.sided”); Champely, 2020).

In Experiment 2, 117 participants completed the experiment, but three were excluded by the same criteria as in Experiment 1. The remaining 114 participants were, by random assignment, in either the Q–Q plot (n = 37), stable Q–Q plot (n = 39), or P–P plot (n = 38) condition.

For the Stable Q–Q plot condition, the x-axis and y-axis used the same range (the minimum of x and y plotting coordinates combined up to the maximum of x and y plotting coordinates combined). The reference line was set to have a y-intercept of 0 and slope of 1, resulting in a consistent diagonal line.

Whereas Q–Q plots show actual versus expected points on the scale of z scores (or similarly, raw scores), P–P plots show actual versus expected points on the scale of percentiles. Because percentiles are a non-linear transformation of z scores, the placement of dots is different. The reference line was identical to that of the Stable Q–Q plot condition.

In Experiment 1, one nonnormal type (γ₁ = 0, γ₂ = 10) was harder to visually discriminate than others, adding an unintended source of noise. To address this issue, this nonnormal type was changed to γ₁ = 0, γ₂ = 20 in Experiment 2.

Participants completed the experiment in groups of up to 11 at a time in a computer classroom. To ensure comprehension of instructions, instructions were followed by a multiple-choice test. If a participant did not achieve 100% correct on this test, the instructions and test repeated until he/she did so. Instructions for all three conditions were identical to those in the Q–Q plot condition of the previous experiment (for details, see https://osf.io/msv72).

Results and discussion

As with Experiment 1, formal hypothesis tests tended to outperform informal graph judgments, with the Shapiro–Wilk test showing the highest mean performance levels. As shown in Table 2, informal judgments of any graph type (even posttraining) had significantly lower discriminability as compared to any formal hypothesis test.

To further examine informal judgments, a 3 (graph type) × 2 (trial block: pretraining vs. posttraining) ANOVA was conducted on AUC. There was a significant main effect of graph type, F(2, 111) = 9.60, p < .001, η_p² = .15, qualified by a significant Graph Type × Trial Block interaction, F(2, 111) = 7.25, p = .001, η_p² = .12, both medium effects. As shown in Fig. 7, at pretraining but not posttraining, Q–Q plots had lower discriminability than Stable Q–Q and P–P plots. That is, at least before training, it was easier to judge plots when they had a stable, consistent reference line, a finding consistent with data on judgments of scatterplots (Doherty & Anderson, 2009), F(2, 111) = 15.23, p < .001, η_p² = .22, with Tukey’s HSD showing significantly lower AUC for Q–Q than stable Q–Q and P–P plots, ps < .001, but no significant difference between Stable Q–Q and P–P plots, p = .75. However, after training, performance was similar across the three graph types, suggesting that the choice of particular Q–Q and P–P plots may have little impact, F(2, 111) = 1.64, p = .20, η_p² = .03. Stable Q–Q plots had the highest mean performance of the three graphs, and so these plots were used in all remaining experiments.

Fig. 7

In Experiment 2, power of hypothesis tests across all possible alpha levels, and power of human decisions across all possible confidence thresholds. Kolm.-Smir. (L) = Kolmogorov–Smirnov (Lilliefors version)

Experiment 3: Ecological validity

The previous experiments suggested that several formal hypothesis tests of normality perform better than informal judgments. Do such findings generalize to more realistic situations? Experiment 3 involved several modifications to address this question.

Researchers often wish to judge normality to inform decisions about other routine hypothesis tests, such as whether two or more means differ in a population. In such a situation, the decision about normality is intended to improve the more important decision about whether the means are equal. So, the goal is not to determine whether the population is exactly normal or not. Rather, the goal is to determine whether the population is close enough to normal for one test—often a parametric test—to produce fewer errors (Type I and/or II) than an alternative.

To represent such a real-world decision, in Experiment 3, participants made decisions about whether a sample came from an approximately normal distribution or not. In particular, approximately normal was operationally defined here as any population distribution shape close enough to normal for a common parametric test to produce more power than its nonparametric analog. Conversely, “not normal” was defined as any population shape different enough from normal that the nonparametric test was more powerful than the parametric one. Specifically, the parametric test here was an independent-samples t test, and nonparametric test was the MWW test. These tests were chosen for two reasons. First, these tests are used for one of the simplest and most common experimental designs—a two-condition between-participant experiment, frequently used for comparison of a treatment group to a control group. Second, both the independent-samples t and MWW tests have acceptable Type I error rates under the conditions studied here, and so their performance can be compared solely on the basis of power (i.e., 1–Type II error probability). So, in addition to discriminability, we also examined the power implications of both informal and formal judgment, that is, how normality judgments would lead to more or less powerful tests of equal means.

To further mimic real-world decisions, in Experiment 3, distribution shapes for stimuli were generated by stratified sampling of combinations of skewness and kurtosis observed in actual psychological and educational data (via Cain et al., 2017). Figure 8 shows the resulting combinations of skewness and kurtosis, along with the distinction between approximately normal (green) and not (red).

Fig. 8

Experiments 3 and 4 used skewness and kurtosis combinations reported in the literature. Green (+) indicates approximately normal combinations, with higher power for an independent-samples t test. Red (▽) indicates not normal combinations, with higher power for a Mann–Whitney–Wilcoxon (MWW) test. Gray (•) indicates less than .01 difference in estimated power. Lower case letters indicate combinations used in Experiment 1 (e.g., n = normal). Gray curves show the boundary for mathematically possible combinations. Figure scales were transformed (Yeo & Johnson, 2000) so outliers would be visible

Additionally, because researchers have incentives to reach valid, replicable conclusions, in Experiment 3, participants were provided with a tangible incentive for performance. Participants bet points on normality judgments, with the number of points bet indicating confidence. The participant who achieved the highest number of points at the end of the experiment was awarded a $75 bonus.

Finally, in many real-world settings, researchers judge normality across various sample sizes. To provide at least some semblance of this real-life complexity, in Experiment 3, each participant judged stimuli of two different sizes (small: n = 30, and large: n = 120). It was expected that both participants and formal hypothesis tests would perform better in the large sample condition, where more information was available. Of primary interest, though, was whether the advantage of formal tests over informal judgment would remain in an experiment that better resembled realistic situations

Method

Participants

Initially, 39 participants were recruited from introductory undergraduate statistics courses in the Math department. No participant met the a priori exclusion criteria described in Experiment 1. One participant fell asleep during the experiment, and so his data were excluded, resulting in a final sample of n = 38. Participants were compensated with course extra credit, and the best-performing participant also received $75.

Design

Stimulus sample size was manipulated within-participants such that half of the trials showed a stable Q–Q plot with a small sample (30 dots) and half with a large sample (120 dots). To give participants a greater chance of matching or beating the performance of formal tests, the pretraining block was replaced with a training block (80 trials with feedback).

Materials

Population distributions for stimuli were based on Cain et al. (2017). Cain and colleagues contacted 503 researchers who had published in the flagship journal of either the Association for Psychological Science (Psychological Science) or the American Educational Research Association (American Educational Research Journal). They requested, among other information, the univariate skewness and kurtosis of all continuous variables used in each publication. Their request yielded 1,567 cases. We excluded 26 cases due to missing values, and seven due to mathematically impossible combinations of skewness and kurtosis (${\gamma}_2<{\gamma}_1^2-2$). In pilot simulations, some extreme combinations of skewness and kurtosis produced tied observations, which led to problems with power calculations. To avoid these problems, we excluded 65 cases where pilot simulations produced more than 10% ties, leaving 1,469 remaining cases.

For each remaining case, first, a super-sample of n = 1,500,000 was generated from a standardized population with that case’s skewness and kurtosis values. This was accomplished via the Pearson distribution family and the PearsonDS package in R (Becker & Klößner, 2016). Next, this super-sample was then divided into 10,000 samples of size n = 30, and 10,000 samples of size n = 120. Each sample was then subdivided into two groups of equal size, representing two independent-samples (ns = 15, and ns = 60, respectively). To make the alternative hypothesis true, one of the two groups had d = .5 added to each observation. Power of the t test was estimated as the proportion of the 10,000 samples that produced a t-test p value less than .05. Power was estimated accordingly for the MWW test. We verified that the Type I error rate was approximately .05 by also conducting these tests where the null was true (i.e., d = 0). All tests showed an estimated Type I error rate less than .06, which is expected, as the simulation margin of error for the proportion was ±.010. However, in 1.7% of cases, the Type I error rate was lower than .04, and this was more common for t tests (1.5%) than for MWW (.2%). These cases were all in the small sample size (n = 30) condition, and they appeared to be outliers because the average Type I error rate was similar for two tests, and even slightly higher on average for t (M = .049) than MWW (M = .047). Nevertheless, with exceptionally low Type I error rates, one could adjust alpha above .05 to achieve higher power while keeping the Type I error rate below .05. We examined this possibility through 10,000 simulations with the outlying cases. Adjusting alpha upward to achieve a Type I error rate of .05 usually improved power for both t tests and MWW, but in no case did it change which test had the highest power. In other words, adjusting alpha in these outlying cases does not change which procedure—t versus MWW—was preferable.

For cases where MWW had higher power, the correct answer was defined as “not normal”; for cases where a t test had higher power, the correct answer was defined as “normal.” The results are summarized in Fig. 8. (The greater advantage of the MWW test in the large sample condition occurred because increasing sample size increased the power of the MWW test at a faster rate than that of the t test).

To generate stimuli, 140 cases were randomly sampled from each of the four combinations of sample size and power advantage (t test vs. MWW), for a total of 560 stimuli. Borderline cases, where the power difference was less than the simulation margin of error (±.010), were excluded from this sampling process (see Fig. 8, gray circles). Stimuli were generated without adding a constant to one group (without adding d = .5) so that the stimuli represented residuals, which are typically evaluated rather than raw data. Of the 560 stimuli, a random sample of 480 was used as critical stimuli, and the remaining were reserved for instruction examples. Presentation order was random with the constraint that each combination of conditions (sample size and normal versus not) was equally represented during each 16 trial subblock.

Procedure

Participants were told that “graphs may have small or large sample sizes (few or many dots).” They were also warned that they might need to be more or less lenient about their decision based on the sample size. On each trial, “Large Sample” or “Small Sample” appeared to the left of the graph.

At the start of the first block, the upper right-hand corner showed “Score: 200.” The Likert scale from left to right was “Normal Wager 3,” “Normal Wager 2,” “Normal Wager 1,” “NOT Normal Wager 1,” “NOT Normal Wager 2,” “NOT Normal Wager 3,” where numbers represented the points bet. Participants were allowed up to 12 seconds to respond. After each response in the training block, “Normal” or “NOT normal” appeared below the graph for 4 seconds. Additionally, in the last 1 second, the change in score appeared below the current score. For example, if a participant chose “Normal Wager 2” but the correct answer was NOT normal, “−2” would appear below the current score total. The next trial would then show the updated current score (e.g., 198). During the posttraining block, no feedback information (including the score and score changes) was shown (for details, see https://osf.io/msv72).

Data analysis

We also examined how informal versus formal decisions could lead to power differences not just in tests of normality, but also in the power of a follow-up test to detect a difference between means. Specifically, for each stimulus, we know (i) the power of an independent-samples t test, and (ii) the power of a MWW test, and hence, which test will have the higher power to detect a difference between means. We also observe (iii) the informal human decisions of normality, and (iv) the formal normality test decisions of normality. We sought to determine if using the formal approach (iv) to select between (i) and (ii) would lead to higher power to detect a difference between means than using the informal approach (iii) to select between (i) and (ii). Additionally, we analyzed the proportion of correction decisions—that is, how often a decision (from iii or iv) led to the more powerful follow-up test (i vs. ii). For formal tests, we report a low discrimination test (Pearson χ²) and high discrimination test (Shapiro–Wilk) to highlight the range of results.

These power and proportion correct analyses require a decision criterion, a threshold between normal and nonnormal decisions. For informal human judgments, we used the threshold between “Normal Wager 1” and “NOT Normal Wager 1” response options. Unfortunately, for formal normality tests, the threshold is more arbitrary, so we examined three: the traditional α = .05, a more stringent α = .005 (Benjamin et al., 2018), and an optimal alpha. Optimal alpha was estimated as the one that maximized power in the long run to detect a difference between means, optimized for this particular set of critical stimuli, where half of stimuli had higher power for a t test, and the other half higher power for a MWW test. Optimal alphas were estimated as .197 and .019 for the Pearson χ² small and large sample conditions, respectively, and .027 and .0002 for the Shapiro–Wilk test (see Supplement 5 for details).

Results and discussion

As shown earlier in Table 2, it was easier to discriminate approximately normal from nonnormal when the stimuli had a larger sample size (i.e., more dots). A paired t test of the AUC showed that stable Q–Q plot judgment of large sample stimuli was significantly higher than that of small sample stimuli (M = .822 and .779), t(37) = 2.11, p = .04, η² = .11, a medium effect.

More importantly, though, the advantage of formal tests over informal judgment remained despite the more realistic decision context. As shown in both Table 2 and Fig. 9a–b, regardless of the stimulus sample size, stable Q–Q plot discriminability was significantly lower than that of all formal hypothesis tests. One-sample t tests confirmed that small sample stimuli discriminability of stable Q–Q plots (M = .779, SE = .015) was significantly lower than that of every formal test (range: .865–.919), all ps < .001. The same was true for large sample stimuli (stable Q–Q plot: M = .822, SE = .013; formal test range: .891–.946), all ps < .001. The best performing tests were the Shapiro–Francia and Shapiro–Wilk tests. Although the Shapiro–Francia test is a simplified version of the Shapiro–Wilk test, the former had higher discriminability than the latter. This pattern could be due to the decision involving approximate rather than strict normality (a judgment that these tests were not specifically designed for), or perhaps to the particular combinations of the skewness and kurtosis commonly found in psychology and education data.

Fig. 9

In Experiments 3 and 4, power of hypothesis tests across all possible alpha levels, and power of human decisions across all possible confidence thresholds. Experiment 3 (a–b) shows performance of undergraduates. Experiment 4 (c–d) shows performance of PhD-holding experts. Kolm.-Smir. (L) = Kolmogorov–Smirnov (Lilliefors version)

The discriminability advantage of formal normality tests led to follow-up tests (t vs. MWW) that were more powerful, though this power advantage was small and not as robust as other patterns. As shown in Table 3, for small samples, human judgment power (M = .345, SE = .003) was nonsignificantly lower than formal test power (range: .342–.350), .11 < ps < .54. For large samples, human judgment power (M = .827, SE = .002) was significantly lower than the power of most formal testing approaches (range: .829–.833), ps < .05, except for the Pearson χ²_{α = .005} and the Shapiro–Wilk_{α = .05}, which human judgment was nonsignificantly lower than, p = .05 and .57, respectively.

Table 3 Power and Proportion Correct in Experiments 3–4

As shown by proportion correct in Table 3, formal normality tests usually led to choosing a more powerful follow-up test than human judgments did. For small samples, human judgment proportion correct (M = .743., SE = .016) was significantly lower than formal test proportion correct (range: .796–.867), ps < .002. For large samples, human judgment proportion correct (M = .789, SE = .014) was significantly lower than most formal tests’ proportion correct (range: .733–.867), ps < .003, with the exception of Shapiro–Wilk_{α = .05}, which had significantly lower proportion correct than human judgment, p < .001.

Experiment 4: Experts

Previous experiments involved visual judgments from relatively novice participants—undergraduates from introductory psychology and introductory statistics courses. Could formal hypothesis tests beat the performance of expert participants? On the one hand, expertise may aid judgments, as experts may have had years of experience, experience immeasurably greater than that obtained through a few hundred trials with feedback. Indeed, there is some evidence that seasoned graduate students and faculty can discriminate scatterplot patterns more accurately than can novices (Lewandowsky & Spence, 1989). On the other hand, though, for judgments of normality, the type of feedback that experts receive is often ambiguous. Researchers almost never see the true shape of the population from which their samples were drawn. Feedback may consist of proxies for this true shape, such as normality test statistics or p values, but even with such proxy feedback, the researcher could, at best, learn to match the performance of formal tests. Because of such limited feedback, experts may still be unable to beat the performance of formal hypothesis tests of normality (see Karelaia & Hogarth, 2008; Shanteau, 1992). To address this issue, Experiment 4 was conducted largely as a replication of Experiment 3, but with a small sample of experts (n = 3) who had doctoral degrees in relevant subjects.

Method

Participants

One participant had a PhD in psychometrics and quantitative psychology; one in mathematics (this participant specialized in statistics); and one in measurement, evaluation, and research methodology. Participants were recruited via emails to the APA Division 5 (Quantitative and Qualitative Methods) LISTSERV and to local experts. Participants were not authors of this paper, nor were they aware of the results of previous experiments. Participants were paid $75 each, plus a $75 bonus for the participant with the highest final score.

Design and materials

Experiment 4 was programmed with jsPsych (de Leeuw, 2015) to allow web-based participation. Critical stimuli were randomly assigned to either the block of 400 training stimuli or the block of 80 posttraining stimuli, but with the constraint that each combination of conditions (sample size, and normal versus not) was equally represented during each of these blocks.

Procedure

Participants took the experiment using a web browser on a desktop or laptop computer. Touch-input devices (e.g., iPad, smartphones) did not function on the website. Participants were instructed beforehand to select a quiet time and place to avoid distraction. We arranged an agreed-upon time with each participant so that we were on-call in case of questions or problems.

The instruction screens noted that the experiment was adapted from one used with undergraduates, and so some parts of the experiment might seem obvious or might seem like a game. After receiving instructions from Experiment 3, additionally, participants were given the definition of approximately normal: “For the purposes of this study, an approximately normal population is defined as one where it is reasonable to use a two-sample t test rather than a nonparametric analog, the Mann–Whitney U test, because the t test tends to be more powerful. Conversely, a nonnormal population is defined here as one where the Mann–Whitney U test tends to be more powerful.” (For details, see https://osf.io/msv72.)

Data analysis

CIs for each individual subject’s discriminability (AUC) were estimated through bootstrapping with 10,000 stratified replicates (see Robin et al., 2011).

Results and discussion

As shown in Fig. 9c–d, the average expert judgment appeared to have less discriminability than most formal tests. Perhaps due to the small number of experts, one-sample t tests showed that human discriminability of small samples (M = .817, SE = .051) and large samples (M = .844, SE = .046) were not significantly lower than the discriminability of formal tests (small sample range: .865–.919, large sample range: .891–.946), ps > .15. As shown by the parentheses in Table 2, there was a wide range of performance among the three experts, but even the best-performing expert had lower discriminability than the Shapiro–Francia test for both sample sizes, and lower than most hypothesis tests (Anderson–Darling, Shapiro–Francia, and Shapiro–Wilk) for the small sample size. For small samples, discriminability of individual experts (.725, .826, .900; individual 95% CIs [.600, .850; .704, .925; .786, .985]) corresponded to the 28.9, 68.4, and 86.8 percentiles of nonexperts (Experiment 3) in the same condition. For large samples, discriminability of individuals experts (.775, .826, .931; individual 95% CIs [.650, .900; .684, .945; .851, .985]) corresponded to the 21.0, 47.4, and 100 percentiles of nonexperts. The best-performing expert was a different individual across the two sample sizes.

As shown in Table 3, small sample human judgment power (M = .325, SE = .001) was significantly lower than formal test power (range: .342–.350), ps < .004. For large samples, human judgment power (M = .829, SE = .006) was not significantly different from formal test power (range: .829–.833), .59 < ps < .89. For small samples, human judgment proportion correct (M = .792, SE = .033) was nonsignificantly different from formal test proportion correct (range: .796–.867), .15 < ps < .91. Likewise, for large samples, human judgment proportion correct (M = .800, SE = .025) was not significantly different from formal test proportion correct (range: .733–.867), .12 < ps < .31.

General discussion

Overall, informal graph judgments tended to be inferior to formal hypothesis tests. Indeed, even the Pearson χ² test, which is one of the oldest and least powered tests of normality, was usually preferable to informal judgment. The inferiority of informal human judgment occurred despite giving participants several crutches, crutches that are rarely if ever available in real-world settings. First, participants were trained with hundreds of examples with feedback, feedback that is almost never available in real life because the researcher rarely gets to see the population from which the sample was drawn. Second, participants were informed that each sample would have an equal chance of coming from a normal population or not. This kind of base-rate information is rarely known in actual research. Third, participants were shown, at most, two different sample sizes (Experiments 3–4), whereas in actual research the sample sizes can vary considerably from study to study, and even from variable to variable within study. In actual research, informal judgment would have to be calibrated to numerous different samples sizes, making learning even more challenging. For these reasons, the human performance observed in the present experiments is likely an overestimate of that achievable in realistic settings.

Three formal tests showed relatively strong performance: Shapiro–Wilk, Shapiro–Francia, and Anderson–Darling tests. These tests performed well not only when the decision was between “normal” versus “not normal” (Experiments 1–2), but also when the decision was between “normal enough for a parametric test” versus not (Experiments 3–4). Likewise, these tests performed well regardless of whether the true population distribution (the alternative hypothesis) consisted of a variety experimenter chosen shapes (Experiments 1–2) or of realistic skewness and kurtosis combinations commonly observed in psychological and educational data (Experiments 3–4). The generality of these results suggests that the Shapiro–Wilk, Shapiro–Francia, and Anderson–Darling tests are all defensible choices (also see Gan & Koehler, 1990; Shapiro & Wilk, 1965; Thode, 2002).

Receiver operating characteristics were crucial for comparing different approaches to assessing normality. They were crucial because overall accuracy is influenced both by a criterion/confidence threshold, which is easy to change, and by each approach’s ability to discriminate (approximately) normal from nonnormal, which is not. By illustrating all possible criteria/confidence thresholds, ROCs showed a clear advantage in discriminability of several formal tests over informal judgments. However, if one were to use a dependent measure other than discriminability, the advantages of formal tests might be obscured. For example, using proportion of correct judgments as the dependent variable could produce an apparent advantage for informal judgments, at least if one sets the alpha level for formal tests to be too high or too low. Indeed, with certain alpha levels, proportion correct could even suggest an apparent advantage of small samples over large ones (see Anderson, Doherty, Berg, & Friedrich, 2005).

ROCs provide a resolution to the sample size paradox that troubles various formal model diagnostics, including normality tests. Rather than treating large ns as worse than small ns, ROCs illustrate that larger sample sizes encourage better discriminability. Larger sample sizes are not problematic in and of themselves; the problem arises if the chosen criterion (α) is too high, allowing too many “not normal” decisions. That is, the real problem that the paradox points to is that the optimal criterion is unclear. However, switching from formal to informal judgment does not solve this criterion problem—it merely hides it. For example, when judging a Q–Q plot, one must still make an arbitrary decision about how close to the reference line is “close enough.” Formal hypothesis tests make this criterion setting explicit, but informal judgment still relies on some criterion, whether explicit or not.

An additional concern with informal judgment of graphs is that those judgments create additional researcher degrees of freedom. Researchers could be biased, perhaps unintentionally, to use these degrees of freedom to produce results that are publishable, but not replicable (John, Loewenstein, & Prelec, 2012; Simmons, Nelson, & Simonsohn, 2011). For example, if a primary test of interest produced nonsignificant results, a researcher may then be tempted to scrutinize the model for assumption violations, using even small deviations from a reference line to justify one or more additional statistical procedures. The same researcher might not have examined model assumptions, or perhaps would have done so with different informal criteria, if the primary test had produced a significant result. If the researcher instead used a formal hypothesis test for model diagnostics, both the test and criterion could be explicitly decided upon beforehand.

While the discriminability advantage of formal tests was clear, the power advantage was more subtle. This could be due to the similar power of the independent-samples t test and MWW test for the stimuli used in Experiments 3 and 4, as the mean absolute power difference was only .086. More substantial differences in power or other outcomes could arise when choosing among more distinct statistical models, or relatedly, when the choice depends on combinations of assumption violations (normality, homoscedasticity, and/or independent observations). The experiments here focused on just a simple decision involving similar models and only one possible assumption violation.

More generally, the current work suggests that formal approaches to model diagnostics might be more fruitful than previously thought. Unfortunately, there could be several barriers to their use. One barrier may be a misconception that parametric tests are, in general, immune to the effects of assumption violations, so long as n is greater than ___ (readers may fill in the blank with 30, 100, 120, or some other rule of thumb). Unfortunately, even with relatively large samples, a simple parametric test can be underpowered relative to an alternative (e.g., Sawilowsky & Blair, 1992). Large samples may also fail to help with confidence intervals or other estimates of interest (e.g., Bishara et al., 2018). In other words, it would be an oversimplification to declare parametric tests robust in general (Bradley, 1978). A second barrier may be the worry that assumption tests increase study-wise Type I error by increasing the number of tests. However, a Type I error on an assumption test is different from one on the test of primary interest (e.g., a t test), and an error on one need not lead to an error on the other. Indeed, the situations that are ambiguous enough to lead to an error on an assumption test are also the situations where assumption violations, if any, are likely to be subtle, and therefore have little impact on the test of interest.

It is more difficult to overcome a final barrier: What is an optimal criterion for an assumption test? One possible approach to the criterion problem would be to sidestep it, and simply use robust methods. To avoid circularity, we took that approach here, for example, by using bootstrapped confidence intervals for the major effects of interest. However, using models with more detailed assumptions can provide more accurate inference and estimation, or at least when those assumptions are met. An alternative approach would be to identify some function to estimate an optimal alpha or other criterion. Such a function may depend on a variety of factors, including the primary hypothesis test of interest (e.g., ANOVA, t test), the alpha level of that test of interest, how well other assumptions are satisfied, the relative sample sizes in multiple group designs, and even on combinations of these factors. It is an open question as to whether these numerous factors could be incorporated into a function simple enough for practical use.

Limitations

First, our conclusions should not be oversimplified to suggest that all graph judgment or all informal judgment is undesirable. After all, our conclusions were reached by both formal methods (e.g., p < .05) and informal ones (ROC plot judgment). Whether a formal decision rule is superior to informal judgment is an empirical question, and one that should be addressed for the particular statistical task of interest (e.g., Coulson, Healey, Fidler, & Cumming, 2010; Fidler & Loftus, 2009).

Second, our experiments and simulations used samples drawn from continuous population distributions. Caution should be used when data consist of short-range Likert scale ratings or other situations where ties are frequent. Frequent ties can distort the expected linear pattern on Q–Q and P–P plots, and they also necessitate modifications to formal assumption tests (e.g., for the Shapiro–Wilk test; see Royston, 1989).

Third, it is possible that participants’ informal judgments would have been better had they been provided with other cues in addition to the graphs, such as combinations of graphs with one or more formal test results. Conversely, it is also possible that they would have been worse (e.g., Goldberg, 1968), as often happens when cues are redundant (Karelaia & Hogarth, 2008). The Shapiro–Francia test is largely redundant with a Q–Q plot, as the Shapiro–Francia test statistic (W') is a measure of the linearity of dots on that plot. Because of such redundancy, Shapiro–Francia and other correlation type tests (e.g., Shapiro–Wilk) seem unlikely to be beaten by informal judgments that combine these test results with some form of Q–Q plot inspection.

Fourth, assumption tests are not always warranted, and there are some situations in which they do more harm than good. A well-known example is the test for homogeneity of variance prior to conducting a two-sample t test. In that situation, the assumption test is unhelpful because the Welch version of the test has no equal variance assumption, and yet performs as well or better than the two-sample t test, even when homogeneity of variance is satisfied (Moser & Stevens, 1992; Zimmerman, 2004). Of course, there is no reason to expect that the pitfalls of assumption tests can be avoided by informal inspections of Q–Q plots or other graphs. Informal judgments can carry the same risks as formal hypothesis tests, and possibly more; if they are less discriminating, they behave as assumption tests, but with additional noise influencing the outcome.

Finally, while power and Type I error are important considerations for choosing a model, numerous other factors might also be considered, such as interpretability, precision of estimates, and prediction error. That is, model choice is a complex, multi-attribute decision problem. Even if the decision ultimately relies on some informal weighting of these many attributes, it could still be advantageous to formalize the judgment of individual attributes.

Conclusions

The relative value of formal tests versus informal statistical judgments may appear obvious, or at least until one recalls the long-standing debates about these issues (Bakan, 1966; Cumming, 2014; Fisch, 1998; Greenwald, Gonzalez, Harris, & Guthrie, 1996; Nelson, Simmons, & Simonsohn, 2018; Skinner, 1956). Experiments that directly compare formal and informal statistical judgment, and particularly within an ROC framework, offer an empirical approach to navigate these debates. The experiments here showed that formal statistical judgment can be more discriminating, resulting in slightly higher power of the chosen statistical model.