The effect of residual stress on the stability of a circular cylindrical tube

Abstract

Residual stresses in an unloaded configuration of an elastic material have a significant influence on the response of the material from that configuration, but the effect of residual stress on the stability of the material, whether loaded or unloaded, has only been addressed to a limited extent. In this paper we consider the level of residual stress that can be supported in a thick-walled circular cylindrical tube of non-linearly elastic material without loss of stability when subjected to fixed axial stretch and either internal or external pressure. In particular, we consider the tube to have radial and circumferential residual stresses, with a simple form of elastic constitutive law that accommodates the residual stress, and incremental deformations restricted to the cross section of the tube. Results are described for a tube subject to a level of (internal or external) pressure characterized by the internal azimuthal stretch. Subject to restrictions imposed by the strong ellipticity condition, the emergence of bifurcated solutions is detailed for their dependence on the level of residual stress and mode number.

1 Introduction

Residual stresses have a significant effect on the mechanical behaviour of materials in which they are supported, as has been reported in a number of recent works, for example Merodio et al. [1] and Merodio and Ogden [2] where the influence of the response of circular cylindrical tubes subject to residual stress under various loading conditions was analysed. Residual stresses can have damaging consequences when generated in components during the manufacturing process, for example. On the other hand, they can improve the properties of structures (for example, in pre-stressed car windscreens). In biological tissues residual stresses are developed during growth and remodelling and have an important influence on the mechanical response of the tissue in normal (or abnormal) physiological conditions. Understanding the influence of residual stresses from a theoretical point of view therefore has important practical consequences.

A theoretical basis for non-linearly elastic solids with residual stress was developed in a series of papers by Hoger, in particular in [3, 4], while for a homogeneously initially stressed material (as distinct from a residually stressed material) further contributions detailing the effect of the initial stress on the propagation of waves were provided by Shams et al. [5], and Ogden and Singh [6], for example.

Although the basic analysis of the effect of residual stress on material response is now well developed, very little has been done on the effect that residual stress has on stability, an exception being the paper by Ciarletta et al. [7], which was concerned with the stability (in two dimensions) of an unloaded circular annulus carrying both radial and circumferential residual stresses.

In the present paper we examine the effect of axial load, internal and external pressure and residual stress on the stability of a circular cylindrical tube of incompressible elastic material based on the linear theory of elastic increments superimposed on the (finitely deformed) circular cylindrical configuration, with attention restricted to increments confined to the radial–circumferential plane.

We begin in Sect. 2 by providing the basic equations of elasticity with residual stress, while in Sect. 2.1 the constitutive equation is specialized in terms of invariants. The theory is then applied in Sect. 3 to the basic configuration of a residually stressed circular cylindrical tube subject to axial load and internal or external pressure. Section 4 summarizes the required incremental equations, which are specialized in detail in Sect. 5 for the case of planar increments (in the radial–circumferential plane). Specific forms of residual stress and constitutive equation to be used for illustration are also provided along with consideration of the restrictions imposed by the strong ellipticity condition. The numerical procedure used for solving the incremental equations and boundary conditions is described in Sect. 6.

Results of the calculations are illustrated in Sect. 6.3 to show the relative influences of the residual stress, the tube thickness, the deformed inner radius of the tube (as a measure of internal or external pressure) and the mode number on the onset of bifurcation, with particular reference to the strong ellipticity condition.

Some brief concluding remarks are provided in Sect. 6.4.

2 Residual stress and elasticity

We consider a solid continuum which, when unloaded, is designated its reference configuration, denoted ${\mathcal {B}}_\mathrm {r}$. Within this configuration it possesses a residual stress distribution, with the residual (Cauchy) stress tensor denoted $\varvec{\tau }$. By definition [3, 4] $\varvec{\tau }$ satisfies the equilibrium equation and zero traction boundary conditions

$$\begin{aligned} \hbox {Div }\varvec{\tau }=\mathbf {0} \quad \text{ in }\quad {\mathcal {B}}_\mathrm {r},\quad \varvec{\tau }\mathbf {N}=\mathbf {0}\quad \text{ on }\quad \partial {\mathcal {B}}_\mathrm {r}, \end{aligned}$$

(1)

where $\partial {\mathcal {B}}_\mathrm {r}$ is the boundary of ${\mathcal {B}}_\mathrm {r}$, which has unit outward normal $\mathbf {N}$, $\hbox {Div }$ being the divergence operator in ${\mathcal {B}}_\mathrm {r}$, i.e. with respect to material position $\mathbf {X}\in {\mathcal {B}}_\mathrm {r}$. It is assumed that there are no intrinsic couple stresses so that $\varvec{\tau }$ is symmetric. Note that residual stresses are necessarily non-uniform, i.e. depend on $\mathbf {X}$, and the material that supports them is inhomogeneous.

When loads are applied, the resulting deformation is measured from ${\mathcal {B}}_\mathrm {r}$ with deformation gradient $\mathbf {F}$, associated with which are the right and left Cauchy–Green deformation tensors, denoted $\mathbf {C}$ and $\mathbf {B}$, respectively, and defined by

$$\begin{aligned} \mathbf {C}=\mathbf {F}^\mathrm {T}\mathbf {F},\quad \mathbf {B}=\mathbf {F}\mathbf {F}^\mathrm {T}. \end{aligned}$$

(2)

The deformed configuration is denoted ${\mathcal {B}}$ and its boundary by $\partial {\mathcal {B}}$, within which the material point $\mathbf {X}$ is located at $\mathbf {x}$, which is given by the deformation function $\varvec{\chi }$, such that $\mathbf {x}=\varvec{\chi }(\mathbf {X})$ and $\mathbf {F}=\hbox {Grad }\mathbf {x}$, $\hbox {Grad }$ being the gradient operator with respect to $\mathbf {X}$.

In this paper we shall assume that the material response relative to ${\mathcal {B}}_\mathrm {r}$ is incompressible, so the constraint

$$\begin{aligned} \det \mathbf {F}=\det \mathbf {C}=1, \end{aligned}$$

(3)

is satisfied for each $\mathbf {X}\in {\mathcal {B}}_\mathrm {r}$.

We suppose that the response to applied loads is purely elastic and characterized in terms of a strain-energy function W defined per unit volume in ${\mathcal {B}}_\mathrm {r}$ and measured therefrom. It depends not only on the deformation gradient $\mathbf {F}$ but also the residual stress $\varvec{\tau }$. Objectivity requires that W depends on $\mathbf {F}$ through $\mathbf {C}$. The dependence on $\varvec{\tau }$ is included explicitly in the arguments of W and we write

$$\begin{aligned} W=W(\mathbf {C},\varvec{\tau }), \end{aligned}$$

(4)

which is automatically objective since $\varvec{\tau }$ is unaffected by rotations in the deformed configuration ${\mathcal {B}}$. Note that the elastic properties of the material relative to ${\mathcal {B}}_\mathrm {r}$ are anisotropic, i.e. $\varvec{\tau }$ has an effect on the constitutive law analogous to that of a structure tensor associated with preferred directions in fibre-reinforced materials, as for example, in [8]. In the special case that $\varvec{\tau }$ specializes to a rank-one tensor, say $\mathbf {M}\otimes \mathbf {M}$, the invariants associated with transverse isotropy are recovered. In general, we may refer to $\varvec{\tau }$ as a generalized structure tensor. The appropriate invariants for a general $\varvec{\tau }$ will be listed in the following section.

Since W is measured from ${\mathcal {B}}_\mathrm {r}$, we impose the condition

$$\begin{aligned} W(\mathbf {I},\varvec{\tau })=0. \end{aligned}$$

(5)

The formulas for the nominal and Cauchy stresses are the same as in standard non-linear elasticity, except by the dependence of W on $\varvec{\tau }$, which has a passive role since it is independent of the deformation. Thus, for the considered incompressible elastic material the nominal stress tensor $\mathbf {S}$ and Cauchy stress tensor $\varvec{\sigma }$ are given by

$$\begin{aligned} \mathbf {S}=\frac{\partial W}{\partial \mathbf {F}}(\mathbf {F},\varvec{\tau })-p\mathbf {F}^{-1}, \quad \varvec{\sigma }={\mathbf {F}}{\mathbf {S}}=\mathbf {F}\frac{\partial W}{\partial \mathbf {F}}(\mathbf {F},\varvec{\tau })-p\mathbf {I}, \end{aligned}$$

(6)

where p is a Lagrange multiplier necessitated by the constraint (3) and $\mathbf {I}$ is now written for the identity tensor in ${\mathcal {B}}$ (which we do not distinguish from that in ${\mathcal {B}}_\mathrm {r}$). For equilibrium in ${\mathcal {B}}$ the equations

$$\begin{aligned} \hbox {Div }\mathbf {S}=\mathbf {0},\quad \text{ div } {\varvec{\sigma }}=\mathbf {0} \end{aligned}$$

(7)

have to be satisfied in the absence of body forces.

When $\mathbf {F}=\mathbf {I}$, each of the expressions in (6) reduces to

$$\begin{aligned} \varvec{\tau }=\frac{\partial W}{\partial \mathbf {F}}(\mathbf {I},\varvec{\tau })-p^{(\mathrm {r})}\mathbf {I}, \end{aligned}$$

(8)

where $p^{(\mathrm {r})}$ is the value of p in ${\mathcal {B}}_\mathrm {r}$. The latter condition imposes restrictions on W in ${\mathcal {B}}_\mathrm {r}$, which will be made explicit in the following.

2.1 Invariant formulation

Based on the general theory of Spencer [9] it can be seen that, for an incompressible material, in three dimensions $W(\mathbf {C},\varvec{\tau })$ depends on 9 invariants generated by the two tensors $\mathbf {C}$ and $\varvec{\tau }$. With the invariant $I_3=\det \mathbf {C}$ omitted because of the constraint (3), these are typically taken to be, for $\mathbf {C}$,

$$\begin{aligned} I_1=\hbox {tr }\mathbf {C},\quad I_2=\frac{1}{2}[(\hbox {tr }\mathbf {C})^2-\hbox {tr }(\mathbf {C}^2)], \end{aligned}$$

(9)

for the combination of $\mathbf {C}$ and $\varvec{\tau }$,

$$\begin{aligned} I_5=\hbox {tr }(\varvec{\tau }\mathbf {C}),\quad I_6=\hbox {tr }(\varvec{\tau }\mathbf {C}^2),\quad I_7=\hbox {tr }(\varvec{\tau }^2\mathbf {C}),\quad I_8=\hbox {tr }(\varvec{\tau }^2\mathbf {C}^2), \end{aligned}$$

(10)

while for $\varvec{\tau }$ we denote the three invariants collectively as

$$\begin{aligned} I_4\equiv \left\{ \hbox {tr }\varvec{\tau },\ \frac{1}{2}[(\hbox {tr }\varvec{\tau })^2-\hbox {tr }(\varvec{\tau }^2)],\ \det \varvec{\tau }\right\} . \end{aligned}$$

(11)

The invariants of $\varvec{\tau }$ are not affected by the deformation, while in the configuration ${\mathcal {B}}_\mathrm {r}$ the other invariants reduce to

$$\begin{aligned} I_1=I_2=3,\quad I_3=1,\quad I_5=I_6=\hbox {tr }\varvec{\tau },\quad I_7=I_8=\hbox {tr }(\varvec{\tau }^2). \end{aligned}$$

(12)

We emphasize that the above set of 9 invariants, or an equivalent set of alternative invariants, forms a complete set of invariants of $\mathbf {C}$ and $\varvec{\tau }$ in three dimensions for an incompressible material. When the dimension of the considered problem is reduced from three to two, such as for plane strain, the number of independent invariants is reduced.

In terms of the invariants the expressions in (6) for the nominal and Cauchy stresses can be expanded in the form

$$\begin{aligned} \mathbf {S}=\sum _{i\,\in \,{\mathcal {I}}}{\bar{W}}_i\frac{\partial I_i}{\partial \mathbf {F}}-p\mathbf {F}^{-1},\quad \varvec{\sigma }={\mathbf {F}}{\mathbf {S}}, \end{aligned}$$

(13)

where ${\mathcal {I}}$ is the index set $\{1,2,5,6,7,8\}$, the notation ${\bar{W}}_i=\partial {\bar{W}}/\partial I_i,\, i\in {\mathcal {I}}$ has been adopted, and W is written ${\bar{W}}(I_1,I_2,I_4,I_5,I_6,I_7,I_8)$ to reflect the dependence on the invariants. Note that the derivative of $I_4$ with respect to $\mathbf {F}$ vanishes and so is not included in the above expression, but $I_4$ is included in the functional dependence of ${\bar{W}}$.

The expressions for $\partial I_i/\partial \mathbf {F},\,i\in {\mathcal {I}}$, required in (13), are given by

$$\begin{aligned} \frac{\partial I_1}{\partial \mathbf {F}}= & {} 2\mathbf {F}^\mathrm {T},\quad \frac{\partial I_2}{\partial \mathbf {F}}=2(I_1\mathbf {F}^\mathrm {T}-\mathbf {C}\mathbf {F}^\mathrm {T}),\end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial I_5}{\partial \mathbf {F}}= & {} 2\varvec{\tau }\mathbf {F}^\mathrm {T},\quad \frac{\partial I_6}{\partial \mathbf {F}}=2(\varvec{\tau }\mathbf {C}\mathbf {F}^\mathrm {T}+\mathbf {C}\varvec{\tau }\mathbf {F}^\mathrm {T}),\end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial I_7}{\partial \mathbf {F}}= & {} 2\varvec{\tau }^2\mathbf {F}^\mathrm {T},\quad \frac{\partial I_8}{\partial \mathbf {F}}=2(\varvec{\tau }^2\mathbf {C}\mathbf {F}^\mathrm {T}+\mathbf {C}\varvec{\tau }^2\mathbf {F}^\mathrm {T}), \end{aligned}$$

(16)

the symmetry of $\varvec{\tau }$ having been used.

The Cauchy stress in (13) then expands in full as

$$\begin{aligned} \varvec{\sigma }= & {} 2 {\bar{W}}_1 \mathbf {B} + 2 {\bar{W}}_2 (I_1 \mathbf {B} - \mathbf {B}^2) + 2 {\bar{W}}_5\varvec{\varSigma }+2 {\bar{W}}_6 (\varvec{\varSigma }\mathbf {B} + \mathbf {B}\varvec{\varSigma })\nonumber \\&+ \,2{\bar{W}}_7 \varvec{\varSigma } \mathbf {B}^{-1} \varvec{\varSigma } + 2 {\bar{W}}_8(\varvec{\varSigma }\mathbf {B}^{-1}\varvec{\varSigma }\mathbf {B} + \mathbf {B} \varvec{\varSigma } \mathbf {B}^{-1}\varvec{\varSigma })-p \mathbf {I}, \end{aligned}$$

(17)

wherein we have introduced the notation $\varvec{\varSigma }=\mathbf {F}\varvec{\tau }\mathbf {F}^\mathrm {T}$ for the Eulerian tensor which is the push-forward of $\varvec{\tau }$. We also recall that $\mathbf {B}={\mathbf {F}}{\mathbf {F}}^\mathrm {T}$ is the left Cauchy–Green tensor.

When evaluated in ${\mathcal {B}}_\mathrm {r}$ the latter reduces to the specialization of (8) as

$$\begin{aligned} \varvec{\tau } = (2 {\bar{W}}_1+4{\bar{W}}_2-p^{(\mathrm {r})}) \mathbf {I} + 2 ({\bar{W}}_5+2 {\bar{W}}_6) \varvec{\tau }+ 2({\bar{W}}_7 +2{\bar{W}}_8)\varvec{\tau }^2, \end{aligned}$$

(18)

where each ${\bar{W}}_i,\,i\in {\mathcal {I}}$, is evaluated for the invariants given by (12). Thus, following [5] with a slightly different notation, we obtain the restrictions

$$\begin{aligned} 2 {\bar{W}}_1 + 4 {\bar{W}}_2 - p^{(\mathrm {r})} = 0, \quad 2({\bar{W}}_5 + 2 {\bar{W}}_6) = 1, \quad {\bar{W}}_7 + 2 {\bar{W}}_8 = 0 \end{aligned}$$

(19)

on the strain-energy function in ${\mathcal {B}}_\mathrm {r}$.

Further details of the residual stress formulation are given in [5] and, for a material also containing a preferred direction, in [6], while an application to a prototype problem involving an inhomogeneous deformation, that of (plane strain) azimuthal shear of a circular cylindrical tube, for a residually stressed material, is provided in [1]. In the following section we consider the specialization of the above equations to a circular cylindrical configuration with the residual stress confined to the cross-sectional plane of the cylinder.

3 Application to a thick-walled tube with residual stress

We now consider a thick-walled circular cylindrical tube which is subject to a uniform axial stretch and radial deformation. Let the cross-sectional geometry of the tube in the configuration ${\mathcal {B}}_{\mathrm {r}}$ be defined by $0<A\le R\le B$, $0\le \varTheta \le 2\pi$, with axial coordinate Z. After deformation the internal and external radii A and B become a and b and since the material is incompressible the deformation is given in terms of cylindrical polar coordinates $r,\theta ,z$ by

$$\begin{aligned} r^2=a^2+\lambda _z^{-1}(R^2-A^2),\quad \theta =\varTheta ,\quad z=\lambda _zZ, \end{aligned}$$

(20)

where the constant $\lambda _z$ is the axial stretch, while b is given by $b^2=a^2+\lambda _z^{-1}(B^2-A^2)$. The circumferential stretch, denoted $\lambda$, is given by $\lambda =r/R$, and by incompressibility the radial stretch is $\lambda ^{-1}\lambda _z^{-1}$.

The residual stress in ${\mathcal {B}}_{\mathrm {r}}$ is taken to consist of radial and circumferential components $\tau _{33}$ and $\tau _{11}$, respectively, with axial component $\tau _{22}=0$. For the most part the components of tensors are signified with indices $p, q, \alpha ,\beta ,...$, etc., which take values 1, 2, 3 in the general case. The components $\tau _{33}$ and $\tau _{11}$ satisfy the equilibrium equation

$$\begin{aligned} \frac{\mathrm {d}\tau _{33}}{\mathrm {d}R}+\frac{1}{R}(\tau _{33}-\tau _{11})=0\quad \text{ for }\ A<R<B, \end{aligned}$$

(21)

with the boundary condition (1)$_2$ specializing to

$$\begin{aligned} \tau _{33}=0\quad \text{ on }\quad R=A\ \text{ and }\ B. \end{aligned}$$

(22)

Note that $\tau _{11}$ and $\tau _{33}$ are the only components of the residual stress since the considered geometry can support neither a shear nor an axial component of residual stress without Z dependence.

The first two invariants in $I_4$ in (11) reduce to just $\tau _{11}+\tau _{33}$ and $\tau _{11}\tau _{33}$ and the third vanishes, while $I_1$ and $I_2$ in (9) become

$$\begin{aligned} I_1=\lambda ^2+\lambda _z^2+\lambda ^{-2}\lambda _z^{-2},\quad I_2= \lambda ^{-2}+\lambda _z^{-2}+\lambda ^2\lambda _z^2, \end{aligned}$$

(23)

and $I_5,\dots ,I_8$ can be expressed in terms of $\tau _{11},\tau _{33}$ and the stretches as

$$\begin{aligned} I_5= & {} \lambda ^{-2}\lambda _z^{-2}\tau _{33}+\lambda ^2\tau _{11},\quad I_6=\lambda ^{-4}\lambda _z^{-4}\tau _{33}+\lambda ^4\tau _{11},\nonumber \\ I_7= & {} \lambda ^{-2}\lambda _z^{-2}\tau _{33}^2+\lambda ^2\tau _{11}^2,\quad I_8=\lambda ^{-4}\lambda _z^{-4}\tau _{33}^2+\lambda ^4\tau _{11}^2. \end{aligned}$$

(24)

Since the invariants depend on only two independent stretches $\lambda$ and $\lambda _z$ together with the residual stress components $\tau _{11}$ and $\tau _{33}$, we introduce the reduced form of the strain-energy function, denoted ${\tilde{W}}(\lambda ,\lambda _z,\tau _{11},\tau _{33})$, and using (17) we then obtain the Cauchy stress differences

$$\begin{aligned} \sigma _{11}-\sigma _{33}=\lambda {\tilde{W}}_\lambda ,\quad \sigma _{22}-\sigma _{33}=\lambda _z{\tilde{W}}_{\lambda _z}, \end{aligned}$$

(25)

the indices 1, 2, 3 corresponding to the coordinates $\theta ,z,r$, respectively. In (25) the subscripts $\lambda$ and $\lambda _z$ signify partial derivatives.

For the considered geometry the equilibrium equation (7)$_2$ reduces to

$$\begin{aligned} \frac{\mathrm {d}\sigma _{33}}{\mathrm {d}r}=\frac{1}{r}(\sigma _{11}-\sigma _{33})=\frac{1}{r}\lambda {\tilde{W}}_\lambda . \end{aligned}$$

(26)

For the moment we assume that the radial deformation is accompanied by both internal and external pressures, denoted $P_a$ and $P_b$ on $r=a$ and $r=b$, respectively. Thus, $\sigma _{33}$ satisfies the boundary conditions

$$\begin{aligned} \sigma _{33}={\left\{ \begin{array}{ll}-P_a&{}\text{ on }\ r=a,\\ -P_b&{}\text{ on }\ r=b.\end{array}\right. } \end{aligned}$$

(27)

Integration of (26) then gives

$$\begin{aligned} P\equiv P_a-P_b=\int _a^b\lambda {\tilde{W}}_\lambda \frac{\mathrm {d}r}{r}. \end{aligned}$$

(28)

Note that positive (negative) P corresponds to an effective internal (external) pressure.

Since $\tau _{22}=0$, when the expressions (25) are evaluated in ${\mathcal {B}}_{\mathrm {r}}$, where $\lambda =\lambda _z=1$, they reduce to

$$\begin{aligned} \tau _{11}-\tau _{33}={\tilde{W}}_\lambda (1,1,\tau _{11},\tau _{33}), \quad -\tau _{33}={\tilde{W}}_{\lambda _z}(1,1,\tau _{11},\tau _{33}), \end{aligned}$$

(29)

which provide restrictions on ${\tilde{W}}$ that specialize those in (19).

The corresponding expression for the reduced axial load on a cross section of the tube is

$$\begin{aligned} F=\pi \int _a^b(2\lambda _z{\tilde{W}}_{\lambda _z}-\lambda {\tilde{W}}_\lambda )r\,\mathrm {d}r. \end{aligned}$$

The latter provides an expression for the reduced axial load required to maintain a fixed value of the axial stretch, while (28) provides an expression for the pressure difference for a prescribed value of the inner radius a and the axial stretch $\lambda _z$, on recalling that the outer radius is given by $b=\sqrt{a^2+\lambda _z^{-1}(B^2-A^2)}$.

4 Incremental equations

In order to examine the linear stability of the basic configuration we need to consider incremental deformations relative to that configuration. Incremental quantities are signified by a superposed dot, so that the incremental displacement is denoted ${\dot{\mathbf {x}}}=\varvec{{\dot{\chi }}}(\mathbf {X})$ and the corresponding increment in the deformation gradient by ${\dot{\mathbf {F}}}$, with ${\dot{\mathbf {F}}}=\hbox {Grad }{\dot{\mathbf {x}}}=\mathbf {L}\mathbf {F}$, where $\mathbf {L}=\hbox {grad }\mathbf {u}$ is the displacement gradient, $\mathbf {u}$ being the Eulerian counterpart of ${\dot{\mathbf {x}}}$ defined by $\mathbf {u}(\mathbf {x})=\varvec{{\dot{\chi }}}(\varvec{\chi }^{-1}(\mathbf {x}))$. Then, on taking the increment of (6)$_1$ we obtain the increment in the nominal stress

$$\begin{aligned} {\dot{\mathbf {S}}}=\varvec{{\mathcal {A}}}{\dot{\mathbf {F}}}+p\mathbf {F}^{-1}{\dot{\mathbf {F}}} \mathbf {F}^{-1}-{\dot{p}}\mathbf {F}^{-1}, \end{aligned}$$

(30)

where ${\dot{p}}$ is the incremental Lagrange multiplier and the fourth-order tensor of elastic moduli $\varvec{{\mathcal {A}}}$ is defined in symbolic and index notation by

$$\begin{aligned} \varvec{{\mathcal {A}}}=\frac{\partial ^2W}{\partial \mathbf {F}\partial \mathbf {F}},\quad {\mathcal {A}}_{\alpha i\beta j}=\frac{\partial ^2W}{\partial F_{i\alpha }F_{j\beta }}. \end{aligned}$$

(31)

The incremental equilibrium equation is $\hbox {Div }{\dot{\mathbf {S}}}=\mathbf {0}$.

On updating the reference configuration from ${\mathcal {B}}_{\mathrm {r}}$ to ${\mathcal {B}}$ the incremental constitutive equation (30) becomes

$$\begin{aligned} {\dot{\mathbf {S}}}_0=\varvec{{\mathcal {A}}}_0\mathbf {L}+p\mathbf {L}-{\dot{p}}\mathbf {I}, \end{aligned}$$

(32)

where ${\dot{\mathbf {S}}}_0$ is the push-forward version of ${\dot{\mathbf {S}}}$ defined by ${\dot{\mathbf {S}}}_0=\mathbf {F}{\dot{\mathbf {S}}}$ and satisfying the Eulerian form $\text{ div } {\dot{\mathbf {S}}}_0=\mathbf {0}$ of the incremental equilibrium equation, while $\varvec{{\mathcal {A}}}_0$ is the corresponding push-forward of $\varvec{{\mathcal {A}}}$ defined in index notation by

$$\begin{aligned} {\mathcal {A}}_{0piqj}=F_{p\alpha }F_{q\beta }{\mathcal {A}}_{\alpha i\beta j}. \end{aligned}$$

(33)

The incremental traction per unit area of the boundary $\partial {\mathcal {B}}$ is $\dot{\mathbf {S}}_0^{\mathrm {T}}\mathbf {n}$ and will be made explicit later for the considered problem, $\mathbf {n}$ being the outward unit normal to $\partial {\mathcal {B}}$.

Let $\mathbf {e}_1$, $\mathbf {e}_2$, $\mathbf {e}_3$ be unit basis vectors in an orthogonal curvilinear coordinate system. Then, in component form, the equilibrium equation $\text{ div } {\dot{\mathbf {S}}}_0=\mathbf {0}$ yields the three scalar equations

$$\begin{aligned} {\dot{S}}_{0ji,j}+{\dot{S}}_{0ji}\mathbf {e}_k\cdot \mathbf {e}_{j,k}+{\dot{S}}_{0kj}\mathbf {e}_i\cdot \mathbf {e}_{j,k}=0, \quad i=1,2,3, \end{aligned}$$

(34)

as in Haughton and Ogden [10], in which summation over repeated indices j and k from 1 to 3 is implied and the subscript notation, j represents the derivative associated with the jth curvilinear coordinate. These components will be made explicit in the following section for the considered cylindrical polar coordinates. Equation (34) is valid for any elastic material whether or not it carries residual stress.

In respect of the invariant expansion, the components ${\mathcal {A}}_{0piqj}$ have been given in [5] in full generality for three dimensions. These are very lengthy and not needed here, but we do note the general connection

$$\begin{aligned} {\mathcal {A}}_{0piqj}-{\mathcal {A}}_{0ipqj}=(\sigma _{pq}+p\delta _{pq})\delta _{ij}-(\sigma _{iq}+p\delta _{iq})\delta _{pj} \end{aligned}$$

(35)

coming from incremental rotational balance equation (see [5]), which will be used here together with the incremental incompressibility condition in the form

$$\begin{aligned} \text{ div } \mathbf {u}=0. \end{aligned}$$

(36)

5 Planar bifurcation

We now order the coordinates as $\theta ,z, r$, associated with the stretches $\lambda ,\lambda _z,\lambda _r$, respectively, and for the associated components of vectors and tensors we adopt the indices 1, 2, 3 in the same order, as already noted.

The unit basis vectors associated with the cylindrical polar coordinates $\theta$, z, r are denoted $\mathbf {e}_1$, $\mathbf {e}_2$, $\mathbf {e}_3$, and the derivatives $(\cdot )_{,k}$ in (34) denoted by subscripts with preceding commas become $\partial /r\partial \theta$, $\partial /\partial z$, $\partial /\partial r$ for $k=1,2,3$, respectively. Here, however, we restrict attention to planar increments in the $(r,\theta )$ plane with all incremental quantities independent of z. Then, for the cylindrical polar coordinates the only non-zero scalar products $\mathbf {e}_i\cdot \mathbf {e}_{j,k}$ in (34) are

$$\begin{aligned} \mathbf {e}_1\cdot \mathbf {e}_{3,1}=-\mathbf {e}_3\cdot \mathbf {e}_{1,1}=\frac{1}{r}. \end{aligned}$$

(37)

In the absence of the incremental axial displacement the incremental displacement $\mathbf {u}$ may be written

$$\begin{aligned} \mathbf {u}=v\mathbf {e}_1+u\mathbf {e}_3, \end{aligned}$$

(38)

with components u and v corresponding to the radial and circumferential directions, respectively, and are in general dependent on both r and $\theta$. The matrix of components of $\mathbf {L}=\hbox {grad }\mathbf {u}$ with respect to the basis vectors $\mathbf {e}_1,\mathbf {e}_2,\mathbf {e}_3$ is

$$\begin{aligned}{}[L_{ij}]=\begin{bmatrix} (u+v_{,\theta })/r &{}\quad 0 &{}\quad v_{,r} \\ 0&{}\quad 0 &{}\quad 0 \\ (u_{,\theta }-v)/r &{}\quad 0 &{}\quad u_{,r} \end{bmatrix}, \end{aligned}$$

(39)

where the subscripts $\theta$, r following a comma indicate the corresponding partial derivatives.

The incremental incompressibility condition (36) specializes to

$$\begin{aligned} (u+v_{,\theta })/r+u_{,r}=0, \end{aligned}$$

(40)

which is satisfied by introducing a function $\phi (\theta , r)$ such that

$$\begin{aligned} u=\frac{\phi _{,\theta }}{r}, \quad v=-\phi _{,r}. \end{aligned}$$

(41)

The incremental equilibrium equations are now used to obtain the equation for $\phi$. First, we note that the equilibrium equation for $i=2$ in (34) is satisfied identically, while the equations for $i=1, 3$ yield

$$\begin{aligned}&{\dot{S}}_{011,1}+{\dot{S}}_{031,3}+\frac{1}{r}({\dot{S}}_{031}+{\dot{S}}_{013})=0, \end{aligned}$$

(42)

$$\begin{aligned}&{\dot{S}}_{013,1}+{\dot{S}}_{033,3}+\frac{1}{r}({\dot{S}}_{033}-{\dot{S}}_{011})=0. \end{aligned}$$

(43)

For the considered underlying cylindrical configuration the components of ${\dot{\mathbf {S}}}_0$ in the above two equations are given by

$$\begin{aligned} {\dot{S}}_{011}= & {} {\mathcal {A}}_{01111}L_{11}+{\mathcal {A}}_{01133}L_{33}+pL_{11}-{\dot{p}}, \end{aligned}$$

(44)

$$\begin{aligned} {\dot{S}}_{013}= & {} {\mathcal {A}}_{01313}L_{31}+{\mathcal {A}}_{01331}L_{13}+pL_{13}, \end{aligned}$$

(45)

$$\begin{aligned} {\dot{S}}_{031}= & {} {\mathcal {A}}_{03131}L_{13}+{\mathcal {A}}_{03113}L_{31}+pL_{31}, \end{aligned}$$

(46)

$$\begin{aligned} {\dot{S}}_{033}= & {} {\mathcal {A}}_{03311}L_{11}+{\mathcal {A}}_{03333}L_{33}+pL_{33}-{\dot{p}}, \end{aligned}$$

(47)

where the components of the elastic modulus tensor $\varvec{{\mathcal {A}}}_0$ are specialized below.

On substitution of these expressions into (42) and (43) and use of the incompressibility condition (40) with (39) we obtain

$$\begin{aligned} {\dot{p}}_{,\theta }= & {} [r({\mathcal {A}}^{\prime }_{03113}+p^{\prime })+{\mathcal {A}}_{01313}](u_{,\theta }-v)/r+(r{\mathcal {A}}^{\prime }_{03131}+{\mathcal {A}}_{03131})v_{,r} +{\mathcal {A}}_{03131}rv_{,rr}\nonumber \\&+({\mathcal {A}}_{01331}+{\mathcal {A}}_{01133}-{\mathcal {A}}_{01111})u_{,r\theta }, \end{aligned}$$

(48)

$$\begin{aligned} {\dot{p}}_{,r}= & {} [r({\mathcal {A}}^{\prime }_{03333}+p^{\prime }-{\mathcal {A}}^{\prime }_{01133})+{\mathcal {A}}_{03333}+{\mathcal {A}}_{01111}-2{\mathcal {A}}_{01133}]u_{,r}/r\nonumber \\&+({\mathcal {A}}_{03333}-{\mathcal {A}}_{01133})u_{,rr}+{\mathcal {A}}_{01313}(u_{,\theta \theta }-v_{,\theta })/r^2+{\mathcal {A}}_{01331}v_{,r\theta }/r, \end{aligned}$$

(49)

respectively, where a prime denotes differentiation with respect to r.

It is now convenient to define the reduced notations

$$\begin{aligned} \alpha ={\mathcal {A}}_{01313},\quad 2\beta ={\mathcal {A}}_{03333}+{\mathcal {A}}_{01111}-2{\mathcal {A}}_{01331}-2{\mathcal {A}}_{01133},\quad \gamma ={\mathcal {A}}_{03131}. \end{aligned}$$

(50)

Then, by eliminating ${\dot{p}}_r$ and ${\dot{p}}_{\theta }$ from (48) and (49) by cross differentiation and then substituting for the expressions (41) in the result, followed by some rearrangements, we obtain the required equation for $\phi$, namely

$$\begin{aligned}&\gamma r^4\phi _{,rrrr}+2\beta r^2\phi _{,rr\theta \theta }+\alpha \phi _{,\theta \theta \theta \theta }+2(r\gamma '+\gamma )r^3\phi _{,rrr}+2(r\beta '-\beta )r\phi _{,r\theta \theta }\nonumber \\&\quad +(2\beta +\alpha -2r\beta ')\phi _{,\theta \theta }+(r^2\gamma ''+r\gamma '-\gamma )(r^2\phi _{,rr}-r\phi _{,r}-\phi _{,\theta \theta })=0. \end{aligned}$$

(51)

The transition to this equation makes use of the equilibrium equation (26), the connections

$$\begin{aligned} {\mathcal {A}}_{01331}+p={\mathcal {A}}_{03131}-\sigma _{33}=\gamma -\sigma _{33},\quad \sigma _{11}-\sigma _{33}=\alpha -\gamma \end{aligned}$$

(52)

from (35), and

$$\begin{aligned} r( {\mathcal {A}}_{01331}+p)'=r\gamma '+\gamma -\alpha ,\quad r^2( {\mathcal {A}}_{01331}+p)''+r\alpha '-\alpha =r^2\gamma ''+r\gamma '-\gamma . \end{aligned}$$

(53)

We now turn to the boundary conditions associated with Eq. (51). For the considered pressure boundary conditions the incremental traction is given by

$$\begin{aligned} \dot{\mathbf {S}}_0^{\mathrm {T}}\mathbf {n}={\left\{ \begin{array}{ll}P_a \mathbf {L}^\mathrm {T}\mathbf {n}&{}\text{ on }\quad r=a,\\ P_b \mathbf {L}^\mathrm {T}\mathbf {n}&{}\text{ on }\quad r=b, \end{array}\right. } \end{aligned}$$

(54)

no incremental pressure being admitted. Hence, in terms of components this gives

$$\begin{aligned} {\dot{S}}_{031}={\left\{ \begin{array}{ll}P_aL_{31}&{}\text{ on }\quad r=a,\\ P_bL_{31}&{}\text{ on }\quad r=b, \end{array}\right. } \qquad {\dot{S}}_{033}={\left\{ \begin{array}{ll}P_aL_{33}&{}\text{ on }\quad r=a,\\ P_bL_{33}&{}\text{ on } \quad r=b. \end{array}\right. } \end{aligned}$$

(55)

By considering the boundary conditions involving ${\dot{S}}_{031}$ with the expression (46) and the connection from (52)$_1$ with the notation (50)$_3$ and using the boundary conditions (27), we obtain

$$\begin{aligned} \gamma (L_{13}+L_{31})=0 \quad \text{ on } \quad r=a,b. \end{aligned}$$

(56)

In general, apart from isolated configurations, we may assume that $\gamma \ne 0$. Then, in terms of $\phi$, (56) becomes

$$\begin{aligned} r^2\phi _{,rr}-r\phi _{,r}-\phi _{,\theta \theta }=0 \quad \text{ on } \quad r=a,b. \end{aligned}$$

(57)

Next, on use of (47) and the incremental incompressibility condition in the form $L_{11}+L_{33}=0$ the boundary conditions involving ${\dot{S}}_{033}$ can be rewritten as

$$\begin{aligned} ({\mathcal {A}}_{03333}-{\mathcal {A}}_{01133}+p)L_{33}-{\dot{p}}=0\quad \text{ on }\quad r=a,b. \end{aligned}$$

(58)

The term in ${\dot{p}}$ is then eliminated by differentiating (58) with respect to $\theta$ and using (48). Then, by using the expressions for the components $L_{ij}$ in terms of the function $\phi$, the boundary conditions (27), and an application of (57) this yields the boundary condition

$$\begin{aligned} \gamma r^3\phi _{,rrr}+(2\beta +\gamma )(r\phi _{,r\theta \theta }-\phi _{,\theta \theta })=0\quad \text{ on }\quad r=a,b. \end{aligned}$$

(59)

We now have a partial differential equation (51) for $\phi$ as a function of r and $\theta$ and two boundary conditions in each of (57) and (59). To make further progress the system of equations and boundary conditions needs to be solved numerically. Towards this we consider solutions for $\phi$ of the form

$$\begin{aligned} \phi =f_n(r)\sin n\theta , \end{aligned}$$

(60)

n being a non-negative integer.

Equation (51) is now expressed in terms of the function $f_n(r)$ and its derivatives as

$$\begin{aligned}&\gamma r^4f_n''''+2(r\gamma '+\gamma )r^3f_n'''+(r^2\gamma ''+r\gamma '-\gamma -2n^2\beta )r^2f_n''\nonumber \\&\quad -\,[r^2\gamma ''+r\gamma '-\gamma +2n^2(r\beta '-\beta )]rf_n'\nonumber \\&\quad +\,n^2(r^2\gamma ''+r\gamma '-\gamma +2r\beta '-2\beta -\alpha +\alpha n^2)f_n=0\quad \text{ for }\quad a<r<b. \end{aligned}$$

(61)

The boundary conditions (57) and (59) become

$$\begin{aligned}&r^2f_n''-rf_n'+n^2f_n=0\quad \text{ on }\quad r=a,b, \end{aligned}$$

(62)

$$\begin{aligned} \gamma&r^3f_n'''-n^2(2\beta +\gamma )rf_n'+n^2(2\beta +\gamma )f_n=0\quad \text{ on }\quad r=a,b. \end{aligned}$$

(63)

The foregoing equations and boundary conditions apply for any radial deformation with $\lambda >0$ and axial stretch $\lambda _z>0$. However, to avoid buckling-type instabilities (z-dependent) associated with axial compression we restrict attention to $\lambda _z\ge 1$ since we are only considering prismatic bifurcations here.

5.1 Specialization of the residual stress and constitutive equation

At this point we specialize the form of the residual stress in order to provide explicit illustrations of the effect of residual stress on the material response. First, we choose a simple form of $\tau _{33}$ satisfying the boundary conditions (22) and then use (21) to determine $\tau _{11}$. Specifically, we take

$$\begin{aligned} \tau _{33}=\nu (R-A)(R-B), \end{aligned}$$

(64)

and hence

$$\begin{aligned} \tau _{11}=\nu [3R^2-2(A+B)R+AB], \end{aligned}$$

(65)

where $\nu$ is a constant, which may be positive or negative.

Plots of $\tau _{11}/\nu$ and $\tau _{33}/\nu$ are shown in Fig. 1. For $\nu >0$, their behaviours are very similar to those arising from the residual stresses calculated for a single-layer artery wall from the so-called ‘opening angle’ method [11] or the assumption that the circumferential stress at a typical physiological pressure is uniform [12], and are therefore realistic in this context. However, it is appropriate to allow for the possibility that $\nu$ be negative in other contexts.

Fig. 1

Plots of the scaled circumferential and radial residual stress components, $\tau _{11}/\nu$ (continuous curve) and $\tau _{33}/\nu$ (dashed curve), respectively, for $A\le R\le B$

In order to obtain explicit results we now consider a simple form of energy function, namely

$$\begin{aligned} {\bar{W}}=\frac{1}{2}\mu (I_1-3)+\frac{1}{2}(I_5-\hbox {tr }\varvec{\tau })+\frac{1}{4}\kappa (I_5-\hbox {tr }\varvec{\tau })^2, \end{aligned}$$

(66)

where $\mu >0$ is a constant and $\kappa$ is a non-negative constant, as introduced in [5] in a slightly different notation, and also adopted in [1] and [2], for example. Thus, ${\bar{W}}=0$ and (19)$_1$ is satisfied with $p^{(\mathrm {r})}=\mu$ in ${\mathcal {B}}_\mathrm {r}$.

From Sect. 3, for the considered deformation we have ${\tilde{W}}(\lambda ,\lambda _z,\tau _{11},\tau _{33})$, which becomes

$$\begin{aligned} {\tilde{W}}= & {} \frac{1}{2}\mu (\lambda ^2+\lambda _z^2+\lambda ^{-2}\lambda _z^{-2}-3)+\frac{1}{2}[(\lambda ^2-1)\tau _{11}+(\lambda ^{-2}\lambda _z^{-2}-1)\tau _{33}]\nonumber \\&\quad +\frac{1}{4}\kappa [(\lambda ^2-1)\tau _{11}+(\lambda ^{-2}\lambda _z^{-2}-1)\tau _{33}]^2, \end{aligned}$$

(67)

and the stress differences (25) become

$$\begin{aligned} \sigma _{11}-\sigma _{33}= & {} \mu (\lambda ^2-\lambda ^{-2}\lambda _z^{-2})+\lambda ^2\tau _{11}-\lambda ^{-2}\lambda _z^{-2}\tau _{33}+\kappa [(\lambda ^2-1)\tau _{11}+(\lambda ^{-2}\lambda _z^{-2}-1)\tau _{33}](\lambda ^2\tau _{11}-\lambda ^{-2}\lambda _z^{-2}\tau _{33}), \nonumber \\\end{aligned}$$

(68)

$$\begin{aligned} \sigma _{22}-\sigma _{33}= & {} \mu (\lambda _z^2-\lambda ^{-2}\lambda _z^{-2})-\lambda ^{-2}\lambda _z^{-2}\tau _{33} -\kappa [(\lambda ^2-1)\tau _{11}+(\lambda ^{-2}\lambda _z^{-2}-1)\tau _{33}]\lambda ^{-2}\lambda _z^{-2}\tau _{33}. \end{aligned}$$

(69)

Noting that the energy function (67) is inhomogeneous, the total energy per unit length of the tube, denoted ${\mathcal {W}}$, is

$$\begin{aligned} {\mathcal {W}}=2\pi \int _A^B {\tilde{W}}R\,\,\mathrm {d}R, \end{aligned}$$

(70)

and this can be obtained explicitly on substitution from (67), use of (64), (65), (20)$_1$ and $\lambda =r/R$ for fixed $\lambda _z$ and given material constants. The resulting expressions are quite lengthy and not therefore included here. For the case $\kappa =0$, Fig. 2a shows example plots of the total energy ${\mathcal {W}}$ divided by $2\pi \mu$, denoted $\bar{{\mathcal {W}}}$, for four values of the dimensionless residual stress parameter ${\bar{\nu }}=\nu A^2/\mu$ with $\lambda _z=1$ and $B/A=1.25$. Thus, the total energy is positive, although for some R and $\lambda$ the local energy (67) can be slightly negative.

For $\kappa > 0$ the additional term is positive and the energy is greater than for the $\kappa =0$ case. In dimensionless form ${\bar{\kappa }}=\kappa \mu$. This is illustrated in Fig. 2b for ${\bar{\kappa }}=0.5$ for four values of ${\bar{\nu }}$. In this case the local energy (67) is positive for all $\lambda$ except for a very small negative value near $\lambda =1$. Example plots of the pressure from Eq. (28) for the energy function (67) with $\lambda _z=1$ using (64) and (65) are shown in Fig. 3.

Fig. 2

Plots of the scaled total energy $\bar{{\mathcal {W}}}={\mathcal {W}}/(2\pi \mu )$ from (70) versus $\lambda$ with $\lambda _z=1$: a $\kappa =0$ for the following values of ${\bar{\nu }}=\nu A^2/\mu$: 5 (blue); 20 (green); 40 (black); 60 (red); b ${\bar{\kappa }}=0.5$ with the following values of ${\bar{\nu }}$: 1 (red); 10 (blue); 20 (green); 40 (black)

Fig. 3

Representative plots of the dimensionless pressure $P^*=P/\mu$ versus ${\bar{a}}$ based on the formula (28) for the energy function (67) with $\lambda _z=1$, $B/A=1.2$ and the following values of ${\bar{\nu }}$ and ${\bar{\kappa }}$: ${\bar{\nu }}=5,{\bar{\kappa }}=0$ (green); ${\bar{\nu }}=6,{\bar{\kappa }}=0.6$ (blue): ${\bar{\nu }}=7,{\bar{\kappa }}=0.8$ (black); ${\bar{\nu }}=8,{\bar{\kappa }}=1$ (red)

5.2 The elasticity tensor and strong ellipticity

For the strain-energy function (66), we obtain, by specializing the general expressions given in [5],

$$\begin{aligned} {\mathcal {A}}_{0piqj}=\mu B_{pq}\delta _{ij}+\varSigma _{pq}\delta _{ij}+\kappa (I_5-\hbox {tr }\varvec{\tau })\varSigma _{pq}\delta _{ij}+2\kappa \varSigma _{pi}\varSigma _{qj}, \end{aligned}$$

(71)

and, since $\tau _{13}=0$, it follows from (50) and (71) that

$$\begin{aligned} \alpha= & {} \lambda ^2\{\mu +\tau _{11}[1+\kappa (I_5-\hbox {tr }\varvec{\tau })]\},\quad \gamma =\lambda ^{-2}\lambda _z^{-2}\{\mu +\tau _{33}[1+\kappa (I_5-\hbox {tr }\varvec{\tau })]\},\nonumber \\ 2\beta= & {} \alpha +\gamma +2\kappa (\lambda ^2\tau _{11}-\lambda ^{-2}\lambda _z^{-2}\tau _{33})^2. \end{aligned}$$

(72)

These expressions are required in Eq. (61) and the boundary conditions (63). Additionally, in (61), recalling that a prime indicates differentiation with respect to r, we require the expressions

$$\begin{aligned}&R'=\lambda \lambda _z, \quad r\lambda ' =-\lambda (\lambda ^2\lambda _z-1),\quad \tau _{11}'=2\nu [3R-(A+B)]R', \end{aligned}$$

(73)

$$\begin{aligned}&\tau _{33}'=\nu [2R-(A+B)]R',\quad \tau _{33}''=\nu [2R-(A+B)]R''+2\nu (R')^2, \end{aligned}$$

(74)

$$\begin{aligned}&\alpha '=2\lambda \lambda '(\mu +\tau _{11})+\lambda ^2\tau _{11}',\quad \gamma '=-2\lambda ^{-3}\lambda _z^{-2}\lambda '(\mu +\tau _{33})+\lambda ^{-2}\lambda _z^{-2}\tau _{33}', \end{aligned}$$

(75)

$$\begin{aligned}&\gamma ''=2\lambda ^{-4}\lambda _z^{-2}[3(\lambda ')^2-\lambda \lambda ''](\mu +\tau _{33})-4\lambda ^{-3}\lambda _z^{-2}\lambda '\tau _{33}'+\lambda ^{-2}\lambda _z^{-2}\tau _{33}''. \end{aligned}$$

(76)

Explicit forms of some of these expressions are fairly lengthy and not listed here but are easily obtained from (72)–(74).

The strong ellipticity condition imposes restrictions on the material response (see, for example, [5]). In general the strong ellipticity condition can be written

$$\begin{aligned} {\mathcal {A}}_{0piqj}n_pn_qm_im_j>0, \end{aligned}$$

(77)

where $m_i$ and $n_i,\,i=1,2,3$, are the components of non-zero vectors $\mathbf {m},\mathbf {n}$ satisfying the incompressibility condition $\mathbf {m}\cdot \mathbf {n}=0$. For $\mathbf {m}$ and $\mathbf {n}$ restricted to the 1, 3 ($\theta ,r$) plane we take $\mathbf {n}=(n_1,0,n_3), \mathbf {m}=(m_1,0,m_3)=(n_3,0,-n_1)$. This yields

$$\begin{aligned} \alpha n_1^4+2\beta n_1^2n_3^2+\gamma n_3^4>0 \end{aligned}$$

(78)

for all non-zero $n_1,n_3$. This requires $\alpha >0$ and $\gamma >0$, and for the expressions given in (72) it follows that $\beta >0$ (note that more generally the inequality $\beta > -\sqrt{\alpha \gamma }$ would be required [13], but is automatically satisfied here).

6 Numerical solution

In order to solve Eq. (61) we form the system of first-order equations

$$\begin{aligned} \mathbf {y}'=\varvec{{\mathcal {M}}}\mathbf {y} \end{aligned}$$

(79)

with dependent variables $\mathbf {y}=(y_1,y_2,y_3,y_4)$, where $y_1=f_n,y_2=y_1',y_3=y_2',y_4=y_3'$, the matrix $\varvec{{\mathcal {M}}}$ being given by

$$\begin{aligned} \varvec{{\mathcal {M}}}=\left[ \begin{array}{cccc}0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1\\ c_1&{}c_2&{}c_3&{}c_4\end{array}\right] \end{aligned}$$

(80)

with

$$\begin{aligned} c_1= & {} -n^2(r^2\gamma ''+r\gamma '-\gamma +2r\beta '-2\beta -\alpha +\alpha n^2)/(\gamma r^4), \end{aligned}$$

(81)

$$\begin{aligned} c_2= & {} [r^2\gamma ''+r\gamma '-\gamma +2n^2(r\beta '-\beta )]/(\gamma r^3), \end{aligned}$$

(82)

$$\begin{aligned} c_3= & {} -(r^2\gamma ''+r\gamma '-\gamma -2n^2\beta )/(\gamma r^2), \end{aligned}$$

(83)

$$\begin{aligned} c_4= & {} -2(r\gamma '+\gamma )/(\gamma r). \end{aligned}$$

(84)

The corresponding boundary conditions (62) and (63) become

$$\begin{aligned} \varvec{{\mathcal {B}}}\mathbf {y}=\mathbf {0}\quad \text{ on }\quad r=a,b, \end{aligned}$$

(85)

where the $2\times 4$ matrix $\varvec{{\mathcal {B}}}$ is

$$\begin{aligned} \varvec{{\mathcal {B}}}=\left[ \begin{array}{cccc}n^2&{} \quad -r &{}\quad r^2&{} \quad 0\\ (2\beta +\gamma )n^2 &{}\quad -(2\beta +\gamma )n^2r &{} \quad 0&{} \quad \gamma r^3 \end{array}\right] . \end{aligned}$$

(86)

6.1 Non-dimensionalization

For the numerical treatment it is convenient to introduce the non-dimensionalizations defined by

$$\begin{aligned}&{\bar{B}}=B/A,\quad {\bar{R}}=R/A,\quad {\bar{r}}=r/A,\quad {\bar{a}}=a/A,\quad {\bar{b}}=b/A, \end{aligned}$$

(87)

$$\begin{aligned}&{\bar{\nu }}=\nu A^2/\mu ,\quad {\bar{\kappa }}=\kappa \mu ,\quad {\bar{\tau }}_{11}=\tau _{11}/\mu ,\quad {\bar{\tau }}_{33}=\tau _{33}/\mu ,\quad {\bar{\alpha }}=\alpha /\mu ,\quad {\bar{\beta }}=\beta /\mu ,\quad {\bar{\gamma }}=\gamma /\mu . \end{aligned}$$

(88)

Note that ${\bar{\nu }}$ and ${\bar{\kappa }}$ were introduced earlier but are included here for completeness. The dimensionless forms of the required derivatives are

$$\begin{aligned} {\bar{\tau }}_{11}'=A\tau _{11}'/\mu ,\quad {\bar{\tau }}_{33}'=A\tau _{33}'/\mu ,\quad {\bar{\alpha }}'=A\alpha '/\mu ,\quad {\bar{\gamma }}'=A\gamma '/\mu ,\quad {\bar{\gamma }}''=A^2\gamma ''/\mu , \end{aligned}$$

(89)

where the prime attached to a quantity with an overbar denotes a derivative with respect to ${\bar{r}}$.

Equation (79) is then written in the dimensionless form

$$\begin{aligned} {\bar{\mathbf {y}}}'=\varvec{\bar{{\mathcal {M}}}}{\bar{\mathbf {y}}}, \end{aligned}$$

(90)

where the components of ${\bar{\mathbf {y}}}$ are given by ${\bar{y}}_1=y_1,{\bar{y}}_2=Ay_2,{\bar{y}}_3=A^2y_3,{\bar{y}}_4=A^3y_4$,

$$\begin{aligned} \varvec{\mathcal {{\bar{M}}}}=\left[ \begin{array}{cccc}0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ {\bar{c}}_1&{}\quad {\bar{c}}_2&{}\quad {\bar{c}}_3&{}\quad {\bar{c}}_4\end{array}\right] , \end{aligned}$$

(91)

and

$$\begin{aligned} {\bar{c}}_1=A^4 c_1,\quad {\bar{c}}_2=A^3 c_2, \quad {\bar{c}}_3=A^2 c_3,\quad {\bar{c}}_4=A c_4. \end{aligned}$$

(92)

In dimensionless form the boundary conditions (93) become

$$\begin{aligned} \varvec{\bar{{\mathcal {B}}}}{\bar{\mathbf {y}}}=\mathbf {0}\quad \text{ on }\ {\bar{r}}={\bar{a}},{\bar{b}}, \end{aligned}$$

(93)

where

$$\begin{aligned} \varvec{\bar{{\mathcal {B}}}}=\left[ \begin{array}{cccc}n^2&{}\quad -{\bar{r}}&{}\quad {\bar{r}}^2&{}\quad 0\\ (2{\bar{\beta }}+{\bar{\gamma }})n^2&{}\quad -(2{\bar{\beta }}+{\bar{\gamma }})n^2{\bar{r}}&{}\quad 0&{}\quad {\bar{\gamma }} {\bar{r}}^3 \end{array}\right] . \end{aligned}$$

(94)

The coefficients in (92) have the forms

$$\begin{aligned} {\bar{c}}_1= & {} -n^2 ({\bar{r}}^2{\bar{\gamma }}''+{\bar{r}}{\bar{\gamma }}'-{\bar{\gamma }}+2{\bar{r}}{\bar{\beta }}'-2{\bar{\beta }}-{\bar{\alpha }}+{\bar{\alpha }}n^2)/({\bar{\gamma }}{\bar{r}}^4) , \end{aligned}$$

(95)

$$\begin{aligned} {\bar{c}}_2= & {} [{\bar{r}}^2{\bar{\gamma }}''+{\bar{r}}{\bar{\gamma }}'-{\bar{\gamma }}+2n^2({\bar{r}}{\bar{\beta }}'-{\bar{\beta }})]/({\bar{\gamma }}{\bar{r}}^3), \end{aligned}$$

(96)

$$\begin{aligned} {\bar{c}}_3= & {} - ({\bar{r}}^2{\bar{\gamma }}''+{\bar{r}}{\bar{\gamma }}'-{\bar{\gamma }}-2n^2{\bar{\beta }})/({\bar{\gamma }}{\bar{r}}^2), \end{aligned}$$

(97)

$$\begin{aligned} {\bar{c}}_4= & {} -2 ({\bar{r}}{\bar{\gamma }}'+{\bar{\gamma }})/({\bar{\gamma }}{\bar{r}}). \end{aligned}$$

(98)

6.2 Restrictions from strong ellipticity

From Sect. 5.2 and (72), the requirement $\alpha >0$ in dimensionless form yields

$$\begin{aligned}&1+{\bar{\nu }} [3{\bar{R}}^2-2({\bar{B}}+1) {\bar{R}}+{\bar{B}}]+{\bar{\kappa }}{\bar{\nu }}^2 [3{\bar{R}}^2-2({\bar{B}}+1) {\bar{R}}+{\bar{B}}]^2(\lambda ^2-1)\nonumber \\&\qquad \quad +\,{\bar{\kappa }}{\bar{\nu }}^2 [3{\bar{R}}^2-2({\bar{B}}+1) {\bar{R}}+{\bar{B}}] [{\bar{R}}^2-({\bar{B}}+1) {\bar{R}}+{\bar{B}}](\lambda ^{-2}\lambda _z^{-2}-1)>0, \end{aligned}$$

(99)

and $\gamma >0$ entails

$$\begin{aligned}&1+{\bar{\nu }} [{\bar{R}}^2-({\bar{B}}+1) {\bar{R}}+{\bar{B}}]+{\bar{\kappa }}{\bar{\nu }}^2 [3{\bar{R}}^2-2({\bar{B}}+1) {\bar{R}}+{\bar{B}}][{\bar{R}}^2-({\bar{B}}+1) {\bar{R}}+{\bar{B}}](\lambda ^2-1)\nonumber \\&\qquad \quad +\,{\bar{\kappa }}{\bar{\nu }}^2 [{\bar{R}}^2-({\bar{B}}+1) {\bar{R}}+{\bar{B}}]^2(\lambda ^{-2}\lambda _z^{-2}-1)>0. \end{aligned}$$

(100)

In each case the inequalities should be satisfied for all ${\bar{R}}\in [1,{\bar{B}}]$ and govern the allowed ranges of values of ${\bar{\nu }},\lambda ,\lambda _z$. For $\kappa =0$ these are independent of the deformation and reduce to

$$\begin{aligned} -1/[{\bar{B}}({\bar{B}}-1)]<{\bar{\nu }}< {\left\{ \begin{array}{ll} 1/({\bar{B}}-1)&{} \text{ if } \ {\bar{B}}\le 2,\\ 3/({\bar{B}}^2-{\bar{B}}+1)&{} \text{ if }\ {\bar{B}}\ge 2,\end{array}\right. } \end{aligned}$$

(101)

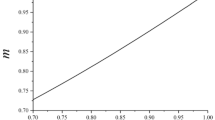
which restricts significantly the allowable values of ${\bar{\nu }}$. For ${\bar{B}}=1.2$, for example, this gives $-25/6<{\bar{\nu }}<5$, and the restrictions become tighter as ${\bar{B}}$ increases, as Fig. 4 shows. Note that the upper condition on the right-hand side of (101) was omitted from equation (62) in [2].

Fig. 4

Plot of ${\bar{\nu }}$ versus ${\bar{B}}$ for the case $\kappa =0$ based on the strong ellipticity restrictions (101)

When $\kappa \ne 0$ the restrictions are different and depend on the deformation. Figure 5 provides example plots of ${\bar{\nu }}$ versus ${\bar{a}}$ (the circumferential stretch on the inner boundary) showing the (shaded) regions where the strong ellipticity condition is satisfied (i.e. $\alpha>0,\gamma >0$). In particular, the representative plots are for $\lambda _z=1$ and ${\bar{B}}=1.2$ for several values of ${\bar{\kappa }}$. Each value of ${\bar{R}}\in [1,1.2]$ yields a different region, and in each case the region shown is that for which strong ellipticity holds for all ${\bar{R}}\in [1,1.2]$. The character of the results is similar for other values of ${\bar{B}}$. Thus, in some cases, the quadratic term in the energy function increases the ranges of values of ${\bar{\nu }}$ and ${\bar{a}}$ for which strong ellipticity holds compared with the case $\kappa =0$, while in other cases the ranges of allowable values of ${\bar{\nu }}$ of ${\bar{a}}$ are reduced. As ${\bar{\kappa }}$ increases the area of the region where strong ellipticity holds becomes smaller and smaller.

Fig. 5

Plots of ${\bar{\nu }}$ versus ${\bar{a}}$ for the fixed value $\lambda _z=1$ with ${\bar{B}}=1.2$ for which the strong ellipticity conditions $\alpha >0$ and $\gamma >0$ are satisfied (within the shaded regions), for the following values of ${\bar{\kappa }}$: a 0.1; b 0.5; c 1; d 5. Subject to ${\bar{a}}\in [0.1,3]$, outside these regions either $\alpha <0$ or $\gamma <0$, or both

The analogues of the case ${\bar{B}}=1.2$ in Fig. 5b for ${\bar{B}}=1.1,1.5$ are shown in Fig. 6. As is the case with $\kappa =0$ (Fig. 4), the region where strong ellipticity holds becomes smaller as ${\bar{B}}$ increases.

Fig. 6

Plots of ${\bar{\nu }}$ versus ${\bar{a}}$ for the fixed value $\lambda _z=1$ with ${\bar{\kappa }}=0.5$ for which the strong ellipticity conditions $\alpha >0$ and $\gamma >0$ are satisfied (within the shaded regions): a ${\bar{B}}=1.1$; b ${\bar{B}}=1.5$. Subject to ${\bar{a}}\in [0.1,3]$, outside these regions either $\alpha <0$ or $\gamma <0$, or both

6.3 Results

The aim now is to determine the numerical solution of the system of equations and boundary conditions (61)–(63) for $f_n(r)$, $n=2, 3, ...$, for different combinations of ${\bar{\nu }}$, ${\bar{B}}$ and ${\bar{a}}$. Note that $n=1$ is not included since this corresponds to a rigid rotation, with $f_1=cr$ for constant c and $u=c\cos \theta ,v=-c\sin \theta$. The dependence of ${\bar{\nu }}$ on ${\bar{a}}$ for given values of ${\bar{B}}$ at the point of onset of bifurcation is determined for different mode numbers, applied (internal or external) pressure (as measured by the dimensionless internal radius ${\bar{a}}$) and fixed axial stretch (exemplified by $\lambda _z=1$). The system is solved for the dimensionless forms (90) with (93) using the routine NDSolve in Mathematica [14].

The results are illustrated for the model (66), first of all with $\kappa =0$, in Fig. 7, for $\lambda _z=1$, where the curves of ${\bar{\nu }}$ versus ${\bar{a}}$ for which bifurcation is possible are plotted for a series of values of the mode number n and for each of ${\bar{B}}=1.1,1.2,1.5$ separately. Results for other values of $\lambda _z\,(>1)$ are very similar and not shown separately. For example, with $\lambda _z=1.5$ the curves are essentially just shifted to the left with minor numerical differences. With reference to the inequalities (101) the limits imposed by strong ellipticity are shown as horizontal red lines in Fig. 7. The valid region in $({\bar{a}},{\bar{\nu }})$ space is between the lines in each case.

As can be seen from Fig. 7 most of the bifurcation curves in the strongly elliptic region are where ${\bar{a}}<1$, i.e. when there is no internal pressure, which is consistent with the situation where there is no residual stress discussed in [10]. However, it can be seen from Fig.  7a, b that there is a small range of negative values of ${\bar{\nu }}$ where bifurcation can occur for ${\bar{a}}>1$, at least for mode number $n=2$. This is not the case in Fig. 7c. In the domain ${\bar{a}}<1$, corresponding to external pressure, and subject to strong ellipticity, as ${\bar{a}}$ is reduced from 1 the $n=2$ mode occurs first, followed by $n=3, 4, ...$ in sequence until there is some interchange of priorities for higher modes. This is of minor theoretical interest since the mode $n=2$ dominates. Note, in particular, with reference to Fig. 7a, b, that within the strongly elliptic region bifurcation may arise for an unloaded cylinder, i.e. when ${\bar{a}}=1$, for limited mode numbers. In the region ${\bar{a}}>1$ and outside the strongly elliptic domain, bifurcation is possible for higher-order mode numbers, depending on the value of the residual stress parameter ${\bar{\nu }}$. To avoid overcrowding, each panel of Fig. 7 shows a representative selection of curves for a limited set of mode numbers n.

Fig. 7

Plot of ${\bar{\nu }}$ versus ${\bar{a}}$ for $\kappa =0$ with $\lambda _z=1$ and the following values of ${\bar{B}}$: a 1.1, b 1.2, c 1.5, for a selection of mode numbers n in each case, indicated by the adjacent numerical value. The region of strong ellipticity lies between the two horizontal red lines. (Color figure online)

Figure 8 illustrates the corresponding results for the model (66) for a non-zero value of ${\bar{\kappa }}$, exemplified by ${\bar{\kappa }}=0.5$, again for ${\bar{B}}=1.1,1.2,1.5$. There are significant similarities with Fig. 7 and this is also the case for larger values of ${\bar{\kappa }}$ (not shown). One difference is that the strong ellipticity domain depends on ${\bar{a}}$ and spreads into a larger area where ${\bar{a}}>1.2$, as shown in more detail in Figs. 5b and 6 (for ${\bar{\kappa }}=0.5$), the pressure then being internal. When ${\bar{a}}=1$ (the unloaded case), the situation is different from that for $\kappa =0$ as no bifurcation curves arise. Higher modes can occur within the strongly elliptic region for ${\bar{a}}$ greater than approximately 1.2, but these are not shown. The area of the strongly elliptic domain decreases as ${\bar{B}}$ increases, as with the case $\kappa =0$.

Fig. 8

Plot of ${\bar{\nu }}$ versus ${\bar{a}}$ for ${\bar{\kappa }}=0.5$ with $\lambda _z=1$ and the following values of ${\bar{B}}$: a 1.1; b 1.2; c 1.5, for a selection of mode numbers n in each case, indicated by the adjacent numerical value. The region of strong ellipticity lies between the two red curves. (Color figure online)

6.4 Concluding remarks

The influence of residual stress on the incremental response and bifurcation of a circular cylindrical tube subject to axial extension and internal or external pressure has been investigated. Incremental deformations superimposed on the cylindrical configuration have been restricted to the planar cross section of the tube, i.e. independent of the axial coordinate z. Results have been presented for an unstretched tube ($\lambda _z=1$) only as results for $\lambda _z>1$ are qualitatively similar, while those for $\lambda _z<1$ require consideration of possible buckling modes (axisymmetric or asymmetric) that depend on z. The results are described for a prototype model of elasticity that incorporates residual stress, and they quantify the dependence of the dimensionless residual stress parameter ${\bar{\nu }}$ on the dimensionless internal radius ${\bar{a}}$ of the tube, which provides a measure of the internal or external pressure, for different tube thickness ratios ${\bar{B}}$ and selected bifurcation mode numbers n. Restrictions imposed by the strong ellipticity condition form a framework for the interpretation of the results. In particular, limits on the range of the allowable residual stress magnitude are determined.

It has been found that, with limited exceptions, it is the case that bifurcation can only occur when the pressure is external, and lower mode numbers have priority, as is the case for the situation without the presence of residual stress [10], where it was shown that bifurcation under internal pressure was excluded. In particular, mode $n=2$ occurs first as the deflation of the tube proceeds from the point where the internal radius is at its initial value (${\bar{a}}=1$). For the considered model, higher modes, i.e. for n greater that about 48, can in principle arise within the strongly elliptic domain, but these are of minor interest and can occur only for small values of ${\bar{\nu }}$. It is worth noting in passing that for very large values of $n\rightarrow \infty$ the only solution of the governing equations is the trivial solution $f_n(r)\rightarrow 0$.

For the special case in which the tube is unloaded ($\lambda _z=1$ and ${\bar{a}}=1$) bifurcation (wrinkling) solutions were obtained for a different model from that adopted here and illustrated in the paper by Ciarletta et al. [7]. We have also obtained solutions for their model and found results which are very similar to those in Figs. 7 and 8.

In a subsequent paper attention will be devoted to axisymmetric and asymmetric modes of bifurcation.