Abstract
It is known that the behavior of the Mitchell order substantially changes at the level of rank-to-rank extenders, as it ceases to be well-founded. While the possible partial order structure of the Mitchell order below rank-to-rank extenders is considered to be well understood, little is known about the structure in the ill-founded case. The purpose of the paper is to make a first step in understanding this case, by studying the extent to which the Mitchell order can be ill-founded. Our main results are (i) in the presence of a rank-to-rank extender there is a transitive Mitchell order decreasing sequence of extenders of any countable length, and (ii) there is no such sequence of length \(\omega _1\).
Similar content being viewed by others
1 Introduction
Extenders are combinatorial objects which play a fundamental role in capturing the strength of various large cardinal axioms, and specifically in capturing the strength of elementary embeddings. Given an elementary embedding \(j : V \rightarrow M\) with critical point \(\kappa \), and an ordinal \(\lambda > \kappa \), the \((\kappa ,\lambda )\)-extender E derived from j is a system of ultrafilters \(E = (E_a \mid a \in [\lambda ]^{<\omega })\), where each \(E_a\) is given by
where \(\xi \ge \kappa \) is the least ordinal such that \(\lambda \le j(\xi )\). For \(a \in [\lambda ]^{<\omega }\), \(\mu _a\) denotes the least \(\mu \) such that \(a \subseteq j(\mu )\). Suppose that \(a \subseteq b\) are elements of \([\lambda ]^{<\omega }\), where \(|b| = n\) and \(I \subseteq n\) is the set of indices (given by the canonical order on \(\lambda \)) for which \(b \upharpoonright I = a\). We note that the map \(\pi _{b,a} : [\mu _b]^{|b|} \rightarrow [\mu _a]^{|a|}\) given by \(\pi _{b,a}(x) = x\upharpoonright I\) satifies that for every \(X \in E_a\), \(\pi _{b,a}^{-1}(X) \in E_b\). Each ultrafilter \(E_a\) is \(\kappa \)-complete, and the system of ultrafilters naturally gives rise to a canonical system of ultrapowers \({\text {Ult}}(V,E_a)\). The manner we derived each \(E_a\) from j implies that \({\text {Ult}}(V,E_a)\) is isomorphic to the subclass \(X_a\) of M given by \(X_a = \{ j(f)(a) \mid f : [\mu _a]^{|a|} \rightarrow V\}\). The functions \(\pi _{b,a}\) allow us to form a natural direct limit of the system of ultrapowers, denoted by \({\text {Ult}}(V,E)\), which is isomorphic to the subclass \(X_E = \bigcup _{a \in [\lambda ]^{<\omega }} X_a\) of M. We denote the transitive collapse of \({\text {Ult}}(V,E)\) (which is the same as the transitive collapse of \(X_E\)) and the resulting ultrapower embedding by \(i_E : V \rightarrow M_E\). It follows from the description of \(X_E\) that if the original embedding \(j : V \rightarrow M\) is \(\lambda \)-strong (i.e., \(V_\lambda \subseteq M\)) then \(V_\lambda \subseteq M_E\). In that sense, we see that the ultrapower of V by the extender E captures the strength of \(j : V \rightarrow M\) up to \(\lambda \). The properties of an extender \(E = (E_a, \pi _{b,a} \mid a \subseteq b \in [\lambda ]^{<\omega })\) as a system of ultrafilters with suitable connecting maps can be formulated directly, without the need of an ambient embedding \(j : V \rightarrow M\). We refer the reader to [9, Section 26] for an extensive introduction to the theory of extenders.
A fundamental notion in the study of extenders is the one of the Mitchell order.
Definition 1.1
Let \(E,E'\) be two extenders. We write \(E \triangleleft E'\) if E is represented in the (well-founded) ultrapower of V by \(E'\).
The Mitchell order \(\triangleleft \) was introduced by Mitchell in [10] to construct canonical inner models with many measurable cardinals. The Mitchell order, which was initially introduced as an ordering on normal measures, has been extended to extenders and plays a significant role in inner model theory. As a prominent notion in the theory of large cardinals, the study of the Mitchell order and its structure has expanded in recent decades. The behaviour of the Mitchell order on extenders depends on the type of extenders in consideration and naturally becomes more complicated when restricted to stronger types of extenders. A fundamental dividing line in the behaviour of the Mitchell order is its well-foundedness: Mitchell [11] has shown that \(\triangleleft \) is well-founded when restricted to normal measures. The question of the well-foundedness of \(\triangleleft \) was further studied by Steel [13], and Neeman [12], who showed that it fails exactly at the level of rank-to-rank extenders.
Definition 1.2
Let E be an extender. We say E is a rank-to-rank extender iff assuming \(\lambda > {\text {crit}} (E)\) is least such that \(i_E(\lambda ) = \lambda \), then \(V_\lambda \subseteq M_E\).
Due to their similarity with embeddings \(j : V \rightarrow M\) with \(V_{\lambda +2} \subseteq M\), which have been shown by Kunen to be inconsistent with ZFC, the large cardinal strength witnessed by rank-to-rank extenders is considered to be located near the top of the large cardinal hierarchy. More precisely, rank-to-rank extenders naturally arise from the large cardinal axiom I2.
The known dividing line of well-foundedness naturally breaks the question of the general possible behaviour into two (i) which well-founded partial orderings can be isomorphic to the Mitchell order on measures/extenders below the rank-to-rank level? and (ii) which ill-founded partial orderings can be isomorphic to the Mitchell order on a set of rank-to-rank extenders?Footnote 1
Concerning question (i), the possible structure of the Mitchell order on normal measures has been extensively studied in [1,2,3,4,5, 11, 14]. It has been shown in [2] that it is consistent for every well-founded partial ordering to be isomorphic to the restriction of \(\triangleleft \) to the set of normal measures on some measurable cardinal \(\kappa \) (the exact consistency strength of this property has not been discovered).
In this work, we make a first step towards expanding the study of the Mitchell order in the ill-founded case, and address question (ii). Specifically, we focus on the extent to which the well-foundedness of the Mitchell order fails on rank-to-rank extenders, by considering possible ordertypes of infinite decreasing chains in \(\triangleleft \). The main results of this paper are the following two theorems.
Theorem 1.3
Assume there exists a rank-to-rank extender E. Then for every countable ordinal \(\gamma \) there is a sequence of rank-to-rank extenders of length \(\gamma \), \((E_\alpha \mid \alpha < \gamma )\), on which the Mitchell order is transitive and strictly decreasing.
Theorem 1.4
There is no \(\omega _1\)-sequence of extenders which is strictly decreasing and transitive in the Mitchell order.
Our presentation of the proof of Theorem 1.4 goes through a proof of a weak version of Steel’s conjecture, which addresses transitive \(\omega \)-sequences of extenders.Footnote 2 This presentation replaces a previous ad-hoc proof. The authors would like to thank Grigor Sargsyan for pointing out the connection with Steel’s conjecture, which led to the current concise proof of Theorem 1.4. The (full) conjecture was recently proved by Goldberg ( [7]) building on his remarkable study of the internal relation.
2 Basic definitions and observations
For notational clarity it will be sometimes convenient for us to use the notation \(\overline{{\text {Ult}}}(V,E)\) for \(M_E\), the transitive collapse of \({\text {Ult}}(V,E)\). For an extender E in a transitive class N, write \(M_E^N\) for the transitive collapse of \({\text {Ult}}(N,E)\) and \(i_E^N : M \rightarrow M_E^N\) for the corresponding ultrapower embedding. For a rank-to-rank extender E we write \(\lambda ^E\) for the least \(\lambda > {\text {crit}} (E)\) such that \(i_E(\lambda ) = \lambda \). Moreover, we write \(\kappa ^E_0 = {\text {crit}} (E)\) and \(\kappa ^E_{n+1} = i_E(\kappa ^E_n)\) for \(n < \omega \), and call \((\kappa ^E_n \mid n < \omega )\) the critical sequence of E. For any rank-to-rank extender E, \(\lambda ^E = \sup _{n<\omega } \kappa ^E_n = {\text {lh}} (E)\).
For every \(n < \omega \) let \(E\upharpoonright \kappa _n^E\) be the cutback of E to the measures \(E_a\), \(a \in [\kappa _n^E]^{<\omega }\). We have that \(M_E = \bigcup _n X_n\) where
By taking \(f = {\text {id}}\), it is clear that \(\kappa _n^E \subseteq X_n\). Let \(N_n\) denote the transitive collapse of \(X_n\) for each \(n<\omega \). We have that \(N_n\) is isomorphic to \(M_{E \upharpoonright \kappa _n^E}\). Moreover, for each \(n < \omega \), \(N_{n+1}\) contains \(V_{\kappa _{n+1}^E}\) and in particular \(i_E``\kappa _n^E \in N_{n+1}\). It follows from a standard argument that \({}^{\kappa _n^E}N_{n+1} \subseteq N_{n+1}\). As the critical point of the inverse of the collapse map \(N_{n+1} \rightarrow X_{n+1}\) is \(>\kappa _n^E\), this implies \({}^{\kappa _n^E}X_{n+1} \subseteq X_{n+1}\).
The following observations will be useful in comparing extenders in different ultrapowers.
Lemma 2.1
Assume that \(N = \bigcup _{n<\omega } X_n\) is an increasing union of classes \(X_n\), N is transitive, and there exists a sequence of cardinals \(\langle \kappa _n \mid n < \omega \rangle \), such that \({}^{\kappa _n} X_{n+1} \subseteq X_{n+1}\) for all \(n < \omega \). Let \(E \in N\) be a rank-to-rank extender of height \({\text {lh}} (E) = \lambda = \bigcup _n \kappa _n\).
-
(1)
For every \(a \in [\lambda ]^{<\omega }\) and \(f : [\mu _a]^{|a|} \rightarrow N\) a function in V, there exists a function \(f_N \in N\) such that \(\{ \nu \in [\mu _a]^{|a|} \mid f(\nu ) = f_N(\nu )\} \in E_a\).
-
(2)
Let \(i_E : V \rightarrow M_E\) and \(i^N_E : N \rightarrow M_E^N\) be the ultrapower embeddings by E of V and N, respectively. For every set \(x \in N\), \(i_E(x) = i^N_E(x)\).
Proof
-
(1)
As \(N = \bigcup _n X_n\) is an increasing union, and \(E_a\) is \(\sigma \)-complete, there exists some n such that the set \(A_n = \{ \nu \in [\mu _a]^{|a|} \mid f(\nu ) \in X_n\}\) belongs to \(E_a\) and \(\mu _a < \kappa _n^E\). Since \(X_{n+1}\) is closed under \(\kappa _n^E\)-sequences, it follows that \(f\upharpoonright A_n : [\mu _a]^{|a|} \rightarrow X_n\) belongs to \(X_{n+1} \in N\). The claim follows.
-
(2)
Let \(\pi : {\text {Ult}}(V,E) \rightarrow M_E\) and \(\pi ^N : {\text {Ult}}(N,E) \rightarrow M_E^N\) denote the transitive collapse embeddings. We have that in fact for any \([a,f]_E\) and \([a,f_N]_E\) for \(a \in [\lambda ]^{<\omega }\), \(f : [\mu _a]^{|a|} \rightarrow x\) in V and \(f_N : [\mu _a]^{|a|} \rightarrow x\) in N with \(\{ \nu \in [\mu _a]^{|a|} \mid f(\nu ) = f_N(\nu )\} \in E_a\),
$$\begin{aligned} \pi ([a,f]_E) = \pi ^M([a,f_N]_E). \end{aligned}$$This follows from a straightforward induction on the rank of \([a,f]_E\) using that for any \([b,g]_E \in [a,f]_E\), g takes values in N, as N is transitive and we may assume that \(g \in N\) by the first part of the lemma. Now this implies \(i_E(x) = i^N_E(x)\).
\(\square \)
Lemma 2.2
Suppose \(E_2,E_1,E_0\) are three rank-to-rank extenders of the same length \(\lambda = \lambda ^{E_i}\), \(i = 0,1,2\), such that \(E_2\) is Mitchell order below \(E_1\), and both \(E_2,E_1\) are Mitchell order below \(E_0\). Then \(M_{E_0}\) also witnesses that \(E_2\) is Mitchell order below \(E_1\).
Proof
The fact \(E_2 \triangleleft E_1\) means that \(E_2\) is represented in the V-ultrapower by \(E_1\), by a function f and a generator a of \(E_1\). Take \(k < \omega \) such that \(a \in [\kappa _{k+1}^{E_1}]^{<\omega }\).
The reason it is not immediate that the relation \(E_2 \lhd E_1\) also holds in \(M_{E_0}\) is that the function f need not belong to \(M_{E_0}\). However, we can argue that \(M_{E_0}\) does see some witnessing function \(f^*\) by using approximations. Assume without loss of generality that \(f(\nu )\) is an extender for every \(\nu \in {\text {dom}}(f)\). Indeed, notice that for every \(n < \omega \), the function \(f_n\) with \({\text {dom}}(f_n) = {\text {dom}}(f)\) such that for every \(\nu \), \(f_n(\nu )\) is the restriction of the extender \(f(\nu )\) to length \(\kappa _{n}^{E_1}\). Clearly, \([a,f_n]^V_{E_1}\) represents the cut back of \(E_2\) to length \(\kappa _{n+1}^{E_1}\). Moreover, \(f_n\) belongs to \(M_{E_0}\) for every \(n < \omega \) since \(V_\lambda \subseteq M_{E_0}\).
Let \(\mathcal {E}(\eta )\) for some ordinal \(\eta \) denote the set of all \((\kappa ,\eta )\)-extenders. Now, working in \(M_{E_0}\) and utilizing the fact that both \(E_1,E_2\) belong to the model, we consider the tree T of all pairs \((\tau ,n)\) such that \(\tau : [\kappa _k^{E_1}]^{|a|} \rightarrow \mathcal {E}(\kappa _n^{E_1})\) satisfies that \([a,\tau ]^{M_{E_0}}_{E_1}\) represents the restriction of \(E_2\) to length \(\kappa _{n+1}^{E_1}\). The tree order \(<_T\) is given by \((\tau ,n) <_T (\tau ',n')\) if \(n < n'\) and \(\tau '(\nu )\) extends \(\tau (\nu )\) for all \(\nu \in {\text {dom}}(\tau )\). It is clear that a cofinal branch in T translates to a function F for which \([a,F]_{E_1}\) represents \(E_2\), and vice versa. Therefore \(f \in V\) witnesses that T has a cofinal branch in V, and thus, by absoluteness of well-foundedness, it must also have one in \(M_{E_0}\). \(\square \)
Steel gives in [13] a folklore example that for rank-to-rank extenders the Mitchell order need not be well-founded. We recall it here because some of the ideas will be used later.
Proposition 2.3
(Folklore) Let E be a rank-to-rank extender. Then there is a strictly decreasing sequence of length \(\omega \) in the Mitchell order on which \(\triangleleft \) is transitive.
Proof
Consider the following sequence of rank-to-rank extenders \((E_n :n < \omega )\). Let \(E_0 = E\) and \(E_{n+1} = i_{E_n}(E_n)\), where \(i_{E_n} :V \rightarrow M_{E_n}\) is the canonical embedding associated to \(E_n\). Then it is straightforward to check that every \(E_n\) is a V-extender and \(E_{n+1} \lhd E_n\) for all \(n<\omega \).
Claim 1
The Mitchell order is transitive on \((E_n :n < \omega )\).
Proof
Let \(n<\omega \). We show that \(E_{n+2} \lhd E_{n}\), the rest follows analogously. By construction \(E_{n+2} \in M_{E_{n+1}}\) and \(E_{n+1} \in M_{E_n}\), we argue that \(E_{n+2} \in M_{E_n}\). Argue that \(i_{E_{n+1}}(E_{n+1}) = i_{E_{n+1}}^{M_{E_n}}(E_{n+1})\), where \(i_{E_{n+1}}^{M_{E_n}} :M_{E_n} \rightarrow M_{E_{n+1}}^{M_{E_n}}\). By Lemma 2.1, applied to \(E = E_{n+1}\) and \(M_{E_n}\), we see that \(E_{n+2} = i_{E_{n+1}}(E_{n+1}) = i_{E_{n+1}}^{M_{E_n}}(E_{n+1})\), and hence \(E_{n+2} \in M_{E_n}\). \(\square \)
\(\square \)
3 Countable decreasing sequences in the Mitchell order
In this section we prove Theorem 1.3 and show that there can be strictly decreasing transitive sequences in the Mitchell order of any countable length.
Before we turn to the proof, we would like to emphasize why we cannot simply extend the construction in Proposition 2.3 to obtain decreasing sequences of extenders in the Mitchell order of arbitrary (countable) length. Let E be a rank-to-rank extender and let \((E_n :n < \omega )\) be the corresponding sequence of extenders constructed in the proof of Proposition 2.3. The critical points of the extenders \(E_n\) are strictly increasing with supremum \(\lambda ^E\). A natural next extender to consider is the image of E under the direct limit embedding obtained by successively applying the \(E_n\)’s (internally, i.e., \(E_1\) is applied to \(M_{E_0}\) and so forth). This, however, does not work outright as this direct limit embedding moves \(\kappa \), the critical point of E, to \(\lambda \). Instead, we will construct a sequence of extenders \((E_n^\prime :n < \omega )\) such that the direct limit embedding j obtained by successively applying the \(E^{\prime }_{n}\) ’s (again, internally) has critical point strictly above \(\kappa \). Now j(E) is a rank-to-rank extender with critical point \(\kappa \) and \(\lambda ^{j(E)} = \lambda \). Moreover, \(j(E) \triangleleft E_n^\prime \) for all \(n<\omega \), so if we let \(E_\omega ^\prime = j(E)\), \((E_n^\prime :n \le \omega )\) is a decreasing sequence of length \(\omega +1\) in the Mitchell order. The proof of Theorem 1.3 elaborates on this idea.
Proof of Theorem 1.3
Let E be a rank-to-rank extender with critical sequence \((\kappa _n \mid n<\omega )\) and \(\lambda ^E = \lambda \). In what follows, all extenders will have the same length \(\lambda \). We start by introducing some notation for sequences of extenders as constructed in the proof of Proposition 2.3. For a rank-to-rank extender F, write \(S^1(F) = i_{F}(F)\) and \(S^{n+1}(F) = i_{S^n(F)}(S^n(F))\). Now, the decreasing sequences in the Mitchell order we construct will be of the following form.
Definition 3.1
Let \(\mathbf {E} = (E_\alpha \mid \alpha < \gamma )\) be a sequence of rank-to-rank extenders. Then we say that \(\mathbf {E}\) is guided by an internal iteration iff there are well-founded models \((M_\alpha \mid \alpha \le \gamma )\), \((M_\alpha ^* \mid \alpha \le \gamma )\) with \(M_0 = M_0^* = V\) and elementary embeddings \(j^*_{\alpha ,\beta } :M_\alpha ^* \rightarrow M_\beta ^*\) for all \(\alpha < \beta \le \gamma \) such that
-
(1)
\(E_{\alpha +1} = S^n(E_\alpha )\) for some \(n \ge 1\) and all \(\alpha +1 < \gamma \),
-
(2)
\(M_{\nu } = M_\nu ^*\) for all limit ordinals \(\nu \le \gamma \) is given as the direct limit of the directed system \(\langle M_\alpha ^* ,j^*_{\alpha ,\beta } \mid \alpha \le \beta < \nu \rangle \).
-
(3)
\(M_{\alpha +1} = M_{E_\alpha }\) and \(M_{\alpha +1}^*\) is the transitive collapse of \({\text {Ult}}(M_\alpha ^*,E_\alpha )\). For notational convenience (see the diagram below) we will use \(M_{\alpha +1}^N\) to denote the transitive collapse of \({\text {Ult}}(N, E_\alpha )\), therefore \(M_{\alpha +1}^* = M_{\alpha +1}^{M_\alpha ^*}\).
-
(4)
for all limit ordinals \(\nu < \gamma \), \(E_\nu = j^*_{0,\nu }(E_0)\) and \({\text {Ult}}(V, E_\nu )\) is well-founded, and
-
(5)
the following diagram commutes and all maps in the diagram are given by internal ultrapowers.

The term guided by an internal iteration refers to the fact that the iteration \(\langle M_\alpha ^*, j^*_{\alpha ,\beta } \mid \alpha \le \beta < \gamma \rangle \) is internal, as shown by the next claim.
Claim 1
For each \(\alpha < \gamma \), \(E_\alpha \in M_\alpha ^*\).
Proof
The claim is immediate when \(\alpha \) is a limit ordinal or \(\alpha = 0\). Let \(\alpha = \beta +1\) be a successor ordinal and assume inductively that \(E_\beta \in M_\beta ^*\).
Suppose first that \(E_\alpha =S^n(E_\beta )\) for \(n = 1\). Then \(E_\alpha = i_{E_\beta }(E_\beta )\), where \(i_{E_\beta } :V \rightarrow M_{E_\beta }\) is the V-ultrapower embedding given by \(E_\beta \). Recall that \(M^*_\alpha = M^{M_\beta ^*}_{E_\beta }\). By applying Lemma 2.1 to \(M = M_\beta ^*\) and \(E = E_\beta \), we conclude that \(E_\alpha = i_{E_\beta }^{M_\beta ^*}(E_\beta ) \in M^{M_\beta ^*}_{E_\beta } = M_\alpha ^*\). We now know that \(S^1(E_\beta ) \in M_{\alpha }^*\), and so for \(n >1\), we can further compute \((S^{n-1})^{M_\alpha ^*}(S^1(E_\beta ))\) inside \(M_{\alpha }^*\), which by applying Lemma 2.1\((n-1)\) consecutive times, results in
\(\square \)
Before we prove the existence of sequences of extenders guided by internal iterations, we show an abstract claim which will allow us to extend any such sequence by one further element. This is shown as in the proof of Theorem 2.2 in [13] (where this particular argument is attributed to Martin). We sketch the proof here for the reader’s convenience.
Claim 2
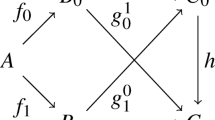
Let \(N \cong {\text {Ult}}(V,E')\) for some rank-to-rank extender \(E'\) of length \(\lambda \), and \(E \lhd F\) rank-to-rank extenders of length \(\lambda \) with \(E,F \in N\). Then the following diagram commutes and all maps are given by internal ultrapowers.

Proof
First, we note that \(\overline{{\text {Ult}}}(M_E^N, i_E(F)) = i_E(M_F^N)\), where we consider \(M_F^N\) as a class of N. Second, we assume \(E \triangleleft F\) in V, which by Lemma 2.2 implies that \(E \triangleleft F\) in N as well, i.e., \(E \in M_F^N\). We can therefore form the internal ultrapower of \(M_F^N\) by E. Let \(i_E^{M_F^N} :M_F^N \rightarrow \overline{{\text {Ult}}}(M_F^N,E)\) be the resulting ultrapower embedding. Finally, we have that every \(x \in i_E(M_F^N)\) can be identified with equivalence classes \([a,f]_E\), where \(a \in [\lambda ]^{<\omega }\) and \(f :[\mu _a]^{|a|} \rightarrow M_F^N\), and by Lemma 2.1, \([a,f]_{E} = [a,g]_E\) for some function \(g \in M_F^N\). It follows that \(i_E(M_F^N)\) identifies with the internal ultrapower \({\text {Ult}}(M_F^N,E)\), and \(i_E \upharpoonright M_F^N\) with \(i_E^{M_F^N}\). \(\square \)
Next, we argue that sequences as in Definition 3.1 are in fact as desired.
Claim 3
If a sequence \({\mathbf {E}} = (E_\alpha \mid \alpha < \gamma )\) of extenders is guided by an internal iteration, the embeddings in the diagram witness that \(E_\beta \lhd E_\alpha \) for all \(\alpha< \beta < \gamma \). In particular, \({\mathbf {E}}\) is a decreasing transitive sequence in \(\triangleleft \).
Proof
Given a finite ordinal \(n < \omega \) and a countable ordinal \(\alpha > n\), Claim 1 implies that \(E_\alpha \lhd E_n\). This is since all maps in the diagram witnessing that \(\mathbf {E}\) is guided by an internal iteration, are internal ultrapowers, and therefore there are internal iterations from \(M_{n+1}\) (the ultrapower of V by \(E_n\)) to \(M_{n+1}^*\) (i.e., vertical maps), and from \(M_{n+1}^*\) to \(M_\alpha ^*\), from which \(E_\alpha \) is taken.
More generally, given countable ordinals \(\beta < \alpha \), we see that \(E_\alpha \lhd E_\beta \) by moving first to the last limit ordinal \(\eta \le \beta \) (i.e., \(\beta = \eta +n\) for some \(n < \omega \)), and apply the proof of Claim 2 to show that the following diagram commutes and its top row is given by an internal iteration of \(M_{E_{\eta +n}} = \overline{{\text {Ult}}}(V, E_{\eta +n})\).

The extenders used to obtain the bottom row of the diagram are \(E_0\), \(E_1\), \(E_2\), \(\dots \), while the extenders used to obtain the top row of the diagram are \(i_{E_{\eta +n}}(E_0), i^{M^*_1}_{E_{\eta +n}}(E_1),i^{M_2^*}_{E_{\eta +n}}(E_2), \dots \).
Finally, we get from \(M_\eta ^*\) to \(M_{\eta +n}^*\) using the same argument described above, for \(n < \alpha \). This suffices to show that \(E_\alpha \lhd E_{\eta +n} = E_\beta \). \(\square \)
We now turn to proving the following claim, which immediately yields the theorem.
Claim 4
Assume there is a rank-to-rank extendere E. For every countable ordinal \(\gamma < \omega _1\) and an ordinal \(\kappa < \lambda = \lambda ^E\), there is a sequence of rank-to-rank extenders \(\mathbf {E} = (E_\alpha \mid \alpha \le \gamma )\) which is guided by an internal iteration, such that the induced embedding \(j^*_{0,\gamma } :V \rightarrow M_\gamma ^*\) satisfies \(\kappa< {\text {crit}} (j^*_{0,\gamma }) < \lambda \) and \(j^*_{0,\gamma }(\lambda ) = \lambda \).
Proof
We prove the claim by induction on \(\gamma < \omega _1\). There is nothing to show for \(\gamma = 0\). Suppose that \(\gamma = 1\). Let \(\kappa < \lambda \) be arbitrary and fix some \(n<\omega \) such that \(\kappa < \kappa _n^E\). Then \(E_0 = S^{n+1}(E)\) and \(E_1 = S^1(E_0)\) giving rise to \(j^*_{0,1} :V \rightarrow M_{E_{0}}\) are as desired.
Now, suppose \(\gamma = \alpha + 1\) and the claim holds for \(\alpha \) witnessed by \((E_\nu \mid \nu \le \alpha )\). Let n be such that \(\kappa < \kappa _n^{E_\alpha }\), the n-th element of \(E_\alpha \)’s critical sequence, and \(E_{\alpha +1} = S^n(E_\alpha )\). Then \({\text {crit}} (E_{\alpha +1}) \ge \kappa _n^\alpha \) and hence, using that inductively \({\text {crit}} (j^*_{0, \alpha }) > \kappa \), we have \({\text {crit}} (j^*_{0, \alpha +1}) > \kappa \). Using Claim 2 the extended sequence \((E_\nu \mid \nu \le \alpha +1)\) is as desired.
Finally, suppose \(\gamma < \omega _1\) is a limit ordinal and fix an increasing sequence \(\langle \alpha _n \mid n < \omega \rangle \), cofinal in \(\gamma \), with \(\alpha _0 = 0\). We also fix a well-ordering \(<_w\) of \(H_{\lambda ^+}\) in V.
By the inductive hypothesis applied to \(\alpha _1\), there is a sequence \({\mathbf {E}}^0\) of rank-to-rank extenders which is guided by an internal iteration and an elementary embedding \(j^*_{0,\alpha _1} :V \rightarrow M_{\alpha _1}^*\) with critical point \(\nu _0 > \kappa \) and \(j^*_{0,\alpha _1}(\lambda )=\lambda \). We pick \(\mathbf {E}^0\) to be the minimal such sequence with respect to \(<_w\). By elementarity of \(j^*_{0,\alpha _1}\), we can apply the inductive hypothesis again inside \(M_{\alpha _1}^*\) to get a sequence \(\mathbf {E}^1\) of rank-to-rank extenders which is guided by an internal iteration and an elementary embedding \(j^*_{\alpha _1,\alpha _2} :M_{\alpha _1}^* \rightarrow M_{\alpha _2}^*\) with critical point \(\nu _1 > j^*_{0,\alpha _1}(\nu _0)\) and \(j^*_{\alpha _1,\alpha _2}(\lambda )=\lambda \). We take \(\mathbf {E}^1\) to be the minimal such sequence in \(M_{\alpha _1}^*\), with respect to \(j_{0,\alpha _1}^*(<_w)\). Repeating this procedure yields a sequence \(((\mathbf {E}^n, j^*_{\alpha _n,\alpha _{n+1}}) \mid n < \omega )\) of sequences of extenders together with elementary embeddings.
Let \((E_\alpha \mid \alpha < \gamma )\) be the concatenation of the sequences \(\mathbf {E}^n\), \(n < \omega \). The choice of \(\mathbf {E}^{n+1}\) to be minimal in \(M_{\alpha _{n}}^*\) with respect to the well ordering \(j_{0,\alpha _n}^*(<_w)\) guarantees that the sequence \(\langle \mathbf {E}^m \mid m > n\rangle \) belongs to \(M_{\alpha _n}^*\), and thus also the tail of the iteration \(\langle M_{\alpha }^*, j^*_{\alpha ,\beta } \mid \alpha _n< \alpha \le \beta < \gamma \rangle \). Note that \({\text {crit}} (j^*_{0,\gamma }) > \kappa \) since \({\text {crit}} (j^*_{\alpha _n, \alpha _{n+1}}) > \kappa \) for all \(n < \omega \). Let \(j^*_{0,\gamma } :V \rightarrow M_\gamma ^* = M_\gamma \) be the direct limit embedding of the system.
The reflecting a minimal counterexample argument used to show that internal iterations by normal ultrafilters are well-founded (see e.g., [8, Theorem 19.7] for normal ultrafilters or [6, Proposition 5.8] for rank-to-rank extenders), can also be used to show that \(M_\gamma \) is well-founded.
Subclaim 1
\(j^*_{0,\gamma }(\lambda ) = \lambda \).
Proof
Suppose not. Then there is some \(\eta < \lambda \) such that \(j(\eta ) \ge \lambda \). But for every \(\eta < \lambda \), there is by choice of the embeddings \(j^*_{\alpha _n,\alpha _{n+1}}\) some \(n < \omega \) such that \(\nu _n = {\text {crit}} (j^*_{\alpha _n,\alpha _{n+1}}) > \eta \), i.e. \(j^*_{\alpha _n,\gamma }(\eta ) = \eta \). \(\square \)
Moreover, it is clear from the construction that, letting \(E_\gamma = j^*_{0,\gamma }(E)\), the resulting sequence \((E_\alpha \mid \alpha \le \gamma )\) of rank-to-rank extenders is guided by an internal iteration. The only condition that needs a small argument is the following.
Subclaim 2
\({\text {Ult}}(V,E_\gamma )\) is well-founded.
Proof
As \(M_\gamma \) is well-founded and \(E_\gamma \) is an extender in \(M_\gamma \), \({\text {Ult}}(M_\gamma , E_\gamma )\) is well-founded. We prove the subclaim by defining an elementary embedding \(\pi :{\text {Ult}}(V,E_\gamma ) \rightarrow {\text {Ult}}(M_\gamma , E_\gamma )\) as follows. For \([a,f]_{E_\gamma }^V \in {\text {Ult}}(V,E_\gamma )\), let
\(\pi \) is well-defined since for \(a \in [\lambda ]^{<\omega }\), \(\mu _a < \lambda \). Therefore, \(j^*_{0,\gamma } \upharpoonright [\mu _a]^{|a|} \in V_\lambda \subseteq M_\gamma \). In addition, \(j^*_{0,\gamma }(f) \circ j^*_{0,\gamma } = j^*_{0,\gamma } \circ f\), so \(\pi \) is elementary. \(\square \)
\(\square \)
This finishes the proof of Theorem 1.3. \(\square \)
4 A bound on the length of decreasing sequences in the Mitchell order
Steel proved in [13] that in a Mitchell order decreasing sequence of rank-to-rank extenders, the extenders cannot all have the same critical point. He conjectured the following stronger statement.
Conjecture 1 (Steel) Suppose that \((E_m \mid m < \omega )\) is a sequence of rank-to-rank extenders which is strictly decreasing in \(\lhd \). Let \(\lambda \) be the unique ordinal such that \(\lambda = \lambda ^{E_m}\) for all sufficiently large m. Then \(\sup _{m < \omega } {\text {crit}} (E_m) = \lambda \).
Theorem 4.1 below establishes Steel’s Conjecture for the special case that the Mitchell order is transitive on the sequence \((E_m \mid m < \omega )\).
Theorem 4.1
Suppose that \((E_m \mid m < \omega )\) is a sequence of rank-to-rank extenders, which is strictly decreasing and transitive in \(\lhd \). Let \(\lambda \) be the unique ordinal such that \(\lambda = \lambda ^{E_m}\) for all sufficiently large m. Then \(\sup _{m < \omega } {\text {crit}} (E_m) = \lambda \).
Proof
Suppose otherwise, and let \(\gamma _0\) be the minimal ordinal for which there exists a \(\lhd \)-decreasing and transitive sequence \(\mathbf {E} = (E_m \mid m < \omega )\) such that \(\gamma _0 = \sup _{m<\omega } \kappa _0^{E_m}< \lambda ^{\mathbf {E}} = \sup _{m<\omega } \lambda ^{E_m}\). We assume without loss of generality that \(\lambda ^{\mathbf {E}} = \lambda ^{E_m}\) for all \(m < \omega \). Let \(n < \omega \) be the integer for which \(\kappa _n^{E_0} \le \gamma _0 < \kappa _{n+1}^{E_0}\). We move to the ultrapower \(M_{E_0}\). By our assumption, \(E_m \in M_{E_0}\) for every \(m > 0\), and by Lemma 2.2, \(M_{E_0}\) sees that \(E_m\) is Mitchell order below \(E_k\) for every \(0< k< m < \omega \). Since \(M_{E_0}\) is not closed under \(\omega \)-sequences of its elements (in V) the sequence \((E_m \mid 1 \le m < \omega )\) need not belong to \(M_{E_0}\). Nevertheless, we may define in \(M_{E_0}\) the tree \(T^*\) of all finite sequences of rank-to-rank extenders \((E_m^* \mid m < N)\), which are strictly Mitchell order decreasing, transitive, have length \(\lambda ^{\mathbf {E}}\), and satisfy \(\gamma _0 \ge \max _{m<N} \kappa _0^{E_m^*}\). The sequence \((E_m \mid 1 \le m < \omega )\) witnesses that \(T^*\) has a cofinal branch in V. So by absoluteness of well-foundedness there is a cofinal branch in \(M_{E_0 }\) as well. We can now reflect this from \(M_{E_0}\) back to V. Using the fact that \(\kappa _n^{E_0} \le \gamma _0 < \kappa _{n+1}^{E_0} = i_{E_0}(\kappa _n^{E_0})\), we conclude that in V, there exists some \(\gamma _{-1} < \kappa _n^{E_0} \le \gamma _0\), and a sequence \(\mathbf {E}^*= (E_m^* \mid m < \omega )\) of rank-to-rank extenders which is strictly \(\lhd \)-decreasing and transitive such that \(\sup _{m<\omega } \kappa _0^{E_m^*} \le \gamma _{-1} < \lambda ^{\mathbf {E}^*}\). This is a contradiction to the minimality of \(\gamma _0\). \(\square \)
Now we can obtain Theorem 1.4 as a corollary.
Proof of Theorem 1.4
Suppose otherwise. Let \(\mathbf {E} = (E_\alpha \mid \alpha < \omega _1)\) be a sequence of extenders which is strictly decreasing and transitive in the Mitchell order. We may assume that all \(E_\alpha \) are rank-to-rank extenders and that there exists some \(\lambda ^{\mathbf {E}}\) such that \(\lambda ^{E_\alpha } = \lambda ^{\mathbf {E}}\) for all \(\alpha < \omega _1\). In particular, \({\text {cf}}(\lambda ^{\mathbf {E}}) = \omega \) and we may choose a cofinal sequence \((\rho _n \mid n < \omega )\) in \(\lambda ^{\mathbf {E}}\). By a straightforward pressing down argument, we can find an uncountable set \(I \subseteq \omega _1\) and some \(n^* < \omega \) such that \(\kappa _0^{E_\alpha } < \rho _{n^*}\) for all \(\alpha \in I\). Taking \((\alpha _n \mid n < \omega )\) to be the first \(\omega \) many ordinals of I, it follows that \((E_{\alpha _n} \mid n < \omega )\) is strictly decreasing and transitive in the Mitchell order, with \(\sup _{n<\omega } \kappa _0^{E_{\alpha _n}} \le \rho _{n^*} < \lambda ^{\mathbf {E}}\). This contradicts Theorem 4.1. \(\square \)
5 Questions
After studying the length of the Mitchell order for rank-to-rank extenders, a natural question that arises is about the structure this order can have.
Question 5.1
Suppose there is a rank-to-rank extender. Can the tree order on the infinite binary tree \(2^{<\omega }\) be realized by a Mitchell order?
We can even ask the following more general question.
Question 5.2
Suppose there is a rank-to-rank extender. Can any tree order on \(\omega \) be realized by a Mitchell order?
Notes
Beyond the possible (partial) ordering structure of the Mitchell order, the investigation can be further extended to non-transitive relations, as the Mitchell order need not be transitive in general (see [13]). This direction is not developed in this paper.
See Sect. 4 for a formulation of Steel’s conjecture.
References
Baldwin, S.: The \(\triangleleft \)-ordering on normal ultrafilters. J. Symb. Logic 50(4), 936–952 (1985)
Ben-Neria, O.: The structure of the Mitchell order-II. Ann. Pure Appl. Logic 166(12), 1407–1432 (2015)
Ben-Neria, O.: The structure of the Mitchell order-I. Isr. J. Math. 214(2), 945–982 (2016)
Cummings, J.: Possible behaviours for the Mitchell ordering. Ann. Pure Appl. Logic 65(2), 107–123 (1993)
Cummings, J.: Possible behaviours for the Mitchell ordering II. J. Symb. Logic 59(4), 1196–1209 (1994). (12)
Dimonte, V.: I0 and rank-into-rank axioms. Bollettino dell’Unione Matematica Italiana 11(3), 315–361 (2018)
Gabriel, G.: The internal relation. Submitted, see arXiv:1810.04290
Jech, T.J.: Set Theory. Springer Monographs in Mathematics. Springer (2003)
Kanamori, A.: The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings. Springer Monographs in Mathematics. Springer (2008)
Mitchell, W.J.: Sets constructible from sequences of ultrafilters. J. Sym. Logic 39(1), 57–66 (1974)
Mitchell, W.J.: Sets constructed from sequences of measures: revisited. J. Sym. Logic 48(3), 600–609 (1983)
Neeman, I.: The Mitchell order below rank-to-rank. J. Symb. Logic 69(4), 1143–1162 (2004)
Steel, J.R.: The well-foundedness of the Mitchell order. J. Symb. Logic 58(3), 931–940 (1993)
Witzany, J.: Any behaviour of the Mitchell ordering of normal measures is possible. Proc. Am. Math. Soc. 124(1), 291–297 (1996)
Acknowledgements
This research was initiated whilst the second-listed author visited the first-listed author at the Hebrew University of Jerusalem in February 2019. She wishes to thank the Hebrew University of Jerusalem for its hospitality. The first-listed author was partially supported by the Israel Science Foundation Grant 1832/19. The second-listed author gratefully acknowledges funding from L’ORÉAL Austria, in collaboration with the Austrian UNESCO Commission and in cooperation with the Austrian Academy of Sciences - Fellowship Determinacy and Large Cardinals. The authors would like to thank Grigor Sargsyan and the referee for many valuable comments and suggestions, which greatly improved the presentation of the paper.
Funding
Open Access funding provided by University of Vienna.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ben-Neria, O., Müller, S. Infinite decreasing chains in the Mitchell order. Arch. Math. Logic 60, 771–781 (2021). https://doi.org/10.1007/s00153-021-00762-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00153-021-00762-x