1 Introduction

Stress gradient elasticity is a generalised continuum theory that has been proposed very recently as a counterpart of Mindlin’s well-known strain gradient elasticity model [14, 25, 26]. Stress gradient elasticity should neither be confused with the Aifantis gradient elasticity model which is a special case of isotropic strain gradient elasticity [13, 29], nor with models based on Laplacians of stress and strain which have been recently recognised as special cases of micromorphic elasticity [7, 10, 16]. The essential feature of the stress gradient continuum is that each material point is endowed with a third rank tensor of additional degrees of freedom complementing its usual displacement. These new degrees of freedom, called microdisplacements in [14], are conjugate to the stress gradient tensor in the generalised work of internal forces. The microstructural origin of the microdisplacements was recently highlighted based on an original homogenisation approach in [18]. In contrast, the strain gradient model is solely based on the classic displacement degrees of freedom.

The resolution of boundary value problems for stress gradient elastic bodies requires the definition of suitable boundary conditions. A debate commenced after the discovery of the stress gradient theory on the possibility of prescribing all stress components at a boundary which emerges in the stress gradient framework [27]. This is in contrast to classic Cauchy mechanics where the traction vector only can be controlled. Proper extensions of Korn’s inequality show that the set of boundary conditions defined in [14] leads to a well-posed boundary value problem, with associated existence and uniqueness theorems [31]. They confirm the possibility of applying extended Neumann conditions in the form of fully prescribed stress components at a boundary.

Applications of stress gradient elasticity have been rather limited up to now. They include prediction of size effects in bending with a comparison with strain gradient and micromorphic approaches [28], and particle size effects in composite materials [33]. The latter reference contains extensions of the Eshelby and Hashin-Shtrikman homogenisation approaches to heterogeneous stress gradient media in a simplified case of isotropic elasticity.

The objective of the present work is to propose the first finite element implementation of stress gradient linearised elasticity theory. The choice of appropriate nodal degrees of freedom and matrix form of the variational formulation of the boundary value problem will be discussed. Validation examples with respect to analytical solutions are provided for simple tension and torsion in a simplified case of isotropic stress gradient elasticity. Free surface boundary conditions will be shown to play an essential role in the modification of the stress distributions compared to classic elasticity. The observed size effects with respect to structure size and the intrinsic length scale of the model will be discussed in detail.

In particular, this contribution is organised as follows: after a brief recapitulation of the fundamentals of the stress gradient theory in Sect. 2, a finite element formulation is discussed in detail in Sect. 3. By making use of the latter, representative boundary value problems are studied in Sect. 4. Moreover, analytical solutions are derived for validation purposes. The findings are summarised and concluding remarks are given in Sect. 5.

1.1 Notation

Let \(\varvec{\alpha }\), \(\varvec{\beta }\), \(\varvec{\gamma }\), \(\varvec{\delta }\), \(\varvec{\zeta }\), \(\varvec{\eta }\) denote arbitrary first order tensors, let the standard dyadic product be indicated by \(\varvec{\alpha }\otimes \varvec{\beta }\) and let the standard single tensor contraction be given by \(\varvec{\alpha }\cdot \varvec{\beta }\). With these definitions at hand, double and triple tensor contractions are understood in the sense \(\left[ \varvec{\alpha }\otimes \varvec{\beta }\right] :\left[ \varvec{\gamma }\otimes \varvec{\delta }\right] = \left[ \varvec{\alpha }\cdot \varvec{\gamma }\right] \,\left[ \varvec{\beta }\cdot \varvec{\delta }\right]\,\,{\text{and}}\) \(\left[ \varvec{\alpha }\otimes \varvec{\beta }\otimes \varvec{\gamma }\right] \therefore \left[ \varvec{\delta }\otimes \varvec{\zeta }\otimes \varvec{\eta }\right] = \left[ \varvec{\alpha }\cdot \varvec{\delta }\right] \,\left[ \varvec{\beta }\cdot \varvec{\zeta }\right] \,\left[ \varvec{\gamma }\cdot \varvec{\eta }\right] \). Moreover, the symmetric part of a second order tensor \(\varvec{\varXi }\) is given by

$$\begin{aligned} \left[ \varXi _{ij} \, \varvec{e}_i \otimes \varvec{e}_j\right] ^{{\rm sym}} = \frac{1}{2}\left[ \varXi _{ij} + \varXi _{ji} \right] \, \varvec{e}_i \otimes \varvec{e}_j, \end{aligned}$$
(1)

with \(\varvec{e}_\bullet \) denoting Cartesian basis vectors. In analogy with second order tensors, the additive spherical-deviatoric decomposition of third order tensors \(\varvec{\mathcal {T}}\) that are symmetric with respect to the first two indices is introduced as

$$\begin{aligned} \varvec{\mathcal {T}}= \varvec{\mathcal {T}}^{{\rm sph}}+ \varvec{\mathcal {T}}^{{\rm dev}}, \quad&\varvec{\mathcal {T}}:\varvec{I}= \varvec{\mathcal {T}}^{{\rm sph}}:\varvec{I}, \\ \varvec{\mathcal {T}}^{{\rm dev}}:\varvec{I}= {\varvec{0}}, \quad&\varvec{\mathcal {T}}^{{\rm sph}}\therefore \varvec{\mathcal {T}}^{{\rm dev}}=0. \end{aligned}$$
(2)

In particular, the spherical part of a symmetric third order tensor in a three-dimensional setting is given by

$$\begin{aligned} \varvec{\mathcal {T}}^{{\rm sph}}&= \frac{1}{4}\Big [ \left[ \varvec{\mathcal {T}}:\varvec{I}\right] \otimes \varvec{I}+ \left[ \varvec{\mathcal {T}}:\varvec{I}\right] \overline{\otimes }\,\varvec{I}\Big ] \\&= \frac{1}{4}\left[ \mathcal {T}_{ilm} \, \delta _{lm} \, \delta _{jk} + \mathcal {T}_{jlm} \, \delta _{lm} \, \delta _{ik}\right] \, \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_k \end{aligned}$$
(3)

where the special dyadic product \(\overline{\otimes }\) was used, see also [14]. In addition to the second order identity tensor

$$\begin{aligned} \varvec{I}= \delta _{ij}\, \varvec{e}_i \otimes \varvec{e}_j \end{aligned}$$
(4)

with \(\delta _{ij}\) denoting the Kronecker-delta, the fourth order symmetric identity tensor

$$\begin{aligned} {\mathbf{\mathsf{I}}}^{{\rm sym}}= \frac{1}{2} \left[ \delta _{ik}\,\delta _{jl}\, + \delta _{il}\, \delta _{jk} \right] \, \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_k \otimes \varvec{e}_l, \end{aligned}$$
(5)

the sixth order symmetric identity tensor

$$\begin{aligned} \varvec{\mathcal {I}}^{{\rm sym}}= \mathsf{{I}} ^{{\rm sym}}_{ijpq}\,\delta _{kr} \, \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_k \otimes \varvec{e}_p \, \otimes \varvec{e}_q \otimes \varvec{e}_r, \end{aligned}$$
(6)

and the sixth order symmetric and deviatoric identity tensor

$$\begin{aligned} \varvec{\mathcal {I}}^{{\rm sym,dev}}&=\left[ \mathsf{{I}} ^{{\rm sym}}_{ijpq}\,\delta _{kr} - \frac{1}{4} \left[ \mathsf{{I}} ^{{\rm sym}}_{pqir}\, \delta _{jk} + \mathsf{{I}} ^{{\rm sym}}_{pqjr}\, \delta _{ik} \right] \right] \\&\quad \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_k \otimes \varvec{e}_p \, \otimes \varvec{e}_q \otimes \varvec{e}_r \end{aligned}$$
(7)

with

$$\begin{aligned} \varvec{\mathcal {T}}^{{\rm dev}}&= \varvec{\mathcal {I}}^{{\rm sym,dev}}\therefore \varvec{\mathcal {T}}\\&= \varvec{\mathcal {I}}^{{\rm sym}}\therefore \varvec{\mathcal {T}}- \frac{1}{2}\, {\mathbf{\mathsf{I}}}^{{\rm sym}}\cdot \left[ \varvec{\mathcal {I}}^{{\rm sym}}\therefore \varvec{\mathcal {T}}\right] :\varvec{I}\end{aligned}$$
(8)

are introduced, see also [33]. Furthermore, (right-)gradient and (right-)divergence operators are denoted as \(\nabla \left( \bullet \right) \) and \(\nabla \cdot \left( \bullet \right) \), respectively.

2 Stress gradient theory

The governing equations of the stress gradient theory as derived in [14] based on variational principles and on the method of virtual power will briefly be recapitulated in this section.

At the outset of the theory, a generalised (volume specific) stress energy density function of the form \(w^*\left( \varvec{\sigma }, \varvec{R}\right) \) is postulated which depends on the symmetric small deformation stress tensor \(\varvec{\sigma }\) and on the third order generalised stress tensor \(\varvec{R}\). The associated minimisation problem of the (generalised) complementary energy functional on the domain \(\mathcal {B}\) is moreover subjected to the extended set of static admissibility conditions

$$\begin{aligned} \nabla \cdot \varvec{\sigma }+\rho \,\varvec{f}= {\varvec{0}} \quad \text {on} \,\,\, \mathcal {B}\, , \end{aligned}$$
(9a)
$$\begin{aligned} \varvec{R}-\left[ \nabla \varvec{\sigma }\right] ^{\rm dev}= {\varvec{0}} \quad \text {on} \,\,\, \mathcal {B}\, , \end{aligned}$$
(9b)

with \(\rho \) denoting the mass density and \(\varvec{f}\) the (mass specific) body force density. Based on the symmetry of the stress tensor and on the observation that the volumetric part of the stress gradient is determined by (9a) since

$$\begin{aligned} \left[ \nabla \varvec{\sigma }\right] :\varvec{I}=\left[ \nabla \varvec{\sigma }\right] ^{\rm sph}:\varvec{I}=\nabla \cdot \varvec{\sigma }= -\rho \,\varvec{f}, \end{aligned}$$
(10)

holds, the third order generalised stress tensor \(\varvec{R}\) is assumed to be symmetric on the first two indices and deviatoric. This entails the assumption that the deviatoric part of the stress gradient contributes to the stress energy density function \(w^*\left( \varvec{\sigma }, \varvec{R}\right) \), in addition to the stress tensor.

In order to derive the primal variational formulation of the stress gradient theory, the static admissibility conditions (9a) and (9b) are multiplied by the kinematic field variables \(\delta \varvec{u}\) and \(\delta \varvec{\varPhi }\), respectively. In analogy with \(\varvec{R}\), the third order tensor field \(\delta \varvec{\varPhi }\) is assumed to be symmetric and deviatoric. By integrating the ensuing equations over the domain \(\mathcal {B}\) with boundary \(\partial \mathcal {B}\) and with outward unit normal vector \(\varvec{n}\), and by applying the divergence theorem one arrives at

$$\begin{aligned}&\underbrace{ \int _{\mathcal {B}}\varvec{\sigma }:\left[ \left[ \nabla \delta \varvec{u}\right] ^{\rm sym}+\nabla \cdot \delta \varvec{\varPhi }\right] + \varvec{R}\therefore \delta \varvec{\varPhi }\, {\rm d}v}_{\displaystyle \mathcal {P}^{(i)}\left( \delta \varvec{u}, \delta \varvec{\varPhi }\right) } \\&\quad = \underbrace{ \int _{\mathcal {B}}\quad \rho \,\varvec{f}\cdot \delta \varvec{u}\, {\rm d}v}_{ \displaystyle \mathcal {P}^{(v)}\left( \delta \varvec{u}\right) } + \underbrace{ \int _{\partial \mathcal {B}}\quad \varvec{\sigma }:\left[ \left[ \delta \varvec{u}\otimes \varvec{n}\right] ^{\rm sym}+ \delta \varvec{\varPhi }\cdot \varvec{n}\right] {\rm d}a}_ { \displaystyle \mathcal {P}^{(c)}\left( \delta \varvec{u}, \delta \varvec{\varPhi }\right) } \end{aligned}$$
(11)

Equation (11) can be interpreted as a virtual work balance for the stress gradient theory, with the virtual work of internal forces \(\mathcal {P}^{(i)}\left( \delta \varvec{u}, \delta \varvec{\varPhi }\right) \), the virtual work of volume distributed forces \(\mathcal {P}^{(v)}\left( \delta \varvec{u}\right) \) and with the virtual work of contact forces \(\mathcal {P}^{(c)}\left( \delta \varvec{u}, \delta \varvec{\varPhi }\right) \). With regard to the virtual work of internal forces \(\mathcal {P}^{(i)}\left( \delta \varvec{u}, \delta \varvec{\varPhi }\right) \), energetic dualities are observed between the stresses \(\varvec{\sigma }\) and the generalised strain tensor

$$\begin{aligned} \varvec{e}= \left[ \nabla \varvec{u}\right] ^{\rm sym}+\nabla \cdot \varvec{\varPhi }, \end{aligned}$$
(12)

and between the generalised stress tensor \(\varvec{R}\) and the kinematic variable \(\varvec{\varPhi }\), which is henceforth referred to as the micro-displacement tensor. The latter observation motivates the introduction of a generalised strain energy density function \(w\left( \varvec{e}, \varvec{\varPhi }\right) \) such that

$$\begin{aligned}\varvec{\sigma }= \frac{\partial w\left( \varvec{e}, \varvec{\varPhi }\right) }{\partial \varvec{e}}, \end{aligned}$$
(13a)
$$\begin{aligned}\varvec{R}= \frac{\partial w\left( \varvec{e}, \varvec{\varPhi }\right) }{\partial \varvec{\varPhi }}. \end{aligned}$$
(13b)

The elasticity potentials \(w^*\left( \varvec{\sigma }, \varvec{R}\right) \) and \(w\left( \varvec{e}, \varvec{\varPhi }\right) \) are related to each other by a Legendre(-Fenchel) transform. Moreover, the specific form of the virtual work of contact forces \(\mathcal {P}^{(c)}\left( \delta \varvec{u}, \delta \varvec{\varPhi }\right) \) stipulates Dirichlet-type boundary conditions in terms of the generalised displacements \( \left[ \delta \varvec{u}\otimes \varvec{n}\right] ^{\rm sym}+ \delta \varvec{\varPhi }\cdot \varvec{n}\) and Neumann-type boundary conditions in terms of the complete stress tensor \(\varvec{\sigma }\). A detailed discussion on the boundary conditions of the stress gradient theory is additionally provided in [14].

3 Finite element formulation

This section focuses on the finite element implementation of the stress gradient theory. In particular, a reformulation of the generalised virtual work equation (11) is discussed in Sect. 3.1 and the corresponding discretised weak form is derived in Sect. 3.2.

3.1 A different view on the virtual work equation

The derivation of the finite element implementation of the stress gradient theory is based on a reformulation of the generalised virtual work equation (11) in terms of one primary field variable \(\varvec{\varPsi }\), hereafter referred to as the generalised displacement field. The generalised displacement field is a tensor field of third order that is symmetric with respect to the first two indices and that was first introduced in the existence and uniqueness proofs of the stress gradient theory presented in [31]. It is constructed so that its deviatoric part is identical with the micro-displacement field, i.e.

$$\begin{aligned} \varvec{\varPsi }^{{\rm dev}}= \varvec{\varPhi }, \end{aligned}$$
(14)

whereas its spherical part is defined in terms of the (classic) displacement field, namely,

$$\begin{aligned} \varvec{\varPsi }^{{\rm sph}}= \frac{1}{2} \left[ \varvec{u}\otimes \varvec{I}+ \varvec{u}\,\overline{\otimes }\, \varvec{I}\right] . \end{aligned}$$
(15)

The other way around, the displacement field can conveniently be reconstructed from the generalised displacement field via

$$\begin{aligned} \varvec{u}= \frac{1}{2}\,\varvec{\varPsi }:\varvec{I}= \frac{1}{2}\,\varvec{\varPsi }^{{\rm sph}}:\varvec{I}, \end{aligned}$$
(16)

and it can be observed that

$$\begin{aligned} \left[ \varvec{u}\otimes \varvec{n}\right] ^{\rm sym}= \varvec{\varPsi }^{{\rm sph}}\cdot \varvec{n}, \end{aligned}$$
(17)

holds, see also [31]. By making use of (12) and by invoking relation

$$\begin{aligned} \left[ \nabla \varvec{u}\right] ^{\rm sym}= \nabla \cdot \varvec{\varPsi }^{{\rm sph}}\end{aligned}$$
(18)

one moreover arrives at the representation of the generalised strain tensor in terms of the generalised displacements

$$\begin{aligned} \varvec{e}= \nabla \cdot \varvec{\varPsi }. \end{aligned}$$
(19)

Finally, inserting (14), (16) and (17) into (11) yields the virtual work balance

$$\begin{aligned}&\int _{\mathcal {B}}\varvec{\sigma }:\left[ \nabla \cdot \delta \varvec{\varPsi }\right] + \varvec{R}\therefore \delta \varvec{\varPsi }\, {\rm d}v\\ &\quad =\int _{\mathcal {B}}\rho \,\varvec{f}\cdot \frac{1}{2}\, \delta \varvec{\varPsi }:\varvec{I}\, {\rm d}v+ \int _{\partial \mathcal {B}}\varvec{\sigma }:\delta \varvec{\varPsi }\cdot \varvec{n}\, {\rm d}a, \end{aligned}$$
(20)

which is particularly useful for the finite element implementation, as it implies that either the (components) of the stress tensor or the corresponding normal projections of the generalised displacement field can independently be prescribed. In this sense, the two-field problem in terms of the displacement field \(\varvec{u}\) and the micro-displacement field \(\varvec{\varPhi }\) is reformulated in terms of one primary field quantity, i.e. in terms of the generalised displacement field \(\varvec{\varPsi }\).

3.2 Discretisation

The virtual work balance (20) serves as the basis for the derivation of the discrete weak form of the stress gradient theory. More specifically speaking, the generalised displacement field and the test function \(\varvec{\eta }\) are discretised by using a finite element approach

$$\begin{aligned}\varvec{\varvec{\varPsi }}^{{\rm h}}= \sum _{B=1}^{{\rm n}_{{\rm en}}}N_B \, \varvec{\varPsi }_B \end{aligned}$$
(21a)
$$\begin{aligned}\varvec{\eta }^{{\rm h}}= \sum _{A=1}^{{\rm n}_{{\rm en}}}N_A \, \varvec{\eta }_A \end{aligned}$$
(21b)

with shape functions \(N_\bullet \), nodal values \(\varvec{\varPsi }_\bullet \) and \(\varvec{\eta }_\bullet \), and with \({\rm n}_{{\rm en}}\) denoting the number of element nodes. By approximating the domain \(\mathcal {B}\) with a finite number of elements \({\rm n_{el}}\), by denoting the respective element domains as \(\mathcal {B}^e\) and by making use of the assembly operator

, (20) and (21b) give rise to the discrete vector of internal forces

(22)

to the discrete vector of volume distributed forces

(23)

and to the discrete vector of contact forces

(24)

Following standard procedure, the resulting system of (in general non-linear) equations is brought into a residual-type format \(\varvec{r}^{\rm h}\) and solved for the list of generalised nodal displacements \({\widehat{\varvec{\varPsi }}}\), namely

$$\begin{aligned} \varvec{r}^{\rm h}= \varvec{f}_{{\rm int}}^{\rm h}- \varvec{f}_{{\rm vol}}^{\rm h}- \varvec{f}_{{\rm con}}^{\rm h}, \quad \varDelta \varvec{r}^{\rm h}\, = \frac{{\rm d}\varvec{r}^{\rm h}}{{\rm d}{\widehat{\varvec{\varPsi }}}} \cdot \varDelta {\widehat{\varvec{\varPsi }}}. \end{aligned}$$
(25)

The linear part of the corresponding Taylor-series expansion \(\varDelta \varvec{r}^{\rm h}\) is given in terms of the generalised stiffness matrix

(26)

where dead-loads have been assumed and with \(\bullet ^{\overset{13}{{\rm T}}}\) indicating a transposition with respect to the first and third index.

4 Representative simulation results

After the specification of the material model and of the constitutive equations in Sect. 4.1, representative simulation results are the focus of this section. In particular, a cylindrical bar under tension is studied by using the proposed finite element formulation in Sect. 4.2 and by means of analytical methods in Sect. 4.3. Breaking the rotational symmetry of the tensile problem, the focus is on a rectangular bar under tension in Sect. 4.4 before the torsion problem of a cylindrical bar is eventually studied in Sect. 4.5. Finite element results shown in this section are based on element-wise mean values.

4.1 Material model

Motivated by the theoretical developments of the stress gradient theory presented in [14, 31, 33], a symmetric positive definite quadratic form for the generalised stress energy density function is assumed

$$\begin{aligned} w^*\left( \varvec{\sigma }, \varvec{R}\right) = \frac{1}{2} \, \varvec{\sigma }:{\mathbf{\mathsf{C}}}\,{\text{:}}\,\varvec{\sigma }+ \frac{1}{2}\, \varvec{R}\therefore \varvec{\mathcal {C}}\therefore \varvec{R}, \end{aligned}$$
(27)

with \({\mathbf{\mathsf{C}}}\) and \(\varvec{\mathcal {C}}\) denoting the compliance and the generalised compliance tensor, respectively. By making use of the Legendre(-Fenchel) transform, the corresponding generalised strain energy density function takes the form

$$\begin{aligned} w\left( \varvec{e}, \varvec{\varPhi }\right) = \frac{1}{2} \, \varvec{e}:{\mathbf{\mathsf{E}}}\,{\text{:}}\,\varvec{e}+ \frac{1}{2}\, \varvec{\varPhi }\therefore \varvec{\mathcal {E}}\therefore \varvec{\varPhi }, \end{aligned}$$
(28)

with the stiffness tensor \({\mathbf{\mathsf{E}}}\) and the generalised stiffness tensor \(\varvec{\mathcal {E}}\) defined as

$$\begin{aligned}{\mathbf{\mathsf{E}}}= {\mathbf{\mathsf{C}}}^{-1} \end{aligned}$$
(29a)
$$\begin{aligned}\varvec{\mathcal {E}}= \varvec{\mathcal {C}}^{-1} \end{aligned}$$
(29b)

In the scope of this work, a classic form for the stiffness tensor \({\mathbf{\mathsf{E}}}\) in terms of the Lamé-type constants \(\lambda \) and \(\mu \), namely

$$\begin{aligned} {\mathbf{\mathsf{E}}}=\lambda \, \varvec{I}\otimes \varvec{I}+ 2\,\mu \, {\mathbf{\mathsf{I}}}^{{\rm sym}}, \end{aligned}$$
(30)

is adopted and the generalised stiffness tensor is assumed to take the form

$$\begin{aligned} \varvec{\mathcal {E}}= \frac{\mu }{\ell ^2}\, \varvec{\mathcal {I}}^{{\rm sym,dev}}, \end{aligned}$$
(31)

with \(\ell \) denoting the material length scale parameter. Moreover, the Lamé-type constants are related to the generalised Young’s modulus and to the generalised Poisson’s ratio via

$$\begin{aligned}\lambda = \frac{E\, \nu }{\left[ 1+\nu \right] \, \left[ 1-2\,\nu \right] } \end{aligned}$$
(32a)
$$\begin{aligned}\mu = \frac{E}{2 \,\left[ 1+\nu \right] } \end{aligned}$$
(32b)

With the specific form of the strain energy density function defined by (28)–(31) at hand, the evaluation of (13) yields the specific form of the stress and generalised stress tensor

$$\begin{aligned}\varvec{\sigma }= {\mathbf{\mathsf{E}}}\,{\text{:}}\,\varvec{e} \end{aligned}$$
(33a)
$$\begin{aligned}\varvec{R}= \varvec{\mathcal {E}}\therefore \varvec{\varPhi }\end{aligned}$$
(33b)
Fig. 1
figure 1

Geometric dimensions (in mm) and boundary conditions of the cylindrical bar under tension

Full size image

4.2 Cylindrical bar under tension

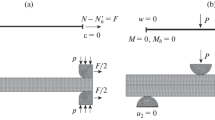
In this section, the tensile problem of a cylindrical bar as depicted in Fig. 1 is studied, with positions and tensor indices referring either to a Cartesian \((x_1, x_2, x_3)\) or to a cylindrical coordinates \((r, \theta , z)\) description. At the left boundary of the bar (\(z={0}\) mm), generalised clamping boundary conditions of the form

$$\begin{aligned} \varvec{\varPsi }\cdot \varvec{n}&= {{\bf 0}}, \\ \left[ \varvec{\varPsi }\cdot \varvec{n}\right] _{ij}&= - \begin{bmatrix} \varPsi _{113} &{} \varPsi _{123} &{} \varPsi _{133} \\ \varPsi _{213} &{} \varPsi _{223} &{} \varPsi _{233} \\ \varPsi _{313} &{} \varPsi _{323} &{} \varPsi _{333} \\ \end{bmatrix} = \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix}, \end{aligned}$$
(34)

are assumed for the generalised displacement field. It is noted that these do, in general, not imply vanishing (classic) displacements since

$$\begin{aligned} \left[ \varvec{u}\right] _{i} = \left[ \frac{1}{2}\varvec{\varPsi }:\varvec{I}\right] _{i}&= \frac{1}{2}\, \begin{bmatrix} \varPsi _{111} + \varPsi _{122} + \varPsi _{133} \\ \varPsi _{211} + \varPsi _{222} + \varPsi _{233} \\ \varPsi _{311} + \varPsi _{322} + \varPsi _{333} \\ \end{bmatrix} \\&= \frac{1}{2}\, \begin{bmatrix} \varPsi _{111} + \varPsi _{122} \\ \varPsi _{211} + \varPsi _{222} \\ \varPsi _{311} + \varPsi _{322} \\ \end{bmatrix}, \end{aligned}$$
(35)

holds. At the right boundary (\(z={100}\) mm), generalised traction boundary conditions of the form

$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=\overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3\otimes \varvec{e}_3, \end{aligned}$$
(36)

with the overbar indicating a prescribed quantity, are applied which result in a total axial force of 660 kN. Moreover, the outer surface of the cylindrical bar (\(r={10}\) mm) is assumed to be stress-free, i.e.

$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=\varvec{\sigma }\otimes \varvec{e}_r={\varvec{0}}. \end{aligned}$$
(37)

In order to study the size-dependent material response, the problem dimensions defined in Fig. 1 are kept fixed and the material length scale parameter \(\ell \) is varied. In particular, the set of material parameters provided in Table 1 is used.

Table 1 Material parameters used in the simulations of the cylindrical bar depicted in Fig. 1
Full size table

The simulation results are based on a finite element discretisation with linear (eight-node) Lagrangian elements, and integrals are evaluated numerically by using a Gaussian quadrature scheme with eight sampling points. Taking into account the rotational symmetry of the problem, the predicted stress distribution in the cross section at \(z={50}\) mm is presented in Fig. 2 with respect to the natural (physical) basis system induced by the cylindrical coordinates.

First, it is observed that the boundary condition (37) causes all coefficients of the stress tensor to approach zero at the boundaries. This is a significant difference compared to the classic Cauchy continuum approach where only the normal projection of the stress tensor can be prescribed and where a constant stress profile \(\sigma _{zz}\approx {2100}\) N/mm\(^{2}\) is expected when an isotropic, linear elastic material response is assumed and when boundary effects are neglected. In contrast, \(\sigma _{zz}\) takes a parabolic profile in the present case, with the extreme value at \(r={0}\) mm and the slope of the profile being functions of the material length scale parameter \(\ell \), see Figs. 2a and 3a. The in-plane coefficients of the stress tensor \(\sigma _{rr}\) and \(\sigma _{zz}\), which would take zero values for a classic Cauchy continuum theory, are depicted in Figs. 2b, c, 3b and c. They show a strong dependence on the material length scale parameter and are observed to be approx. two orders of magnitude smaller than the axial stresses. Due to the vanishing stress boundary condition at \(r={10}\) mm, it is moreover observed that the element-wise mean values of all coefficients of the stress tensor approach zero at the boundary, with the resolution being limited by the finite element discretisation. In addition, the radial displacement as a function of the material length scale parameter is provided in Fig. 2d. The corresponding profile becomes linear for smaller values of the internal length scale.

Fig. 2
figure 2

Finite element solution of the tensile problem depicted in Fig. 1 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\))

Full size image
Fig. 3
figure 3

Stress distribution predicted by finite element calculations of the tensile problem depicted in Fig. 1 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\), \(\ell ={1.0}\) mm)

Full size image

4.3 Comparison of simulation results and analytical solution in the case of vanishing Poisson’s ratio

In order to derive an analytic solution for the boundary value problem depicted in Fig. 1, a class of axisymmetric stress states is considered in the form

$$\begin{aligned} \varvec{\sigma }= \sigma _r(r) \, \varvec{e}_r\otimes \varvec{e}_r+ \sigma _\theta (r) \, \varvec{e}_\theta \otimes \varvec{e}_\theta + \sigma _z(r) \, \varvec{e}_z\otimes \varvec{e}_z, \end{aligned}$$
(38)

where the stress components \(\sigma _r=\sigma _{r\,r}, \sigma _\theta =\sigma _{\theta \theta }\) and \(\sigma _z= \sigma _{zz}\) are unknown functions of \(r\) in the cylindrical coordinate system \((r,\theta ,z)\). Subject to the assumptions of quasi-statics and vanishing body forces, see (9b) and (10), the generalised stress tensor is computed as

$$\begin{aligned} \varvec{R}&= \nabla \varvec{\sigma }= \frac{\partial \varvec{\sigma }}{\partial r}\otimes \varvec{e}_r+ \frac{1}{r}\frac{\partial \varvec{\sigma }}{\partial \theta }\otimes \varvec{e}_\theta + \frac{\partial \varvec{\sigma }}{\partial z}\otimes \varvec{e}_z\\&= \left[ \sigma _r' \, \varvec{e}_r\otimes \varvec{e}_r+ \sigma _\theta ' \, \varvec{e}_\theta \otimes \varvec{e}_\theta + \sigma _z' \, \varvec{e}_z\otimes \varvec{e}_z\right] \otimes \varvec{e}_r\\&\quad+ \frac{\sigma _r-\sigma _\theta }{r} \left[ \varvec{e}_r\otimes \varvec{e}_\theta + \varvec{e}_\theta \otimes \varvec{e}_r\right] \otimes \varvec{e}_\theta \end{aligned}$$
(39)

with primes denoting derivatives with respect to \(r\). By additionally invoking the static balance equation for the active stress components, i.e.

$$\begin{aligned} \sigma _r' + \frac{\sigma _r-\sigma _\theta }{r} = 0, \end{aligned}$$
(40)

the generalised stress tensor can be rewritten as

$$\begin{aligned} \varvec{R} =\sigma _r' \,& \left[ \varvec{e}_r\otimes \varvec{e}_r\otimes \varvec{e}_r-\varvec{e}_r\otimes \varvec{e}_\theta \otimes \varvec{e}_\theta - \varvec{e}_\theta \otimes \varvec{e}_r\otimes \varvec{e}_\theta \right] \\ +\sigma _\theta ' \,\,\,& \, \varvec{e}_\theta \otimes \varvec{e}_\theta \otimes \varvec{e}_r+ \sigma _z' \, \varvec{e}_z\otimes \varvec{e}_z\otimes \varvec{e}_r. \end{aligned}$$
(41)

For the computation of the third order tensor \(\varvec{\varPhi }\) of microdisplacements, it is necessary to evaluate the divergence of the generalised stress tensor

$$\begin{aligned} \nabla \cdot \varvec{R}= &\frac{\partial \varvec{R}}{\partial r}\cdot \varvec{e}_r+ \frac{1}{r} \frac{\partial \varvec{R}}{\partial \theta }\cdot \varvec{e}_\theta + \frac{\partial \varvec{R}}{\partial z}\cdot \varvec{e}_z \\ &= \left[ \sigma _r''+\frac{3\,\sigma _r'}{r}\right] \varvec{e}_r\otimes \varvec{e}_r \\ & + \left[ \sigma _\theta ''+\frac{\sigma _\theta '}{r}-\frac{2\,\sigma _r'}{r}\right] \varvec{e}_\theta \otimes \varvec{e}_\theta \\& + \left[ \sigma _z''+\frac{\sigma _z'}{r}\right] \varvec{e}_z\otimes \varvec{e}_z \end{aligned}$$
(42)

where the equilibrium equation (40) has again been taken into account.

The displacement vector and its gradient are taken in the form

$$\varvec{u}= u_r(r)\, \varvec{e}_r+ u_{z}(z) \, \varvec{e}_z,$$
(43a)
$$\nabla \varvec{u}= u_r' \, \varvec{e}_r\otimes \varvec{e}_r+ \frac{u_r}{r}\,\varvec{e}_\theta \otimes \varvec{e}_\theta + {\frac{\partial u_z}{\partial z}} \, \varvec{e}_z\otimes \varvec{e}_z.$$
(43b)

Under simple tensile/compression loading conditions, the displacement gradient contribution \(\frac{\partial u_z}{\partial z} = {{\bar{\varepsilon }}}\) is prescribed. The generalised strain tensor can now be computed by making use of (12), (29)–(33) and by assuming that \(\ell \) and \(\mu \) are constant in space, i.e.

$$\begin{aligned} \varvec{e}&= \left[ \nabla \varvec{u}\right] ^{\rm sym}+ \nabla \cdot \varvec{\varPhi }= \left[ \nabla \varvec{u}\right] ^{\rm sym}+\ell ^2 \mu ^{-1}\,\nabla \cdot \varvec{R}\\&= \frac{1+\nu }{E} \, \varvec{\sigma }- \frac{\nu }{E}\, {\rm tr}\left( \varvec{\sigma }\right) \, \varvec{I}. \end{aligned}$$
(44)
Fig. 4
figure 4

Finite element vs. analytic solution of the simple tensile problem depicted in Fig. 1 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0\))

Full size image

Combining (42)–(44) leads to the differential system

$$ E\,u_r' +2 \left[ 1+\nu \right] \, \ell ^2 \, \left[ \sigma _r'' +\tfrac{3\,\sigma _r'}{r}\right] = \sigma _r- \nu \left[ \sigma _\theta + \sigma _z\right]$$
(45a)
$$E\, \tfrac{u_r}{r} + 2 \left[ 1+\nu \right] \ell ^2\left[ \sigma _{\theta \theta }'' + \tfrac{\sigma _\theta '}{r} - \tfrac{2\,\sigma _r'}{r}\right] =\sigma _\theta - \nu \left[ \sigma _r + \sigma _z\right]$$
(45b)
$$E\,{{\bar{\varepsilon }}} + 2 \,\left[ 1+\nu \right] \,\ell ^2\left[ \sigma _z''+\frac{\sigma _z'}{r}\right] = \sigma _z- \nu \left[ \sigma _r + \sigma _\theta \right] $$
(45c)

This system must be complemented by the balance relation (40) in order to be solved for the four unknown functions \(u_r,\sigma _r, \sigma _\theta , \sigma _z\). In accordance with Fig. 1, vanishing stress boundary conditions are prescribed at the outer boundary of the cylindrical bar with radius \(r_{{\rm m}}\), i.e.

$$\begin{aligned} \sigma _r(r_{{\rm m}}) = \sigma _\theta (r_{{\rm m}})= \sigma _z(r_{{\rm m}}) = 0. \end{aligned}$$
(46)

It can be shown that the functions \(\sigma _r= \sigma _\theta =0\) are no solutions of the system, with the considered boundary conditions, except in the very special case \(\nu =0\). This is in contrast to simple tension in a cylindrical bar for the Cauchy continuum.

In the particular case \(\nu = 0\) the system simplifies and it is found that \(u_r= 0\), that \(\sigma _r= \sigma _\theta = 0\) and that the axial stress is solution of the ordinary differential equation

$$\sigma _z'' + \frac{1}{r} \,\sigma _z' - \frac{1}{\tilde{\ell }^{2} }\, \sigma _z+ \frac{E}{\tilde{\ell}^{2} } \,{{\bar{\varepsilon }}} = 0\,$$
(47)

with

$$\begin{aligned} \tilde{\ell }=\sqrt{2}\,\ell . \end{aligned}$$
(48)

A particular solution is the classic one \(\sigma _z(r) = E\,{{\bar{\varepsilon }}}\), which, however, does not fulfil the boundary condition of vanishing stresses at \(r= r_{{\rm m}}\). With the scaling \(x=r/\tilde{\ell }\) and with the notation \(y(x) = \sigma _z(\tilde{\ell }\, x)\) being adopted, the homogeneous equation to solve is given by

$$\begin{aligned} x y'' + y' - x y = 0, \end{aligned}$$
(49)

where primes indicate derivatives with respect to x. This is a special case of the modified Bessel’s equation

$$\begin{aligned} x^2 y'' + xy' - \left[ x^2+\alpha ^2\right] \, y = 0 \end{aligned}$$
(50)

with \(\alpha = 0\), see [1]. The solution is given by a linear combination of modified Bessel functions, also denoted as hyperbolic Bessel functions, of the first and second kind: \(I_0(x)\) and \(K_0(x)\). The function \(K_0\) is singular at \(x=0\) and cannot appear in the solution of the considered boundary value problem. Thus, the solution is of the form

$$\begin{aligned}&\sigma _z(r) =y(r/\tilde{\ell }) = C_1\,I_0(r/\tilde{\ell }) + C_2 \\&\text {with}\quad \sigma _z(r=0) = \sigma _0,\quad \sigma _z(r_{{\rm m}}) = 0 \end{aligned}$$
(51)

where \(\sigma _0\) is the stress value at the centre that can be related to the stress value \(E\,{{\bar{\varepsilon }}}=C_2\). Finally, this gives

$$\begin{aligned} C_1 = \frac{-\,\sigma _0}{I_0(r_{{\rm m}}/\tilde{\ell })-1}, \quad C_2 = \sigma _0\, \frac{I_0(r_{{\rm m}}/\tilde{\ell })}{I_0(r_{{\rm m}}/\tilde{\ell })-1} . \end{aligned}$$
(52)

Figure 4 shows the excellent agreement between the analytical and finite element solutions for three different length scales and vanishing Poisson’s ratio. Regarding the analytical solution of the tensile problem given by (51) and (52), it is moreover observed that the solution converges to the one of a classic Cauchy continuum for \(\tilde{\ell }\rightarrow 0^+\), except for an increasingly thin boundary layer that occurs due to the vanishing stress boundary condition at the outer surface. In addition to the latter results, the convergence of the finite element results towards the analytical solution upon mesh refinement is studied in the Appendix.

4.4 Rectangular bar under tension

Breaking the rotational symmetry of the boundary value problem discussed in Sects. 4.2 and 4.3, the tensile problem of a rectangular bar with a square cross section sketched in Fig. 5 is studied in this section. In accordance with the previous sections, generalised clamping boundary conditions are assumed at the left boundary (\(z={0}\) mm), and generalised traction boundary conditions that result in a total axial force of 840 kN are applied at the right boundary (\(z={100}\) mm). At the remaining boundaries, homogeneous generalised Neumann boundary conditions are assumed. The material parameters are chosen in accordance with Table 1, the bar is discretised by using linear (eight-node) Lagrangian elements, and a Gaussian quadrature scheme with eight sampling points is used for numerical integration.

Fig. 5
figure 5

Geometric dimensions (in mm) and boundary conditions of the rectangular bar under tension

Full size image
Fig. 6
figure 6

Stress distribution predicted by finite element calculations of the tensile problem depicted in Fig. 5 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\)) with zero stress boundary conditions on \(\partial \mathcal {B}_1\)–\(\partial \mathcal {B}_4\). The results are shown on the deformed cross-section, with the deformation scaled by a factor of 50 for visualisation purposes

Full size image

The finite element results are presented with respect to the Cartesian basis specified in Fig. 5 and are evaluated for the cross section at \(z={50}\) mm to reduce the influence of boundary effects. The simulation results are summarised in Fig. 6 and differ significantly from the homogeneous, uniaxial stress state expected in the case of a classic Cauchy continuum with an isotropic, linear-elastic material model: (1) A strongly inhomogeneous axial stress field \(\sigma _{33}\) is observed in Fig. 6a–c. The axial stress takes its maximum value in the centre of the cross section and approaches zero at the boundaries. In accordance with the observations for the cylindrical bar in Sect. 4.2, the slope and the maximum value of the \(\sigma _{33}\) profile depend on the material length scale parameter \(\ell \) which penalises stress gradients in an energetic manner. (2) Significant in-plane stresses are observed in Fig. 6d–i. (3) The complex stress state in the cross-section is associated with a complex deformation of the cross-section which, in particular, does not remain square. The latter deformation mode becomes more pronounced with increasing values of the material length scale parameter \(\ell \). Moreover, no warping of the cross section’s surface with unit normal vector \(\varvec{e}_3\) is observed.

In contrast, the homogeneous uniaxial stress state that is expected (at a distance from the clamped boundary) in the case of a classic Cauchy continuum with an isotropic linear-elastic material model can be recovered by taking into account a different set of boundary conditions. More specifically speaking, the bar is again assumed to be clamped (in a generalised sense) at the left boundary (\(x_3={0}\) mm)

$$\begin{aligned} \varvec{\varPsi }\cdot \varvec{n}=- \, \varvec{\varPsi }\cdot \varvec{e}_3= {\varvec{0}} \end{aligned}$$
(53)

and homogeneous traction boundary conditions

$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}= \overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3\otimes \varvec{e}_3 \end{aligned}$$
(54)

are assumed at the right boundary (\(x_3= {100}\) mm). At the remaining boundaries, generalised stress boundary conditions that are consistent with the expected uni-axial stress state are prescribed, i.e.

$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=-\, \overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3\otimes \varvec{e}_1 \quad \text {on}\quad \partial \mathcal {B}_1 \end{aligned}$$
(55a)
$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=-\, \overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3\otimes \varvec{e}_2 \quad \text {on}\quad \partial \mathcal {B}_2 \end{aligned}$$
(55b)
$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=\quad \overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3\otimes \varvec{e}_1 \quad \text {on}\quad \partial \mathcal {B}_3 \end{aligned}$$
(55c)
$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=\quad \overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3\otimes \varvec{e}_2 \quad \text {on}\quad \partial \mathcal {B}_4 \end{aligned}$$
(55d)

The simulation results that were calculated with the set of boundary conditions (53)–(55), cf. Fig. 5, and with \(\ell ={1.0}\) mm are provided in Fig. 7. For an applied axial load of 840 kN, the uniaxial stress state at a distance from the clamped boundary is given by

$$\begin{aligned} \varvec{\sigma }= \overline{\sigma }_{33}\, \varvec{e}_3\otimes \varvec{e}_3 = {2100}~\text {N}/\text {mm}^{2} \, \varvec{e}_3\otimes \varvec{e}_3, \end{aligned}$$
(56)

as indicated by light grey colour. In addition, an inhomogeneous stress distribution due to the clamping conditions is observed in the vicinity of the left boundary.

Fig. 7
figure 7

Stress distribution predicted by finite element calculations of the tensile problem depicted in Fig. 5 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\), \(\ell ={1.0}\) mm) with boundary conditions according to (53)–(55)

Full size image

4.5 Torsion test

The torsion problem of a cylindrical bar as depicted in Fig. 8 is analysed in this section. The bar is assumed to be clamped (in a generalised sense) at the left boundary. The remaining boundary, except for the right end of the cylindrical bar where a torque is induced by means tangential forces, is assumed to be stress free. In particular, traction boundary conditions at the surface with outward unit normal vector \(\varvec{n}=\varvec{e}_r\), in the vicinity of the right boundary (\(z={100}\) mm), of the form

$$\begin{aligned} \varvec{\sigma }\otimes \varvec{n}=\overline{\sigma }_{\theta r}\, \left[ \varvec{e}_\theta \otimes \varvec{e}_r+ \varvec{e}_r\otimes \varvec{e}_\theta \right] \otimes \varvec{e}_r \end{aligned}$$
(57)

are applied that result in a torque of approx. 1100 N m with respect to the \(\varvec{e}_z\)-axis. Moreover, by making use of the relation between the Cartesian and polar basis

$$\varvec{e}_r= \cos \left( \theta \right) \,\varvec{e}_1 + \sin \left( \theta \right) \, \varvec{e}_2 \,,$$
(58a)
$$\varvec{e}_\theta= - \sin \left( \theta \right) \, \varvec{e}_1 + \cos \left( \theta \right) \,\varvec{e}_2 \,,$$
(58b)
$$\begin{aligned} \varvec{e}_z= \varvec{e}_3, \end{aligned}$$
(58c)

the boundary condition (57) can alternatively be expressed as

(59)

The corresponding coefficient matrix with respect to the Cartesian basis system takes the form

$$\begin{aligned}&\left[ \varvec{\sigma }\otimes \varvec{n}\right] _{ij1} =\\&\quad \begin{bmatrix} -2\,\sin \left( \theta \right) \, \cos \left( \theta \right) &{} \left[ \cos ^2\left( \theta \right) -\sin ^2\left( \theta \right) \right] &{} 0 \\ \left[ \cos ^2\left( \theta \right) -\sin ^2\left( \theta \right) \right] &{} 2\, \sin \left( \theta \right) \, \cos \left( \theta \right) &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix} \cos \left( \theta \right) \, \overline{\sigma }_{\theta r} \end{aligned}$$
(60a)
$$\begin{aligned}&\left[ \varvec{\sigma }\otimes \varvec{n}\right] _{ij2} =\\&\quad\begin{bmatrix} -2\,\sin \left( \theta \right) \, \cos \left( \theta \right) &{} \left[ \cos ^2\left( \theta \right) -\sin ^2\left( \theta \right) \right] &{} 0 \\ \left[ \cos ^2\left( \theta \right) -\sin ^2\left( \theta \right) \right] &{} 2\, \sin \left( \theta \right) \, \cos \left( \theta \right) &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix} \,\sin \left( \theta \right) \, \overline{\sigma }_{\theta r} \end{aligned}$$
(60b)
$$\begin{aligned}\left[ \varvec{\sigma }\otimes \varvec{n}\right] _{ij3} = \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{bmatrix} \end{aligned}$$
(60c)

The material parameters are chosen according to Table 1, and a Gaussian quadrature scheme with eight sampling points and discretisations based on linear (eight-node) Lagrangian elements are used.

Fig. 8
figure 8

Geometric dimensions (in mm) and boundary conditions of the cylindrical bar under torsion

Full size image

The simulation results are summarised in Figs. 9 and 10 with respect to a cylindrical basis system and are evaluated for the cross section at \(z={50}\) mm. Due to the boundary conditions at the outer surface of the cylinder, the in-plane shear stress \(\sigma _{\theta z}\) does not linearly increase on the interval \(r\in \left[ {0}~\mathrm{mm}, {10}~\mathrm{mm}\right] \) as would be the case for a classic Cauchy continuum with an isotropic, linear elastic material model. In contrast, a parabolic profile that approaches zero at the centre (\(r={0}\) mm) and at the outer radius (\(r={10}\) mm) is observed in Fig. 9, with the slope and the maximum shear stress value depending on the material length scale \(\ell \). In addition, the shear stress distribution in the cross section is provided in Fig. 10 for the three different values of the length scale parameter studied.

Fig. 9
figure 9

Shear stress distribution predicted by finite element simulations of the torsion problem depicted in Fig. 8 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\))

Full size image
Fig. 10
figure 10

Shear stress distribution predicted by finite element simulations of the torsion problem depicted in Fig. 8 (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\))

Full size image

4.6 Comparison with the analytic solution in torsion

The stress tensor takes the form

$$\begin{aligned} \varvec{\sigma }= \tau \, \left[ \varvec{e}_\theta \otimes \varvec{e}_z+ \varvec{e}_z\otimes \varvec{e}_\theta \right] \end{aligned}$$
(61)

where \(\tau = \sigma _{\theta z}\) is the unknown function to be determined. The static balance equations, in the absence of body forces, require that \(\tau \) is a function of the sole variable \(r\). Under these conditions, the stress gradient is deviatoric and one finds that

$$\begin{aligned} \varvec{R}= \nabla \varvec{\sigma }= \tau ' \,&\left[ \varvec{e}_\theta \otimes \varvec{e}_z\otimes \varvec{e}_r+ \varvec{e}_z\otimes \varvec{e}_\theta \otimes \varvec{e}_r\right] \\ -\frac{\tau }{r}\,&\left[ \varvec{e}_r\otimes \varvec{e}_z\otimes \varvec{e}_\theta + \varvec{e}_z\otimes \varvec{e}_r\otimes \varvec{e}_\theta \right] \end{aligned}$$
(62)

where \(\tau '\) denotes the derivative of the stress component with respect to \(r\). Its divergence is then computed as

$$\begin{aligned} \nabla \cdot \varvec{R}= \left[ \tau '' + \frac{\tau '}{r}-\frac{\tau }{r^2}\right] \, \left[ \varvec{e}_\theta \otimes \varvec{e}_z+ \varvec{e}_z\otimes \varvec{e}_\theta \right] . \end{aligned}$$
(63)

On the other hand, the displacement vector is described by a single function \(u_\theta (r,z)\) in the form

$$\begin{aligned} \varvec{u}= u_\theta (r,z) \, \varvec{e}_\theta \end{aligned}$$
(64)

from which the infinitesimal strain tensor is computed as

$$\begin{aligned} \left[ \nabla \varvec{u}\right] ^{\rm sym}= \frac{1}{2} \left[ \frac{\partial u_\theta }{\partial r} - \frac{u_\theta }{r}\right] \,& \left[ \varvec{e}_r\otimes \varvec{e}_\theta + \varvec{e}_\theta \otimes \varvec{e}_r\right] \\ +\frac{1}{2} \frac{\partial u_\theta }{\partial z}\; & \left[ \varvec{e}_z\otimes \varvec{e}_\theta + \varvec{e}_\theta \otimes \varvec{e}_z\right] . \end{aligned} $$
(65)

Assuming that \(\ell \) and \(\mu \) are constant in space, the generalised strain tensor can now be expressed as

$$\begin{aligned} \varvec{e} &= {} \left[ \nabla \varvec{u}\right] ^{\rm sym}+ \nabla \cdot \varvec{\varPhi }= \left[ \nabla \varvec{u}\right] ^{\rm sym}+\ell ^2 \mu ^{-1}\,\nabla \cdot \varvec{R} \\ &= {} \displaystyle \frac{1}{2} \left[ \frac{\partial u_\theta }{\partial r} - \frac{u_\theta }{r}\right] \, \left[ \varvec{e}_r\otimes \varvec{e}_\theta + \varvec{e}_\theta \otimes \varvec{e}_r\right] \\& {} \quad+ \left[ \frac{1}{2} \frac{\partial u_\theta }{\partial z} + \ell ^2 \mu ^{-1} \left[ \tau '' + \left[ \frac{\tau }{r}\right] '\right] \right] \left[ \varvec{e}_z\otimes \varvec{e}_\theta + \varvec{e}_\theta \otimes \varvec{e}_z\right] \, . \end{aligned}$$
(66)

In the analysed torsion case, generalised Hooke’s law (33a) simplifies to

$$\begin{aligned} \varvec{e}= \frac{1}{2\,\mu } \, \varvec{\sigma }. \end{aligned}$$
(67)

By taking into account (61), (66) and (67), the differential system of two equations

$$\begin{aligned} \frac{\partial u_\theta }{\partial r} - \frac{u_\theta }{r}= 0 \end{aligned}$$
(68a)
$$\begin{aligned} \mu \,\frac{\partial u_\theta }{\partial z} + 2\,\ell ^2 \left[ \tau '' + \left[ \frac{\tau }{r}\right] '\right] - \tau=0 \end{aligned}$$
(68b)

is thus derived. It follows from (68a) that \(u_\theta (r,z) = \alpha (z)\,r\) where \( \alpha \) is a function of the sole variable \(z\). Furthermore, (68b) shows that this function reduces to \( \alpha (z) = \alpha _0 \, z\). Equation (68b) can now be written in the form

$$\begin{aligned} \mu \,\alpha _0 \,r+2\,\ell ^2\left[ \tau '' + \left[ \frac{\tau }{r}\right] '\right] - \tau = 0. \end{aligned}$$
(69)

A particular solution of this equation is the well-known linear field from classic elasticity

$$\begin{aligned} \tau \left( r\right) = \mu \, \alpha _0 \, r. \end{aligned}$$
(70)

The remaining homogeneous ordinary differential equation to be solved is then

$$\begin{aligned} r^2\tau ''+r\tau '-\left[ 1+\frac{r^2}{\tilde{\ell }^2}\right] \tau = 0, \end{aligned}$$
(71)

where definition (48) was used. The change of variable \(r= \tilde{\ell }\, x\) and the definition \(y(x) = \tau (\tilde{\ell }\,x)\) lead to the ordinary differential equation

$$\begin{aligned} x^2\,y''+x\,y'-\left[ 1+x^2\right] y = 0, \end{aligned}$$
(72)

where primes indicate derivatives with respect to x. According to [1], the solutions are given by modified Bessel functions of order one, i.e.

$$\begin{aligned} y(x) = C_1 \,I_1(x)+C_2 \, Y_1(ix) \end{aligned}$$
(73)

with \(Y_1(ix) = -\,I_1(x) -\frac{2i}{\pi }\, K_1(x)\). The modified Bessel function of the second kind \(K_1\) is singular at \(x=0\) and is therefore not acceptable for the considered bar. The solution of the torsion problem thus takes the form

$$\begin{aligned} \tau (r)= {} \mu \, \alpha _0 \, r+ C_1 \, I_1(r/\tilde{\ell }) \end{aligned}$$
(74)
$$\begin{aligned}= {} \mu \, \alpha _0 \, r_{{\rm m}}\left[ \displaystyle \frac{r}{r_{{\rm m}}} - \displaystyle \frac{I_1(r/\tilde{\ell })}{I_1(r_{{\rm m}}/\tilde{\ell })}\right] \end{aligned}$$
(75)

where the constant \(C_1\) was determined from the condition \(\tau (r=r_{{\rm m}}) = 0\).

The solution is found to be such that \(\tau (r=0) = 0\), with the vanishing shear stress at the tube’s axis being a consequence of the specific form of the analytical solution and not imposed to the governing differential equation. In accordance with the tensile problem discussed in Sect. 4.3, it is moreover observed that the analytical solution (75) converges towards the one of a classic Cauchy continuum in the limit \(\tilde{\ell }\rightarrow 0^+\), except for an increasingly thin boundary layer that occurs due to the vanishing stress boundary condition at the outer surface. In addition, the convergence of the finite element results towards the analytical solution upon mesh refinement is exemplarily shown for \(\ell ={1.0}\) mm in the Appendix.

The next step consists in evaluating the torque resulting from the computed shear stress function. The only non-vanishing component of this vector is \(M\,\varvec{e}_z\) and given by

$$M= {} \int _S r^2 \, \tau \, {\rm d}r{\rm d}\theta$$
(76)
$$= {} \mu \, \alpha _0 \,\frac{\pi \, r_{{\rm m}}^{4}}{2} + 2 \,\pi \, C_1\int _0^{r_{{\rm m}}}r^2 \,I_1(r/\tilde{\ell })\,{\rm d}r$$
(77)
$$= {} \mu \, \alpha _0 \,\frac{\pi \, r_{{\rm m}}^{4}}{2} + 2\,\pi \, \tilde{\ell }^{\,3} \, C_1 \int _0^{x_{{\rm m}}}x^2 \, I_1(x)\,{\rm d}x$$
(78)

with \(x_{{\rm m}}= r_{{\rm m}}/\tilde{\ell }\). The last integral can be evaluated exactlyFootnote 1 by means of two successive integrations by parts as

$$\begin{aligned} \int _0^{x_{{\rm m}}}x^2\, I_1(x){\rm d}x= x_{{\rm m}}^2 \, I_0(x_{{\rm m}})-2\, x_{{\rm m}}\, I_1(x_{{\rm m}}). \end{aligned}$$
(79)

The torque can now be related to the torsion angle per unit length, \( \alpha _0\), as

$$\begin{aligned} M= \mu \, \alpha _0 \, \frac{\pi \, r_{{\rm m}}^4}{2} \left[ 1 - 4\, \frac{\tilde{\ell }^2}{r_{{\rm m}}^2} \left[ \frac{r_{{\rm m}}}{\tilde{\ell }}\frac{I_0(r_{{\rm m}}/\tilde{\ell })}{I_1(r_{{\rm m}}/\tilde{\ell })}-2\right] \right] . \end{aligned}$$
(80)

The torque value was prescribed in the finite element analysis of Sect. 4.5. The value \( \alpha _0\) can be computed from (80) and completely determines the shear stress field (75). A comparison of the analytical and numerical shear stress profiles is plotted in Fig. 11 for three values of the intrinsic length scale. Excellent agreement is obtained, which shows that the usual linear shear stress profile is replaced by a non-monotonic distribution with a boundary layer close to the free surface.

Fig. 11
figure 11

Comparison between the analytic and numerical predictions for the shear stress distribution in torsion for the stress gradient continuum endowed with three different intrinsic length scales (\(E={210{,}000}\) N/mm\(^2\), \(\nu =0.3\))

Full size image

4.7 Smaller is softer

The torsion stiffness \(\mathcal {J}_\ell \) can be defined from relation (80). It is a function of the wire radius and of the characteristic length of the stress gradient elastic continuum. Specifically speaking,

$$\begin{aligned} \mathcal {J}_\ell = \mathcal {J}_0\left[ 1 - 4\frac{\tilde{\ell }^2}{r_{{\rm m}}^2}\left[ \frac{r_{{\rm m}}}{\tilde{\ell }}\frac{I_0(r_{{\rm m}}/\tilde{\ell })}{I_1(r_{{\rm m}}/\tilde{\ell })}-2\right] \right] , \end{aligned}$$
(81)

holds, with \(\mathcal {J}_0\) denoting the usual torsion stiffness of a cylindrical bar

$$\begin{aligned} \mathcal {J}_0= \mu \frac{\pi \, r_{{\rm m}}^4}{2}. \end{aligned}$$
(82)

A tensile stiffness of the cylindrical bar can also be defined from the solution found in Sect. 4.3. The stress distribution was given by (51) and (52). Alternatively, it can be expressed in terms of the stress value \(E\,{{\bar{\varepsilon }}}\), where \({{\bar{\varepsilon }}}\) is the prescribed axial displacement gradient, namely

$$\begin{aligned} \sigma _z(r/\tilde{\ell }) = E\, {{\bar{\varepsilon }}} \left[ 1- \frac{I_0(r/\tilde{\ell })}{I_0(r_{{\rm m}}/\tilde{\ell })} \right] . \end{aligned}$$
(83)

The tensile stiffness of the bar is defined as the ratio of the applied force \(F\) and the prescribed relative displacement \(\delta = L\,{{\bar{\varepsilon }}}\), with \(L\) denoting the length of the bar. In the case of a Cauchy continuum, it is well-known that the reference stiffness is

$$\begin{aligned} \mathcal {K}_0= E\,\frac{\pi \,r_{{\rm m}}^2}{L}. \end{aligned}$$
(84)

For the stress gradient continuum, the total force is computed as

$$\begin{aligned} F&= {} \int _S \sigma _z \, r\, {\rm d}r\,{\rm d}\theta\\ &= {} 2\,\pi \,E\,{{\bar{\varepsilon }}}\int _0^{r_{{\rm m}}} r\left[ 1- \frac{I_0(r/\tilde{\ell })}{I_0(r_{{\rm m}}/\tilde{\ell })}\right] \, {\rm d}r \end{aligned}$$
(85)
$$\begin{aligned}&= {} 2\,\pi \, E\, {{\bar{\varepsilon }}} \,\tilde{\ell }^{\,2}\int _0^{x_{{\rm m}}} x\left[ 1-\frac{I_0(x)}{I_0(x_{{\rm m}})}\right] \, {\rm d}x \\&= {} \pi \, E\,{{\bar{\varepsilon }}}\, r_{{\rm m}}^2\left[ 1 - \frac{2\,I_1(x_{{\rm m}})}{x_{{\rm m}}\,I_0(x_{{\rm m}})} \right] . \end{aligned}$$
(86)

It follows that

$$\begin{aligned} \mathcal {K}_\ell = E\frac{\pi \, r_{{\rm m}}^2}{L} \left[ 1 - \frac{2\,I_1(x_{{\rm m}})}{x_{{\rm m}}\,I_0(x_{{\rm m}})} \right] , \end{aligned}$$
(87)

with the relative tensile stiffness defined as

$$\begin{aligned} \frac{\mathcal {K}_\ell }{\mathcal {K}_0} = \left[ 1 - \frac{2\,I_1\,(x_{{\rm m}})}{x_{{\rm m}}\,I_0(x_{{\rm m}})} \right] . \end{aligned}$$
(88)

The tensile and torsion relative stiffnesses are plotted in Fig. 12. The curves clearly reveal a smaller is softer tendency, meaning that the stiffness decreases when the intrinsic length scale increases. It is particularly remarkable that the bar stiffness tends towards zero when the length scale increases or when the bar radius decreases. This effect stems from the existence of a boundary layer with vanishing stress whose thickness becomes dominant for small bar radii or large intrinsic length scales.

The limit case of torsion for large radii or small internal length scales is also interesting. The usual stiffness \(\mathcal {J}_0\) is retrieved in this limit case in spite of the presence of a stress gradient. The reason is that, at the limit, the shear stress is a linear function implying that the divergence of the stress gradient and of microdisplacements (see (63)) vanishes, leaving the usual strain tensor unaffected.

A comparison can be drawn with solutions according to existing strain gradient elasticity models, including Mindlin’s original theory [25] or Aifantis simplified model [13]. No size effect is expected in tension in strain gradient elasticity at least for long enough bars fulfilling Saint-Venant’s conditions. The softening effect obtained in torsion according to stress gradient elasticity is in striking contrast to the predictions of strain gradient elasticity which are notoriously associated with a smaller is stiffer effect, see [6]. Solutions of the torsion problem of strain gradient elastic bars have been provided in [2, 20, 32]. A torsion stiffening effect is predicted by strain gradient elasticity when the bar radius has the same order of magnitude as the intrinsic length scale and below. The linear stress profile is still valid in a strain gradient elastic circular cylindrical bar because it fulfils all required higher order boundary conditions. This is in contrast to the stress gradient solution worked out in the previous section. However, the torsion stiffness is increased by a contribution of the higher order elasticity moduli [19, 20], at least if the bar is long enough to fulfil the Saint-Venant conditions, see [23] which focuses on special boundary conditions at the bar’s ends. This relative stiffness enhancement is proportional to \(\left[ 1+ a\, x_{{\rm m}}^{-2}\right] \), where \(x_{{\rm m}}\) is the ratio of the bar radius divided by one strain gradient elastic length scale, and where a is a factor depending on the specific strain gradient model considered. This implies that the relative stiffness approaches infinity for vanishingly small radii or very large intrinsic length scales. It is recalled that the stress gradient elasticity theory predicts a vanishing relative stiffness under these conditions. Finite element solutions of the torsion problem of strain gradient elastic bars were presented in [5], confirming the absence of warping for circular bars and computing the warping of elliptical sections.

Fig. 12
figure 12

Relative stiffness of a cylindrical bar in tension or in torsion as a function of the ratio between the bar radius \(r_{{\rm m}}\) and the intrinsic length scale \(\tilde{\ell }=\sqrt{2}\,\ell \)

Full size image

5 Closure

In this contribution, a finite element implementation of the stress gradient theory was proposed and studied in detail. The implementation relied on a reformulation of the governing set of field equations (of the stress gradient theory) in terms of one primary, tensor-valued field variable of third order. Since the latter field variable was based on the classic displacement field and on a micro-displacement field-type quantity, it was referred to as a generalised displacement field. It was then shown that a reformulation of the weak form of the balance equations in terms of the generalised displacement field is particularly suitable for a finite element-based implementation, especial with regard to (the implementation of) boundary conditions. More specifically speaking, a peculiarity of the stress gradient theory as opposed to the classic Cauchy continuum was that the complete stress tensor could be prescribed at the boundaries. With the finite element implementation at hand, representative boundary value problems were studied in detail. In particular, a cylindrical bar under tension was analysed for which an analytical solution by means of Bessel functions could be derived for validation purposes in the case of a circular cross section. Breaking the rotational symmetry of the bar, the study of a rectangular bar under tension revealed a significantly different deformation behaviour as compared to a classic Cauchy continuum. These results strongly differ from strain gradient elasticity which does not predict any size effect for a bar in tension, at least in the sense of Saint-Venant. Finally, the (unusual) shear stress distribution in a cylindrical bar under torsion was studied by means of numerical and analytical methods. Note that the analytical solution of the simple tension problem was provided explicitly for a circular bar in the special case of vanishing Poisson’s ratio. In contrast, the solution presented for torsion loading in isotropic stress gradient elasticity is general.

The stress gradient continuum represents a generalisation of a classic Cauchy continuum. Amongst others, it allows for generalised boundary conditions in terms of the complete stress tensor and naturally accounts for a material length scale. The simulation examples provided in this work illustrate a remarkable feature of stress gradient elasticity which predicts that smaller is softer in the presence of stress free boundaries. This is in contrast to smaller is stiffer effects according to strain gradient elasticity. Free boundary layer effects can be accounted for by means of second strain gradient elasticity and essentially lead to an increase of the tensile stiffness of a bar [9, 22]. Smaller is softer effects have been reported in materials science for the apparent Young’s modulus of nanowires in [36] in relation to free surface effects, see [9] and references quoted therein. This trend was also observed in the plasticity of bulk metallic glasses according to [17]. It may also be relevant in the context of boundary layer effects in elastic composite materials, see the bending-gradient theory for thick heterogeneous plates discussed in [30]. Additionally, both smaller is stiffer as well as smaller is softer effects have been reported in bending experiments on human cortical bone samples [8, 35]. These seemingly contradictory results prompted the analyses presented in [34], which suggests by employing simple analytical laminate beam theories and finite element-based studies of two-dimensional beam-type samples with periodic heterogeneities that the latter experimental findings can be explained by the particular properties of the material surface. From a modeling point of view, recent research efforts moreover focus on the combination of gradient and nonlocal elasticity theories to account for both smaller is softer as well as smaller is stiffer effects that may, possibly, be related to different material length scales, [3]. Applications of nonlocal strain gradient theories to simulate beam- and shell-type nanoscale structures are discussed in, for example, [11, 24], and it remains to be shown how these theories are related to the stress gradient theory that serves as the basis for the present contribution.

In addition, the simplified isotropic elasticity law used in the present work involving a single additional intrinsic length scale should be extended to more general sixth order tensors of stress gradient elasticity, including isotropy and anisotropy [4, 14]. Furthermore, more complex geometries and loadings will be investigated in future works so as to reveal the full potential of the stress gradient theory. Another challenging issue to be considered is the introduction of nonlinear aspects of the stress gradient theory into the proposed finite element approach, regarding either the finite deformation framework established in [15] or plasticity theory [12]. The latter would allow for a comparison between stress gradient plasticity and strain gradient plasticity predictions for a wealth of physical situations which were explored in the past only in the case of strain gradient approaches [6, 21].