Abstract
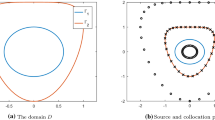
The problem of detecting and localizing a cavity, a crack, or an inclusion in an elastic body by means of partially overdetermined data given on its outer boundary is considered. The input data can be obtained in a single static experiment. A new approach for solving this problem is proposed. The capabilities of the proposed approach are illustrated by the example of the problem for detecting a cavity in an elastic plate.
Similar content being viewed by others
REFERENCES
D. Colton and A. Kirsch, “A simple method for solving inverse scattering problems in the resonance region,” Inverse Probl. 12, 383–393 (1996).
D. Colton, M. Piana, and R. Potthast, “A simple method using Morozov’s discrepancy principle for solving inverse scattering problems,” Inverse Probl. 13, 1477–1493 (1997).
T. Arens, “Linear sampling methods for 2D inverse elastic wave scattering,” Inverse Probl. 17, 1445–1464 (2001).
A. Kirsch, “Characterization of the shape of a scattering obstacle using spectral data of the far field operator,” Inverse Probl. 14, 1489–1512 (1998).
N. Grinberg, “Obstacle visualization via the factorization method for the mixed boundary value problem,” Inverse Probl. 18, 1687–1704 (2002).
R. Potthast, “A survey on sampling and probe methods for inverse problems,” Inverse Probl. 22, R1–R47 (2006).
S. H. Dehghan Manshadi, N. Khaji, and M. Rahimian, “Cavity/inclusion detection in plane linear elastic bodies using linear sampling method,” J. Nondestruct. Eval. 33, 93–103 (2014).
A. Kirsch, “The factorization method for a class of Inverse elliptic problems,” Math. Nachr. 278, 258–277 (2005).
E. I. Shifrin, “Factorization method in the geometric inverse problem of static elasticity,” Mech. Solids 51 (5), 562–570 (2016).
H. Ammari, H. Kang, G. Nakamura, and K. Tanuma, “Complete asymptotic expansions of solutions of the system of elastostatics in the presence of an inclusion of small diameter and detection of an inclusion,” J. Elast. 67, 97–129 (2002).
H. Kang, E. Kim, and J.-Y. Lee, “Identification of elastic inclusions and elastic moment tensors by boundary measurements,” Inverse Probl. 19, 703–724 (2003).
H. Ammari and H. Kang, Reconstruction of Small Inhomogeneities from Boundary Measurements (Springer, Berlin, 1846).
H. Ammari and H. Kang, Polarization and Moment Tensors: with Applications to Inverse Problems and Effective Medium Theory (Springer, New York, 2007).
M. Ikehata, “Enclosing a polygonal cavity in a two-dimensional bounded domain from cauchy data,” Inverse Probl. 15, 1231–1241 (1999).
M. Ikehata, “A regularized extraction formula in the enclosure method,” Inverse Probl. 18, 435–440 (2002).
A. Karageorghis, D. Lesnic, and L. Marin, “The method of fundamental solutions for the detection of rigid inclusions and cavities in plane linear elastic bodies,” Comput. Struct. 106–107, 176–188 (2012).
A. Karageorghis, D. Lesnic, and L. Marin, “A moving pseudo-boundary method of fundamental solutions for void detection,” Numer. Methods Partial Differ. Equations 29, 935–960 (2013).
A. Karageorghis, D. Lesnic, and L. Marin, “The method of fundamental solutions for three-dimensional inverse geometric elasticity problems,” Comput. Struct. 166, 51–59 (2016).
S. Andrieux and A. Ben Abda, “Identification of planar cracks by complete overdetermined data: inversion formulae,” Inverse Probl. 12, 553–563 (1996).
S. Andrieux, A. Ben Abda, and H. D. Bui, “Reciprocity principle and crack identification,” Inverse Probl. 15, 59–65 (1999).
R. V. Goldstein, E. I. Shifrin, and P. S. Shushpannikov, “Application of invariant integrals to the problems of defect identification,” Int. J. Fract. 147, 45–54 (2007).
E. I. Shifrin, “Ellipsoidal defect identification in an elastic body from the results of a uniaxial tension (compression) test,” Mech. Solids 45 (3), 417–426 (2010).
E. I. Shifrin and P. S. Shushpannikov, “Identification of a spheroidal defect in an elastic solid using a reciprocity gap functional,” Inverse Probl. 26, 055001 (2010).
E. I. Shifrin and P. S. Shushpannikov, “Identification of an ellipsoidal defect in an elastic solid using boundary measurements,” Int. J. Solids Struct. 48, 1154–1163 (2011).
E. I. Shifrin and P. S. Shushpannikov, “Reconstruction of an ellipsoidal defect in anisotropic elastic solid, using results of one static test,” Inverse Probl. Sci. Eng. 21, 781–800 (2013).
E. I. Shifrin and P. S. Shushpannikov, “Identification of small well-separated defects in an isotropic elastic body using boundary measurements,” Int. J. Solids Struct. 50, 3707–3716 (2013).
E. I. Shifrin and P. S. Shushpannikov, “Identification of finitely many small defects in an anisotropic linearly elastic body from a single static test,” Mech. Solids 50 (4), 421–431 (2015).
E. I. Shifrin and A. V. Kaptsov, “Identification of multiple cracks in 2D elasticity by means of the reciprocity principle and cluster analysis,” Inverse Probl. 34, 015009 (2018).
M. Bonnet and A. Constantinescu, “Inverse problems in elasticity,” Inverse Probl. 21, R1–R150 (2005).
M. Burger, “A level set method for inverse problems,” Inverse Probl. 17, 1327–1355 (2001).
M. Burger, “Levenberg-marquardt level set methods for inverse obstacle problems,” Inverse Probl. 20, 259–282 (2004).
H. Ben Ameur, M. Burger, and B. Hackl, “Level set methods for geometric inverse problems in linear elasticity,” Inverse Probl. 20, 673–696 (2004).
V. A. Kozlov, V. G. Maz’ya, and A. V. Fomin, “An iterative method for solving the Cauchy problem for elliptic equations,” Comput. Math. Math. Phys. 31 (1), 45–52 (1991).
A. Cimetiere, F. Delvare, M. Jaoua, and F. Pons, “Solution of the cauchy problem using iterated Tikhonov regularization,” Inverse Probl. 17, 553–570 (2001).
T. N. Baranger and S. Andrieux, “An optimization approach for the Cauchy problem in linear elasticity,” Struct. Multidiscip. Optim. 35, 141–152 (2008).
C.-S. Liu and S. N. Atluri, “Numerical solution of the Laplacian Cauchy problem by using a better postconditioning collocation Trefftz method,” Eng. Anal. Boundary Elements 37, 74–83 (2013).
R. V. Kohn and M. Vogelius, “Relaxation of a variational method for impedance computed tomography,” Commun. Pure Appl. Math. 40, 745–777 (1987).
A. N. Tikhonov, and V. Ya. Arsenin, Solution of Ill-Posed Problems (John Wiley and Son, New York, 1977).
P. C. Hansen, “Analysis of discrete ill-posed problems by means of the L-curve,” SIAM Rev. 34, 561–580 (1992).
P. C. Hansen, “The L-curve and its use in the numerical treatment of inverse problems,” in Computational Inverse Problems in Electrocardiography, Ed. by P. Johnston (WIT Press, Southampton, 2001), pp. 119–142.
Funding
The work цфы supported by the State Taskб state registration no. AAAA-A20-120011690132-4б and by the Russian Foundation for Basic Researchб project no. 19-01-00100.
Professor Efim Il’ich Shifrin, the renowned expert in the mechanics of deformable solids and in the fracture mechanics, the author of more than 200 papers in mechanics and applied mathematics, the member of the editorial board of the journal Prikladnaya Matematika i Mekhanika, and the active reviewer and author of the journal, turned 70 on April 14, 2020.
The editorial board and editorial staff of Prikladnaya Matematika i Mekhanika, colleagues, and disciples would like to thank him for his dedicated work, as well as wish him good health and further creative successes.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by E. Oborin
About this article
Cite this article
Kasparova, E.A., Shifrin, E.I. Solution for the Geometric Elastostatic Inverse Problem by Means of Not Completely Overdetermined Boundary Data. Mech. Solids 55, 1298–1307 (2020). https://doi.org/10.3103/S0025654420080117
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.3103/S0025654420080117