Skip to main content
SpringerLink
Log in

An efficient numerical algorithm for the study of time fractional Tricomi and Keldysh type equations

  • Original Article
  • Published:
Engineering with Computers Aims and scope Submit manuscript

Abstract

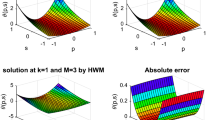
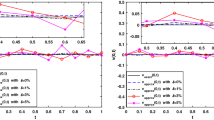
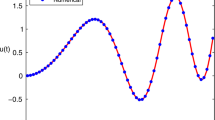
This work addresses a hybrid scheme for the numerical solutions of time fractional Tricomi and Keldysh type equations. In proposed methodology, Haar wavelets are used for discretization in space while \(\theta\)-weighted scheme coupled with second order finite differences and quadrature rule are employed for temporal discretization and fractional derivative respectively. Stability of the proposed scheme is described theoretically and validated computationally which is an essential chunk of the current work. Efficiency of the suggested scheme is endorsed through resolutions level and time step size. Goodness of the obtained solutions confirmed through computing error norms \({\mathbb E}_{\infty }\), \({\mathbb E}_2\) and matching with existing results in literature. Moreover, convergence rate is also checked for considered problems. Numerical simulations show good performance for both 1D and 2D test problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier, New York

    MATH  Google Scholar 

  2. Oldham K, Spanier J (1974) The fractional calculus theory and applications of differentiation and integration to arbitrary order. Elsevier, New York

    MATH  Google Scholar 

  3. He J (1998) Nonlinear oscillation with fractional derivative and its applications. In: International conference on vibrating engineering, vol 98, Dalian, China, pp 288–291

  4. He J (1999) Some applications of nonlinear fractional differential equations and their approximations. Bull Sci Technol 15(2):86–90

    Google Scholar 

  5. Mainardi F (2012) Fractional calculus: some basic problems in continuum and statistical mechanics. arXiv:1201.0863 (arXiv preprint)

  6. Baillie RT (1996) Long memory processes and fractional integration in econometrics. J Econom 73(1):5–59

    Article  MathSciNet  Google Scholar 

  7. Rossikhin YA, Shitikova MV (1997) Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids

  8. Magin RL (2004) Fractional calculus in bioengineering, part 2. Crit Rev Biomed Eng 32:2

    Google Scholar 

  9. Metzler R, Klafter J (2004) The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J Phys A Math Gener 37(31):R161

    Article  MathSciNet  Google Scholar 

  10. Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations. Wiley, New York

    MATH  Google Scholar 

  11. Hesameddini E, Rahimi A, Asadollahifard E (2016) On the convergence of a new reliable algorithm for solving multi-order fractional differential equations. Commun Nonlinear Sci Numer Simul 34:154–164

    Article  MathSciNet  Google Scholar 

  12. Kemppainen JT, Ruotsalainen KM (2011) On the spline collocation method for the single layer equation related to time-fractional diffusion. Numer Algorithms 57(3):313–327

    Article  MathSciNet  Google Scholar 

  13. Chen S, Liu F, Anh V (2011) A novel implicit finite difference method for the one-dimensional fractional percolation equation. Numer Algorithms 56(4):517–535

    Article  MathSciNet  Google Scholar 

  14. Huang J, Zhao Y, Arshad S, Li K, Tang Y (2019) Alternating direction implicit schemes for the two-dimensional time fractional nonlinear super-diffusion equations. J Comput Math 37:3

    Article  MathSciNet  Google Scholar 

  15. Wang Y-M, Ren L (2019) Efficient compact finite difference methods for a class of time-fractional convection-reaction-diffusion equations with variable coefficients. Int J Comput Math 96(2):264–297

    Article  MathSciNet  Google Scholar 

  16. Chen S, Liu F, Zhuang P, Anh V (2009) Finite difference approximations for the fractional Fokker–Planck equation. Appl Math Modell 33(1):256–273

    Article  MathSciNet  Google Scholar 

  17. Ford NJ, Xiao J, Yan Y (2011) A finite element method for time fractional partial differential equations. Fract Calc Appl Anal 14(3):454–474

    Article  MathSciNet  Google Scholar 

  18. Jiang Y, Ma J (2011) High-order finite element methods for time-fractional partial differential equations. J Comput Appl Math 235(11):3285–3290

    Article  MathSciNet  Google Scholar 

  19. Zhao Z, Li C (2012) Fractional difference/finite element approximations for the time-space fractional telegraph equation. Appl Math Comput 219(6):2975–2988

    MathSciNet  MATH  Google Scholar 

  20. Li L, Xu D, Luo M (2013) Alternating direction implicit Galerkin finite element method for the two-dimensional fractional diffusion-wave equation. J Comput Phys 255:471–485

    Article  MathSciNet  Google Scholar 

  21. Agrawal OP (2000) A general solution for the fourth-order fractional diffusion-wave equation. Fract Calc Appl Anal 3(1):1–12

    MathSciNet  MATH  Google Scholar 

  22. Huang Q, Huang G, Zhan H (2008) A finite element solution for the fractional advection–dispersion equation. Adv Water Resour 31(12):1578–1589

    Article  Google Scholar 

  23. Zheng Y, Li C, Zhao Z (2010) A note on the finite element method for the space-fractional advection diffusion equation. Comput Math Appl 59(5):1718–1726

    Article  MathSciNet  Google Scholar 

  24. Deng W (2009) Finite element method for the space and time fractional Fokker–Planck equation. SIAM J Numer Anal 47(1):204–226

    Article  MathSciNet  Google Scholar 

  25. Uddin M, Haq S (2011) Rbfs approximation method for time fractional partial differential equations. Commun Nonlinear Sci Numer Simul 16(11):4208–4214

    Article  MathSciNet  Google Scholar 

  26. Abbaszadeh M, Dehghan M (2020) Direct meshless local Petrov–Galerkin (DMLPG) method for time-fractional fourth-order reaction-diffusion problem on complex domains. Comput Math Appl 79(3):876–888

    Article  MathSciNet  Google Scholar 

  27. Hussain M, Haq S, Ghafoor A (2019) Meshless spectral method for solution of time-fractional coupled KDV equations. Appl Math Comput 341:321–334

    MathSciNet  MATH  Google Scholar 

  28. Soman K (2010) Insight into wavelets: from theory to practice. PHI Learning Pvt, Ltd, New York

    Google Scholar 

  29. Oruç Ö (2018) A computational method based on Hermite wavelets for two-dimensional Sobolev and regularized long wave equations in fluids. Numer Methods Partial Differ Equ 34(5):1693–1715

    Article  MathSciNet  Google Scholar 

  30. Secer A, Ozdemir N (2019) An effective computational approach based on Gegenbauer wavelets for solving the time-fractional KDV-Burgers–Kuramoto equation. Adv Differ Equ 2019(1):386

    Article  MathSciNet  Google Scholar 

  31. Xu X, Xu D (2018) Legendre wavelets direct method for the numerical solution of time-fractional order telegraph equations. Mediterr J Math 15(1):27

    Article  MathSciNet  Google Scholar 

  32. Ghafoor A, Haq S, Hussain M, Kumam P, Jan MA (2019) Approximate solutions of time fractional diffusion wave models. Mathematics 7(10):923

    Article  Google Scholar 

  33. Chen C, Hsiao C (1997) Haar wavelet method for solving lumped and distributed-parameter systems. IEE Proc Control Theory Appl 144(1):87–94

    Article  MathSciNet  Google Scholar 

  34. Cattani C (2001) Haar wavelet splines. J Interdiscip Math 4(1):35–47

    Article  MathSciNet  Google Scholar 

  35. Cattani C (2004) Haar wavelets based technique in evolution problems. In: Proceedings-Estonian Academy of Sciences Physics Mathematics, vol 53. Estonian Academy Publishers, 1999, pp 45–63

  36. Lepik Ü (2007) Numerical solution of evolution equations by the Haar wavelet method. Appl Math Comput 185(1):695–704

    MathSciNet  MATH  Google Scholar 

  37. Lepik Ü (2011) Solving PDES with the aid of two-dimensional Haar wavelets. Comput Math Appli 61(7):1873–1879

    Article  MathSciNet  Google Scholar 

  38. Hosseini VR, Chen W, Avazzadeh Z (2014) Numerical solution of fractional telegraph equation by using radial basis functions. Eng Anal Bound Elem 38:31–39

    Article  MathSciNet  Google Scholar 

  39. Zhang X, Liu J, Wen J, Tang B, He Y (2013) Analysis for one-dimensional time-fractional tricomi-type equations by LDG methods. Numer Algorithms 63(1):143–164

    Article  MathSciNet  Google Scholar 

  40. Zhang X, Huang P, Feng X, Wei L (2013) Finite element method for two-dimensional time-fractional tricomi-type equations. Numer Methods Partial Differ Equ 29(4):1081–1096

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Numerical Sciences, Kohat University of Science and Technology, Kohat, KP, 26000, Pakistan

    Abdul Ghafoor & Amir Rasool

  2. Faculty of Engineering Sciences, GIK Institute, Topi, KP, 23640, Pakistan

    Sirajul Haq

  3. Department of Mathematics, Cankaya University, 06530, Balgat, Ankara, Turkey

    Dumitru Baleanu

  4. Institute of Space Sciences, Magurele, Bucharest, Romania

    Dumitru Baleanu

Authors
  1. Abdul Ghafoor
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sirajul Haq
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Amir Rasool
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dumitru Baleanu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abdul Ghafoor.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ghafoor, A., Haq, S., Rasool, A. et al. An efficient numerical algorithm for the study of time fractional Tricomi and Keldysh type equations. Engineering with Computers 38, 3185–3195 (2022). https://doi.org/10.1007/s00366-020-01257-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00366-020-01257-8

Keywords

Search

Navigation