Leveraging circuit theory and nonlinear dynamics for the efficiency improvement of energy harvesting

Abstract

We study the performance of vibrational energy harvesting systems with piezoelectric and magnetic inductive transducers, assuming the power of external disturbance concentrated around a specific frequency. Both linear and nonlinear harvester models are considered. We use circuit theory and equivalent circuits to show that a large improvement in both the harvested energy and the power efficiency is obtained, for linear systems, through a proper reactive modification of the load. For nonlinear systems, we use methods of nonlinear dynamics to derive analytical formulae for the output voltage, the harvested energy and the power efficiency. We show that also for the nonlinear case, the modified load significantly boosts the performance.

1 Introduction

Bolstered by the rapid deployment of the Industry 4.0 paradigm, the proliferation of Internet of Things (IoT) applications is expected to reach 31 billion connected devices by 2020, and 75 billion devices by 2025 [1]. At the very foundation of IoT lies the idea that a network of devices with embedded electronics, sensors, actuators and software are connected and interact via the Internet [2,3,4]. Among the many challenges posed by IoT, the problem of how to supply power to this network of wireless nodes is of paramount importance. Although the power needed to operate each device is small, typically in the microwatt to milliwatt range, their huge number, their often remote and difficult to access location and their ongoing miniaturization make old fashioned solutions, e.g., batteries, quite rarely a viable approach. A striking example are wearable systems, which are both portable and wireless, and thus where batteries would be an obvious choice. Unfortunately, the progress in energy storage density has, for the moment, been unable to keep the pace and batteries remain, with respect to other electronic components, bulky and heavy [5, 6].

A significant literature body, see, e.g., [7,8,9], suggests that electronic systems capable to wirelessly exchange not only information but also energy may represent a valid alternative. Yet another solution is to design systems capable of self-powering, by scavenging energy from the surrounding environment. The collected power can be used as a direct power source, or at least to extend the battery lifespan for those systems where continuous operation without maintenance is required. The set of technical solutions exploiting this idea is referred to as energy harvesting [10,11,12].

Energy harvesting (EH) technologies exploit different physical principles, depending upon the external power source to be tapped. Irrespective of the working principle, a common issue of EH apparatuses is the limited power density of the source. However, although negligible at the macroscale, energy dispersed in the environment is significant at the microscale, making EH technologies a viable solution to powering small autonomous devices.

Among the many possible sources, kinetic energy plays a very prominent role, because of its comparatively large power density and its widespread availability. Kinetic energy exists in the form of mechanical vibrations, regular or random displacements and driving forces. It can be found in mechanical structures, due to impacts or periodic motions, in buildings and bridges, due to traffic and wind, in vehicles, due to road asperity and engine induced vibrations, as well as in human body motion [13,14,15,16].

Kinetic energy harvesters rely on some kind of oscillating structure to capture vibrations, and on a transducer that converts kinetic energy into electrical power. Linear energy harvesters require a fine tuning of the oscillator’s resonant frequency, to match the spectral range of environmental vibrations where most of the energy is concentrated. In many applications, this is a key limiting factor, due to geometrical and dimensional constraints. In fact, the rule of thumb is that the smaller is the size of an object, the larger its resonant frequency will be. Thus, it is very difficult to design energy harvesters that are both miniaturized and that work efficiently at low frequencies, making, for instance, the realization of wearable electronics that scavenge energy from human body motion very challenging. In this respect, it has been suggested that nonlinear oscillators can perform better than linear ones [17,18,19,20,21,22]. When compared to their linear counterparts, nonlinear energy harvesters show a wider steady-state frequency bandwidth and may exhibit multi-stability and even chaotic dynamics, thus suggesting that they can be more efficient especially in random and non-stationary vibratory environments [23,24,25,26].

Oscillators periodically exchange energy between two different forms. The losses taking place during each oscillation cycle, both dissipated by internal resistances and delivered to the load, can be significantly less than the total energy involved in the oscillation. For example, an LC oscillator characterized by a quality factor Q loses approximately a fraction 1/Q of its energy per oscillation cycle. The remaining power bounces back and forth between the source and the load. It is well known from circuit theory that, in order to maximize the power efficiency, it is necessary to minimize the power that merely flows in the circuit with no useful contribution, a procedure known as power factor correction.

In this paper, we apply circuit theory and nonlinear dynamics methods to improve the efficiency of EH systems. We study the equivalent circuits (ECs) for two well-known energy harvesters: piezoelectric and magnetic inductive. Using circuit theory, we show that for linear harvesters, a simple modification of the load inspired by previous works [27,28,29,30,31] allows to improve the maximum collected power and the power efficiency. In the nonlinear case, using nonlinear dynamics methods we solve the state equations and find analytical formulae for the harvested power and the power efficiency. We show that, similarly to the linear case, properly modifying the load increases both the harvested power and the power efficiency.

The paper is organized as follows. In Sect. 2, we present the harvester models and ECs for both piezoelectric- and magnetic induction-based devices, showing how nonlinearities in the mechanical part (stiffness of the rod and in the springs, respectively) can be accounted for in the circuit equations. In Sect. 3, we investigate the linear limit. We apply standard circuit theory to solve the governing equations, and we show how the harvested energy and power efficiency can be maximized by a proper adaptation of the load. In Sect. 4, we study the nonlinear case. We show that the governing equations can be put in a standard form, valid for both the piezoelectric- and the magnetic inductance-based harvesters. We use tools of nonlinear dynamics to solve the state equations, and we derive analytical formulae for the harvested power and power efficiency. We show that even for the nonlinear harvester, the adapted load outperforms a purely resistive load. Finally, Sect. 5 is devoted to conclusions.

2 Harvester modeling

An EH device for mechanical vibration scavenging is composed by an oscillator that captures kinetic energy from environmental vibrations, and by a transducer, responsible for the conversion of kinetic energy into usable electrical power. Transducers may exploit different physical principles for energy conversion including piezoelectric, magnetic induction and electrostatic transduction methods.

Fig. 1

Schematic representation of a piezoelectric energy harvester

2.1 Piezoelectric energy harvester

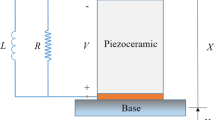
A schematic representation of a piezoelectric energy harvester is shown in Fig. 1.

A simple piezoelectric energy harvester is composed by a cantilever beam, covered by a layer of piezoelectric material, fixed at one end to a moving support with an inertial mass m at the opposite end to increase the oscillation amplitude. Vibrations of the support produce oscillations of the cantilever, inducing mechanical stress and strain in the piezoelectric material that are converted into electrical currents.

A more sophisticated setup is shown in Fig. 1 [23, 32]. A thin beam covered by piezoelectric layers and with an inertial mass m is clamped at both ends. An external static load can be applied to one end, to tune the natural frequency of the beam and to introduce a cubic nonlinearity. Under the influence of an external dynamic excitation, the beam undergoes oscillations around a static position defined by the axial load. If the mass of the cantilever and the effect of gravity are neglected, the equation of motion for the mechanical system reads [18, 33]

$$\begin{aligned} m \, \ddot{x} = -U'(x) - \gamma \, \dot{x} - k_v \, v(t) + F_{\text {in}} \end{aligned}$$

(1)

where x is the displacement from the vertical equilibrium position, U(x) is the elastic potential of the cantilever beam and the prime denotes the first derivative, $\gamma$ is the friction coefficient, $k_v\,v(t)$ describes the action of the piezoelectric layer onto the mechanical system (v(t) is the transducer voltage), and $F_{\text {in}}$ is the external perturbation.

The energy of ambient vibrations is typically spread over a wide frequency range, suggesting to model perturbation as white Gaussian noise. However, such random process can be represented as a superposition of harmonic (sinusoidal) signals with random phases and frequencies [34]. For the sake of simplicity, we consider here a vibration energy concentrated around a single frequency, and thus, we model vibrations as a simple harmonic driving force.

The piezoelectric device is characterized by an internal capacitance $C_2$, an internal resistance, here assumed to be negligible for the sake of simplicity, and a coupling with the mechanical part represented by parameter $k_c$.

The EC for the electromechanical system is shown in Fig. 2, where the parallel branches on the right represent the piezoelectric device, feeding a generic load.

Fig. 2

EC for the piezoelectric harvester

Applying Kirchhoff voltage law (KVL) to the left loop yields

$$\begin{aligned} \ddot{q}_1 = - \dfrac{1}{L_1} v_1(q_1) - \dfrac{R_1}{L_1} \dot{q}_1 - \dfrac{k_v}{L_1} v_2 + \dfrac{1}{L_1} v_{\text {in}} \end{aligned}$$

(2)

where $\dot{q}_1 = i_1(t)$, and $v_1(q_1)$ is the voltage–charge characteristic of the capacitor $C_1$. It is straightforward to verify that (1) and (2) are equivalent provided $x = q_1$, $m=L_1$, $U'(x)=v_1(q_1)$, $\gamma =R_1$, $F_{\text {in}} = v_{\text {in}}$ and $v=v_2$.

Application of Kirchhoff current law (KCL) to node a on the right yields

$$\begin{aligned} \dot{v}_2 = \dfrac{k_c}{C_2} \dot{q}_1 - \dfrac{1}{C_2} i_2 \end{aligned}$$

(3)

Usually, purely resistive loads are considered [18, 33]. However, we will show that both the harvested power and the harvester efficiency can be significantly boosted if the load has a reactive component.

2.2 Electromagnetic energy harvester

Examples of electromagnetic energy harvesters are given in [35, 36], with the schematic representation shown in Fig. 3. A small magnet with mass m is placed inside a tube, connected to vibrating supports through springs, and with a coil wrapped around the tube. An alternative setup, where the magnet is suspended in the tube by a magnetic field generated by other magnets, is described in [19]. Vibrations of the supports produce oscillations of the suspended magnet, inducing a current in the surrounding coil through Faraday’s law. The equation of motion for the magnet is

$$\begin{aligned} m \, \ddot{y} = - U'(y) - c \, \dot{y} - r_1 \, i(t) + F_{\text {in}} \end{aligned}$$

(4)

where y is the displacement, U(y) is the elastic potential of the springs, c is the friction constant, $r_1 i(t)$ describes the interaction with the coil through magnetic induction, and $F_{\text {in}}$ is the external perturbation.

Fig. 3

Schematic representation of an electromagnetic energy harvester

Figure 4 shows the EC for the electromagnetic harvester, where the loop on the right describes the magnetic induced current in the coil, providing power to the load.

Fig. 4

EC for the electromagnetic harvester

Applying KVL to the loop on the left gives

$$\begin{aligned} \ddot{q}_1 = - \dfrac{1}{L_1} v_1(q_1) - \dfrac{R_1}{L_1} \dot{q}_1 - \dfrac{r_1}{L_1} i_2 + \dfrac{1}{L_1} v_{\text {in}} \end{aligned}$$

(5)

which maps onto (4) provided $y = q_1$, $m= L_1$, $U'(y) = v_1(q_1)$, $c = R_1$, $i=i_2$ and $F_{\text {in}} = v_{\text {in}}$

Applying KVL to the loop on the right yields

$$\begin{aligned} \dot{i}_2 = \dfrac{r_2}{L_2} \dot{q}_1 - \dfrac{1}{L_2} v_2 \end{aligned}$$

(6)

We notice that (2)–(3) and (5)–(6) are completely analogous.

3 Small signal analysis

We begin to study the small signal limit, where it can be assumed that all one-port components have linear characteristics.

3.1 Piezoelectric energy harvester

Consider the EC in Fig. 2. At steady state in the phasor domain,¹ denoting by $Y_2$ the load admittance, the state equations read

$$\begin{aligned} \left[ \begin{array}{cc} R_1 + j X_1 &{} k_v\\ -k_c &{} G_2 + j B_2 \end{array}\right] \left[ \begin{array}{c} I_1 \\ V_2 \end{array}\right] = \left[ \begin{array}{c} V_{\text {in}} \\ 0 \end{array}\right] \end{aligned}$$

(7)

where $X_1$ is the reactance of the left loop

$$\begin{aligned} X_1 = \omega L_1 - \dfrac{1}{\omega C_1} \end{aligned}$$

(8)

$\omega$ and $V_{\mathrm{in}}$ are the angular frequency and amplitude of the external forcing term, respectively, while $G_2 = \text {Re}\{Y_2\}$ is the conductance of the load, and $B_2 = \omega C_2 + \text {Im}\{Y_2\}$ is the susceptance of the right part.

The relevant transfer functions are

$$\begin{aligned} Y_{\text {in}}(\omega )&= \dfrac{I_1}{V_{\text {in}}} = \dfrac{G_2 + j B_2}{(R_1+j X_1)(G_2 + j B_2) + k_v \, k_c} \end{aligned}$$

(9)

$$\begin{aligned} H(\omega )&= \dfrac{V_2}{V_{\text {in}}} = \dfrac{k_c}{(R_1+j X_1)(G_2 + j B_2) + k_v \, k_c} \end{aligned}$$

(10)

Assuming that the resonator on the left works at the resonance frequency $\omega _0 = 1/\sqrt{L_1C_1}$ and that $\omega _0=\omega$ to maximize energy collection, using phasors and (10), the average power delivered to the load is

$$\begin{aligned} P_{\text {out}} =&{ \dfrac{1}{2} \, \text {Re}[V_2 \, I_2^*] = \dfrac{1}{2} G_2 \, |V_2|^2} = \dfrac{1}{2} G_2 \, |H|^2 \, |V_{\text {in}}|^2 \nonumber \\ =&\dfrac{1}{2} \, \dfrac{G_2 k_c^2}{K^2 + R_1^2 B_2^2} \, |V_{\text {in}}|^2 \end{aligned}$$

(11)

where $K=R_1G_2+k_vk_c$. Conversely, using (9) the average power injected by the voltage source is

$$\begin{aligned} P_{\text {in}} =&{\dfrac{1}{2} \, \text {Re}[V_{\text {in}} \, I_1^*] = \dfrac{1}{2} \, \text {Re}[Y_{\text {in}}^*] \, |V_{\text {in}}|^2 } \nonumber \\ =&\dfrac{1}{2} \, \dfrac{G_2 K + R_1 B_2^2}{K^2 + R_1^2 B_2^2} \, |V_{\text {in}}|^2 \end{aligned}$$

(12)

so that the power efficiency reads

$$\begin{aligned} \eta _{\text {pz}} = \dfrac{P_{\text {out}}}{P_{\text {in}}} = \dfrac{G_2 k_c^2}{G_2 K + R_1 B_2^2} \end{aligned}$$

(13)

As a result, both the average dissipated power $P_{\text {out}}$ and the power efficiency $\eta _{\text {pz}}$ are maximized when the susceptance $B_2$ is null.² This condition cannot be attained by a resistive load, as customarily assumed [20, 33, 35,36,37]. Conversely, maximum dissipated power and efficiency are achieved if the load is composed by a resistor $R_2 = 1/G_2$ connected in parallel with an inductor $L_2$ with inductance $L_2 = 1/(\omega _0^2 C_2) = L_1 C_1/C_2$, as shown in Fig. 8b. In this case, the circuit in Fig. 2 is composed by two resonators with the same resonant frequency connected through the controlled sources.

A realistic transducer model must represent a passive element, so that it does not supply energy to the rest of the circuit. According to the passive sign convention [38], the average power dissipated by the controlled sources is

$$\begin{aligned} P_{k_v} + P_{k_c}&= \dfrac{1}{2} (k_v-k_c) \, \text {Re}\{V_2 \, I_1^*\}\nonumber \\&= \dfrac{1}{2} (k_v-k_c) \text {Re}\{ H(\omega ) \, Y^*_{\text {in}}(\omega )\} |V_{\text {in}}|^2 \end{aligned}$$

(14)

In particular, at the resonance frequency

$$\begin{aligned} P_{k_v} + P_{k_c} = \dfrac{1}{2} (k_v-k_c) \dfrac{G_2 \,k_c}{(R_1 \,G_2 + k_v k_c)^2 } |V_{\text {in}}|^2 \end{aligned}$$

(15)

Equation (15) implies that the transducer is passive if and only if $k_v \ge k_c$. Considering that dissipation is accounted for by $R_1$, it can be assumed that the transducer’s energy balance is null for all frequencies, thus implying $k_v = k_c$. For this reason, in many models one parameter only is used to describe the transducer [23, 31, 39].

Maximum average dissipated power is obtained with the load conductance

$$\begin{aligned} G_2 = \dfrac{k_v^2}{R_1} \end{aligned}$$

(16)

corresponding to a maximum average absorbed power

$$\begin{aligned} P_{\text {out}}^{\text {max}} = \dfrac{|V_{\text {in}}|^2}{8R_1} \end{aligned}$$

(17)

and to the expected 50% efficiency [38].

Efficiency higher than 50% can obviously be attained, either decreasing $R_1$ ($G_2$ being kept fixed) or vice versa increasing $R_2$ ($R_1$ being kept fixed). In fact, from (13) with $B_2 = 0$ S we have $\partial \eta _{\text {pz}}/\partial R_1<0$ and $\partial \eta _{\text {pz}}/\partial G_2<0$. In particular, in the limit $G_2 \ll k_ck_v/R_1$, we have $K \approx k_v k_c$ and $\eta _{\text {pz}} \rightarrow 1$. However, higher efficiency can be attained only giving up the maximum power transfer to the load, as from (11) we find that $\partial P_{\text {out}}/\partial G_2 \ne 0$ for $G_2 \ne k_ck_v/R_1$.

Figure 5 shows the Bode diagram for the magnitude of transfer functions $Y_{\text {in}}(\omega )$ and $H(\omega )$ for the cases of a resistive and of a resistive–inductive load. Parameter values have been normalized (including time) so that $\omega _0=1$ rad/s.

Fig. 5

Magnitude Bode diagram for transfer functions $Y_{\text {in}}(\omega )$ (above), and $H(\omega )$ (below), for a resistive (red) and a resistive–reactive load (blue). Parameter values are $L_1 = 0.4$ H; $C_1 = 2.5$ F; $L_2 = 0.2$ H; $C_2 = 5$ F; $R_1 = 0.04~\varOmega$; $G_2 = 1.5625$ S; $k_v = k_c = 0.25$ . (Color figure online)

Fig. 6

Output average power (above) and power efficiency (below) for a resistive load (red) and a resistive–reactive load (blue) versus the frequency of the external forcing. Parameter values are the same used in Fig. 5. Output average power (above) is calculated assuming $V_{\mathrm{in}} = 1$V . (Color figure online)

Figure 6 shows the average dissipated (output) power $P_{\text {out}}$ and the power efficiency $\eta _{\text {pz}}$ as a function of the external forcing term frequency. For the resistive load case, the average dissipated power is maximized by a proper matching of the resonance frequency to the forcing term. This can be done, for instance, by an appropriate choice of the inertial mass m. However, power efficiency is maximum at zero frequency and decreases rapidly as the forcing frequency increases. On the contrary, the resistive–reactive load not only has higher average dissipated power but, more importantly, both dissipated power and efficiency are maximum at the same frequency, provided that the mechanical and the electrical parts are tuned to the same resonance frequency. These findings are in agreement with previous works [31, 39].

Finally, 7 shows the averaged power delivered to the load and the power efficiency, as functions of the inductance $L_2$ for the resistive–reactive load in Fig. 8b. It can be seen that both $P_{\text {out}}$ and $\eta _{\text {pz}}$ are maximum for $L_2=L_1 C_1/C_2 = 0.2$ S, so that $B_2 =0$ S. It can also be seen that both the output power and the efficiency converge to constant values for large $L_2$, corresponding to the values of a purely resistive load. (For $L_2\rightarrow +\infty$, the inductor is equivalent to an open circuit.)

Fig. 7

Average (output) power delivered to the load (above), and power efficiency (below), as functions of the inductance $L_2$ for the resistive–reactive load in Fig. 8b. Average output power (above) is calculated assuming $V_{\text {in}} = 1$ V. Other parameter values are the same used in Fig. 5

3.2 Electromagnetic energy harvester

The analysis of the electromagnetic energy harvester is completely analogous. Consider the EC shown in Fig. 4. Denoting as $Z_2$ the load impedance, at steady state in the phasor domain the state equations read

$$\begin{aligned} \left[ \begin{array}{cc} R_1 + j X_1 &{} r_1\\ -r_2 &{} R_2 + j X_2 \end{array}\right] \left[ \begin{array}{c} I_1 \\ I_2 \end{array}\right] = \left[ \begin{array}{c} V_{\text {in}} \\ 0 \end{array}\right] \end{aligned}$$

(18)

where $X_1$ and $X_2$ are the reactances of the left and right loops, respectively

$$\begin{aligned} X_1&= \omega L_1 - \dfrac{1}{\omega C_1} \end{aligned}$$

(19)

$$\begin{aligned} X_2&= \omega L_2 + \text {Im}\{Z_2\} \end{aligned}$$

(20)

and $R_2 = \text {Re}\{Z_2\}$.

The relevant transfer functions are

$$\begin{aligned} Y_{\text {in}}(\omega )&= \dfrac{I_1}{V_{\text {in}}} = \dfrac{R_2 + j X_2}{(R_1+j X_1)(R_2 + j X_2) + r_1 \, r_2} \end{aligned}$$

(21)

$$\begin{aligned} Y_{\text {out}}(\omega )&= \dfrac{I_2}{V_{\text {in}}} = \dfrac{r_2}{(R_1+j X_1)(R_2 + j X_2) + r_1 \, r_2} \end{aligned}$$

(22)

Assuming that the resonator on the left works at the resonance frequency and denoting by $R^2 = R_1 R_2 + r_1 r_2$, the average power delivered to the load is

$$\begin{aligned} P_{\text {out}} = \dfrac{1}{2} \dfrac{R_2 r_2^2}{R^4+R_1X_2^2}|V_{\text {in}}|^2 , \end{aligned}$$

(23)

whereas the average injected power is

$$\begin{aligned} P_{\text {in}} = \dfrac{1}{2} \dfrac{R^2 R_2 + R_1 X_2^2}{R^4 + R_1^2 X_2^2} |V_{\text {in}}|^2 \end{aligned}$$

(24)

with power efficiency

$$\begin{aligned} \eta _{\text {em}} = \dfrac{R_2 r_2^2}{R^2 R_2 + R_1 X_2^2} \end{aligned}$$

(25)

Similarly to the piezoelectric energy harvester case, to maximize the average dissipated power and the power efficiency, the reactance $X_2$ must vanish. This can be obtained connecting a capacitor with capacitance $C_2 = 1/(\omega _0^2L_2)=C_1L_1/L_2$, in series with the resistor, as shown in Fig. 8c. In this way, the EC in Fig. 4 is composed of two resonators, connected through the controlled sources, characterized by the same resonance frequency $\omega _0$.

For the magnetic induction energy harvester, the average power dissipated by the transducer is

$$\begin{aligned} P_{r_1} + P_{r_2}&= \dfrac{1}{2} \left( r_1 \text {Re}\{I_2 \, I_1^*\} - r_2 \text {Re}\{I_1 \, I_2^* \} \right) \nonumber \\&= \dfrac{1}{2} \left( r_1 \, \text {Re}\{Y_{\text {out}}(\omega )\, Y_{\text {in}}^*(\omega ) \} \right. \nonumber \\&\qquad \left. -\, r_2 \, \text {Re}\{Y_{\text {in}}(\omega ) \, Y_{\text {out}}^*(\omega )\} \right) |V_{\mathrm{in}}|^2 \end{aligned}$$

(26)

At the resonance frequency

$$\begin{aligned} \begin{aligned} P_{r_1} + P_{r_2} = \dfrac{1}{2} (r_1-r_2) \dfrac{R_2 \,r_2}{(R_1\,R_2 + r_1 \, r_2)} |V_{\mathrm {in}}|^2 \end{aligned} \end{aligned}$$

(27)

thus the transducer is passive for all frequencies if and only if $r_1 \ge r_2$.

Assuming $r_1=r_2$, the maximum average dissipated power is obtained if the load has resistance

$$\begin{aligned} R_2 = \dfrac{r_1^2}{R_1} \end{aligned}$$

(28)

so that

$$\begin{aligned} P_{\text {out}}^{\text {max}} = \dfrac{|V_{\text {in}}|^2}{8 R_1} \end{aligned}$$

(29)

and the efficiency reaches the theoretical maximum of 50%.

Fig. 8

Loads for the cases under consideration. a Resistive load considered in previous works. b Matched RL load for the piezoelectric energy harvester. c Matched RC load for the electromagnetic energy harvester

4 Nonlinear energy harvester analysis

The main drawback of linear energy harvesters is the limited working bandwidth. Linear resonators are designed to work efficiently at a specific, resonance frequency $\omega _0$. The amplitude response decreases quickly away from $\omega _0$, dropping dramatically outside the passband. Several works [17,18,19,20,21,22] suggest that nonlinear resonator-based harvesters may overcome this limitation. Exploiting the hysteretic amplitude response of a nonlinear resonator, it is in principle possible to increase the collected power, trading off the efficiency at a specific frequency against a larger bandwidth.

The idea is illustrated in Fig. 9, where the typical frequency response (amplitude versus frequency of the forcing term) of linear (black line) and nonlinear (blue and red lines) oscillators is compared. For similar values of the parameters, a linear oscillator in general exhibits an higher amplitude response than the nonlinear counterpart, but the amplitude decreases quickly out of a frequency interval, the passband width $B_\mathrm{L}$. Conversely, a nonlinear oscillator is in general characterized by a lower maximum amplitude, and by a wider passband width $B_\mathrm{N}$ where the amplitude response remains significant.

Fig. 9

Qualitative representation of the amplitude vs frequency response for a linear (black) and a nonlinear (blue-red) periodically driven resonator. Blue lines represent stable periodic responses, whereas the red line is an unstable response. $B_\mathrm{L}$ and $B_\mathrm{N}$ denote the passband width for the linear and the nonlinear resonator, respectively . (Color figure online)

4.1 Nonlinear piezoelectric energy harvester

Consider the piezoelectric energy harvester, modeled by the EC shown in Fig. 2, with the resistive–inductive load in Fig. 8b. Nonlinearity in the stiffness of the beam is taken into account considering a capacitor with nonlinear voltage–charge characteristic. We assume a Duffing-type cubic stiffness term, describing the hardening spring effect observed in many mechanical systems [40]

$$\begin{aligned} v_1(q_1) = \dfrac{1}{C_1} q_1 + \dfrac{1}{{{\widetilde{C}}}_1} q_1^3 \end{aligned}$$

(30)

Similarly, the inductor in the load is assumed to have a nonlinear current–flux characteristic, matching the nonlinearity of the capacitor

$$\begin{aligned} i_{L_2} = \dfrac{1}{L_2} \phi _2 + \dfrac{1}{{{\widetilde{L}}}_2} \phi _2^3 \end{aligned}$$

(31)

Applying KVL to the left loop, KCL to node a, and rearranging the terms, we obtain the dynamic equations

$$\begin{aligned} \ddot{q}_1 + \dfrac{1}{L_1 C_1} q_1&= \dfrac{1}{L_1} v_{\text {in}} - \dfrac{R_1}{L_1} \dot{q}_1 - \dfrac{1}{L_1 {{\widetilde{C}}}_1} q_1^3 - \dfrac{k_v}{L_1} {\dot{\phi }}_2 \end{aligned}$$

(32)

$$\begin{aligned} \ddot{\phi }_2 + \dfrac{1}{L_2 C_2} \phi _2&= - \dfrac{G_2}{C_2} {\dot{\phi }}_2 - \dfrac{1}{{{\widetilde{L}}}_2 C_2} \phi _2^3 + \dfrac{k_c}{C_2} \dot{q}_1 \end{aligned}$$

(33)

Making the substitution $x_1 = q_1$, $x_2 = \phi _2$, assuming $v_{\text {in}}(t)/L_1 = \varepsilon A \cos (\omega \, t)$ and introducing the new parameters³:

$$\begin{aligned} \dfrac{1}{\sqrt{L_1 C_1}}&= \omega _1&\dfrac{1}{\sqrt{L_2 C_2}}&= \omega _2&\dfrac{R_1}{L_1}&= \varepsilon \gamma _1 \\ \dfrac{G_2}{C_2}&= \varepsilon \gamma _2&\dfrac{1}{L_1 \widetilde{C}_1}&= \varepsilon \delta _1&\dfrac{1}{{{\widetilde{L}}}_2 C_2}&= \varepsilon \delta _2 \\ \dfrac{k_v}{L_1}&= \varepsilon \sigma _1&\dfrac{k_c}{C_2}&= \varepsilon \sigma _2 \end{aligned}$$

equations (32) and (33) become

$$\begin{aligned} \ddot{x}_1 + \omega _1^2 \, x_1&= \varepsilon \left( A \cos (\omega \, t) -\gamma _1 \dot{x}_1 - \delta _1 x_1^3 - \sigma _1 \dot{x}_2 \right) \end{aligned}$$

(34)

$$\begin{aligned} \ddot{x}_2 + \omega _2^2 \, x_2&= \varepsilon \left( - \gamma _2 \dot{x}_2 - \delta _2 x_2^3 + \sigma _2 \dot{x}_1\right) \end{aligned}$$

(35)

4.2 Nonlinear electromagnetic energy harvester

Consider the electromagnetic energy harvester and its EC shown in Fig. 4, with the resistive–capacitive load in Fig. 8 c. In full analogy with the previous case, nonlinearity in the spring stiffness is accounted for by the nonlinear voltage–charge characteristic of the capacitor (30). We also assume that capacitor $C_2$ in the matched load has a similar characteristic

$$\begin{aligned} v_2(q_2) = \dfrac{1}{C_2} q_2 + \dfrac{1}{{{\widetilde{C}}}_2} q_2^3 \end{aligned}$$

(36)

Applying KVL to both loops, and rearranging the terms, we obtain the equations

$$\begin{aligned} \ddot{q}_1 + \dfrac{1}{L_1 C_1} q_1&= \dfrac{1}{L_1} v_{in} - \dfrac{R_1}{L_1} \dot{q}_1 - \dfrac{1}{L_1 {{\widetilde{C}}}_1} q_1^3 - \dfrac{r_1}{L_1} \dot{q}_2 \end{aligned}$$

(37)

$$\begin{aligned} \ddot{q}_2 + \dfrac{1}{L_2 C_2} q_2&= - \dfrac{R_2}{L_2} \dot{q}_2 - \dfrac{1}{L_2 {{\widetilde{C}}}_2} q_2^3 + \dfrac{r_2}{L_2} \dot{q}_1 \end{aligned}$$

(38)

Assuming again $v_{\text {in}}(t)/L_1 = \varepsilon A \cos (\omega \, t)$, making the substitution $x_i = q_i$ and introducing the new parameters

$$\begin{aligned} \dfrac{1}{\sqrt{L_i C_i}} = \omega _i \quad \dfrac{R_i}{L_i} = \varepsilon \gamma _i \quad \dfrac{1}{L_i {{\widetilde{C}}}_i} = \varepsilon \delta _i \quad \dfrac{r_i}{L_i} = \varepsilon \sigma _i \end{aligned}$$

for $i=1,2$, we obtain, again, equations (34) and (35), although with a different meaning of variables and parameters.

Therefore, we can use the same dynamical system to study both the piezoelectric and the electromagnetic energy harvester.

4.3 Analysis

We shall find an approximate solution to equations (34)-(35) exploiting a perturbative method [40] adapted to the case under study. Let’s rewrite the equations in the form

$$\begin{aligned} \ddot{x}_i + \omega _i^2 \, x_i = \varepsilon \left( A_i \cos (\omega t) - \gamma _i \dot{x}_i - \delta _i x_i^3 - \sigma _i \dot{x}_j \right) \end{aligned}$$

(39)

with $i=1,2$, $j \ne i$ and

$$\begin{aligned} A_i = \left\{ \begin{array}{lr} A &{} \text {for} \; i= 1\\ 0 &{} \text {for} \; i= 2 \end{array} \right. \qquad \sigma _i = \left\{ \begin{array}{lr} \sigma _1 &{} \text {for} \; i= 1\\ -\sigma _2 &{} \text {for} \; i= 2 \end{array} \right. \end{aligned}$$

(40)

We introduce the invertible coordinate transformation⁴

$$\begin{aligned} \left( \begin{array}{c} u_i \\ v_i \end{array} \right) = \left( \begin{array}{cc} \cos (\omega t) &{}\quad -\dfrac{1}{\omega } \sin (\omega t) \\ -\sin (\omega t) &{}\quad - \dfrac{1}{\omega } \cos ( \omega t) \end{array} \right) \left( \begin{array}{c} x_i \\ \dot{x}_i \end{array} \right) \end{aligned}$$

(41)

In the new rotating reference frame, the unforced system is stationary. Taking time derivatives

$$\begin{aligned} \dot{u}_i =&-\dfrac{1}{\omega } \left( \ddot{x}_i + \omega ^2 x_i \right) \sin (\omega t) \end{aligned}$$

(42)

$$\begin{aligned} \dot{v}_i =&-\dfrac{1}{\omega } \left( \ddot{x}_i + \omega ^2 x_i \right) \cos (\omega t) \end{aligned}$$

(43)

introducing $\varOmega _i = (\omega _i^2-\omega ^2)/\varepsilon$, and using (39) we obtain

$$\begin{aligned} \dot{u}_i&= - \dfrac{\varepsilon }{\omega } \left( A_i \cos (\omega t) - \gamma _i \dot{x}_i - \delta _i x_i^3 - \varOmega _i x_i - \sigma _i \dot{x}_j\right) \nonumber \\&\quad \times \sin (\omega t) \end{aligned}$$

(44)

$$\begin{aligned} \dot{v}_i&= - \dfrac{\varepsilon }{\omega } \left( A_i \cos (\omega t) - \gamma _i \dot{x}_i - \delta _i x_i^3 - \varOmega _i x_i + \sigma _i \dot{x}_j\right) \nonumber \\&\quad \times \cos (\omega t) \end{aligned}$$

(45)

Inverting (41) and substituting into (44)–(45), we obtain a system of non-autonomous ordinary differential equations in the unknowns $u_i$ and $v_i$.

For small value of $\varepsilon$, Eqs. (44) and (45) can be averaged introducing a limited error. Integrating each function with respect to t from 0 to $T= 2\pi /\omega$ while holding $u_i$ and $v_i$ constant, we obtain the autonomous system⁵

$$\begin{aligned} \dot{u}_i&= - \dfrac{\varepsilon }{2 \omega } \left( \gamma _i \, \omega \, u_i + \dfrac{3}{4} \delta _i (u_i^2+v_i^2) v_i + \varOmega _i v_i + \sigma _i \, \omega \, u_j \right) \end{aligned}$$

(46)

$$\begin{aligned} \dot{v}_i&= - \dfrac{\varepsilon }{2 \omega } \left( A_i + \gamma _i \, \omega \, v_i - \dfrac{3}{4} \delta _i (u_i^2+v_i^2) u_i - \varOmega _i u_i \right. \nonumber \\&\quad \left. + \sigma _i \, \omega \, v_j\right) \end{aligned}$$

(47)

Introducing polar coordinates

$$\begin{aligned} u_i = a_i \cos \varphi _i \qquad v_i = a_i \sin \varphi _i , \end{aligned}$$

(48)

a straightforward calculation gives

$$\begin{aligned} \dot{a}_i&= - \dfrac{\varepsilon }{2 \omega } \left( A_i \sin \varphi _i + \gamma _i \, \omega \, a_i + \sigma _i \, \omega \, a_j \cos (\varphi _i - \varphi _j) \right) \end{aligned}$$

(49)

$$\begin{aligned} {\dot{\varphi }}_i&= - \dfrac{\varepsilon }{2 \omega } \left( \varOmega _i -\dfrac{A_i}{a_i} \cos \varphi _i + \dfrac{3}{4} \delta _i a_i^2 \right. \nonumber \\&\quad \left. +\, \sigma _i \omega \dfrac{a_j}{a_i} \sin (\varphi _i - \varphi _j) \right) \end{aligned}$$

(50)

The equilibrium points of equations (49) and (50) correspond to oscillations of constant amplitude in the original equations. They are found solving the system ($\psi = \varphi _2 - \varphi _1$)

$$\begin{aligned}&A \sin \varphi _1 + \gamma _1 \omega \, a_1 + \sigma _1 \omega \, a_2 \cos \psi = 0 \end{aligned}$$

(51)

$$\begin{aligned}&\gamma _2 \omega \, a_2 - \sigma _2 \omega \, a_1 \cos \psi = 0 \end{aligned}$$

(52)

$$\begin{aligned}&- A \cos \varphi _1 + \dfrac{3}{4} \delta _1 \, a_1^3 + \varOmega _1 a_1 - \sigma _1 \omega \, a_2 \sin \psi = 0 \end{aligned}$$

(53)

$$\begin{aligned}&\dfrac{3}{4} \delta _2 \, a_2^3 + \varOmega _2 a_2 - \sigma _2 \omega \, a_1 \sin \psi = 0 \end{aligned}$$

(54)

Equations (52) and (54) imply

$$\begin{aligned} \cos \psi&= \dfrac{\gamma _2}{\sigma _2} \dfrac{a_2}{a_1} \end{aligned}$$

(55)

$$\begin{aligned} \sin \psi&= \dfrac{\frac{3}{4} \delta _2 a_2^3 + \varOmega _2 \, a_2}{\sigma _2 \omega a_1} \end{aligned}$$

(56)

Squaring and summing, we obtain the first equation for the steady-state amplitudes

$$\begin{aligned} \gamma _2^2 \omega ^2 a_2^2 + \left( \dfrac{3}{4} \delta _2 a_2^3 + \varOmega _2 a_2\right) ^2 - \sigma _2^2 \omega ^2 a_1^2 = 0 \end{aligned}$$

(57)

Substituting (55) and (56) into (51) and (53), respectively, rearranging the terms, squaring and summing, we find the second amplitude equation

$$\begin{aligned}&- A^2 a_1^2 + \left( \gamma _1 \omega a_1^2 + \gamma _2 \omega \dfrac{\sigma _1}{\sigma _2} a_2^2 \right) ^2 + \nonumber \\&\quad +\, \left( \dfrac{3}{4} \delta _1 a_1^4 + \varOmega _1 a_1^2 - \dfrac{\sigma _1}{\sigma _2} a_2 \left( \dfrac{3}{4} \delta _2 a_2^3 + \varOmega _2 a_2 \right) \right) ^2 = 0 \end{aligned}$$

(58)

The nonlinear algebraic system (57)–(58) can be solved numerically, finding the steady-state amplitudes $a_1$ and $a_2$. These, in turn, allow to compute the phase shifts $\varphi _1$ and $\varphi _2$ through (55)–(56), and finally the state variables

$$\begin{aligned}&i_1(t) = \dot{x}_1(t) = -\omega a_1 \sin (\omega t + \varphi _1) \end{aligned}$$

(59)

$$\begin{aligned}&\left. \begin{array}{c} v_2(t) \\ i_2(t) \end{array} \right\} = \dot{x}_2(t) = -\omega a_2 \sin (\omega t + \varphi _2) \left\{ \begin{array}{c} \text {for \, pz}\\ \text {for \, em} \end{array} \right. \end{aligned}$$

(60)

The average injected power for both the piezoelectric and the electromagnetic energy harvester is

$$\begin{aligned} P_{\text {in}}&= \dfrac{1}{T}\int _0^T v_{\text {in}}(t) \, \dot{q}_1(t) {\text {d}}t \nonumber \\&= - \dfrac{\varepsilon A \, L_1 \omega a_1}{T}\int _0^T \sin (\omega t + \varphi _1) \cos (\omega t) {\text {d}}t \nonumber \\&= -\dfrac{\varepsilon A L_1 \omega \, a_1}{2} \sin \varphi _1 =\dfrac{\varepsilon L_1 \omega ^2}{2\sigma _2} \left( \gamma _1 \sigma _2 a_1^2 + \gamma _2 \sigma _1 a_2^2 \right) \end{aligned}$$

(61)

where the inverse of (41) has been used, together with (51) and (55).

The average dissipated power for the piezoelectric harvester is

$$\begin{aligned} P_{\text {out}}^{\text {pz}}&= \dfrac{1}{T} \int _0^T \dfrac{v_2(t)^2}{R_2} {\text {d}}t \nonumber \\&= \dfrac{\omega ^2 a_2^2}{T R_2} \int _0^T \sin ^2(\omega t + \varphi _2) {\text {d}}t = \dfrac{\omega ^2 a_2^2}{2 R_2} \end{aligned}$$

(62)

with power efficiency

$$\begin{aligned} \eta _{\text {pz}} = \dfrac{\sigma _2 \, G_2 \,a_2^2}{\varepsilon L_1 \left( \gamma _1 \sigma _2 a_1^2 + \gamma _2 \sigma _1 a_2^2 \right) } \end{aligned}$$

(63)

For the electromagnetic energy harvester, the average dissipated power is

$$\begin{aligned} P_{\text {out}}^{\text {em}} = \dfrac{1}{T} \int _0^T R_2 \, \dot{q}_2(t)^2 {\text {d}}t = \dfrac{\omega ^2 R_2 a_2^2}{2} \end{aligned}$$

(64)

with power efficiency

$$\begin{aligned} \eta _{\text {em}} = \dfrac{\sigma _2 \, R_2 \, a_2^2}{\varepsilon L_1 \left( \gamma _1 \sigma _2 a_1^2 + \gamma _2 \sigma _1 a_2^2 \right) } \end{aligned}$$

(65)

To confirm our theoretical prediction, we have performed extensive numerical simulations. The following results refer to the case of the piezoelectric EH model. Based on the analogy shown at the beginning of this section, the results can be easily adapted to the case of electromagnetic energy harvester.

Fig. 10

Input current amplitude for the nonlinear coupled resonators. Lines derive from the theoretical analysis, while symbols result from numerical simulations: Blue circles refer to the resistive–inductive load. Parameters are $\delta _1 = 0.1$, $\delta _2= 0.5$, $V_{\text {in}}=1$ V, and other parameters are the same as in Fig. 5 . (Color figure online)

Fig. 11

Output voltage amplitude comparison for a nonlinear resonator-based energy harvester: Resistive load versus resistive–inductive load. Black diamonds refer to the resistive load. Parameters are the same as in Fig. 10

Figures 10 and 11 show the amplitude response for the current $i_1(t)$ and the voltage $v_2(t)$, respectively, as a function of the voltage source angular frequency $\omega$, for the piezoelectric nonlinear energy harvester.

As expected, both curves show the hysteretic behavior due to the nonlinear stiffness. Stability and bifurcation analysis for the averaged system are determined computing the eigenvalues of the Jacobian matrix of system (49)–(50). For small values of the forcing frequency, there is only one solution, which is a stable equilibrium point of the averaged system and corresponds to stable periodic oscillations of $i_1(t)$ and $v_2(t)$ (increasing full black line), with the same period of the forcing term. At the critical value $\omega _{SN_1} \simeq 1.31$, a saddle node bifurcation, identified by a null eigenvalue, occurs. Two new, initially coincident, equilibrium points emerge that separate and become distinct when $\omega$ is further increased. The smaller amplitude corresponds to a stable equilibrium point (decreasing full line), while the larger amplitude is a saddle (dashed line). At the critical value $\omega _{SN_2} \simeq 1.57$ rad/s, the unstable saddle collides with the larger, stable equilibrium point, and they vanish through a second saddle node bifurcation. The small, stable equilibrium point ultimately survives as the only solution. Theoretical predictions of our perturbation approach are compared with the results obtained from the numerical integration of equations (32)-(33) (symbols). Numerical solutions were obtained applying a continuation method, using the solution for a certain value of the forcing frequency as the initial condition for the following value of this parameter. Obviously, the saddle-type limit cycle cannot be detected neither through forward nor backward time integration. Moreover, as the parameter $\omega$ approaches the critical value $\omega _{SN_2}$, it becomes increasingly difficult to follow the large stable solution, because its basin of attraction becomes smaller (this solution and the unstable saddle-type limit cycle get closer to each other), and trajectories are attracted toward the small stable limit cycle.

For comparison purposes, Fig. 11 also shows the output voltage for the resistive load case. This value has been calculated solving numerically the ODE system (2)-(3) for the resistive load. The output voltage curve shows a clear resemblance to the linear case, though with a high, long right tale. This behavior is due to the resonance between the output voltage $v_2(t)$ and the nonlinear hysteretic behavior of the current $i_1(t)$. The maximum amplitude is also shifted toward higher frequency values. More importantly, the matched RL load case clearly outperforms the resistive load case in a wide frequency interval.

Figure 12 shows the output average power as a function of the forcing frequency, for both the resistive–reactive and the purely resistive load. For the RL load, we have calculated the output power for both the stable (full line) and the unstable (dashed line) limit cycles, although only stable solutions are accessible for the system. The theoretical result given by (62) is compared with the numerical values obtained evaluating

$$\begin{aligned} P_{\text {out}} = \dfrac{1}{T} \int _0^T G_2 \, {\dot{\phi }}_2^2(t) \, \mathrm{d}t \end{aligned}$$

(66)

where $T = 2\pi /\omega$ is the period of the oscillation, and ${\dot{\phi }}_2(t)$ is calculated through numerical integration of the state equations (32)–(33) (symbols). It is worth noticing that the nonlinearity introduces a double peak in the average output power.

Fig. 12

Output average power as a function of forcing frequency, for both the resistive–reactive RL load, and the resistive R load. Parameters are the same as in Fig. 10

In the nonlinear case, the optimal value of the load resistance $R_2$ maximizing the average dissipated power cannot be found analytically. In fact, $R_2$ influences the value of $a_2$, which is found numerically and that, in turns, determines the output power. The dependence of the average output power and power efficiency on the output conductance is shown in Figs. 13 and 14, respectively, for a fixed value of the input frequency $\omega$. Both the cases of resistive–reactive and purely resistive load are considered. Again, the RL load solution determines a larger average output power together with a better efficiency over the whole range of values considered for $G_2$. Notice also that maximum power and power efficiency are obtained at a lower conductance with respect to the linear case.

Fig. 13

Output average power as a function of the load conductance $G_2$ for $\omega =1$. Solid line (theoretical result from (62)) and circles (numerical simulations) refer to the resistive–inductive load, and red diamonds refer to the resistive load (numerical simulations only). Parameters are the same as in Fig. 10

Fig. 14

Power efficiency comparison as a function of the load conductance $G_2$ for $\omega =1$. Solid line (theoretical result from (62)) and circles (numerical simulations) refer to the resistive–inductive load, and black diamonds refer to the resistive load (numerical simulations only). Parameters are the same as in Fig. 10

In Fig. 15, we show the power efficiency as a function of the source angular frequency $\omega$, here represented for the optimal value of $G_2$ valid for the linear harvester, i.e., $G_2=k_vk_c/R_1=1.56$ S. Even for the nonlinear case, the efficiency reaches an upper limit of about $50\%$ at the resonance frequency, showing a very good agreement between the theoretical prediction from (63) and the results of the numerical simulations. It is worth noticing that although the average output power shows a double peak in Fig. 12, the efficiency is single peaked, because the average input power is strictly increasing up to the bifurcation frequency $\omega _{SN_2}$.

For comparison, we also show the result of the numerical simulations for the purely resistive load, which is almost identical to the linear case, being the system only weakly nonlinear.

Fig. 15

Power efficiency comparison as a function of the forcing frequency. Solid line (theoretical result from (63)) and circles (numerical simulations) refer to the resistive–inductive load, and red diamonds refer to the resistive load (numerical simulations only). Parameters are the same as in Fig. 10

Finally, Fig. 16 shows the average power delivered to the load (above), and the power efficiency (below), as functions of the load inductance $L_2$, for the nonlinear piezoelectric harvester. Theoretical predictions are obtained solving (57) and (58), and then, $P_{\text {out}}$ and $\eta$ are computed from (62) and (63), respectively. Results show a good agreement with the numerical experiments. Because the system is weakly nonlinear, the curves show a clear resemblance with the corresponding curves for the linear harvester. It can be seen that both $P_{\text {out}}$ and $\eta$ reach a maximum for $L_2$ close to the optimal value for linear systems $L_2 = L1 C_1 /C_2$. Moreover, both the average power and efficiency converge to constant values for large values of $L_2$. As explained for the linear system, this is due to the fact that the inductor becomes equivalent to an open circuit for $L_2 \rightarrow + \infty$.

Fig. 16

Average power delivered to the load (above) and power efficiency (below) as functions of the load inductance $L_2$, for $\omega =1$. Solid lines are theoretical result from (62) and (63), respectively. Blue circles refer to numerical simulations. Parameters are the same as in Fig. 10

5 Conclusions

We have analyzed vibrational energy harvesting systems with piezoelectric and magnetic inductive transducers, assuming the power of external disturbance concentrated around a specific frequency.

Typically, energy harvesters are modeled as oscillators, either linear or nonlinear, coupled to first-order systems that describe the transducer’s dynamics. For linear harvester, we used circuit theory to show that the harvested energy can be maximized by a proper matching of the load, usually assumed to be a simple resistor. Analogously to the power factor correction procedure, a reactive passive component can be added that maximizes the average power delivered to the load. As a result, the energy harvester is modeled by two coupled oscillators that must be designed to have the same resonance frequency. This solution allows for maximum power collection by the non-degenerate resistive load in the presence of finite losses of the harvester. Moreover, the maximum 50% efficiency under maximum power transfer condition can be achieved at the same resonant frequency.

For the nonlinear system, we used nonlinear dynamics methods to derive analytical formulae for the output, the harvested energy and the power efficiency. In full analogy with the linear case, modifying the load increases the harvested energy and power efficiency. As opposed to the linear case, however, the efficiency can reach values above 50%, again assuming realistic values for both the load and the harvester losses.

Appendix: State equations for the electrical domain

In this “Appendix,” we derive the state equations for both the mechanical and electrical domains of the piezoelectric and the electromagnetic energy harvesters.

For the piezoelectric energy harvester, the state equations for the electromechanical system are (1), (3) that we rewrite in the form

$$\begin{aligned} \ddot{x} =&-\dfrac{U'(x)}{m} - \dfrac{\gamma }{m} \dot{x} - \dfrac{k_v}{m}v_2 + \dfrac{1}{m} F_{\mathrm{in}} \end{aligned}$$

(67a)

$$\begin{aligned} \dot{v}_2 =&\dfrac{k_c}{C_2} \dot{x} - \dfrac{1}{C_2} i_2 \end{aligned}$$

(67b)

For the resistive load in Fig. 8a, $i_2 = G_2 v_2$, thus obtaining the electromechanical model equations in [18, 33]. For the RL load in Fig. 8b, applying KCL yields $i_2 = G_2 v + i_{L_2}$. Using the constitutive relation for the inductor $\phi _2 = L_2 i_{L_2}$, and the flux–voltage relationship ${\dot{\phi }}_2 = v$, equations (67) become

$$\begin{aligned} \ddot{x} =&-\dfrac{U'(x)}{m} - \dfrac{\gamma }{m} \dot{x} - \dfrac{k_v}{m}{\dot{\phi }}_2 + \dfrac{1}{m} F_{\mathrm{in}} \end{aligned}$$

(68a)

$$\begin{aligned} \ddot{\phi }_2 =&\dfrac{k_c}{C_2} \dot{x}- \dfrac{1}{L_2 C_2} \phi _2 - \dfrac{G_2}{C_2} {\dot{\phi }}_2 \end{aligned}$$

(68b)

For the electromagnetic energy harvester, the electromechanical equations are (4) and (6) that we rewrite in the form

$$\begin{aligned} \ddot{y} =&-\dfrac{U'(y)}{m} - \dfrac{c}{m} \dot{y} - \dfrac{r_1}{m} i_2 + \dfrac{F_{\mathrm{in}}}{m} \end{aligned}$$

(69a)

$$\begin{aligned} \dot{i}_2 =&\dfrac{r_2}{L_2} \dot{y} - \dfrac{v_2}{L_2} \end{aligned}$$

(69b)

For the resistive load in Fig. 8a, $v_2 = R_2 i_2$.

For the RC load in Fig. 8c, applying KVL yields $v_2 = R_2 i_2 + v_{C_2}$. Using the constitutive relation for the capacitor $q_2 = C_2 v_{C_2}$, and the current–charge relationship $\dot{q}_2 = i_{2}$, equation (69) becomes

$$\begin{aligned} \ddot{y} =&-\dfrac{U'(y)}{m} - \dfrac{c}{m} \dot{y} - \dfrac{r_1}{m} \dot{q}_2 + \dfrac{F_{in}}{m} \end{aligned}$$

(70a)

$$\begin{aligned} \ddot{q}_2 =&\dfrac{r_2}{L_2} \dot{y} - \dfrac{1}{L_2 C_2} q_2 - \dfrac{R_2}{L_2} \dot{q}_2 \end{aligned}$$

(70b)