4D Chern–Simons theory and affine Gaudin models

Abstract

We relate two formalisms recently proposed for describing classical integrable field theories. The first (Costello and Yamazaki in Gauge Theory and Integrability, III, 2019) is based on the action of four-dimensional Chern–Simons theory introduced and studied by Costello, Witten and Yamazaki. The second (Costello and Yamazaki, in Gauge Theory and Integrability, III, 2017) makes use of classical generalised Gaudin models associated with untwisted affine Kac–Moody algebras.

1 Introduction and summary

It was shown by Costello [11, 12], and further developed recently in [48, 13, 14] by Costello, Witten and Yamazaki that various integrable lattice models can be understood as originating from a four-dimensional variant of Chern–Simons theory on the product $M :=\Sigma \times C$ of a real two-dimensional manifold $\Sigma$ and a Riemann surface C equipped with a non-vanishing meromorphic 1-form $\omega$. It was also recently shown in [8] that integrable lattice models with boundaries can be accounted for by putting the gauge theory on an orbifold $(\Sigma \times \mathbb {C})/\mathbb {Z}_2$.

Very recently in [15], Costello and Yamazaki extended this approach to describe also integrable field theories on $\Sigma$, with spectral plane C, by starting from the same variant of Chern–Simons theory on $\Sigma \times C$ as in [11, 12, 48, 13, 14].

The purpose of this note is to show that the framework of [15] is intimately related to the description of classical integrable field theories that we proposed in [47], which is based on Gaudin models associated with untwisted affine Kac–Moody algebras. Since the latter underlies a number of important conjectures and problems in both mathematics and mathematical physics, including the ODE/IM correspondence [25], the problem of non-ultralocality [47] and the formulation of a geometric Langlands correspondence over complex surfaces, establishing its connection to 4D Chern–Simons theory is likely to provide deep insights into these difficult problems.

In order to explain this connection in more detail, we first recall how the gauge theory on $\Sigma \times C$ is defined more explicitly.

For concreteness, we shall let $\Sigma = \mathbb {R}\times S^1$ with global coordinates $(\tau , \sigma )$ and let $C = \mathbb {C}P^1$ be the Riemann sphere with holomorphic coordinate z on $\mathbb {C}= \mathbb {C}P^1\setminus \{ \infty \}$. We also fix a choice of meromorphic differential $\omega$ on $\mathbb {C}P^1$ which can be expressed in coordinates as

$$\begin{aligned} \omega = \varphi (z) dz, \end{aligned}$$

where $\varphi$ is a meromorphic function on $\mathbb {C}P^1$. As noted in [15], in order to be able to describe a broad family of classical integrable field theories it is crucial in the present context to allow $\omega$ to have zeroes.

Let $\mathfrak {g}$ be a semisimple Lie algebra over $\mathbb {C}$ and $\langle \cdot , \cdot \rangle : \mathfrak {g}\times \mathfrak {g}\rightarrow \mathbb {C}$ be a non-degenerate invariant symmetric bilinear form on $\mathfrak {g}$. We extend it to a symmetric bilinear pairing $\langle \cdot , \cdot \rangle : \mathfrak {g}\otimes \Omega ^p(M) \times \mathfrak {g}\otimes \Omega ^q(M) \rightarrow \Omega ^{p+q}(M)$.

The bulk action functional of four-dimensional Chern–Simons theory introduced and studied in [11, 12, 48, 13, 14, 15], for a $\mathfrak {g}$-valued 1-form A on M, reads

$$\begin{aligned} S_\mathrm{bulk}[A] = \frac{\mathrm{i}}{4\pi } \int _{\Sigma \times \mathbb {C}P^1} \omega \wedge CS(A), \qquad CS(A) :=\left\langle A, dA + \frac{2}{3} A \wedge A \right\rangle . \end{aligned}$$

(1.1)

The normalisation factor in front of the action is chosen to match the conventions of [47]. It is interesting to note that it coincides, up to an integer factor, with the normalisation of the action (in the case when $\omega = dz$) motivated from the extension of the standard Chern–Simons action to loop groups [48].

The action (1.1) is trivially invariant under the transformation $A \mapsto A + \varpi$ for any 1-form $\varpi = f \, dz \in \Omega ^1(\Sigma \times \mathbb {C}P^1)$ proportional to dz. We can use this freedom to eliminate the (1, 0)-component of A along $\mathbb {C}P^1$ and thereby fix it to be of the form $A = A_\tau d\tau + A_\sigma d\sigma + A_{\bar{z}} d\bar{z}$. The action is then invariant under gauge transformations of these remaining three components.

The equation of motion $\omega \wedge F = 0$, derived by extremising (1.1), expresses the fact that A is a flat connection on $\Sigma$ which varies meromorphically on $\mathbb {C}P^1$. This strongly suggests that, when working in the gauge where $A_{\bar{z}} = 0$, one can interpret $A_\tau d\tau + A_\sigma d\sigma$ as the Lax connection of some classical integrable field theory. Indeed, the proposal of [15] is to describe integrable field theories in this way, as arising from the introduction of specific surface defects along $\Sigma$ in the four-dimensional Chern–Simons theory on $M = \Sigma \times \mathbb {C}P^1$.

However, in order to completely characterise the integrable structure of a classical integrable field theory, it is necessary to move to the Hamiltonian framework and to identify the Poisson bracket of $A_\sigma$ with itself. There then exist sufficient conditions on the form of this Poisson bracket [37, 38] ensuring that the integrals of motion constructed from $A_\sigma$ are in involution.

In Sect. 2 we perform a Hamiltonian analysis of the four-dimensional Chern–Simons theory of [11, 12, 48, 13, 14, 15], with $\omega$ a generic meromorphic differential on $\mathbb {C}P^1$. There are first-class constraints associated with the gauge invariance of this theory and second-class constraints coming from the fact that the Lagrangian CS(A) is linear in the time derivative of A. We impose natural gauge fixing conditions and determine the corresponding Dirac bracket $\{ \cdot , \cdot \}^\star$ on the reduced phase space. The latter is parametrised by the $\mathfrak {g}$-valued field $A_\sigma$ which, having fixed the gauge, is now meromorphic and such that:

(1.2)

We find that the Dirac bracket on the reduced phase space takes the form

(1.3)

where the $\mathcal {R}$-matrix is given explicitly by

(1.4)

The factor of $2 \pi$ in (1.4) is also there to match the conventions of [47].

In other words, the first result of this note is that the spatial component $A_\sigma$ of the Chern–Simons 1-form A can be interpreted as the Lax matrix of a non-ultralocal classical integrable field theory with twist function $\varphi$.

Furthermore, by adding to the bulk Hamiltonian associated with the action (1.1) a suitable boundary term, fixed by the requirement that the total Hamiltonian has well-defined functional derivatives [41], we find that the Hamiltonian on the reduced phase space is

$$\begin{aligned} H = -\frac{1}{2} \sum _{x \in \varvec{\zeta }} \epsilon _x \int _{S^1} d\sigma \, {{\,\mathrm{res}\,}}_x \langle A_\sigma , A_\sigma \rangle \omega , \end{aligned}$$

(1.5)

where $\varvec{\zeta }$ is the set of zeroes of $\omega$ and $\{ \epsilon _x \}_{x \in \varvec{\zeta }}$ is a set of complex numbers entering through the choice of gauge fixing conditions imposed.

Let $\widetilde{\mathfrak {g}}$ be the untwisted affine Kac–Moody algebra corresponding to $\mathfrak {g}$. We showed in [47] (see also [17, 33]) that classical integrable field theories with the properties (1.3)–(1.5) can be understood as realisations of various generalisations of the Gaudin model associated with $\widetilde{\mathfrak {g}}$. Since this result is quite technical, but essential to the discussion, we will recall its main features in Sect. 3.

The result of this note therefore establishes that the general formalisms of [15] and [47] provide equivalent descriptions of classical integrable field theories in the Lagrangian and Hamiltonian formulations, respectively.

More precisely, the action functional (1.1) of [15] can be used to describe those classical integrable field theories which:

• (i) can be realised as a non-cyclotomic affine Gaudin model in the sense of [47],

• (ii) satisfy the additional technical condition (1.2).

We do not discuss here the case of cyclotomic affine Gaudin model, let alone dihedral ones, in the terminology of [47]. See Sect. 4.2 for a discussion of this point.

It is, however, interesting to note that the condition (1.2) is known not to hold for certain classical integrable field theories which nevertheless do admit an affine Gaudin model description. This is, for instance, the case for affine Toda field theories which can be described as cyclotomic (in fact dihedral) affine Gaudin models [47]. The generalisation of the present work to the cyclotomic case could therefore provide an explanation as to why these theories, including sine-Gordon theory, do not admit straightforward interpretations in terms of four-dimensional Chern–Simons theory [15].

We end with some comments and discussion of possible future work in Sect. 4.

2 Hamiltonian analysis of four-dimensional Chern–Simons theory

2.1 Bulk action

In order to move to the Hamiltonian framework, we begin by isolating the global time coordinate on the cylinder by writing $A = A_\tau d\tau + \hat{A}$ with $\hat{A} :=A_\sigma d\sigma + A_{\bar{z}} d \bar{z}$, and for any $\eta \in \mathfrak {g}\otimes \Omega ^p(M)$ we let $d\eta = d\tau \wedge \partial _\tau \eta + \hat{d}\eta$, with $\hat{d}\eta :=d\sigma \wedge \partial _\sigma \eta + dz \wedge \partial _z \eta + d\bar{z} \wedge \partial _{\bar{z}} \eta$.

We have

$$\begin{aligned} CS(A) = - d\tau \wedge \big ( \langle \hat{A}, \partial _\tau \hat{A} \rangle - 2 \langle A_\tau , \hat{F} \rangle \big ) + \hat{d} \langle A_\tau d\tau , \hat{A} \rangle + \langle \hat{A}, \hat{d} \hat{A} \rangle , \end{aligned}$$

where $\hat{F} :=\hat{d} \hat{A} + \hat{A} \wedge \hat{A}$. The last term in CS(A) can be ignored since it will drop out when taking the wedge product with $\omega$. The bulk action functional (1.1) can then be rewritten as

$$\begin{aligned} S_\mathrm{bulk}[A] = \frac{\mathrm{i}}{4\pi } \int _{\mathbb {R}\times S^1 \times \mathbb {C}P^1} d\tau \wedge \omega \wedge \big ( \langle \hat{A}, \partial _\tau \hat{A} \rangle - 2 \langle A_\tau , \hat{F} \rangle \big ) \end{aligned}$$

(2.1)

where we ignored a ‘boundary term’. Indeed, even though $S^1 \times \mathbb {C}P^1$ has no boundary per se, using Stokes theorem we generate a term of the form $d \tau \wedge \hat{d} \omega \wedge \langle A_\tau , \hat{A} \rangle$ in the integrand. Explicitly, we have

$$\begin{aligned} \int _{S^1 \times \mathbb {C}P^1} \omega \wedge \hat{d} \langle A_\tau , \hat{A} \rangle = - \int _{S^1 \times \mathbb {C}P^1} \hat{d}\big (\omega \wedge \langle A_\tau , \hat{A} \rangle \big ) + \int _{S^1 \times \mathbb {C}P^1} \hat{d} \omega \wedge \langle A_\tau , \hat{A} \rangle , \end{aligned}$$

with the first term vanishing because $\partial (S^1 \times \mathbb {C}P^1) = \emptyset$. But $\hat{d} \omega$ is a distribution on $\mathbb {C}P^1$ with support at the poles of $\omega$, so the integral in the second term above localises at these poles. We shall therefore refer to such terms as ‘boundary terms’.

Remark 2.1

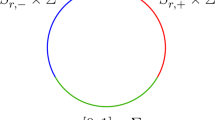
One could equally describe these ‘boundary terms’ as actual boundary terms. Let $D_r$ be the union of small discs of radius $r > 0$ around each of the poles of $\omega$, and take the integral in (2.1) to be over $M_r :=S^1 \times \mathbb {C}P^1{\setminus }D_r$ instead. Then

$$\begin{aligned} \int _{M_r} \omega \wedge \hat{d} \langle A_\tau , \hat{A} \rangle = - \int _{M_r} \hat{d}\big (\omega \wedge \langle A_\tau , \hat{A} \rangle \big ) + \int _{M_r} \hat{d} \omega \wedge \langle A_\tau , \hat{A} \rangle , \end{aligned}$$

where now the second term on the right hand side vanishes because $\hat{d} \omega$ has support inside $D_r$. On the other hand, the first term now gives a boundary integral which in the limit when $r \rightarrow 0$ coincides with the ‘boundary term’ identified above. More generally, in order to allow other singularities in the fields $A_\tau$ or $\hat{A}$, as we will do when imposing a gauge fixing condition on $A_\tau$ later in Sect. 2.7, we should also include in $D_r$ small discs of radius r around these additional points.

Writing $\hat{A}$ in terms of its components and working up to ‘boundary terms’ in the above sense, we can express the action (2.1) more explicitly as

$$\begin{aligned} S_\mathrm{bulk}[A] = \int _{\mathbb {R}\times S^1 \times \mathbb {C}P^1} d\tau \wedge d\sigma \wedge dz \wedge d\bar{z} \, \mathcal {L}_\mathrm{bulk}(A), \end{aligned}$$

(2.2a)

where the bulk Lagrangian is given by

$$\begin{aligned} \mathcal {L}_\mathrm{bulk}(A)&:=\frac{\mathrm{i}\varphi }{4\pi } \langle A_{\bar{z}}, \partial _\tau A_\sigma \rangle - \frac{\mathrm{i}\varphi }{4\pi } \langle A_\sigma , \partial _\tau A_{\bar{z}} \rangle \nonumber \\&\quad - \frac{\mathrm{i}}{2\pi } \langle A_\tau , \partial _{\bar{z}} (\varphi A_\sigma ) - \varphi \partial _\sigma A_{\bar{z}} - [\varphi A_\sigma , A_{\bar{z}}] \rangle . \end{aligned}$$

(2.2b)

2.2 Phase space

The conjugate momentum of the three $\mathfrak {g}$-valued fields $A_\tau$, $A_\sigma$ and $A_{\bar{z}}$ is given, respectively, by the $\mathfrak {g}$-valued fields

$$\begin{aligned} \Pi _\tau :=\frac{\partial {\mathcal {L}}(A)}{\partial (\partial _\tau A_\tau )} = 0, \qquad \Pi _\sigma :=\frac{\partial {\mathcal {L}}(A)}{\partial (\partial _\tau A_\sigma )} = \frac{\mathrm{i}\varphi }{4 \pi } A_{\bar{z}}, \qquad \Pi _{\bar{z}} :=\frac{\partial {\mathcal {L}}(A)}{\partial (\partial _\tau A_{\bar{z}})} = - \frac{\mathrm{i}\varphi }{4 \pi } A_\sigma . \end{aligned}$$

The initial phase space is parametrised by three pairs of $\mathfrak {g}$-valued conjugate fields $A_i, \Pi _i \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})$ for $i \in \{ \tau , \sigma , \bar{z} \}$, whose canonical Poisson brackets can be expressed using standard tensorial index notation as

(2.3)

where $\delta _{\sigma \sigma ^{\prime }} :=\frac{1}{2\pi } \sum _{n \in \mathbb {Z}} e^{\mathrm{i}n (\sigma - \sigma ^{\prime })}$ is the Dirac comb, i.e. the Dirac $\delta$-distribution on $S^1$, and $\delta _{zz^{\prime }}$ is the Dirac $\delta$-distribution on $\mathbb {C}P^1$ with the properties that

$$\begin{aligned} \int _{S^1} d\sigma \, f(\sigma , z) \delta _{\sigma \sigma ^{\prime }} = f(\sigma ^{\prime }, z), \qquad \int _{\mathbb {C}P^1} dz \wedge d\bar{z} \, f(\sigma , z) \delta _{zz^{\prime }} = f(\sigma , z^{\prime }) \end{aligned}$$

for any $f \in C^\infty (S^1 \times \mathbb {C}P^1)$. Also, C denotes the split Casimir of $\mathfrak {g}$.

There are three primary constraints

$$\begin{aligned} \Pi _\tau \approx 0, \qquad {\mathcal {C}}_\sigma :=A_{\bar{z}} - \frac{4 \pi }{\mathrm{i}\varphi } \Pi _\sigma \approx 0, \qquad {\mathcal {C}}_{\bar{z}} :=\Pi _{\bar{z}} + \frac{\mathrm{i}\varphi }{4 \pi } A_\sigma \approx 0. \end{aligned}$$

(2.4)

The last two constraints are second class and their Poisson bracket

is invertible. We can therefore set them to zero strongly, which we shall do, provided that we work with the corresponding Dirac brackets, given by

(2.5a)

(2.5b)

Let ${\mathcal {P}}$ denote the resulting phase space, parametrised by the fields $A_\tau$, $\Pi _\tau$, $A_{\bar{z}}$ and $\Pi _{\bar{z}}$ satisfying the Dirac brackets (2.5). We shall refer to the latter just as a Poisson bracket from now on, but still keep denoting it as $\{ \cdot , \cdot \}^*$ to distinguish it from the original Poisson bracket (2.3) since (2.5b) is now different.

Note that we have thus far fixed the last two of the primary constraints in (2.4), so there remains the primary constraint $\Pi _\tau \approx 0$.

2.3 Differentiable functionals

Given any pair of functionals $\mathscr {F}, \mathscr {G} : \mathcal {P}\rightarrow \mathbb {C}$, it follows from (2.5) that their Poisson bracket reads

$$\begin{aligned} \{ \mathscr {F}, \mathscr {G} \}^*&= 2 \pi \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta A_\tau }, \frac{\delta \mathscr {G}}{\delta \Pi _\tau } \bigg \rangle \!\bigg \rangle - 2 \pi \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta \Pi _\tau }, \frac{\delta \mathscr {G}}{\delta A_\tau } \bigg \rangle \!\bigg \rangle \nonumber \\&\quad + \pi \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta A_{\bar{z}}}, \frac{\delta \mathscr {G}}{\delta \Pi _{\bar{z}}} \bigg \rangle \!\bigg \rangle - \pi \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta \Pi _{\bar{z}}}, \frac{\delta \mathscr {G}}{\delta A_{\bar{z}}} \bigg \rangle \!\bigg \rangle , \end{aligned}$$

(2.6)

where we have introduced the notation

$$\begin{aligned} \langle \!\langle X, Y \rangle \!\rangle :=\int _{S^1 \times \mathbb {C}P^1} d\sigma \wedge dz \wedge d\bar{z} \, \langle X, Y \rangle \end{aligned}$$

(2.7)

for any $\mathfrak {g}$-valued distributions X, Y on $S^1 \times \mathbb {C}P^1$ for which this integral makes sense.

However, problems could arise if the variational derivatives of $\mathscr {F}$ and $\mathscr {G}$ involve distributions with overlapping supports. The right-hand side of (2.6) would then be the integral of a product of such distributions, which is typically ill-defined.

In light of Remark 2.1, such distributions can be interpreted as ‘boundary terms’. The treatment of boundary terms in the Hamiltonian framework was understood in the seminal work of Regge and Teitelboim [41] in the context of general relativity; see also [9, 10]. The application of these ideas to ordinary Chern–Simons theory, directly relevant to the present discussion, was considered in [2, 3]; see also [4].

We shall say, in the spirit of [41], that a functional $\mathscr {F} : \mathcal {P}\rightarrow \mathbb {C}$ is differentiable if its variational derivatives do not involve ‘boundary terms’, i.e. if we can write

$$\begin{aligned} \delta \mathscr {F} = \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta A_\tau }, \delta A_\tau \! \bigg \rangle \!\bigg \rangle + \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta A_{\bar{z}}}, \delta A_{\bar{z}} \! \bigg \rangle \!\bigg \rangle + \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta \Pi _\tau }, \delta \Pi _\tau \! \bigg \rangle \!\bigg \rangle + \bigg \langle \!\bigg \langle \frac{\delta \mathscr {F}}{\delta \Pi _{\bar{z}}}, \delta \Pi _{\bar{z}} \! \bigg \rangle \!\bigg \rangle \end{aligned}$$

but where the variational derivatives $\delta \mathscr {F}/ \delta A_i$ and $\delta \mathscr {F}/ \delta \Pi _i$ are smooth functions for $i \in \{ \tau , \bar{z} \}$, though possibly with singularities at finitely many points.

The resolution of the problem alluded to above is that the Poisson bracket $\{ \mathscr {F}, \mathscr {G} \}^*$ is only defined between differentiable functionals $\mathscr {F}$ and $\mathscr {G}$. If a functional $\mathscr {F}$ is not differentiable then one should find a suitable boundary term to add to it, so as to cancel off any unwanted boundary terms in its variation $\delta \mathscr {F}$. This will ensure that it has well-defined Poisson brackets with any other differentiable functional.

2.4 Bulk Hamiltonian

The bulk Hamiltonian density is given by the Legendre transform of the bulk Lagrangian (2.2b), namely

$$\begin{aligned} \mathcal {H}_\mathrm{bulk}(A) :=\langle \Pi _\tau , \partial _\tau A_\tau \rangle + \langle \Pi _\sigma , \partial _\tau A_\sigma \rangle + \langle \Pi _{\bar{z}}, \partial _\tau A_{\bar{z}} \rangle - \mathcal {L}_\mathrm{bulk}(A) = \langle A_\tau , \gamma \rangle . \end{aligned}$$

Here, we have introduced the $\mathfrak {g}$-valued field

$$\begin{aligned} \gamma :=- 2 \partial _{\bar{z}} \Pi _{\bar{z}} - \frac{\mathrm{i}}{2 \pi } \varphi \, \partial _\sigma A_{\bar{z}} + 2 [\Pi _{\bar{z}}, A_{\bar{z}}]. \end{aligned}$$

Therefore, the bulk Hamiltonian of four-dimensional Chern–Simons theory reads

$$\begin{aligned} H_\mathrm{bulk} :=\langle \!\langle A_\tau , \gamma \rangle \!\rangle . \end{aligned}$$

(2.8)

We will come back to the issue of the differentiability of this functional in Sect. 2.8 after fixing the value of $A_\tau$ in Sect. 2.7.

2.5 Gauge invariance

There is just one constraint on the phase space $\mathcal {P}$, namely $\Pi _\tau \approx 0$, which we should ensure is preserved under time evolution. We have

$$\begin{aligned} \{ H_\mathrm{bulk}, \Pi _\tau \}^*= \gamma . \end{aligned}$$

This is, however, not quite a pure constraint since it already contains the necessary ‘boundary terms’ to ensure that $\langle \! \langle \varepsilon , \gamma \rangle \!\rangle$, for all $\varepsilon \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})$, is a differentiable functional in the sense of Sect. 2.3, cf. the computation in Sect. 2.8 below.

On the other hand, $\gamma$ is the correct ‘improved’ generator of gauge transformations. Indeed, by using (2.5b) we obtain

(2.9a)

(2.9b)

It follows that the expression $\frac{1}{2\pi } \langle \!\langle \varepsilon , \gamma \rangle \!\rangle$, for every $\varepsilon \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})$, generates a gauge transformation of four-dimensional Chern–Simons theory since

$$\begin{aligned} \frac{1}{2\pi } \{ \langle \!\langle \varepsilon , \gamma \rangle \!\rangle , A_\sigma (\sigma , z) \}^*&= [\varepsilon (\sigma , z), A_\sigma (\sigma , z)] - \partial _\sigma \varepsilon (\sigma , z),\\ \frac{1}{2\pi } \{ \langle \!\langle \varepsilon , \gamma \rangle \!\rangle , A_{\bar{z}}(\sigma , z) \}^*&= [ \varepsilon (\sigma , z), A_{\bar{z}}(\sigma , z)] - \partial _{\bar{z}} \varepsilon (\sigma , z). \end{aligned}$$

In particular, the bulk Hamiltonian (2.8) is thus a pure gauge transformation with the field $A_\tau$ playing the role of the gauge parameter.

Moreover, the Poisson bracket of $\gamma$ with itself reads

(2.10)

from which it follows that, for any $\varepsilon , {\tilde{\varepsilon }} \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})$, we have

$$\begin{aligned} \{ \langle \!\langle \varepsilon , \gamma \rangle \!\rangle , \langle \!\langle {\tilde{\varepsilon }}, \gamma \rangle \!\rangle \}^*= - 2 \pi \langle \!\langle [\varepsilon , {\tilde{\varepsilon }}, \gamma \rangle \!\rangle + \mathrm{i}\langle \!\langle (\partial _{\bar{z}} \varphi ) \varepsilon , \partial _\sigma {\tilde{\varepsilon }} \rangle \!\rangle . \end{aligned}$$

(2.11)

The second term on the right-hand side is a ‘boundary term’ localised at the poles of the differential $\omega$, cf. the analogous central extension in the Poisson algebra of the ‘improved’ constraints in ordinary Chern–Simons theory [2, 3].

Let $C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})_\omega$ denote the subspace of $C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})$ consisting of those functions which vanish at the poles of $\omega$ (and whose multiplicities at these zeroes is given by the orders of the corresponding poles of $\omega$). The central extension term in (2.11) is then absent if either $\varepsilon$ or ${\tilde{\varepsilon }}$ belongs to $C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})_\omega$. In particular, we see that the true bulk constraint can be described as the smearing $\langle \!\langle \varepsilon , \gamma \rangle \!\rangle \approx 0$ with all possible $\varepsilon \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})_\omega$. This is then first class by (2.11). By an abuse of language, we will still refer to this constraint as $\gamma \approx 0$.

Using (2.10), we find that

$$\begin{aligned} \{ H_\mathrm{bulk}, \gamma \}^*\approx - \mathrm{i}(\partial _{\bar{z}} \varphi ) \partial _\sigma A_\tau . \end{aligned}$$

Thus, for each $\varepsilon \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})_\omega$ we have $\{ H_\mathrm{bulk}, \langle \!\langle \varepsilon , \gamma \rangle \!\rangle \}^*\approx 0$, and hence, there are no tertiary constraints.

2.6 Gauge fixing

We would like to fix the gauge invariance associated with the constraint $\gamma \approx 0$ identified in Sect. 2.5. Concretely, letting $\varvec{z}$ denote the set of poles of $\varphi$ we will fix the constraint $\gamma (\sigma , z) \approx 0$ for $z \not \in \varvec{z}$, which is clearly first class by (2.10).

We shall do this by imposing the gauge fixing condition

$$\begin{aligned} A_{\bar{z}} \approx 0. \end{aligned}$$

(2.12)

This choice is motivated by the fact that, following [15], one would like to interpret the gauge field A of four-dimensional Chern–Simons theory as the Lax connection of an integrable field theory. Since the latter only has $d\sigma$ and $d\tau$ components, we should bring A to this form also by moving to the gauge (2.12). It follows from (2.9b) that

(2.13)

We can thus impose the constraint $\gamma \approx 0$ together with the gauge fixing condition (2.12) strongly, provided that we work with the appropriate new Dirac bracket $\{ \cdot , \cdot \}^\star$. To define it, we note that (2.13) is invertible since

where we have used the fact that

$$\begin{aligned} - \frac{1}{2 \pi \mathrm{i}} \partial _{\bar{z}} \bigg ( \frac{1}{z - z^{\prime }} \bigg ) = \delta _{zz^{\prime }}. \end{aligned}$$

(2.14)

The subscript ‘ on $\langle \!\langle \cdot , \cdot \rangle \!\rangle$, as defined in (2.7), is used here to indicate that the integration is taken over $d\sigma ^{\prime } \wedge dz^{\prime } \wedge d\bar{z}^{\prime }$ and the bilinear form $\langle \cdot , \cdot \rangle$ is applied to the second tensor factor.

The new Dirac bracket of any $\mathfrak {g}$-valued observables U and V is then defined by

In order to compute the Dirac bracket of the field $\Pi _{\bar{z}}$ with itself, we note from (2.9a), and using the last constraint in (2.4), that

Using the above definition for the Dirac bracket $\{ \cdot , \cdot \}^\star$, we obtain

(2.15)

which is valid for $z, z^{\prime } \not \in \varvec{z}$. In view of the constraint ${\mathcal {C}}_{\bar{z}} \approx 0$ in (2.4), this is equivalent to the non-ultralocal algebra (1.3) with $\mathcal {R}$-matrix as in (1.4).

The slightly unconventional factor of $2 \pi$ in (1.4) matches with the conventions of [47], where (1.3) was derived from purely algebraic considerations, as we shall recall in Sect. 3.1. Note that here $\delta _{\sigma \sigma ^{\prime }}$ denotes the Dirac comb, whereas in [47] we used it to denote the unnormalised Dirac comb, which in the present conventions is $2 \pi \delta _{\sigma \sigma ^{\prime }}$.

We have now imposed the constraint $\gamma \approx 0$ strongly, or more precisely $\langle \!\langle \varepsilon , \gamma \rangle \!\rangle \approx 0$ for every $\varepsilon \in C^\infty (S^1 \times \mathbb {C}P^1, \mathfrak {g})_\omega$. Using the gauge fixing condition (2.12), this gives

$$\begin{aligned} \langle \!\langle \varepsilon , \partial _{\bar{z}} \Pi _{\bar{z}} \rangle \!\rangle \approx 0. \end{aligned}$$

(2.16)

It follows that $\Pi _{\bar{z}}$ is meromorphic on $\mathbb {C}P^1$ with the same pole structure as $\varphi$. By virtue of the definition of the constraint ${\mathcal {C}}_{\bar{z}} \approx 0$ in (2.4), this is equivalent to (1.2).

Remark 2.2

The condition (1.2) can also be seen in the Lagrangian formalism from the equation of motion $\omega \wedge F = 0$. In the gauge (2.12), this implies that the connection $A_\tau d \tau + A_\sigma d \sigma$ is flat and that $\varphi \partial _{\bar{z}} A_\sigma = \varphi \partial _{\bar{z}} A_\tau = 0$. In other words, $A_\sigma$ and $A_\tau$ are meromorphic with poles at the zeroes of $\varphi$ (with the order of each pole coinciding with the multiplicity of the corresponding zero of $\varphi$).

2.7 Fixing the Lagrange multiplier

Note that we still have the first class primary constraint $\Pi _\tau \approx 0$. The effect of the corresponding gauge transformation is just to change the Lagrange multiplier $A_\tau$ in the bulk Hamiltonian. We shall impose it strongly by fixing the Lagrange multiplier.

Let $\varvec{\zeta }$ denote the set of zeroes of $\omega$. We shall assume, for the sake of clarity of the presentation, that $\varvec{\zeta } \subset \mathbb {C}$, i.e. infinity is not a zero, and moreover that all the zeroes are simple. The latter means that $\varphi (x) = 0$ while $\varphi ^{\prime }(x) \ne 0$ for $x \in \varvec{\zeta }$. The arguments given below and in Sect. 2.8 generalise straightforwardly to the generic case.

Having imposed the constraint ${\mathcal {C}}_{\bar{z}} \approx 0$ in (2.4) strongly, we have

$$\begin{aligned} A_\sigma (\sigma , z) \approx \frac{4 \pi \mathrm{i}}{\varphi (z)} \Pi _{\bar{z}}(\sigma , z) = \sum _{x \in \varvec{\zeta }} \frac{4 \pi \mathrm{i}}{\varphi ^{\prime }(x)} \frac{\Pi _{\bar{z}}(\sigma , x)}{z - x}. \end{aligned}$$

(2.17)

The second equality is obtained by performing a partial fraction expansion, noting that $\Pi _{\bar{z}}$ and $\varphi$ have the same pole structure. The explicit form above follows from assuming that $\varphi$ has simple zeroes at points in the set $\varvec{\zeta } \subset \mathbb {C}$. Note that (2.17) is exactly equation (2.39) from [17], in view of the discussion of Sect. 3.1 below.

As noted in Remark 2.2, in the Lagrangian formalism two of the three equations of motion on A impose that both components $A_\sigma$ and $A_\tau$ are meromorphic with poles at the zeroes of $\varphi$. We see that relation (2.17) is compatible with this property. Similarly, we shall fix the Lagrangian multiplier $A_\tau$ to be meromorphic with poles at the zeroes of $\varphi$. More precisely, choosing a set $\{ \epsilon _x \}_{x \in \varvec{\zeta }}$ of complex numbers, we shall use the gauge fixing condition

$$\begin{aligned} A_\tau (\sigma , z) \approx - \sum _{x \in \varvec{\zeta }} \frac{4 \pi \mathrm{i}\epsilon _x}{\varphi ^{\prime }(x)} \frac{\Pi _{\bar{z}}(\sigma , x)}{z - x}. \end{aligned}$$

(2.18)

(Note that this coincides, up to a sign in the definition of the $\epsilon _x$, with (2.40) from [17] by the same remark as for (2.17) above.) In other words, we take a linear combination of the singular parts at each $x \in \varvec{\zeta }$ of the partial fraction decomposition (2.17) with coefficients $\epsilon _x$. Since we are setting the Lagrange multiplier $A_\tau$ equal to a meromorphic function with poles in $\varvec{\zeta }$, we are technically only specifying its ‘boundary value’ at the points in $\varvec{\zeta }$. In any case, there is no need to specify its value as a whole on $\mathbb {C}P^1$ since we are already working on the constraint surface $\gamma \approx 0$. We will motivate the choice (2.18) shortly in Sect. 2.8, but for the time being it is interesting to compare with the choices made in [15].

To compare with [15], let us split the set $\varvec{\zeta }$ into two disjoint subsets as $\varvec{\zeta } = \varvec{\zeta }_+ \sqcup \varvec{\zeta }_-$ and take $\epsilon _x = \pm 1$ for $x \in \varvec{\zeta }_\pm$. Let us also note in passing that the latter condition was shown in [17] to imply that the resulting model is relativistic. It follows from comparing (2.17) with (2.18) that $A_\tau \pm A_\sigma$ is regular at each $x \in \varvec{\zeta }_\pm$ and has a simple pole at every $x \in \varvec{\zeta }_\mp$. This is to be compared with the boundary conditions imposed on the fields $A_\tau \pm A_\sigma$ at the zeroes of $\omega$ in [15], where $|\varvec{\zeta }|$ is even and $|\varvec{\zeta }_+| = |\varvec{\zeta }_-|$. Note, however, that by contrast with [15] we do not choose to work in a gauge in which the pair of fields $A_\sigma \pm A_\tau$ both vanish at the poles of $\omega$. We will come back to this point in Sect. 4.1 below. Choosing the right gauge in the Hamiltonian formalism is essential since it is known, see e.g. [1], that the form of the Poisson bracket (1.3)–(1.4) is very sensitive to this choice.

Introducing a Dirac bracket to impose $\Pi _\tau \approx 0$ strongly, together with its gauge fixing condition (2.18), it is immediate that the Dirac bracket (2.15) is unmodified.

2.8 Reduced dynamics

In a classical field theory with no local degrees of freedom, such as (1.1), it is the choice of boundary condition on the Lagrange multipliers in the Hamiltonian, such as $A_\tau$ here, which completely determines the dynamics on the reduced phase space. In this sense, the gauge fixing condition (2.18) was chosen so as to produce the correct dynamics on the reduced phase space, as we now show.

The variation of the bulk Hamiltonian (2.8) reads

$$\begin{aligned} \delta H_\mathrm{bulk}&= \langle \!\langle \gamma , \delta A_\tau \rangle \!\rangle + \left\langle \!\left\langle \frac{\mathrm{i}}{2 \pi } \varphi \partial _\sigma A_\tau + 2 [A_\tau , \Pi _{\bar{z}}], \delta A_{\bar{z}} \right\rangle \!\right\rangle + 2 \langle \!\langle [A_{\bar{z}}, A_\tau ] + \partial _{\bar{z}} A_\tau , \delta \Pi _{\bar{z}} \rangle \!\rangle . \end{aligned}$$

The first term vanishes on the constraint surface. Among all of the other terms, the only potentially problematic one is the one involving $\partial _{\bar{z}} A_\tau$ since it could correspond to a ‘boundary term’, cf. Remark 2.1. And indeed, by using the explicit form of the gauge fixing condition (2.18) and using the identity (2.14 we can rewrite it as

$$\begin{aligned} 2 \langle \!\langle \partial _{\bar{z}} A_\tau , \delta \Pi _{\bar{z}} \rangle \!\rangle&= - 4 \pi \sum _{x \in \varvec{\zeta }} \frac{4 \pi \epsilon _x}{\varphi ^{\prime }(x)} \int _{S^1 \times \mathbb {C}P^1} d\sigma \wedge dz \wedge d\bar{z} \, \delta _{z x} \langle \Pi _{\bar{z}} (\sigma , x), \delta \Pi _{\bar{z}}(\sigma , z) \rangle \\&= \delta \Bigg ( \!\! - \frac{1}{2}\sum _{x \in \varvec{\zeta }} \frac{\epsilon _x}{\varphi ^{\prime }(x)} \int _{S^1} d\sigma \, \langle 4 \pi \Pi _{\bar{z}} (\sigma , x), 4 \pi \Pi _{\bar{z}}(\sigma , x) \rangle \Bigg ). \end{aligned}$$

This suggests adding a boundary term to the bulk Hamiltonian $H_\mathrm{bulk}$, given in (2.8), to cancel off this boundary term in the above variation $\delta H_\mathrm{bulk}$. Explicitly, we define the new Hamiltonian

$$\begin{aligned} H :=\langle \!\langle A_\tau , \gamma \rangle \!\rangle + \frac{1}{2}\sum _{x \in \varvec{\zeta }} \frac{\epsilon _x}{\varphi ^{\prime }(x)} \int _{S^1} d\sigma \langle 4\pi \Pi _{\bar{z}}(\sigma , x), 4\pi \Pi _{\bar{z}}(\sigma , x) \rangle , \end{aligned}$$

which is now differentiable in the sense of [41], see Sect. 2.3.

The Hamiltonian on the reduced phase space is then given by

$$\begin{aligned} H \approx \frac{1}{2}\sum _{x \in \varvec{\zeta }} \frac{\epsilon _x}{\varphi ^{\prime }(x)} \int _{S^1} d\sigma \langle 4\pi \Pi _{\bar{z}}(\sigma , x), 4\pi \Pi _{\bar{z}}(\sigma , x) \rangle . \end{aligned}$$

This can equally be rewritten as

$$\begin{aligned} H \approx \sum _{x \in \varvec{\zeta }} \epsilon _x {{\,\mathrm{res}\,}}_x \bigg ( \frac{1}{2}\varphi (z)^{-1} \int _{S^1} d\sigma \langle 4\pi \Pi _{\bar{z}}(\sigma , z), 4\pi \Pi _{\bar{z}}(\sigma , z) \rangle \bigg ) dz. \end{aligned}$$

(2.19)

which is equivalent to (1.5) using the constraint ${\mathcal {C}}_{\bar{z}} \approx 0$. In this final form (2.19), it is straightforward to show that the result also holds, as written, in the more generic situation when $\omega$ is allowed to have multiple zeroes including at infinity.

3 Connection with affine Gaudin models

We showed in Sect. 2.6 that the non-ultralocal Poisson algebra (1.3), with $\mathcal {R}$-matrix given by (1.4), naturally arises as the Poisson structure on the reduced phase space of four-dimensional Chern–Simons theory. We then showed in Sect. 2.8 that for a suitable choice of gauge fixing conditions (closely related to conditions imposed in [15]), the Hamiltonian on the reduced phase space takes the very specific form (1.5).

By contrast, in [47] we gave a very different, more algebraic, interpretation of this same non-ultralocal Poisson algebra (1.3)–(1.4) and Hamiltonian (1.5). We will briefly review this below. In short, classical integrable field theories with properties (1.3)–(1.5) can equally be understood as particular representation of generalised (non-cyclotomic) affine Gaudin models.

3.1 Non-ultralocal algebra

The object which naturally enters in the formalism of [47] is not so much the field $A_\sigma$ but rather the combination ${\mathcal {L}} :=4 \pi \mathrm{i}\Pi _{\bar{z}} = \varphi A_\sigma$. Its Poisson bracket, which follows immediately form (2.15), can be written as

(3.1)

We have explicitly removed the superscript ‘$\star$’ on the Poisson bracket since in what follows we no longer want to think of it as a Dirac bracket on a reduced phase space.

To explain the origin of the Poisson bracket (3.1) from Gaudin models associated with the untwisted affine Kac–Moody algebra $\widetilde{\mathfrak {g}}:=\mathfrak {g}\otimes \mathbb {C}[t, t^{-1}] \oplus \mathbb {C}\mathsf {K}\oplus \mathbb {C}\mathsf {D}$, we briefly recall how these are defined.

Let $\{ I_a \}$ be a basis of $\mathfrak {g}$ and denote $\{ I^a \}$ its dual basis with respect to the bilinear form $\langle \cdot , \cdot \rangle$. Note that, in terms of these, we can write the split Casimir of $\mathfrak {g}$ introduced in Sect. 2.2 as $C = I_a \otimes I^a$, where the sum over the repeated index a is implicit.

A basis $\{ I_{\widetilde{a}} \}$ of $\widetilde{\mathfrak {g}}$ is then given by $I_{a, -n} :=I_a \otimes t^{-n}$ for $n \in \mathbb {Z}$ together with $\mathsf {K}$ and $\mathsf {D}$. Its dual basis with respect to the standard bilinear form $(\cdot | \cdot ) : \widetilde{\mathfrak {g}}\times \widetilde{\mathfrak {g}}\rightarrow \mathbb {C}$ on $\widetilde{\mathfrak {g}}$, which we denote by $\{ I^{\widetilde{a}} \}$, consists of $I^a_n :=I^a \otimes t^n$ for $n \in \mathbb {Z}$ together with $\mathsf {D}$ and $\mathsf {K}$.

Now the Lax matrix of the affine Gaudin model takes the form

$$\begin{aligned} L(z) :=I_{\widetilde{a}} \otimes {\mathcal {L}}^{\widetilde{a}}(z) \end{aligned}$$

(3.2)

where the infinite sum over the repeated index $\widetilde{a}$ is implicit. The ${\mathcal {L}}^{\widetilde{a}}(z)$ are given by very explicit rational functions on $\mathbb {C}P^1$ which are valued in the algebra of observables ${\mathcal {A}}$ of the Gaudin model. For instance, in the simplest case of Gaudin models with regular singularities the algebra of observables ${\mathcal {A}}$ is a completion of $S(\widetilde{\mathfrak {g}})^{\otimes N}$ where $N \in \mathbb {Z}_{\ge 1}$ is the number of sites, which are located at $\varvec{z} = \{ z_i \}_{i=1}^N$. We then have

$$\begin{aligned} {\mathcal {L}}^{\widetilde{a}}(z) = \sum _{i=1}^N \frac{I^{\widetilde{a}(i)}}{z - z_i} \end{aligned}$$

where $I^{\widetilde{a}(i)}$ denotes the copy of the basis element $I^{\widetilde{a}} \in \widetilde{\mathfrak {g}}$ in the $i^\mathrm{th}$ copy of $S(\widetilde{\mathfrak {g}})$ in the N-fold tensor product $S(\widetilde{\mathfrak {g}})^{\otimes N}$. Explicit and simple expressions for ${\mathcal {L}}^{\widetilde{a}}(z)$ also exist for other generalisations of the Gaudin model. However, since these are not directly relevant for the present discussion, we refer the reader to [47] for the details. For our purposes, the key property that we shall need of these functions is that the Poisson brackets of the fundamental fields of the Gaudin model (in the above example these are $I^{\widetilde{a}(i)}$) can be packaged into the following form [47]

(3.3)

where $\widetilde{C} :=I_{\widetilde{a}} \otimes I^{\widetilde{a}}$ is the split Casimir of $\widetilde{\mathfrak {g}}$.

The connection with (3.1) is now apparent. Explicitly, let us consider the natural representation $\varrho$ of $\widetilde{\mathfrak {g}}$ in terms of $\mathfrak {g}$-valued connections on $S^1$, given explicitly in the basis $\{ I_{\widetilde{a}} \}$ by

$$\begin{aligned} I_{a, -n} \longmapsto I_a \otimes e^{- \mathrm{i}n \sigma }, \qquad \mathsf {K}\longmapsto 0, \qquad \mathsf {D}\longmapsto - \mathrm{i}\partial _\sigma , \end{aligned}$$

where $\sigma$ is a coordinate on $S^1 = \mathbb {R}/ 2 \pi \mathbb {Z}$. Applying $\varrho$ to both tensor factors of the split Casimir of $\widetilde{\mathfrak {g}}$ yields

As recalled above, the definition of $\delta _{\sigma \sigma ^{\prime }}$ used here is $\frac{1}{2\pi }$ times the one in [47].

Likewise, applying $\varrho$ to the first tensor factor of the formal Lax operator (3.2) gives

where again we refer to [47] for the explicit forms of the rational functions ${\mathcal {D}}(z)$, ${\mathcal {K}}(z)$ and ${\mathcal {L}}^a_n(z)$ valued in the algebra of observables $\mathcal {A}$ of the affine Gaudin model.

To describe a specific classical integrable field theory, we should also introduce a representation $\hat{\pi }$ of the Poisson algebra ${\mathcal {A}}$. This should send ${\mathcal {K}}(z)$, which is valued in the centre of ${\mathcal {A}}$, to a complex number valued rational function. In the example of a Gaudin model with regular singularities mentioned above, this takes the form

$$\begin{aligned} {\mathcal {K}}(z) = \sum _{i=1}^N \frac{\mathsf {K}^{(i)}}{z - z_i}, \end{aligned}$$

and the central elements $\mathsf {K}^{(i)}$ should be realised as complex numbers. Furthermore, $\hat{\pi }$ should realise each $\mathcal {L}^a_n(z)$, $n \in \mathbb {Z}$ in terms of the Fourier modes of the various fields of the classical integrable field theory in question. Explicitly, $\hat{\pi }$ is given by

$$\begin{aligned} {\mathcal {K}}(z) \longmapsto \mathrm{i}\varphi (z), \qquad I_a \sum _{n \in \mathbb {Z}} e^{- \mathrm{i}n \sigma } \otimes {\mathcal {L}}^a_n(z) \longmapsto {\mathcal {L}}(\sigma , z), \end{aligned}$$

(3.4)

where ${\mathcal {L}}(z)$ is the $\mathfrak {g}$-valued Lax matrix of the classical integrable field theory and $\varphi (z)$ is its twist function. Combining this with the representation $\varrho$, we have

In other words, the twist function naturally arises as one of the components of the Lax matrix of the affine Gaudin model.

Applying $\varrho$ to the first and second tensor factors of the Poisson bracket relation (3.3), labelled respectively by and , as well as applying $\hat{\pi }$ to the third factor which is not explicitly labelled, we now obtain the non-ultralocal Poisson algebra (3.1).

3.2 Quadratic Hamiltonians

So far we have only described, though somewhat implicitly (but more explicitly in the case of regular singularities), the kinematics of affine Gaudin models.

The dynamics of an affine Gaudin model is defined by its quadratic Hamiltonians. These are conveniently defined, by using the Lax matrix (3.2), as the coefficients in the partial fraction expansion of the rational function

$$\begin{aligned} S_1(z) :=\frac{1}{2}(L(z) | L(z)) = {\mathcal {K}}(z) {\mathcal {D}}(z) + \frac{1}{2}\sum _{n \in \mathbb {Z}} \langle I_a, I_b \rangle {\mathcal {L}}^a_{-n}(z) {\mathcal {L}}^b_n(z), \end{aligned}$$

(3.5)

where the bilinear form $(\cdot | \cdot )$ on $\widetilde{\mathfrak {g}}$ is being applied to the pair of first factors of the Lax matrices in (3.2). It follows directly from (3.3) that the quadratic Hamiltonians generate a Poisson commutative subalgebra of ${\mathcal {A}}$ [47].

Since (3.5) is a rational function valued in ${\mathcal {A}}$, we can apply to it the representation $\hat{\pi }$ which, after also multiplying through by the inverse twist function, gives [17]

$$\begin{aligned} \varphi (z)^{-1} \hat{\pi } \big ( S_1(z) \big ) = \hat{\pi } \big ( {\mathcal {D}}(z) \big ) + \frac{1}{2}\varphi (z)^{-1} \int _{S^1} d\sigma \langle {\mathcal {L}}(\sigma , z), {\mathcal {L}}(\sigma , z) \rangle . \end{aligned}$$

The first term on the right-hand side has poles only at the sites $\varvec{z} = \{ z_i \}_{i =1}^N$, namely at the poles of the twist function $\varphi$, and is thus regular at the set $\varvec{\zeta }$ of zeroes of $\varphi$. Taking the residue at any $x \in \varvec{\zeta }$, we obtain

$$\begin{aligned} {{\,\mathrm{res}\,}}_x \varphi (z)^{-1} \hat{\pi } \big ( S_1(z) \big ) dz = {{\,\mathrm{res}\,}}_x \bigg ( \frac{1}{2}\varphi (z)^{-1} \int _{S^1} d\sigma \langle \mathcal {L}(\sigma , z), {\mathcal {L}}(\sigma , z) \rangle \bigg ) dz. \end{aligned}$$

Recalling that we identified ${\mathcal {L}} = 4 \pi \mathrm{i}\Pi _{\bar{z}}$ in Sect. 3.1, it now follows that the Hamiltonian (2.19) of four-dimensional Chern–Simons theory on the reduced phase space is given by a linear combination of the quadratic Gaudin Hamiltonians, explicitly

$$\begin{aligned} H \approx - \sum _{x \in \varvec{\zeta }} \epsilon _x {{\,\mathrm{res}\,}}_x \varphi (z)^{-1} \hat{\pi } \big ( S_1(z) \big ) dz. \end{aligned}$$

This completes the proof of the main result, namely that the classical integrable field theory on the reduced phase space of four-dimensional Chern–Simons theory identified in Sect. 2 can indeed be described as a realisation of an affine Gaudin model.

Let us note in passing that higher-spin local integrals of motion in classical Gaudin models of affine type are also intrinsically associated with the set $\varvec{\zeta }$. Indeed, explicit expressions for these were constructed in [34], in the case when $\mathfrak {g}$ is of classical type, generalising the original construction of [21] on the principal chiral model. Specifically, there exists certain polynomials in the Lax matrix $\mathcal {L}(\sigma , z)$, whose degrees are related to the set of exponents of $\widetilde{\mathfrak {g}}$, and the evaluation of which at the points in $\varvec{\zeta }$ yield the higher local conserved charges. It would be interesting to understand their appearance from the point of view of four-dimensional Chern–Simons theory.

4 Discussion

4.1 Formal Gaudin model and realisations

Loosely speaking, one talks about a given classical integrable field theory as ‘being’ an affine Gaudin model if it has all the properties listed in (1.3)–(1.5). However, it is convenient to distinguish the affine Gaudin model formulated at the abstract level of affine Kac–Moody algebras from the classical integrable field theory itself. For this reasons, quantities expressed at the level of Kac–Moody algebras were referred to as being formal in [47].

As recalled in Sect. 3, in order to go from the formal affine Gaudin model to a concrete classical integrable field theory, one needs to make a choice of representation $\hat{\pi }$ of the algebra of formal observables ${\mathcal {A}}$, cf. (3.4). And although the twist function $\varphi$ is an important ingredient in the definition of $\hat{\pi }$ it does not, by itself, define $\hat{\pi }$. Indeed, one also needs a realisation of the formal fields of the Gaudin model in terms of the fundamental fields of a given theory, represented by the second equation in (3.4).

In particular, different classical integrable field theories may share the same twist function. Indeed, given a twist function with at most double poles, there are often various natural ways of defining a corresponding realisation $\hat{\pi }$. A list of possibilities, which is by no means complete, was given in [17].

One way of defining $\hat{\pi }$ is to try to associate with every double pole of $\varphi$, or with pairs of simple poles of $\varphi$, a copy of the cotangent bundle $T^*{\mathcal {L}} G$ of the loop group ${\mathcal {L}} G$ where G is a real Lie group with Lie algebra $\mathfrak {g}$, which we take here to be real. A general recipe for doing so was given in [46] building on the earlier constructions in [18, 19].

Concretely, the group valued field $g_i$ parameterising the base of the copy of $T^*{\mathcal {L}} G$ associated with a given double pole $z_i$ of $\varphi$ can be defined by the requirement that the gauge transformation of the Lax matrix by $g_i$ vanishes at $z_i$. Likewise, the group valued field $g_i$ associated with simple poles $z_i^\pm$ is defined by requiring that the gauge transformation of the Lax matrix by $g_i$ evaluated at the pair of points $z^\pm _i$ takes value in a subalgebra complementary to $\mathfrak {g}$ in $\mathfrak {g}^\mathbb {C}$ or to $\mathfrak {g}_\mathrm{diag}$ in $\mathfrak {g}\oplus \mathfrak {g}$. See [46] for details.

The proposals of [15] for constructing the group valued fields (called $\sigma _i$ there) in both the double and simple pole cases, i.e. rational and trigonometric cases, are very reminiscent of the above general constructions. This serves to highlight again the very close similarity between the two formalisms of [15, 47].

Let us also mention that one particular family of classical integrable field theories that were shown in [17] (see also [46]) to be realisations of affine Gaudin models are the so called ‘$\lambda$-deformations’ of the principal chiral model [44], of the symmetric space $\sigma$-models [30] and also of the semi-symmetric space $\sigma$-models [31]; see also [7] for the $\lambda$-deformation of the pure-spinor superstring on $AdS_5 \times S^5$. It was argued in [42, 43] that the $\lambda$-deformation can be seen as the theory at the boundary of a ‘doubled’ ordinary Chern–Simons theory. It would be interesting to understand the connection with the present analysis in the context of $\lambda$-deformations.

4.2 Dihedral equivariance

It will be interesting to generalise the analysis of the present note to four-dimensional Chern–Simons theory on the orbifold $\Sigma \times \mathbb {C}P^1/\mathbb {Z}_T$ for $T \in \mathbb {Z}_{\ge 2}$, where $\mathbb {Z}_T$ here only acts on $\mathbb {C}P^1$ by contrast with the orbifolds considered in [8]. This should amount to $A_\sigma$ being equivariant under an action of the cyclic group $\mathbb {Z}_T$ in the sense that

$$\begin{aligned} \check{\sigma }(A_\sigma (\sigma , z)) = A_\sigma (\sigma , \omega z), \end{aligned}$$

(4.1)

where $\omega$ is a $T^\mathrm{th}$-root of unity and $\check{\sigma }$ a $\mathbb {Z}_T$-automorphism of $\mathfrak {g}$.

In the language of [47], this would then correspond to considering the family of $\mathbb {Z}_T$-cyclotomic affine Gaudin models. The latter encompasses all symmetric and semi-symmetric space $\sigma$-models and in particular the $\sigma$-model of the superstring on $AdS_5 \times S^5$ [45], but also affine Toda field theories.

We have also not addressed the issue of reality conditions here. In the setting of [47], these are characterised by the Lax matrix $A_\sigma$ also being equivariant under an action of $\mathbb {Z}_2$, namely

$$\begin{aligned} \check{\tau }(A_\sigma (\sigma , z)) = A_\sigma (\sigma , \bar{z}), \end{aligned}$$

(4.2)

where $\check{\tau }$ is an anti-linear involution of the complex Lie algebra $\mathfrak {g}$ that specifies the choice of real form of $\mathfrak {g}$.

The conditions (4.1) and (4.2) put together imply that $A_\sigma$ is, in fact, equivariant under an action of the dihedral group $D_{2T} = \mathbb {Z}_T \rtimes \mathbb {Z}_2$. It was shown, more precisely, in [47] that many classical integrable field theories of interest admit a description as dihedral affine Gaudin models. It will be interesting to connect such affine Gaudin models to four-dimensional Chern–Simons theory. We leave this for future work.

4.3 (Dis)order defects and (non-)ultralocality

There are two types of classical integrable field theories discussed in [15], corresponding to two types of surface defects, namely the order and disorder ones, that can be added to the four-dimensional Chern–Simons theory described by the bulk action (1.1). It follows from the results of this note that this dichotomy is essentially the same as the usual one between the ultralocal and non-ultralocal models.

Indeed, the order defects were considered only in the cases when $\omega$ has no zeroes, as in the original papers [11, 12, 48, 13, 14] on lattice models—see Sect. 4.4 below. Among those, the two cases covered by the formalism of this note are $\omega = dz$ (rational) and $\omega = dz / z$ (trigonometric). In the former case $\varphi (z) = 1$ so that the $\delta ^{\prime }$-term in the Poisson bracket (1.3) of the Lax matrix is absent. In the latter case, the coefficient of the $\delta ^{\prime }$-term in (1.3) is constant, i.e. independent of the spectral parameters, and can typically be eliminated by a suitable gauge transformation. A prime example of this, albeit in the cyclotomic case, is given by KdV theory [5].

As noted in [15], however, the collection of classical integrable field theories that can be described using order defects is very limited. Indeed, most theories of interest are described instead, in the language of [15], using so called disorder defects. These were considered in the case when the 1-form $\omega$ has zeroes. As we have shown, this is in perfect agreement with the observation made in [47] that a very large family of classical integrable field theories are described by affine Gaudin models, which are intrinsically non-ultralocal. Indeed, the fact that many known non-ultralocal models were recovered in [15], including the multi-parameter family of coupled integrable $\sigma$-models introduced in [16], is what originally prompted us to seek a deeper connection between the formalisms of [15, 47].

Turning to the problem of quantising these classical integrable field theories, one can expect the quantum inverse scattering method [24, 32, 22, 20, 23], i.e. RTT formalism, to apply as usual in the ultralocal setting. In particular, this formalism should have a reinterpretation in the language of four-dimensional Chern–Simons theory as was the case for lattice models in [14].

In the non-ultralocal setting, however, we expect new techniques to be required, which are ultimately related to the problem of $\omega$ having zeroes.

4.4 Zeroes of the differential $\omega$

The presence of zeroes in $\omega$ is known to pose problems in the perturbative quantisation of four-dimensional Chern–Simons theory. Indeed, it was argued heuristically, e.g. in [13], that since the action (1.1) depends on $\omega$ through the ratio $\omega /\hbar$, its zeroes correspond to points where $\hbar \rightarrow \infty$. In light of the discussion of Sect. 4.3, this issue can be seen as a reformulation of the long-standing open problem of quantising non-ultralocal integrable field theories, which in turn is equivalent to the problem of quantising (dihedral) affine Gaudin models [47].

It is interesting that in the lattice model context of [11, 12, 48, 13, 14], restricting attention to Riemann surfaces C admitting a non-vanishing differential $\omega$, so as to avoid these difficulties, has led to rediscovering the classification of skew-symmetric solutions to the Yang-Baxter equation due to Belavin and Drinfel’d [6].

By contrast, the presence of zeroes in $\omega$ is clearly needed in the context of classical integrable field theories. In the language of [15], it is thus expected that quantising non-ultralocal integrable field theories will require a non-perturbative definition of quantum four-dimensional Chern–Simons theory with action (1.1) for generic $\omega$.

On the other hand, approaching the problem from the perspective of affine Gaudin models, we anticipate from [LVY1, LVY2] that in studying quantum Gaudin models associated with the affine Kac–Moody algebra $\widetilde{\mathfrak {g}}$, the role of the zeroes of the twist function $\varphi$ should be replaced by twisted homology cycles in $\mathbb {C}P^1{\setminus } \varvec{z}$. This may also shed some light on how to tackle the problem from the point of view of four-dimensional Chern–Simons theory.

Finally, it is also expected that Langlands duality should play a central role in the study of Gaudin models in affine type, see for instance [FF, FH, LVY1, LVY2], by direct analogy with the well-studied case of Gaudin models in finite type [FFR, F1, F2, MV1, MV2]. It would therefore be very interesting to see the emergence of Langlands duality also from the four-dimensional Chern–Simons theory.