High-throughput bandstructure simulations of van der Waals hetero-bilayers formed by 1T and 2H monolayers

Abstract

Vertically stacked van der Waals heterostructures made of two-dimensional compounds are almost an infinite playground for the fabrication of nano-engineered materials for the most diverse applications. Unfortunately, high-throughput electronic structure theory, which often serves as a guidance for material design, is not practical in this case. In fact, the compositional and structural complexity of van der Waals heterostructures make the number of prototypes to calculate combinatorially large. In this work a method is developed to compute the bandstructure of van der Waals heterostructures with an arbitrary composition and geometry using minimal computational resources. Such scheme is applied to the systematic study of a library of two-dimensional hexagonal XY₂ compounds. The method is based on the density functional theory and on the assumption that the inter-layer electronic interaction is limited to classical electrostatic screening. Our analysis enables us to identify and categorize a large range of van der Waals bilayer heterostructures with electronic band gaps of different nature ranging from 0.1 to 5.5 eV and various types of band line-up.

Introduction

Two-dimensional (2D) materials have unique physical/chemical properties that originate from their extreme quantum confinement and, for that reason, appear as appealing candidates for the next generation of optoelectronic and nanoelectronic devices.¹ Research in this area of materials science has been kicked off by the isolation of graphene from graphite, and a second strong stimulus has been provided by the isolation of transition metal dichalcogenides (TMDs). This latter is a relatively large family of compounds offering tuneable band gaps, strong light–matter interaction and high charge-carrier mobility. Furthermore, piezoelectricity, valleytronics, superconductivity, and charge density wave have all been found in single and/or a few layers TMDs.^2,3,4,5,6,7 The two most common TMDs monolayers (MLs) polytypes are octahedral (1T) and trigonal prismatic (2H). Both configurations are characterized by one transition-metal atomic layer sandwiched between two layers of chalcogen ions.

In addition to their remarkable intrinsic properties, 2D materials also pave the way to a vast family of hybrid crystals, known as van der Waals heterostructures (vdWHs).^8,9 Such heterostructures are formed by vertically stacking two or more different 2D MLs. Importantly, the layers interact with each other only via weak vdW forces, since the surfaces have no dangling bond. This means that the formation of heterogeneous vdW-bonded stacks is almost completely chemical agnostic, so that potentially any arbitrary combination of MLs can be obtained. Given the large number of ML types available and the broad variety of their properties, the concept of vdWHs appears ideal to the rational design and engineering of nanomaterials for devices. At the same time, however, the possible combinatorial space is enormous. Furthermore, MLs can be arranged in a broad variety of crystallographically inequivalent ways, so that for the same combination many polymorphs may exist. Heterostructures made of graphene, h-BN, MoS₂, MoSe₂, WS₂, and WSe₂ have all been intensively investigated.^10,11,12,13 Nevertheless, the full potential of vdWHs has not been entirely exploited in the absence of high-throughput methods to rapidly chart the enormous compositional and configurational space available.

An accurate calculation of their electronic bandstructure is essential to understand and predict the properties of vdWHs. Standard density functional theory (DFT) within the generalized gradient approximation (GGA) routinely underestimates the band gaps, so that it is suitable for extracting only structural and mechanical information, in particular if the GGA is corrected for dispersive forces. At the same time higher level methods, such as hybrid-functionals DFT and GW many-body perturbation theory, are numerically expensive and cannot be deployed over the entire compositional space of the vdWHs. Furthermore, vdWHs made of different MLs are only rarely lattice matched so that real stacks can have extremely large in-plane supercells. The situation is further aggravated by the fact that often different stack geometries are very close in energy so that the study of the electronic properties require some level of compositional average. This means that the calculation of the bandstructure of vdWHs in a high-throughput mode remains an impractical task even for modern super computers.

In this work, we have developed a high-throughput method to calculate the bandstructure of vdWHs at a very low computational cost, which can then be used for a rapid and effective screening for potential applications. This is based on the concept that, except for dielectric screening, the interlayer interaction affects little the bandstructure of the layers forming an heterostructure.¹⁴ A database, containing 93 2D parental compounds, all with hexagonal lattice, has been first constructed. This contains the mechanical and electronic properties of such 93 materials computed with DFT at the level of both semi-local and hybrid functionals. Semiconducting MLs are then selected to generate more than 700 bilayer vdWHs, constructed to have the smallest possible unit cell compatible with low strain. We have then identified a large range of vdWHs with electronic band gaps ranging from 0.1 to 5.5 eV. These include several structures with direct band gap and various types of band line-up. Our work thus offers a map to navigate the extremely large compositional space of vdWHs and enable the rapid screening of structures with the desired electronic properties.

Note that our work is by no mean the only one proposing a high-throughput strategy for the analysis of the electronic properties of vdWHs. For instance, Haastrup et al. have created a very comprehensive database of computed properties of 2D materials (C2DB), which can be combined to evaluate the properties of prototype heterostructures.¹⁵ In particular C2DB is a powerful tool to determine both the band alignment and the band gap of heterogeneous structures. Here we go a step further. Our method, in fact, has been designed to compute, not only the alignment and the gap, but most importantly the entire band structure of any given vdWH, regardless of its composition, unit cell and layers orientation. This is a crucial aspect, since often the structural details of a heterostructure determine the electronic properties.¹⁶ The key enabler of such calculation consists in mapping the band energy dispersion of the monolayers over the entire 2D irreducible Brillouin zone, something that is usually not performed as standard in band structure theory.

The paper is organized as follows. In the next section we present the mechanical and electronic properties of the 93 compounds included in the database. Among them, 38 MLs are nonmagnetic and nonmetallic (having nonzero band gap) and these are used to form 703 bilayer combinations. Results for the 703 vdWHs are discussed next. These include several combinations (292) presenting type-II band alignment, many never seen before. Such band structures are categorized by band-gap type, size and according to the details of the band alignment. The we proceed by a short discussion. Finally, we report computational aspects of our work, in particular the strategy used for the construction of the vdWHs and the band-folding scheme adopted to extract the band structure of the bilayers from those of the constituent MLs.

Results

Targets of the screening process

Despite the fact that atomically thin materials offer a broad range of properties and have attracted tremendous research interest, only a handful of them has been considered as building block for heterostructures. The problem is that there are several hundreds compounds that can be isolated in a single layer form.^17,18 This number becomes even larger when one also considers hypothetical single layers constructed by chemical similarity to existing compounds.¹⁵ For this reason the combinatorial space of the possible heterostructures is enormous, and it then appears clear that a consistent and comprehensive exploration is needed to fully map the properties of the possible vdWHs and to determine where to direct the fabrication effort. This is the main target of our work, which focuses on the sub-class of existing and exfoliatable 2D materials having either 1T- or 2H-type layers with chemical formula of XY₂ [see Fig. 1(a) for the atomic structure]. Due to their structural similarities the heterostructures formed by vertically stacking XY₂ MLs can preserve the hexagonal symmetry.

Fig. 1: Atomic structures of the monolayers and possible band alignments of the vdWHs.

a Atomic arrangement of the prototypes 1T and 2H monolayers. In the figure the lattice constant, a, the layer thickness, h, and the inter-layer distance d, are indicated. b Possible band alignments for a two-layer heterojunction. Conduction bands are in red and valence ones in blue. In the case of type-II band alignment we have defined the band offsets for the conduction and valence band, respectively as, ΔE_v and ΔE_c.

2D hexagonal X Y ₂ database

The ML building blocks for our vdWHs have been chosen from the MaterialsCloud 2D materials database¹⁷, in which the structure of 2D materials in their ML form is extracted from that of the experimentally existing parental bulk compounds. These comprise both 1T (80 in total) and 2H (16) ML structure [see Table 1], and mostly include di-chalcogenides and di-halides made with transition-metal and rare-earth ions. A few compounds have a central chalcogenide ion and two metallic external surfaces (e.g., OTl₂). Among the materials chosen 7 of them have been reported to present both a 1T and a 2H geometry: CrSe₂, GeI₂, MoS₂, NbS₂, NbSe₂, TaS₂, and TaSe₂. Most of the MLs investigated here are also part of C2DB,¹⁵ with the exceptions being OTl₂, STl₂, YbI₂, and 2H-GeI₂. Note that C2DB contains the electronic structure of 350 1T and 348 2H MLs, many of which have never been synthesised and remain theoretical prototypes.

Table 1 Mechanical and electronic properties of 93 hexagonal XY₂ 2D materials MLs important for hetero-structure engineering.

In an heterostructure the vdW forces do not only provide the binding between the layers, but also affect their electronic and optical properties, mostly through the geometry relaxation induced by the interlayer interaction. Thus, it is important to determine the strength of such dispersive interactions. The layers’ binding energy, E_b, and the inter-layer distance, d, are two important quantities that characterize the interlayer bonding in heterostructures [see Fig. 1(a) for the definition of the various structural quantities]. Here the binding energy is calculated by using the total energy of the relaxed ML as reference, namely it is

$${E}_{{\rm{b}}}=({E}_{{\rm{crystal}}}-{E}_{{\rm{ML}}})/S\ ,$$

(1)

where E_crystal is the DFT energy per layer in the relaxed bulk crystal structure (total energy divided by number of layers in unit-cell), E_ML is the energy of the relaxed ML and S is the surface area. With this definition E_b is slightly larger than that obtained by simply separating the layers of the bulk 3D structures. If multiple bulk crystal structures exist for a given material, the lowest energy bulk structure will be used as unique reference. Note that E_b is calculated only for homogeneous compounds and not for the hetero-bilayers.

Our results are summarized in Fig. 2, where we plot the layer thickness, h and the binding energy, E_b, as a function of the interlayer distance, d. The various compounds are color-coded differently depending on the corresponding chalcogen or halide element, since these form the most external atomic layers in the 2D MLs. The figure also include data for 2D compounds having the external surfaces made of metal ions [NBa₂, NCa₂, NSr₂, OTl₂, and STl₂]. These are grouped under “other”. In general, as expected, we find that both h and d increase with the atomic number of the chalcogen/halide element, as a consequence of the larger ionic radii. Oxides appear to form rather tight monolayers with a strongly confined planar structure (h is small) regardless of the inter-layer distance, while halide-based 2D compounds on average present thicker MLs. Similarly, the interlayer distance of halide-based compounds is consistently larger than that of their chalcogen-based counterpart. We could not find a particular correlation between d and the in-plane lattice constant a (not shown here), indicating that the metal ion also plays a significant role in determine the geometry.

Fig. 2: Binding properties of the 2D compounds used as building blocks for constructing the vdWHs.

a layer’s thickness, h, against the inter-layer distance, d. b the binding energy, E_b, against the inter-layer distance.

Moving to the binding energy we note that, again as expected, structures presenting a small interlayer distance also display large binding energies. As a consequence we find larger E_b for compounds incorporating heavier chalcogen/halide elements. An anomaly to this trend is found for 2D materials presenting metallic edges, namely for XY₂ compounds where Y is a metal. In these the binding energies are in excess of 100 meV per Ų, making them hard to exfoliate and unsuitable for constructing vdWHs. The post-transition metals Thallium is the only exception with OTl₂ and STl₂ having E_b of 31 meV per Ų and 35 meV per Ų, respectively, i.e., values similar to what found for transition-metal di-chalcogenides.

The bandstructures of the MLs are calculated next for the GGA-relaxed structures, initially at the GGA level. Among the 93 MLs studied 49 are found to have nonzero band-gap, while 44 are metals. Interestingly 23 MLs are predicted to show a net spin moment, 11 of them have nonzero band-gap, 6 are metallic and 6 present a half-metal bandstructure. In general, our results agree well with those reported in Mounet’s work.¹⁷ It is important to note that the GGA may fail in predicting the correct magnetic ground state, and consequently often also the correct metallic state, in particular for compounds containing tightly bound orbitals, such as rare earths. Hence, we will not consider magnetic compounds when constructing the vdWHs. Also note that the typical GGA band gaps are usually severely smaller than the actual ones. For this reason the bandstructure and geometry of the remaining compounds will be re-calculated at the HSE06 level (see later).

Upon forming a vdWH the MLs involved will undergo some form of strain. In fact, the size of the actual unit cell of the vdWH will be determined by a competition between the strength of the dispersive forces binding the layers and the energy costs associated to the strain. The minimum of the binding potential between the layers is usually found at high-symmetry positions (e.g., the stack geometry found in bulk), for which the size of the vdWH unit cell is minimal. These configurations, however, will be found only if the binding energy is sufficiently large to overcome the energy necessary to modify the in-plane lattice parameter of the free-standing MLs to that of the final vdWH. Thus it is important to study the dependence of the MLs’ total energy on the strain, ε.

We perform GGA calculations for MLs strained in the range [−3%, +3%] in steps of 0.5% applied to both the x and y axis. The atomic positions are relaxed for any in-plane lattice constant and the strain coefficient, α, is obtained with a quadratic fit of the total energy against strain,

$$E={E}_{0}+\alpha {\varepsilon }^{2}\ .$$

(2)

The elastic modulus, α_s, is then calculated as the strain coefficient per unit area, α_s = α/s, and it can be thought as the 2D analog of the bulk modulus. Our results are summarised in Table 1. In general, we find a broad range of stiffnesses with α_s values going from 1.4 eV per Ų (1T-TmI₂) to 11.11 eV per Ų (2H-WS₂). Such α_s distribution is thus about twice as wide as that found for the binding energy, E_b, indicating that the response to strain is the key property in determining the structure of possible vdWHs. We consistently find the di-chalcogenides to be stiffer than the halides, with α_s increasing as the atomic number of the main-group ion is reduced. In the case both the 1T and 2H structure can be stabilized, we find the 2H polymorph to be more stiff than the corresponding 1T. Completing the information reported in Table 1 are the computed equilibrium lattice constants, a₀, the cell magnetic moment, μ, and both the direct and indirect GGA band gap, E_g and E_d. Finally, for some of the magnetic MLs, e.g., CoI₂ and FeI₂, the coefficient α_s is not defined. This is because strain induces a spin transition so that the energy-versus-strain curves discontinuously jump at some critical strain. One could then perform a fixed-spin calculation and compute α_s for the different magnetic states. Since, we have excluded magnetic compounds from the construction of the vdWHs, we have not performed such calculations.

Since our chosen MLs are a subset of those contained in the MaterialsCloud 2D materials database, it is useful at this point to compare our results with those of ref. ¹⁷. In particular the comparison concerns the GGA band information, E_g and E_d, and the binding energy, E_b. In general we find an almost perfect agreement between our computed band gaps and optical band gaps, indicating that the differences in GGA-DFT implementation between our work and ref. ¹⁷ play little role. A good agreement, although not perfect, is also found for the binding energy. In this case the deviations are in the region of 20% with the exception of NBa₂, NCa₂, NSr₂, and a few group-V dichalcogenides, for which we compute a binding energy about twice as large as those reported MaterialsCloud. These differences are attributed to the different XC functionals used to describe van der Waals interaction, namely the DF2C09¹⁹ and rVV10²⁰ in ref. ¹⁷ and the Tkatchenko–Scheffler method with Hirshfeld partitioning²¹ in our work. Note that such differences are fully in line with the reported spread of values associated to the different mainstream van der Waals functionals²² and so they should be considered as normal. Indeed they are small enough not to jeopardise our ability to distinguish the compounds easy to exfoliate from the others. A full comparison of our results with those of ref. ¹⁷ is provided in the Supplementary Table S1.

In order to correct for the shortfalls of the GGA in predicting band properties we have repeated our calculations by using the hybrid HSE06 functional. This time we have considered only those compounds presenting a GGA nonmetallic bandstructure and no magnetism. The chosen ML structures have been relaxed again with HSE06 and then the bands have been calculated. In a few cases, e.g., 2H-CrSe₂, materials predicted nonmagnetic by GGA display a spin-polarized ground state when the electronic structure is computed by HSE06. These have also been excluded from any further analysis. In general, we find the difference between the lattice parameters calculated by GGA and HSE06 to be of the order of 0.5%, with the largest difference of 3% being reported for OTl₂. Such small structural variations are in line with what expected from the functionals used. Note that there is no clear trend when comparing structural parameters obtained with GGA and HSE06, although HSE06 seems, on average, to slightly reduce the lattice parameters.

Going to the bandstructure we find, as expected, that HSE06 opens the GGA band gap without affecting too much the band curvature. Out of the 93 initial compounds only 38 are predicted nonmetallic and nonmagnetic. These include 1T-TiS₂ and 1T-HfTe₂, which the GGA returns semi-metals and HSE06 semiconductors. The inclusion of spin–orbit coupling in general reduces the band gap by shifting the valence band maximum (VBM) on average by 0.17 eV. Such shift is more pronounced for compounds made of heavy ions and the maximum shift of 0.52 eV is found for PtTe₂. Notably, only the MLs with 2H structure break inversion symmetry and their bandstructure shows spin-splitting along the Γ-K line.²³ A full summary of the electronic properties of the nonmetallic MLs is presented in Table 2. From the table we notice that there is only a limited number of direct-gap insulators/semiconductors. These are confined to W- and Mo-based di-chalcogenides (MoS₂, MoSe₂, MoTe₂, WS₂, WSe₂, WTe₂), all presenting 2H structure and band gap at the K point, and to a few 1T halides (CdBr₂, CdCl₂, HgBr₂, MgBr₂, MgCl₂, ZnCl₂) with band gap at Γ. The only exception is OTl₂, which strictly speaking possesses an indirect gap, but whose valence band top is extremely flat.

Table 2 Electronic properties of 38 nonmetallic and nonmagnetic MLs.

Most of our candidates (34 out of 38) have also been studied in C2DB¹⁵ using the HSE functional. A detailed comparison between our calculated band gaps, E_g and E_d, position of the valence band, E_v, and valence band shift is provided in the Supplementary Table S2, showing again an overall very good agreement, and therefore little dependence on the specific DFT implementation. As expected the corresponding GW band gaps, also computed in C2DB, are typically larger than the HSE06 ones, by a factor of about 1.3. It is worth remarking at this point, that our aim here is to compute the entire band-structure of the hetero-bilayers and not just the band lineup. For this reason we compute the bands over a uniform k-mesh spanning the entire irreducible Brillouin zone, so that we could not simply use the data reported in literature, such as those in C2DB.

The curvature of the VBM and of the conduction band minimum (CBM) is described by the electron and hole effective mass tensor. This is calculated from the HSE06 band structure including spin orbit interaction as

$${m}_{ij}^{* }={\left(\frac{{\partial }^{2}{E}_{\overrightarrow{k}}}{\partial {k}_{i}\partial {k}_{j}}\right)}^{-1}\ ,$$

(3)

where ${E}_{\overrightarrow{k}}$ is the band energy for the wave-vector $\overrightarrow{k}$, whose cartesian coordinate is (k_x, k_y). The second order derivatives are calculated by three-point-stencil differentiation, namely ${m}^{* }={[({E}_{k+\delta k}+{E}_{k-\delta k}-2{E}_{k})/(\delta {k}^{2})]}^{-1}$, with δk chosen close to the grid size of the energy surface. In Table 2 we report the eigenvalues of such 2D effective mass tensor. In general, we find that most of the MLs present a rather dispersive electron and hole band, with effective mass values below the free electron mass. Low effective mass values, indicative of potentially large mobilities, are found for W- and Mo-based di-chalcogenides, which present similar band dispersion at the VBM and CBM. Other compounds feature low effective masses only for either the valence (e.g., 1T-TiS₂) or the conduction band (e.g., 1T-STl₂), suggesting the possibility of large variation in mobility depending on the nature of the charge carrier. Finally, there are a few MLs presenting very high effective masses at the VBM and extremely anisotropic band curvatures (YbI₂, OTl₂, STl₂, PtO₂, and PtS₂). These MLs possess a high density of states (DOS) at the valence top, therefore, they have high and fast photo-responses. The high DOS is also potentially useful for thermoelectrics applications.

Finally we characterize the bandstructure by looking at their dependence on strain. In practice we monitor the energy of the VBM and the CBM and their positions in k-space as a function of strain. For small strains such dependence is approximately linear and one can write

$${E}_{\alpha }={k}_{\alpha }\varepsilon +{E}_{\alpha }^{0},$$

(4)

where α = v and c for the VBM and CBM, respectively. Thus, the coefficients k_c and k_v describe the response of the electronic structure to strain, a quantity that is related to the electron–phonon coupling at the top of the band. By definition the bang-gap strain coefficient is k_g = k_c − k_v. Sometime the band edges of some MLs move across two high-symmetry k-points under strain, causing the E_α(ε) to be discontinuous. In these cases we limit the calculation of Eq. (4) to strains small enough to keep the band extreme always at the same k-point. In general, we find that ∣k_c∣ > ∣k_v∣ for all the 2H structures (except GeI₂ and HfTe₂), while in the case of 1T MLs the situation is less clear. The largest coefficients are found for the conduction band of the W- and Mo-based di-chalcogenides, which are also among the most rigid compounds (see α_s in Table 1). In contrast selenides and tellurides made with either late (Pd, Pt, Sn) or group-four transition metals (Zr and Hf) display the strongest response to strain in the valence band: 1T-HfSe₂, 1T-PdTe₂, 1T-PtTe₂, 1T-SnSe₂, ZrSe₂, and 2H-HfTe₂. Note that the coefficient k_v and k_c have been computed at the GGA level, because of the HSE06 computational costs associated to the geometrical relaxations.

Selected bilayer vdWHs

In order to validate our noninteracting model we need to understand how the band edges of MLs drift in energy upon forming bilayer vdWHs. Thus, we have explicitly computed the electronic structure of all the possible heterogeneous bilayers constructed by using 10 of the ML prototypes contained in the database with either 2H (MoS₂, MoSe₂, WS₂, WSe₂) and 1T structure (GeI₂, HfS₂, PtSe₂, SnS₂, SnSe₂, and ZrS₂). By using the coincidence lattice method described before, we construct bi-layer configurations with the smallest in-plane area (smallest unit cell) and presenting a maximum strain not in excess of 2% (the strain on both the MLs forming the vdWH should be lower than 2%). This exercise is performed at the GGA level only. Figure 3 provides an idea of how many structures can be constructed according to this criterion for the case of MoS₂/SnS₂ bi-layers. In the figure we represent all the possible bi-layer supercells containing less than ~2000 atoms as a function of the twisting angle [Fig. 3(b)] and the in-plane strain [Fig. 3(c)]. The two forming MLs have a lattice mismatch of the order of 15%, a value that yields supercells with limited number of atoms for a twisting angle of 30^∘ [see Fig. 3(a)] and strains just in excess of 1%. The figure clearly shows that vdWHs can be formed for any angle and with arbitrarily small strains, as long as these contain a large number of atoms. For instance we have found that 560 structures can be designed with a twisting angle comprised between 0^∘ and 30^∘, strains smaller than 2% and containing <2000 atoms.

Fig. 3: Analysis of the possible MoS₂/SnS₂ bi-layers supercells.

a a sketch of a supercell with a twisting angle θ = 30^∘. The lattices of MoS₂ and SnS₂ are represented by orange and purple grids, respectively. The distribution of supercells for MoS₂/SnS₂ bi-layers, where the individual layers are strained by <2%: b number of atoms against the twisting angle; c number of atoms against the in-plane lattice strain, ε₁₁.

The bandstructures of the bilayer vdWHs are then obtained after geometrical optimization using Perdew, Burke and Ernzerhof (PBE) including vdW corrections. Among the 45 possible different vdWHs we find that eight are type-I, 35 type-II, and 2 type-III. We have then analyzed the position of the band edges of such vdWHs and compared them with those of the constituent monolayers [see Fig. 4(a)]. In general, we find that being part of a hetero-bi-layers affects little the position of the bands of the monolayers, as long as they do not have broken gaps (in Type-III junction). The average variation of the band edges among the materials investigated, whether in a ML form or as part of a bi-layer vdWH, is 0.11 eV for the VBM and 0.12 eV for the CBM. Since the MLs are typically under strain in a vdWH we have corrected the position of their band edges by using the strain coefficients, k_v and k_c. Such correction, however, does not change the average band-edge variations, indicating that strain is not the primary source of band-energy change when single layers form a vdWH. Figure 4(b) explores whether the band-energy change is directly correlated with the vdWH inter-layer distance, but no notable correlation is found. It is thus likely that the band-edge shift taking place in a vdWH is mostly due to the dielectric screening of the two layers¹⁴.

Fig. 4: Band information of the 45 vdWHs investigated.

a Band-edge energies of the vdWH against those of the constituent monolayers. b Band-edge deviation against inter-layer distance. Here we have defined ${{\Delta }}E={E}_{{\rm{ML}}}^{\alpha }-{E}_{{\rm{vdWH}}}^{\alpha }$, with ${E}_{{\rm{ML}}}^{\alpha }$ (${E}_{{\rm{vdWH}}}^{\alpha }$) being the band edge energy for the monolayer (vdWH) and α = VBM and CBM. The different colors identify the band-gap type of the heterostructure.

Finally, as far as the two type-III bilayers are concerned, 1T-SnSe₂/2H-WSe₂ and 1T-ZrS₂/2H-WSe₂, both present a shift in the valence band of about ~0.3 eV, with an analogous shift of ~0.3 eV found in the conduction band of 1T-ZrS₂/2H-WSe₂. Such large deviation is not unexpected considering that charge transfer can take place in the type-III lineup, an effect that is not described by our non-interacting model.

Non-interacting band structures and type-II vdWHs

We have just established that in type-I and type-II bi-layer vdWHs the VBM and CBM appear to be positioned rather close to their monolayer values. This suggests that Anderson’s rule is largely valid²⁴. Therefore, we can provide an accurate estimate of the vdWHs bands by simply superimposing those of the constituent monolayers, after the appropriate band folding. This essentially implies that, in first approximation, the two layers do not interact with each other. Importantly, such “non-interacting” approximation offers us the opportunity of a high-throughput screening of the possible vdWHs, where the electron energy surfaces of the MLs can be calculated by using expensive but highly accurate methods, while the simulation of heterostructures of large size is performed at a very moderate cost.

A database of bilayer vdWHs is thus generated by using the 38 nonmetallic and nonmagnetic MLs identified before, giving a total of 703 (38 × 37/2 = 703) combinations. These are enough so that an appropriate choice of the MLs forming the interface allows one to have a sophisticated control of the band gap and bands offset. For each combination, one configuration with minimum supercell area is created and the two arrays of indices n₁ − n₄ and m₁ − m₄ are calculated by using the coincidence lattice method [see first part of “Methods”]. The electronic band structure along the Γ − M − K − Γ path of the supercell is then calculated. Note that the absolute band gap between the VBM and the CBM is the same regardless of the epitaxy and orientation of the stacking. The minimum direct gap, however, depends on the relative alignment. There are 349 type-I, 292 type-II, and 62 type-III junctions (see Supplementary Table S3−S5 for details). A summary of the band gaps and band offsets of all 292 type-II vdWHs are plot in Fig. 5(a) [see Fig. 1(b) for a definition of the band offsets].

Fig. 5: Band information for the 292 type-II bi-layer vdWHs constructed with the non-interacting model.

a Band gaps and band offsets. The band gaps are shown as a color code, with the scale reported on the right-hand side. Solid symbols are for direct-gap vdWHs, while the hollow ones are for indirect. b The distribution of band gaps among 641 type-I and type-II vdWHs. The red portion of each bar represents number of type-I vdWHs, while the blue (sky blue) one indicates the number of type-II vdWHs with direct (indirect) band gap.

The range of band gaps found for such type-II vdWHs is broad, going from ~0 eV of YbI₂/SnSe₂ to 5.5 eV of MgBr₂/ZnCl₂. This means that potentially there are inter-layer absorption transitions ranging from the near infrared to the ultraviolet. Looking at the band offsets it appears that most of the bi-layer vdWHs have offsets within 1 eV. Interestingly the distribution of the offsets is not uniform and we find that junctions tend to have a valence-band offset, ΔE_v larger than that of the conduction band, ΔE_c. It is also interesting to observe that there is a significant number of junctions presenting ΔE_v ~ ΔE_c, although for these usually the band gap is small, in particular when the offset is large. Note that the band offsets are critical to determine several properties of the vdWHs, such as quantum confinement, dopability, and chemical activity. Figure 5(b) shows the distribution of vdWHs according to their band gap. The majority of the bilayer vdWHs has band gap below 2 eV and there are very few structures with E_g larger than 3 eV. The peak in the distribution corresponds to the interval 1.4−1.6 eV, where one finds about half of the structures with type-I bands alignment.

We now proceed to further analyze two subgroups of the possible type-II heterojunctions, namely vdWHs with a direct band gap and those presenting a planar unit cell identical to the primitive cell. A primitive-cell heterojunction is formed when two hexagonal MLs have very similar lattice constants. In this work, the lattice difference tolerance is 2%. Such MLs then have the possibility to bind to each other in the same way as in a homo-bilayer or in bulk. In these junctions the typical separation between the two layers is minimal and the inter-layer coupling is maximised. For example, it has been shown that the binding energy of MoS₂ bilayers can be reduced by about 20%, when the layers are oriented in a highly mismatched configuration.²⁵ By comparing the lattice constants of the various MLs, we find that 66 MLs pairs are able to form primitive-cell vdWHs with 30 of them being of type-II. Figure 6(a) shows the “network” of all type-II primitive-cell vdWHs, where we represent the constituent 1T MLs in red and the 2H in blue, while a solid (dashed) line indicates a direct-gap (indirect-gap) vdWH. Thus we find that 13 MLs pairs have direct or pseudo-direct band gap, while the remaining are indirect. Here a band gap is defined ‘pseudo-direct’ when either the conduction or valence band is very flat and the energy difference between the minimal indirect gap and the direct one is <0.1 eV.

Fig. 6: Summary of the electronic properties of type-II heterostructures with minimal unit cell and band edges at Γ.

a “Network” representation of the vdWHs having an in-plane unit cell corresponding to the ML primitive cell. Red (blue) compounds are 1T (2H) type. The dashed lines indicate that the MLs pair forms a vdWH with indirect band gap, while the solid ones are for direct vdWHs. b Band alignment for MLs with band edges at Γ (solid blocks). Blue blocks represent the valence bands and red blocks the conduction ones. A hollow block indicates that the corresponding band edge is not at Γ.

The structural and electronic properties of such heterostructures are reported in Table 3. The 13 direct-band-gap type-II heterostructures appear particularly appealing for optoelectronics applications. Three of them are made of pairs of 2H MLs, namely MoS₂/WS₂, MoSe₂/WSe₂, and MoTe₂/WTe₂, and have been extensively studied in the past.^2,3,16,26,27 In addition, we have also found ten more primitive-cell vdWHs made entirely of 1T MLs. These bi-layer vdWHs are rarely considered in research. Among them, PtTe₂/GeBr₂ has small gap of 0.38 eV but very large valence offset of 2.72 eV. STl₂/GeBr₂ and YbI₂/HgBr₂ have bad gap ~1 eV and ΔE_c ~ 2 eV. There are also four bilayers having very large band gaps, namely ZnI₂/GeBr₂, CdI₂/HgBr₂, MgI₂/HgBr₂, and MgBr₂/CdCl₂. The last three 1T vdWHs bilayers, YbI₂/1T-GeI₂, STl₂/CdBr₂, and YbI₂/CdI₂, all have type-II gap at around 1.6 eV, namely in the middle of the solar spectrum and rather close to that found for the Mo- and W-based chalcogenides heterostructures. In particular, YbI₂/1T-GeI₂ and YbI₂/CdI₂ appear interesting, since they both enjoy band offsets in the eV range, namely the indirect inter-layer band gap absorption edge should be well separated from any absorption transitions taking place over an individual ML.²⁸

Table 3 Properties of the type-II vdWHs made of 38 nonmetallic MLs and identified with the non-interacting method.

A second interesting class of vdWHs is populated by those structures for which the constituent MLs have band edges at different positions in k-space, but band folding makes them type-II with direct band gap. In this case the actual nature of the band gap depends on the specific type of supercell, meaning that the same materials combination may or may not form a direct-band-gap structure depending on how the bands of the constituent MLs fold. Clearly, for extremely large supercells the Brillouin zone of the heterostructure will be extremely small and band folding will yield almost flat bands and hence a direct band gap. Thus, we consider here only those hetero-bilayers in which the unit cell is equal or smaller than 3 × 3 of the constituent MLs primitive cell. Again results are presented in Table 3. This class contains a broad variety of structures made with MLs of either 1T and 2H symmetry and mixed 1T−2H composition. Their band gaps range from 0.17 eV for 1T-PtTe₂/1T-PbI₂ to 3.48 eV for 1T-CaI₂/1T-CdBr₂, with a large variety of band offsets. Notably, several of them have band offsets larger than 1 eV for both the valence and the conduction band. These include small band gap (E_g < 1 eV) junctions, namely 1T-YbI₂/1T-HfS₂, 1T-YbI₂/1T-SnS₂, 1T-STl₂/1T-PtO₂, 1T-YbI₂/1T-PtO₂, and 1T-YbI₂/2H-MoS₂, and the intermediate-gap 1T-PtO₂/1T-NiO₂. Note that the presence of quite a few structures containing 1T-YbI₂ is explained by fact that 1T-YbI₂ displays a very flat valence band, so that virtually all vdWHs made with it present a direct band gap. Given their highly tuneable band structures, this class provides a good materials platform for sensing applications.

The last class is composed by vdWHs, whose constituent MLs have the relevant band edge at the Γ point. In this case one will find the band extremes still at the Γ point regardless of the band folding, namely regardless of the size of the supercell. As such crystal momentum conservation is always preserved for the Γ-Γ transition, despite the rotations and translations needed to construct the heterostructure unit cell. It is thus expected that the properties determined by transitions at the band edge are little affected by the type of stack considered. This means there is no need to maintain special inter-layer configurations in fabrication and processing. Figure 6(b) shows the band edge alignment of all MLs which have VBM and/or CBM at Γ. The information is also useful if the building blocks are not limited to 1T and 2H MLs. Γ-Γ vdWHs are listed in Table 3.

Finally, a complete view of all the structures investigated can be obtained by looking at Fig. 7, where we present the band-gap type and the actual band-gap value for all the possible combinations obtainable with the 38 MLs building blocks.

Fig. 7: Summary of all the possible vdWHs made with 38 ML building blocks.

MLs written in red have 1T structure, while those in blue are 2H. a The band-alignment type, with color code shown on the bottom (the diagonal is left empty). b The actual value of the band gaps as a heat map.

Discussion

In this work MLs having 1T and 2H geometries form a database of hexagonal XY₂ 2D compounds, which is then used to construct bi-layer vdWHs. The electronic properties of the MLs and those of the parental 3D counterparts are simulated with DFT, both at the GGA and hybrid functional levels. In particular for each compound we compute the binding energy, the electronic band structure, the elastic modulus, the effective masses and the variation in band-edge energy with strain. MLs presenting an nonmetallic GGA band structure and nonmagnetic ground state are then selected to form the vdWHs.

Firstly, we have explicitly computed the electronic structure of 45 vdWH hetero-bilayers. Interestingly, their band edges are found close to those of the constituting MLs, once the variation of the extremal energies with strain is taken into account and with the remaining discrepancy being attributed to dielectric screening. This fact offers the conceptual foundation of our next set of calculations, where the electronic band structure of of vdWHs is approximated with that of the constituent MLs, after appropriate band folding. Thus, by using the coincidence lattice methods we have constructed 703 prototypes of vdWHs with minimal unit cell and lattice strain never exceeding 2%. The electronic structures of all the vdWHs are carefully analyzed. In particular, we have identified a number of different groups, classified according to their band-gap type and unit-cell size. Of special interest are vdWHs with a direct band gap and an in-plane cell identical to that of the ML. This is populated by the well-known Mo- and W-based dichalcogenides, but also includes ten transition–metal–halides combinations, such as YbI₂/1T-GeI₂, STl₂/CdBr₂, and YbI₂/CdI₂.

Although the analysis here is limited to MLs with a hexagonal cell forming bi-layer structures, our non-interacting method is applicable to any vdW crystal interface, where the constituents have arbitrary planar symmetry and the heterostructure contains single-, double-, or many-layer flake types. It can also be used recursively for multi-components vdW super-structures. Our work thus provides a complete navigation map for vdWHs, for which the composition space is enormous and not accessible by direct electronic structure theory.

Methods

Construction of the interface

The coincidence lattice method,^29,30 which is illustrated in brief here, is used to construct vertically stacked vdWHs. Consider two 2D crystals, A and ${\bf{A}}^{\prime}$, described by their corresponding basis vectors (${\overrightarrow{a}}_{1}$, ${\overrightarrow{a}}_{2}$) and (${\overrightarrow{a}}_{1}^{\prime}$, ${\overrightarrow{a}}_{2}^{\prime}$). An arbitrary superlattice of A can be defined by means of two new linearly independent basis vectors, (${\overrightarrow{A}}_{1}$, ${\overrightarrow{A}}_{2}$), as [see Fig. 8(a)]

$$\begin{array}{l}{\overrightarrow{A}}_{1}={n}_{1}{\overrightarrow{a}}_{1}+{n}_{2}{\overrightarrow{a}}_{2}\ ,\\ {\overrightarrow{A}}_{2}={n}_{3}{\overrightarrow{a}}_{1}+{n}_{4}{\overrightarrow{a}}_{2}\ ,\end{array}$$

(5)

so that the superlattice is uniquely specified by the set of integer indices {n₁, n₂, n₃, n₄}. Similarly, for the crystal ${\bf{A}}^{\prime}$ we can define the superlattice basis vectors

$$\begin{array}{l}{\overrightarrow{A}}_{1}^{\prime}={m}_{1}{\overrightarrow{a}}_{1}^{\prime}+{m}_{2}{\overrightarrow{a}}_{2}^{\prime}\ ,\\ {\overrightarrow{A}}_{2}^{\prime}={m}_{3}{\overrightarrow{a}}_{1}^{\prime}+{m}_{4}{\overrightarrow{a}}_{2}^{\prime}\ .\end{array}$$

(6)

If ${\overrightarrow{A}}_{1}={\overrightarrow{A}}_{1}^{\prime}$ and ${\overrightarrow{A}}_{2}={\overrightarrow{A}}_{2}^{\prime}$, the two crystals share a common superlattice. In practice, the pairs of vectors describing the two crystals A and ${\bf{A}}^{\prime}$ will be considered “equal”, if their difference is smaller than a pre-defined length and angle tolerance. Note that, since the ${\bf{A}}^{\prime}$ lattice can present any orientation with respect to the lattice A, the searching for common superlattices should be carried out for all the relative angles between A and ${\bf{A}}^{\prime}$. In this work, we set the length tolerance to 2%, the angle tolerance to 0.05^∘, and the relative angle between uneven compounds, the so-called twisting angle, are changed from 0^∘ to 30^∘ with a 0.1^∘ step. The twisting angle describes the relative rotation of the primitive lattice vectors of the two layers with respect to each other [see Fig. 3(a)], and note that the crystals considered here have a rotational period of 60^∘, namely a sixfold symmetry.

Fig. 8: Construction of the supercell and band folding.

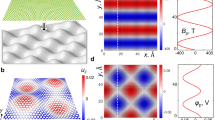
a An hexagonal lattice in real space and the associated $\sqrt{3}\times \sqrt{3}$ supercell. The indices of the supercell are [2, 1, −1, 1] [see Eq. (5)]. b Demonstration of BZ folding. The region enclosed by the black dashed line is the first BZ of the primitive cell, while the red hexagons denote the BZs of the $\sqrt{3}\times \sqrt{3}$ supercell. The blue, orange and green regions denote the IRBZ of the supercell, its replicas placed within the first BZ of the primitive cell, and its equivalent placed inside the IRBZ of the primitive cell. c The electron energy surface of the highest 2H-MoS₂ occupied band plotted over the IRBZ. Some high-symmetry points are shown.

Bandstructure folding

For a 2D crystal with basis vectors ${\overrightarrow{a}}_{1}$ and ${\overrightarrow{a}}_{2}$ the supercell basis vectors are defined by the indices {n_i} introduced in Eq. (5). Thus, the area of the supercell, S, is N_f times that of the primitive cell s, S = N_fs, with N_f = n₁n₄ − n₂n₃. The number of electronic bands in the supercell is also N_f times that contained in the primitive cell. The reciprocal basis vectors of the supercell are

$$\begin{array}{l}{\overrightarrow{B}}_{1}=({n}_{4}{\overrightarrow{b}}_{1}-{n}_{3}{\overrightarrow{b}}_{2})/{N}_{{\rm{f}}}\ ,\\ {\overrightarrow{B}}_{2}=(-{n}_{2}{\overrightarrow{b}}_{1}+{n}_{1}{\overrightarrow{b}}_{2})/{N}_{{\rm{f}}}\ ,\end{array}$$

(7)

where ${\overrightarrow{b}}_{1}$ and ${\overrightarrow{b}}_{2}$ are the reciprocal lattice vectors associated to the primitive cell (described by ${\overrightarrow{a}}_{1}$ and ${\overrightarrow{a}}_{2}$). In reciprocal space the area of the first Brillouin zone (BZ) of the supercell is 1/N_f of that of the primitive cell. Importantly, since considering a supercell representation of the electronic structure does not alter the nature of the eigenstates, one can always map the bandstructure calculated within one representation into that obtained over a different one by applying the appropriate symmetry operations. This process is called “folding” of the bandstructure. In order to obtain the N_f-folded electron energies at a point in the first BZ of the supercell, the electron energies of all its replicas that fall within the first BZ of the primitive cell must be considered. As a result of symmetry, this operation is often performed inside the irreducible Brillouin zone (IRBZ) instead of the first BZ. The idea behind the BZ folding is presented in Fig. 8(b).

We have adopted such band-folding strategy and constructed the bandstructure of supercells by folding that of the corresponding primitive cell. For this operation the knowledge of the bandstructure along the high-symmetry points of the primitive hexagonal unit cell (e.g., Γ, M, and K) is not sufficient, and one needs the electron energies computed over the entire IRBZ of the primitive cell. As such here we evaluate the electron energy surfaces of the relevant bands over a 40 × 40 rectangular grid containing the IRBZ [see Fig. 8(c)].

Computational details

The all-electron DFT code FHI-AIMS is used throughout this work.³¹ This is a particularly convenient choice, since all-electron simulations use a common vacuum level, defined by the free-electron energy, so that the band edges obtained with different simulations can be lined up. The “tight” version of the FHI-AIMS numerical atom-centered orbits³² is used as basis set. The number of k-points along the planar x- and y-axis is determined by the lattice constant, namely it is k_x = k_y = 4⋅⌈15/a⌉, where a is the in-plane lattice constant in Å. The lattice constant along the out-of-plane z-axis is set to be 30 Å for all MLs, a value that ensures the periodic replica to be separated from each other by at least 25 Å. The number of k-points along z-axis is k_z = ⌈k⋅a/c⌉ for the bulk form of the 2D compounds, where c is the lattice constant along z.

The geometries of the MLs and their parental 3D crystals are first optimized by using the GGA of the exchange-correlation functional as parametrized by PBE.³³ In addition, the Tkatchenko-Scheffler method, based on the Hirshfeld partitioning scheme, is used to account for vdW corrections.²¹ In the case of magnetic ions, such as V, Cr, Mn, Fe, Co, Ni, and rare earth elements, the spin moments are initially assigned according to Hund’s rule and then converged self-consistently without constrains. The electronic structure of the potential building blocks of the vdWHs are then re-computed with the HSE06 functional.³⁴ By introducing a screened exact-exchange energy, the HSE06 Kohn-Sham eigenvalues provide a good estimation of the electron quasi-particle energies. Spin–orbit coupling is also considered and it is applied as a non-self-consistent perturbation after the convergence of the electronic structure,³⁵ since it has little effect in determining the self-consistent charge density. The electron energy surface is calculated at the HSE06 level only for nonmetallic MLs with zero spin moment.