1 Introduction

Under the action of the intraocular pressure (IOP) due to internal fluids, the cornea shell assumes a spherical shape by exploiting the spatial perfection of the collagen network contained in the stroma [1]. Collagen is the protein, organized in thin fibrils, delegated to furnish mechanical stiffness to tissues. In the human cornea, more than 60% of the collagen fibrils are randomly distributed over the plane tangent to the mid-surface of the shell. The remaining 40% of the fibrils are arranged according to an orthogonal pattern, oriented at the center in the nasal-temporal (NT) direction and superior–inferior (SI) directions, and in circumferential–radial directions at the periphery [2,3,4]. The local orthogonality of the collagen fibrils guarantees the preservation of a mechanically stable spherical shape, and allows the correct deviation of the light rays onto the retina. Alterations of the collagen architecture are associated with changes of the corneal shape and vision impairment. Exemplary keratoconus refers to an impairing condition characterized by a marked loss of fibril organization leading to a conical shape of the cornea and to a local thinning of the tissue. Effects on vision are irregular astigmatism and strong myopia [5]. Yet, the etiology of keratoconus has not been clarified: chemical, genetic, and mechanical causes are under investigation. To clarify the biological mechanisms that lead to keratoconus onset and development would be useful to develop a numerical model of the cornea that accounts for material and geometry modification.

To date, most of the numerical models of the cornea consider physiological conditions. Examples in the recent literature include idealized continuum models based on anisotropic hyperelasticity [6, 7] or on stochastic fiber distributions [8,9,10], patient-specific models [11,12,13,14,15], and diagnostics and surgery planning [16,17,18,19,20]. None of them, however, has been developed with the ability to model the degenerative process leading to ectasia and keratoconus. As matter of facts, degeneration that induces tissue thinning and geometry reshaping is not an easy task and cannot be achieved by means of continuum models.

In the view of proposing an alternative and predictive approach based on micromechanical considerations, we revisit a structural model of the orthogonally arranged collagen architecture of the stroma recently proposed [21], conceived to deploy a realistic shape of the keratoconus by selective reduction of the mechanical stiffness of structural elements. We assume that, at the state of advanced conus, the maximum stiffness and minimum stiffness of both fibrils and crosslinks correspond to the values obtained in the numerical simulations in [21], where we explored the mechanical effects of the stiffness reduction. Specifically, in [21] the stiffness of all the truss elements was varied within a wide range of values, considering all possible combinations, and the crosslinks connecting the two fibril sets were identified as the key element responsible for pathology onset. In fact, the reduction of the fibril stiffness alone does not lead to the formation of a marked cone. Thus, in the present simulation, the stiffness of all truss elements is allowed to reduce in the radial direction from the limbus, where it preserves the maximum value, to the center of the conus, where it reaches the minimum value.

The microstructural model of the stromal collagen described in [21] is here enriched with a novel mechano-reaction–diffusion mechanism that describes a progressive reduction of the stiffness, leading to geometrical changes of the cornea corresponding to the pathologies known as ectasia and keratoconus. The microstructural model is based on the spatial replication of a unit cell made of trusses describing two sets of fibrils and chemical bonds (crosslinks) connecting them, Fig. 1a. The spatial trusswork is superposed to a continuum model of the cornea, Fig. 1b, where a reaction–diffusion process involving a concentration-like scalar field takes place. The concentration-like field is intended as a measure of the material degeneration that affects the stiffness of the crosslinks. The evolution of the scalar field determines the biomechanical response of the cornea.

Fig. 1
figure 1

a Structure of the hexahedron unit cell: collagen fibrils F1 (solid blue) and collagen fibrils F2 (solid red); in-plane orthogonal crosslinks C1 (dashed blue) and C2 (dashed red) between the fibrils of the same set; in-plane diagonal crosslinks SS (solid gray) between fibrils of the same set; out-of-plane diagonal crosslinks S12 (solid orange) between fibrils of two different sets. b Computational domain representing the continuum patient-specific cornea model. (Color figure online)

Full size image

Biological phenomena associated to non-equilibrium chemical processes are well described mathematically by reaction–diffusion (RD) equation systems [22,23,24]. The dynamics of chemical species responsible for the formation of crosslinks between fibrils can be framed into a reaction–diffusion equation, a mathematical tool useful to manage the different scales involved in the process by preserving the validity of the continuum approach [25,26,27].

In a simplified scenario, supported by a recent study on ectatic corneas [28], we can define two stable states for the crosslink network: a healthy state and a degenerate state where the shape markedly changes due to a stiffness reduction. The attainment of the degenerate state is dependent on a threshold of a variable measuring the level of the damage. Thus, we adopt a phenomenological approach considering a nonlinear reaction–diffusion process describing the space–time propagation of the degeneration variable governing the local stiffness, of both collagen fibrils and chemical crosslink bonds, varying in the limits of the ranges discussed in [21].

The reaction–diffusion equation, well known to be able to represent diverse biological dynamics from subcellular chemical reactions to population dispersal [29], is here adopted with the goal to characterize the critical level of degenerated stiffness that corresponds to the threshold between a physiological configuration and keratoconus. The problem, albeit formulated here in terms of a unique scalar variable not yet identifiable as a particular chemical/biological agent, is of great interest to clinical applications and represents a first step towards the definition of a biomechanical motivation to the keratoconus onset. Thus, the stiffness is assumed to be a function of the scalar variable.

The solution of the problem is sought in a weakly coupled manner, by solving the reaction–diffusion equation over the continuum domain assumed rigid, and subsequently by solving a static problem on the trusswork by reducing the stiffness of each truss according to the degradation function evaluated at the barycenter of the truss. The present investigation proposes a numerical approach that can be easily extended to other studies concerning the multiphysics of the human cornea, in order to understand the development of pathologies and to predict their evolution in a patient-specific context.

The paper is organized as follows. Material models and numerical methods are described in Sect. 2. Numerical results are collected in Sect. 3. A critical discussion on the proposed model is reported in Sect. 4.

2 Materials and methods

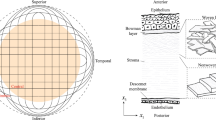
We consider a patient-specific geometry, characterized by the main geometrical data listed in Table 1. The model and its components are visualized in Fig. 2. The orthonormal reference system is centered at the posterior limbus plane and the z axis is oriented along the optical axis. The solid model of the patient-specific cornea is discretized in finite elements to solve the diffusion–reaction problem. On the same geometry, a microstructural model of the collagen architecture that provides the structural stiffness to the cornea is constructed according to the features described in [21], to solve the mechanical problem. As mentioned in the introduction, the trusswork model accounts only for the 40% of collagen fibrils present in the human stroma, therefore only 40% of the IOP-induced load is considered.

Fig. 2
figure 2

Reference system, lateral and nasal-temporal section views of the human cornea model considered in this study. Patient-specific geometry (top row); corresponding finite element discretization (middle row); collagen reinforcement trusswork (bottom row). Blue trusses are constrained at one end. (Color figure online)

Full size image
Table 1 Geometry of the patient-specific cornea model (all sizes in mm)
Full size table

2.1 Trusswork model

The micromechanical model of the collagen reinforcement follows the geometry of the patient-specific cornea, Fig. 2 (top). The trusswork is obtained by combining unit cells with the hexahedron topology shown in Fig. 1a. The unit cell consists of sixteen trusses of six different types. F1 (blue) and F2 (red) refer to collagen fibrils, lying on two distinct planes. C1 crosslink connects the F1 fibrils with coplanar orthogonal links; C2 crosslinks connect the F2 fibrils of the same plane with coplanar orthogonal links; SS crosslinks connect the fibrils of the same set with coplanar diagonal links; S12 crosslinks connects the F1 and F2 fibrils with out-of-plane diagonal links. The hexahedral cell repeated over the shell geometry, Fig. 2 (bottom row) defines a structure mechanically stable.

The two sets of fibrils are oriented in the NT and SI directions, respectively, in the central part, and in the circumferential and radial directions, respectively, at the limbus. The separation between the anterior and posterior truss-discretized surfaces corresponds to the corneal thickness, set to 0.5 mm. Trusses are connected with hinges, pinned at the limbus. All the links are allowed to work in tension and in compression. The trusswork geometry adopted for the calculations includes the repetition of 48 unit cells in the NT and SI directions, counting 5000 nodal points and 28,600 trusses. In agreement with the trusswork theory, the load can be only applied to the hinges in the form of point loads. The load equivalent to the 40% of the IOP (we remind that the trusswork represents only the organized collagen fibrils) is applied to the posterior surface of the model in the normal direction with respect to the continuum surface.

We apply the linear elastic theory for trussworks, and the solution is obtained in terms of nodal displacements as

$$\begin{aligned} {\varvec{K}}{\varvec{U}}= {\varvec{F}}\,, \end{aligned}$$
(1)

where \({\varvec{K}}\) is the stiffness matrix, \({\varvec{U}}\) the array of unknown displacements, and \({\varvec{F}}\) the array of the external loads. The i truss is characterized by the stiffness \(k_i = E_i A_i/h_i\), where \(E_i\) is the equivalent Young modulus and \(A_i\) the equivalent cross-section area, and \(h_i\) is the length of the truss. The input data for the model are further simplified introducing an equivalent rigidity parameter \(S_i = E_i A_i\). Clearly, each truss is representative of a certain amount of components, and the mechanical parameters must be obtained by a suitable homogenization of the actual properties of the components. The estimate of the material parameters has been done on the basis of experimental results of [30,31,32]; a detailed discussion can be found in [21]. The use of the uniaxial stiffness concept greatly reduces the number of parameters necessary for the analysis, while providing the sufficient flexibility to model the bulging of the keratoconus, experimentally observation to be related to a weakening of the stroma crosslinks [33].

2.2 Bistable reaction–diffusion constitutive modeling

Reaction–diffusion (RD) equations are parabolic partial differential equations describing the dynamics of nonlinear concentration of one or more substances. The most general RD constitutive model valid for a single species c, that in the present context is assumed to model a degeneration-like variable, reads:

$$\begin{aligned} \dfrac{\partial c}{\partial t} = \underbrace{\nabla \cdot ({\varvec{D}}\,\nabla c)}_{\text {Diffusion}} + \underbrace{F(c)}_{\text {Reaction}} \,, \qquad c=c({\varvec{x}},t)\in [0,1] \,, \end{aligned}$$
(2)

where \({\varvec{x}}\) denotes an orthonormal basis vector, t the time, and \({\varvec{D}}\) the diffusion tensor. According to Fick’s law, the concentration flux is given by \({\varvec{D}}\,\nabla c\). The concentration flux is, in general, a function of position and time, and may reproduce anisotropic, inhomogeneous, and fractional diffusion processes, as well as self-diffusion or stress-assisted diffusion [27, 34,35,36,37]; \(\nabla (\bullet )\) and \(\nabla \cdot \) denote the gradient and divergence operators, respectively, in the spatial configuration; the source F(c) governs the reaction process, and controls the local evolution or regression of the concentration field.

In a first approach, we take an ansatz by considering an insulated tissue and adopting homogeneous and isotropic diffusion, with normalized bistable reaction kinetics, and zero-flux boundary conditions:

$$\begin{aligned} \dfrac{\partial c}{\partial t}&= D \nabla ^2 c + A c (1-c)(c-\alpha ) \quad \mathrm{in} \,\, \varOmega , \end{aligned}$$
(3a)
$$\begin{aligned} \nabla c&= \mathbf{0} \quad \mathrm{on} \,\, \partial \varOmega , \end{aligned}$$
(3b)

where \(\varOmega \) and \(\partial \varOmega \) are the computational domain and its boundary, respectively. It follows that the zero-dimensional dynamical system, obtained by setting the scalar diffusion parameter \(D=0\), is characterized by two stable fixed points, at the concentrations \(c=0\) and \(c=1\), and one unstable fixed point, at the concentration \(c=\alpha \). The coefficient \(\alpha \) plays the role of a critical value that defines the threshold for the onset of a propagating concentration front-wave.

The three constitutive parameters \(A,D,\alpha \) must be able to model a realistic space–time evolution of the degeneration field; the time and space scales (month and mm) are chosen to capture the desired degradation process leading to the conus formation.

We trigger the process with an isotropic Gaussian-like initial condition, \(c_0\), centered at \(\{x_0, y_0\}\) and uniformly distributed across the cornea thickness:

$$\begin{aligned} c_0 = \hat{c} \,\exp {\left[ -\dfrac{(x-x_0)^2}{\sigma ^2} - \dfrac{(y-y_0)^2}{\sigma ^2} \right] } \,. \end{aligned}$$
(4)

The center is displaced 0.5 mm form the apex of the cornea, in the NT direction (cf. [21]). The variance is \(\sigma ^2=2\) mm\(^2\), and the amplitude of the peak of the concentration is \(\hat{c}=0.8\). In [21] it was observed that the most effective (in terms of conus shape) stiffness decrease from limbus to center follows a parabolic law; in the present calculation the parabolic radial variation of the stiffness cannot be assured—and probably it is not reached—since the spatial distribution obeys the solution of the reaction–diffusion equation not available explicitly. The diffusion problem has been solved with a finite elements analysis, by discretizing the continuum domain in 7701 quadratic tetrahedra and 12,917 nodes. We used a direct solver MUMS, with time steps not larger than 0.5 month. The mesh size was chosen after a few preliminary calculations that ensured the insensitivity to further mesh refinement. Figure 3 collects six sequential snapshots of the propagating degeneration variable, obtained for \(A=1.\)/month, \(D = 0.1\) mm\(^2\)/month, and \(\alpha = 0.1\). The resulting concentration front-wave will cover the entire surface of the cornea in fifty months.

Fig. 3
figure 3

View of the concentration field evolution \(c({\varvec{x}})\) at selected time-frames, \(t=0,5,10,15,17,20\) months

Full size image

3 Results

We present the results of sequential quasi-static analyses of the trusswork that account for the reduction of the truss stiffness \(S_i(c)\) according to the time evolution of the degradation field shown in Fig. 3. We focus on the initial stages of the evolution of the pathology, with the goal to identify the critical condition that corresponds to the formation of a marked conus.

The diffusion and the mechanical problems are weakly coupled, since the solid domain adopted for the solution of the diffusion problem is not affected by the changes of configuration induced by the stiffness reduction. We assign to each truss set a range of variability for the stiffness. The upper value of the stiffness, or reference stiffness \(S_\mathrm{r}\), is attained when there is no degradation; the lower value of the stiffness, or diseased stiffness \(S_\mathrm{d}\), is attained when the degradation is full. In each analysis, the stiffness k of each truss is modified according to the value assumed by the degradation variable c at the barycenter of the truss, using a linear interpolation:

$$\begin{aligned} S(c) = S_{\text {r}} (1 - c) + S_{\text {d}} c \,. \end{aligned}$$
(5)

A set of calculations has been carried out in order to characterize the range of variability of the stiffness of the trusses, using as starting point the results provided in [21]. The ranges of truss stiffness obtained from the preliminary analyses are collected in Table 2.

Table 2 Reference and diseased truss stiffness
Full size table

The reduction of the stiffness is different for the six sets of trusses. Collagen undergoes a reduced damage with respect to the crosslink bonds. Specifically, (i) the fibril sets F1 and F2 may reduce up to 30% of the original stiffness, since it is expected that collagen is still able to sustain the load; (ii) C1 and C2 crosslinks, connecting the fibrils of the same family, may reduce up to 87% of the original stiffness; (iii) SS crosslinks may reach up to 90% reduction, in compliance with the experimentally observation that reveals disorganization of the fibrils when crosslink bonds are missing.

The tuned reduction of the truss stiffness provides the attainment of the conical shape of the cornea as observed in keratoconus. Alternative choices lead to unrealistic shapes of the cornea, not observed in the pathological conditions. The stiffness of the trusses may be further reduced, leading to more pronounced conus as may be observed in advanced stages of the illness.

Fig. 4
figure 4

Cone configurations at four selected stages of propagation of the degeneration field (top row collects the iso-surfaces extracted from Fig. 3). From left to right, images show the configuration at 1, 3, 5, 7 months from the disease onset, top view (middle row) and side view (bottom row). The color refers the cornea displacements in mm

Full size image

Figure 4 shows a representative example of the results of the coupled analysis. The evolution of the degradation field (visualized as iso-surfaces in the top row images) drives the localized weakening with the cornea’s associated conic shape (central row images, top view; bottom row images, lateral view). At the early stages, within the first three months from disease onset, the trusswork reveals the presence of a restricted weakened area, and finds the equilibrium configuration without the formation of a marked conus that compromises all the field of vision, reflecting the clinical observations where the early pathology does not induce vision loss, making it difficult to be self-diagnosed. According to the chosen parameters, a marked change of the configuration of the cornea is observed at the fifth month. The condition becomes more evident at the seventh month when we recognize a fully developed conus with the classical shape documented in the clinical literature.

Computations allow to quantify the progress of the pathology by introducing a scalar measure of the extension of the degenerated tissue. The analysis of the configurations of the cornea may allow to identify a threshold to separate mild conditions from serious conditions.

We introduce a volumetric measure of the diffusion of the degeneration field that can be regarded as a synthetic index of the severity of the pathology. The measure is defined as the volume of the portion of the corneal tissue where the degeneration field is greater than a threshold \(\tilde{c}\), indicator of a dangerous level of the scalar field c. The extension of the cornea volume with \(c\ge \tilde{c}\) is an indicator of the level of invasiveness of the pathology. For example, setting a mild (high value) threshold \(\tilde{c}=0.8\), at month five the degradation field spreads over 1.9% of the entire cornea, and at month seven over 3.8% of the whole domain. Setting a more severe (low value) threshold, \(\tilde{c}=0.5\), at month five the degradation field covers 7.7% of the cornea volume, and at month seven reaches 10.7%. At later stages, i.e., at month twelve, more than 20% of the structure is compromised with a degeneration of the corneal stiffness, condition that leads to the formation of a marked conus.

Fig. 5
figure 5

Space–time plot of the degradation evolution on the middle surface of the cornea, using a curvilinear spatial abscissa (arc length)

Full size image

The concentration threshold can be related to the velocity of the propagation of the wave-front in the space–time plot of Fig. 5. The figure shows the time evolution of the degradation field over the mid-surface of the cornea, starting from a Gaussian-like initial condition. The slope of the shaded area represents the average velocity of the wave-front, or degradation speed in mm/month. For the chosen parameters, the degradation speed is \(\sim 0.13\) mm/month. The knowledge of the degradation speed allows to predict the time frame to reach the full evolution of the pathology. Fig. 5 highlights (i) the pre-critical time interval, an early stage of the pathology where the diagnosis is difficult because of the lack of evidence of conical shape, (ii) a critical time interval, where the pathology diagnosis is facilitated by the insurgence of optical aberrations, and a non-invasive surgical treatment will avoid the progression of the degeneration, and (iii) a post-critical stage, where the pathology is fully revealed by the advanced state of the conus, and keratoplasty will remain the only possible treatment.

4 Discussion

We presented a weakly coupled continuum-discrete model of the human cornea that models the time evolution of degenerative pathologies of the cornea related to a loss of cohesion between collagen fibrils. The continuum is used to solve a reaction–diffusion equation of a scalar field representing the degeneration, while the discrete trusswork model (representative of the structurally organized collagen) is used to solve the coupled quasi-static equilibrium. The effect of the degeneration field is to reduce selectively the stiffness of the structural components of the trusswork.

Within the necessary limitations due to the adoption of two different discretizations and for the simplicity of the treatment of the corneal tissue, the results are interesting, capture the features of the time progression of the keratoconus, and suggest the definition of a scalar threshold that distinguishes between the three stages of the illness.

The limitations of the model include the full disregarding of the stochastic nature of the material properties, typical of all biological tissue, characterized by dispersion of the fibril orientation and here assumed to have a deterministic configuration. Furthermore, anisotropy and inhomogeneity of the healthy tissue have been neglected. The main consequence of this assumption is the impossibility to estimate quantitatively the stress from the weakened and deformed trusswork. Furthermore, the model does not allow to understand the individual degeneration of the multiple layers of the cornea, that in this approach are disregarded.

The simplifications are, however, acceptable because the goal of this study is the quantitative estimate only of the “observable” geometrical parameters, i.e., the shape of the cornea, in terms of reduction of the stiffness of the bonds (crosslinks) between collagen fibrils. Interestingly, keratoconus seems to be related to the reduction of the number of natural crosslinks that allows the organization of the collagen in sub-planar structures (lamellae) superposed in multiple stacks. Our model reveals that keratoconus can be ascribed to the lack of cohesion between adjacent lamellae [21]. In the present contribution we try to provide an explanation of the reduction of the crosslink bonds observed in keratoconus [33] in terms of diffusion of the “concentration” of an enzymatic or chemical species. At the moment, we have not in mind any particular substance. Playing with a scalar field, it is possible to characterize a volumetric risk index associated to the extension of the volume of the degenerated cornea.

In a future development of the present work, we plan to overcome some of the limitations induced by the oversimplified assumptions. At the constitutive level, we want to introduce anisotropy in the reaction–diffusion model to provide preferential paths of diffusion of the scalar field. Anisotropy needs to be identified in terms of patient-specific architecture of the trusswork, by associating the model to advanced imaging of the cornea microstructure. Indeed, the reaction–diffusion model in Eq. (3a) is defined in terms of diffusion tensor, which may be extended to account for anisotropy. Inhomogeneities that may privilege the onset of the pathology in a particular site are also a feature that must be considered.

Computational improvements include the full coupling of the discrete-continuum model in the view to adopt a monolithic approach for the solution, relevant in the case on anisotropy and inhomogeneities.