Development of Dynamic Model and Analytical Analysis for the Diffusion of Different Species in Non-Newtonian Nanofluid Swirling Flow

Usman, Auwalu Hamisu; Khan, Noor Saeed; Humphries, Usa Wannasingha; Shah, Zahir; Kumam, Poom; Khan, Waris; Khan, Amir; Rano, Sadiya Ali; Ullah, Zafar

doi:10.3389/fphy.2020.616790

ORIGINAL RESEARCH article

Front. Phys., 22 February 2021
Sec. Interdisciplinary Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.616790

Development of Dynamic Model and Analytical Analysis for the Diffusion of Different Species in Non-Newtonian Nanofluid Swirling Flow

Auwalu Hamisu Usman^1,2

Noor Saeed Khan^1,3,4,5* www.frontiersin.org

Usa Wannasingha Humphries¹* www.frontiersin.org

Zahir Shah^4,6 www.frontiersin.org

Poom Kumam^1,3,4,7* www.frontiersin.org

Waris Khan⁸ www.frontiersin.org

Amir Khan⁹ www.frontiersin.org

Sadiya Ali Rano² www.frontiersin.org

Zafar Ullah⁵

¹Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
²Department of Mathematical Sciences, Bayero University, Kano, Nigeria
³KMUTT-Fixed Point Theory and Applications Research Group, Theoretical and Computational Science Center (TaCS), Science Laboratory Building, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
⁴Center of Excellence in Theoretical and Computational Science (TaCS-CoE), SCL 802 Fixed Point Laboratory, Science Laboratory Building, King Mongkut’s University of Technology Thonburi (KMUTT), Bangkok, Thailand
⁵Division of Science and Technology, Department of Mathematics, University of Education Lahore, Lahore, Pakistan
⁶Department of Mathematics, University of Lakki Marwat, Lakki Marwat, Pakistan
⁷Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
⁸Department of Mathematics and Statistics, Hazara University Mansehra, Khyber Pakhtunkhwa, Pakistan
⁹Department of Mathematics and Statistics, University of Swat, Khyber Pakhtunkhwa, Pakistan

The analysis is carried out to analyze the flow through double stretchable rotating disks with the theory of radiative Cross nanofluid under the influence of variable thermal conductivity, the Hall current, Arrhenius activation energy, and binary chemical reactions. The Buongiorno nanofluid model is adopted for the governing equations of the problem which are transformed into ordinary differential equations through similarity transformations and then solved using the homotopy analysis method. The impact of dimensionless parameters on all profiles and physical quantities is presented and discussed. The radial velocity of the two disks increases with their corresponding ratio stretching rate parameter and decreases with the Hall parameter and the bioconvection Rayleigh number. The heat transfer at the lower disk enhances with the variable thermal conductivity parameter, while at the upper disk, opposite trend is observed. Mass transfer increases with the chemical reactions and temperature difference parameters at the lower disk and decreases with Arrhenius activation energy, whereas an opposite trend is observed at the upper disk. The local density number is enhanced for the larger values of Peclet and Lewis numbers. The comparison of the present work with the published literature authenticates the validation of the present work.

Introduction

Cross [1] carried out an innovative work on the Cross model in 1965. Cross fluid is a separate generalization of non-Newtonian fluid types, which has served as a model offering a wide range of shearing rates for the dilatant and pseudoplastic origin of the fluids. A variety of applications involves polymerization in the Cross-fluid model. Xie and Jin [2] reported a Cross rheological equation analysis for the surface free layer of non-Newtonian fluid. Manzur et al. [3] studied the Cross-fluid model with flow through the extended vertical sheet stretching layer by examining the mixed convection and radiative heat transfer. Abbas et al. [4] considered the Cross nanofluid flow subject to entropy generation mathematical modeling and analysis. Hayat et al. [5] performed a numeric simulation of MHD stagnation of Cross-fluid model flow and heat transfer in a stretched surface. Naz et al. [6] studied the Cross nanofluid dynamics with magnetohydrodynamics, entropy, and gyrotactic motile microbiological characteristics.

The thermal transformation process is characterized by the thermal conductivity of the basic fluid due to poor thermal conductivity of nonmetallic materials such as mud, oils, and glycol mixture in contrast to some metallic materials like copper, aluminum, iron, bronze, etc. The properties of low thermal-conducting nanoparticles, usually made up of oxides and metals, significantly increase the base fluid thermal conductivity. The conductivity and convection coefficients of metals and oxides increase the efficiency of heat transfer in nanofluids. Choi and Eastman [7] in 1995 first suggested the term “nanofluid” by using very small (1–100 nm) nanoparticles added to the base fluid. Boungiorno [8] suggested the slips mechanisms like inertia, dissipation, magnus, fluid drainage, gravity, Brownian diffusion, and thermophoresis effects in the dynamics of nanofluids. Kuznetsov and Nield [9] used the Buongiorno model to address the nanoparticles’ effects on natural convective boundary flow via a vertical plate. The main work focusing on normal cases using nanofluids for all purposes began in 1995 with Choi and Eastman on their study to assign the suspension of solid nanoparticles to the base fluid, where they found that the thermal conductivity of the water– ${Al}_{2} O_{3}$ blend was increased by 20% for a concentration of the volumes in the range of 1–5% of ${Al}_{2} O_{3}$ . Turkyilmazoglu [10] reported the study of nanofluid flow and heat transfer due to a rotating disk. Ahmad et al. [11] presented a numerical study of generalized non-Newtonian unsteady 3D magneto-nanoparticles liquid flow. Hafeez et al. [12] investigated the rotational flow of Oldroyd-B nanofluid under Cattaneo–Christov double diffusion theory. Khan et al. [13] reported a 3D numerical unsteady Sisko magneto-nanofluid flow study with heat absorption and temperature-dependent thermal conductivity. More nanofluid studies can be found in Refs. 14–21.

Bioconvective phenomena are common in suspension, usually due to the swimming of microorganisms that are marginally denser than water. If the upper surface of the suspension is too thick due to the accumulation of microorganisms, it becomes brittle and the microorganisms collapse to induce the bioconvection. The development of gyrotactic nanofluid microorganisms enables mass transfer, microscale mixing, primarily in microvolumes, and improves nanofluid stability. Li and Xu [22] studied the unsteady mixed bioconvection flow of a nanofluid between two contracting or expanding rotating disks. Qayyum et al. [23] examined the analysis of radiation in a suspension of nanoparticles and gyrotactic microorganism for rotating disk of variable thickness. Shehzad et al. [24] investigated the Maxwell nanofluid bioconvection on isolated rotating disks under the influence of the double-diffusive Cattaneo–Christov theory. Khan et al. [25] reported the study of entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. More studies on bioconvection can be found in Refs. 26–30.

Scientists and engineers, particularly in the areas of oil, chemical and petroleum engineering, oil and water emulsion, cooling reactors, geothermal, mechanical chemistry, and material degradation, have been very interested in multi-specific applications such as energy activation and species response. Generally, the relation between chemical reactions and mass transfer is highly complex and can only be studied by producing and digesting reagent species at different fluid flow and mass transfer rates. Arrhenius [31] for the first time suggested the concept of activation energy. However, Bestman [32] recognized a principal model of a boundary layer of flow problem due to binary chemical reactions with Arrhenius activation energy. Shahzad et al. [33] investigated the transport of radiative heat transfer with entropy generation and activation energy in dissipative nanofluid flow. Dhlamini et al. [34] suggested the mixed convective nanofluid flow with convective boundary conditions under binary chemical reaction and Arrhenius activation energy. Azam et al. [35] investigated the Arrhenius activation energy effects on radiative Cross-nanofluid axisymmetric flow through covalent bonding development. More studies on Arrhenius activation energy and binary chemical reaction can be seen in Refs. 36–40.

The idea of flow into a rotating disk system is an important area for future industrial process optimization and development. Scientists all over the world have drawn attention to this idea with the applications in the fields of electrochemistry, energy engineering, aerodynamics, chemical engineering, food processing, and medical equipment. To the best of knowledge, Karman [41] initially investigated the flow of liquid through an infinite disk with the introduction of famous similarity transformations in his study. Hayat et al. [42] investigated the viscous dissipation in the second-grade fluid flow in rotating disk with the Joule heating. Yao and Lian [43] reported the flow due to rotation, in which they provided analytical and numerical solutions when the fluid is rigidly rotated. Hayat et al. [44] investigated the flow between two stretchable rotating disks with the Cattaneo–Christov heat flux model. More studies on a rotating disk system can be consulted in Refs. 45 and 46.

In the light of the abovementioned literature, no one has, to the best of our knowledge, studied the flow between two stretchable rotating disks under the radiative Cross-nanofluid theory in the following context. The objective, here is, to explore the flow of Cross nanofluid in the presence of variable thermal conductivity, the Hall effect, and Arrhenius activation energy effect. The Buongiorno nanofluid model is used to develop Brownian diffusion and thermophoresis effects in both the energy and concentration equations. The problem is solved through HAM [47, 48] presented by Liao in 1992. However, due to its rapid convergence, various researchers [49–74] used HAM and various potential techniques to solve their problems. The effects of the parameters on the profiles are explained through graphs and tables whose detail is given in the Discussion section.

Problem Formulation

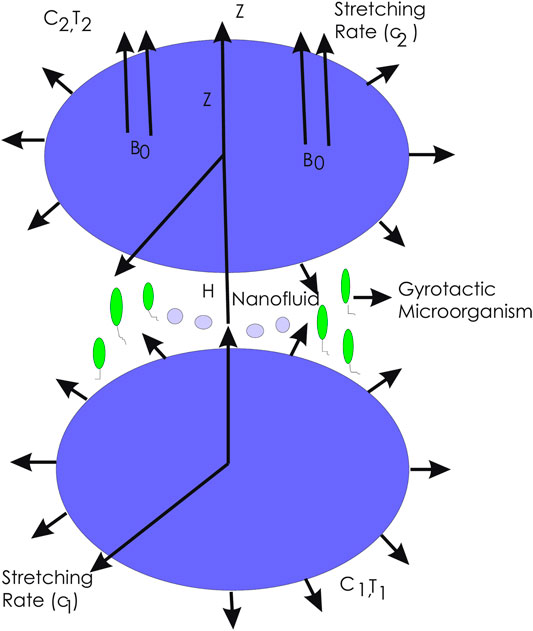
A three-dimensional, steady, axisymmetric motion of MHD flow of incompressible radiative Cross nanofluid through rotating double disks is considered. The lower disk is at the plane $z = 0$ . Fluid motion is subjected to rotation in axial direction of the disks having amplitude $ε_{o}$ and angular velocities $γ_{1}$ and $γ_{2}$ lower and upper disks, respectively. Investigations are made by considering cylindrical coordinates. The velocity components $(u, v, w)$ along the directions of $(r, ϑ, z)$ , respectively. Let $(T_{1}, T_{2})$ indicate the constant temperatures prescribed for both the low and upper disks where $T_{1} > T_{2}$ , and the concentrations in the lower and upper disks are represented by $(C_{1}, C_{2})$ . By regarding the flow to be axisymmetric, thus, the tangential coordinate derivatives with respect to $ϑ$ are omitted. The magnetic field $B_{o}$ with uniform intensity acts in the axial direction. Furthermore, due to the low Reynolds number, the induced magnetic field is zero, and there is also an exclusion of the electrical field. Nanofluid dilution to consider viscosity dispersion is used to prevent bioconvection instability. The nanoparticles suspended in the base fluid are also expected to be stable so that they do not affect the swimming pathway and the velocity of the microorganisms. $N_{1}$ and $N_{2}$ are the motile gyrotactic microorganism distributions on the lower and upper disks, respectively. Figure 1 shows the physical form of the problem. The guiding principles are the governing equations that follow the Buongiorno nanofluid model.

FIGURE 1

FIGURE 1. Geometry of the problem.

The Hall current is influencing many fields such as medical sciences and engineering. Cosmological fluid dynamics, geophysics, and the Hall accelerator can be listed as various engineering applications of the Hall current. The Hall current is induced by the significantly strong magnetic field. Generalized form of Ohm’s law in the existence of the electric fields is given by

J + \frac{σ μ_{e}}{B_{o}} (J \times B) = σ [μ_{e} V \times B + \frac{1}{e n_{e}} \nabla p_{e}], (1)

assuming that the thermoelectric pressure and ion slip conditions for weakly ionized gas are negligible. Hence, the equations reduced in the form as

J_{r} = \frac{σ μ_{e} B_{o}}{1 + m^{2}} (m v - u) and J_{z} = \frac{σ μ_{e} B_{o}}{1 + m^{2}} (m u + v), (2)

where $ω_{e}$ is the electron’s cyclotron frequency, $e$ is the electron collision time, $p_{e}$ is the pressure of the electron, $n_{e}$ is the electron’s density number, $μ_{e}$ is the magnetic permeability, and $σ$ is the electrical conductivity of fluid. The Hall parameter here is defined as $m = ω_{e} τ_{e}$ .

The Cauchy stress tensor (Cross-viscosity model) is displayed as

τ = - p I + μ (\dot{γ}) A_{1}, (3)

where $μ$ is the viscosity, $I$ is the identity matrix, $p$ is the pressure, and $A_{1}$ is the first Rivlin–Ericksen tensor given as

A_{1} = \nabla V + {(\nabla V)}^{T}, (4)

where $\nabla V$ stands for the velocity gradient. For generalized Newtonian fluid subclass (Cross fluid), the viscosity rheology equation is

μ = μ_{\infty} + \frac{μ_{o} - μ_{\infty}}{1 + {(Γ \dot{γ})}^{n}}, (5)

by taking viscosity infinite shear rate to zero $(μ_{\infty} = 0)$ , the stress tensor now becomes

τ = - p I + μ_{o} {[1 + {(Γ \dot{γ})}^{n}]}^{- 1} A_{1} . (6)

Taking the assumption $Γ = 0$ , the original Newtonian model is obtained. It is apparent that the Cross fluid chooses to act as shear thinning fluid for the range $0 < n < 1$ ; that is, $n$ is the power law index for Cross fluid used for choosing to behave like shear thinning in the range of 0 and 1.

The Cross-viscosity model shear rate in the existence of simulation is given as

\dot{γ} = \sqrt{\frac{1}{2} \sum_{i} \sum_{j} {\dot{γ}}_{i j} {\dot{γ}}_{j i}} = \sqrt{\frac{1}{2} t r (A_{1}^{2})}, (7)

where $t r (A_{1}^{2})$ is the trace of the matrix $A_{1}^{2}$ .

Now the continuity, momentum, energy, concentration, and gyrotactic microorganism equations [1, 3, 5, 6, 34] are

\frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0, (8)

\begin{array}{l} u \frac{\partial u}{\partial r} + w \frac{\partial u}{\partial z} - \frac{v^{2}}{r} = - \frac{1}{ρ_{n f}} \frac{\partial p}{\partial r} + ν_{n f} \frac{\partial}{\partial z} [\frac{{(\frac{\partial u}{\partial z})}^{}}{1 + (Γ {\frac{\partial u}{\partial z})}^{n}}] - \frac{σ_{n f} B_{o}^{2}}{ρ_{n f} (1 + m^{2})} (u - m v) \\ + \frac{1}{ρ_{n f}} [(1 - C_{2}) ρ_{n f} β (T - T_{2}) - (ρ_{p} - ρ_{n f}) (C - C_{2}) - (N - N_{2}) (ρ_{m} - ρ_{n f})] g, \end{array} (9)

u \frac{\partial v}{\partial r} + w \frac{\partial v}{\partial z} + \frac{v u}{r} = ν_{n f} \frac{\partial}{\partial z} [\frac{\partial v / \partial z}{1 + {(Γ \partial v / \partial z)}^{n}}] - \frac{σ_{n f} B_{o}^{2}}{ρ_{n f} (1 + m^{2})} (v + m u), (10)

u \frac{\partial w}{\partial r} + w \frac{\partial w}{\partial z} = - \frac{1}{ρ_{n f}} \frac{\partial p}{\partial z} + ν_{n f} \frac{\partial}{\partial z} [\frac{{(\frac{\partial u}{\partial z})}^{}}{1 + (Γ {\frac{\partial u}{\partial z})}^{n}}], (11)

\begin{array}{l} (u \frac{\partial T}{\partial r} + w \frac{\partial T}{\partial z}) = \frac{μ_{o}}{{(ρ c_{p})}_{n f}} [\frac{{(\frac{\partial u}{\partial z})}^{2}}{1 + (Γ {(\frac{\partial u}{\partial z})}^{n})}] + [\frac{K (T)}{r} \frac{\partial T}{\partial r} + \frac{\partial}{\partial r} [K (T) \frac{\partial T}{\partial r}] + \frac{\partial}{\partial z} [(K (T) \frac{\partial T}{\partial z})]] + \\ τ 〈 D_{B} {\frac{\partial T}{\partial z} \frac{\partial C}{\partial z} + \frac{\partial T}{\partial r} \frac{\partial C}{\partial r} + \frac{D_{T}}{T_{2}} [{(\frac{\partial T}{\partial z})}^{2} + {(\frac{\partial T}{\partial r})}^{2}]} 〉 + \frac{σ_{n f} B_{o}^{2} (v^{2} + u^{2})}{{(ρ c_{p})}_{n f}} - \frac{1}{{(ρ c_{p})}_{n f}} \frac{\partial (r q_{r}),}{\partial r} \end{array} (12)

\begin{array}{l} u \frac{\partial C}{\partial r} + w \frac{\partial C}{\partial z} = D_{B} (\frac{\partial^{2} C}{\partial r^{2}} + \frac{1}{r} \frac{\partial C}{\partial r} + \frac{\partial^{2} C}{\partial z^{2}}) + \frac{D_{T}}{T_{2}} (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r} + \frac{\partial^{2} T}{\partial z^{2}}) \\ - k_{r}^{2} (C - C_{2}) {(\frac{T}{T_{2}})}^{m_{1}} \exp [\frac{- E_{a}}{K_{1} T}], \end{array} (13)

u \frac{\partial N}{\partial r} + w \frac{\partial N}{\partial z} + \frac{b W_{c}}{(C_{1} - C_{2})} [\frac{\partial}{\partial z} (N \frac{\partial C}{\partial z})] = D_{m} (\frac{\partial^{2} N}{\partial z^{2}}), (14)

where $K (T)$ denotes the variable thermal conductivity and is defined as

K (T) = k_{n f} (1 + ε \frac{T - T_{2}}{T_{1} - T_{2}}) .

The boundary conditions are

\begin{array}{l} u = c_{1} r, v = r γ_{1}, w = 0, T = T_{1}, C = C_{1}, N = N_{1}, a t z = 0 \\ u = c_{2} r, v = r γ_{2}, w = 0, T = T_{2}, C = C_{2}, N = N_{2}, a t z = H . \end{array} (15)

The following transformations are used

\begin{array}{l} u = r γ_{1} f^{'} (ζ), v = r γ_{1} g (ζ), w = - 2 H γ_{1} f (ζ), P = ρ_{n f} γ_{1} v_{n f} [p_{o} (ζ) + \frac{r^{2} ε_{o}}{2 H^{2}}], \\ θ (ζ) = \frac{T - T_{2}}{T_{1} - T_{2}}, ϕ (ζ) = \frac{C - C_{2}}{C_{1} - C_{2}}, χ (ζ) = \frac{N - N_{2}}{N_{1} - N_{2}}, ζ = \frac{z}{H} . \end{array} (16)

Equation 8 is satisfied through Eq 16, and the remaining Eqs 9–15 provide Eqs 17–23, respectively, as

[1 + (1 - n) {(W e f^{″})}^{n}] f^{‴} - {[1 + {(W e f^{″})}^{n}]}^{2} [\begin{array}{l} Re ({f^{'}}^{2} - 2 f f^{″} - g^{2}) + \frac{Re M}{(1 + m^{2})} (f^{'} - m g) + \\ λ (θ - N_{r} ϕ - R_{b} χ) - ε \end{array}] = 0, (17)

[1 + (1 - k) {(W e g^{'})}^{n}] g^{″} + Re [(f g^{'} - f^{'} g) - \frac{M}{1 + m^{2}} (g + m f^{'})] {[1 + {(W e f^{″})}^{n}]}^{2} = 0, (18)

P = 4 Re f f^{'} + [\frac{1 + (1 + n) {(- 2 β_{1} W e f^{'})}^{n}}{{[1 + {(- 2 β_{1} W e f^{'})}^{n}]}^{2}}] = 0, (19)

(1 + \frac{ε - 1}{δ} + R d) θ^{″} + ε ({θ^{'}}^{2} + θ θ^{″}) + \Pr [\begin{array}{l} E c β_{2} [\frac{{f^{″}}^{2}}{1 + {(W e f^{″})}^{n}}] + N b ϕ^{'} θ^{'} + N t θ^{2} \\ + Re E c [M ({f^{'}}^{2} + g^{2}) - f f^{'}] \end{array}] = 0, (20)

ϕ^{″} + \frac{N t}{N b} θ^{″} + Re S c f^{'} ϕ^{'} - S c σ {(1 + δ θ)}^{m_{1}} Exp (- \frac{E}{1 + δ θ}) = 0, (21)

χ^{″} + 2 Re L e f χ^{'} - P e [χ^{'} ϕ^{'} + H (ϕ^{'} χ + N_{δ} ϕ)] = 0, (22)

with boundary conditions

\begin{array}{l} f (0) = 0, f^{'} (0) = s_{1}, g (0) = 0, p (0) = 1, θ (0) = 1, ϕ (0) = 1, χ (0) = 1 \\ f (1) = 0, f^{'} (1) = s_{2}, g (1) = γ, θ (1) = 0, ϕ (1) = 0, χ (1) = 0, \end{array} (23)

\begin{array}{l} where W e = \frac{Γ r γ_{1}}{H}, Re = \frac{H^{2} γ_{1}}{ν_{n f}}, M = \frac{σ_{n f} B_{o}^{2}}{ρ_{n f} γ_{1}}, λ = \frac{(1 - C_{2}) g β (T_{1} - T_{2}) H^{2}}{r γ_{1} ν_{n f}}, s_{1} = \frac{c_{1}}{γ_{1}}, s_{2} = \frac{c_{2}}{γ_{2}}, \\ N r = \frac{(ρ_{p} - ρ_{n f}) (C_{1} - C_{2})}{β ρ_{n f} (1 - C_{2}) (T_{1} - T_{2})}, R b = \frac{(ρ_{m} - ρ_{n f}) (C_{1} - C_{2})}{β ρ_{n f} (1 - C_{2}) (T_{1} - T_{2})}, R d = \frac{16 σ^{*} T_{2}^{3}}{3 k^{*} k_{n f}}, E c = \frac{r^{2} γ_{1}^{2}}{{(ρ c_{p})}_{n f} (T_{1} - T_{2})}, \\ \Pr = \frac{ν_{n f}}{α}, N t = \frac{τ D_{T} (T_{1} - T_{2})}{T_{2} ν_{n f}}, N b = \frac{τ D_{B} (C_{1} - C_{2})}{ν_{n f}}, β_{1} = \frac{H}{r}, β_{2} = \frac{μ_{o}}{{(ρ c_{p})}_{n f}}, S c = \frac{ν_{n f}}{D_{B}}, σ = \frac{k_{r}^{2} H^{2}}{ν_{n f}} \\ δ = \frac{T_{1} - T_{2}}{T_{2}}, E = \frac{E_{a}}{T_{2} K_{1}}, L e = \frac{ν_{n f}}{D_{m}}, P e = \frac{b W_{c}}{D_{m}}, N_{δ} = \frac{N_{2}}{N_{1} - N_{2}}, γ = \frac{γ_{2}}{γ_{1}} \end{array} (24)

Physical Quantities

The physical quantities of interests are given below.

Skin Friction Coefficients

These are defined as

C_{f_{L}} = \frac{τ_{w}}{ρ_{n f} {(r γ_{1})}^{2}} |_{z = 0}, C_{f_{U}} = \frac{τ_{w}}{ρ_{n f} {(r γ_{2})}^{2}} |_{z = H}, where τ_{w} = {(τ_{z r}^{2} + τ_{z θ}^{2})}^{\frac{1}{2}} . (25)

Therefore, the skin friction coefficients for the lower and upper disks are respectively, as

C_{f_{L}} = \frac{v_{n f}}{(r γ_{1}) H} {{[f^{″} (0)]}^{2} + {[g^{'} (0)]}^{2}}^{\frac{1}{2}} = \frac{1}{{Re}_{r}} {{[f^{″} (0)]}^{2} + {[g^{'} (0)]}^{2}}^{\frac{1}{2}}, (26)

C_{f_{U}} = \frac{v_{n f}}{(r γ_{2}) H} {{[f^{″} (1)]}^{2} + {[g^{'} (1)]}^{2}}^{\frac{1}{2}} = \frac{1}{{Re}_{r}} {{[f^{″} (1)]}^{2} + {[g^{'} (1)]}^{2}}^{\frac{1}{2}}, (27)

where ${Re}_{r} = r γ_{i} H / v_{n f}, i = 1,2, \dots,$ is defined as the local Reynolds number.

Nusselt Number

These are defined as

N u_{r_{1}} = \frac{H q_{m}}{k_{n f} (T_{1} - T_{2})} |_{z = 0}, where q_{m} = - k_{n f} \frac{\partial T}{\partial z} |_{z = 0} = - k_{n f} \frac{(T_{1} - T_{2})}{H} θ^{'} (0), so N u_{r_{1}} = - θ^{'} (0), (28)

N u_{r_{2}} = \frac{H q_{m}}{k_{n f} (T_{1} - T_{2})} |_{z = H}, where q_{m} = - k_{n f} \frac{\partial T}{\partial z} |_{z = H} = - k_{n f} \frac{(T_{1} - T_{2})}{H} θ^{'} (1), N u_{r_{2}} = - θ^{'} (1) a . (29)

Sherwood Number

These are defined as

S h_{r_{1}} = \frac{H q_{b}}{D_{B} (C_{1} - C_{2})} |_{z = 0}, where q_{b} = - D_{B} \frac{\partial C}{\partial z} |_{z = 0} = - D_{B} \frac{(C_{1} - C_{2})}{H} ϕ^{'} (0), so S h_{r_{1}} = - ϕ^{'} (0), (30)

S h_{r_{2}} = \frac{H q_{b}}{D_{B} (C_{1} - C_{2})} |_{z = H}, where q_{b} = - D_{B} \frac{\partial C}{\partial z} |_{z = H} = - D_{B} \frac{(C_{1} - C_{2})}{H} ϕ^{'} (1), so S h_{r_{2}} = - ϕ^{'} (1) . (31)

Local Density Motile Flux

These are defined as

S n_{r_{1}} = \frac{H q_{m}}{D_{m} (N_{1} - N_{2})} |_{z = 0}, where q_{m} = - D_{m} \frac{\partial N}{\partial z} |_{z = 0} = - D_{m} \frac{(N_{1} - N_{2})}{H} χ^{'} (0), so S n_{r_{1}} = - χ^{'} (0), (32)

S n_{r_{2}} = \frac{H q_{m}}{D_{m} (N_{1} - N_{2})} |_{z = H}, where q_{m} = - D_{m} \frac{\partial N}{\partial z} |_{z = H} = - D_{m} \frac{(N_{1} - N_{2})}{H} χ^{'} (1), s o S n_{r_{2}} = - χ^{'} (1) . (33)

Solution of the Problem by HAM

The current problem is solved with the HAM (homotopy analysis method) software in Mathematica 10 computer-based programing. HAM has been used to solve the problem because this method has the following good aspects.

Without discretization and linearization of the nonlinear differential equations, this technique is applicable to the system for the best answer.

This technique is also applicable to those systems which have small or large natural parameters.

This technique produces the convergent solution of the problem.

This method is free from a set of base functions and linear operators.

Taking the initial guesses and the linear operators as

\begin{array}{l} f_{o} (ζ) = s_{1} ζ - (2 s_{1} + s_{2}) ζ^{2} + (s_{1} + s_{2}) ζ^{3}, g_{o} (ζ) = 1 - ζ + γ ζ, θ_{o} (ζ) = 1 - ζ, \\ ϕ_{o} (ζ) = 1 - ζ, χ_{o} (ζ) = 1 - ζ, \end{array} (34)

L_{f} = f^{'}, L_{g} = g′, L_{θ} = θ^{″}, L_{ϕ} = ϕ^{″}, and L_{χ} = χ^{″}, (35)

which satisfy the following properties

\begin{array}{l} L_{f} [C_{1} + C_{2} ζ + C_{3} ζ^{2} + C_{4} ζ^{3}] = 0, L_{g} [C_{5} + C_{6} ζ] = 0, \\ L_{θ} [C_{7} + C_{8} ζ] = 0, L_{ϕ} [C_{9} + C_{10} ζ] = 0, L_{χ} [C_{11} + C_{12} ζ] = 0, \end{array} (36)

where ${C_{i}}_{i = 1}^{12}$ are the arbitrary constants.

The zeroth order form of the problems is given as

(1 - q) L_{f} [f (ζ, q) - f_{o} (ζ)] = q ℏ_{f} N_{f} [f (ζ, q), θ (ζ, q), ϕ (ζ, q), χ (ζ, q)], (37)

(1 - q) L_{g} [g (ζ, q) - g_{o} (ζ)] = q ℏ_{g} N_{g} [f (ζ, q), g (ζ, q)], (38)

(1 - q) L_{θ} [θ (ζ, q) - θ_{o} (ζ)] = q ℏ_{θ} N_{θ} [f (ζ, q), g (ζ, q), θ (ζ, p), ϕ (ζ, q)], (39)

(1 - q) L_{ϕ} [ϕ (ζ, q) - ϕ_{o} (ζ)] = q ℏ_{ϕ} N_{ϕ} [f (ζ, q), θ (ζ, q), ϕ (ζ, q)], (40)

(1 - q) L_{χ} [χ (ζ, q) - χ_{o} (ζ)] = q ℏ_{χ} N_{χ} [f (ζ, q), ϕ (ζ, q), χ (ζ, q)], (41)

\begin{array}{l} f (0, q) = 1, f^{'} (1, q) = 0, f^{'} (0, q) = 1, g (0, q) = 1, g (1, q) = 0, \\ θ (0, q) = 1, θ (1, q) = 0, ϕ (0, q) = 1, ϕ (1, q) = 0, χ (0, q) = 1, χ (1, q) = 0, \end{array} (42)

where $q$ is an embedding parameter in this case, and $ℏ_{f}, ℏ_{g}, ℏ_{θ}, ℏ_{ϕ}, ℏ_{χ}$ are the nonzero auxiliary parameters. $N_{f}, N_{g}, N_{θ}, N_{ϕ}, N_{χ}$ are the nonlinear operators and can be obtained through Eqs 17–22 by adopting the procedure in Ref. 47.

For $q = 0$ and $q = 1$ , the following form is obtained

\begin{array}{l} f (ζ, 0) = f_{0} (ζ), θ (ζ, 0) = θ_{0} (ζ), g (ζ, 0) = g_{0} (ζ), ϕ (ζ, 0) = ϕ_{0} (ζ), χ (ζ, 0) = χ_{0} (ζ), \\ f (ζ, 1) = f (ζ), θ (ζ, 1) = θ (ζ), ϕ (ζ, 1) = ϕ (ζ), χ (ζ, 1) = χ (ζ) . \end{array} (43)

Obviously, when $q$ is increased from $0 to 1$ , then $f (ζ, q), g (ζ, q), θ (ζ, q), ϕ (ζ, q), χ (ζ, q)$ vary from $f_{o} (ζ), g_{o} (ζ), θ_{o} (ζ), ϕ_{o} (ζ), χ_{o} (ζ)$ to $f (ζ), g (ζ), θ (ζ), ϕ (ζ), χ (ζ)$ . Through Taylor’s series expansion, the expressions in the above equations become as

f (ζ, q) = f_{o} (ζ) + \sum_{m = 1}^{\infty} f_{m} (ζ) q^{m}, f_{m} (ζ) = \frac{1}{m!} \frac{\partial^{m} f (ζ, q)}{\partial ζ^{m}} |_{q = 0}, (44)

g (ζ, q) = g_{o} (ζ) + \sum_{m = 1}^{\infty} g_{m} (ζ) q^{m}, g_{m} (ζ) = \frac{1}{m!} \frac{\partial^{m} g (ζ, q)}{\partial ζ^{m}} |_{q = 0}, (45)

θ (ζ, q) = θ_{o} (ζ) + \sum_{m = 1}^{\infty} θ_{m} (ζ) q^{m}, θ_{m} (ζ) = \frac{1}{m!} \frac{\partial^{m} θ (ζ, q)}{\partial ζ^{m}} |_{q = 0}, (46)

ϕ (ζ, q) = ϕ_{o} (ζ) + \sum_{m = 1}^{\infty} ϕ_{m} (ζ) q^{m}, ϕ_{m} (ζ) = \frac{1}{m!} \frac{\partial^{m} ϕ (ζ, q)}{\partial ζ^{m}} |_{q = 0}, (47)

χ (ζ, q) = χ_{o} (ζ) + \sum_{m = 1}^{\infty} χ_{m} (ζ) q^{m}, χ_{m} (ζ) = \frac{1}{m!} \frac{\partial^{m} χ (ζ, q)}{\partial ζ^{m}} |_{q = 0} . (48)

The convergence of the series in Eqs 44–48 depends strongly upon $ℏ_{f}, ℏ_{g}, ℏ_{θ}, ℏ_{ϕ}, ℏ_{χ}$ . By considering that $ℏ_{f}, ℏ_{g}, ℏ_{θ}, ℏ_{ϕ}, ℏ_{χ}$ are selected properly so that the series in Eqs 44–48 converge at $q = 1$ , then these have the following forms

f (ζ) = f_{o} (ζ) + \sum_{m = 1}^{\infty} f_{m} (ζ), g (ζ) = g_{o} (ζ) + \sum_{m = 1}^{\infty} g_{m} (ζ), θ (ζ) = θ_{o} (ζ) + \sum_{m = 1}^{\infty} θ_{m} (ζ),

ϕ (ζ) = ϕ_{o} (ζ) + \sum_{m = 1}^{\infty} ϕ_{m} (ζ), χ (ζ) = χ_{o} (ζ) + \sum_{m = 1}^{\infty} χ_{m} (ζ) . (49)

The result of the problems at order $m$ deformations can be constructed as follows

L_{f} [f_{m} (ζ) - η_{m} f_{m - 1} (ζ)] = ℏ_{f} R_{f}^{m} (ζ), (50)

L_{g} [g_{m} (ζ) - η_{m} g_{m - 1} (ζ)] = ℏ_{g} R_{g}^{m} (ζ), (51)

L_{θ} [θ_{m} (ζ) - η_{m} θ_{m - 1} (ζ)] = ℏ_{θ} R_{θ}^{m} (ζ), (52)

L_{ϕ} [ϕ_{m} (ζ) - η_{m} ϕ_{m - 1} (ζ)] = ℏ_{ϕ} R_{ϕ}^{m} (ζ), (53)

L_{χ} [χ_{m} (ζ) - η_{m} χ_{m - 1} (ζ)] = ℏ_{χ} R_{χ}^{m} (ζ), (54)

\begin{array}{l} f_{m} (0) = f^{'} (0) = f^{'} (1) = 0, g_{m} (0) = g_{m} (1) = 0, θ_{m} (0) = θ_{m} (1) = 0, \\ ϕ_{m} (0) = ϕ_{m} (1) = 0, χ_{m} (0) = χ_{m} (1) = 0, \end{array} (55)

where $R_{f}^{m} (ζ), R_{g}^{m} (ζ), R_{θ}^{m} (ζ), R_{ϕ}^{m} (ζ), and R_{χ}^{m} (ζ)$ can be calculated through Eqs 17–22 with the procedure as in Ref. 47 and $η_{m} = {\begin{cases} 0, m \leq 1 \\ 1, m > 1 \end{cases}}$ .

By solving the $m^{t h}$ order deformation problems, the general solutions are

f_{m} (ζ) = f_{m}^{*} (ζ) + C_{1} + C_{2} ζ + C_{3} ζ^{2} + C_{4} ζ^{3}, (56)

g_{m} (ζ) = g_{m}^{*} (ζ) + C_{5} + C_{6} ζ, (57)

θ_{m} (ζ) = θ_{m}^{*} (ζ) + C_{7} + C_{8} ζ, (58)

ϕ_{m} (ζ) = ϕ_{m}^{*} (ζ) + C_{9} + C_{10} ζ, (59)

χ_{m} (ζ) = χ_{m}^{*} (ζ) + C_{11} + C_{12} ζ . (60)

in which $f_{m}^{*} (ζ), g_{m}^{*} (ζ), θ_{m}^{*} (ζ), ϕ_{m}^{*} (ζ), χ_{m}^{*} (ζ)$ are the special solutions.

Results and Discussion

Velocity Profile

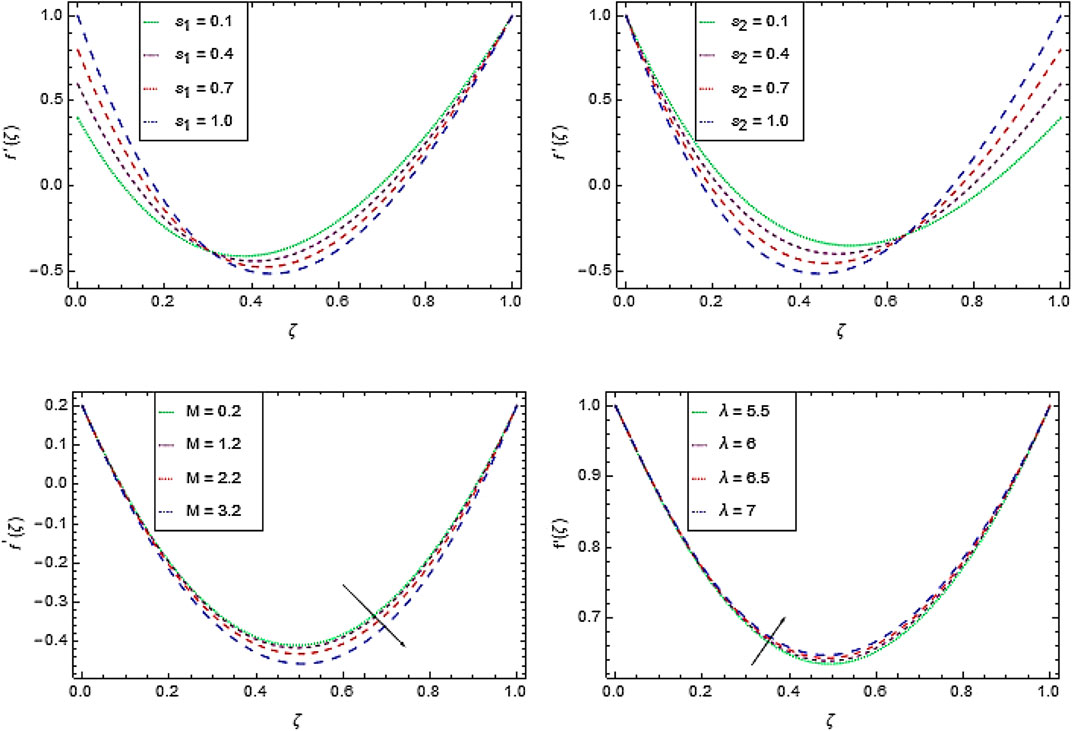
Figures 2A–D depict the effect of $s_{1}$ , $s_{2}$ , $M$ , and $λ$ on radial velocity profile $f^{'} (ζ)$ . Figure 2A reveals that the $f^{'} (ζ)$ increases at the lower disk by increasing the values of stretching parameter $s_{1}$ and decreases near the upper disk. $f^{'} (ζ)$ takes negative value near the lower disk due to the high stretching and rotation at the upper disk. From Figure 2B, it is evident that by increasing stretching parameter $s_{2}$ , $f^{'} (ζ)$ enhances near the surface of the upper disk because the stretching rate is greater there. The result is resembled with Figures 4 and 6 of Hayat et al. [44]. Figure 2C shows that $f^{'} (ζ)$ decreases by increasing magnetic field parameter $M$ . In the hydromagnetic case, the fluid velocity is much smaller than that in the case of hydrodynamic. This is because of the strength of Lorentz force that grows stronger when $M$ increases. Thus, increasing $M$ means increasing the resistive force (Lorentz force) that causes friction between the fluid and the surface, resulting in the reduction of radial velocity. Figure 2D shows that $f^{'} (ζ)$ enhances with the increase in $λ$ values. Figures 3A,B show the effect of bioconvection Rayleigh number $R b$ and Weissenberg number $W e$ on $f^{'} (ζ)$ . Figure 3A shows that $f^{'} (ζ)$ decreases as the convection power of the bioconvection worked against the convection of the buoyancy force. Figure 3B shows that by increasing the values of Weissenberg number $W e$ , the velocity of Cross nanofluid is decreased, which indicates a thinning liquid shear.

FIGURE 2

FIGURE 2. $f^{'} (ζ)$ as a function of (A) $s_{1}$ , (B) $s_{2}$ , (C), and $M$ (D) $λ$ .

FIGURE 3

FIGURE 3. $f^{'} (ζ)$ as a function of (A) $R b$ , (B) $W e$ , and $g (ς)$ as a function of (C) $γ$ and (D) $m$ .

FIGURE 4

FIGURE 4. $P (ς)$ as a function of (A) $Re$ (B) $W e$ .

FIGURE 5

FIGURE 5. $θ (ζ)$ as a function of (A) $ε$ , (B) $E c$ , (C) $N b$ , and (D) $N t$ .

Figure 3C discloses that the rotation paves a long way to enhance the velocity component $g (ς)$ . The rotation parameter $γ$ is defined as $γ = γ_{1} / γ_{2}$ and has rotatory motion with the essential reliable results. If $γ = 0$ , then there is no rotation at all and the system remains at rest. $γ$ > 0 shows that the direction of motion at both of the disks is same, and precisely, $γ = 1$ is the same direction and velocity of motion. It is easily understood that rotation directions from both disks are crucial to the motion of the disks. If the two disks rotate within the same direction, the rotation of the fluid in the disks will be at angular velocity. Particularly, the motion of the two disks will be different more likely to be higher in the upper disk, the radial flow is inwardly close to lower disk whereas outwardly close to the upper disk. When the rotation of the lower disk is faster, the liquid flows inward to the lower disk and outward to the upper disk. After all, the two disks attracted to each other, showing that the pressure decreases between the two disks. The plane between the two disks in which the tangential velocity is zero in magnitude is in the opposite direction to each of the disks. Thus, the radial velocity of the fluid is near the plane. Both disks are currently repelling each other, resulting in an increase in pressure. From Figure 3D, it is observed that the azimuthal velocity $g (ς)$ is an increasing function of the Hall parameter $m$ . The last term $M / 1 + m^{2} (g + m f^{'})$ in Eq. 18 mathematically proves that the velocity $g (ς)$ is increased as the Hall parameter $m$ increases, provided that the magnetic field is strong, that is, the magnetic field parameter $M$ is positive and high enough. It is noted that when there is no magnetic field, that is, if $M = 0$ , then the term $M / 1 + m^{2} (g + m f^{'})$ vanishes consequently and there is no Hall effect.

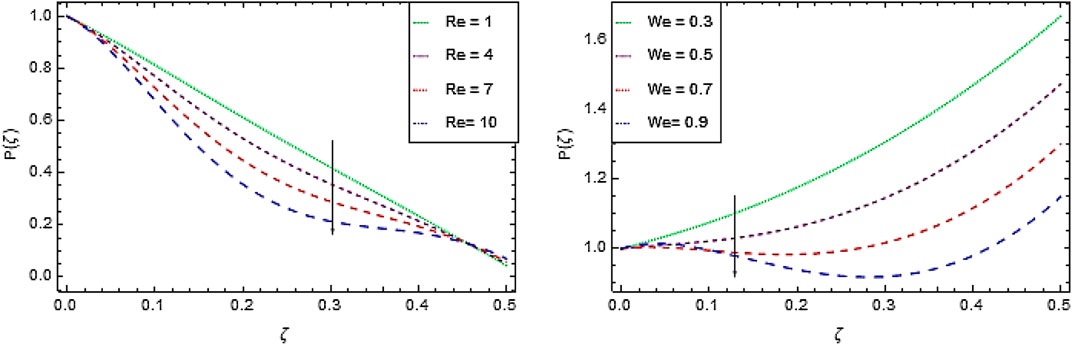
Pressure Profile

Figures 4A,B depicts the effect of Reynolds number $Re$ and Weissenberg number $W e$ on pressure profile $P (ς)$ . Figure 4A reveals that $P (ς)$ decreases by increasing the values of $W e$ . From Figure 4B, similar trend is observed by increasing the values of $Re$ . Physically, when the pressure of the flow decays, the flow velocity also decreases, indicating the thinning of the liquid shear.

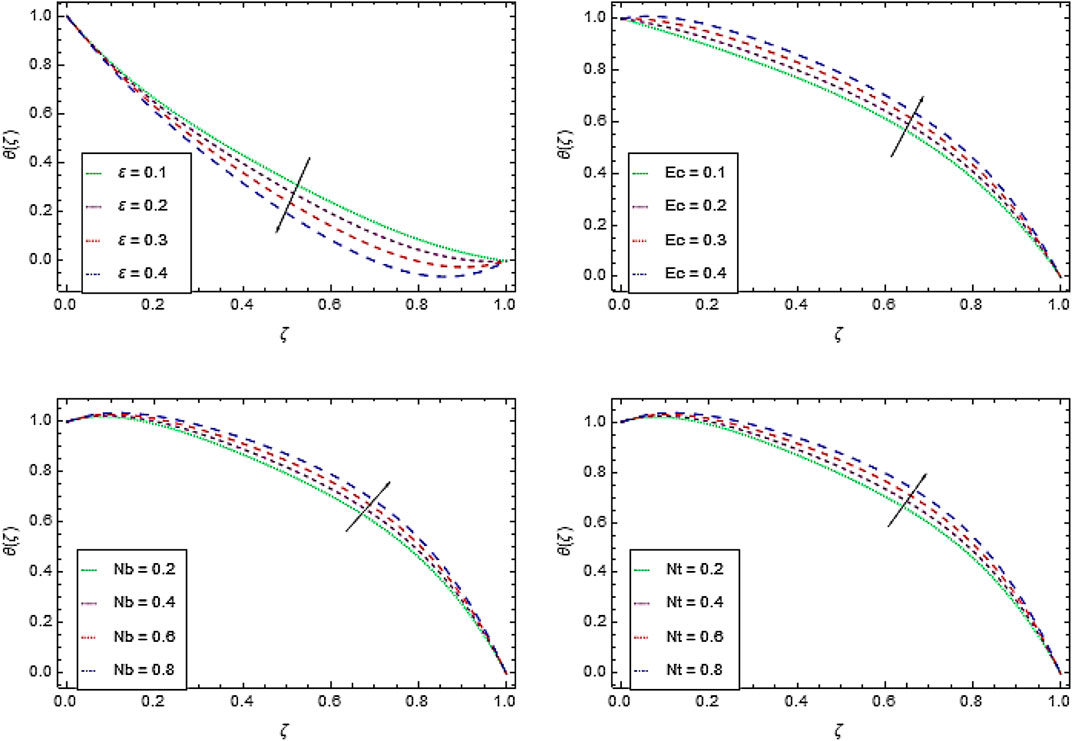
Temperature Profile

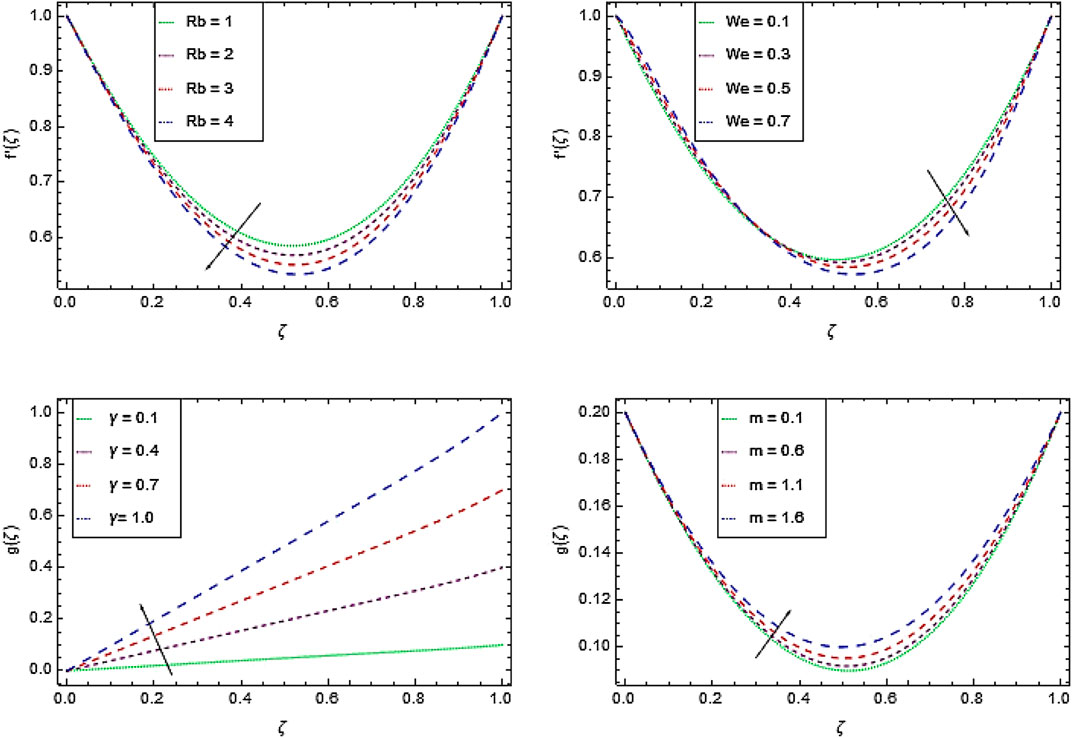
The temperature decreases by increasing the values of thermal conductivity parameter $ε$ as seen in Figure 5A. Fluid thermal conductivity is directly related to $ε$ , and because of this, large heating amount takes place, and then transferred to the fluid through the disk surface due to the increase in temperature $θ (ζ)$ . Figure 5B shows that when Eckert number $E c$ increases, the temperature $θ (ζ)$ is increased. $E c$ is the link between the enthalpy flow and the kinetic energy. Work vs. viscous liquid stress is used to convert kinetic energy (KE) into internal energy. The reason is that mechanical energy is converted into thermal energy, so this effect increases the temperature $θ (ζ)$ due to heat dissipation. Figure 5C demonstrates that Brownian motion parameter $N b$ has the effect of increasing the temperature of the fluid. The fluid particles develop random motion as the value of $N b$ increases, leading to a higher temperature distribution $θ (ζ)$ . There is a significant increase in temperature with higher values of the thermophoresis parameter $N t$ as shown in Figure 5D. Essentially, rising in the value of $N t$ means the reinforcement of the thermophoresis forces that tend to transport heat in nanoparticles.

FIGURE 6

FIGURE 6. $ϕ (ζ)$ as a function of (A) $E$ , (B) $σ$ , (C) $δ$ , and (D) $N b$ .

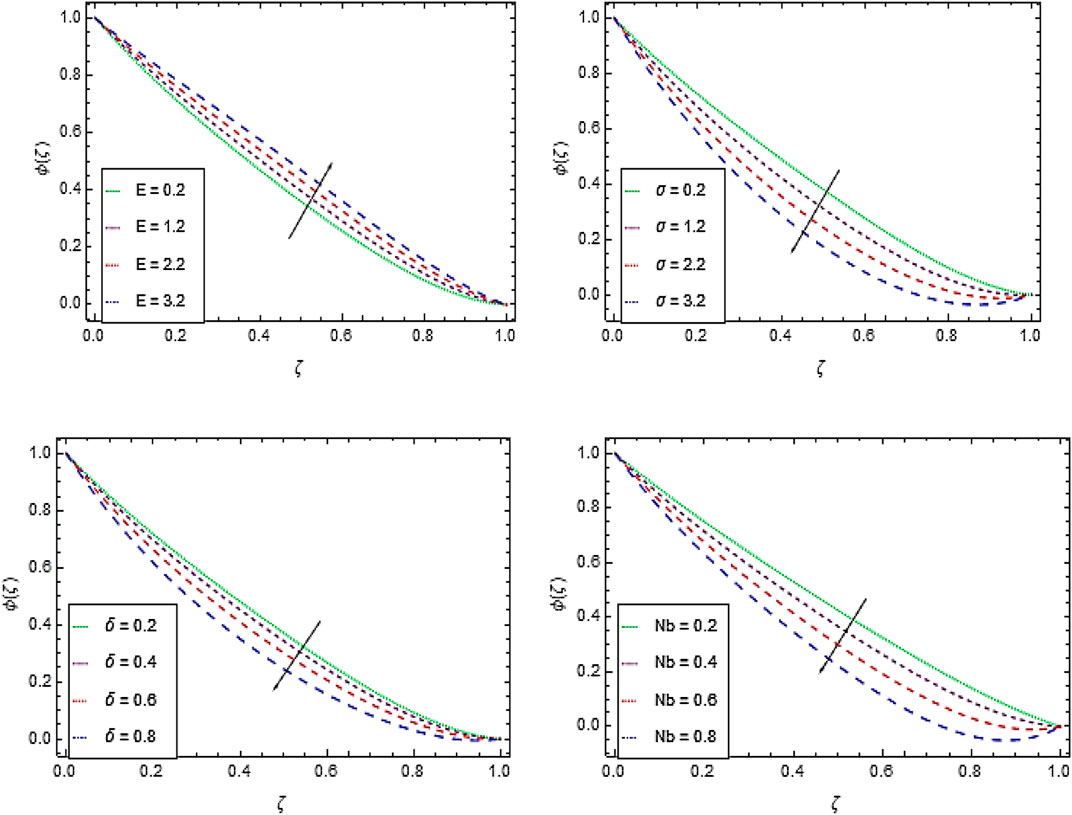
Nanoparticles Concentration Profile

The increase in Arrhenius activation energy $E$ causes the nanoparticles concentration $ϕ (ζ)$ to increase in the boundary layer as shown by Figure 6A. Essentially, a larger estimate of the Arrhenius activation energy parameter reduces the value of the modified Arrhenius function that drives the associative chemical reaction. Figure 6B shows that the nanoparticles concentration $ϕ (ζ)$ found to be a decreasing function of dimensionless chemical reaction rate $σ$ . As a result, the concentration of fluid decays to a higher estimate of the chemical reaction rate parameter. Larger values of $σ$ are associated with a major devastating chemical reaction that dissolves liquid species quite productively. Figure 6C shows that the nanoparticle concentration $ϕ (ζ)$ of fluid is observed to decreasing by a higher estimate of temperature difference parameter $δ$ . The concentration of the nanoparticles decreases by the Brownian motion parameter $N b$ as shown by Figure 6D. In addition, it is observed that an increase in $N b$ corresponds to an increase in the rate at which nanoparticles in the base liquid move at different velocity in random directions.

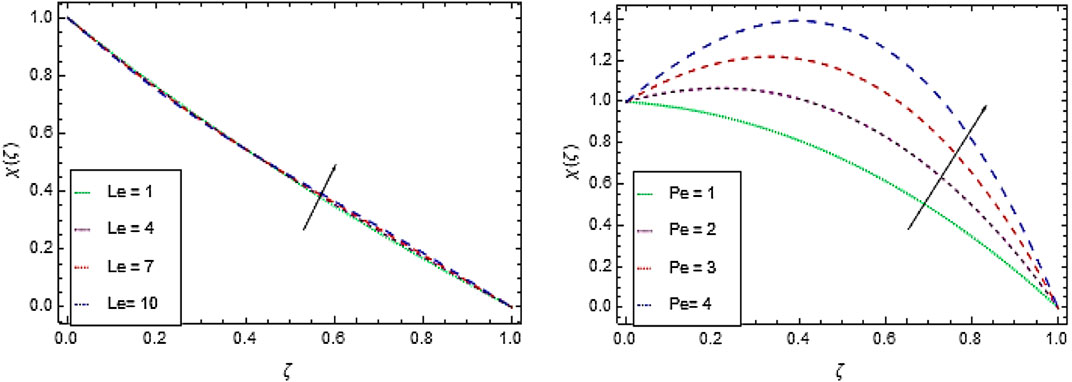
Gyrotactic Microorganism Concentration Profile

Heat treatment makes the system quite fragile and improves production of bioconvection. Figure 7A shows that the increment in the motile microorganism’s concentration $χ (ζ)$ occurs by increasing the values of Lewis number $L e$ . That is, the increments in the diffusion of microorganisms can be measured, thus increasing the density and boundary layer thickness of motile microorganism’s concentration. Figure 7B presents that the increment in the density of the motile microorganisms occurs quickly by increasing the Peclet number $P e$ . This shows a strong relation between the nanoparticles field $ϕ (ζ)$ and the microorganism’s field $χ (ζ)$ .

FIGURE 7

FIGURE 7. $χ (ζ)$ as a function of (A) $L e$ and (B) $P e$ .

FIGURE 8

FIGURE 8. Streamlines for (A) $m = 0.2,$ $h = - 0.1,$ for the upper disk (B) $h = - 0.4,$ for the lower disk.

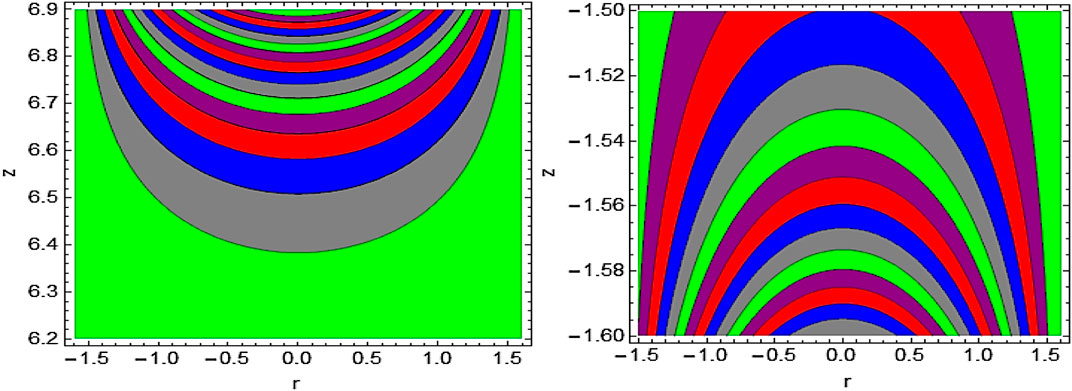
Streamlines

The trapping for different values of the Hall parameter $m$ is shown in Figures 8A and 8B. It is observed from these figures that the size of the trapping bolus is higher at the lower disc than in the upper disc for the flow channel.

Validation of the Present Work and Physical Quantities

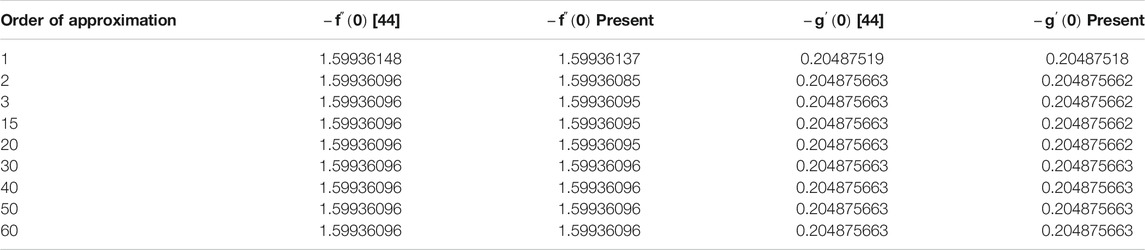
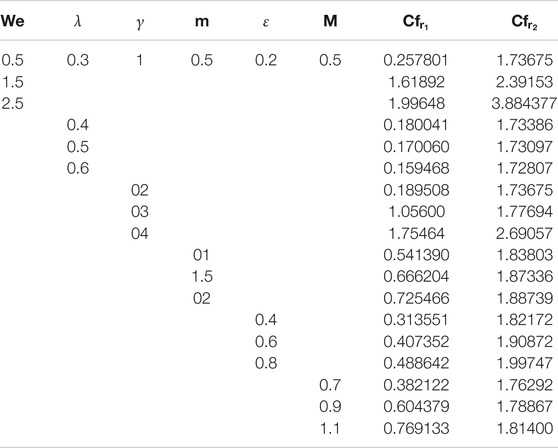
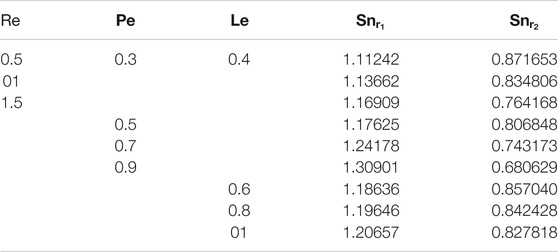
The comparison between the present work and the previous work is shown in Table 1. The results show that there is a close agreement of the present problem. The numerical values of the skin frictions on both the disks are displayed in Table 2. The lower disk skin friction is increased with $W e$ , $γ$ , $m$ , $ε$ , and $M$ , while the opposite trend is observed for $λ$ . However, the observations on the upper disk were found to be the same with the lower disk. It is examined in Table 3 that the rate of heat transport on the lower disk is decreased with $E c, N t, and N b$ , while the opposite effect is shown with $R d$ , $\Pr$ , and $ε$ . The observations here are that the rate of heat transport on the upper disk is increased by $E c, N t, and N b$ , while the decreasing effect is shown by $R d$ , $\Pr$ , and $ε$ . The local Sherwood number for the upper disk is decreased with higher values of $σ, N t, δ, and S c$ and is increased with $E and N b$ as shown in Table 4. Local density number is enhanced for larger values of $P e, L e$ , and $Re$ at the lower disk, and opposite trend is observed at the upper disk as shown in Table 5.

TABLE 1

TABLE 1. Comparison of the present work with the existing literature.

TABLE 2

TABLE 2. Effects of parameters $W e$ , $λ$ , $γ$ , $m$ , $ε$ , and $M$ on skin friction coefficients $C f_{x}$ .

TABLE 3

TABLE 3. Effects of parameters $E c$ , $R d$ , $N t$ , $N b$ , $ε$ , and $\Pr$ on local Nusselt number $N u_{x}$ .

TABLE 4

TABLE 4. Effect of parameters $σ$ , $E$ , $N t$ , $N b$ , $δ$ , and $S c$ on local Sherwood number $S h_{x}$ .

TABLE 5

TABLE 5. Effects of parameters $Re$ , $P e$ , and $L e$ on motile density number $S n_{x}$ .

Conclusion

The current work has analyzed the influence of variable thermal conductivity, the Hall current, and activation energy on the flow of double stretchable rotating disks under the theory of radiative Cross nanofluid in the presence of a uniform magnetic field. The fluid functions have been analyzed using graphs and tables explaining the details of the findings in the Discussion section. In summary,

The Cross-nanofluid velocity decreases at the boundary layer with the magnetic field parameter $M$ . Radial velocity is proportional to $s_{1}, s_{2}, λ, and W e$ and inversely proportional to $m and R b$ .

The azimuthal velocity $g$ is accelerated by increasing the disk rotation parameter and the Hall effect parameter.

Pressure profile $P (ς)$ decreases with $Re$ and $W e$ .

The temperature of the Cross nanofluid enhances with increasing the $ε, E c, N b, N t$ parameters.

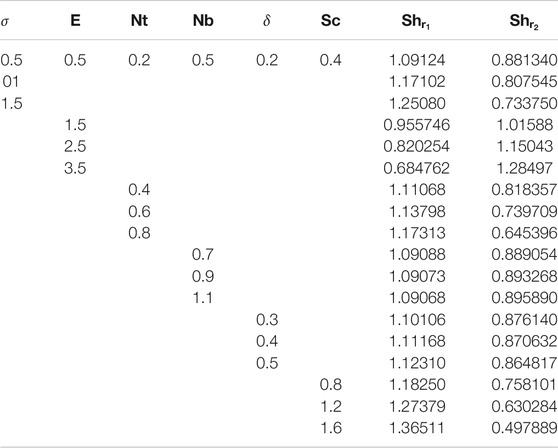
The nanofluid concentrations decreases with higher values of $δ, σ, N b$ while increases with higher values of $E$ .

Motile gyrotactic microorganism’s density increases through larger value of $L e$ and it decreases with $P e and Re$ .

The lower disk skin frictions is increased with $W e$ , $γ$ , $m$ , $ε$ , and $M$ , while the opposite trend is observed for $λ$ ; however, at the upper disk, the case is opposite.

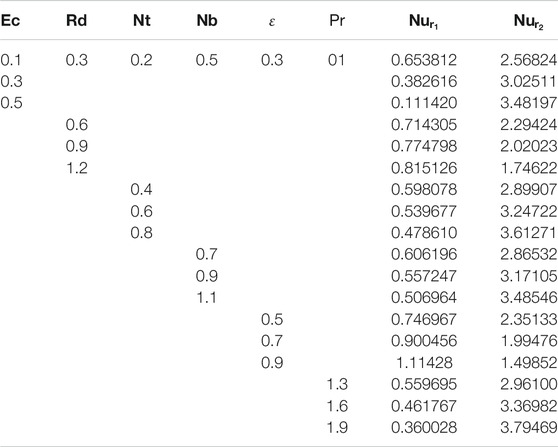
The rate of heat transport on the lower disk decreases with $E c, N t, and N b$ , while the opposite effects are shown with $R d$ , $\Pr$ , and $ε$ ; however, at the upper disk, the case is opposite.

The local density number is enhanced for the larger values of $P e, L e$ , and $Re$ at the lower disk, and opposite trend is observed at the upper disk.

There exists a nice agreement between the present and published work in Table 1.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding authors.

Author Contributions

NK, AU, UH, ZS, PK, WK, AK, SR, ZU completed the research work.

Funding

The research is funded by Petchra Pra Jom Klao Doctoral Scholarship for Ph.D. program of King Mongkut’s University of Technology Thonburi (KMUTT) (Grant No. 13/2562) and Theoretical and Computational Science (TaCS) Center. The authors appreciate the financial support allotted by King Mongkut’s University of Technology Thonburi through the “KMUTT 55th Anniversary Commemorative Fund.” The first author is supported by the Petchra Pra Jom Klao Doctoral Scholarship Academic for PhD studies at KMUTT. This research was accomplished with the help of the Theoretical and Computational Science (TaCS) Center, Faculty of Science, KMUTT.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest

Acknowledgments

The authors are obliged to the respectable editor and referees for their important and fruitful comments to enhance the quality of this article. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005.

Glossary

$u, v, w$ velocity components

$ρ_{n f}$ density of fluid

$v_{n f}$ kinematic viscosity

$μ_{n f}$ dynamic viscosity

$n$ power law index

$B_{o}$ uniform magnetic field strength

${(ρ c_{p})}_{n f}$ heat capacity of nanofluid

$τ$ ratio of heat capacity

${(ρ c_{p})}_{p}$ effective heat capacity

$k_{n f}$ thermal conductivity

$σ^{*}$ Stefan–Boltzmann constant

$D_{T}$ thermophoresis effect

$T$ temperature

$C$ concentration

$N$ motile gyrotactic microorganisms

$ζ$ dimensionless variable

$f, g$ dimensionless velocities

$θ$ dimensionless temperature

$ϕ$ dimensionless concentration

$χ$ dimensionless motile microorganisms

$P$ fluid pressure

$W e$ Weissenberg number

$k_{r}^{2}$ reaction rate

$E$ Arrhenius activation energy dimensionless Arrhenius activation energy

$β$ ratio of viscosities

$Le$ Lewis number

$Pe$ Peclet number

$γ$ rotation parameter

$s_{1}$ lower disk rotation rate

$s_{2}$ upper disk rotation rate

$k^{*}$ mean absorption coefficient

$Γ$ time material constant

$D_{B}$ Brownian motion

$\Pr$ Prandtl number

$M$ magnetic parameter

$N r$ Buoyancy ratio parameter

$λ$ mixed convection parameter

$R b$ Rayleigh number bioconvection

$N b$ Brownian motion parameter

$N t$ thermophoresis parameter

$E c$ Eckert number

$S c$ Schmidt number

$σ$ dimensionless chemical reaction rate

$E$ Arrhenius activation energy dimensionless Arrhenius activation energy

$δ$ temperature difference parameter

$N_{δ}$ microorganisms concentration variance parameter

$β_{1}$ dimensionless parameter 1

$β_{2}$ dimensionless parameter 2

$R d$ thermal radiation parameter

$ε$ thermal conductivity parameter

$K (T)$ variable thermal conductivity

$τ_{w}$ wall shear stress

$q_{w}$ wall heat flux

$C f_{x}$ skin friction coefficient

$N u_{x}$ local Nusselt number

$S h_{x}$ Sherwood number

$S n_{x}$ local density number

${Re}_{x}$ local Reynolds number

References

1. Cross MM. Rheology of non-newtonian fluids: a new flow equation for pseudoplastic systems. J Colloid Sci (1965) 20:417–37. doi:10.1016/0095-8522(65)90022-x

CrossRef Full Text | Google Scholar

2. Xie J, Jin Y-C. Parameter determination for the cross rheology equation and its application to modeling non-Newtonian flows using the WC-MPS method. Eng Appl Comput Fluid Mech (2016) 10:111–29. doi:10.1080/19942060.2015.1104267

CrossRef Full Text | Google Scholar

3. Manzur M, Khan M, Rahman Mu. Mixed convection heat transfer to cross fluid with thermal radiation: effects of buoyancy assisting and opposing flows. Int J Mech Sci (2018) 138–139:515–23. doi:10.1016/j.ijmecsci.2018.02.010

CrossRef Full Text | Google Scholar

4. Abbas SZ, Khan WA, Sun H, Ali M, Irfan M, Shahzed M, et al. Mathematical modeling and analysis of cross nanofluid flow subjected to entropy generation. Appl Nanosci (2020) 10:3149–60. doi:10.1007/s13204-019-01039-9

CrossRef Full Text | Google Scholar

5. Hayat T, Khan MI, Tamoor M, Waqas M, Alsaedi A. Numerical simulation of heat transfer in MHD stagnation point flow of cross fluid model towards a stretched surface. Results Phy (2017) 7:1824–7. doi:10.1016/j.rinp.2017.05.022

CrossRef Full Text | Google Scholar

6. Naz R, Noor M, Hayat T, Javed M, Alsaedi A. Dynamism of magnetohydrodynamic cross nanofluid with particulars of entropy generation and gyrotactic motile microorganisms. Int Commun Heat Mass Tran (2020) 110:104431. doi:10.1016/j.icheatmasstransfer.2019.104431

CrossRef Full Text | Google Scholar

7. Choi SU, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticles (1995). Report Nos. ANL/MSD/CP-84938; CONF-951135-29. Lemont, IL: Argonne National Lab.

Google Scholar

8. Buongiorno J. Convective transport in nanofluids. J Heat Trans-T ASME (2006) 128:240–50. doi:10.1115/1.2150834

CrossRef Full Text | Google Scholar

9. Kuznetsov AV, Nield DA. Natural convective boundary-layer flow of a nanofluid past a vertical plate. Int J Therm Sci (2010) 49(2):243–7. doi:10.1016/j.ijthermalsci.2009.07.015

CrossRef Full Text | Google Scholar

10. Turkyilmazoglu M. Nanofluid flow and heat transfer due to a rotating disk. Comput Fluids (2014) 94:139–46. doi:10.1016/j.compfluid.2014.02.009

CrossRef Full Text | Google Scholar

11. Ahmad L, Khan M, Khan WA. Numerical investigation of magneto-nanoparticles for unsteady 3D generalized Newtonian liquid flow. Eur Phys J Plus (2017) 132(9):373. doi:10.1140/epjp/i2017-11658-6

CrossRef Full Text | Google Scholar

12. Hafeez A, Khan M, Ahmed A, Ahmed J. Rotational flow of Oldroyd-B nanofluid subject to Cattaneo-Christov double diffusion theory. Appl Math Mech (2020) 41:1083–94. doi:10.1007/s10483-020-2629-9

CrossRef Full Text | Google Scholar

13. Khan M, Ahmad L, Gulzar MM. Unsteady Sisko magneto-nanofluid flow with heat absorption and temperature dependent thermal conductivity: a 3D numerical study. Results Phy (2018) 8:1092–103. doi:10.1016/j.rinp.2018.01.034

CrossRef Full Text | Google Scholar

14. Ahmad L, Khan M. Numerical simulation for MHD flow of Sisko nanofluid over a moving curved surface: a revised model. Microsyst Technol (2019) 25(6):2411–28. doi:10.1007/s00542-018-4128-3

CrossRef Full Text | Google Scholar

15. Khan M, Ahmed J, Sultana F, Sarfraz M. Non-axisymmetric Homann MHD stagnation point flow of Al₂O₃-Cu/water hybrid nanofluid with shape factor impact. Appl Math Mech (2020) 41:1125–38. doi:10.1007/s10483-020-2638-6

CrossRef Full Text | Google Scholar

16. Khan M, Irfan M, Khan WA, Ahmad L. Modeling and simulation for 3D magneto eyring-powell nanomaterial subject to nonlinear thermal radiation and convective heating. Results Phy (2017) 7:1899–906. doi:10.1016/j.rinp.2017.06.002

CrossRef Full Text | Google Scholar

17. Ahmed A, Khan M, Ahmed J. Thermal analysis in swirl motion of Maxwell nanofluid over a rotating circular cylinder. Appl Math Mech (2020) 41:1417–30. doi:10.1007/s10483-020-2643-7

CrossRef Full Text | Google Scholar

18. Khan M, Ahmad L, Khan WA. Numerically framing the impact of radiation on magnetonanoparticles for 3D Sisko fluid flow. J Braz Soc Mech Sci Eng (2017) 39:4475–87. doi:10.1007/s40430-017-0842-5

CrossRef Full Text | Google Scholar

19. Ahmed J, Khan M, Ahmad L. Radiative heat flux effect in flow of Maxwell nanofluid over a spiraling disk with chemically reaction. Phys Stat Mech Appl (2020) 551:123948. doi:10.1016/j.physa.2019.123948

CrossRef Full Text | Google Scholar

20. Ahmed J, Shahzad A, Farooq A, Kamran M, Khan SUD, Khan SUD. Thermal analysis in swirling flow of titanium dioxide–aluminum oxide water hybrid nanofluid over a rotating cylinder. J Therm Anal Calorim (2020):1–11. doi:10.1007/s10973-020-10190-3

CrossRef Full Text | Google Scholar

21. Ahmed J, Shahzad A, Farooq A, Kamran M, Khan SUD, Khan SUD. Radiative heat transfer in Homann stagnation-point flow of hybrid nanofluid. Appl Nanosci (2020) 10:1–10. doi:10.1007/s13204-020-01464-1

CrossRef Full Text | Google Scholar

22. Li JJ, Xu H, Raees A, Zhao QK. Unsteady mixed bioconvection flow of a nanofluid between two contracting or expanding rotating discs. Z Naturforsch (2016) 71:261–72. doi:10.1515/zna-2015-0518

CrossRef Full Text | Google Scholar

23. Qayyum S, Imtiaz M, Alsaedi A, Hayat T. Analysis of radiation in a suspension of nanoparticles and gyrotactic microorganism for rotating disk of variable thickness. Chin J Phys (2018) 56:2404–23. doi:10.1016/j.cjph.2018.06.020

CrossRef Full Text | Google Scholar

24. Shehzad SA, Reddy MG, Rauf A, Abbas Z. Bioconvection of Maxwell nanofluid under the influence of double diffusive Cattaneo–Christov theories over isolated rotating disk. Phys Scr (2020) 95:045207. doi:10.1088/1402-4896/ab5ca7

CrossRef Full Text | Google Scholar

25. Khan NS, Shah Q, Bhaumik A, Kumam P, Thounthong P, Amiri I. Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci Rep (2020) 10:1–26. doi:10.1038/s41598-020-61172-2 |

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Khan NS, Shah Q, Sohail A. Dynamics with Cattaneo–Christov heat and mass flux theory of bioconvection Oldroyd-B nanofluid. Adv Mech Eng (2020) 12. doi:10.1177/1687814020930464

CrossRef Full Text | Google Scholar

27. Khan NS. Mixed convection in mhd second grade nanofluid flow through a porous medium containing nanoparticles and gyrotactic microorganisms with chemical reaction. Filomat (2019) 33:4627–53. doi:10.2298/fil1914627k

CrossRef Full Text | Google Scholar

28. Zuhra S, Khan NS, Islam S. Magnetohydrodynamic second-grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comput Appl Math (2018) 37:6332–58. doi:10.1007/s40314-018-0683-6

CrossRef Full Text | Google Scholar

29. Zuhra S, Khan NS, Shah Z, Islam S, Bonyah E. Simulation of bioconvection in the suspension of second grade nanofluid containing nanoparticles and gyrotactic microorganisms. AIP Adv (2018) 8:105210. doi:10.1063/1.5054679

CrossRef Full Text | Google Scholar

30. Palwasha Z, Islam S, Khan NS, Ayaz H. Non-Newtonian nanoliquids thin-film flow through a porous medium with magnetotactic microorganisms. Appl Nanosci (2018) 8:1523–44. doi:10.1007/s13204-018-0834-5

CrossRef Full Text | Google Scholar

31. Arrhenius S. Über die dissociationswärme und den Einfluss der temperatur auf den dissociationsgrad der elektrolyte. Z Phys Chem (1889) 4:96–116. doi:10.1515/zpch-1889-0108

CrossRef Full Text | Google Scholar

32. Bestman AR. Natural convection boundary layer with suction and mass transfer in a porous medium. Int J Energy Res (1990) 14:389–96. doi:10.1002/er.4440140403

CrossRef Full Text | Google Scholar

33. Shahzad M, Sun H, Sultan F, Khan WA, Ali M, Irfan M. Transport of radiative heat transfer in dissipative cross nanofluid flow with entropy generation and activation energy. Phys Scr (2019) 94:115224. doi:10.1088/1402-4896/ab2caf

CrossRef Full Text | Google Scholar

34. Dhlamini M, Kameswaran PK, Sibanda P, Motsa S, Mondal H. Activation energy and binary chemical reaction effects in mixed convective nanofluid flow with convective boundary conditions. J Comput Des Eng (2019) 6:149–58. doi:10.1016/j.jcde.2018.07.002

CrossRef Full Text | Google Scholar

35. Azam M, Xu T, Shakoor A, Khan M. Effects of Arrhenius activation energy in development of covalent bonding in axisymmetric flow of radiative-cross nanofluid. Int Commun Heat Mass Tran (2020) 113:104547. doi:10.1016/j.icheatmasstransfer.2020.104547

CrossRef Full Text | Google Scholar

36. Khan NS, Shah Z, Islam S, Khan I, Alkanhal T, Tlili I. Entropy generation in MHD mixed convection non-newtonian second-grade nanoliquid thin film flow through a porous medium with chemical reaction and stratification. Entropy (2019) 21:139. doi:10.3390/e21020139

CrossRef Full Text | Google Scholar

37. Khan NS, Kumam P, Thounthong P. Second law analysis with effects of Arrhenius activation energy and binary chemical reaction on nanofluid flow. Sci Rep (2020) 10:1226–6. doi:10.1038/s41598-020-57802-4 |

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Abdelmalek Z, Mahanthesh B, Md Basir MF, Imtiaz M, Mackolil J, Khan NS, et al. Mixed radiated magneto Casson fluid flow with Arrhenius activation energy and Newtonian heating effects: flow and sensitivity analysis. Alex Eng J (2020) 59:3991–4011. doi:10.1016/j.aej.2020.07.006

CrossRef Full Text | Google Scholar

39. Khan NS, Zuhra S, Shah Q. Entropy generation in two phase model for simulating flow and heat transfer of carbon nanotubes between rotating stretchable disks with cubic autocatalysis chemical reaction. Appl Nanosci (2019) 9:1797–822. doi:10.1007/s13204-019-01017-1

CrossRef Full Text | Google Scholar

40. Khan NS, Shah Z, Shutaywi M, Kumam P, Thounthong P. A comprehensive study to the assessment of Arrhenius activation energy and binary chemical reaction in swirling flow. Sci Rep (2020) 10:1–21. doi:10.1038/s41598-020-64712-y |

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Kármán TV. Über laminare und turbulente Reibung. Z Angew Math Mech (1921) 1:233–52. doi:10.1002/zamm.19210010401

CrossRef Full Text | Google Scholar

42. Hayat T, Khan MI, Alsaedi A, Khan MI. Joule heating and viscous dissipation in flow of nanomaterial by a rotating disk. Int Commun Heat Mass Tran (2017) 89:190–7. doi:10.1016/j.icheatmasstransfer.2017.10.017

CrossRef Full Text | Google Scholar

43. Yao B, Lian L. A new analysis of the rotationally symmetric flow in the presence of an infinite rotating disk. Int J Mech Sci (2018) 136:106–11. doi:10.1016/j.ijmecsci.2017.12.023

CrossRef Full Text | Google Scholar

44. Hayat T, Qayyum S, Imtiaz M, Alsaedi A. Flow between two stretchable rotating disks with Cattaneo-Christov heat flux model. Results Phys (2017) 7:126–33. doi:10.1016/j.rinp.2016.12.007

CrossRef Full Text | Google Scholar

45. Khan M, Ahmed J, Ahmad L. Chemically reactive and radiative von Kármán swirling flow due to a rotating disk. Appl Math Mech (2018) 39:1295–310. doi:10.1007/s10483-018-2368-9

CrossRef Full Text | Google Scholar

46. Hafeez A, Khan M, Ahmed J. Oldroyd-B fluid flow over a rotating disk subject to Soret–Dufour effects and thermophoresis particle deposition. Proc IME C J Mech Eng Sci (2020) 24. doi:10.1177/0954406220946075

CrossRef Full Text | Google Scholar

47. Liao SJ. The proposed homotopy analysis technique for the solution of nonlinear problems. [PhD thesis]. Shanghai (China): Shanghai Jiao Tong University (1992).

Google Scholar

48. Liao S-J. An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int J Non Lin Mech (1999) 34:759–78. doi:10.1016/s0020-7462(98)00056-0

CrossRef Full Text | Google Scholar

49. Shah Z, Gul T, Khan AM, Ali I, Islam S, Husain F. Effects of hall current on steady three-dimensional non-Newtonian nanofluid in a rotating frame with Brownian motion and thermophoresis effects. J Eng Technol (2017) 6:e296. doi:10.1115/1.2969753

Google Scholar

50. Usman AH, Humphries UW, Kumam P, Shah Z, Thounthong P. Double diffusion non-isothermal thermo-convective flow of couple stress micropolar nanofluid flow in a Hall MHD generator system. IEEE Access (2020) 8:78821–35. doi:10.1109/access.2020.2986021

CrossRef Full Text | Google Scholar

51. Khan NS, Shah Q, Sohail A, Kumam P, Thounthong P, Bhaumik A, et al. Lorentz forces effects on the interactions of nanoparticles in emerging mechanisms with innovative approach. Symmetry (2020) 12:1700. doi:10.3390/sym12101700

CrossRef Full Text | Google Scholar

52. Shah Z, Islam S, Gul T, Bonyah E, Altaf Khan M. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys (2018) 9:1201–14. doi:10.1016/j.rinp.2018.01.064

CrossRef Full Text | Google Scholar

53. Usman AH, Shah Z, Humphries UW, Kumam P, Thounthong P. Soret, Dufour, and activation energy effects on double diffusive convective couple stress micropolar nanofluid flow in a Hall MHD generator system. AIP Adv (2020) 10:075010. doi:10.1063/5.0014897

CrossRef Full Text | Google Scholar

54. Zuhra S, Khan NS, Islam S, Nawaz R. Complexiton solutions for complex KdV equation by optimal homotopy asymptotic method. Filomat (2019) 33:6195–211. doi:10.2298/fil1919195z

CrossRef Full Text | Google Scholar

55. Khan NS, Zuhra S, Shah Z, Bonyah E, Khan W, Islam S, et al. Hall current and thermophoresis effects on magnetohydrodynamic mixed convective heat and mass transfer thin film flow. J Phys Commun. (2019) 3:035009. doi:10.1088/2399-6528/aaf830

CrossRef Full Text | Google Scholar

56. Khan NS, Kumam P, Thounthong P. Renewable energy technology for the sustainable development of thermal system with entropy measures. Int J Heat Mass Tran (2019) 145:118713. doi:10.1016/j.ijheatmasstransfer.2019.118713

CrossRef Full Text | Google Scholar

57. Khan NS, Gul T, Islam S, Khan I, Alqahtani A, Alshomrani A. Magnetohydrodynamic nanoliquid thin film sprayed on a stretching cylinder with heat transfer. Appl Sci (2017) 7:271. doi:10.3390/app7030271

CrossRef Full Text | Google Scholar

58. Khan NS. Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Braz J Phys (2018) 48:227–41. doi:10.1007/s13538-018-0567-7

CrossRef Full Text | Google Scholar

59. Khan NS, Gul T, Islam S, Khan W. Thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin film second-grade fluid of variable properties past a stretching sheet. Eur Phys J Plus (2017) 132:11. doi:10.1140/epjp/i2017-11277-3

CrossRef Full Text | Google Scholar

60. Palwasha Z, Khan NS, Shah Z, Islam S, Bonyah E. Study of two-dimensional boundary layer thin film fluid flow with variable thermo-physical properties in three dimensions space. AIP Adv (2018) 8:105318. doi:10.1063/1.5053808

CrossRef Full Text | Google Scholar

61. Khan NS, Gul T, Islam S, Khan A, Shah Z. Brownian motion and thermophoresis effects on MHD mixed convective thin film second-grade nanofluid flow with Hall effect and heat transfer past a stretching sheet. J Nanofluids (2017) 6:812–29. doi:10.1166/jon.2017.1383

CrossRef Full Text | Google Scholar

62. Khan NS, Zuhra S, Shah Z, Bonyah E, Khan W, Islam S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv (2019) 8:115302. doi:10.1063/1.5055690

CrossRef Full Text | Google Scholar

63. Khan NS, Gul T, Kumam P, Shah Z, Islam S, Khan W, et al. Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies (2019) 12:1459. doi:10.3390/en12081459

CrossRef Full Text | Google Scholar

64. Khan NS. Study of two dimensional boundary layer flow of a thin film second grade fluid with variable thermo-physical properties in three dimensions space. Filomat (2019) 33:5387–405. doi:10.2298/fil1916387k

CrossRef Full Text | Google Scholar

65. Khan NS, Zuhra S. Boundary layer unsteady flow and heat transfer in a second-grade thin film nanoliquid embedded with graphene nanoparticles past a stretching sheet. Adv Mech Eng (2019) 11:1–11. doi:10.1177/1687814019884428

CrossRef Full Text | Google Scholar

66. Khan NS, Gul T, Islam S, Khan W, Khan I, Ali L. Thin film flow of a second-grade fluid in a porous medium past a stretching sheet with heat transfer. Alex Eng J (2017) 57:1019–31.

Google Scholar

67. Zuhra S, Khan NS, Alam A, Islam S, Khan A. Buoyancy effects on nanoliquids film flow through a porous medium with gyrotactic microorganisms and cubic autocatalysis chemical reaction. Adv Mech Eng (2020) 12:1–17. doi:10.1177/1687814019897510

CrossRef Full Text | Google Scholar

68. Zuhra S, Khan NS, Khan MA, Islam S, Khan W, Bonyah E. Flow and heat transfer in water based liquid film fluids dispensed with graphene nanoparticles. Results Phys (2018) 8:1143–57. doi:10.1016/j.rinp.2018.01.032

CrossRef Full Text | Google Scholar

69. Liaqat A, Asifa T, Ali R, Islam S, Gul T, Kumam P, et al. A new analytical approach for the research of thin-film flow of magneto hydrodynamic fluid in the presence of thermal conductivity and variable viscosityZAMM J Appl Math Mech (2020):1–13. doi:10.1002/zamm.201900292

CrossRef Full Text | Google Scholar

70. Liaqat A, Khan NS, Ali R, Islam S, Kumam P, Thounthong P. Novel insights through the computational techniques in unsteady MHD second grade fluid dynamics with oscillatory boundary conditions. Heat Transf (2020) 1–23. doi:10.1002/htj.21989

Google Scholar

71. Khan NS, Liaqat A, Ali R, Kumam P, Thounthong P. A novel algorithm for the computation of systems containing different types of integral and integro-differential equations. Heat Transf (2020) 1–14. doi:10.1002/htj.22018

Google Scholar

72. Khan NS, Kumam P, Thounthong P. Computational approach to dynamic systems through similarity measure and homotopy analysis method for the renewable energy. Crystals (2020) 1–25. doi:10.3390/cryst10121086

CrossRef Full Text | Google Scholar

73. Khan NS, Gul T, Khan MA, Bonyah E, Islam S. Mixed convection in gravity-driven thin film non-Newtonian nanofluids flow with gyrotactic microorganisms. Results Phys (2017) 7:4033–49. doi:10.1016/j.rinp.2017.10.017

CrossRef Full Text | Google Scholar

74. Khan NS, Kumam P, Thounthong P. Magnetic field promoted irreversible process of water based nanocomposites with heat and mass transfer flow. Sci Rep (2021) 7(1):1692. doi:10.1038/s41598-020-80554-0

CrossRef Full Text | Google Scholar

Keywords: nanofluid, nanofluid (Buongiorno model), heat transfer, gyrotactic microorganism, rotating/stretching surface

Citation: Usman AH, Khan NS, Humphries UW, Shah Z, Kumam P, Khan W, Khan A, Rano SA and Ullah Z (2021) Development of Dynamic Model and Analytical Analysis for the Diffusion of Different Species in Non-Newtonian Nanofluid Swirling Flow. Front. Phys. 8:616790. doi: 10.3389/fphy.2020.616790

Received: 13 October 2020; Accepted: 23 December 2020;
Published: 22 February 2021.

Edited by:

Antonio F. Miguel, University of Evora, Portugal

Reviewed by:

Latif Ahmad, Shaheed Benazir Bhutto University, Pakistan
Eda Aydin, Ontario Tech University, Canada
Jawad Ahmed, University of Engineering and Technology, Pakistan

Copyright © 2021 Usman, Khan, Humphries, Shah, Kumam, Khan, Khan, Rano and Ullah. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Usa Wannasingha Humphries, usa.wan@kmutt.ac.th; Noor Saeed Khan, noorsaeedkhankhattak@gmail.com; Poom Kumam, poom.kum@kmutt.ac.th

ORIGINAL RESEARCH article

Development of Dynamic Model and Analytical Analysis for the Diffusion of Different Species in Non-Newtonian Nanofluid Swirling Flow

Introduction

Problem Formulation

Physical Quantities

Skin Friction Coefficients

Nusselt Number

Sherwood Number

Local Density Motile Flux

Solution of the Problem by HAM

Results and Discussion

Velocity Profile

Pressure Profile

Temperature Profile

Nanoparticles Concentration Profile

Gyrotactic Microorganism Concentration Profile

Streamlines

Validation of the Present Work and Physical Quantities

Conclusion

Data Availability Statement

Author Contributions

Funding

Conflict of Interest

Acknowledgments

Glossary

References

People also looked at