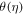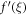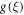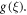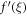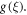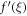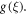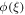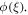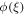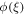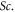Abstract
In this research article, three-dimensional Casson nanofluid under influences of Arrhenius stimulation energy and thermal radiation is considered. The flow is induced by a turning disk. Temperature, velocity, and concentration slips at the outward of the turning disk are deliberated. The effect of Brownian movement and thermophoresis is examined due to the nanosized particles in a Casson fluid dispersed over the turning disk. The appropriate transformation methods for reducing a set of Partial differential equations (PDEs) to nonlinear Ordinary differential equations (ODEs) and further solved by the homotopy analysis method (HAM). Numerical simulation using Schmidt number, magnetic, Casson, Brownian movement, and thermophoresis parameters on outspread, temperature, tangential velocities, and nanoparticles are portrayed. Local Nusselt number, Skin friction, and Sherwood number are plotted and investigated. The graphical results show that the tangential velocity of nanofluids decreases because of an addition in Reynolds' number, while the radial velocity displays the converse patterns. The tangential and radial velocities reduce with the increment magnetic factor. It is also perceived that an augmentation in estimations of radiation parameters enhances the heat transfer rate. Increasing the values of non-dimensional activation energy raises the mass transfer rate.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Nomenclature
| Symbol | Discription |
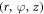
| Polar coordinates |
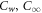
| Concentration near and far away the surface respectively |
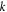
| Thermal conductivity |
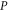
| Pressure (dimensionless) |

| Concentration and temperature of the fluid respectively |
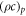
| Effective heat capacity of nanoparticles |
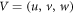
| Velocity field |
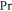
| Prandtl number |
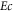
| Eckert number |
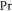
| Prandtl number |

| Schmidt number |
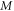
| Magnetic field constraint |
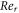
| Reynolds number |
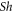
| Sherwood number |
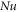
| Nusselt number |

| Skin friction coefficient |

| Temperatures near and far away the surface respectively |
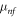
| Dynamic viscosity of nanofluid |
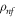
| Density of nanofluid |
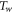
| Surface temperature |

| Surface concentration |
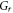
| Grashof number |
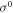
| Stefan-Boltzmann constant |
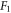
| Inertia coefficient |
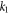
| Porosity parameter |
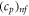
| specific heat at constant pressure of nanoparticles |
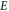
| Nondimensional activation energy |
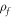
| Density |
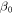
| Applied magnetic field |

| Velocity slip parameter |
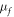
| Dynamic viscosity |
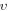
| Kinematic viscosity |
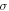
| Electrical conductivity |

| Thermal slip parameter |

| Temperature difference parameter |
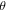
| Fluid temperature (dimensionless) |
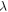
| Casson fluid parameter |
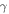
| Concentration slip parameter |
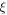
| Similarity variable |
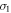
| Chemical reaction constraint |
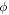
| fluid concentration (dimensionless) |
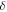
| Temperature difference parameter |
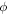
|
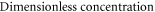
|
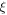
| Similarity variable |
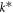
| permeability of porous medium |

| Thermal conductivity of nanofluid |
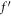
|
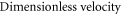
|
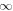
| Ambient condition |
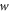
| Condition on surface |
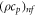
| volumetric heat capacity of nanofluid |
| ' | Differentiate with respect to ξ |
| R | Radiation parameter |
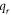
| Rosseland approximation |
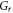
| Grashof number |
1. Introduction
Nanofluids have increased wonderful consideration from scientists because of their rousing warmth move in different modern and manufacturing applications. Basic working liquids, for example, water, ethylene glycol, and motor oils have confined warm exhibitions which bound their use in cutting edge cooling solicitations. Nanofluids comprise nanoscale particles, for example, alumina, copper, metal oxides, carbon nanotubes, carbides, and nitrides which improve the warm conductivity of base liquids. These nanofluids have broad uses in present-day frameworks of warming and freezing, hybrid-powered engines, sunlight based cells, cancer therapy, and generation of new fuels, drug delivery, and medication. The major effort on nanofluid was structured by Choi [1] which was also got in altered behaviors. Because of these different uses of nanofluids, numerous investigations related to the progression of nanofluids have been led. For representation, Prasannakumara et al [2] have inspected the limit stratum stream and warmth move of liquid elements deferral with nanoparticles above a nonlinearly extending slip. The intriguing slip highlights of thermophoresis development and Brownian movement were inspected by Buongiorno [3]. The exceptional contour aspects of different nanoparticles over a warmed divider stream have been concentrated by Turkyilmazoglu [4]. Bhatti and Rashidi [5] incorporated the possible effects of bottle dissemination and warm contamination inflow of Williamson nanofluid over a permeable extending surface.
Table 1. Effect of different physical factors over 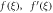 and g(ξ) when
and g(ξ) when 
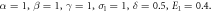
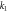
| λ | Rer | M |

|
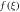
|

|

|
|---|---|---|---|---|---|---|---|
| 0.1 | 0.3 | 1 | 0.5 | 2 |

|

|
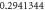
|
| 1.0 |
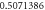
|
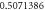
|
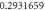
| ||||
| 1.2 |

|
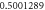
|

| ||||
| 0.4 |
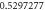
|
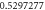
|
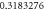
| ||||
| 0.5 |
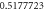
|
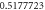
|

| ||||
| 0.7 |
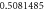
|

|

| ||||
| 2 |
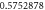
|

|

| ||||
| 3 |
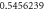
|
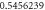
|
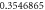
| ||||
| 4 |
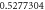
|
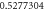
|
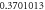
| ||||
| 0.6 |
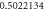
|
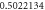
|
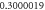
| ||||
| 1.1 |
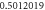
|
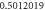
|

| ||||
| 1.6 |
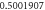
|
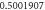
|

| ||||
| 4 |
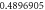
|
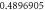
|
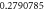
| ||||
| 5 |
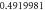
|
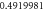
|

| ||||
| 6 |
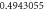
|
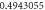
|

|
Further, magnetohydrodynamics (MHD) is a field of liquid mechanics that incorporates the marvels emerging when an attractive field is applied to an electrically leading liquid. The examination in the field of MHD grew exceptionally quick as of late (Davidson [6]). The investigation of stream and warmth move of an electrically leading liquid within the sight of a magnetic field past a warmed surface has applications in assembling procedures, for example, the nuclear reactor, cooling of the metallic plate, expulsion of polymers, and so on. The MHD stream in electrically leading liquid can control the pace of warmth move at the surface and subsequently wanted cooling impact can be accomplished. Xie and Jian [7] talked about the MHD two-layer electroosmotic flow with entropy age through small scale equal channels. Khan et al [8] inspected the 3D steady MHD stream of Powell Eyring nanofluid with convective and nanoparticles mass flux circumstances. Ellahi et al [9] inspected warmth spread in a limit level stream with MHD and entropy age impacts. Jawad et al have [10] have explored entropy age and warmth move examination in MHD unsteady turning stream for watery deferrals of carbon nanotubes with nonlinear current emission and viscous dissemination impact.
Table 2. Effect of different physical constraints over temperature profile 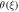 when
when 
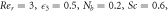

| Pr |
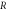
|
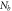
|
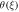
|
|---|---|---|---|
| 2.5 | 0.5 | 0.1 |
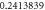
|
| 3.5 |

| ||
| 4.5 |

| ||
| 1.0 |
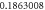
| ||
| 1. 3 |

| ||
| 1. 5 |
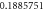
| ||
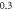
|

| ||
| 0.4 |
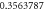
| ||
| 0.7 |
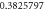
|
The issue of the liquid stream over a pivoting circle is one of the classical problems in liquid mechanics, which has both hypothetical and pragmatic qualities. Numerous sorts of examination have been completed on flow over a turning plate in hypothetical orders and because of various pragmatic applications in certain zones, for example, electronic gadgets, pivoting apparatus, gas turbine rotors, turning air cleaning machines, food handling, precious stone development procedures, and clinical equipment, such stream is additionally significant in the industrial forms. The imaginative thought of a thin-film flow through a turning circle was first detailed by Emslie et al [11]. By seeing the stability between viscid and outward strength throughout the plate turn course permit them to streamline the leading conditions and presumed that the film consistency holds as it flimsy increasingly more ceaselessly. In the electrical business, the appropriateness of the turn covering procedure was investigated through exploratory translations and hypothetical examinations by Washo [12]. Jenekhe [13] and Flack et al [14] broadened crafted by Emslie et al [11] by fusing the bulk exchange and non-Newtonian liquid models. The came about oily conditions were handled with a finite difference structure. Wang et al [15] concentrated arithmetically on the issue of the fluid thin film created above an accelerating pivoting plate. The asymptotic arrangement on account of values of quickening, slim and dense constraints was likewise acquired. Andersson et al [16] gained the mathematical just as the asymptotic arrangement of fluid thin film stream because of a turning circle with attractive field impacts. The integration pattern is useful to tackle the streaming unruly because a pivoting plate including the alterations as recommended by von Karman [17] was analyzed by Cochran [18]. Mellor et al [19] considered the stream between a fixed and a turning plate, which clarifies that there can be numerous answers for Re according to their arithmetical calculation. The specific arithmetical result for the warmth interchange tool between two co-pivotal turning plates was clarified by Arora and Stokes [20]. Darcy-Forchheimer model for nanoliquids comprising CNTs as nanoparticles is used by Hayat et al [21] to clarify the stream designs because of the disk turn with partial slip. Selimefendigil et al [22] mathematically investigated the blended convective MHD CuO-nanofluid move over an adaptable walled lid-driven enclosure in the presence of volumetric heat optimization by incorporating the impact of Brownian motion. Turkyilmazoglu [23] researched the arrangement of an electrically directing liquid stream and broadened the Karman viscid pump problem by captivating the stream over an outwardly extendible turning plate affected by a uniform vertical attractive impact and inspected the attractive consequences for the stream. The consistent progression of an incompressible force law liquid because of a pivoting vast plate was concentrated by Ming et al [24]. Ali et al [25] examined the MHD mixed convective Cu-water nanoliquid flow because of a turning rounded cylinder through a trapezoidal container saturated with a permeable medium. Asma et al [26] have inspected magnetohydrodynamic viscous nanoliquid 3D stream by whirling plate with thermal immersion/generation, binary chemical response, and Arrhenius actuation vitality. Ahmed et al [27] have thought unstable thin leading film of Maxwell nanofluid stream over a turning circle within the sight of nonlinear warm radiation, variable attractive field, and Joule heating. Tulu et al [28] have considered CNTs with ethylene glycol nanofluid stream and warmth move because of the stretchable pivoting circle with the Cattaneo Christov heat flux model. Jawad et al have [29] have portrayed a 3D MHD nanofluid thin-film stream with warmth and mass exchange over a slanted permeable pivoting disk.
Table 3. Effect of various physical factors over concentration profile  When
When 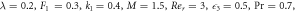


|
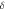
|
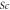
|
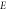
|

|
|---|---|---|---|---|
| 0.3 | 1.0 | 0.7 | 0.1 |
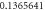
|
| 0.4 |
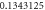
| |||
| 0.5 |

| |||
| 2.0 |

| |||
| 3.0 |
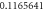
| |||
| 3.5 |
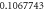
| |||
| 1.0 |

| |||
| 1. 3 |

| |||
| 1.6 |

| |||
| 0.3 |
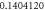
| |||
| 0.4 |

| |||
| 0.5 |
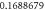
|
Gajjela et al [30] presented a diverse convection stream of stagnation—point couple stress nanofluid with an extending cylinder. The effects of flexible thermal conductivity, viscid heating, and an inside heat source are furthermore examined. Magagula et al [31] have investigated the double dispersed bioconvection phenomena for a Casson nanofluid flow over a nonlinearly stretching sheet. Nayaka et al [32] have examined a fixed and active tactic on thermal study on Darcy–Forchheimer flow of copper–water nanofluid related with non-linear thermal radiation and entropy minimization because of a turning disk. Shaw et al [33] have analyzed the Marangoni flow with microgravity and earth gravity, which causes undesirable effects in crystal growth experiments. Noor et al [34] deliberated magnetohydrodynamic Casson nanofluid squeezing flow with velocity slip in a permeable medium under the effect of chemical reaction and viscous dissipation. Buongiorno's nanofluid model is in this study. Noor et al [35] explored an unsteady squeezing flow of magnetohydrodynamic (MHD) Casson nanofluid with thermal radiation, heat generation/absorption effects and chemical reaction. The effects of joule and viscous dissipation are also scrutinized.
The key purpose of the existing article is to discuss the three-dimensional Casson nanofluid under influences of Arrhenius stimulation energy and thermal radiation. The flow is induced by a turning disk. Temperature, velocity, and concentration slips at the outward of the turning disk are deliberated. Brownian motion and thermophoresis is assessed by seeing nanosized particles in a Casson fluid dispersed over the turning disk. We used appropriate transformations methods for reducing a set of Partial differential equations (PDEs) to nonlinear Ordinary differential equations (ODEs) which were further corroborated by the homotopy analysis method (HAM). Numerical perceptions using Schmidt number, magnetic, Casson, Brownian movement, and thermophoresis parameters focus on outspread, temperature, tangential velocities, and nanoparticle focus are portrayed.
Table 4. Influence of various physical factors over Skin friction 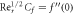 and
and  when
when 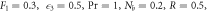
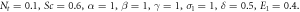
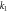
|

|
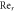
|
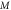
|
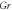
|
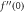
|
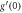
|
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 1.0 | 0.1 | 2.0 |

|
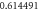
|
| 1.0 |
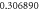
|
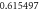
| ||||
| 1.2 |
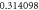
|
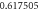
| ||||
| 0.4 |

|
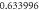
| ||||
| 0.5 |
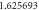
|
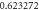
| ||||
| 0.6 |
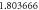
|
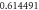
| ||||
| 2.0 |
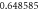
|
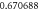
| ||||
| 3.0 |
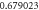
|
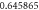
| ||||
| 4.0 |

|

| ||||
| 0.5 |
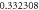
|
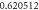
| ||||
| 1.1 |
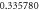
|

| ||||
| 1.6 |
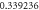
|
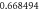
| ||||
| 4.0 |
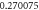
|
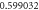
| ||||
| 5.0 |
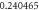
|
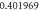
| ||||
| 6.0 |
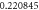
|

|
2. Problem formulation
The present study investigates the MHD steady 3D progression of Casson nanoliquid has quipped above pivoting disk for z > 0. Thermal radiation impacts and Arrhenius activation energy are presented.
Brownian motion and thermophoretic impact additionally exist. Magnetic field 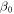 is applied in z-direction (see figure 1). The velocity
is applied in z-direction (see figure 1). The velocity 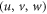 is in the directions of
is in the directions of 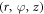 correspondingly.
correspondingly.
Figure 1. Graphic demonstration of the flow.
Download figure:
Standard image High-resolution imageThe governing equations of the said problem are:
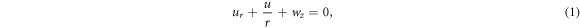
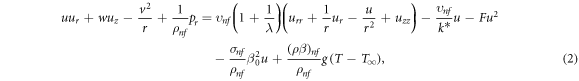
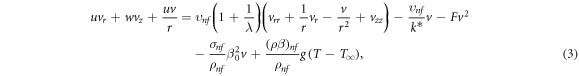
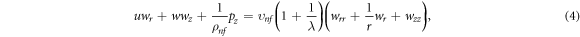


The BCs are [26]:
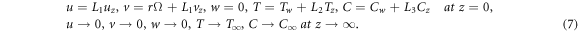
The variables for problem [26]

Using equation (8) in equations (1)–(6) take the form:

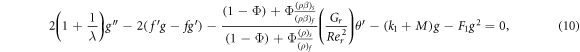

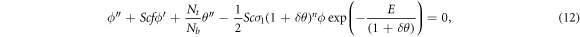
Similarly using equation (8) in equation (7) the subjected BCs are transformed as;
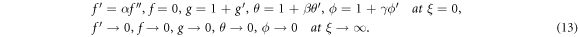
The dimensionless quantities are defined as:

Above the symbols 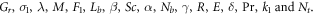 are denote Grashof number, chemical reaction parameter, Casson factor, magnetic parameter, inertia coefficient, thermal slip, velocity slip constraint, Schmith number, Brownian movement, concentration slip factor, radiation factor, nondimensional activation energy, temperature difference, Prandtl number, porosity parameter and for thermophoretic factor.
are denote Grashof number, chemical reaction parameter, Casson factor, magnetic parameter, inertia coefficient, thermal slip, velocity slip constraint, Schmith number, Brownian movement, concentration slip factor, radiation factor, nondimensional activation energy, temperature difference, Prandtl number, porosity parameter and for thermophoretic factor.
3. Physical quantities of interest
The skin friction  Sherwood
Sherwood 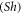 and Nusselt numbers
and Nusselt numbers 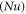 are:
are:
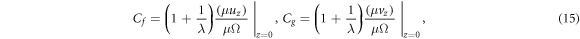
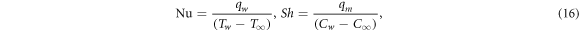
Where  are, wall heat flux and wall mass flux, respectively, and are given by
are, wall heat flux and wall mass flux, respectively, and are given by
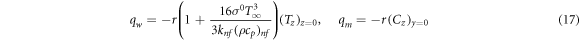
Using equation (8), one obtains [30]

Where 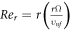 is the local Reynolds number.
is the local Reynolds number.
4. Analytical method
An ideal analytical of homotopy analysis method (HAM) is implemented to obtain the solution for fluid velocity, temperature and concentration. Equations (9)–(12) with boundary conditions (13) are solved by HAM. For this point, we used the Mathematica programming. The initial conditions are selected as follows
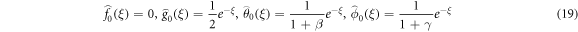
The essential inference of the model equation is given below.
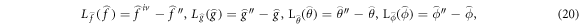
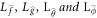 are suggested as
are suggested as
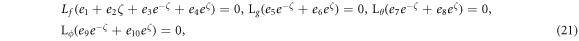
The non-linear operatives are rationally chosen as 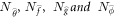 and organize:
and organize:

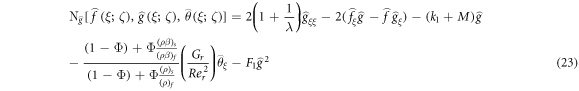
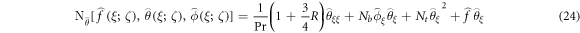
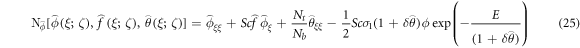
For equations (9)–(12) the 0th-order system is written as

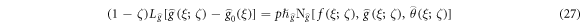
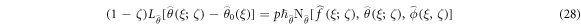

Whereas BCs are:
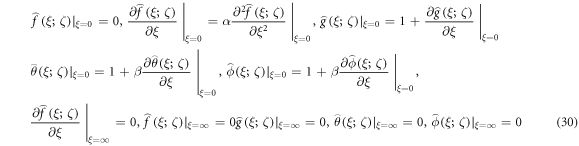
While the implanting constraint is ![$\zeta \in [0,1],$](https://content.cld.iop.org/journals/2399-6528/5/2/025008/revision5/jpcoabe4e0ieqn197.gif) to regulate for the solution convergence
to regulate for the solution convergence 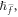
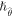 and
and 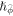 are utilized. When
are utilized. When 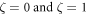 we have:
we have:
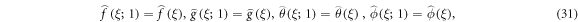
Enlarge the  and
and  over Taylor's series for
over Taylor's series for 
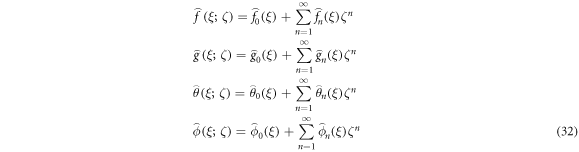
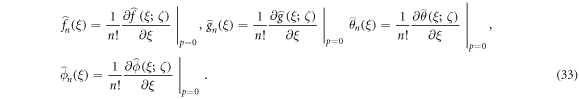
Whereas BCs are:
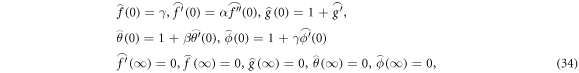
Now

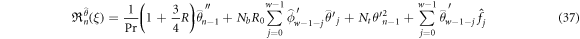
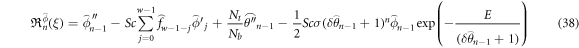
While
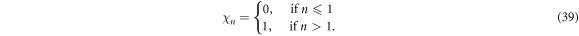
5. Results and discussions
The different outcomes of the current examination are displayed graphically.
5.1. Velocity distribution
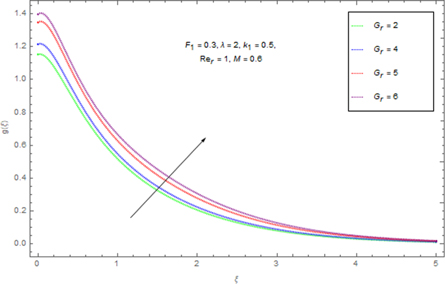
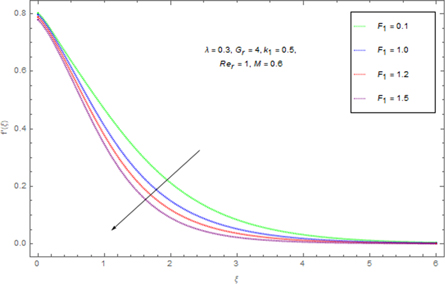
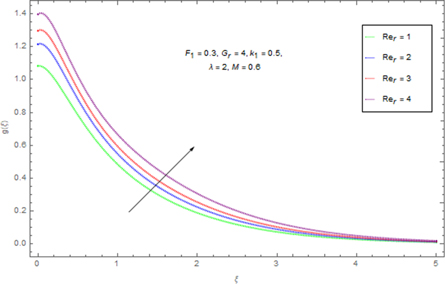
Figure 1 denoted the schematic depiction of the flow problem. Figure 2 describes the variation of the spiral segments of velocity distribution for several Gr due to turning disk. This demonstrates velocity profiles expand with enlargement of Gr for both radiative nanofluids. Greater Gr accounts for the larger diversities of the comparative spiral velocity components compared with the smaller Gr case. Figure 3 illustrates the diversity of the tangential segment of g(ξ) for nanoliquid past a whirling plate. It is perceived that g(ξ) upsurges due to the development of Gr for nanoliquid. But, noteworthy relative g(ξ) display as we transfer from the exterior of the plate towards the ambient liquid. Figure 4 depicts the g(ξ) for nanofluid because of various qualities of the permeable matrix. Augmentations in k1 produce a decrease in g(ξ). Figure 5 shows the reaction of f'(ξ) for different values of the inertia coefficient F1 past a pivoting plate. It is uncovered from the figure that increases in F1 a decrease f'(ξ) for nanofluid. Nonetheless, the decaying of f'(ξ) is bigger for higher F1. Then, the comparative velocity of f'(ξ) for nanofluid of concern for all F1 is irrelevant. Elevated F1 outcomes in easing g(ξ) profiles all through the stream system. However, higher estimations of F1 lead the bigger falls of g(ξ) in figure 6. Figure 7 shows the distinctive highlights of f'(ξ) for nanoliquid for different Rer
due to the pivoting disk. Obviously f'(ξ) is a falling capacity of Rer
. Figure 8 outlines the behavior of g(ξ) for numerous Rer
due to the prolonging of the whirling plate. This state g(ξ) is an intensifying the volume of Rer
for the two sorts of nanoliquid. Various estimations of Rer
set up discrete layers of profiles of g(ξ). Expanded Rer
upgrades g(ξ) for nanofluid. Amplification is higher more prominent Rer
for nanofluid. The fairly bigger relative velocity of g(ξ) is attained for higher Rer
. Figures 9 and 10 are considered to scrutinize the effect of λ on CF. It is clear from these figures 9 and 10 that increasing the value of λ results in lessening liquid velocity which resist the fluid flow. As Casson factor approaches larger estimations, liquid jumps to act like a Newtonian fluid. Physically, an upsurge in λ means  a decline in the yield stress, hence a decrease in boundary layer thickness is noted.
a decline in the yield stress, hence a decrease in boundary layer thickness is noted.
Figure 2. Effect of Gr on f'(ξ).
Download figure:
Standard image High-resolution imageFigure 3. Impact of Gr on g(ξ).
Download figure:
Standard image High-resolution imageFigure 4. Impact of k1 on g(ξ).
Download figure:
Standard image High-resolution imageFigure 5. Outcome of F1 on f'(ξ).
Download figure:
Standard image High-resolution imageFigure 6. Impact of F1 on g(ξ).
Download figure:
Standard image High-resolution imageFigure 7. Impact of Rer on f'(ξ).
Download figure:
Standard image High-resolution imageFigure 8. Impact of Rer on g(ξ).
Download figure:
Standard image High-resolution imageFigure 9. Effect of λ on f'(ξ).
Download figure:
Standard image High-resolution imageFigure 10. Impact of λ on g(ξ).
Download figure:
Standard image High-resolution imageTable 5. Validation of result by comparisons of result for Nusselt number with past results.

|
|
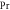
|
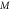
|
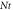
|

|
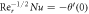
|

|
|---|---|---|---|---|---|---|---|
| Present Result | Past Result [30] | ||||||
| 0.2 | 0.32662 | 0.32660 | |||||
| 0.5 | 0.30365 | 0.30363 | |||||
| 0.8 | 0.28727 | 0.28724 | |||||
| 0.0 | 0.30503 | 0.30502 | |||||
| 0.7 | 0.24435 | 0.24434 | |||||
| 1.4 | 0.17577 | 0.17575 | |||||
| 0.5 | 0.25000 | 0.24999 | |||||
| 1.0 | 0.29225 | 0.29224 | |||||
| 1.5 | 0.32296 | 0.32294 | |||||
| 0.1 | 0.46189 | — | |||||
| 0.5 | 0.46258 | — | |||||
| 0.9 | 0.46327 | — | |||||
| 0.5 | 0.25918 | 0.25916 | |||||
| 0.7 | 0.23880 | 0.23879 | |||||
| 1.0 | 0.21026 | 0.21025 | |||||
| 0.5 | 0.26360 | 0.26358 | |||||
| 0.7 | 0.23689 | 0.23687 | |||||
| 1.0 | 0.20069 | 0.20068 |
5.2. Temperature profile 
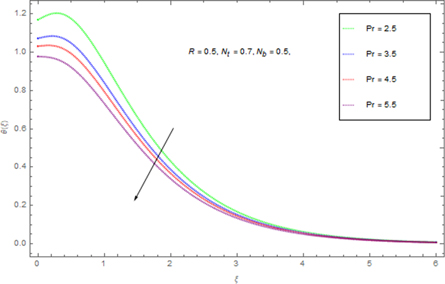
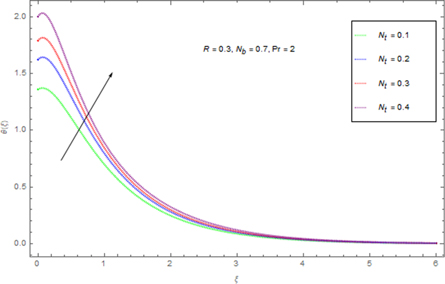
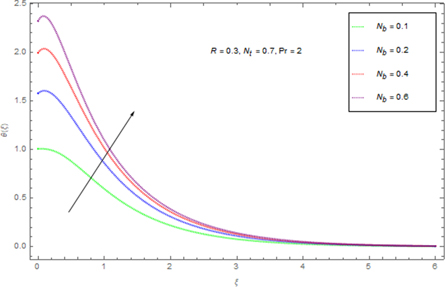
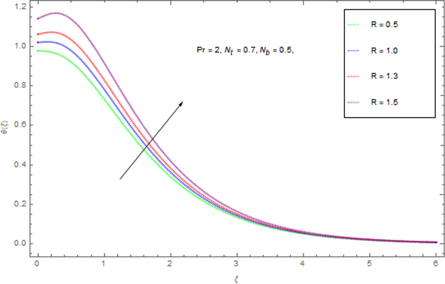
Figure 11 presents an assortment in the temperature field θ(ξ) for contrasting Pr. Here θ(ξ) is reduced through Pr. Advanced guesses of Pr yield progressively delicate updraft diffusivity which thinks about to a decline in thermal level. Temperature of the fluid diminishes for greater Pr because with a growing Pr the thermal diffusivity decreases. In fact, the particles are able to conduct less heat, and subsequently temperature declines. The impression o Nt on θ(ξ) is delineated in figure 12. As the thermophoresis factor rises, the profiles jump stirring away from the boundary exemplifying a development in the thermal boundary layer thickness. Figure 13 portrays assortment in temperature θ(ξ) for indisputable guesses of Brownian development Nb . Physically an uneven motion of nanoparticles develops by growing Brownian movement constraint because of which collision of particles occurs. As an outcome, kinetic energy is altered into heat energy which causes augmentation in heat distribution and allied layer wideness. Figure 14 shows a graphical portrayal of the θ(ξ) of radiative nanofluids for various radiation parameters R due to the spreading of the porous whirling plate. By upgrade of R expansions the non-dimensional liquid temperature θ(ξ), prompting rising related layers for nanofluid. For increasing values of R, θ(ξ) significantly increases for nanofluid.
Figure 11. Effect of Pr on θ(ξ).
Download figure:
Standard image High-resolution imageFigure 12. Influence of Nt on θ(ξ).
Download figure:
Standard image High-resolution imageFigure 13. Outcome of Nb on θ(ξ).
Download figure:
Standard image High-resolution imageFigure 14. Effect of R on θ(ξ).
Download figure:
Standard image High-resolution image5.3. Concentration profile 
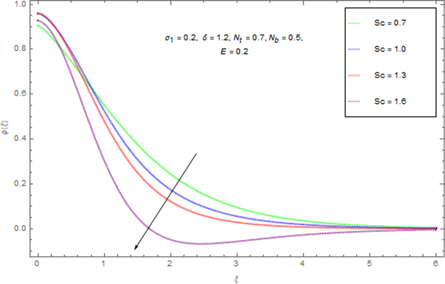
Since figure 15, shows that the bigger Schmidt Sc displays decline in concentration ϕ(ξ). Figure 16 shows that how thermophoresis Nt
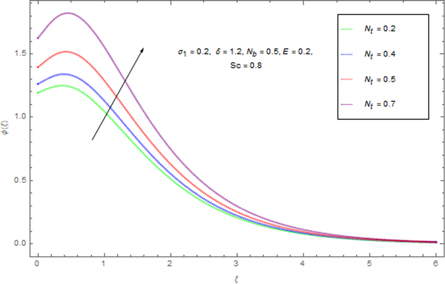
impacts ϕ(ξ). By enlightening Nt
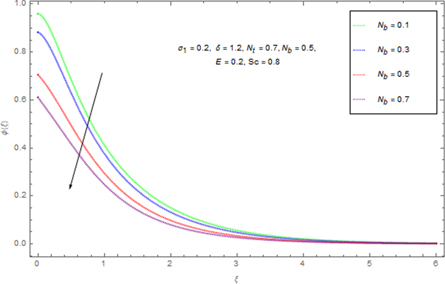
, the ϕ(ξ) and connected layer are prolonged. Figure 17 depicts the influence of Brownian enlargement Nb
on ϕ(ξ). It is obviously perceived that a decreasingly delicate ϕ(ξ) is conveyed by using a higher Brownian improvement Nb
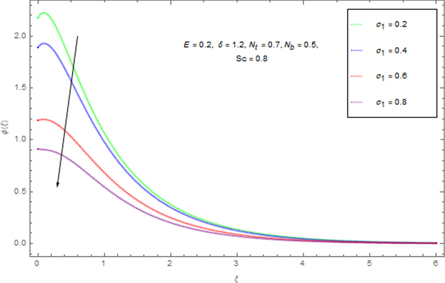
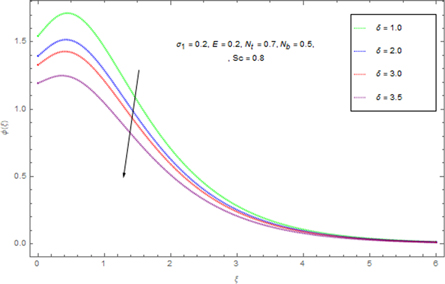
. Figure 18 elucidates the effect of non-dimensional E on concentration ϕ(ξ). An enhancement in actuation vitality E decays modified Arrhenius work  The Arrhenius activation energy is characterized as the minimum energy required beginning a chemical response and it is for the most part meant by. It very well may be additionally characterized as the height of the potential obstruction (energy hindrance) isolating two minima of the possible energy of the products and reactants in a response. Figure 19. Shows the effect of chemical response factor on the concentration field. Chemical response upsurges the rate of interfacial mass transfer. The reaction decreases the local concentration, thus amassed the concentration gradient and its flux. As an outcome, the concentration of the chemical species in the boundary layer drops with an intensification in chemical reaction constraint. Figure 20 clarifies the effect of δ on ϕ(ξ). Here ϕ(ξ) is viewed as a reducing limit of δ.
The Arrhenius activation energy is characterized as the minimum energy required beginning a chemical response and it is for the most part meant by. It very well may be additionally characterized as the height of the potential obstruction (energy hindrance) isolating two minima of the possible energy of the products and reactants in a response. Figure 19. Shows the effect of chemical response factor on the concentration field. Chemical response upsurges the rate of interfacial mass transfer. The reaction decreases the local concentration, thus amassed the concentration gradient and its flux. As an outcome, the concentration of the chemical species in the boundary layer drops with an intensification in chemical reaction constraint. Figure 20 clarifies the effect of δ on ϕ(ξ). Here ϕ(ξ) is viewed as a reducing limit of δ.
Figure 15. Result of Sc on ϕ(ξ).
Download figure:
Standard image High-resolution imageFigure 16. Outcome of Nt on ϕ(ξ).
Download figure:
Standard image High-resolution imageFigure 17. Outcome of Nb on ϕ(ξ).
Download figure:
Standard image High-resolution imageFigure 18. Impact of E on ϕ(ξ).
Download figure:
Standard image High-resolution imageFigure 19. Effect of σ1 on ϕ(ξ).
Download figure:
Standard image High-resolution imageFigure 20. Impression of δ on ϕ(ξ) w.
Download figure:
Standard image High-resolution image6. Table discussions
Table 1 defined the influence of 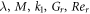 axial velocity
axial velocity  and tangential velocity
and tangential velocity  For growing estimation
For growing estimation 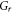 axial velocity
axial velocity 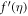 and tangential velocity
and tangential velocity 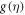 are upsurges, for amassed estimation of
are upsurges, for amassed estimation of 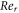 tangential components of velocity
tangential components of velocity  is upsurges and declines both
is upsurges and declines both  and
and  for amassed estimations of
for amassed estimations of  for amassed approximation of
for amassed approximation of 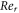 axial
axial  is diminishes. Table 2 designates the effect of
is diminishes. Table 2 designates the effect of  on
on  By cumulative estimations of
By cumulative estimations of 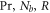 temperature are upsurges for
temperature are upsurges for  and decreases for Pr. Table 3 displays the effect of
and decreases for Pr. Table 3 displays the effect of 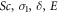 on
on 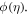 For amassed estimations of E concentration is an upsurge and declines for
For amassed estimations of E concentration is an upsurge and declines for  Table 4, examine the influence of
Table 4, examine the influence of 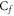 and
and  in the impact of different factors. The possessions of
in the impact of different factors. The possessions of 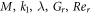 on skin friction for the dissimilar approximations are presented in table 4. It is observed that the growing values of
on skin friction for the dissimilar approximations are presented in table 4. It is observed that the growing values of 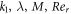 upsurges the
upsurges the 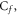 while
while  is decreases function of
is decreases function of  It is supposed that the amassed values of
It is supposed that the amassed values of 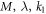 upsurges the
upsurges the  while
while 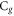 is decreases function of
is decreases function of  We have analyzed the variety of Nusselt and Sherwood numbers with their outcomes as appeared in tables 5 and 6. We can understand from these tables our results tie with present values from a constraining perspective. The trivial difference is because of the decision of the numerical method utilized in both efforts. Their estimations are acquired by utilizing an algorithm (shooting method with R-K scheme) while we have utilized the homotopy analysis method in Mathematica subject to Casson nanofluid stream actuated by the solid turning disk.
We have analyzed the variety of Nusselt and Sherwood numbers with their outcomes as appeared in tables 5 and 6. We can understand from these tables our results tie with present values from a constraining perspective. The trivial difference is because of the decision of the numerical method utilized in both efforts. Their estimations are acquired by utilizing an algorithm (shooting method with R-K scheme) while we have utilized the homotopy analysis method in Mathematica subject to Casson nanofluid stream actuated by the solid turning disk.
Table 6. Validation of result by comparisons of result for Sherwood number with past results.
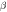
|
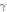
|
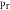
|

|

|
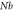
|

|
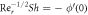
|
|---|---|---|---|---|---|---|---|
| Present Result | Past Result [30] | ||||||
| 0.2 | 0.27595 | 0.27593 | |||||
| 0.5 | 0.26947 | 0.26945 | |||||
| 0.8 | 0.26499 | 0.26498 | |||||
| 0.0 | 0.27013 | 0.27012 | |||||
| 0.7 | 0.25396 | 0.25394 | |||||
| 1.4 | 0.23737 | 0.23735 | |||||
| 0.5 | 0.22945 | 0.22944 | |||||
| 1.0 | 0.26638 | 0.26636 | |||||
| 1.5 | 0.31278 | 0.31276 | |||||
| 0.1 | 0.23052 | — | |||||
| 0.5 | 0.23137 | — | |||||
| 0.9 | 0.23221 | — | |||||
| 0.5 | 0.22216 | 0.22215 | |||||
| 0.7 | 0.22565 | 0.22564 | |||||
| 1.0 | 0.22289 | 0.22288 | |||||
| 0.5 | 0.30344 | 0.30342 | |||||
| 0.7 | 0.31889 | 0.31887 | |||||
| 1.0 | 0.32979 | 0.32978 |
7. Conclusions
This article's expected major results include:
- Higher Magnetic field show diminishing pattern for
 and
and 
- Increases in values of
 represent a decreasing in
represent a decreasing in  and
and 
- Higher values of
 express an increasing in
express an increasing in  and
and 
- Increments in Rer
represent a decreasing in
 and inverse impact for
and inverse impact for 
- Advanced Pr relates to more fragile temperature.
- Concentration
 is a diminishing component of higher Sc.
is a diminishing component of higher Sc. - Greater E displays more concentration

- Higher R shows an increasing pattern for the

- Concentration
 portrays diminishing conduct for bigger δ and σ1.
portrays diminishing conduct for bigger δ and σ1. - Stronger temperature dissemination is perceived for Nb and Nt .
- Concentration
 shows inverse behavior for Nb
and Nt
.
shows inverse behavior for Nb
and Nt
. - Concentration
 is a diminishing component of higher
is a diminishing component of higher 
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Funding statement
The author(s) received no specific funding for this study.
Conflict of interest
The authors have no conflict of interest.