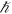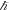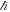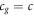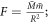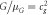Abstract
In this paper, we will demonstrate, based on reasoning as well as mathematical evidence and experimental observations, why Newtonian gravity moves at the speed of light and is not, as previously thought, instantaneous. The misunderstanding that Newtonian gravity is instantaneous has constrained our progress in understanding gravity to its full extent. We will show that all of Newton's gravitational phenomena contain the Planck length and the speed of gravity; this speed of gravity is identical to the speed of light. A series of gravitational phenomena that are considered to be non-Newtonian and most often explained by the theory of general relativity actually contain no information about the speed of gravity. However, all observable gravitational phenomena which we will look at here can be predicted from the Planck length and the speed of gravity alone, and we can easily extract both of them from gravitational phenomena with no knowledge of any physics constants. In addition, we can also measure the speed of light from electromagnetic phenomena and then extract the Planck length from any of Newton's gravitational phenomena with no knowledge of G or 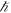 .
.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Background
Today, Newton's formula for gravitational force is well-known as:
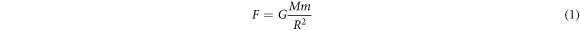
where G is Newton's gravitational constant, M and m are two masses, and R is the distance center to center between the two masses. This is perhaps the second most commonly known physics formula after Einstein's  . Therefore, one might think there is nothing new to discover about it. However, such a view will be strongly challenged in this paper. It seems clear from the formula that gravity is a function of the masses and the distance between them. The speed of light (or any other speed) does not appear anywhere in the formula and one soon gets the impression that Newton's gravitational force formula: 1) says nothing about the speed of gravity, and 2) would be inconsistent with a finite speed of gravity. This was highlighted by Good in 1975 [1], for example:
. Therefore, one might think there is nothing new to discover about it. However, such a view will be strongly challenged in this paper. It seems clear from the formula that gravity is a function of the masses and the distance between them. The speed of light (or any other speed) does not appear anywhere in the formula and one soon gets the impression that Newton's gravitational force formula: 1) says nothing about the speed of gravity, and 2) would be inconsistent with a finite speed of gravity. This was highlighted by Good in 1975 [1], for example:
"We may fairly conclude that a finite rate of propagation of gravitation is inconsistent with Newton's inverse square law or any other force that is function of distance only."
This reflects the view held in modern physics to this day, and is also the dominant line of thought in standard university textbooks on gravity, for example [2, 3]. At first glance, the argument looks fully valid and sound, but as we will later see, it is, in fact, flawed due to a failure to understand the Newtonian gravitational formula in depth. Another argument often used to claim that Newton's gravitational force is instantaneous—and therefore that the speed of gravity is infinite—is from the so-called Newtonian field equation, which is derived from the Gaussian law. This is given by

where Mi
is the mass inside the Gauss surface, and  is the gravitational acceleration vector. This can also be written in differential form (the Poisson equation) as
is the gravitational acceleration vector. This can also be written in differential form (the Poisson equation) as
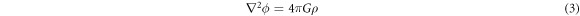
Here ϕ is the gravitational field, a scalar field, and ρ is the mass density. It seems that if one changes the mass density, then the gravitational field will change instantaneously. It has, therefore, been concluded that Newtonian gravity is instantaneous, and it implicitly assumes that the speed of gravity moves at an infinite speed; see [4], for example, who states: "In Newton's theory of gravity, perturbations in the gravitational field propagate at infinite speed." This view reflects the consensus on gravity among researchers in the field. The same idea is conveyed in popular media platforms such as Wikipedia: "In modern terms, Newtonian gravitation is described by the Poisson equation, according to which, when the mass distribution of a system changes, its gravitational field instantaneously adjusts. Therefore, the theory assumes the speed of gravity to be infinite.", Wikipedia 17 Jan 2021. We are not quoting Wikipedia for its reliability in scientific information, but simply to show this assumption that the speed of gravity in Newton is infinite is widespread across scientific journals and also among "popular-science" distributors.
Laplace [5], in 1805, may have been the first to indicate that Newtonian gravity might be infinite in velocity. In 1890, Maurice Lévy [6] was potentially the first to suggest that the speed of gravity is equal to the speed of light, and in 1904, Poincare [7] argued that, based on relativity theory, the speed of gravity could not be faster than the speed of light in a vacuum.
The speed of light in Einstein's [8] theory of general relativity is assumed to be the same as the speed of light in a vacuum, see also [9, 10]. For many years, there has been a considerable debate over whether the speed of gravity is the same as the speed of light, or if it is significantly different, see [11–13]. Recent experimental research [14] has been able to determine the difference between the speed of gravity and the speed of light as being between 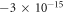 and
and 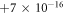 times the speed of light. Therefore, the speed of gravity is very likely to be equal to the speed of light, as predicted by general relativity. However, if that is the case then one might ask, "How can a theory that assumes the infinite speed of gravity still be so accurate for many gravitational phenomena, particularly since Newton's infinity is much higher than the speed of light. Does this mean that Newtonian gravitational phenomena, such as the orbital velocity of the Moon, is independent, or close to independent, of the velocity of gravity?" We will answer this and many other questions related to the speed of gravity in this paper.
times the speed of light. Therefore, the speed of gravity is very likely to be equal to the speed of light, as predicted by general relativity. However, if that is the case then one might ask, "How can a theory that assumes the infinite speed of gravity still be so accurate for many gravitational phenomena, particularly since Newton's infinity is much higher than the speed of light. Does this mean that Newtonian gravitational phenomena, such as the orbital velocity of the Moon, is independent, or close to independent, of the velocity of gravity?" We will answer this and many other questions related to the speed of gravity in this paper.
Returning to Newton's formula for gravitational force, equation (1) is actually not the formula Newton presented. The formula he showed [15] in Principia was simply
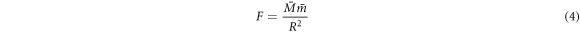
where  and
and 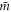 are the two masses. Here we are using a slightly different notation for mass than in equation (1) because Newton's definition of mass was not the same as the modern definition of mass. Newton actually only stated this formula through words (and not equations) in Principia [15]—which is to say, Newton neither invented, nor did he use, a gravitational constant. Even so, he was still able to predict such things as the relative mass between planets, see Principia and also [16]. It is often claimed that Cavendish [17] in 1798 was the first to measure Newton's gravitational constant, but in fact Cavendish did not mention, measure, or use a gravitational constant. Still, it is true that a Cavendish apparatus can indeed be used to find the value of the so-called Newton's gravitational constant, which was actually first introduced in 1873 by Cornu and Baille [18] in the formula
are the two masses. Here we are using a slightly different notation for mass than in equation (1) because Newton's definition of mass was not the same as the modern definition of mass. Newton actually only stated this formula through words (and not equations) in Principia [15]—which is to say, Newton neither invented, nor did he use, a gravitational constant. Even so, he was still able to predict such things as the relative mass between planets, see Principia and also [16]. It is often claimed that Cavendish [17] in 1798 was the first to measure Newton's gravitational constant, but in fact Cavendish did not mention, measure, or use a gravitational constant. Still, it is true that a Cavendish apparatus can indeed be used to find the value of the so-called Newton's gravitational constant, which was actually first introduced in 1873 by Cornu and Baille [18] in the formula  , where f was the gravitational constant. This is basically identical to Newton's gravitational force formula as we know it today. The current notation for the gravitational constant of G was possibly first introduced by Boys in 1894 [19]. Many scientists used the notation f for the gravitational constant well into the early 20th century; Max Planck, for example, employed it as late as 1928, [20]. Naturally, whether one uses the notation f or G for the gravitational constant is purely cosmetic. What is however important here is that the gravitational constant first came into existence in 1873, almost two hundred years after Newton introduced his formula for gravitational force, and also that "Newton's" gravitational constant is partly related to the fact that, in the 1870s, a definition of mass incorporating the kilogram came into use internationally (in various parts of the world).
, where f was the gravitational constant. This is basically identical to Newton's gravitational force formula as we know it today. The current notation for the gravitational constant of G was possibly first introduced by Boys in 1894 [19]. Many scientists used the notation f for the gravitational constant well into the early 20th century; Max Planck, for example, employed it as late as 1928, [20]. Naturally, whether one uses the notation f or G for the gravitational constant is purely cosmetic. What is however important here is that the gravitational constant first came into existence in 1873, almost two hundred years after Newton introduced his formula for gravitational force, and also that "Newton's" gravitational constant is partly related to the fact that, in the 1870s, a definition of mass incorporating the kilogram came into use internationally (in various parts of the world).
Nonetheless, it is important to understand that, in 1873, there was no clear understanding of what mass entailed at a deeper level. Newton himself had introduced the term mass in Principia and defined it as a quantity of matter ("quantities material"). Less well known among most researchers today is that Newton maintained the view that matter ultimately consists of indivisible particles with a spatial dimension, something he claimed in the third part of Principia, which concerns gravity, and this was the principle behind all of his philosophy. In Newton's view, mass had to be somehow linked to the quantity of these indivisible particles in a given object (or clump of matter). However, these particles were assumed to be extremely small, so there would be no way to observe them directly. In Principia, Newton also mentions indivisible time, or indivisible moments. Overall, it is not completely clear what mass is in Newton's theory, but he repeatedly points out in Principia that weight is proportional to the quantity of matter; in his own words,"I have always found that the quantity of matter to be proportional to their weight." So, if we know the weight of two bodies (measured at the same distance from a gravity object, e.g., Earth), then we know their relative mass. We can easily find the relative mass of planets and the Sun, for example, using Newton's principles without any knowledge of the misnamed gravitational constant that was introduced in 1873. The mass of the Earth relative to the Sun is given by
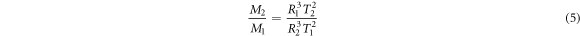
where T2 and T1 are the orbital times of the Moon around the Earth, and the Earth around the Sun, R2 is the distance from the center of the Earth to the Moon, and R1 is the distance from the center of the Sun to the Earth. We can find the distances with parallax, which was part of the method Newton used when he found the relative mass of the planets, as shown in Principia. The orbital time of the Moon around the Earth is approximately 27 days, and the orbital time of the Earth around the Sun is 365 days; the distance of the Earth to the Moon is approximately 384,400 km, and the distance of the Earth to the Sun is approximately 149,597,870 km. This gives us 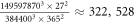 , which is basically the same as the well-known mass of the Sun relative to the Earth. Even in Newton's time, one could gauge the approximate diameter of the Earth and the Sun and Newton also calculated the relative density between the Earth and the Sun. In Principia, he gives the number 4, which is very close to today's measurement of 3.91. The point here is simply that we can complete many gravitational predictions using Newton's original theory, even without the gravitational constant.
, which is basically the same as the well-known mass of the Sun relative to the Earth. Even in Newton's time, one could gauge the approximate diameter of the Earth and the Sun and Newton also calculated the relative density between the Earth and the Sun. In Principia, he gives the number 4, which is very close to today's measurement of 3.91. The point here is simply that we can complete many gravitational predictions using Newton's original theory, even without the gravitational constant.
However, there was one significant challenge that Newton was not able to solve: finding the density of the Earth relative to a known uniform substance, such as water, lead, or gold. It would take another hundred years or so to accomplish this, which Cavendish was able to achieve in 1798 by using what is today known as a Cavendish apparatus. By means of this apparatus, Cavendish could measure the gravitational effect from a clump of a known uniform material (the large balls in the apparatus), such as iron, mercury, lead or gold. Then he could find the density of the Earth relative to this clump (sphere) of uniform known substance, but again this was accomplished with no knowledge of a gravitational constant. The gravitational constant G is needed when one defines mass as kilograms (kg), something which we will return to soon.
As noted previously, the adjusted Newtonian formula with a gravitational constant was first published in 1873. Sixteen years later, Max Planck [21, 22] assumed that there were three universal constants; the gravitational constant G, the Planck constant 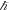 , and the speed of light c. Based on dimensional analysis, he then found a unique length
, and the speed of light c. Based on dimensional analysis, he then found a unique length 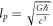 , time:
, time: 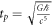 , and mass:
, and mass:  . These are today known as Planck units. It is worth mentioning that, in 1883, Stoney [23] had already used G, and c, as well as the elementary charge and the Coulomb constant to come up with similar natural units. However, the consensus among physicists today is that Planck units seem to be more essential than Stoney units—a view we share, and will also soon back up with derivations combined with observations and scientific arguments.
. These are today known as Planck units. It is worth mentioning that, in 1883, Stoney [23] had already used G, and c, as well as the elementary charge and the Coulomb constant to come up with similar natural units. However, the consensus among physicists today is that Planck units seem to be more essential than Stoney units—a view we share, and will also soon back up with derivations combined with observations and scientific arguments.
After publishing his theory of general relativity theory, in 1916, Einstein claimed that a quantum gravity theory was the natural next step; in his own words:
Because of the intra-atomic movement of electrons, the atom must radiate not only electromagnetic but also gravitational energy, if only in minute amounts. Since, in reality, this cannot be the case in nature, then it appears that the quantum theory must modify not only Maxwell's electrodynamics but also the new theory of gravitation.
In 1922, Eddington [24] suggested that the Planck length played a central role in a quantum gravity theory, stating:
But it is evident that this length (the Planck length) must be the key to some essential structure. It may not be an unattainable hope that someday a clearer knowledge of the process of gravitation may be reached.
Other prominent physicists such as Bridgman [25] (who received the 1946 Nobel Prize in Physics) ridiculed this idea and claimed the Planck units were merely mathematical artifacts coming out of dimensional analyses, see also [26]. Today, most physicists think the Planck length is the smallest possible length, see for example [27–29]. However, a minority of physicists, for example Unzicker [30] claim that Planck units are not useful. Unzicker bases his claim on the view that "there is not the remotest chance of testing the validity of the Planck units". His point is reminiscent of Einstein's claim relative to the ether: If the ether cannot be detected or lead to observable predictions, then why not simply abandon it?
Still, many physicists think that the Planck units probably do play an important role and have attempted to build theories incorporating them. One strain of super string theory, for example, assumes that there are only two universal fundamental constants, namely the Planck length and the speed of light [31], although such theories have not yet shown any breakthroughs in observable predictions and the jury is still out on this topic. Several quantum gravity theories predict that Lorentz symmetry will be broken at the Planck scale, see [32]. However, despite extensive experimental research, there has as yet been no evidence of this. At the moment, little has changed since the introduction of the Planck units and although a series of physicists have claimed they potentially play an important role, there has been no proof of this based on experimental research. It is a consensus among physicists today that, as yet, Planck units have only been found through dimensional analysis. However, this view has recently been challenged by Haug, who has claimed that one can easily find the Planck length from gravity observations with no prior knowledge of G or 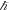 , see [33, 34]. If this is truly the case, then it is a breakthrough in understanding the Planck scale. As we will see, this is also important for understanding Newton's theory of gravity from a deeper perspective.
, see [33, 34]. If this is truly the case, then it is a breakthrough in understanding the Planck scale. As we will see, this is also important for understanding Newton's theory of gravity from a deeper perspective.
2. Newton's theory of gravity is only understood from the surface, not in depth
Returning to the modern version of Newton's gravitational formula, 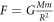 , before we can use this formula to predict any observable gravitational phenomena we have to calibrate it to a gravity observation to find G. We can say G is the missing information in the formula that is found from calibration in order to make the formula work. When the formula is first calibrated to one gravity observation using a Cavendish apparatus, for example, then it can be used to predict a series of other observable gravitational phenomena, such as orbital velocity and gravitational acceleration. We also know what units G must be in in order for it to be consistent with the outputs such as orbital velocity. If the mass is in kg, then G must have the following units
, before we can use this formula to predict any observable gravitational phenomena we have to calibrate it to a gravity observation to find G. We can say G is the missing information in the formula that is found from calibration in order to make the formula work. When the formula is first calibrated to one gravity observation using a Cavendish apparatus, for example, then it can be used to predict a series of other observable gravitational phenomena, such as orbital velocity and gravitational acceleration. We also know what units G must be in in order for it to be consistent with the outputs such as orbital velocity. If the mass is in kg, then G must have the following units 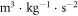 for
for  to come out as a velocity (length divided by time). Still, the modern Newtonian gravity theory does not tell us anything about what this gravity constant really represents. We know with very high probability it is a constant, and if it is calibrated to one gravity observation, it can be used to accurately predict a series of other gravity observations. Furthermore, it does not seem to change over time, so we can be highly confident that it is a constant. However, the universe itself does not invent constants and it is unlikely that anything in the universe consists of
to come out as a velocity (length divided by time). Still, the modern Newtonian gravity theory does not tell us anything about what this gravity constant really represents. We know with very high probability it is a constant, and if it is calibrated to one gravity observation, it can be used to accurately predict a series of other gravity observations. Furthermore, it does not seem to change over time, so we can be highly confident that it is a constant. However, the universe itself does not invent constants and it is unlikely that anything in the universe consists of  . Is there anything directly observable that is, in fact, meters cubed divided by kg and seconds squared? Even if we could not see it, can you imagine anything in the universe with such properties? I personally cannot. However, I can imagine something with a length, my shoes, for example. I can imagine something with weight, like my shoes. I can imagine a speed, as this is simply how far something has moved during a selected time duration. But I cannot imagine anything that is
. Is there anything directly observable that is, in fact, meters cubed divided by kg and seconds squared? Even if we could not see it, can you imagine anything in the universe with such properties? I personally cannot. However, I can imagine something with a length, my shoes, for example. I can imagine something with weight, like my shoes. I can imagine a speed, as this is simply how far something has moved during a selected time duration. But I cannot imagine anything that is  . Our point is that there could be something more fundamental behind G, that G is simply what is missing in the gravitational formula when we have decided to define mass as kg.
1
Moreover, although this is missing, whatever it may be, it can be found indirectly by calibrating the model to gravitational observations. We could also point to the kg masses M and m in the modern Newton formula, and ask, "What exactly do they represent?" We could also ask, "What is a kg?" But even though the kg definition did not exist in Newton's time, Newton was clear on the idea that weight is proportional to mass, and mass is a quantity of matter. We could even delve deeper and ask, "What is matter?" Today, we have a partial understanding that matter has particle-wave duality properties. So, when we write
. Our point is that there could be something more fundamental behind G, that G is simply what is missing in the gravitational formula when we have decided to define mass as kg.
1
Moreover, although this is missing, whatever it may be, it can be found indirectly by calibrating the model to gravitational observations. We could also point to the kg masses M and m in the modern Newton formula, and ask, "What exactly do they represent?" We could also ask, "What is a kg?" But even though the kg definition did not exist in Newton's time, Newton was clear on the idea that weight is proportional to mass, and mass is a quantity of matter. We could even delve deeper and ask, "What is matter?" Today, we have a partial understanding that matter has particle-wave duality properties. So, when we write 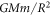 , we can say this is just a formula that we partly understand, and that fits observations. An important question is whether or not we can understand the formula from a deeper perspective and thereby obtain new insight into the formula and gravity itself. As will be seen, we believe we can do so!
, we can say this is just a formula that we partly understand, and that fits observations. An important question is whether or not we can understand the formula from a deeper perspective and thereby obtain new insight into the formula and gravity itself. As will be seen, we believe we can do so!
Looking at the predictions from Newton's gravity formula, table 1 shows a series of observable and several non-observable gravitational phenomena.
Table 1. The table shows a series of gravitational effects that can be predicted from Newton's formula. As expected, the speed of light (gravity) does not appear in any of the formulas.
| Gravity force |
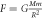
|
| Field equation |
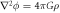
|
| Observable Predictions: | Formula: |
| Gravity acceleration |

|
| Orbital velocity |
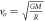
|
| Orbital time |
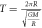
|
| Velocity ball Newton cradle a |
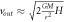
|
| Frequency Newton spring |
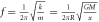
|
| Periodicity pendulum (clock) b |

|
| Non-Observable Predictions: | Formula: |
| Escape velocity |
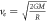
|
a
H is the height of the ball drop. This is a very good approximation when  .
b
This was actually derived by Huygens [35] some years before Newton. L is the length of the pendulum. This is a very accurate approximation for a small angle, and it is actually exact for a full circle, see [36].
.
b
This was actually derived by Huygens [35] some years before Newton. L is the length of the pendulum. This is a very accurate approximation for a small angle, and it is actually exact for a full circle, see [36].
In addition, in none of these formulas do we see the speed of light. This is not surprising, as all of these formulas for observable gravitational phenomena can be derived from Newton's gravity force formula. But again, what does G truly represent? And what is a mass from a deeper perspective? As stated by Prof. Jammer [37] in his work on mass, "mass is a mess"—his point is that we still do not really understand what mass is, something we will get back to soon.
3. Extracting the speed of light (gravity) times half the Schwarzschild radius from Newton-type gravity observations with no prior knowledge of any physical constants
In table 2, we can see that all of Newton's gravitational phenomena are only a function of the speed of light c (gravity?) and the Schwarzschild radius, as well as such variables as the distance to the center of the gravity object, R, or the length of a pendulum, and L, or the height from which we are dropping a ball in a Newton cradle.
Table 2. The table shows a series of gravitational effects that can be predicted from Newton's formula. However, we have rewritten this and shown that they can be written as a function of the speed of gravity cg and half of the Schwarzschild radius.
| Gravity force |
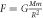
|
| Field equation |
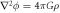
|
| Observable Predictions: | Formula: |
| Gravity acceleration |
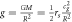
|
| Orbital time |
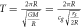
|
| Orbital velocity |

|
| Velocity ball Newton cradle a |
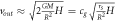
|
| Frequency Newton spring |

|
| Periodicity pendulum (clock) b |
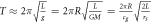
|
| Non-Observable Predictions: | Formula: |
| Escape velocity |
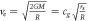
|
a
Very good approximation when  as it is in any normal Newton cradle.
b
This was actually derived by Huygens [35] some years before Newton. This is very accurate when the angle of the Pendulum is small, as it is in any normal Pendulum clock, which is why Pendulum clocks are quite accurate time keepers.
as it is in any normal Newton cradle.
b
This was actually derived by Huygens [35] some years before Newton. This is very accurate when the angle of the Pendulum is small, as it is in any normal Pendulum clock, which is why Pendulum clocks are quite accurate time keepers.
The Schwarzschild radius is, through general relativity theory, given by 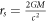 . That is to say, if we need to predict it from standard gravity theory, where we already have calibrated and found G, we also need to know the kg mass of the gravitational object and the speed of light. In this context, it is worth noting that the Schwarzschild radius is not unique to general relativity theory. In 1783, geologist John Michell [38] wrote a letter to Cavendish where he had calculated that the diameter of a sphere with the same mass density of the Sun had to be 500 times the diameter of the Sun in order for the escape velocity to be larger than the speed of light. Therefore, he predicted that such a sun would be dark, as not even light could escape. A sphere with 500 times the radius (and diameter) of the Sun has a volume of
. That is to say, if we need to predict it from standard gravity theory, where we already have calibrated and found G, we also need to know the kg mass of the gravitational object and the speed of light. In this context, it is worth noting that the Schwarzschild radius is not unique to general relativity theory. In 1783, geologist John Michell [38] wrote a letter to Cavendish where he had calculated that the diameter of a sphere with the same mass density of the Sun had to be 500 times the diameter of the Sun in order for the escape velocity to be larger than the speed of light. Therefore, he predicted that such a sun would be dark, as not even light could escape. A sphere with 500 times the radius (and diameter) of the Sun has a volume of  and if it has the same density of the Sun, it has a mass of
and if it has the same density of the Sun, it has a mass of 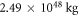 . The escape velocity at the radius of this star is the speed of light, so if the radius of this star was any smaller than that and still the same mass, then the escape velocity from the surface of this star would be higher than c, which is why Michell predicted it would be a dark sun (star). The radius of this object that he predicted using Newtonian mechanics is the same as the radius we get from general relativity and its Schwarzschild solution to predict the radius where the escape velocity is c. However, the Newtonian mechanical solution does not take into account relativistic effects and it would be reasonable to discuss whether or not it is valid. We have recently [34] shown that one can make relativistic corrections to the Newton mechanics, and that the radius when the escape velocity is c will then be half of the Schwarzschild radius. The main point is that we do not need to know general relativity to find such a radius. In fact, we do not need any of these theories to find such a radius (only to predict such a radius)—best known under the name "Schwarzschild radius". One can also find the Schwarzschild radius indirectly from gravitational observations with no knowledge of G, c, or M. If we observe the light bending from the Sun, for example, we will find that the light is bent by approximately 1.75 arcseconds, as first observed by Eddington [39]. Then, from this observation with no knowledge of G, c, or even M, we can find the Schwarzschild radius to be
. The escape velocity at the radius of this star is the speed of light, so if the radius of this star was any smaller than that and still the same mass, then the escape velocity from the surface of this star would be higher than c, which is why Michell predicted it would be a dark sun (star). The radius of this object that he predicted using Newtonian mechanics is the same as the radius we get from general relativity and its Schwarzschild solution to predict the radius where the escape velocity is c. However, the Newtonian mechanical solution does not take into account relativistic effects and it would be reasonable to discuss whether or not it is valid. We have recently [34] shown that one can make relativistic corrections to the Newton mechanics, and that the radius when the escape velocity is c will then be half of the Schwarzschild radius. The main point is that we do not need to know general relativity to find such a radius. In fact, we do not need any of these theories to find such a radius (only to predict such a radius)—best known under the name "Schwarzschild radius". One can also find the Schwarzschild radius indirectly from gravitational observations with no knowledge of G, c, or M. If we observe the light bending from the Sun, for example, we will find that the light is bent by approximately 1.75 arcseconds, as first observed by Eddington [39]. Then, from this observation with no knowledge of G, c, or even M, we can find the Schwarzschild radius to be  . This means the Schwarzschild radius of the Sun is
. This means the Schwarzschild radius of the Sun is
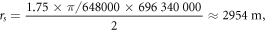
extracted directly from an observation, and not predicted based on prior knowledge of G, c, and M. The multiplication of 1.75 with π and division by 648 000 is just to turn the arcseconds into numbers of radians.
We can now just observe the orbital velocity of the Earth around the Sun  , where T is the orbital time of the Earth, 365 days, and
, where T is the orbital time of the Earth, 365 days, and  is the distance from the Earth to the Sun, and then put this into the orbital time formula that we get from Newton, which can be solved with respect to the speed of gravity cg
if we know the Schwarzschild radius. This formula is given in table 3, that is simply the formula in table 2 solved with respect to cg
, which gives
is the distance from the Earth to the Sun, and then put this into the orbital time formula that we get from Newton, which can be solved with respect to the speed of gravity cg
if we know the Schwarzschild radius. This formula is given in table 3, that is simply the formula in table 2 solved with respect to cg
, which gives
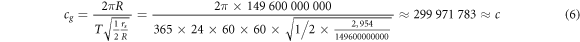
Table 3. The table shows how we can extract the speed of gravity from a series of gravitational phenomena by combining two gravity observations without knowledge of any physical constants.
| Gravity force |
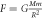
|
| Field equation |
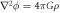
|
| Observable Predictions: | Formula: |
| Gravity acceleration |
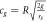
|
| Orbital time |

|
| Orbital velocity |

|
| Velocity ball Newton cradle |

|
| Frequency Newton spring |

|
| Periodicity pendulum (clock) |

|
| Combined with deflection: | Formula: |
| Gravity acceleration |
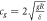
|
| Orbital time |
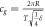
|
| Orbital velocity |
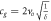
|
| Velocity ball Newton cradle |
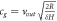
|
| Frequency Newton spring |

|
| Periodicity pendulum (clock) |
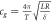
|
| Combined with red-shift: | Formula: |
| Gravity acceleration |
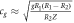
|
| Orbital time |

|
| Orbital velocity |
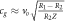
|
| Velocity ball Newton cradle |
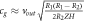
|
| Frequency Newton spring |
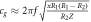
|
| Periodicity pendulum (clock) |

|
That is to say, we have found the speed of gravity from a Newtonian observation, namely the orbital time of the Earth, combined with a length we found from the gravity deflection of the Sun. To review, we combined two observations of gravitational phenomena, namely the orbital time of the Earth (which has been known for thousands of years) and the deflection angle of light from the Sun that has been observed accurately since Eddington's experiment in 1919. The small difference between this estimated speed and the speed of light is due to measurement errors. The same can be performed with all of Newton's gravitational phenomena, as shown in table 3, but we do need to combine this with observations that supposedly have only been predicted by GR. Furthermore, we do not need to predict these observations, but only to observe them; we have extracted the speed of gravity from observing gravitational phenomena alone. As we will demonstrate, all of Newton's gravitational phenomena (at least the ones in the table above) contain both the speed of gravity and the Schwarzschild radius; the Schwarzschild radius, as we will also explain, is directly linked to the Planck length that we can extract by observing gravity phenomena with no knowledge of G, c, 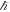 , or any other physical constants.
, or any other physical constants.
That all of Newton's gravitational phenomena contain the speed of light (gravity) embedded within them should be an important revelation. Some may claim that we are merely using a mathematical trick here, since we are relying on the Schwarzschild radius, which theoretically is given by  . So, are we not simply taking something that is related to GR, where the speed of gravity is indeed assumed to be
. So, are we not simply taking something that is related to GR, where the speed of gravity is indeed assumed to be  , and therefore able to derive cg
from GR? We will demonstrate that such a view is wrong. First of all, we are not using any GR predictions; we are just using an observation from the Sun's deflection of light, or alternatively observing gravitational red-shift by measuring the frequency of a light beam at two altitudes, or by observing two atomic clocks at different altitudes. In other words, we are not relying on general relativity theory to do this. Second, the c2 in the GR formula to predict deflection, or the Schwarzschild radius is used to obtain the speed of light out of the formula, not into the formula, as one might think. This is because both G and M contain the speed of light (gravity) embedded—something we will soon discuss and demonstrate. One can already get a good intuition from this because all of Newton's observational phenomena are directly or indirectly linked to velocity. The orbital velocity, the escape velocity, the periodicity of a pendulum, and the orbital time are all linked to velocity, so it would not be surprising if these velocities were linked to a more fundamental velocity, namely the speed of light (gravity). On the other hand, light deflection is an angle, and the Schwarzschild radius is a length only, so why should these contain the speed of light (gravity)? We will quickly look at a few more ways to find the Schwarzschild radius without the knowledge of any physical constants.
, and therefore able to derive cg
from GR? We will demonstrate that such a view is wrong. First of all, we are not using any GR predictions; we are just using an observation from the Sun's deflection of light, or alternatively observing gravitational red-shift by measuring the frequency of a light beam at two altitudes, or by observing two atomic clocks at different altitudes. In other words, we are not relying on general relativity theory to do this. Second, the c2 in the GR formula to predict deflection, or the Schwarzschild radius is used to obtain the speed of light out of the formula, not into the formula, as one might think. This is because both G and M contain the speed of light (gravity) embedded—something we will soon discuss and demonstrate. One can already get a good intuition from this because all of Newton's observational phenomena are directly or indirectly linked to velocity. The orbital velocity, the escape velocity, the periodicity of a pendulum, and the orbital time are all linked to velocity, so it would not be surprising if these velocities were linked to a more fundamental velocity, namely the speed of light (gravity). On the other hand, light deflection is an angle, and the Schwarzschild radius is a length only, so why should these contain the speed of light (gravity)? We will quickly look at a few more ways to find the Schwarzschild radius without the knowledge of any physical constants.
The gravitational red-shift is given by
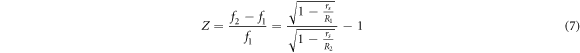
where  , and f2 and f1 are the observed photon frequencies at respectively R2 and R1. Solved with respect to the Schwarzschild radius, this gives
, and f2 and f1 are the observed photon frequencies at respectively R2 and R1. Solved with respect to the Schwarzschild radius, this gives

in a weak gravitational field (such as, for example, on the surface of the Earth), we have the very good approximation

And the only thing we need to find the speed of gravity from a Newtonian observable gravity phenomenon is to extract the Schwarzschild radius from the observational values. In the last section of table 3, we have combined observations of standard Newtonian gravity phenomena with observations of red-shift. This will give us the speed of gravity. Again, the reason we have to combine two gravitational phenomena to find cg
is that we need a gravitational phenomenon that depends on and therefore contains information about the speed of gravity in addition to another gravitational phenomenon that does not depend on the speed of gravity, such as gravitational deflection and gravitational red-shift. As stated previously, we can extract the speed of gravity from all of these phenomena with no prior knowledge of G, c,  , or the kg mass of the object in question. This alone is very important and strongly points towards the idea that Newtonian phenomena contain the speed of gravity. Furthermore, the speed of gravity that we can extract in this way is very close to the speed of light, only measurement errors potentially make it inexact.
, or the kg mass of the object in question. This alone is very important and strongly points towards the idea that Newtonian phenomena contain the speed of gravity. Furthermore, the speed of gravity that we can extract in this way is very close to the speed of light, only measurement errors potentially make it inexact.
4. The Newton gravity constant must be a universal composite constant
The Planck length is given by the Planck formula to be  . There is nothing mathematically wrong by solving this with respect to G, which gives
. There is nothing mathematically wrong by solving this with respect to G, which gives
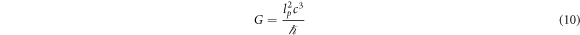
Many will here likely protest, as they will claim the only way to find the Planck length is first by knowing G, and then making G a function of lp
, which will actually just lead to a circular problem. However, if one can find the Planck length totally independent of any knowledge of G, then there is no such circular problem. We will demonstrate here that we can find the Planck length independent of any knowledge of G, and even without any knowledge of G,  , or c. Still, it would be totally absurd to claim that G is a composite constant, as one clearly did not know anything about the Planck constant or the Planck length when G was introduced in 1873. However, even if Newton's formula, when used together with kg mass definition of mass, missed the value of several constants, there is nothing wrong in claiming that all of these constants were found as a composite value from calibration without being aware of that directly, see [40]. That is to say, they could be extracted from gravity. Assume that in reality we have
, or c. Still, it would be totally absurd to claim that G is a composite constant, as one clearly did not know anything about the Planck constant or the Planck length when G was introduced in 1873. However, even if Newton's formula, when used together with kg mass definition of mass, missed the value of several constants, there is nothing wrong in claiming that all of these constants were found as a composite value from calibration without being aware of that directly, see [40]. That is to say, they could be extracted from gravity. Assume that in reality we have
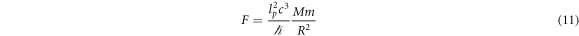
then we could set 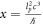 and then have
and then have  , basically the exact Newton formula and see if we could calibrate the unknown x to a gravitational phenomenon with a Cavendish apparatus. Next we would check to see if we could use the formula with a calibrated value of x to predict other gravitational phenomena. If this works, it might indicate that we had found the value of lp
, c, and
, basically the exact Newton formula and see if we could calibrate the unknown x to a gravitational phenomenon with a Cavendish apparatus. Next we would check to see if we could use the formula with a calibrated value of x to predict other gravitational phenomena. If this works, it might indicate that we had found the value of lp
, c, and 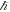 in the calibration, not as their separate values, but rather their values as a composite (so, indeed, simply G). This would mean that one does not need to know c and lp
separately for any Newtonian phenomena. Newton did not know or suggest that gravity moves at the speed of light, nor did the researchers who introduced the gravitational constant.
2
The fact that the gravitational constant came before the Planck length does not mean that it is more fundamental than the Planck length. On the contrary, we live in a world where what we tend to observe is far away from the subatomic world. Therefore, it is natural that we perturb and examine the surface of reality before we can understand what is going on at a deeper level.
in the calibration, not as their separate values, but rather their values as a composite (so, indeed, simply G). This would mean that one does not need to know c and lp
separately for any Newtonian phenomena. Newton did not know or suggest that gravity moves at the speed of light, nor did the researchers who introduced the gravitational constant.
2
The fact that the gravitational constant came before the Planck length does not mean that it is more fundamental than the Planck length. On the contrary, we live in a world where what we tend to observe is far away from the subatomic world. Therefore, it is natural that we perturb and examine the surface of reality before we can understand what is going on at a deeper level.
Continuing the analysis, in our view, the mass can be expressed by taking advantage of the Compton [41] wavelength formula 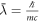 . Solving this with respect to m we get
. Solving this with respect to m we get
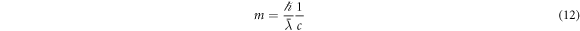
This formula is valid for all rest-masses, at least as long as we only are interested in them in the form of kg, and kg is proportional to the mass as pointed out by Newton. Naturally, based on this different masses are measured in the same gravitational field. Be aware that the de Broglie [42, 43] wavelength formula 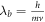 is not valid for rest-mass particles, as one cannot divide by zero (v = 0), see an in-depth discussion of this in [33, 34]. We can now express Newton's formula as
is not valid for rest-mass particles, as one cannot divide by zero (v = 0), see an in-depth discussion of this in [33, 34]. We can now express Newton's formula as
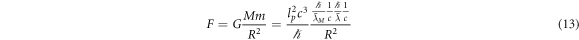
where 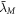 and
and 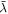 are the reduced Compton wavelengths of the large mass and small mass, respectively. This is, in our view, what the modern Newton formula truly represents, as understood from a deeper perspective. We can now see that it contains the speed of light. However, the Newton gravitational force itself is never directly observable or measurable. Directly observable gravitational phenomena that can also be predicted from Newton's formula can be found in table 1. Note that we always have GM and not GMm in any directly observable gravitational phenomena. The small mass always cancels out in derivations to obtain formulas that predict something observable. In real two-body problems, when both masses (that are significantly large) act significantly on each other, the gravity parameter is
are the reduced Compton wavelengths of the large mass and small mass, respectively. This is, in our view, what the modern Newton formula truly represents, as understood from a deeper perspective. We can now see that it contains the speed of light. However, the Newton gravitational force itself is never directly observable or measurable. Directly observable gravitational phenomena that can also be predicted from Newton's formula can be found in table 1. Note that we always have GM and not GMm in any directly observable gravitational phenomena. The small mass always cancels out in derivations to obtain formulas that predict something observable. In real two-body problems, when both masses (that are significantly large) act significantly on each other, the gravity parameter is  that is to say, in all directly observable gravity phenomena (or at least all those we have looked at), we have GM and not GMm. Further,
that is to say, in all directly observable gravity phenomena (or at least all those we have looked at), we have GM and not GMm. Further, 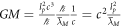 . As all observable Newtonian phenomena (again, at least all those we have looked at) contain
. As all observable Newtonian phenomena (again, at least all those we have looked at) contain 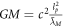 , this means they contain two constants: the speed of light and the Planck length. They also contain the speed of light and the Schwarzschild radius, as we already have demonstrated, since
, this means they contain two constants: the speed of light and the Planck length. They also contain the speed of light and the Schwarzschild radius, as we already have demonstrated, since 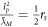 .
.
Table 4 shows that all Newton's gravitational observations need the Planck length and the speed of gravity (light) to be predicted; see the end results. This also means that these observations contain both the Planck length and the speed of gravity. To extract only the speed of gravity, we need a way to find the Planck length in isolation so we can separate the speed of gravity (light) from 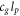 , which we get from Newton's gravitational phenomena. We see from the table that gravitational deflection, time dilation, and red-shift only contain the Planck length (plus some variables) and not the speed of gravity (light). All of them contain
, which we get from Newton's gravitational phenomena. We see from the table that gravitational deflection, time dilation, and red-shift only contain the Planck length (plus some variables) and not the speed of gravity (light). All of them contain 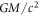 in their traditional formulation, but here we see the real reason for this, namely to get c2 out of
in their traditional formulation, but here we see the real reason for this, namely to get c2 out of 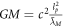 ,
,  .
.
Table 4. The table shows that any gravitational observations we can make contain GM and not GMm; GM contains and needs less information than is required to find G and M.
| Modern Newton: | |
| Mass |
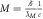 (kg) (kg) |
| Non observable (contains GMm) | |
| Gravitational constant |
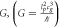
|
| Gravity force |

|
| Field equation | Gauss "law": 
|
| Observable predictions, identical for the two methods: (contains only GM) | |
| Gravity acceleration |
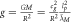
|
| Orbital velocity |
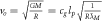
|
| Orbital time |
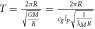
|
| Velocity ball Newton cradle |
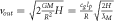
|
| Frequency Newton spring |
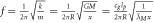
|
| Periodicity pendulum (clock) |

|
| Observable predictions (from GR): (contains only GM) | |
| Gravitational red-shift |
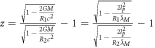
|
| Time dilation |
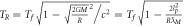
|
| Gravitational deflection (GR) |
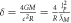
|
| Advance of perihelion |

|
Since the gravitational deflection, time dilation, and red-shift are only dependent on the Planck length (plus some variables), we can, from observing any of these phenomena, extract the Planck length with no knowledge of any other physical constants. For example, if we have observed the deflection of light from the Sun, then we can find the Planck length. If we solve the formula in the table with respect to lp , we get
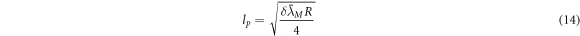
where δ is the observed deflection, R is the distance from the center of the gravitational object to where the light beam passes by the Sun, and 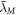 is the Compton wavelength of the Sun. We can measure the radius of the Sun with parallax and other methods; and we can also observe the deflection of the Sun. The question is, how can we find the Compton wavelength of the Sun that is also in this formula? Some may think that the Sun cannot have a Compton wavelength. It is true that the Sun cannot have one physical Compton wavelength, but the Sun consists of atoms that again consist of elementary particles that have a Compton wavelength. There is a way to aggregate the Compton wavelengths of these particles to obtain the aggregated Compton wavelength of the Sun, or any other mass. The Compton wavelength of a composite mass can be found from the Compton wavelengths making up the composite mass through the following formula (see also [33])
is the Compton wavelength of the Sun. We can measure the radius of the Sun with parallax and other methods; and we can also observe the deflection of the Sun. The question is, how can we find the Compton wavelength of the Sun that is also in this formula? Some may think that the Sun cannot have a Compton wavelength. It is true that the Sun cannot have one physical Compton wavelength, but the Sun consists of atoms that again consist of elementary particles that have a Compton wavelength. There is a way to aggregate the Compton wavelengths of these particles to obtain the aggregated Compton wavelength of the Sun, or any other mass. The Compton wavelength of a composite mass can be found from the Compton wavelengths making up the composite mass through the following formula (see also [33])
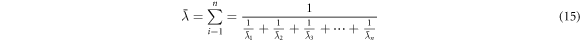
This formula is fully consistent with standard mass addition because we have
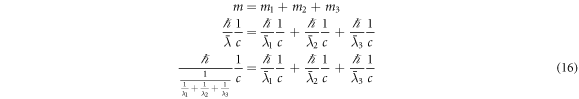
If we know the mass of the Sun in kg and the Planck constant (to do this we also first need to find G), we can simply find the reduced Compton wavelength of the Sun by  . However, there is also a way to find the Compton wavelength of the Sun with no knowledge of G or
. However, there is also a way to find the Compton wavelength of the Sun with no knowledge of G or 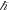 or any knowledge of the kg mass of the Sun. From Compton's 1923 paper, we can find that the Compton wavelength of the electron is given by
or any knowledge of the kg mass of the Sun. From Compton's 1923 paper, we can find that the Compton wavelength of the electron is given by
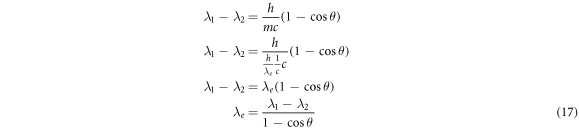
That is to say, we need to shoot photons at an electron and measure the wavelength (frequency) of the photon before and after the impact with the electron. In addition, we need to measure the angle θ, i.e., the angle between the incoming and outgoing photons we shoot at the electron. Pay attention to the fact that we do not require information about the kg mass of the electron in order to do this, nor do we need the Planck constant, or the speed of light. It can be discussed whether we need knowledge of the speed of light to find the wavelength here, but remember we have already extracted cg
from gravitational phenomena with no knowledge of c as shown in table 3, so we do not need to observe c from electromagnetism phenomena to find 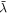 , we can get cg
from gravitational observations and also use it here.
, we can get cg
from gravitational observations and also use it here.
Next, we have that the cyclotron frequency is given by
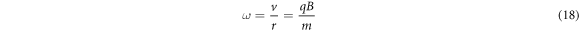
An electron and a proton have the same charge, so the cyclotron ratio is equal to their mass ratio. This is well known, as one has also used cyclotron frequencies to find the well-known proton electron ratio (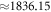 ) by this method, see [44]. Furthermore, their mass ratio is equal to their Compton wavelength ratio
) by this method, see [44]. Furthermore, their mass ratio is equal to their Compton wavelength ratio
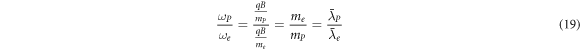
where  is the reduced Compton wavelength of the proton and
is the reduced Compton wavelength of the proton and 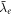 is the reduced Compton wavelength of the electron. So, we now have the reduced Compton wavelength of a proton without knowledge of any prior physical constants. If we need to know the reduced Compton wavelength of the Earth, we could theoretically count all the protons in the Earth. There is nothing in the laws of physics to prevent this, even if it is technically impossible. One would then by formula 15 know the Compton wavelength of the Earth. However, there is a simpler way that could potentially be achieved in practice. One could count the number of protons in a small mass the size of roughly half a kg, for example, (without knowing anything about kg); what we need is a handful of uniform matter to be used in a Cavendish apparatus. Next, we will use this mass as the gravitational object (the large mass) in the Cavendish apparatus. There is naturally a challenge in counting the number of protons in a mass of even such a size, but it is not impossible. In recent years, silicon (
is the reduced Compton wavelength of the electron. So, we now have the reduced Compton wavelength of a proton without knowledge of any prior physical constants. If we need to know the reduced Compton wavelength of the Earth, we could theoretically count all the protons in the Earth. There is nothing in the laws of physics to prevent this, even if it is technically impossible. One would then by formula 15 know the Compton wavelength of the Earth. However, there is a simpler way that could potentially be achieved in practice. One could count the number of protons in a small mass the size of roughly half a kg, for example, (without knowing anything about kg); what we need is a handful of uniform matter to be used in a Cavendish apparatus. Next, we will use this mass as the gravitational object (the large mass) in the Cavendish apparatus. There is naturally a challenge in counting the number of protons in a mass of even such a size, but it is not impossible. In recent years, silicon (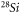 ) crystal balls have been turned into almost perfect spheres. As the material is very uniform and we know the volume very accurately and the silicon atom structure, we have therefore been able to count the number of atoms, based on this, see [45, 46]. To count the number of atoms is, therefore, not pure theory, other potential methods also exist—see for example [47]. If we know the number of atoms in a piece of matter, we know its Compton wavelength (without having to rely on the Planck constant).
) crystal balls have been turned into almost perfect spheres. As the material is very uniform and we know the volume very accurately and the silicon atom structure, we have therefore been able to count the number of atoms, based on this, see [45, 46]. To count the number of atoms is, therefore, not pure theory, other potential methods also exist—see for example [47]. If we know the number of atoms in a piece of matter, we know its Compton wavelength (without having to rely on the Planck constant).
Next, we can find the gravitational acceleration of the sphere, in which we have counted the number of atoms by using a Cavendish apparatus. The gravitational acceleration is given by
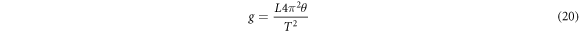
where θ is the angle of the arm in the apparatus, T is the time of the oscillation period, and L is the length between the two small balls in the apparatus. This is found without any knowledge of G, or the Planck constant, or c. This is the gravitational acceleration field from the large balls in the Cavendish apparatus at radius R1, which is the distance from the large ball to the small ball in the Cavendish apparatus when the arm is deflected.
Next, the Compton wavelength (and the reduced Compton wavelength) in the masses are proportional to the gravitational acceleration:
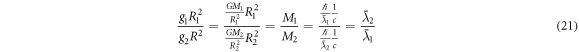
We can therefore easily determine the Compton wavelength of the Earth, or the Sun, for example, when we know the number of atoms in a clump of uniform matter on Earth. Since the Compton wavelength was the last needed input into the formula 14, this means that we have a method for finding the Planck length totally independent of any knowledge of G,  , and potentially also c, from gravitational deflection.
, and potentially also c, from gravitational deflection.
We can also find the Planck length directly from measuring the gravitational frequency shift (red-shift) of a laser beam sent out from altitude R2 and received at altitude R1. In a weak gravitational field, we get
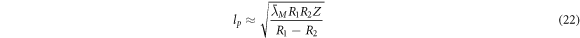
where Z is the observed red-shift, and  is the reduced Compton wavelength of the mass causing the gravitational field we are performing the measurement in, e.g., the Earth.
is the reduced Compton wavelength of the mass causing the gravitational field we are performing the measurement in, e.g., the Earth.
So, from gravitational bending of light (deflection), gravitational red-shift, gravitational time dilation, and the perihelion of Mercury, we can find the Planck length with no prior knowledge of any other physical constants, see the bottom of table 4. We can predict the same observations with only one constant, namely the Planck length. This strongly supports the idea that these particular gravitational phenomena do not contain the speed of gravity. Because how can it be that we can obtain the Planck length in this way without separating out any other constants, such as G,  , or c? To understand why, let us first look at the gravitational deflection. According to general relativity, this requires two constants G and c (or actually three, as the Planck constant is embedded in G as well as in M) to be predicted. This is because we have
, or c? To understand why, let us first look at the gravitational deflection. According to general relativity, this requires two constants G and c (or actually three, as the Planck constant is embedded in G as well as in M) to be predicted. This is because we have 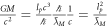 , and we see that the c2 in the nominator cancels out the embedded c2 in GM, and the embedded
, and we see that the c2 in the nominator cancels out the embedded c2 in GM, and the embedded 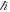 in G cancels out with the Planck constant in the mass. Gravitational deflection seems to only depend on one constant, and that is the Planck length in addition to variables such as the distance from the center of the Sun to where the light beam is deflected and a variable deciding the size of the mass, namely the Compton wavelength of the mass in question. Moreover, based on our deeper understanding, we suspect we can probably guarantee that one cannot extract G from only observing deflection, because G is not in the deflection, only part of G, namely the Planck length. Nor can anyone likely extract the speed of gravity only from observing gravity deflection, red-shift, or time dilation without adding in other constants, or by multiplying with a known mass, as mass in kg contains
in G cancels out with the Planck constant in the mass. Gravitational deflection seems to only depend on one constant, and that is the Planck length in addition to variables such as the distance from the center of the Sun to where the light beam is deflected and a variable deciding the size of the mass, namely the Compton wavelength of the mass in question. Moreover, based on our deeper understanding, we suspect we can probably guarantee that one cannot extract G from only observing deflection, because G is not in the deflection, only part of G, namely the Planck length. Nor can anyone likely extract the speed of gravity only from observing gravity deflection, red-shift, or time dilation without adding in other constants, or by multiplying with a known mass, as mass in kg contains 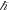 and c embedded. This is because these observations in our view likely contain no information about the speed of light or the speed of gravity; all they contain in the form of constants seems to be the Planck length. This also means that in standard gravity theory one is using unnecessary information to arrive at the correct prediction. In standard theory, one is indirectly using three constants to predict all gravitational phenomena, G, c, and
and c embedded. This is because these observations in our view likely contain no information about the speed of light or the speed of gravity; all they contain in the form of constants seems to be the Planck length. This also means that in standard gravity theory one is using unnecessary information to arrive at the correct prediction. In standard theory, one is indirectly using three constants to predict all gravitational phenomena, G, c, and  , since the kg mass is linked to the Planck constant, as is clear from the new kg definition of mass that came into play in 2019, see [48, 49]. In reality, we only need two constants, namely lp
and c, that can be found from gravity observations alone, with no prior knowledge of any other constants. These two constants are also much more intuitive than either G or
, since the kg mass is linked to the Planck constant, as is clear from the new kg definition of mass that came into play in 2019, see [48, 49]. In reality, we only need two constants, namely lp
and c, that can be found from gravity observations alone, with no prior knowledge of any other constants. These two constants are also much more intuitive than either G or  . The Planck length is the shortest possible length, and we all have quite good intuition as to what a length is, and c is how far something (light and something related to gravity) can travel during a predefined time window. Again, G, on the other hand, gives little or no intuition from its output units
. The Planck length is the shortest possible length, and we all have quite good intuition as to what a length is, and c is how far something (light and something related to gravity) can travel during a predefined time window. Again, G, on the other hand, gives little or no intuition from its output units 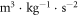 . If anyone can tell me of anything physical that they can observe directly that corresponds to such a unit combination, I would be happy to hear about it.
. If anyone can tell me of anything physical that they can observe directly that corresponds to such a unit combination, I would be happy to hear about it.
Classic Newton gravitational phenomena, as we can see from table 4, contain both the speed of gravity and the Planck length, and we need to know the Planck length (or the Schwarzschild radius) in order to separate out the speed of gravity from these observations. We can also find the Planck length from Newton's gravitational phenomena if we know the speed of light, for example, from simply measuring the speed of light.
Table 5 shows how we can extract 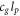 , as well as lp
and therefore also cg
and lp
separately, by observing only two gravity observations and with no knowledge of G, c, or
, as well as lp
and therefore also cg
and lp
separately, by observing only two gravity observations and with no knowledge of G, c, or 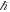 . From these two constants, we can then predict any other observable gravitational phenomena, as can be seen from table 4.
. From these two constants, we can then predict any other observable gravitational phenomena, as can be seen from table 4.
Table 5. The table shows how we can extract  from a series of gravitational observations, and further how we can extract the Planck length isolated from some other gravitational observations. This means that we can also isolate cg
and lp
by performing two gravitational observations and without any knowledge of G,
from a series of gravitational observations, and further how we can extract the Planck length isolated from some other gravitational observations. This means that we can also isolate cg
and lp
by performing two gravitational observations and without any knowledge of G, 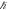 , c, or any other constant. Again, these can be used to predict any gravitational phenomena. This means that Newton's gravitational phenomena contain the speed of gravity and that the speed of Newtonian gravity is
, c, or any other constant. Again, these can be used to predict any gravitational phenomena. This means that Newton's gravitational phenomena contain the speed of gravity and that the speed of Newtonian gravity is 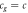 .
.
| Modern Newton: | |
| Mass |
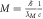 (kg) (kg) |
| Non observable (contains GMm) | |
| Gravitational constant |
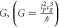
|
| Gravity force |

|
| Field equation | Gauss "law": 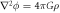
|
| Planck length times speed of gravity from: | |
| Gravity acceleration |
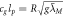
|
| Orbital velocity |

|
| Orbital time |
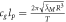
|
| Velocity ball Newton cradle |
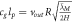
|
| Frequency Newton spring |
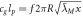
|
| Periodicity Pendulum (clock) |
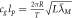
|
| Planck length from: | |
| Gravitational red-shift |
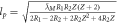
|
| Gravitational red-shift weak field approx..: |
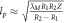
|
| Time dilation |

|
| Time dilation weak field approx.: |

|
| Gravitational deflection (GR) |

|
| Advance of perihelion Mercury |
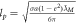
|
5. The Newtonian field equation in a new light
We can also rewrite the Gaussian law of gravity based on the composite view of 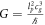 and this gives
and this gives

In other words, the speed of light appears in the field equation. It is probably inaccurate to conclude, as has been done in the past, that Newtonian gravity is instantaneous and the implicit speed of gravity in Newton's formulation is therefore infinite. This would mean that we should put  , and this would lead to an infinitely strong gravitational field, something that is absurd and not in line with Newtonian theory. If we set
, and this would lead to an infinitely strong gravitational field, something that is absurd and not in line with Newtonian theory. If we set 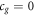 , then the gravitational field would be zero, which is also absurd and not in line with Newton predictions, or observations. Only when we have
, then the gravitational field would be zero, which is also absurd and not in line with Newton predictions, or observations. Only when we have 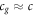 can the equation be used for a series of predictions that are consistent with observations. In other words, Newtonian gravity that is hidden and embedded in
can the equation be used for a series of predictions that are consistent with observations. In other words, Newtonian gravity that is hidden and embedded in  as well as in
as well as in 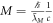 contains the speed of light,
contains the speed of light,  . See also Unnikrishnan and Gillies[50] that we would say indirectly could be interpreted
3
as that G embedded contains
. See also Unnikrishnan and Gillies[50] that we would say indirectly could be interpreted
3
as that G embedded contains  . Newtonian gravity is consistent with the concept that gravity moves at the speed of light.
. Newtonian gravity is consistent with the concept that gravity moves at the speed of light.
We can also rewrite the standard Newton field equation based on standard mass, given that any mass in kg can be expressed as  , which we get from the Compton wavelength formula, and in addition the knowledge that the Schwarzschild radius can be written as
, which we get from the Compton wavelength formula, and in addition the knowledge that the Schwarzschild radius can be written as 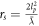 , and that again by understanding the gravity constant is a composite constant,
, and that again by understanding the gravity constant is a composite constant, 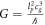 . Based on this we get
. Based on this we get

and since 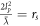 we can re-write this as
we can re-write this as
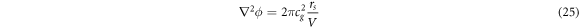
Now there is no hidden c or cg
anywhere in the formula, in contrast to 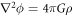 , where the speed of light (gravity) is concealed inside both G and ρ. We see that the Newtonian field equation rewritten in this form must be dependent on the speed of gravity, and if we try to calibrate it to any observation we find that cg
must be c. In this formula, we have the Schwarzschild radius, so some might think we will need general relativity to find the input to this field equation. However, we will then ask the reader to read section 3 again, which shows, in brief, how an identical radius was predicted based on Newtonian mechanics in 1784. In addition, we do not actually need to predict such a radius because we can find it from gravity observations, as described in section 3.
, where the speed of light (gravity) is concealed inside both G and ρ. We see that the Newtonian field equation rewritten in this form must be dependent on the speed of gravity, and if we try to calibrate it to any observation we find that cg
must be c. In this formula, we have the Schwarzschild radius, so some might think we will need general relativity to find the input to this field equation. However, we will then ask the reader to read section 3 again, which shows, in brief, how an identical radius was predicted based on Newtonian mechanics in 1784. In addition, we do not actually need to predict such a radius because we can find it from gravity observations, as described in section 3.
Again, if we set the speed of gravity in the field equation to infinite, as the research community has indirectly thought is the speed of gravity in Newtonian theory, then we get  , which gives an infinite strong gravity field; this makes no sense, nor does it fit observations. Alternatively, if we set
, which gives an infinite strong gravity field; this makes no sense, nor does it fit observations. Alternatively, if we set 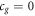 , we get a gravitational field of zero. This also makes no sense. The only value for cg
that fits observations is
, we get a gravitational field of zero. This also makes no sense. The only value for cg
that fits observations is  . In other words, Newtonian gravity is clearly fully consistent with the idea that the speed of gravity is c. To what degree this equation is consistent with special relativity theory or not would lead to a long discussion that is outside the scope of this article. However, the first impression is that it is indeed consistent, or at least to a good degree, as long as the velocities of masses M and m are much smaller than c, (
. In other words, Newtonian gravity is clearly fully consistent with the idea that the speed of gravity is c. To what degree this equation is consistent with special relativity theory or not would lead to a long discussion that is outside the scope of this article. However, the first impression is that it is indeed consistent, or at least to a good degree, as long as the velocities of masses M and m are much smaller than c, (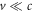 ). To make it "fully" compatible with relativistic effects, one can guess that one would get far further by simply adding relativistic masses to the formula. That is to say, to replace M and m with
). To make it "fully" compatible with relativistic effects, one can guess that one would get far further by simply adding relativistic masses to the formula. That is to say, to replace M and m with 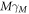 and m with
and m with  , where
, where 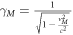 and
and  . This would give
. This would give
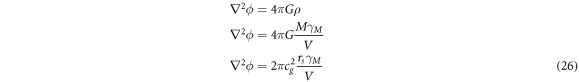
which has been performed in a recent working paper of ours [51] that is currently in review. To our surprise, the predictions for supernovas (580 supernova 1A data points) then essentially fit observed data perfectly without the need for dark energy. One should, however, not come to any preliminary conclusions on how complete or incomplete such a relativistic adjustment will be. What is important in this paper is that Newtonian gravity is clearly consistent with the concept that the speed of gravity is the same as the speed of light; actually, this is what is indirectly predicted by Newton gravity.
Interestingly, general relativity, for example, leads to the same escape velocity that one can obtain from Newton's gravitational formula, see for example [52]. How can it be that GR and Newton give the same escape velocity, if GR assumes the speed of gravity 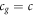 and Newton assumes the speed of gravity is infinite? This simply does not make logical sense. It is clear to us that Newton's formulation embedded in it contains the speed of gravity, not based on assumptions behind the foundation of the model, but by calibration of what is missing in the model that one gets through the composite constant G. This is, however, only fully understood when one understands that G is a composite constant of the form
and Newton assumes the speed of gravity is infinite? This simply does not make logical sense. It is clear to us that Newton's formulation embedded in it contains the speed of gravity, not based on assumptions behind the foundation of the model, but by calibration of what is missing in the model that one gets through the composite constant G. This is, however, only fully understood when one understands that G is a composite constant of the form  (or
(or 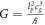 which is the same when we have
which is the same when we have  ) and that any kg mass can be described as
) and that any kg mass can be described as 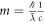 .
.
6. Rethinking Newtonian gravity and returning to the original Newton formula
Haug [34] has suggested that the reason one must multiply G by M is to turn what we have reason to think is an incomplete kg mass definition  into a complete mass definition. The gravity constant G is actually needed for removing the Planck constant from the kg mass and getting the Planck length into it. A long series of gravitational phenomena are linked to the Planck length, so one cannot make most gravity predictions without it. For the output numbers, we obtain the same output if we have placed the Planck length into the formula indirectly without knowing it, through a composite constant, or if we do it directly. The direct approach, as we will soon show, gives deeper insight into gravity. In the same paper, Haug has suggested that the mass actually used in all gravity calculations indirectly is what he has coined collision-time mass,
into a complete mass definition. The gravity constant G is actually needed for removing the Planck constant from the kg mass and getting the Planck length into it. A long series of gravitational phenomena are linked to the Planck length, so one cannot make most gravity predictions without it. For the output numbers, we obtain the same output if we have placed the Planck length into the formula indirectly without knowing it, through a composite constant, or if we do it directly. The direct approach, as we will soon show, gives deeper insight into gravity. In the same paper, Haug has suggested that the mass actually used in all gravity calculations indirectly is what he has coined collision-time mass, 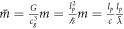 . Based on this, this new mass definition that is embedded in the standard gravity theory, we get an alternative Newton-like gravity formula, namely
. Based on this, this new mass definition that is embedded in the standard gravity theory, we get an alternative Newton-like gravity formula, namely
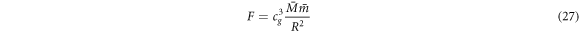
This formula has different output units and numerical output than the standard modern Newtonian gravitational formula. Still, based on this formula, we get the same predictions for any observable gravitational phenomena as in Newton. This can be seen in table 6. We see that both the standard Newtonian formula, as well as our alternative Newtonian formula, provide outputs that are only dependent on the Planck length and the speed of gravity. The end result of all predictions is the same from the standard modern Newtonian formula and this new alternative.
Table 6. The table shows that any observable gravity phenomena (we look at here) are linked to the Planck length and the speed of gravity, which is equal to the speed of light. For all observable gravity phenomena, we have GM and not GMm. This means that the embedded Planck constant cancels out, and all observable gravity phenomena are linked to the Planck length and the speed of gravity that, again, are identical to the speed of light. When this is understood, one can even rewrite Newton and GR gravity formulas in a simpler form that still gives all the same results.
| Modern Newton: | Alternative: | |
| Mass |
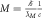 (kg) (kg) |
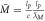 (collision-time, see [34]) (collision-time, see [34]) |
| Non observable (contains GMm) | ||
| Gravitational constant |
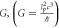
|

|
| Gravity force |
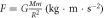
|

|
| Field equation | Gauss "law": 
| Gauss "law": 
|
where 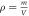 , mass density , mass density | where 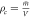 , mass density , mass density | |
| Observable predictions, identical for the two methods: (contains only GM) | ||
| Gravity acceleration |
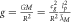
|
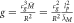
|
| Orbital velocity |
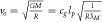
|
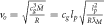
|
| Orbital time |

|
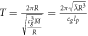
|
| Velocity ball Newton cradle |
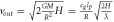
|

|
| Frequency Newton spring |
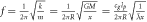
|
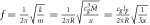
|
| Periodicity Pendulum (clock) |
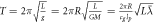
|
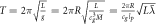
|
| Observable predictions (from GR): (contains only GM) | ||
| Gravitational red-shift |
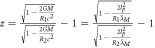
|

|
| Time dilation |

|

|
| Gravitational deflection (GR) |
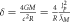
|
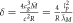
|
| Advance of perihelion |
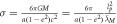
|

|
| Indirectly/"hypothetical" observable predictions: (contains only GM) | ||
| Escape velocity |
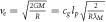
|

|
| Schwarzschild radius |

|
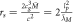
|
| Gravitational parameter |
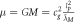
|

|
| Two body problem |

|
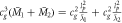
|
| Quantum analysis: | ||
| Constants needed |
G,  , and c or lp
, , and c or lp
,  , and c , and c
| lp and c, for some phenomena only lp |
| Variable needed | one for mass size | one for mass size |
This also means that all of Newton's observed phenomena contain information about the speed of gravity equal to that of light and the Planck length. To extract only the speed of gravity from Newton's observable gravitational phenomena, we need to somehow independently find the Planck length; this can be achieved from light defection, red-shift, time dilation, or the precession of Mercury. These observations are only dependent on one physical constant, the Planck length, and therefore they also contain this constant. As we have stated, it can be extracted from them without knowledge of any other constant, as can be seen in table 6.
We can also derive a field equation using the Gaussian law from our new mass definition; this gives
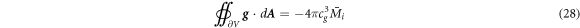
where 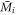 is the mass in terms of collision time inside the Gaussian surface, and
is the mass in terms of collision time inside the Gaussian surface, and  is the gravitational acceleration vector. This can be written in differential form (the Poisson equation) as
is the gravitational acceleration vector. This can be written in differential form (the Poisson equation) as
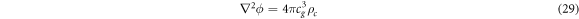
where  is the mass density, but mass is defined as collision-time and not as kg. The collision-time mass has many implications for physics and seems to lead to a unified theory. This is not the topic of this paper, but more information about this subject can be found in our recent paper [34].
is the mass density, but mass is defined as collision-time and not as kg. The collision-time mass has many implications for physics and seems to lead to a unified theory. This is not the topic of this paper, but more information about this subject can be found in our recent paper [34].
In the case where one uses the same unit for length and time (that is to say, if the length unit is how long the light moved in the chosen upon time unit), then the speed of gravity (light) is  and the formula above (27) simplifies to Newton's original formula
and the formula above (27) simplifies to Newton's original formula
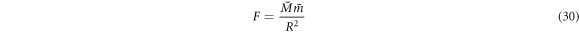
This formula can still be used to predict all Newton's gravitational phenomena. To use time units linked to the length units based on the speed of light, we first need to know the speed of light. This was at least theoretically possible in Newton's time. Back then, they knew the approximate distance from the Earth to the Sun by parallax, and Newton explicitly points out in Principia that the time it takes for light to get from the Sun to the Earth is 7 to 8 minutes. Then all one has to do is to decide on any chosen length unit; I could take off my shoe, for example, and state that this will be the length unit. Next, we will divide the length from the Sun to Earth (that we got by parallax) by this length unit. Finally, take 8 minutes and divide it by the ratio we have obtained, and now we have a time unit linked to the length unit that is also linked to the speed of light. We do not, in any way, claim that Newton did this, but clearly it would have been possible at that time as well.
When we combine Newton's original formula with modern knowledge of the Compton wavelength and how to find it for larger masses, as shown in this paper, then one can even use Newton's gravitational phenomena to find the Planck length with no knowledge or observation of non-Newtonian gravitational phenomena, as we demonstrate in an example below.
6.0.1. Example of finding the Planck length from Newton's original formula
Assume that we first measure the electron's Compton wavelength; it is 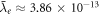 meters. Next, we find the cyclotron frequency of electrons and protons and find that the ratio is about 1,836.15. This means the Compton wavelength of a proton is
meters. Next, we find the cyclotron frequency of electrons and protons and find that the ratio is about 1,836.15. This means the Compton wavelength of a proton is  meters. Then, we count the number of atoms in a clump of uniform atoms. Assume, for example, a silicon sphere; if we count
meters. Then, we count the number of atoms in a clump of uniform atoms. Assume, for example, a silicon sphere; if we count 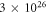 protons (or neutrons, which we assume have same mass as protons). The Compton wavelength of this mass will then be approximately
protons (or neutrons, which we assume have same mass as protons). The Compton wavelength of this mass will then be approximately 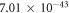 . Now we will find the gravitational acceleration from this mass using a Cavendish apparatus. It is given by
. Now we will find the gravitational acceleration from this mass using a Cavendish apparatus. It is given by
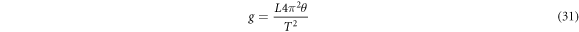
Assume the distance between the small balls in the apparatus is 0.2 meters and the distance between the large sphere and the small sphere, when the arm with the small balls is deflected, is 0.2 meters. Time must be measured in units of 3.3 nanoseconds, if we want to use same time unit as length units, as we have chosen meters as the length unit. This leads to a gravitational acceleration indirectly observed (from the measures in the Cavendish apparatus) of 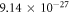 meters per 3.3 nanoseconds squared. We naturally do not need nanosecond accurate measurements to find this, as we must measure over a considerably longer period in a Cavendish apparatus, but by mathematics we will convert our measurement into units per nanoseconds. Therefore, this part could even have been achieved in Cavendish's time.
meters per 3.3 nanoseconds squared. We naturally do not need nanosecond accurate measurements to find this, as we must measure over a considerably longer period in a Cavendish apparatus, but by mathematics we will convert our measurement into units per nanoseconds. Therefore, this part could even have been achieved in Cavendish's time.
To continue, we need to measure the gravitational acceleration on the surface of the Earth, which can be done with two time gates and a drop ball, it is approximately 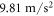 which is equal to
which is equal to  meter per 3.3 nanoseconds squared. The Earth's Compton wavelength is now
meter per 3.3 nanoseconds squared. The Earth's Compton wavelength is now 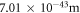 divided by
divided by
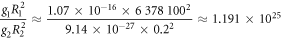
which gives 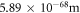 . If we now take the gravitational acceleration on Earth, which was approximately
. If we now take the gravitational acceleration on Earth, which was approximately 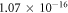 meter per 3.3 nanoseconds, we can find the Planck length simply from the formula
meter per 3.3 nanoseconds, we can find the Planck length simply from the formula
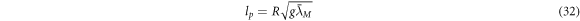
which, in the case of the gravitational field of Earth, is

From this constant (the Planck length) alone, we can predict all observable gravitational phenomena, based on time units linked to length units through the speed of light. Be aware that this only works if one uses for the speed of gravity the same unit for length and time, which mean  , and, in order to use such units, we need to know the speed of light, which we can naturally get from simply measuring the speed of light. So, Newton's formula used in this way would indirectly mean that we already know the speed of light, assuming that gravity moves at the same speed, and where we are using a time unit that is linked to the length unit through the speed of light.
, and, in order to use such units, we need to know the speed of light, which we can naturally get from simply measuring the speed of light. So, Newton's formula used in this way would indirectly mean that we already know the speed of light, assuming that gravity moves at the same speed, and where we are using a time unit that is linked to the length unit through the speed of light.
Newton's original formula from this perspective is entirely correct. If used as it was originally presented, with the mass definition we have introduced, it automatically assumes that gravity is the same as the speed of light. It is necessary to know the speed of light, but not the speed of gravity to operate the formula. One needs to know the speed of light in order to use a time unit that is linked to the length unit through the speed of light.
Combined with modern knowledge of the Compton wavelength that can be found independent of G,  , Newton's formula gives us the most important of all constants, namely the Planck length. From the Planck length alone, we can then predict all observable gravitational phenomena.
, Newton's formula gives us the most important of all constants, namely the Planck length. From the Planck length alone, we can then predict all observable gravitational phenomena.
7. Combining information from electromagnetism with Newtonian gravity to easily find the plank length with no knowledge of G or 
Since a series of Newtonian gravitational phenomena will be dependent on the speed of gravity cg
and the Planck length, and since  , we can extract the Planck length easily from them by extracting the speed of gravity through measuring the speed of light (electromagnetism), as shown in table 7. Be aware that if cg
was significantly different from c, we would not be able to extract the Planck length. We can check this with data from observations, such as how long it takes for the Earth to go around the Sun and we will see that the number obtained is actually the Planck length. This is revolutionary because it means when we observe any gravitational phenomena, we are actually detecting the Planck scale.
, we can extract the Planck length easily from them by extracting the speed of gravity through measuring the speed of light (electromagnetism), as shown in table 7. Be aware that if cg
was significantly different from c, we would not be able to extract the Planck length. We can check this with data from observations, such as how long it takes for the Earth to go around the Sun and we will see that the number obtained is actually the Planck length. This is revolutionary because it means when we observe any gravitational phenomena, we are actually detecting the Planck scale.
Table 7. The table shows how we can easily extract the Planck length from observation of Newtonian gravitational phenomena by extracting the speed of gravity from measuring the speed of light.
Planck length independent found independent of G and 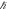 : : | |
| Gravity acceleration |
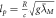
|
| Orbital velocity |
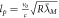
|
| Orbital time |

|
| Velocity ball Newton cradle a |
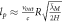
|
| Frequency Newton spring b |
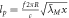
|
| Periodicity pendulum c (clock) |

|
| Periodicity Moon pendulum d (clock) |
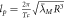
|
a
Very good approximation when  .
b
Where x is the height of the drop above R.
c
Very good approximation when the pendulum angle is small, as it is in a pendulum clock.
d
If using a 360-degree pendulum clock, then the Huygens formula is actually exact, and the Moon-Earth system, for example, can be seen as such a clock (assuming perfect circular orbit), see [36].
.
b
Where x is the height of the drop above R.
c
Very good approximation when the pendulum angle is small, as it is in a pendulum clock.
d
If using a 360-degree pendulum clock, then the Huygens formula is actually exact, and the Moon-Earth system, for example, can be seen as such a clock (assuming perfect circular orbit), see [36].
7.0.2. Example
First, we can find the Compton wavelength of the Earth with the method previously described in this paper; it is  , which is independent of knowledge of
, which is independent of knowledge of  or G. Second, we will measure the distance to the Moon from the Earth by parallax, for example,
or G. Second, we will measure the distance to the Moon from the Earth by parallax, for example, 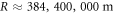 . Next, we measure the orbital time of the Moon around the Earth, which is 27.322 days. We measure the speed of light and plug this into formula orbital time, which gives
. Next, we measure the orbital time of the Moon around the Earth, which is 27.322 days. We measure the speed of light and plug this into formula orbital time, which gives
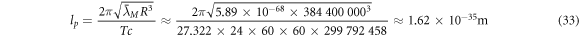
which is very close to the Planck length given by the NIST reference value of the Planck length of  , one standard uncertainty of
, one standard uncertainty of 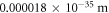 , and relative standard uncertainty of
, and relative standard uncertainty of 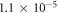 . That means that even our "rough" calculations are well inside the known standard uncertainty. It is important to note that we have not fudged or altered any formula here in a type of physics numerology, but have instead formulated it based on deeper reasoning about mass, G, and the Newton formula to find these simple relations. The important feature here is not that we can calculate the Planck length, but that we can do so from a Newtonian observation, without knowledge of any constant other than c. Here we assume that we obtained c by measuring the speed of light.
. That means that even our "rough" calculations are well inside the known standard uncertainty. It is important to note that we have not fudged or altered any formula here in a type of physics numerology, but have instead formulated it based on deeper reasoning about mass, G, and the Newton formula to find these simple relations. The important feature here is not that we can calculate the Planck length, but that we can do so from a Newtonian observation, without knowledge of any constant other than c. Here we assume that we obtained c by measuring the speed of light.
We can also find the proton Compton wavelength the standard way by  . Next, we count the number of protons in a handful of matter used in the large ball in the Cavendish apparatus; we can then find the Compton wavelength of the Earth, as described in this paper. When this is plugged into the formula above, we would also find the Planck length with no knowledge of G, but with knowledge of
. Next, we count the number of protons in a handful of matter used in the large ball in the Cavendish apparatus; we can then find the Compton wavelength of the Earth, as described in this paper. When this is plugged into the formula above, we would also find the Planck length with no knowledge of G, but with knowledge of  and c. However, we have already shown in this paper how we can also find the Planck length with no knowledge of G,
and c. However, we have already shown in this paper how we can also find the Planck length with no knowledge of G,  , or c.
, or c.
8. Standard uncertainty in lp and G and their connection
Assume we have measured the Planck length (with a standard uncertainty of  ) from some of the possibilities above. The relative uncertainty in the gravitational constant must then be
) from some of the possibilities above. The relative uncertainty in the gravitational constant must then be
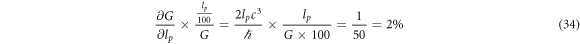
In other words, the standard uncertainty in the Newton gravitational constant will always be twice that of the standard uncertainty in the Planck length measurements. This is in line with what is found in NIST (2018) CODATA, which reports a relative standard uncertainty for the gravitational constant of 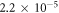 and
and  for the Planck length.
for the Planck length.
It is well known that the relative standard uncertainty for the gravitational constant is much higher than in the fine structure constant or the elementary charge, for example. This paper does not give any immediate procedures for improving on measures in G or lp
, but our findings, at least indirectly, explain why the uncertainty in G is so high. Measuring G is basically measuring  it is directly linked to measuring the smallest of all observable lengths, which we can do through gravity. The fact that there is high uncertainty in measuring the smallest of all units is not a surprise. However, our new approach may potentially also help researchers develop even more accurate methods in the future.
it is directly linked to measuring the smallest of all observable lengths, which we can do through gravity. The fact that there is high uncertainty in measuring the smallest of all units is not a surprise. However, our new approach may potentially also help researchers develop even more accurate methods in the future.
9. Summary of select findings
As we have discussed, we summarize some of our most important findings below:
- Newton's gravitational phenomena contains the speed of gravity, which is equal to the speed of light combined with the Planck length. In order to isolate the speed of gravity (light), we need to find the Planck length in isolation, which can be done from observation (no prediction needed) of gravity deflection, time dilation, red-shift, or the perihelion of Mercury observations. That is to say, we can find both the speed of gravity and the Planck length from gravity observations alone with no knowledge of any physics constants. This is in strong contrast to the general consensus in physics, where it has been assumed that one needs to know G, c, and
 to find the Planck length.
to find the Planck length. - We can also find the Planck length directly from any Newtonian gravity observation simply by knowing the speed of light from electromagnetic phenomena, and variables such as the distance center to center between the two masses. This is revolutionary, as one then can find the Planck length only from knowing the speed of light; there is no need for knowledge or findings of G or
 . Since we can extract the Planck length from Newtonian phenomena by taking out the speed of light, this strongly indicates that the speed of light was already embedded in Newton's gravitational phenomena, noting that we had to extract it to find something as essential as the Planck length. This strongly indicates that Newtonian gravity is moving at the speed of light.
. Since we can extract the Planck length from Newtonian phenomena by taking out the speed of light, this strongly indicates that the speed of light was already embedded in Newton's gravitational phenomena, noting that we had to extract it to find something as essential as the Planck length. This strongly indicates that Newtonian gravity is moving at the speed of light. - The c2 in general relativity prediction formulas of deflection, red-shift, and time dilation is not there to get c into these phenomena for predictive purposes, but to get c out of GM, since GM from a quantum perspective is
 , and that means we have
, and that means we have  , which does not contain c.
, which does not contain c. - The speed of gravity equal to c is hidden and embedded in G and M and therefore modern physics has mistakenly thought that Newtonian gravity moves at infinite speed. We naturally do not mean that Newton himself assumed that gravity moves at the speed of light—it is when one calibrates the model to a gravity observation, e.g. using a Cavendish apparatus, that one gets what is missing into the formula. Newton's formula, which is concealed by calibration inside G, contains both
 and lp
, something that we can now fully understand.
and lp
, something that we can now fully understand. - We can predict deflection, gravitational time-dilation, and red-shift from one constant alone, the Planck length, which we also can extract from any of these phenomena without prior knowledge of G, c, or
 .
. - It looks like we cannot extract the speed of gravity
 only by observations from a Newtonian type gravity observation in combination with gravity deflection, time dilation, red-shift without using other constants or things that contains c embedded, such as mass.
only by observations from a Newtonian type gravity observation in combination with gravity deflection, time dilation, red-shift without using other constants or things that contains c embedded, such as mass. - Newton neither invented nor did he use a gravitational constant. His formula was
 this formula can be used to predict any Newtonian gravitational phenomena and also to find the Planck length, if we have measured the speed of light from electromagnetic phenomena and use a time unit linked to the length based on the speed of light; that is, setting
this formula can be used to predict any Newtonian gravitational phenomena and also to find the Planck length, if we have measured the speed of light from electromagnetic phenomena and use a time unit linked to the length based on the speed of light; that is, setting  . In order to find the Planck length, we must combine this with knowledge of the Compton wavelength.
. In order to find the Planck length, we must combine this with knowledge of the Compton wavelength. - When we understand that the gravitational constant, in reality, is a composite universal constant
 , we understand that Newton's field equation is only consistent with observations if the speed of gravity is equal to the speed of light. Again, modern physics seems to have been misled by G and M, which, if not broken down further, conceals the fact that, by calibration, Newton's formula takes in the speed of gravity equal to the speed of light as well as the Planck length.
, we understand that Newton's field equation is only consistent with observations if the speed of gravity is equal to the speed of light. Again, modern physics seems to have been misled by G and M, which, if not broken down further, conceals the fact that, by calibration, Newton's formula takes in the speed of gravity equal to the speed of light as well as the Planck length. - Our findings strongly support that all observable gravity phenomena constitute a detection of the Planck scale, as pointed out by Haug [34].
10. Conclusion
We have demonstrated that the speed of gravity, together with the Planck length, is embedded and hidden in Newtonian gravity. All observable gravitational phenomena that we have presented here can be predicted solely by two physical constants: lp
and 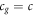 . This is the same scenario as predicted by some aspects of super string theory, but those approaches do not seem to have led anywhere. Newton did not assume that gravity moves at the speed of light when deriving his formula. Still, the speed of gravity being equal to the speed of light is embedded in the formula because one obtains what is missing into the formula through a composite constant that is calibrated to a gravity observation. Both the Planck length and the speed of gravity are needed, and one puts them into the formula by calibrating to a Newton-type gravitational phenomenon to an observed gravitational observation, with a Cavendish apparatus for example.
. This is the same scenario as predicted by some aspects of super string theory, but those approaches do not seem to have led anywhere. Newton did not assume that gravity moves at the speed of light when deriving his formula. Still, the speed of gravity being equal to the speed of light is embedded in the formula because one obtains what is missing into the formula through a composite constant that is calibrated to a gravity observation. Both the Planck length and the speed of gravity are needed, and one puts them into the formula by calibrating to a Newton-type gravitational phenomenon to an observed gravitational observation, with a Cavendish apparatus for example.
For three hundred years, we have looked at the Newton formula without understanding what it represents at a deeper level. This paper should bring us closer to what Newtonian gravity truly represents. After calibration, Newton's formula is fully consistent with the idea that the speed of gravity moves at the speed of light. However, for planets and stars moving relative to the observer, one potentially also needs to take relativistic masses into account. This view has implications for how we consider general relativity in the future, and also the idea that G simply represents a composite universal constant.
11. Conflict of Interest
The author declares that there is no conflict of interest regarding the publication of this paper.
12. Credit
Thanks to Victoria Terces for helping me edit this manuscript, and thanks to two anonymous referees for their useful comments.
Footnotes
- 1
The same is naturally the case if we come up with similar mass definitions, such as pounds; the units of the gravity constant would then be
 .
. - 2
Actually, Newton knew the approximate speed of light—as he stated in Principia it would take approximately 7 to 8 minutes for the light from the Sun to reach the Earth.
- 3
They show that
 , we will claim their
, we will claim their  embedded in it simply contains
embedded in it simply contains  , so that one is left with
, so that one is left with  .
.