Criteria of Fractal Reconstruction and Suppressing Background Events with the SePaC Method

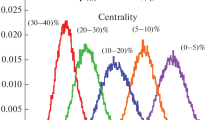
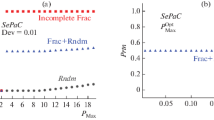
Abstract

This work analyzes the $SePaC$ method of fractals and various background events (mixed, random, and distributed according to Gauss’s law, as well as by power and exponential laws) in order to search and reconstruct fractal structures. It is shown that some of the background events are reconstucted as fractals. Dimensional distributions of various events are considered. It is found that these distributions for fractals and background events are different. Characteristics are proposed that describe the features of fractal structures. They are compared for fractals and background events. Criteria for background suppression are proposed and the results of their application are presented. It is found that the application of the criteria changes the distribution of background events by dimension, and the use of a combination of criteria suppresses the background.

Appendices

APPENDIX A

One distinctive feature of fractals is the difference between topological and fractal dimensions. The topological dimensions of a point, line, and plane are equal to zero, one, and two, respectively. The fractal dimension is determined by the dynamics of object formation. Fractals are characterized by different dimensions: Hausdorff–Besicovich, Minkowski (box-dimension), etc. [24, 25].

Hausdorff–Besicovitch dimension ${{D}_{H}}$ is called fractal and is defined as the value $d$ at which measure ${{M}_{H}}$ has a finite value

$${{M}_{H}} = \mathop {\lim}\limits_{\epsilon \to 0} \mathop {\inf}\limits_C \sum\limits_{i = 1}^N {l_{i}^{d}} .$$

(7)

Here, operator $\inf$ means the minimum of all possible coverings $C$ of the considered set. $N$ is the number of probes with size ${{l}_{i}} < \epsilon$ covering the object. The quantity ${{\epsilon }^{{ - 1}}}$ is called the resolution.

Minkowski dimension (box dimension) ${{D}_{b}}$ is determined by the formula

$${{D}_{b}} = - \mathop {\lim}\limits_{l \to 0} \frac{{\ln{N}(l)}}{{\ln{l}}}.$$

(8)

Here $N(l)$ is the number of probes of size $l$ covering the object.

For fractals with independent division (Appendix B), the box dimension coincides with the Hausdorff–Besicovich dimension, and for fractals with dependent and combined division (Appendix B), they are different (${{D}_{b}} > {{D}_{H}}$). Box dimension is a rougher characteristic, since it assumes the same size of fractal elements at the same level.

APPENDIX B

In this paper, we consider various types of fractals (fractals with independent, dependent, and combined divisions), which are varieties of Cantor sets (Cantor dust). Fractals with dependent and combined division are called fractals with unequal ratios.

Consider fractals with independent division. The most famous representative of this type is the triadic Cantor set, the formation process of which is shown in Fig. 9a. The original element is a unit line $[0;1]$ along the axis $X$. Let us conditionally divide it into three parts, corresponding to the formation of a fractal with a base ${{P}_{F}} = 3$. Let us delete the second part and leave the first and third. Let us call this procedure the act of dividing a fractal element in the process of its formation. The resulting structure is denoted by $S = (101)$, where $\left\langle {\left\langle 1 \right\rangle } \right\rangle$ denotes for the remainder and $\left\langle {\left\langle 0 \right\rangle } \right\rangle$ denotes for the excluded. The number of units in the structure determines the number of new elements in each act of division. At the next levels, the division process is repeated. The new elements are the same size, equal to ${1 \mathord{\left/ {\vphantom {1 {{{P}_{F}}}}} \right. \kern-0em} {{{P}_{F}}}}$ the size of the parent, and are divided independently.

Fig. 9.

Process of formation of fractals with independent (a), dependent (b), and combined (c) division.

Figure 9b shows the formation of a fractal with dependent division. Original element (line $[0;1]$) is conventionally divided into four parts (base ${{P}_{F}} = 4$). The first, third, and fourth parts remain at the first level (structure $S = (1011)$). At the next levels, the division process is repeated, taking into account that the segment consisting of the third and fourth parts represents a single object (dependent division). The number of new elements in each act of division is determined by the number of segments, not units in the structure. New elements differ in size (${1 \mathord{\left/ {\vphantom {1 {{{P}_{F}}}}} \right. \kern-0em} {{{P}_{F}}}}$ and ${2 \mathord{\left/ {\vphantom {2 {{{P}_{F}}}}} \right. \kern-0em} {{{P}_{F}}}}$ on the size of the parent).

The formation of a fractal with combined division is shown in Fig. 9c. The original element is conventionally divided into five parts (${{P}_{F}} = 5$). The second, third, and fourth parts remain at the first level ($S = (0111)$), forming a segment. At the next levels, a combined division of the segment occurs; namely, the second part is divided independently, and the third and fourth as a single object (dependently). The resulting elements differ in size (${1 \mathord{\left/ {\vphantom {1 {{{P}_{F}}}}} \right. \kern-0em} {{{P}_{F}}}}$ and ${2 \mathord{\left/ {\vphantom {2 {{{P}_{F}}}}} \right. \kern-0em} {{{P}_{F}}}}$ on the size of the parent). The number of new elements in each division does not correspond to either the number of units in the structure or the number of segments. To determine them, a full enumeration of various options for selecting them from a segment is required. Note that the $SePaC$ method tests hypotheses of independent and dependent division and approximately reconstructs fractals with combined division.