Methodology of the Construction of Computational Scenarios for Modeling Extreme States in Living Systems

Abstract

We consider a methodology for organizing hybrid computing structures to simulate abrupt changes in controlled natural processes and analyzing phases of extreme environmental phenomena. Systems of differential equations with the dynamically redefinable right-hand side at special moments (events) are used. The truth conditions for transitions are obtained from computing other equations for additional characteristics of the state of a generation. Threshold states in process modeling are the result of the inclusion of trigger functions. Their values on the right-hand side are specifically different from the neutral value only in narrow ranges of the space of changing characteristics of a hybrid system and depend on the initial conditions. The restricted limits of functions and their domain of values rest on the core of the threshold effects for the simulated biosystem, which are observed under special conditions. The method allows us to implement actual qualitative changes in management scenarios as bifurcations of the appearance (reduction) of equilibrium states or the boundary crisis of a complex attractor consisting of intervals scattered in a limited area. Computational scenarios for different population processes are investigated. The collapse of fish stocks is described in the model by the examples of cod in the North Atlantic and sturgeon in the Caspian Sea. The rapid outbreak of their abundance is modeled according to observations on the pulsation of the population size of pests of relict evergreen forests. The threshold scenario of the outbreak of insects in the scenario ends spontaneously due to the local exhaustion of forest resources with a sharp transition to fluctuations of the pest, which are ordinary for the environment. The methodology of organizing the structure for the population model is summarized to predict a wide range of extreme processes related to rapid changes in controlled biological systems and the spread of unwanted biological invasions.

INTRODUCTION

The paper is devoted to the development of modeling techniques to describe cases of the unsteady development of environmental processes and predict their abrupt qualitative changes. The method rests on various real examples.

Modern ecosystems function without a balanced equilibrium of their constituents, and the task of the rational use of bioresources becomes more difficult. There are sharp transitions, and these phenomena do not fit into regular fluctuations in the population of species. Changes in the evening out the diversity of species in ecosystems under human pressure are occurring rapidly. The astatic nature of the new environment does not prevent the adaptation of the species-invaders [1]. Traditional models of mathematical biology are not applicable to analyze situations in which sudden changes are taking place. Rapid shifts in population trends for different species are similar [2]; this will give mathematicians the opportunity to classify these transformations in terms of dynamic system theory. In the paper, we focus on the formation of specific computational model scenarios, which include factors of life cycle stages and changes in the population’s characteristics during adaptation. We consider the relevance of decision making by experts in the management of bioresources and regulation of long-term fisheries when trying to achieve the optimal exemption.

The aim of this paper is to develop a way to organize a hybrid computing structure that allows computer experiments to describe transitions to the unsteady dynamics of different forms and take into account nonlinear effects in meaningful ecological processes. We develop a mathematical apparatus in stages and note the variability of the choice of functions. As a result of a series of modifications and the development of a practical justification for real data, the idea of modeling techniques will be applicable to a wide range of problems of ecodynamics. Of interest is the approach that gives experts an algorithm to expand models in order to describe other special situations and extreme events in addition to the cases we have considered: outbreaks with a single peak and a population collapse.

Episodic extreme events have significant implications for the evolution of ecosystems. An aggressive predator without biotic resistance with a single outbreak destroys its new habitat, just as the poisonous crown-of-thorns starfish Acanthaster planci devastates coral reefs for years to come [3]. According to the logistics law, population growth should slow down at the equilibrium, but in reality the complete destruction of the ecosystem sometimes happens as in the textbook example of the extinction of deer on Bering Island. The threshold effects in regulating the efficiency of reproduction are an important cause of such extreme events both in the rapid spread of some species and in the rapid disappearance of others. There are interesting examples where unwanted species invasions are successfully stopped by biological suppression (releasing efficient natural enemies).

Traditional methods of modeling population invasions face a set of challenges when it is necessary to achieve an adequate description of extreme states in biosystems. Individuals are nonidentical by their reproductive characteristics. In a small group, the variance is stronger. The problem of the heterogeneity of individuals in models is partly solved in [4]. The second difficulty is that individual insects and fish undergo change in the life cycle. An entire population adapts to both the biotic environment and the loss of the largest individuals by fishing. The problem of modeling a complex life cycle is fundamental and is related to a population’s coevolution [5]. The resistance of predators and parasites in the new environment is seen theoretically as a motivating factor for adaptation and further species formation [6]. We can predict the moments of transitions to the suboptimal conditions of the interaction of species with the help of models if we compare model scenarios, including different strategies for managing bioresources.

We discuss the benefits of the approach to computing population’s basic characteristics, where we use auxiliary and evolutionary factors to predict a generation’s survival and final reproductive efficiency. The technique differs in the way predicative changes are organized using traditional differential equations with a hybrid timeframe. The novelty lies in the idea of constructing a redefinable computational structure separately from the basic equation, which varies the form, and several auxiliary equations. An example of the implementation of new ideas will be the formation of a structure of differential equations of generational dynamics in three forms for all stages of development. Transitions are controlled by the rate of the individual growth of generational organisms. The structure of the model is complemented by special functions; “trigger” effect in different practical tasks is activated at different stages of ontogenesis. The practical result is to model two current scenarios of biological cybernetics: the collapse of large fish stocks and an unexpected outbreak of dangerous insects destroying hectares of valuable evergreen forest.

As a result, we show that the state of collapse is caused by the difficult problem of developing a relevant management strategy in the exploitation of bioresources. Experts need to make a decision on production quotas now, and a reliable assessment of the biosystem’s response to the new impact can be obtained several years later. We explain the reasons why the two population models chosen for one management task are often contradictory and incompatible with each other on the important properties of qualitative changes in the behavior of their trajectories.

1. METHODOLOGY FOR BUILDING HYBRID STRUCTURES IN ECODYNAMICS

Systemically or sporadically, there is a change in the factors prevailing in a generation’s survival. A complex life cycle is an adaptation of species; therefore, the formation of a hybrid (continuous-event) structure of computation follows evolutionarily set ecological mechanisms. The actual task of the first stage of our work is to achieve a purposeful mathematical description of the threshold effects, i.e., those internal critical states that determine the qualitative change in the nature of developing the biological process. We can observe the threshold phenomena only in the narrow ranges of the characteristics of the state of the ecosystem process itself.

Important threshold effects include a sharp increase in the efficiency of reproduction observed in species during evolutionary adaptation to the breeding environment and weakening of the overwhelming biotic factor. An alternative threshold effect is a drop in survival at the early stages of ontogenesis in a small group. The threshold of a phenomenon is that when a population is reduced by a factor of three the number of new generations falls by a factor of five, which causes problems in the recovery of the population. As groups get larger, their number becomes smaller as shown in [7]. The frequency of encounters between predator and prey decreases with the aggregation of the prey. Food provision and security in the early stages of development in the group are increased. There is a positive effect of the aggregate group, when for the efficient growth of offspring we need to maintain a large population of the group. We cannot artificially again recreate large flocks at once. The group effect can become symmetrically negative due to competition factors.

The method of analyzing nonlinear processes is better built based on a mathematical description of the survival of generations of populations in early ontogenesis. The theory of optimal spawning of stock is based on predicting the survival of larvae and young fish [8]. According to Sir R. May’s concept of the “critical period” [9], in fertile fish species, fluctuations in survival at the larval stage play a significant role in the appearance of fluctuations in the total population. The average survival rate from spawn to sevruga fry according to T. Usova is 1% with the optimal flood mode [10]; hence, a survival rate of 1.5% becomes a significant success of the species in reproduction.

In the computational structure, we need to calculate the formation of a sexually mature generation, setting very different rates of attrition of the stages of development. When computing, it is relevant for the new models to explicitly distinguish the transitions between continuous equations for all stages of ontogenesis (making the system hybrid and eventful) [11].

In the case of changing conditions and factors in the ecological and physiological development of species, it is justified to form computational models as structures with switches. The term hybrid system refers to a wide variety of all structures with switches, different breaks, and regular impulses [12]. Hybrids include logic–dynamic systems in which the discrete part is described by logical variables [13]. We prefer to talk about our calculations as about predictively redefinable changes in the state of the system.

The complex of equations and rules we develop as logical functions will continue to be considered as a group of scenarios in the iterative form. The discrete component of the model has more convenient opportunities to change behavior in bifurcations. We can achieve balance, cyclical dynamics, or chaotic movement of different types. The shape of the boundary of the attraction areas of different attractors influences the behavior of a trajectory [14]. When analyzing models, we need to understand what we consider reasonable behavior of the hybrid model, and which nonlinear effects need to be excluded from the final discussion of the results.

We use the form of time with both discrete and continuous components for building a population model with pronounced stages of development in the life cycle. We need to adapt this well-known approach in modeling with complex time for biological problems. Discrete effects in the simulated process are manifested during the ontogenesis of the existing generation, and then there is an event, namely, the emergence of a new generation. Accordingly, different events are present within the interval of the ontogenesis of a generation and at the same time there are also interinterval switches. The structure of the time segments is important, because some intervals are the biological characteristics of populations and others are adaptation intervals depending on the conditions of generational development. Therefore, we use both the time-breaking into the frames of life of generations and calculations of events within the interval of the ontogenesis of the species.

The discrete elements of events need to be numbered according to their position in the sequence of frames in the continuous current of the total model time visible to an observer. To build a model of populations with pronounced stages of life cycle development, we develop a form of time in a more complex way than just alternating intervals in hybrid systems. We use the split: framing the hierarchy of continuous periods of time and inside large frames we leave room for numbered events tⁱ. We formalize the hybrid-event time, which is used in the calculations by our programming environment, as a multiset, namely, the combination of finite sequences of ordered elements

$$\bigcup\limits_n {\{ Gap\_Lef{{t}_{n}},{{{\{ {{t}_{0}},...,{{t}^{i}},{{t}^{{i + 1}}},...,{{t}^{I}},T\} }}_{n}},Gap\_Righ{{t}_{n}}\} } ,$$

(1.1)

where i is the serial number of the intraframe event ($0 < i \leqslant I < \infty$), n is the number of the time frame in the computational experiment, I is the number of events that are possible inside the frame, T is the point of completion of calculations in the frame in the units of model time (biologically, event T is interpreted as the achievement of the breeding season by a sexually mature generation), $Gap\_Left$ is a technical gap at the left boundary of the frame, and $Gap\_Right$ is an analogous gap (at the right boundary of the continuous frame) adjacent to the left gap of the next frame. For hybrid automata with normal event transitions between states, the number of events does not have to be tightly fixed or limited, but in our software implementation there is a framed time with internal events. Therefore, number I should be limited, because it is impossible to divide the ontogenesis interval t into an infinite number of constituents. There can be no events between t^I and moment $T$ that ends the frame. This is the difference between our method with the hierarchy of events from the theory of classical hybrid models such as the well-known task of calculating the trajectory after a ball bounces off an elastic surface.

The moment denoted in (1.1) by t₀ is a special event of the initialization of a model, which is always present by default, regardless of the existence of other events; this remark refers also to moment T, which a priori is presented in the software implementation of framed time. The form of time with a continuous and discrete component leaves gaps–boundaries $Gap\_Left[N(0) = f(\lambda ,q)$; w(0) = w₀] and $Gap{\kern 1pt} \_{\kern 1pt} Right$[t = 0] on the right and left of a continuous frame. The frame is adjacent to analogously numbered gaps between the adjacent time frames; the right gap of the nth frame becomes adjacent to the left gap of the (n + 1)th frame. Gaps that are not included in a frame, are required by us, because the boundaries of each period of time are included in the frame itself. Technical moments are required to zero out variables–counters and to perform adjustments at specified transition points to the calculation of the development of the next contiguous generation with t = 0. In experiments with external control, gaps are required to account for the removal or release of a batch of individuals when calculating N(0).

In hybrid models, little attention is paid to the time intervals in managing the change in continuous process, but formalizing significantly helps to set up and debug the operation of transitions. With (1.1), we create a hierarchy of events, ${{t}^{1}},{{t}^{2}},...,{{t}^{I}}$, which are specified by the calculations. We attribute the external management of the process in scenarios to interframe transitions. By this method, we make a simple fixation of the moment to move to the calculation of the dynamics of the next generation in the population age structure and determine the initial state for the number of individuals of the generation.

The first idea of our method is that the population process model is formed using a dynamically redefinable system. The attrition factors significantly vary among the three stages of ontogenesis. In the tasks of fish or insects, the key biological aspect, the stages of their life, allows us to consider the effects of changes in their life cycle as a factor of nonlinear dynamics. Various stages of the life of species with a deep transformation of the structure of the body have a different ecology and physiology; they become predators or victims.

The biological justification for the method is based on the theory of the “stock–recruitment relationship” from the famous work [15] in its modern representation [16]. The perceptions of the role of a functional dependence in the efficiency of reproduction are used to predict the level of exploitation of many stocks of valuable fish species; however, resource management based on statistical data analysis [17] is not always successful. Traditionally, the accepted designations are used for the indicators: S for stock and R for recruitment. Assume that at the initial moment there is a fairly significant parental stock of population S₀ with the average fertility λ. The task of prediction is to establish (according to the observational data) a functional relationship for the amount of the expected recruitment R by time T (the achievement of a sexually mature state by a generation). Further, it is necessary to investigate the effect of this functional link on the position of the equilibrium or fluctuation of the population, including complex cases: the phenomena of collapse and outbreak. The task of regulating fishing requires the use of the bifurcation theory.

The importance of stage ontogenesis is noted by many authors in the analysis of restocking [18]. The second idea of our methodology is to set events on the set of ratios between model values that are not necessarily related to the model time. These events are followed by changes in the process of calculating equations. To build a model, we propose a predictively redefinable computing structure with three successive generational state modes: from $N(0) = \lambda S$ to $R = N(T)$. The model of the attrition of the population from the original value N(0) is written by a differential equation with the set of consecutive forms for its variable right-hand side. In addition, as part of the base model, we specify a variety of predicates for changing the calculation mode: transition to another form of the right-hand side of the equation. We determine the logical functions themselves separately.

Assume that the limit on the number of stages I = 3 and intraframe events $i \in \{ 1,2,3\}$ holds for the correspondence of segments within the frame to the number of stages of ontogenesis. We present the basic skeleton model with three nonspecific generalized stages of the development of ontogenesis determined on a fixed time interval “glued” from floating subintervals: in a series of numbered frames

$$t \in [0,T] \subset \bigcup\limits_{n = 1}^{{{n}_{\infty }}} {\{ {{{[{{t}_{0}},{{t}^{1}},{{t}^{2}},{{t}^{3}},T]}}_{n}}\} } .$$

To be clear, the following base model includes two intraframe events and is defined by three forms of the right-hand side of one differential equation:

$$\frac{{dN}}{{dt}}{{ = }_{{}}}\left\{ \begin{gathered} - ({{\alpha }_{1}}w(t)N(t) + \beta )N(t),\quad {{A}_{1}}(t),{{Z}_{1}}(t), \hfill \\ - {{\alpha }_{2}}N(t){\text{/}}w(\tau ) - \beta N(t),\quad {{A}_{2}}(t),{{Z}_{2}}(t,w(t)), \hfill \\ - {{\alpha }_{3}}w(t)N(t - \eta ) - \beta ,\quad {{A}_{3}}(w(t)),{{Z}_{3}}(t) \hfill \\ \end{gathered} \right.$$

(1.2)

with the inclusion of the lag η < τ related to exhaustion of resources by the previous stages; w(τ) is an important indicator of the attained size by the end of the first stage of development of individuals. In (1.2), the main value N(t) is the current generation size: $N(t) < N(0)$$\forall t > 0$. Descending coefficients ${{\alpha }_{1}} > {{\alpha }_{2}} > {{\alpha }_{3}}$ and β are differently interpreted indicators of juvenile mortality depending on the population. The time subinterval τ is the duration of the first embryonic stage of development without external nutrition to the stage of active larvae.

In our method, reconstructions in (1.2) are performed between modes of the change of state (the rate of attrition changes). The method differs from the organization of direct transitions between the states themselves as is programmed in the discrete-event models. The form for the algorithmic implementation of the model in the computing environment is a hybrid machine [19]. We present such a transition machine in the AnyLogic environment as a graph with oriented arcs: the directions of the transformation of the right-hand side of the initial position by the order of activation of the nodes of the graph. With at least one input arc, the active node of the hybrid machine corresponds to the current mode of the change of state, of one of the three forms of equations in (1.2) set by us. In a computing environment, we can make changes both when we enter the node of the machine and when we exit. The start and completion of the activity of each form of the right-hand side is controlled by the predicates, the logical functions of the arcs that take the meanings of true of false depending on the fulfilment of the ratios between the variables included in the predicates. For each form, ratios are organized for the launch ${{A}_{1}},{{A}_{2}},{{A}_{3}}$ and completion of the calculations ${{Z}_{1}},{{Z}_{2}},{{Z}_{3}}$. We call pairs of predicates ${{A}_{i}},{{Z}_{i}}$ together the rules of activation of transitions between modes of a change in state:

$${{A}_{1}}(t = 0),\quad {{\bar {Z}}_{1}}(t < \tau );\quad {{A}_{2}}(t = \tau ),\quad {{\bar {Z}}_{2}}(w(t) < {{w}_{k}});\quad {{A}_{3}}(w(t) = {{w}_{k}}),\quad {{\bar {Z}}_{3}}(\tau < t < T).$$

(1.3)

The predicates in (1.3) use the threshold level w_k for the exit of the generation from the pressure of juvenile “quadratic” mortality factors. The presence of threshold w_k follows from the dynamics of the dimensional development indicator $w(t) = f(N(t))$. In (1.3), we write predicates for the completion with logical denial, because the transition to the next form (or stopping the machine and reinitializing the internal variables) will be possible when the ratios are violated, because the form of the right-hand side is calculated on the principle “as long as the conditions are fulfilled.” For each form of the right-hand side of (1.2) in the transitions, the intermediate initial conditions are recalculated: ${{N}_{1}}(0){{{\text{|}}}_{{t = t_{{}}^{1}}}} = N{{{\text{|}}}_{{t = \tau }}}$.

Pairing with previous end values on each subinterval is performed. The last event fixes the state at the end of the calculations. In the simple case, the stop occurs on the right boundary of the given interval [0, T]. A strict sequence of switches within [0, T] (as shown in the case of the model of transition between stages of ontogenesis) for machines is not a mandatory condition [20]. We can implement an arbitrary order for selecting the right-hand sides from a variety of possible sides.

In order to implement hybrid systems, modifications of the Godunov scheme are used in the approximation of boundary problem solutions [21]. The methodology is developed, and even the theory of Lyapunov’s functions is generalized for such systems [22]. When implementing computing systems with switches, we should consider avoiding the continuous-time degeneration mode, namely, the well-known Zeno paradox [23]. The numerical algorithm can wander in the neighborhood of the break conditions, while the lengths of continuous segments will tend to zero with an infinite number of such bars; therefore, hybrid systems use methods of predetermination of states [24] and stitching of trajectories.

The truth for starting and finishing predicates is checked by the time frames (we call such transitions time-forced) or is determined by the internal dependences (relation-forced). It is more interesting when the transition occurs after comparing the ratios of values in the internal model variables than from time. Next, we describe the values related to the calculations of auxiliary equations and the modeling methods for the growth rate w(t).

2. THE RELATION BETWEEN AUXILIARY EQUATIONS AND PREDICATES

The third idea of the methodology: it is necessary to supplement the calculation of the reduction in population by calculating other biological indicators in order to be able to apply predicate sets from (1.3). The model’s auxiliary indicators should be easily measurable.

The most important indicator is the rate of the average weight growth of generations, which is shown for different biological objects [25]. The paper [26] investigates the dependence of the mortality of fish larvae on their average weight. The effect on the survival of the factor related to competition for resources between the individual generation was established experimentally for the rate of development of the caterpillars of pests and ladybugs in the [27]. We solve the basic hybrid structure (1.2) numerically in relation to the auxiliary indicator of the dimensional characteristics of the generation. We write an additional equation of the system for the pace of individual development $w(t)$ as follows:

$$\frac{{dw}}{{dt}} = \frac{\rho }{{\sqrt[3]{{{{{(N(t) + \delta )}}^{2}}}}}},$$

(2.1)

where δ is an amendment, $w(0) = {{w}_{0}}$, and $\rho \gg \delta$ is fixed and reflects the availability of food resources; this can be applied in most cases where the rate of replenishment of feed objects is high, as for the case of large marine fish. It is justified that there is an achievable threshold level of the weight of the body $\bar {w}$. When this state is achieved, individuals of the generation no longer experience the pressure of mortality factors, which are squarely dependent on the population and are called compensatory. Individuals become able to move, avoid encounters with predators, or are no longer vulnerable to attacks of parasites that afflict the larvae stages.

Variant (2.1) considers the static conditions. We can set the available food resources in the numerator dynamically: $\rho (t)$—by the third equation. If it is assumed that the feed base tends to a stationary equilibrium $\rho (t) \to \Upsilon$, then we can use simple equations of cybernetic self-regulation. Here, the Ferhulst model is applicable with the most popular quadratic form of self-regulation of the population in the following form:

$$\frac{{d\rho }}{{dt}} = \vartheta \rho (t)\left( {1 - \frac{{\rho (t)}}{\Upsilon }} \right) - \varsigma N(t),$$

(2.2)

where $\vartheta$ is a reproductive parameter comparable to the feed consumption factor ς, while parameter $\Upsilon$ is the balance value of equilibrium, meaning the saturation capacity of the ecological niche. The environmental conditions of bioresource management can be related to climatic or seasonal changes, where the vibrational dynamics of feed resources is important. We can use a one-lag equation $\dot {\rho } = \vartheta f(N(t - \xi ))$ instead of (2.2). For example, we can directly introduce lag ξ into Eq. (2.2) and apply the properties of the Hutchinson equation model with the feed withdrawal factor ς:

$$\frac{{d\rho }}{{dt}} = \vartheta \rho (t)\left( {1 - \frac{{\rho (t - \xi )}}{\Upsilon }} \right) - \varsigma N(t).$$

(2.3)

The behavior of (2.3) depends on the value of the product of the model parameters $\vartheta \xi$ (see [28]). With increasing $\vartheta \xi$, we observe the usual Andronov–Hopf bifurcation with the occurrence of an orbitally stable cyclical trajectory, which is denoted by ${{\rho }_{*}}(t;\vartheta \xi )$, instead of fading vibrations. The asterisk–subscript usually denotes a cyclical trajectory; and an asterisk–superscript; a stationary point of iterations. With increasing $\vartheta \xi$, the trajectory of the cycle ${{\rho }_{*}}(t;\vartheta \xi )$ takes an inharmonic (relaxation) form with an increase in the amplitude of vibrations at extremely low $\min {{\rho }_{*}}(t;\vartheta \zeta ) \to 0 + \varepsilon$.

Instead of the quadratic function, we can use the more complex self-regulation function

$$\frac{{d\rho }}{{dt}} = \vartheta \rho (t - \xi ){{e}^{{ - b\rho (t - \xi )}}} - \varsigma N(t) - \chi \rho (t).$$

(2.4)

Equation (2.4) includes an independent mortality rate $\chi ,\chi < \varsigma$, which reflects the deliberate removal of a resource available to the population. Lag ξ here does not carry an important interpretation but is required for the phenomenological description of unforced fluctuations of the abundance of resources. However, the most obvious options for lag equations in numerical modeling have a significant disadvantage. If it is necessary to increase the period between the peaks of fluctuations with the growth of $\vartheta \xi$, a rapid increase in the amplitude of the cycle ${{\rho }_{*}}(t)$ is found. The minima become extremely small: $\mathop {\lim }\limits_{\xi \vartheta \to \infty } \min {{\rho }_{*}}(t) = 0$. Low resource values ρ are unacceptable for the calculations of (2.2). Such a model is not correlated to the ecological reality: then the whole generation would die at once; therefore, in some small rivers of Canada, there are no “even” (or “odd”) populations of pink salmon, whose life cycle is strictly two years.

We propose a new special equation for the vibrational version of the resource dynamics model for the particular average growth of individuals of the generation, where the current difference of $\Upsilon - {{N}^{2}}(t - \xi )$ is an important factor:

$$\frac{{d\rho }}{{dt}} = \vartheta \rho (t)\left( {\frac{{\Upsilon - {{N}^{2}}(t - \xi )}}{{\Upsilon + \mu {{N}^{3}}(t - \xi )}}} \right) - \varsigma N(t).$$

(2.5)

In (2.5), after the bifurcation of the birth of the cycle, we get relaxation oscillations (the Λ-shaped peaks of a significant amplitude of a nonharmonic shape with the scaling factor μ < 1) starting from a zero threshold near equilibrium with the lost stability. The situation corresponds to the autumn minimum of feed, and this is usual for plankton. Variant (2.5) without a lack of deep lows of fluctuations is relevant for the set of tasks with the seasonal variability of $\rho$, where several generations are formed in different conditions. However, the method allows us to set variations for providing resources with a simple tool. We can change the value of the feed base $\rho$ for various generations by the table function when changing frames.

As a result of the numerical solution of the Cauchy problem (1.2) with (2.1) for all significant $N(0)$ (natural numbers), we obtain the functional dependence $N(0) \to N(T) \equiv \varphi (N(0))$ on the initial (eggs or spawn) group of individuals. Then we can again calculate $N(0) = \lambda S$ for the next iteration; here, S is traditionally the population of mature reserves. The biological justification for the calculation of R = $N(T) = \varphi (N(0))$ in the form of an evolutionary operator for the analysis of iterations ${{R}_{{n + 1}}} = \varphi ({{R}_{n}})$ rests on the principles of the theory of the formation of the replenishment of commercial stock and the role of the nonlinear nature of dependences $R = f(S)$ in the expert management of fishery bioresources (this theory is described in [29]).

The behavior of iterations is subject to fundamental theorems but it is insufficient to use well-known properties of the occurrence of cycles of even and odd periods in order to describe current examples from the dynamics of insects and fish. In smooth dependences, it is necessary to add features to describe the jumpy trajectory changes. We have to avoid jumpy changes in the internal parameters of the hybrid system to preserve the theoretical validity of the entire methodology. It is completely unrealistic to change the key characteristics $\lambda ,{{w}_{0}}$ and τ. In complex biological systems, individual population parameters do not change suddenly but the functions of regulation are adjusted; they determine the direction of the evolutionary trend [30].

3. THE VARIABILITY OF THE MODELING METHOD

The rate of generational growth can be described in different ways: the classic equation of the balance of anabolism and catabolism by L. von Bertalanffy or another predicative structure from a set of forms of the right-hand side of the equation with time-lapse transitions between them. The task of such equations is to describe the factors of indirect regulation of the generation; and in the basic model, the direct factors of attrition. The hybrid system can include specific forms of regulating survival in addition to the typical quadratic form. The method, which allows us to expand the basic model, makes the idea relevant for the extreme dynamics of many species with a high level of fertility λ; i.e., for outbreaks of insects with an incomplete cycle of transformation. Many harmful phytophagous insects are regulated by parasites. Riders and wasps usually attack one of the stages of development (most often eggs) [31]. The reaction of parasites is conditioned by the presence in mass of available victims, which are easier for them to detect in clusters than in a homogeneous distribution. In modeling the rate of attrition, the effect of a mass attack can be taken into account by including N(0) in the equation but only in the first stage:

$$\frac{{dN}}{{dt}} = - ({{\alpha }_{1}}w(t)N(0) + \beta )N(t),\quad 0 < t < \tau .$$

(3.1)

This method takes into account the features of the regulation of the survival of eggs for insect pests. The survival rate of small insects is due to the density of immobile victims in an attack by their enemies; this is used in the deliberate release of parasites for the artificial biological suppression of many butterflies.

Hybrid time modeling is realistic in describing the evolution of the stages of life and the variability of the number of auxiliary equations. We show how to take into account (pointwise) the critical factor, which is important only for one of the stages.

4. THE METHOD OF INCLUDING TRIGGER FUNCTIONS

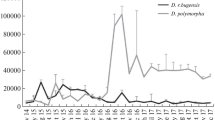
It is known from the practice of observations that if the population size is small, the role of adverse environmental factors in the reproduction of populations increases many times. A disproportionate reduction in fish restocking cannot be foreseen in advance by correlational methods. Suddenly, the efficiency of the natural spawning of Acipenser stellatus sevruga decreased as can be seen in the population of young fish that migrate from the river to the Caspian Sea. The decrease occurred sharply when the size of the spawning stock of sevruga became less than the threshold (420 000 individuals) due to systematic overfishing. Figure 1 presents the data from [32] (processed by us using the moving average method) on the sevruga reproduction at the spawning grounds of the Lower Volga.

Fig. 1.

Efficiency graph of sevruga reproduction in Volga with two peaks.

The graph shows valuable and rare data and allows us to directly assess the form of dependence in the efficiency of replenishment up to 2007; here, this dependence has two explicit peaks. For other cases, we do not have a way to solve the reverse problem, i.e., unequivocally restore the functional dependence using the data of observations. If the population is stable in a state of equilibrium, then in the graph we see only condensations of points at the equilibrium; however, Acipenser stellatus sevruga of the Caspian Sea is now threatened with complete extinction, because fishing in the Volga has not been stopped in a timely manner and illegal fishing continues in this sea.

The need to take into account the threshold changes in the parameters is important in explaining the problem of the low efficiency of artificial reproduction of sturgeon in the Caspian Sea. The hydrological regime of the Volga River was broken in the 1960s. Since the late 1970s, artificial reproduction has been used to increase sturgeon catches to 30 000 tones, but catches from 1979 have continued to decline steadily until the ban on fishing. Ichthyologists could not explain such a low return rate of fish ripe for spawning from the Caspian Sea back to the Volga from the volume of the initial output of young fish [33]. Inflating expectations of the commercial return from artificial reproduction became one of the reasons for the degradation of valuable populations. When predicting the volume of stocks and the proportion of catches, ichthyologists rest on the expected industrial return indicator, which is determined by correlational dependences [34].

The problem of predicting the fate of the Caspian sturgeon has led to another idea of our approach: the introduction of trigger functions to the basic predictively redefinable dynamic system with hybrid time. At their core, these are dynamic factors for iterations ${{\varphi }^{n}}({{x}_{0}};{{\Psi }_{t}}),{{\Psi }_{t}} \ne \text{const}$ but with a limited impact area on the admissible set of values of the argument. The functions will retain their value throughout the combined generation model time-frame interval but will vary in the next numbered elements of the set ${{\{ [{{t}_{0}},...,{{t}^{i}},{{t}^{{i + 1}}},...,T]\} }_{n}}$ from frame to frame. The triggers need to be selected (separately from the conditions of each environmental task) in the model at the desired stage of development. A stage requires only one trigger.

In our generational attrition equation, there are two mortality rates: quadritically dependent on intraspecies interactions $\alpha {{N}^{2}}$ and independent linear $\beta N.$ For the third stage, we do not use the quadratic factor of the decline in (1.2). The term $\alpha w$ takes into account the rapid exhaustion of the resources required for development as the biomass of fish increases. It turned out that it makes sense to take into account the loss of reproduction for migratory fish at a low density, which entered the spawning ground in the river at moment t₀. The effect of the loss of reproductive activity of the fish is implemented in the model by an additional dynamic factor $\Psi [S]$ functionally dependent on the state of stock S. It is included in the term βN, which takes into account the generation’s mortality independent of density:

$$\frac{{dN}}{{dt}} = - \alpha w(t){{N}^{2}}(t) - \Psi [S]\beta N(t).$$

(4.1)

In (4.1), $\Psi [S]$ is given in brackets, because the value of the parental stock is unchanged in the calculation of the loss of the recruitment: $S = {\text{const}},$ $t \in [0,T]$. The effect of the demographic pit for sevruga (Fig. 1) is limited in the model by the range for the following values taken by the function Ψ: $\forall S \in {{{\mathbf{Z}}}^{ + }}$ $\Psi (S) \in [2,1)$. By the statement of the task, we can limit values of the parent population S to a subset of natural numbers S < S_max. Assume that $\Psi (S) = 1 + \exp ( - \sigma {{S}^{2}})$ depends on the size of the parent population S. From the current value of S, we determine the initial conditions N(0).

According to our idea, the region of admissible trigger functions for the first stage on the right should have a unit limit. The trigger Ψ should become neutral if it is no longer necessary:

$$\Psi (S) = 1 + \exp ( - \sigma {{S}^{2}}),\quad {{\lim }_{{S \to \infty }}}\Psi (S) = 1,\quad \Psi (0) = 2,$$

(4.2)

where the parameter σ < 1 directly reflects the severity of the threshold effect. The biological cause of the effect described by the method comes from a decrease in the probability of spawning pairs forming over the course of spawning grounds. Here are some examples of hybrid structures and trigger functions to simulate two critical situations for bioresource management. This effect leads to the presence of the critical population size, which is necessary for the stable existence of the population. The hypothesis that such a minimum population exists is being confirmed increasingly often. In 2020, news agencies reported that the largest freshwater fish, namely, the chinese paddlefish of the Psephurus gladius species was officially recognized as extinct.

5. THE PRACTICE OF USING A HYBRID STRUCTURE AND A VARIETY OF ATTRACTORS

The combined model’s numerical solution allows us to calculate the resulting $N(T) = R$ for an admissible initial stock. We use this dependence of φ as an evolution operator for functional iterations: ${{R}_{{n + 1}}} = \varphi ({{R}_{n}}) - {{q}_{n}}{{R}_{n}}$ ($n = 1,2,3...,{{n}_{\infty }}$), where $q \in [0,1)$ is the share of the commercial withdrawal. In regulated fishing, q catches are calculated for each season n. Magnitude ${{n}_{\infty }}$ is specified here as the number of iterations for which we will consider that the state of the trajectory in computational experiments is asymptotic; for most calculations ${{n}_{\infty }} = {{10}^{4}}$ is sufficient, while we use ${{n}_{\infty }} = {{10}^{6}}$ to establish signs of the chaotic behavior of iterations according to the fact of the exponential dispersal of similar trajectories (the well-known physical criterion of chaos [35]).

In the hybrid model, the calculation of the decline of successive generations with the removal of fishing is set with the expression for the initial conditions of the first stage of development: ${{N}_{{n + 1}}}{{{\text{|}}}_{{t = 0}}} = (1 - {{q}_{n}})\lambda {{N}_{n}}{{{\text{|}}}_{{t = Tn}}}$. Changes in managing the impact of the strategy of fishery q_n will not be difficult to vary in special gaps during the computational experiment.

The model can implement the current nonlinear effects. The chaotization of the trajectory through a cascade of bifurcations of doubling a period can be obtained in the iterations of the known dependences to calculate the replenishment of fish stocks, as in ${{x}_{{n + 1}}} = a{{x}_{n}}{{e}^{{ - b{{x}_{n}}}}},$ a > e², and in ${{x}_{{n + 1}}} = {{{{a{{x}_{n}}} \mathord{\left/ {\vphantom {{a{{x}_{n}}} {1 + \left( {{{x}_{n}}{\text{/}}B} \right)}}} \right. \kern-0em} {1 + \left( {{{x}_{n}}{\text{/}}B} \right)}}}^{b}}$, b > 2, where a is the reproductive potential and b reflects the pressure of environmental factors. We do not consider that this property with a fractal attractor and a continuum of unstable trajectories is relevant to our tasks. Compared to the nonlinear iterative models from the review [36], which were earlier used in the calculations, we obtain the original properties of the dynamics of the model’s trajectories; these properties are interesting for the problem of predicting the event of the collapse of fish stocks.

We use (1.2) and (2.1) with supplement (4.1) and (4.2); we find the separation of the phase space for the trajectory by at least one unstable point. Such a stationary point $x_{r}^{*} = \phi (x_{r}^{*})$, whose neighborhood are left by trajectories at any small perturbations, is called a repeller as opposed to a stable attracting set, namely, the attractor Λ. It can be said that the repeller of a dynamic system is an invariant set that turns into an attractor over time [37]. In a simple case, a repeller acts as a boundary, when the starting points close to each other ${{x}_{{01}}} \in (x_{r}^{*} + \varepsilon )$ and ${{x}_{{02}}} \in (x_{r}^{*} - \varepsilon )$ are simply monotonically attracted to different attractors, or $\mathop {\lim }\limits_{n \to \infty } {{\phi }^{n}}({{x}_{{01}}}) = - \infty$ and $\mathop {\lim }\limits_{n \to \infty } {{\phi }^{n}}({{x}_{{02}}}) = + \infty$.

We distinguish unsustainable stationary points of iterations: isolated repellers without points-prototypes or open repeller points with points-prototypes (right or left of themselves) and prototypes of these prototypes. An important condition for a dependence is the position of the extrema ${{R}_{{\min }}} > {{R}_{{\max }}}$.

It is important for us that if the point $\exists {{x}_{{r2}}}$ is a direct prototype, which under the influence of the evolution operator ϕ is mapped into the repeller point $\phi ({{x}_{{r2}}}) = x_{r}^{*}$; then it also belongs to an invariant set of iterations. A repeller can have more than one direct prototype, and each is related to an invariant set of points-prototypes ${{\phi }^{{ - n}}}(x_{r}^{*})$ not attracted to attractors. Because of the properties of the prototype combinations at such points-repellers, the boundary of the attraction area of the attractors is complicated. A scenario is possible when the attractor crosses its boundary.

A bifurcation is simply a qualitative reconstruction of a phase portrait of a dynamic system, and bifurcations allow us to see changes in the behavior of the trajectory. Continuous and discrete systems have different bifurcation systems, although two of three of them appear similar. We will use bifurcations in the construction of scripted models and to describe situations with the control. As a criterion for stability in stationary iteration points, we use the value of the derivative $\phi {\kern 1pt} '({{x}^{*}}) \in ( - 1,1)$ [38]. The concept of a “strange attractor” with the property of local instability is widely known. Strictly speaking, a strange attractor does not have to be chaotic [39] but in the present paper we consciously do not develop this theme which was popular in the last century. The use of fractal-like objects in ecodynamic models was considered in [40]. The presence of chaotic attractors in biological models has been greatly overestimated, because such a behavior leads to contradictions when compared to real observations of water-bodies when changing their trophic status, known in the biological literature as the “paradox of enrichment” [41]. We do not consider the emergence of a global strange attractor to be an advantage for the model of a particular population of sevruga or cod.

The model dependence from (1.2)–(2.1) with the trigger component (4.1) and (4.2) has more than one maximum, and iterations have two areas of attraction of alternative attractors. The nonunimodal function does not meet the conditions of the Signer theorem [42], which are necessary for the implementation of the scenario of transition to a global chaotic attractor through a cascade of bifurcations of the doubling of the cycle period: according to Feigenbaum’s theory of the formation of the cycle of the infinite period p at the finite growth of the parameter [43]. If the Signer criteria are violated at some point when the parameters change, there will be two alternative cycles of period p = 2.

In the work of A.M. Blokh and M.Yu. Lyubich [44], which summarizes the results of J. Guckenheimer [45], it is shown that for functional iterations there can be four topological types of attractors: the simple equilibrium x* (end-period cycle); an attractor homeomorphic to the Cantor set (this is not a dense set anywhere, without internal points); and an interval attractor as a combination of an infinite set of incoherent segments that can create all the points ${{\phi }^{{ - n}}}(x_{r}^{*})$. The fourth type is the solenoid attractor.

The model can have the ability to form a chaotic movement due to the many points that do not fall into the attraction area of the attractors, because they are prototypes of unstable stationary point-repellents. When the position of the extremes of our dependence $\varphi (\lambda S)$ changes, these boundary $\partial \Omega$ points for the area of attraction $\Omega$ form a continual set of unattracted points. There is a different type of transitional chaotic movement than in Feigenbaum’s theory on the accumulation of a doubling of the cascade of bifurcations. For iterations ${{x}_{n}} = f({{x}_{n}}) \pm \iota$, three types of metamorphosis of the attractors can appear. The bifurcations of stationary iteration points can be direct and reverse. A direct bifurcation is a doubling of the cycle period ${{p}_{m}} = {{2}^{{i + 1}}}$ and a reverse bifurcation is a halving of the period ${{p}_{m}} = {{2}^{{i - 1}}}$. For a reverse bifurcation, it is not necessary to reduce the control parameter; there are iterations where when the parameter increases first there is a cascade of increase of the cycle period ${{p}_{m}} = {{2}^{{i + 1}}}$ and then a cascade of changes of the period with it decreasing in powers of two ${{p}_{m}} = {{2}^{{i - 1}}}$.

Attractors, as compact subsets of the phase space, can instantly lose the property of invariance $f(\Lambda ) \in \Lambda$ if they get a nonempty intersection $\Lambda \cap \partial \Omega \ne \emptyset$ with the boundary $\partial \Omega$ of the closed area $\Omega ,\forall {{x}_{0}} \in \Omega \mathop {\lim }\limits_{n \to \infty } {{\phi }^{n}}({{x}_{0}}) = \Lambda$; this depends on the properties of their area of attraction Ω. The boundary $\partial \Omega$ is not included in this set of points of the region of attraction Ω and can be a point or a set of locally incoherent points (as in our example) or form a fractal structure as the known closed set of Julia, which itself cannot be drawn.

Thus, specific applications overlap again with the fundamental problems of dynamic systems. For example, if we consider iterations of the function${{f}^{{(3)}}}(x;a) \equiv f(f(f(x;a))),$ $f(x;a) = ax{{e}^{{ - bx}}},$ $0 < b < 1$ at the value of the bifurcation parameter $a = {{a}_{3}},\;{\kern 1pt} {{a}_{3}} = 22$, 255 such that ${{f}^{n}}(x_{1}^{*};{{a}_{3}}) = {{f}^{{n + 3}}}(x_{1}^{*};{{a}_{3}})$, then the areas of attraction of the three stable stationary points $x_{1}^{*},\;x_{2}^{*},\;x_{3}^{*}$ at the iterations ${{x}_{{n + 1}}} = {{f}^{{(3)}}}({{x}_{n}};a)$ will be mixed (intermingled basins of attraction according to the terminology in [46]). In this case, for each point $\forall {{x}_{{01}}} \in {{\Omega }_{1}}$, $\mathop {\lim }\limits_{n \to \infty } {{f}^{{(3)n}}}({{x}_{{01}}}) = x_{1}^{*}$, there is an arbitrarily small (ε > 0) neighborhood and the condition for the starting points holds: $\exists {{x}_{{02}}},\;{{x}_{{03}}} \in {{x}_{0}} \pm \varepsilon ,$ ${{x}_{{02}}} \in {{\Omega }_{2}}$ ${{x}_{{03}}} \in {{\Omega }_{3}}$.

6. NONLINEAR DYNAMICS OF THE REAL COLLAPSE OF BIORESOURCES

We develop a model of a bioresource depletion scenario that does not last long, as it did with the stocks of sturgeon fish in the Caspian Sea, but happens suddenly for ichthyologists: in the form of a collapse.

A sharp collapse is fundamentally different from the gradual monotonic depletion of fish stocks. The degradation of cod fishing stocks in the North Atlantic in 1992 is the largest collapse in terms of economic consequences [47]. In Canada at the end of 1992, 25 000 employees lost their jobs from the end of the centuries-old fishing industry.

Wikipedia has devoted a detailed article to the collapse of cod, which presents the graph of the dynamics of catches before the collapse of the fishery; however, the graph from Wikipedia does not contain the complete data. Figure 2 is much more informative for analysis. The solid line in Fig. 2 shows the dynamics of real catches and the dots show the size of the quota for catches (in thousands of tons). The dashed line indicates the calculated estimated value of cod stocks, which (as it turned out after the collapse) did not correspond to the true situation. Obviously, the estimate of stock S is overly optimistic, the expected stock–recruitment curve f(S) for cod is above the real curve, and the curve’s extrema close to the thresholds of the stock were not estimated.

Fig. 2.

Dynamics of collapse of cod stocks of 1992 on Atlantic coast of Canada according to [48].

According to the graphs in Fig. 2, there were two sharp drops in catches in the North Atlantic cod population (without the recovery of fish stocks); therefore, in the computational scenario, also two transformations of the phase portrait of the dynamic system must be found.

After the first drop of catches in the 1970s, fishermen could not catch the quota allocated to them for five years. Estimates of the optimal withdrawal are calculated using the standard cohort models and statistical forecasting methods. Then the catches found equilibrium with the estimates of quotas. For a long time in the 1980s, the quota of cod was mastered and barely changed for ten years. Suddenly, the fishing industry collapsed. The authors of [48] the article in which we found the graph, pessimistically predicted the recovery of cod fishing in Newfoundland over the next nine years; however, the recovery had not taken place even by 2018. The moratorium on catching fish was initially imposed for two years. None of the experts-biologists predicted such a long period of degradation of valuable bioresources. Usually, fish stocks decrease gradually and monotonically year-after-year. Collapses previously occurred with herring and anchovy, i.e., short-cycle fish, and they restored their stocks by themsleves. The Atlantic halibut Hippoglossus hippoglossus, once related to a valuable and abundant fishing species, could not recover after the collapse.

The Gadus morhua cod is a predator with a long life cycle and has only been fished for a few generations. In addition to the reduction of the population, there have been changes in the genetic structure of the population. Individual cods began to gain weight more slowly but their puberty decreased and their life cycle decreased. Such shifts in the characteristics of ontogenesis can be described by an extended set of parameters of the auxiliary equations of our hybrid computational structure. Experts continue to discuss the hidden causes of the local disaster even 29 years later.

7. ANALYSIS OF THE COMPUTATIONAL SCENARIO OF THE COLLAPSE OF BIORESOURCES

For the mathematical implementation of such a scenario of collapse having two stages, we propose a scenario with two transformations in the dynamics of the iterations. The relation must have four nontrivial stationary $\varphi (R_{i}^{*}) = R_{i}^{*}$ states: $R_{1}^{*} < R_{2}^{*} < R_{3}^{*} < R_{4}^{*}$. By the first change, we perform the reverse tangential bifurcation (the iterative analog of the saddle-node bifurcation) with the reduction of the attractive state of equilibrium to an unstable point with its disappearance. In this case, we write down the reduction of the local attractor $R_{4}^{*}$ in such a way that $\forall {{R}_{0}} > R_{3}^{*}\mathop {\lim }\limits_{n \to \infty } {{\varphi }^{n}}({{R}_{0}}) = R_{4}^{*}$ and ${\text{|}}\varphi {\kern 1pt} '(R_{4}^{*}){\text{|}} < 1$. By reduction we mean changes when two points $R_{4}^{*}$ and $R_{3}^{*}$ merge into one $R_{w}^{*}$ unstable point $\varphi (R_{4}^{*}) = \varphi (R_{3}^{*}) = R_{w}^{*}$, and then this point $R_{w}^{*}$ disappears: $\varphi (R_{w}^{*}) < R_{w}^{*}$. The curve lies below the bisector of the coordinate angle: $\varphi (R > {{R}_{{\min }}})$ < R. The second purposeful transformation of the phase portrait implements the boundary crisis of the interval attractor Λ. All points of Λ are concluded after reduction $R_{4}^{*}$ over the interval between the maps ${{R}_{{\min }}}$ and ${{R}_{{\max }}}$ of the extrema of $\varphi$ in such a way that $\Lambda \subset [\varphi ({{R}_{{\min }}}),\varphi ({{R}_{{\max }}})]$.

The interval attractor Λ arises after the reduction of a stable point $R_{4}^{*}$, along with an unstable point $R_{3}^{*}$ in the area that includes a stationary point $R_{2}^{*}$ with prototypes, because it is a repeller open both on the right and on the left. For such a reconstruction of the phase portrait, at least three unstable stationary points are required while maintaining the stability of the zero equilibrium. The behavior of iterations when we change a parameter depends on whether the repeller $R_{1}^{*}$ has prototypes on the right. The hybrid system allows us to scale a dependence along the R axis and purposefully change the positions of the extrema $\varphi (\lambda S)$ when changing the trigger function parameter σ (as shown in Fig. 3). We will see, depending on the parameters σ and β of the repellent (on the graph of the crossing point with the bisector coordinate angle) that are isolated or having point-prototypes. Figures 3a and 3b show forms of the dependency $\varphi (\lambda S)$ in the AnyLogic instrumental environment relative to the bisector of the coordinate angle shown in the graphs. Note that λ is a parameter that can change the position of the extrema of φ. We can obtain this difference of forms in the stock–recruitment curves in Fig. 3 by changing σ and the impact of $\Psi [S]\beta$ in the right-hand side of Eq. (4.1).

Fig. 3.

Transformation of extrema and equilibriums in functional dependence $\varphi (S)$ relative to bisector of coordinate angle: (1) model dependence and (2) bisector $\varphi (S) = S$.

The graphs in Fig. 3 change the relative position of the repellents and extrema. In Fig. 3b, repeller $R_{1}^{*}$ is isolated, while in Fig. 3a, the repeller $R_{1}^{*}$ is open. This property is important for modeling extreme scenarios, because the point $R_{1}^{*}$ in the model is always unstable: ${\text{|}}\varphi {\kern 1pt} '(R_{1}^{*}){\text{|}} > 1$. The trigger function $\Psi$ does not change the relative position of the fourth stable equilibrium of the large population $R_{4}^{*}$ but acts on the position of the extremum $\min \varphi (\lambda S)$ relative to the unstable equilibrium: the repellent $R_{1}^{*}$. The position of the first repeller $R_{1}^{*}$ is more important for quality dynamics than the positions of the remaining repellers.

Assume that initially in the neighborhood of the maximum, our stock–recruitment model curve slightly exceeds the third equilibrium $\varphi (\max\varphi (N(0)) \pm \varepsilon ) > R_{3}^{*}$, i.e., $R_{3}^{*}$ has two direct point-prototypes. If the original state of population R₀ corresponds to the range ${{R}_{0}} \in (R_{1}^{*},R_{3}^{*}) \cap \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\}$, then in the series of aperiodic fluctuations, the trajectory achieves a state that corresponds to the level of a high stable population $R_{4}^{*}$. In the scenario, the set $\{ {{\varphi }^{{ - n}}}(R_{2}^{*})\}$ is important, i.e., the set of the always existing prototype points of the repeller $R_{2}^{*}$. None of them are attracted to the attractors at any R₀ but make local breaks in its area of attraction.

In the computational experiment, we assign the parameters of the scenario where the fishery’s population after an unstable regime has recovered to a stable equilibrium and ecological optimum. Consequently, catches ${{Y}_{n}} = {{R}_{n}}{{q}_{n}}$ are increasing. After assessing the positive trend, experts make an informed decision to increase the annual quota ${{\bar {q}}_{n}}$. Next season’s catches set a historic peak, but then start to clearly decline. In the iterations, the stock successfully passes the local minimum without getting directly into the neighborhood of the critical state $R_{1}^{*}$. Fishing forecasts are guaranteed to take into account the efficiency of the reproduction in previous years. Catches after the fall noticeably begin to return to their former indicators and there is no apparent reason to radically revise the share of withdrawals ${{\bar {q}}_{n}}$. Such a recovery is deceptive. In reality, the duration of the growth of Y_n is related to random factors.

The value of the stock after the intensification of the fishery breaks into an aperiodic small-scale regime with a fickle amplitude of fluctuations. In the case of the belated establishment of the previous rational share of withdrawal, after the fluctuations there is a sharp second drop or collapse in the catch.

Figure 4 presents a computational scenario of a irrevocable population crisis with intermediate fluctuations in the expert management of the intensity of the fishery. It is assumed that the fishery is able to entirely master the quota allocated for exemption, regardless of economic costs and loss of profitability of the fishing.

Fig. 4.

Computational scenario of dynamics of catches in development of collapse of cod stocks in North Atlantic.

The duration of phases of the process in Fig. 4 depends on the initial increase in ${{\bar {q}}_{n}}$. For any population, its state will begin to shift to the left along the curve $\varphi (\lambda S)$. At first, the reduction takes place monotonically but in the case of threshold effects, sharply. The threshold effects will not appear immediately after the quota is increased. The feedback in ecosystems takes place with a delay [49]. A greater time range is needed to adequately assess the population’s response to the impact of changes in the level of fishing than the regulatory organization can afford to spend on making decisions. The scenario shows that experts in determining the impact of fishing are clearly unable to have the relevant information to make the management decisions. The problem can be overcome by the use of historical analogies as well as the method of compiling a table of the described characteristic situations with different impacts on the exploited stocks of the Gadus morhua cod and the corresponding response changes in the population’s characteristics.

The scenario confirmed the hypothesis that the collapse of stocks of large long-lived fish is a natural process and is stretched in stages, which we describe as follows.

Stage I. Stable population after an increase in withdrawals falls into an aperiodic mode. We observe the mode of change at a lower five-year average but with the illusion of active recovery. Recall that in the aperiodic mode the behavior of the trajectory outwardly resembles stochastic fluctuations due to the strong dependence of the movement of the trajectory ${{\varphi }^{n}}({{R}_{0}})$ on proximity to$R_{2}^{*}$ when falling in the neighborhood of the repeller.

Stage II. Unless a timely moratorium is imposed, stage II of degradation will occur decisively in (on average) nine model seasons, with the transition over the threshold of critical equilibrium $R_{1}^{*}$ > minφ(λS). In the shown scenario, the share of 0.61 is sustained, but at q = 0.63 the process—that eventually leads to a collapse—is developing. The dynamics of the trajectory is accompanied by a special type of known sensitivity property related to the selection of the starting points for chaotic systems. In computational experiments, the time spent in the fluctuation mode will always be slightly different.

8. DISCUSSION OF THE COMPUTATIONAL SCENARIO OF A COLLAPSE

The hybrid structure allowed the computational experiment to reproduce the scenario of collapse of the stock in regulated fishing. The collapse of cod off the coast of Canada was triggered by the notion that the bioresources were too well-maintained [50]. There was an overestimation of the rate of recovery of cod stocks, which was calculated by the cohort models [51]. Before the critical threshold, the efficiency of the population’s reproduction, according to many models, is sufficiently high, leading to inflated expectations in the forecasts. The moratorium on cod fishing was introduced with the expectation of entry into the reproductive age of virtual “reserve” generations. In theory, the generations not caught in fisheries should breed, but these virtual reserves have not had the effect of recovery. Similarly, with two phases the collapse takes place of fisheries with different life cycles: cod, king crab, halibut, southern bluefin tuna Thunnus maccoyii, and the local population of redlip mullet Planiliza haematocheilus of the Azov Sea [52].

The methods of estimating stocks and sturgeon of the Caspian Sea and cod in Canada significantly overstated their real numbers, although different methods were used. The official catch of cod was stopped too late. In the sturgeon of the Caspian, the phase of pseudo-stabilization of the stock extended over a period of 15 years: from 1977 to 1992 [53]. The phase of sharp decline in the catch in two populations of sturgeon of Volga is similar to the final of the collapse of cod on Atlantic coast of Canada; from a thriving state it went immediately into the stage of degradation.

The dynamics of the degradation of the population of the Huso huso Caspian belugas differ both in terms of the prolonged and gradual depletion of reserves. The computational experiment of the protracted collapse in Fig. 5 does not show the dynamics of catches (as in the previous experiment) but just the dynamics of the population size by generation. The withdrawal rate in the scenario is slightly higher than the critical one. The graph of the generational change in Fig. 5 much more clearly shows the distinct aperiodic mode of fluctuations with a significant amplitude of the magnitude of the annual recruitment.

Fig. 5.

Scenario of model of population dynamics in three-phase collapse of Caspian Sea sturgeon fish stocks.

For sturgeon, we can talk about modeling the case of a prolonged degradation of three phases by the scenario presented in Fig. 5. The fertility rate λ of sturgeon and sevruga is 1.4 times higher than the given rate of the fertility of cod; this will determine such a long-term sliding reduction in the population right up to the sharp drop at the end. The downward curve of Caspian sturgeon catches is smoothed by the artificial release of the young fish [54] and the predictable effect of the acceleration of puberty of these fish [55]. The cod population is unexpectedly slowly for ichthyologists recovering after its collapse, while the sturgeon of the Caspian Sea is threatened with complete extinction.

The aperiodic mode established by the exponential dispersal ${{R}_{0}},{{R}_{0}} + \varepsilon$ is caused by the incoherent nature of the attraction area of the attractor $R_{4}^{*}$. The area does not include the set of unattractive (to the attractor) prototypes of two unstable points: $\Delta = \{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{3}^{*})\}$. In the case of a negative external impact on the survival of fish, the configuration of stationary points $\varphi (R)$ scaled along the ordinate axis changes. For $\varphi (R)$, the local reverse tangential bifurcation is possible: when merging $R_{3}^{*},$ and $R_{4}^{*}$ with the disappearance of a stable stationary point $R_{4}^{*}$, while retaining the remaining points $R_{1}^{*}$ and $R_{2}^{*}$. Transformations cause the fish population to stay with a smaller S in the fluctuation mode of a significant amplitude in recruitment. In the phase space, the mode is matched by the interval attractor of the third topological type in the theorem of J. Guckenheimer [45].

The duration of the oscillations depends on the position of $\varphi$ in the minimum. If $\varphi ({{R}_{{\min }}}) < R_{1}^{*}$, then the boundary crisis of the interval attractor is implemented. Point $R_{1}^{*}$ is the unsustainable critical equilibrium; if ${{R}_{0}} < R_{1}^{*} - \varepsilon$, then irreversible degradation is implemented ${{R}_{0}} \notin \Delta ,{{\psi }^{n}}({{R}_{0}}) \to 0$. There is also an interior crisis of the attractor; in our model this phenomenon does not arise.

In the scenario of a boundary crisis, the attractor $\Lambda$ comes into contact with the boundary of its area of attraction and loses the invariance property $\varphi (\Lambda ) \in \Lambda$. When $\exists {{R}_{0}} \in \Lambda ,\varphi ({{R}_{0}}) < R_{1}^{*}$, there is an unattraction set ${\text{M}} \in {{\Omega }_{1}}$ consisting of the points ${\rm M},{\rm M} \cap \Delta = \emptyset$ but with chaotic properties. In the neighborhood of multiple repellent points $\Delta$ a limited number of steps ${{n}_{\Delta }} < \kappa$ contain the trajectory of iterations ${{\varphi }^{n}}({{R}_{0}})$, but the chaotization ends by the state ${{\varphi }^{\kappa }}({{R}_{0}}) = 0,$ $\kappa < \infty$. The duration of the degrading transition mode κ to a zero population size is not permanent in computational scenarios due to the sensitive dependence on the change in the original state of the trajectory for small perturbations: ${{R}_{0}} \pm \varepsilon$.

9. MODIFICATION OF THE TRIGGER FUNCTION FOR THE PEST OUTBREAK MODEL

The concept of the technique allows us to simulate an alternative extreme situation in the life of populations. Outbreaks of the pest population represent a global problem. Outbreaks in insects vary in the phases of dangerous local phenomena: from the moment that they are launched, transition to the so-called eruptive dynamics, and exit to the peak and to the stage of completion. Insect outbreaks represent a distinct transition regime. An outbreak of any insects must end naturally for internal biosystem reasons.

One of the most common scenarios for the transition to the rapid-growth phase (population outbreak) is the threshold scenario. The chresthomatic situation of overcoming the threshold of small and sedentary insects of the Psyllidae family is described by the example of the analysis of pest outbreaks of eucalyptus trees in Australia [56]. In Fig. 6, the Roman numbers show the typical phases of an outbreak: from the prethreshold state I to the completion state VII. We present this threshold mathematically as an unstable equilibrium at iterations of complex functional dependence. The problem is that the threshold must be overcome spontaneously. The outbreak in Fig. 6 starts without an external influence. The outbreak is an infrequent extreme phenomenon. Unattracted sets of prototype points at unstable stationary points make the entire area a fractal repeller.

Fig. 6.

Scenario of threshold transition to forest pest outbreak in Australia according to [56].

The chaotic repellent $\Delta$ obtained in the hybrid model (because of the locally incoherent boundary of the areas of attraction of the two alternative attractors) perfectly overcomes the problem of the computational modeling of transitions.

Additionally, a method with transient chaos in a limited interval of a discrete component of time (the number of model seasons u) will simulate the climatic volatility of the breeding environment of insects sensitive to rainfall.

In the previously proposed model with the function Ψ, there is a solution when the spontaneous overcoming of equilibrium $R_{3}^{*}$ triggers a pest outbreak with a way to a sustainable equilibrium of a large population $R_{4}^{*}$. However, we solve only the first part of the problem of outbreak modeling in such a way: the transition to the eruptive phase III. Soon, such phenomena end for two reasons: the ecosystem will not survive such a state for long and the forest will lose foliage. The larvae of the nymphs of psyllids are not able to eat all the foliage; however, because of the damage to the leaves, there is a rapid spread of phytopathogenic infections. The population will quickly destroy the resources it needs. The rate of the spread of psyllids in the forest is limited, and the insects themselves are susceptible to infections when they are crowded in damaged plants.

It is necessary to describe the spontaneous end of the outbreak of insects in forests. To describe a sharp reduction of the survival in feeding psyllid larvae, we once more modify model (1.2) in a different way using our universal method:

$$\Xi (N(\tau )) = 1 + \frac{{\exp ({{c}_{1}}N(\tau ))}}{{l + {{c}_{2}}\exp ({{c}_{1}}N(\tau ))}},\quad \mathop {\lim }\limits_{N(\tau ) \to \infty } \Xi (N(\tau )) = 1 + \frac{1}{{{{c}_{2}}}},$$

(9.1)

where parameter c₂ > 1 characterizes the rapidity of the exhaustion of resources and c₁ is a scaling factor for the approximation of the function $\Xi (N(\tau ))$ to the abscissa axis. Parameter l varies the level of population at which the effect will noticeably manifest itself. We implement the trigger function Ξ for the development stage II. The function Ξ in the calculations will also change the frame. For pests, the second stage requires an abundance of food resources most of all; therefore, at the maximum of the outbreak, the survival of this stage due to (9.1) in the calculations will be clearly reduced:

$$\frac{{dN}}{{dt}} = - {{\alpha }_{2}}N(t)\Xi (N(\tau )){\text{/}}w(\tau ) - \beta N(t),\quad \tau < t < T.$$

(9.2)

In the model computational experiment (1.2) and (2.1) with two trigger modifications (4.1) and (4.2), together with (9.1) and (9.2), we will describe a spontaneous, unpredictable transition of the trajectory from chaotic dynamics to sustainable equilibrium $R_{4}^{*}$ across the threshold ${{\varphi }^{u}}(R) > R_{3}^{*},$ $u < \infty$ that will be the peak phase of the outbreak after intermediate stabilization at point $R_{3}^{*}$. The dynamics of the outbreak with a long peak is shown in the model scenario in Fig. 7.

Fig. 7.

Modelling passage of phases of single outbreak of insect population.

The neighborhood of the open repeller $R_{3}^{*}$ is an indicator of the beginning of the rapid increase in population. The trajectory near $R_{3}^{*}$ in the scenario in Fig. 7 is found for a long time. The experiment shows the internal time of the computational environment. Number u is sufficient to predict dangerous conditions. The threshold for launching an outbreak in psyllids is created by an system of bioregulators: host–parasite–superparasite. The second-order wasp parasites from Australia’s large family of parasitic webbed-winged Ichneumonidae do not allow the primary parasites to multiply rapidly, which should suppress pests of the eucalyptus forest. The balance with a large population can only appear stable. In the new model scenario, any upper equilibrium will disappear due to the action of Ξ, but not immediately, because the reproductive activity of the populations is variable (but remains a fairly conservative characteristic on the scale of related generations).

In the asymptotic of our scenario, the trajectory will return to the aperiodic movement in the interval attractor, namely, the set of incoherent intervals, which will be the difference of the set of points $\Phi$ on the segment between the limiting points-repellers:

$$\Phi = [R_{1}^{*},R_{3}^{*}]{{\backslash }}\{ {{\varphi }^{{ - n}}}(R_{2}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{3}^{*})\} \cup \{ {{\varphi }^{{ - n}}}(R_{1}^{*})\} .$$

(9.3)

In the resulting scenario presented in Fig. 7, the outbreak is a rare and isolated event. In reality, the start and the completion of outbreaks in different species are diverse and it is impossible to single out a generalized single version. In boreal forests, where the wintering-generation factor is important, destructive outbreaks of the spruce leaf roller or gypsy moth occur in a different scenario [57]. Often, outbreaks take the form with a series of individual peaks of activity, which are estimated by the areas of the affected forest. The time period between the neighboring peaks of outbreaks can reach 15 years. Phase VII in [56] shows an example of the variability of an outbreak: the rapid repeat peak of insects.

CONCLUSIONS

The original computational modeling technique is demonstrated by the examples of two practically important processes in aquatic and forest living systems. We obtain a computational structure that is rightly called a dynamic system with the redefinable evolutionary operator $\varphi$. The situations that we model are related to the extreme and transitional dynamics of ecosystems. It has been shown that nonlinear environmental effects and outbreak phases can be mathematically defined by the set of phase-portrait bifurcations in functional iterations. For many species of insects and fish, we can numerically calculate just the fluctuations of juvenile survival rate; however, it is relevant to assess their condition for sexually mature recruitment and to investigate the efficiency of the formation of the new generations of populations.

Our methodology includes the following six principles of the building structure and ways of analyzing the behavior of the population models in the parameter space.

1. Multicomponent time, which allows us to highlight events in continuous intervals, namely, time frames. With form (1.1), it is convenient to introduce the event component while managing the change in a continuous process, to manage the exploitation level.

2. Use auxiliary indicators in calculations in the formation of predicates to override or stop the operation of equations that describe the population.

3. Introduce triggering functions. Such functions Ξ and Ψ pointwise describe the threshold changes in continuous processes in narrow values of the population.

4. External factors in the changing environment should be taken into account indirectly in auxiliary equations if necessary.

5. The discrete component of the trajectory to describe the simulated environmental phenomena is analyzed using all the substantiated metamorphoses of the functional iteration behavior. Tools are given to us by the fundamental theorems of nonlinear dynamics [58]. It should be taken into account in this item of our methodology that not all nonlinear effects of dynamic systems receive a core biological interpretation [59]. Some effects in biosystem models are superfluous.

6. We study several variants of models with control as a scenario study. In the experiments, we include the logic of decision making by experts in the external impact on bioresources, i.e., in the development of a new policy of the regulation of quotas in catching fish or the establishment of restrictive measures during epidemics.

In the practical part of the simulation, comparative analysis of the scenarios and the search for common grounds in the dynamics of change for radically different populations (such as cod off the coast of Canada, Caspian sturgeon, or psyllids in the forests of Australia) are promising. Unlike the collapse of cod, there was sufficient time to make the necessary administrative decisions in order to prevent the degradation of sturgeon in the Caspian Sea.

A model of a population outbreak that spontaneously ends is obtained. In this method, we do not need to include the change in parameters due to external factors that cause reproductive activity to stop. Triggering functions with restricted limits will allow performing targeted bifurcations such as the disappearance of the excess equilibrium point. The right-hand side is rebuilt predictively. A predicate of a hybrid machine can be true when one or several, or at least one of several, conditions hold. Predicates are applied to the analysis of situations of the collapse of bioresources: rapid and unexpected degradation of fish stocks, which is not replaced by recovery contrary to the forecasts and calculations of experts. Our scenario shows that catching fish adjusted according to the optimality principles does not prevent the development of a collapse of the stock. The regulation of exemptions with the introduction of quotas will not be fundamentally safe. An excess by Δq = 4.5% of the planned quota q does not seem to be critical to experts; however, in the return forecasts, they take into account this 4.5% of the stock as breeding individuals. According to the forecasts, the recruitment from the lost fish is expected; therefore, the error in estimates will increase rapidly. A similar mounting error in stock estimates is specified in [60] for the Paralithodes camtschaticus crab near the coast of Alaska. A strong restriction on the technical capabilities of fishing is seen as more rational. The limit on the size of the fishing gear, fuel reserves onboard, or the time of the ships at sea is promising. Remote monitoring allows monitoring ships.

We used a continuous-eventful representation of the time, where the calculated ith event is followed by the reconstruction of the right-hand side; therefore, we talk about predictive-redefinable computational hybrid structures. The selection of regulators for baseline equations can be adapted to a wide class of models (which is absent in the previous version of the paper) with control [61], which use solutions of differential equations sequentially on a set of time intervals, or simple transition functions in [62].

A model is easily modified by expanding the set of auxiliary equations by already known models; e.g., we initially propose to use Eq. (2.5) in order to describe long cycles of the forest pest Choristoneura freemani butterfly in [63], which in resonant oscillations causes large-scale forest lesions. Then the independent model of cyclicity is included in the hybrid structure.

In the modification of hybrid models, other amendments from the set of external factors to the auxiliary equations of reproduction regulation of bioresources can be included. In model scenarios, it is prospective to analyze several fairly common and dangerous environmental situations of a man-made environmental change [64]. For example, in predicative structures it is convenient to take into account the effect of the phenomenon of eutrophication of reservoirs on the survival of young fish, which is important in the situation of limiting oxygen access to spawn clutches [65]. It is interesting to estimate the rate of recovery of the biological productivity of rivers and lakes in the same way as the rate of special bioremediation of reservoirs after their hydrocarbon contamination [66]. The most relevant of the possible biological applications of predicatively overridable systems at present is the simulation of the activity of different types of cells of the immune system, producing a response to an unknown infection. Dangerous complications of COVID-19 in a pandemic of the new virus are caused by the excessive cascading reaction of immune cells: cytokine storm [67]. Hypercytokinaemia triggers the rapid respiratory distress syndrome ARDS [68], when lungs quickly lose the functionality. The COVID-19 epidemic in different countries follows different scenarios. The updated infection statistics confirms that the basic SIRS-models of epidemics [69] with their oscillational regimes do not have the adequacy for real-world situations.

In one paper we managed to combine methodological problems of modeling two fundamentally different biological situations. A mass reproduction and a sharp drop in the efficiency of reproduction are expressed as consequences of the action of threshold mechanisms of regulation. The analysis of two textual scenarios of outbreak and collapse confirms the hypothesis that very different extreme situations in species from far from each other taxonomic groups have a commonality in terms of nonlinear dynamics and are expressed by a similar sequence of bifurcations.