Two-Motzkin-Like Numbers and Stieltjes Moment Sequences

Abstract

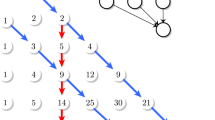
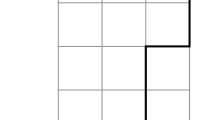
First, we introduce the two-Motzkin-like number as the weight of vertically constrained Motzkin-like path with no leading vertical steps from (0, 0) to (n, 0) consisting of up steps, down steps, horizontal steps, vertical steps in the down direction and vertical steps in the up direction. Secondly, we provide sufficient conditions under which the two-Motzkin-like numbers (resp. the q-analogue of the two-Motzkin-like numbers) are Stieltjes moment sequences (resp. are q-Stieltjes moment sequences) and therefore infinitely log-convex sequences. As applications, on the one hand, we show that many well-known counting coefficients, including the central trinomial $\left( {\begin{array}{c}2n\\ 2n\end{array}}\right) _{2}$ and pentanomial $\left( {\begin{array}{c}2n\\ 4n\end{array}}\right) _{4}$ numbers of even indices respectively are Stieltjes moment sequences and, therefore, infinitely log-convex sequences in a unified approach. On the other hand, we prove that the sequence of polynomials of square trinomials $\sum _{k=0}^{2n}\left( {\begin{array}{c}n\\ k\end{array}}\right) ^{2} _{2}q^{k}$ are q-Stieltjes moment sequence of polynomials. Finally, we provide a criterion for linear transformations and convolutions preserving Stieltjes moment sequences in more generalized triangular array.

Appendix A: Other Stieltjes Moment Sequences in OEIS

$$\begin{aligned} \begin{array}{|c|c|c|c|c|} \hline a_{n} &{} \sum _{k=0}^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) M_{k} &{} \sum _{k=0}^{n}\left( {\begin{array}{c}n\\ k\end{array}}\right) C_{k} &{} \sum _{k=0}^{2n}\left( {\begin{array}{c}n\\ k\end{array}}\right) _{2}\left( {\begin{array}{c}2k\\ k\end{array}}\right) &{} \sum _{k=0}^{2n}\left( {\begin{array}{c}n\\ k\end{array}}\right) _{2}B_{k} \\ \hline \text {OEIS} &{} A270561 &{} A007317 &{} A082760 &{} A207864\\ \hline \end{array} \end{aligned}$$