1 Introduction

Phase retrieval generally alludes to the non-linear inverse problem of recovering some signal (which in this paper will be modelled by \(x \in {\mathbb {C}}^L\)) from phaseless measurements. Some of its more well-known applications include ptychography for coherent diffraction imaging [16, 20, 24, 29] and audio processing [12, 14, 18]. It has been shown that the phase retrieval problem for frames in finite-dimensional Hilbert spaces [7] and a forteriori in finite-dimensional reflexive Banach spaces [2] is always stable, which elicits the question: Why are we concerned with stability estimates for phase retrieval from discrete Gabor measurements at all? The reason is that phase retrieval for frames in infinite-dimensional spaces is always unstable [2, 7] and in addition one can construct sequences of finite-dimensional subspaces of infinite-dimensional Hilbert spaces along with frames for which the stability constant of phase retrieval increases exponentially in the dimension of the constructed subspaces [7]. Recent research [1] into the infinite-dimensional phase retrieval problem has however led us to believe that the instability of phase retrieval is not an insurmountable obstacle to reconstruction. It was shown that stability can be restored for examples that exhibit a disconnectedness in the measurements by only reconstructing the phase semi-globally or in an atoll sense. Furthermore, it was shown in [15] that such disconnectedness in the measurements is the only source of instabilities for phase retrieval.

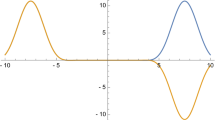
A simple example of instability can be obtained by considering the Gaussian functions \(g(t) := \mathrm {e}^{-\pi t^2}\) in conjunction with the signals

$$\begin{aligned} f_\lambda ^+(t) := g(t-\lambda ) + g(t+\lambda ) \qquad \text{ and } \qquad f_\lambda ^-(t) := g(t-\lambda ) - g(t+\lambda ) \end{aligned}$$

depicted in Fig. 1. When \(\lambda \) increases, the Gaussian bumps in the signals \(f_\lambda ^\pm \) start to move further apart effectively generating what we call a time gap whose length depends linearly on \(\lambda \). It can be shown, see [3], that the measurements generated by the continuous Gabor transform with Gaussian window of the signals \(f_\lambda ^\pm \) have distance on the order of \(\mathrm {e}^{-\lambda ^2}\) in the standard Sobolev space \(W^{1,2}({\mathbb {R}}^2)\) and that one can therefore not stably retrieve \(f_\lambda ^\pm \) from continuous Gabor transform measurements. Similar phenomena can be observed for the discrete setting considered in this paper and we do therefore propose a similar paradigm as in [1] and try to recover signals in a semi-global fashion that is not common in the phase retrieval literature up to this point. Note that in audio processing, it is natural to consider (audio) signals up to semi-global phase as human listeners are not able to distinguish between two signals which differ by semi-global phase [1].

Fig. 1
figure 1

A simple example for instability of phase retrieval with continuous Gabor measurements

Full size image

One should note that in recent years a variety of stability result for phase retrieval have been proven. Some highlights of this research include:

  1. i.

    The PhaseLift method [8, 11] which guarantees stable recovery from \({\mathcal {O}}(L)\) randomly chosen Gaussian measurements with high probability [9].

  2. ii.

    The research on polarisation for phase retrieval [4, 5, 22, 26] in which the authors supplement an existing measurement ensemble in order to obtain a phase retrieval problem that is efficiently and stably solvable.

  3. iii.

    Wirtinger flow and related methods [10, 27, 28] which offer stability guarantees for sufficiently many randomly chosen Gaussian measurements.

  4. iv.

    The eigenvector-based angular synchronisation approach [17] which relies on a certain weak form of invertibility of the phase retrieval problem to prove a stability result for deterministic measurement systems.

  5. v.

    The very recent work [25] in which the stability of phase retrieval from (random) frames whose frame vectors are uniformly distributed on the unit sphere (but not necessarily independent) is considered.

In some way or another, all of these results are based on different setups than ours: As opposed to the papers referenced in item i., iii. and v. we will not work with a probabilistic measurement system but with a deterministic one. We will also not supplement our measurement ensemble as is done in the results referenced in item ii. and we will not work with the weak form of invertibility that is present in the paper referenced in item iv. In fact, we will consider the two well-known Formulae (1) and (2) presented in Sect. 2 which are heavily used to develop methods for exact phase retrieval from Gabor measurements in the literature [13, 19, 21]. We show that through further analysis of the Formulae (1) and (2), one can derive stability results for some of those methods and therefore also for phase retrieval in general. Our stability results are designed for bandlimited signals and come with constants that scale in the square root of the space dimension at the cost of relaxing the notion of stability to resemble the one proposed in [1].

Outline In Sect. 2, we present the reader with the uniqueness results and the formulae on which our stability results hinge. In Sect. 3, we utilise the ambiguity function relation (2) in order to show that phase retrieval can be stably done for bandlimited signals based on the considerations in [6, 23]. In Sect. 4, we use the autocorrelation relation (1) in order to show that phase retrieval can be done stably for bandlimited signals utilising results from [13, 19]. As the proofs of our main results are a bit technical, they appear separately in Sect. 5.

2 Prerequisites

Throughout this paper, we fix the dimension \(L \in {\mathbb {N}}\) and let \(x,\phi \in {\mathbb {C}}^L\). We define the discrete Gabor transform (DGT) of x with window function \(\phi \) to be

$$\begin{aligned} {\mathcal {V}}_\phi [x](m,n) := \frac{1}{\sqrt{L}} \cdot \sum _{\ell =0}^{L-1} x(\ell ) \overline{\phi (\ell -m)} \mathrm {e}^{-2\pi \mathrm {i} \frac{\ell n}{L}}, \qquad m,n=0,\dots ,L-1. \end{aligned}$$

Here and throughout this paper, the indexing is understood to be periodic. In particular, we use the convention \(\phi (\ell ) = \phi (\ell \mod L)\), for \(\ell \in {\mathbb {Z}}\). A helpful way of looking at the DGT is to view it as a collection of windowed Fourier transforms. For this purpose, we denote \(x_m(\ell ) := x(\ell ) \overline{\phi (\ell -m)}\), for \(\ell ,m \in \{0,\dots ,L-1\}\), and obtain

$$\begin{aligned} {\mathcal {V}}_\phi [x](m,n) = {\mathcal {F}}\left[ x_m \right] (n), \qquad m,n = 0,\dots ,L-1, \end{aligned}$$

where \({\mathcal {F}} : {\mathbb {C}}^L \rightarrow {\mathbb {C}}^L\) denotes the discrete Fourier transform (DFT)

$$\begin{aligned} {\mathcal {F}}[x](k) := \frac{1}{\sqrt{L}} \cdot \sum _{\ell =0}^{L-1} x(\ell ) \mathrm {e}^{-2\pi \mathrm {i}\frac{\ell k}{L}}, \qquad k=0,\dots ,L-1, \end{aligned}$$

with inverse

$$\begin{aligned} {\mathcal {F}}^{-1}[x](\ell ) = \frac{1}{\sqrt{L}} \cdot \sum _{k=0}^{L-1} x(k) \mathrm {e}^{2\pi \mathrm {i}\frac{k \ell }{L}}, \qquad \ell =0,\dots ,L-1. \end{aligned}$$

We will frequently use the two-dimensional discrete Fourier transform which is the composition of two DFTs as defined above. Additionally, we define the ambiguity function of a signal x via \({\mathcal {A}}[x] := {\mathcal {V}}_x[x]\). We are interested in the recovery of signals \(x \in {\mathbb {C}}^L\) from the measurements

$$\begin{aligned} M_\phi [x](m,n) := \left|{\mathcal {V}}_\phi [x](m,n) \right|^2, \qquad m,n=0,\dots ,L-1. \end{aligned}$$

It is immediately obvious that \(x \in {\mathbb {C}}^L\) and any signal \(\mathrm {e}^{\mathrm {i} \alpha } x\), with \(\alpha \in {\mathbb {R}}\), yield the same measurements \(M_\phi [ \mathrm {e}^{\mathrm {i} \alpha } x ] = M_\phi [x]\). Therefore, to have any chance of recovery, we will actually view \(M_\phi \) as an operator defined on the quotient space \({\mathbb {C}}^L / {\mathcal {S}}^1\), where \({\mathcal {S}}^1\) denotes the unit circle. Under various assumptions, which we will lay out in the following, one can show that \(M_\phi : {\mathbb {C}}^L / {\mathcal {S}}^1 \rightarrow {\mathbb {R}}_+^{L \times L}\) is an injective operator and that phase retrieval is therefore possible up to a global phase factor. In addition, it was shown in [7] that

$$\begin{aligned} \inf _{\alpha \in {\mathbb {R}}} \Vert x - \mathrm {e}^{\mathrm {i} \alpha } y\Vert _2 \lesssim \Vert \left|{\mathcal {V}}_\phi [x] \right|- \left|{\mathcal {V}}_\phi [y] \right|\Vert _\mathrm {F}, \end{aligned}$$

for all \(x,y \in {\mathbb {C}}^L\), where \(\Vert \cdot \Vert _\mathrm {F}\) denotes the Frobenius norm and the estimate depends on a constant which might increase exponentially in the space dimension L. Our phase retrieval problem is therefore possibly ill-conditioned.

As mentioned before, the number of known uniqueness results has seen a stark rise in the past few years. In the following, we want to mention those that inspired our stability estimates. Let us start by remarking that almost all uniqueness results can be traced back to two consequential formulae which are well-known in the literature. The first of these relates the Gabor measurements to the autocorrelation of \(x_m\). In what follows, time-reversal of a signal will be denoted by \(x^\#(\ell ) = \overline{x(-\ell )}\).

Lemma 2.1

For any \(x \in {\mathbb {C}}^L\),

$$\begin{aligned} {\mathcal {F}}^{-1}\left[ M_\phi [x](m,\cdot ) \right] (n) = \frac{1}{\sqrt{L}} \cdot \left( x_m *x_m^\# \right) (n), \qquad m,n=0,\dots ,L-1. \end{aligned}$$
(1)

Proof

See Appendix B. \(\square \)

The right-hand side in the above result is the aforementioned autocorrelation of \(x_m\):

$$\begin{aligned} \left( x_m *x_m^\# \right) (n) = \sum _{\ell =0}^{L-1} x(\ell )\overline{x(\ell -n)} \phi (\ell -n-m) \overline{\phi (\ell -m)}, \qquad m,n = 0,\dots ,L-1. \end{aligned}$$

The second of these formulae relates the Gabor measurements to the ambiguity function of x and the ambiguity function of \(\phi \).

Lemma 2.2

For any \(x \in {\mathbb {C}}^L\), the following holds:

$$\begin{aligned} {\mathcal {F}}\left[ M_\phi [x]\right] (m,n) = {\mathcal {A}}[x](-n,m) \overline{{\mathcal {A}}[\phi ](-n,m)}, \qquad \text{ for } m,n = 0,\dots ,L-1. \end{aligned}$$
(2)

Proof

See Appendix B. \(\square \)

Next, we will consider the uniqueness results from [6, 23] which are based on equation (2).

Corollary 2.3

(Theorem 2.2 in [6], p. 547) Suppose that \(\phi \) satisfies

$$\begin{aligned} {\mathcal {A}}[\phi ](m,n) \ne 0, \qquad \text{ for } m,n=0,\dots ,L-1. \end{aligned}$$

Then, x is uniquely determined by the measurements \(M_\phi [x]\) up to global phase.

While this result is exceptionally nice in the sense that it does not impose any requirements on the signal, it is quite restrictive in its requirements on the window function \(\phi \). For instance, windows \(\phi \) with support length \(|{\text {supp}} \phi |\) smaller than L/2 will always have zero entries in their ambiguity function.

Corollary 2.4

(Theorem 2.4 in [6, p. 549]) Let \(x \in {\mathbb {C}}^L\) be nowhere-vanishing, i.e. \({\text {supp}} x = \{0,\dots ,L-1\}\), and

$$\begin{aligned} {\mathcal {A}}[\phi ](m,n) \ne 0, \qquad \text{ for } m=0,1,~n=0,\dots ,L-1. \end{aligned}$$

Then, x is uniquely determined by the measurements \(M_\phi [x]\) up to global phase.

This result is in some sense orthogonal to Corollary 2.3: Its requirements on the window function are moderate while its requirements on the signal are rather restrictive. Of course, we might also infer a variety of results that are based on different trade-offs between restrictions on the window and restrictions on the signal. For this purpose, we introduce the parameter \(\Delta \in {\mathbb {N}}_0\). It corresponds to the maximum number of adjacent zeroes across which we may propagate phase in the reconstruction procedure used in the proof of the following corollary. Stated a bit more precisely: If x is a signal of which we only know its measurements \(M_\phi [x]\), then it follows from \({\mathcal {A}}[\phi ](0,\cdot )\) being nowhere-vanishing (and the use of the ambiguity function relation) that we can reconstruct the magnitudes of x. Therefore, it suffices to propagate phase between the entries of x to reconstruct x up to global phase. When we assume that \({\mathcal {A}}[\phi ](m,\cdot )\) is nowhere-vanishing, for some m, then we allow (according to the ambiguity function relation) the phase propagation from the entry with index \(\ell \) to the entry with index \(\ell + m\) (and to the entry with index \(\ell - m\)). Whether this allows us to reconstruct x up to global phase depends on the set of m for which \({\mathcal {A}}[\phi ](m,\cdot )\) is nowhere-vanishing and on the support set of x. This is the central idea on which the following corollary is built:

Corollary 2.5

Let \(\Delta \in {\mathbb {N}}_0\) and let \(x,y,\phi \in {\mathbb {C}}^L\) be such that \(M_\phi [x] = M_\phi [y]\) and

$$\begin{aligned} {\mathcal {A}}[\phi ](m,n) \ne 0, \qquad \text{ for } m \in \{0,\dots ,\Delta +1\},~n\in \{0,\dots ,L-1\}. \end{aligned}$$

Furthermore, let \(G = (V,E)\) denote the graph with vertex set \(V = {\text {supp}} x\) and edge set \(E \subset V \times V\) such that

$$\begin{aligned} (\ell ,k) \in E \Leftrightarrow |\ell - k |\in (0,\Delta +1] \cup [L-\Delta -1,L), \end{aligned}$$

i.e. two vertices are connected if and only if they are at most \(\Delta +1\) apart. If \(\{V_k\}_{k=1}^K\) constitute the vertex sets of the connected components of G, then for each \(k \in \{1,\dots ,K\}\) there exists an \(\alpha _k \in {\mathbb {R}}\) such that

$$\begin{aligned} x(\ell ) = \mathrm {e}^{\mathrm {i} \alpha _k} y(\ell ), \qquad \ell \in V_k. \end{aligned}$$

Proof

See Sect. 5. \(\square \)

Remark 2.6

The corollary above is more general than Corollaries 2.3 and 2.4. Indeed, if \(\Delta \ge \tfrac{L}{2}-1\), then G is connected. In fact, one can see from the definition of the edge set that G is the complete graph on the vertex set \({\text {supp}} x\). In particular, Corollary 2.3 follows. If \(\Delta = 0\) and x is nowhere-vanishing, then G is the circle graph on L vertices and is thus connected. In this way, we recover Corollary 2.4.

Finally, we will work with a uniqueness result first proven in [13] and later generalised in [19] based mostly on Eq. (1). Consider the following statement.

Corollary 2.7

(Theorem 1 in [13, p. 639]) Let \(n_0, \ell _\phi \in \{0,\dots ,L-1\}\) be such that \(\ell _\phi < L/2\) and suppose that \(\ell _\phi -1\) and L are coprime. If

$$\begin{aligned} {\text {supp}} \phi = \{n_0, \dots , n_0 + \ell _\phi \} \end{aligned}$$

and \({\mathcal {F}}[|\phi |^2]\) and x are nowhere-vanishing, then x is uniquely determined by the measurements \(M_\phi [x]\) up to global phase.

The work in [19] shows that one can also derive this result as part of a graph-theoretical formulation for phase retrieval.

Corollary 2.8

(Theorem 3.1 in [19, p. 373]) Let \(n_0, \ell _\phi \in \{0,\dots ,L-1\}\) be such that \(\ell _\phi < L/2\) and suppose that

$$\begin{aligned} {\text {supp}} \phi = \{n_0, \dots , n_0 + \ell _\phi \} \end{aligned}$$

and \({\mathcal {F}}[|\phi |^2]\) is nowhere-vanishing. Let the graph \(G = (V,E)\) defined by having the vertex set \(V = {\text {supp}} x\) and an edge between \(\ell , k \in V\) if

$$\begin{aligned} |\ell -k |\in \{\ell _\phi , L-\ell _\phi \} \end{aligned}$$

be connected. Then, x is uniquely determined by the measurements \(M_\phi [x]\) up to global phase.

3 Stability Estimates Based on the Ambiguity Function Relation

3.1 Stability for a Single Island

First, we derive stability estimates by employing equation (2) and Corollaries 2.3–2.5. In doing this, we want to start with the very simple setup of Corollary 2.4.

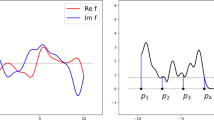
One can immediately see that there are some intricacies to the phase retrieval problem for signals \(x \in {\mathbb {C}}^L\). One of those is dealing with entries \(x(\ell )\) of x which have small (or even vanishing) magnitude. For these entries, extracting the phase of \(x(\ell )\) is unstable (or even impossible). See Fig. 2 for a depiction of this situation. Because of this, we will mostly work with a graph capturing only the larger entries of the signals.

Fig. 2
figure 2

For \(x(\ell ), \eta \in {\mathbb {C}}\), the difference in absolute values satisfies \(||x(\ell ) |- |x(\ell ) + \eta ||\le |\eta |\) such that the map \(|\cdot |: {\mathbb {C}} \rightarrow {\mathbb {R}}_+\) can be seen to be stable. On the other hand, the function which maps complex numbers to their phase is unstable at the origin: To see this, we can choose \(x(\ell ) = (-1+\mathrm {i})\epsilon \), \(\eta = 2\epsilon \) such that \(|\alpha - \beta |= \pi / 2 \ge \pi / (4\epsilon ) \cdot |\eta |\), where \(\alpha , \beta \in (-\pi ,\pi ]\) denote the principal values of the arguments of \(x(\ell ), x(\ell ) + \eta \in {\mathbb {C}}\), respectively

Full size image

Definition 3.1

Let \(\Delta \in {\mathbb {N}}_0\) and \(\delta > 0\). We call the graph \(G_\delta = (V_\delta ,E)\) defined by having the vertex set

$$\begin{aligned} V_\delta = \{ \ell \in \{0,\dots ,L-1\} \;\vert \; |x(\ell ) |\ge \delta \} \end{aligned}$$

and an edge between \(\ell ,k \in V\) if

$$\begin{aligned} |\ell - k |\in (0,\Delta +1] \cup [L-\Delta -1,L), \end{aligned}$$

the essential support graph of x with time separation parameter \(\Delta \). We will also simply call the essential support graph of x with time separation parameter zero the essential support graph of x.

The stability estimates we derive hold for bandlimited signals defined as follows:

Definition 3.2

Let \(B \in {\mathbb {N}}_0\). We call \(x \in {\mathbb {C}}^L\) B-bandlimited if

$$\begin{aligned} {\text {supp}} {\mathcal {F}}[x] \subset \{-B,\dots ,B\} \mod L. \end{aligned}$$

One important property of bandlimited signals is that their ambguity function does not have full support (when \(4B < L\)).

Proposition 3.3

Let \(x \in {\mathbb {C}}^L\) be B-bandlimited, for some \(B \in {\mathbb {N}}_0\). Then, it holds for all \(m \in \{0,\dots ,L-1\}\) that

$$\begin{aligned} {\text {supp}} {\mathcal {A}}[x](m,\cdot ) \subset \{-2B,\dots ,2B\} \mod L. \end{aligned}$$

We included a proof of this basic proposition in Appendix B. In the following, we will work with the \(\ell ^2\)-norm on subsets S of \(\{0,\dots ,L-1\}\). For such sets, we define

$$\begin{aligned} \Vert x \Vert _{\ell ^2(S)} := \left( \sum _{\ell \in S} |x(\ell ) |^2 \right) ^\frac{1}{2}. \end{aligned}$$

We may now prove the following result on the stability of magnitude retrieval:

Lemma 3.4

(Stability of magnitude retrieval) Let \(\delta > 0\) and let \(x,y \in {\mathbb {C}}^L\) be B-bandlimited, for some \(B \in {\mathbb {N}}_0\). Define \(G_\delta = (V_\delta ,E)\) to be the essential support graph of x and let \(\phi \in {\mathbb {C}}^L\) be such that

$$\begin{aligned} \min _{n \in \{-2B,\dots ,2B\}} |{\mathcal {A}}[\phi ](0,n) |\ge \frac{1}{c}, \end{aligned}$$

for some \(c > 0\). Then,

$$\begin{aligned} \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )} \le \frac{c}{\delta } \left\Vert M_\phi [x]-M_\phi [y] \right\Vert _\mathrm {F}. \end{aligned}$$

Proof

Let us start with the simple fact that for \(\ell \in V_\delta \) (cf. Definition 3.1),

$$\begin{aligned} \left||x(\ell ) |- |y(\ell ) |\right|= \frac{\left||x(\ell ) |^2 - |y(\ell ) |^2 \right|}{\left||x(\ell ) |+ |y(\ell ) |\right|} \le \frac{1}{\delta } \left||x(\ell ) |^2 - |y(\ell ) |^2 \right|. \end{aligned}$$

Thus, we have

$$\begin{aligned} \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )} \le \frac{1}{\delta } \left\Vert |x |^2 - |y |^2 \right\Vert _{\ell ^2(V_\delta )} \le \frac{1}{\delta } \left\Vert |x |^2 - |y |^2 \right\Vert _2. \end{aligned}$$

Next, suppose that \(4B < L\). Employing Plancherel’s theorem, the ambiguity function relation and Proposition 3.3, we find

$$\begin{aligned}&\left\Vert |x |^2 - |y |^2 \right\Vert _2^2 = \left\Vert {\mathcal {A}}[x](0,\cdot ) - {\mathcal {A}}[y](0,\cdot ) \right\Vert _2^2 = \sum _{n = 0}^{L-1} \left|{\mathcal {A}}[x](0,n) - {\mathcal {A}}[y](0,n) \right|^2 \\&\quad = \sum _{n = -2B}^{2B} \left|{\mathcal {A}}[x](0,n) - {\mathcal {A}}[y](0,n) \right|^2 = \sum _{n = -2B}^{2B} \left|\frac{{\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] (n,0)}{{\mathcal {A}}[\phi ](0,n)} \right|^2 \\&\quad \le c^2 \sum _{n = -2B}^{2B} \left|{\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] (n,0) \right|^2 \le c^2 \left\Vert {\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] \right\Vert _2^2 \\&\quad = c^2 \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _2^2. \end{aligned}$$

The proof for \(4B \ge L\) is even simpler: In this case \({\mathcal {A}}[\phi ](0,\cdot )\) is lower bounded everywhere. \(\square \)

Remark 3.5

Note that we need to restrict our stability result to the essential support \(V_\delta \) of x because the square root \(t \mapsto \sqrt{t}\) is not Lipschitz continuous. For this reason, we obtain the dependence of our stability result on \(\delta \). We note that in the above proof, we derive

$$\begin{aligned} \left\Vert |x |^2 - |y |^2 \right\Vert _2 \le c \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _2. \end{aligned}$$

Hence, magnitude retrieval is, in fact, stable even when we consider small entries as long as we compare the squared magnitudes of the signals with the squared absolute values of the Gabor transform.

Next, we turn to the retrieval of the phases. First, in accordance with Corollary 2.4, we will only use the entries of \({\mathcal {A}}[x](1,\cdot )\) (and of \({\mathcal {A}}[x](0,\cdot )\)) for our recovery which allows us to do phase propagation on adjacent entries. To be precise, we can propagate the phase from \(x(\ell )\) to \(x(\ell +1)\) (or back), for any \(\ell \in \{0,\dots ,L-1\}\). Mathematically this fact can be captured with the help of the essential support graph \(G_\delta \) of x with time-separation parameter zero, i.e. \(\Delta = 0\). In the following, we will call the connected components of \(G_\delta \) temporal islands.

Theorem 3.6

(Stability of phase retrieval on a single temporal island) Let \(\delta > 0\) and let \(x,y \in {\mathbb {C}}^L\) be B-bandlimited, for \(B \in {\mathbb {N}}_0\). For \(G_\delta = (V_\delta , E)\) the essential support graph of x, assume that the subgraph induced by the vertex set \(S_\delta = V_\delta \cap {\text {supp}} y\) is connected. If \(\phi \in {\mathbb {C}}^L\) is such that

$$\begin{aligned} \min _{\begin{array}{c} m \in \{0,1\}\\ n \in \{-2B,\dots ,2B\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |\ge \frac{1}{c}, \end{aligned}$$

for some \(c > 0\), then

$$\begin{aligned} \inf _{\alpha \in {\mathbb {R}}} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _{\ell ^2(V_\delta )} \le \frac{c}{\delta } \left( 1 + \frac{\sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}. \end{aligned}$$

Proof

See Sect. 5. \(\square \)

Remark 3.7

The stability constant derived in the above result is

$$\begin{aligned} \frac{c}{\delta } \left( 1 + \frac{\sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta } \right) \end{aligned}$$

and consists of a contribution from the magnitude retrieval estimate in Lemma 3.4 and the phase retrieval estimate presented in Sect. 5. The contribution from the phase retrieval estimate contains a factor \(\sqrt{2 |S_\delta |}\) which can be interpreted as a mild ill-conditioning of phase retrieval as it might scale like \(L^\frac{1}{2}\). Additionally, the phase retrieval estimate contains a factor \(1/\delta \) which captures the dependence on the size of the magnitudes of x.

Fig. 3
figure 3

Visualisation of the magnitudes of the ambiguity functions of some commonly used window functions in a logarithmic scale (we plot \(20 \log _{10} |{\mathcal {A}}[\phi ] |\))

Full size image

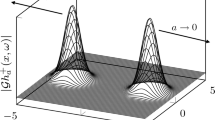
For a visualisation, we plot the magnitudes ambiguity functions of four commonly used window functions \(\phi \in {\mathbb {C}}^L\) in Fig. 3. For reference, we use \(L = 1024\) and the windows

$$\begin{aligned} \phi _{\mathrm {gauss}}(\ell )= & {} \mathrm {e}^{-\pi \frac{(\ell -512)^2}{32^2}}, \qquad \phi _{\mathrm {hamming}}(\ell ) := {\left\{ \begin{array}{ll} \frac{25}{46} \!-\! \frac{21}{46} \cos \left( \frac{2 \pi \ell }{63} \right) &{} \text{ if } \ell \!=\! 0,\dots ,63, \\ 0 &{} \text{ else }, \end{array}\right. } \\ \phi _\mathrm {hann}(\ell ):= & {} {\left\{ \begin{array}{ll} \frac{1}{2} - \frac{1}{2} \cos \left( \frac{2 \pi \ell }{63} \right) &{} \text{ if } \ell = 0,\dots ,63, \\ 0 &{} \text{ else }, \end{array}\right. }\\ \phi _{\mathrm {rectangular}}(\ell ):= & {} {\left\{ \begin{array}{ll} 1 &{} \text{ if } \ell = 0,\dots ,63, \\ 0 &{} \text{ else }. \end{array}\right. } \end{aligned}$$

Example 3.8

We want to present an example to clarify the statement of Theorem 3.6. For this purpose, we let \(L \in {\mathbb {N}}\), with \(L \ge 6\), be arbitrary but fixed and consider the rectangular window of length two

$$\begin{aligned} \phi (\ell ) := {\left\{ \begin{array}{ll} 1 &{} \text{ if } \ell = 0,1, \\ 0 &{} \text{ else }. \end{array}\right. } \end{aligned}$$

Note that the choice of the rectangular window of length two is rather arbitrary. One could, in fact, perform similar calculations with most other common window functions as long as one picks the window in such a way that its time support is small enough. We observe that, for large L, the rectangular window of length two will have a small time support (by which we mean that \(|{\text {supp}} \phi |= 2\) is small compared to L) and a large frequency support (by which we mean that \(|{\text {supp}} {\mathcal {F}}[\phi ] |\), which is readily seen to be L or \(L-1\) depending on whether L is even or odd, is comparable to L). This property of the rectangular window of length two will carry over to its ambiguity function in the sense that even for large B, we find that

$$\begin{aligned} \min _{\begin{array}{c} m \in \{0,1\}\\ n \in \{-2B,\dots ,2B\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |\end{aligned}$$

is rather large and thereby the constant c in Theorem 3.6 is rather small. So let \({{\widetilde{c}}} > 1\) and \(B \in {\mathbb {N}}_0\) be such that \(\tfrac{L}{{{\widetilde{c}}}} \le 6B \le L\). Then, we find that

$$\begin{aligned} \min _{\begin{array}{c} m \in \{0,1\}\\ n \in \{-2B,\dots ,2B\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |= \frac{1}{\sqrt{L}}. \end{aligned}$$

Therefore, it follows that Theorem 3.6 holds with \(c = \sqrt{L}\), i.e. for \(\delta > 0\) and \(x,y \in {\mathbb {C}}^L\) B-bandlimited such that the subgraph of the essential support graph of x induced by the vertex set \(S_\delta = V_\delta \cap {\text {supp}} y\) is connected, we have

$$\begin{aligned} \inf _{\alpha \in {\mathbb {R}}} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _{\ell ^2(V_\delta )} \le \frac{\sqrt{L}}{\delta } \left( 1 + \frac{\sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}. \end{aligned}$$

It follows that for the rectangular window of size two and for \(6B \le L\), the stability constant scales linearly in L. The dimension of the space of B-bandlimited signals is \(d:=2B+1\) and therefore it follows from \(\tfrac{L}{{{\widetilde{c}}}} \le 6B\) that

$$\begin{aligned}&\inf _{\alpha \in {\mathbb {R}}} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _{\ell ^2(V_\delta )}\\&\quad \le \frac{\sqrt{6(d-1)}}{\delta } \left( 1 + \frac{\sqrt{6{\widetilde{c}} (d-1)} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}. \end{aligned}$$

Example 3.9

We also want to give an example which elaborates on the dependence of the stability constant on \(\delta ^{-1}\). On first glance, it might look like this dependence is only due to our analysis (the propagation of phases between adjacent entries.) However, this is not the case. Consider the rectangular window \(\phi \) of length two along with the signals

$$\begin{aligned} x(\ell ) = {\left\{ \begin{array}{ll} 1 &{} \text{ if } \ell = 0, \\ \delta &{} \text{ if } \ell = 1, \\ 1 &{} \text{ if } \ell = 2, \\ 0 &{} \text{ else, } \end{array}\right. } \qquad y(\ell ) = {\left\{ \begin{array}{ll} 1 &{} \text{ if } \ell = 0, \\ \delta &{} \text{ if } \ell = 1, \\ -1 &{} \text{ if } \ell = 2, \\ 0 &{} \text{ else, } \end{array}\right. } \end{aligned}$$

where \(\delta \in (0,1)\). Then, we have

$$\begin{aligned} \inf _{\alpha \in {\mathbb {R}}} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _2 = 2. \end{aligned}$$

In addition, we have

$$\begin{aligned} \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _\mathrm {F} = 2 \sqrt{2} \frac{\delta }{\sqrt{L}}. \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} \frac{\inf _{\alpha \in {\mathbb {R}}} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _2}{\left\Vert M_\phi [x] - M_\phi [y] \right\Vert _\mathrm {F}} = \sqrt{\frac{L}{2}} \cdot \delta ^{-1} \end{aligned}$$
(3)

is a lower bound for the stability constant. Note that this example is independent of the reconstruction technique we have chosen.

3.2 Multiple Islands and Frequency Gaps

The phase propagation procedure presented as part of the proof of Theorem 3.6 carries over quite naturally to the case where the graph \(G_\delta = (V_\delta ,E)\) is disconnected rather than connected. We say the graph \(G_\delta \) has multiple temporal islands. It is of course interesting to consider this case, as there is a wide range of signals for which G will be disconnected. For instance, recordings of human speech will typically consist of multiple temporal islands as speakers tend to leave short gaps (i.e. modes of silence) in between words. In addition, a discretisation of the signal \(f_\lambda ^+\) from the introduction (see Fig. 4) will yield two temporal islands.

Fig. 4
figure 4

The function \(f_\lambda ^+\) from the introduction after discretisation. Entries of the resulting signal that fall below a certain threshold \(\delta > 0\) are coloured in grey. The remaining entries are coloured in black and make up the vertex set \(V_\delta \). In this picture, we can clearly see the two temporal islands

Full size image

Theorem 3.10

(Stability of phase retrieval on multiple temporal islands) Let \(\delta > 0\) and let \(x,y \in {\mathbb {C}}^L\) be B-bandlimited, for \(B \in {\mathbb {N}}_0\). For the essential support graph \(G_\delta = (V_\delta , E)\) of x, assume that the subgraph induced by the vertex set \(S_\delta = V_\delta \cap {\text {supp}} y\) has K connected components whose vertex sets are denoted by \(\{S_k\}_{k=1}^K\). If \(\phi \in {\mathbb {C}}^L\) is such that

$$\begin{aligned} \min _{\begin{array}{c} m \in \{0,1\}\\ n \in \{-2B,\dots ,2B\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |\ge \frac{1}{c}, \end{aligned}$$

for some \(c > 0\), then

$$\begin{aligned} \inf _{\alpha _1,\dots ,\alpha _K \in {\mathbb {R}}} \sum _{k=1}^K \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha _k} y \right\Vert _{\ell ^2(S_k)} \le \frac{c \sqrt{K}}{\delta } \left( 1 + \frac{\sqrt{ 2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}. \end{aligned}$$

Proof

See Theorem 3.11. \(\square \)

Furthermore, one should note that until now we have only worked with minimal restrictions on the ambiguity function \({\mathcal {A}}[\phi ]\) of the window \(\phi \), i.e. we have only utilised the ambiguity function for \(m=0,1\). In the following, we want to generalise our result to be able to use \({\mathcal {A}}[\phi ](m,n)\) for \(m=0,\dots ,\Delta +1\). In particular, we may be able to harness Corollary 2.5 in order to propagate phase stably across a section of the signal in which the entries consistently fall below a threshold \(\delta \). To precisely describe this phase propagation procedure, we make use of the essential support graph of signals x with time-separation parameter \(\Delta \).

Theorem 3.11

(Main theorem) Let \(\Delta \in {\mathbb {N}}_0\), let \(\delta > 0\) and suppose that \(x,y \in {\mathbb {C}}^L\) are B-bandlimited, for \(B \in {\mathbb {N}}_0\). Let \(G_\delta = (V_\delta , E)\) be the essential support graph of x with time-separation parameter \(\Delta \) and assume that the subgraph induced by the vertex set \(S_\delta = V_\delta \cap {\text {supp}} y\) has K connected components whose vertex sets are denoted by \(\{S_k\}_{k=1}^K\). If \(\phi \in {\mathbb {C}}^L\) is such that

$$\begin{aligned} \min _{\begin{array}{c} m \in \{0,\dots ,\Delta +1\}\\ n \in \{-2B,\dots ,2B\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |\ge \frac{1}{c}, \end{aligned}$$
(4)

for some \(c > 0\), then

$$\begin{aligned}&\inf _{\alpha _1,\dots ,\alpha _K \in {\mathbb {R}}} \sum _{k=1}^K \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha _k} y \right\Vert _{\ell ^2(S_k)}\\&\quad \le \frac{c \sqrt{K}}{\delta } \left( 1 + 2 \sqrt{\frac{L+\Delta }{2+\Delta } } \frac{\Vert x \Vert _{\ell ^2(S_\delta )}}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}. \end{aligned}$$

Proof

See Sect. 5. \(\square \)

Remark 3.12

Alternatively, one can show

$$\begin{aligned}&\inf _{\alpha _1,\dots ,\alpha _K \in {\mathbb {R}}} \sum _{k=1}^K \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha _k} y \right\Vert _{\ell ^2(S_k)}\\&\quad \le \frac{c}{\delta } \left( \sqrt{K} + \sum _{k=1}^K \frac{\sqrt{2 |S_k |} \Vert x \Vert _{\ell ^2(S_k)}}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _2 \end{aligned}$$

under the assumptions laid out in Theorem 3.11. We prefer the result above as it is more compact. Note that neither of these results is stronger or weaker than the other.

We note that one can obtain dual results to the above by considering \({\mathcal {F}}[x]\) instead of x. A straight-forward calculation (see proof of Proposition 3.3) yields

$$\begin{aligned} {\mathcal {A}}[x](m,n) = \mathrm {e}^{-2\pi \mathrm {i}\frac{mn}{L}} {\mathcal {A}}[{\mathcal {F}}[x]](n,-m), \qquad m,n = 0,\dots ,L-1. \end{aligned}$$

In this light, it is not surprising that we can derive stability results for recovering \({\mathcal {F}}[x]\) from the measurements \(M_\phi [x]\) resembling the theorems derived above. Note that in this way, one can also show the following dual of the ambguity function relation:

$$\begin{aligned} {\mathcal {F}}\left[ M_\phi [x]\right] (m,n) = {\mathcal {A}}[{\mathcal {F}}[x]](m,n) \overline{{\mathcal {A}}[{\mathcal {F}}[\phi ]](m,n)}, \qquad m,n = 0,\dots ,L-1. \end{aligned}$$

Theorem 3.13

(Stability for frequency gaps) Let \(B, \Delta \in {\mathbb {N}}_0\), let \(\delta > 0\) and suppose that \(x,y \in {\mathbb {C}}^L\) have their support contained in \(\{-B,\dots ,B\} \mod L\). Let \(G_\delta = (V_\delta , E)\) be the essential support graph of \({\mathcal {F}}[x]\) with time-separation parameter \(\Delta \) and assume that the subgraph induced by the vertex set \(S_\delta = V_\delta \cap {\text {supp}} {\mathcal {F}}[y]\) has K connected components whose vertex sets are denoted by \(\{S_k\}_{k=1}^K\). If \(\phi \in {\mathbb {C}}^L\) is such that

$$\begin{aligned} \min _{\begin{array}{c} m \in \{-2B,\dots ,2B\}\\ n \in \{0,\dots ,\Delta +1\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |\ge \frac{1}{c}, \end{aligned}$$

for some \(c > 0\), then

$$\begin{aligned}&\inf _{\alpha _1,\dots ,\alpha _K \in {\mathbb {R}}} \sum _{k=1}^K \left\Vert {\mathcal {F}}[x] - \mathrm {e}^{\mathrm {i} \alpha _k} {\mathcal {F}}[y] \right\Vert _{\ell ^2(S_k)}\\&\quad \le \frac{c \sqrt{K}}{\delta } \left( 1 + 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _2}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _2. \end{aligned}$$

Remark 3.14

In the preceding pages, we have presented approaches for phase retrieval for signals with multiple temporal or frequency islands. Unfortunately, it is not so clear how to extend this work to the more general case of time-frequency atolls considered in [1, 15]. It is likely that one has to come up with a different approach that allows one to do phase propagation in frequency and time direction simultaneously to actually handle time-frequency atolls.

We want to end this section by remarking that from our proof strategy for the frequency result a straight-forward dual version of Corollary 2.5 follows.

Corollary 3.15

Let \(\Delta \in {\mathbb {N}}_0\) and let \(x,y,\phi \in {\mathbb {C}}^L\) be such that \(M_\phi [x] = M_\phi [y]\). Assume that the window \(\phi \) satisfies

$$\begin{aligned} {\mathcal {A}}[\phi ](m,n) \ne 0, \qquad \text{ for } m \in \{0,\dots ,L-1\},~n\in \{0,\dots ,\Delta +1\}. \end{aligned}$$

Define \(G = (V,E)\) as the graph with vertex set \(V = {\text {supp}} {\mathcal {F}}[x]\) and edge set \(E \subset \{0,\dots ,L-1\} \times \{0,\dots ,L-1\}\) given by

$$\begin{aligned} (\ell ,k) \in E \Leftrightarrow |\ell - k |\in (0,\Delta +1] \cup [L-\Delta -1,L). \end{aligned}$$

If \(\{V_k\}_{k=1}^K\) are the vertex sets of the connected components of G, then for all \(k \in \{1,\dots ,K\}\) there exists an \(\alpha _k \in {\mathbb {R}}\) such that

$$\begin{aligned} {\mathcal {F}}[x](\ell ) = \mathrm {e}^{\mathrm {i} \alpha _k} {\mathcal {F}}[y](\ell ), \qquad \ell \in V_k. \end{aligned}$$

4 Stability Estimates Based on the Autocorrelation Relation

The goal of this section is to apply the techniques we have developed thus far to the setup proposed in [19]. Our approach will be designed to work for bandlimited signals \(x \in {\mathbb {C}}^L\) which potentially have very small entries. In doing so, we do not need to require that the Fourier transform of the absolute value squared of the window is nowhere-vanishing. We emphasise these particularities as the stability result developed in [19] (Theorem 4.2 on p. 375) relies on window functions for which \({\mathcal {F}}[|\phi |^2]\) is nowhere-vanishing, and while one may apply it to signals \(x \in {\mathbb {C}}^L\) with very small entries, the resulting stability constant will be ill-behaved as it depends inversely on \(\min _{\ell \in {\text {supp}} x} |x(\ell ) |^2\).

Recall from Sect. 2 that the authors of [19] consider the graph \(G = (V,E)\) with vertex set \(V := {\text {supp}}(x)\) and an edge between \(\ell ,k \in V\) if

$$\begin{aligned} |\ell -k |\in \{\ell _\phi , L-\ell _\phi \}, \end{aligned}$$

where \(\ell _\phi +1\) denotes the support length of the window function. They do then propose to reconstruct the magnitude of a signal \(x \in {\mathbb {C}}^L\) using the ambiguity function relation (2) (as in Sect. 3) and propagate phase from one entry of x to another if their indices have distance \(\ell _\phi \) using Eq. (1). As before, we will work with local lower bounds on the ambiguity function of the window and the signal in order to ensure that all the aforedescribed steps can be carried out stably.

In order to introduce the local lower bounds on the signal, we will have to modify the graphs presented in [19] slightly: Let us consider a signal \(x \in {\mathbb {C}}^L\), a tolerance parameter \(\delta > 0\) and a window function \(\phi \in {\mathbb {C}}^L\) such that

$$\begin{aligned} {\text {supp}}(\phi ) = \{n_0, \dots , n_0+\ell _\phi \} \mod L, \end{aligned}$$

for \(n_0, \ell _\phi \in \{0,\dots ,L-1\}\) such that \(2 \ell _\phi < L\). Introduce the graph \(G_\delta = (V_\delta ,E)\) with vertex set

$$\begin{aligned} V_\delta := \left\{ \ell \in \{0,\dots ,L-1\} \;|\; |x(\ell ) |\ge \delta \right\} \end{aligned}$$

and an edge between \(\ell ,k \in V\) if

$$\begin{aligned} |\ell - k |\in \{\ell _\phi , L-\ell _\phi \}. \end{aligned}$$

Under these assumptions, we can state the following stability estimate whose proof is inspired by the proof of Corollary 2.8:

Theorem 4.1

Let \(\ell _\phi ,n_0 \in {\mathbb {N}}_0\) such that \(2 \ell _\phi < L\). Furthermore, let \(\delta > 0\) and let \(x,y \in {\mathbb {C}}^L\) be B-bandlimited, for \(B \in {\mathbb {N}}_0\). Suppose that the subgraph induced by the vertex set \(S_\delta = V_\delta \cap {\text {supp}} y\) is connected and that the window \(\phi \) satisfies

$$\begin{aligned} {\text {supp}}(\phi ) = \{n_0, \dots , n_0+\ell _\phi \} \mod L \end{aligned}$$

as well as

$$\begin{aligned} \min _{k \in \{-2B,\dots ,2B\}} \left|{\mathcal {F}}\left[ |\phi |^2 \right] (k) \right|\ge \frac{1}{c}, \end{aligned}$$

for some \(c > 0\). Then,

$$\begin{aligned} \inf _{\alpha \in {\mathbb {R}}} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _{\ell ^2(V_\delta )} \le \frac{1}{\delta } \left( c + \frac{2 \sqrt{|S_\delta |L} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta |\phi (n_0) \phi (n_0 + \ell _\phi ) |} \right) \left\Vert M_\phi [x]-M_\phi [y] \right\Vert _\mathrm {F}. \end{aligned}$$

Proof

See Sect. 5. \(\square \)

Remark 4.2

The stability constant in this result is

$$\begin{aligned} \frac{1}{\delta } \left( c + \frac{2 \sqrt{|S_\delta |L} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta |\phi (n_0) \phi (n_0 + \ell _\phi ) |} \right) . \end{aligned}$$

The part of the constant due to magnitude retrieval is exactly the same as in the results in Sect. 3. The part of the constant stemming from phase retrieval is a slight modification from the constants in Sect. 3. It is mostly the term \(|\phi (n_0)\phi (n_0 + \ell _\phi ) |\) in the denominator that deserves some attention. It is clear that phase propagation based on the relation

$$\begin{aligned} {\mathcal {F}}^{-1}\left[ M_\phi [x](n,\cdot ) \right] (\ell _\phi ) = x(n_0 + \ell _\phi + n)\overline{x(n_0 + n)}\phi (n_0)\overline{\phi (n_0+\ell _\phi )} \end{aligned}$$

will be unstable whenever the ends of the window \(\phi (n_0)\) and \(\phi (n_0 + \ell _\phi )\) are close to zero. In particular, the reconstruction method proposed by the authors of [13, 19] benefits from windows for which \(|\phi (n_0) \phi (n_0 + \ell _\phi ) |\) is large such as the Hamming or rectangular window.

As remarked before, in contrast to the stability result in [19], our result is applicable even when the Fourier transform of the magnitude squared of the window function \({\mathcal {F}}[|\phi |^2]\) has vanishing entries at the cost of only being applicable to bandlimited signals. We should also note that in [19] the stability constant for the phase retrieval estimate scales like \(\sqrt{|{\text {supp}} x |} \cdot L^3\) (which becomes \(L^{7/2}\) for nowhere-vanishing signals) whereas our stability constant merely scales like \(\sqrt{|S_\delta |L}\) (which becomes L for signals whose entries have absolute values in excess of the threshold \(\delta \)).

Remark 4.3

(On disconnected graphs and duality results) Finally, we would like to note that one can prove a result resembling Theorem 4.1 in the case where \(S_\delta \) has \(K \in {\mathbb {N}}\) connected components whose vertex sets are denoted by \(S_1,\dots ,S_K \subset S_\delta \).

Similarly, we may utilise Lemma 2.1 in order to deduce that

$$\begin{aligned} {\mathcal {F}}\left[ M_\phi [x](\cdot ,n) \right] (m) = \frac{1}{\sqrt{L}} \cdot \sum _{k=0}^{L-1} {\mathcal {F}}[x](k) \overline{ {\mathcal {F}}[x](k-m) } {\mathcal {F}}[\phi ](k-m-n) \overline{ {\mathcal {F}}[\phi ](k-n) } \end{aligned}$$

holds, for \(x,\phi \in {\mathbb {C}}^L\) and \(m,n = 0,\dots ,L-1\). This in turn can be used to deduce a stability result which is essentially the Fourier-dual of Theorem 4.1.

5 Proofs of the Main Results

Proof of Corollary 2.5

By the ambiguity function relation and our assumptions, we find that

$$\begin{aligned} {\mathcal {A}}[x](m,n) = {\mathcal {A}}[y](m,n), \qquad \text{ for } m \in \{0,\dots ,\Delta +1\}, ~n\in \{0,\dots ,L-1\}. \end{aligned}$$

Therefore,

$$\begin{aligned} x(\ell ) \overline{x(\ell -m)} = y(\ell ) \overline{y(\ell -m)}, \qquad \text{ for } \ell \in \{0,\dots ,L-1\},~m \in \{0,\dots ,\Delta +1\},\nonumber \\ \end{aligned}$$
(5)

and in particular x and y have the same magnitudes. Let us now consider \(k \in \{1,\dots ,K\}\) as well as some \(\ell _0\) in \(V_k\). We have \(|x(\ell _0) |= |y(\ell _0) |\) and hence \(x(\ell _0) = \mathrm {e}^{\mathrm {i} \alpha _k} y(\ell _0)\), for some \(\alpha _k \in {\mathbb {R}}\). As \(V_k\) is the vertex set of a connected component of G, it follows that for all \(\ell \in V_k \setminus \{\ell _0\}\), there exists a (simple) path from \(\ell _0\) to \(\ell \). Therefore, we can consider \(\ell \in V_k \setminus \{\ell _0\}\) and let \((u_0,\dots ,u_n)\) be the vertex sequence of the path from \(u_0 = \ell _0\) to \(u_n = \ell \). For \(j \in \{0,\dots ,n-1\}\) one has, by definition of the edge set, that

$$\begin{aligned} |u_{j+1} - u_j |\in (0,\Delta +1] \cup [L-\Delta -1,L). \end{aligned}$$

Thus, there exists an \(m_j \in \{1,\dots ,\Delta +1\}\) such that \(u_{j+1} - u_j = m_j \mod L\) or \(u_j - u_{j+1} = m_j \mod L\). In either case, it follows from Eq. (5) that \(x(u_{j+1}) \overline{x(u_j)} = y(u_{j+1}) \overline{y(u_j)}\). By induction on j, we find that \(x(\ell ) = \mathrm {e}^{\mathrm {i} \alpha _k} y(\ell )\). \(\square \)

Proof of Theorem 3.6

The case \(4B \le L\) is similar to the case \(4B > L\) but simpler: Indeed consider \(4B \le L\). In this case, we have

$$\begin{aligned} \min _{\begin{array}{c} m \in \{0,1\}\\ n \in \{0,\dots ,L-1\} \end{array}} |{\mathcal {A}}[\phi ](m,n) |\ge \frac{1}{c} \end{aligned}$$

by assumption. Therefore, we can replace all sums over \(\{-2B,\dots ,2B\}\) by sums over \(\{0,\dots ,L-1\}\) in this proof. So let us consider \(4B > L\): Let \(\alpha \in {\mathbb {R}}\) be arbitrary. Employing Proposition A.1, we have

$$\begin{aligned} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha } y \right\Vert _{\ell ^2(V_\delta )} \le \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )} + \left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$
(6)

The magnitude difference is estimated as in Lemma 3.4. For the estimate of the phase difference, we develop inequalities in the following. Let \(\ell ,k \in S_\delta \). According to Proposition A.2, we have

$$\begin{aligned} \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|\le \left|\frac{x(k)}{|x(k) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(k)}{\vert y(k) |} \right|+ \frac{ 2 \left|x(\ell ) \overline{x(k)} - y(\ell ) \overline{y(k)} \right|}{ |x(\ell )x(k) |}. \end{aligned}$$

Using the above inequality recursively, one obtains that for all \(M \in {\mathbb {N}}\) and \(u_0,u_1,\dots ,u_M \in S_\delta \):

$$\begin{aligned}&\left|\frac{x(u_M)}{|x(u_M) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(u_M)}{|y(u_M) |} \right|\le \left|\frac{x(u_0)}{|x(u_0) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(u_0)}{|y(u_0) |} \right|\nonumber \\&\quad +\,2 \sum _{j=0}^{M-1} \frac{ \left|x(u_{j+1}) \overline{x(u_j)} - y(u_{j+1}) \overline{y(u_j)} \right|}{|x(u_{j+1}) x(u_j) |}. \end{aligned}$$
(7)

Suppose now that \(\ell _0\) is chosen such that any other vertex \(\ell \in S_\delta \) has graph distance (in the induced subgraph) at most \(|S_\delta |/2 \) from \(\ell _0\). Then, for any \(\ell \in S_\delta \setminus \{ \ell _0 \}\), there exists \(M(\ell ) \in {\mathbb {N}}\), with \(M(\ell ) \le |S_\delta |/ 2\), and a sequence \(u_0^\ell = \ell _0, u_1^\ell , \dots , u_{M(\ell )}^\ell = \ell \) in \(S_\delta \) such that (cf. Definition 3.1 with \(\Delta = 0\))

$$\begin{aligned} |u_{j+1}^\ell - u_j^\ell |\in \{1,L-1\}, \qquad \text{ for } j = 0,\dots ,M(\ell )-1. \end{aligned}$$

Therefore, there exists a sequence \(\sigma _1^\ell ,\dots ,\sigma _{M(\ell )}^\ell \) in \(\{ -1,1 \}\) such that

$$\begin{aligned} u_{j+1}^\ell - u_j^\ell = \sigma _{j+1}^\ell \mod L, \qquad \text{ for } j = 0,\dots ,M(\ell )-1. \end{aligned}$$

Now, let \(\alpha \in {\mathbb {R}}\) be such that

$$\begin{aligned} \left|\frac{x(\ell _0)}{|x(\ell _0) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell _0)}{|y(\ell _0) |} \right|= 0. \end{aligned}$$

Then, we have for any \(\ell \in S_\delta \), according to the above considerations (and inequality (7)), that

$$\begin{aligned} \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|\le 2 \sum _{j=1}^{M(\ell )} \frac{ \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell )} \right|}{|x(u_j^\ell ) x(u_j^\ell - \sigma _j^\ell ) |}. \end{aligned}$$

For the second term of the right-hand side of inequality (6) this yields

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2 \left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left( \sum _{j=1}^{M(\ell )} \frac{ \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell )} \right|}{ |x(u_j^\ell ) x(u_j^\ell - \sigma _j^\ell ) |} \right) ^2 \right) ^\frac{1}{2}. \end{aligned}$$

Applying Jensen’s inequality on the square of the inner sum and noting that \(M(\ell ) \le |S_\delta |/ 2\), we obtain

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \sqrt{2 |S_\delta |} \left( \sum _{\ell \in S_\delta } \sum _{j=1}^{M(\ell )} \frac{ \left|x(\ell ) \right|^2 }{ |x(u_j^\ell ) x(u_j^\ell - \sigma _j^\ell ) |^2 } \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell )} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

Since \(u^\ell _j \in S_\delta \), for \(j \in \{1,\dots ,M(\ell )\}\), we can further estimate

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{\sqrt{2 |S_\delta |}}{\delta ^2} \left( \sum _{\ell \in S_\delta } \sum _{j=1}^{M(\ell )} \left|x(\ell ) \right|^2 \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell )} \right|^2 \right) ^\frac{1}{2} \end{aligned}$$

and with \(\sigma ^\ell _j \in \{ \pm 1 \}\), for \(j \in \{1,\dots ,M(\ell )\}\), we also get

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{\sqrt{2 |S_\delta |}}{\delta ^2} \left( \sum _{\sigma \in \{-1,1\}} \sum _{\ell \in S_\delta } \sum _{j=1}^{M(\ell )} \left|x(\ell ) \right|^2 \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma )} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

There are no repetitions in the sequences \(u^\ell _1,u^\ell _2,\dots ,u^\ell _{M(\ell )}\) and hence

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{\sqrt{2 |S_\delta |}}{\delta ^2} \left( \sum _{\sigma \in \{-1,1\}} \sum _{\ell \in S_\delta } \sum _{u \in S_\delta } \left|x(\ell ) \right|^2 \left|x(u) \overline{x(u - \sigma )} - y(u) \overline{y(u - \sigma )} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

Therefore, we have

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{ \sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )} }{ \delta ^2 } \left( \sum _{\sigma \in \{-1,1\}} \sum _{u = 0}^{L-1} \left|x(u) \overline{x(u - \sigma )} - y(u) \overline{y(u - \sigma )} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

Suppose now that \(4B < L\). By Plancherel’s theorem, it holds that

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{ \sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )} }{ \delta ^2 } \left( \sum _{\sigma \in \{-1,1\}} \sum _{n = 0}^{L-1} \left|{\mathcal {A}}[x](\sigma ,n) - {\mathcal {A}}[y](\sigma ,n) \right|^2 \right) ^\frac{1}{2} \\&\quad = \frac{ \sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )} }{ \delta ^2 } \left( \sum _{\sigma \in \{-1,1\}} \sum _{n = -2B}^{2B} \left|{\mathcal {A}}[x](\sigma ,n) - {\mathcal {A}}[y](\sigma ,n) \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

It follows from the ambiguity function relation and the lower bound on the ambiguity function of the window on \(\{0,1\} \times \{-2B,\dots ,2B\}\) that

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le c \cdot \frac{ \sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )} }{ \delta ^2 } \left( \sum _{\sigma \in \{-1,1\}} \sum _{n = -2B}^{2B} \left|{\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] (n,-\sigma ) \right|^2 \right) ^\frac{1}{2} \\&\quad \le c \cdot \frac{ \sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )} }{ \delta ^2 } \cdot \left\Vert {\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] \right\Vert _{\mathrm {F}} \\&\quad = c \cdot \frac{ \sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )} }{ \delta ^2 } \cdot \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}, \end{aligned}$$

where we have used Plancherel’s theorem in the last equality. \(\square \)

Proof of Theorem 3.11

Let \(k \in \{1,\dots ,K\}\) and \(\alpha _k \in {\mathbb {R}}\). As in the proof of Theorem 3.6, we start by splitting the estimate into a phase and a magnitude estimate using Proposition A.1:

$$\begin{aligned} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha _k} y \right\Vert _{\ell ^2(S_k)} \le \left\Vert |x |- |y |\right\Vert _{\ell ^2(S_k)} + \left( \sum _{\ell \in S_k} |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

As the connected components \(\{S_k\}_{k=1}^K\) are disjoint subsets of \(V_\delta \), we can use Jensen’s inequality to see that

$$\begin{aligned} \sum _{k=1}^K \left\Vert |x |- |y |\right\Vert _{\ell ^2(S_k)} \le \sqrt{K} \left( \sum _{k=1}^K \left\Vert |x |- |y |\right\Vert _{\ell ^2(S_k)}^2 \right) ^\frac{1}{2}&= \sqrt{K} \left\Vert |x |- |y |\right\Vert _{\ell ^2(\bigcup _{k=1}^K S_k)} \\&\le \sqrt{K} \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )}. \end{aligned}$$

Employing Lemma 3.4, we obtain for the magnitude retrieval estimate

$$\begin{aligned} \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )} \le \frac{c}{\delta } \left\Vert M_\phi [x]-M_\phi [y] \right\Vert _\mathrm {F}. \end{aligned}$$

The phase difference is estimated just like in Theorem 3.6: First, observe that there must exist a vertex \(\ell _0 \in S_k\) such that any other vertex \(\ell \in S_k\) has graph distance \(M(\ell )\) at most \(\tfrac{L+\Delta }{2+\Delta }\) from \(\ell _0\). Indeed, consider the following argument: The worst case which could happen is that we need to connect the vertex 0 to the vertex \(\lfloor L/2 \rfloor \). By definition of the graph, it will take us exactly one step to go from 0 to any \(\ell \in \{1,\dots ,\Delta +1\} \cap S_k\); it will take us exactly two steps to go from 0 to \(\Delta + 2\), if the latter is in \(S_k\); and it will take us at most three steps to go from 0 to \(\ell \in \{\Delta +3,2\Delta +3\} \cap S_k\). Following this logic, it is not too hard to see that it will take us at most 2n steps to go from 0 to \(n(\Delta +2)\), if the latter is in \(S_k\), and it will take us at most \(2n+1\) steps to go from 0 to \(\ell \in \{n(\Delta +2)+1,\dots ,(n+1)(\Delta +2)-1\} \cap S_k\). So, if there exists an element \(n \in {\mathbb {N}}\) such that \(n(\Delta +2) = \lfloor L/2 \rfloor \), then it will take us at most

$$\begin{aligned} 2n = \frac{2 \lfloor L/2 \rfloor }{\Delta + 2} \le \frac{L}{\Delta +2} \le \frac{L+\Delta }{2 + \Delta } \end{aligned}$$

steps to connect 0 and \(\lfloor L/2 \rfloor \). Similarly, if there is an element \(n \in {\mathbb {N}}_0\) such that \(\lfloor L/2 \rfloor \in \{n(\Delta +2)+1,\dots , (n+1)(\Delta +2)-1\}\), then there is a \(\beta \in \{1,\dots ,\Delta +1\}\) such that

$$\begin{aligned} 2n+1 = \frac{2 \lfloor L/2 \rfloor - 2\beta }{\Delta + 2} + 1 \le \frac{L - 2}{\Delta + 2} + 1 = \frac{L + \Delta }{\Delta +2}. \end{aligned}$$

So for any \(\ell \in S_k \setminus \{\ell _0\}\), there exists a path \(u_0^\ell = \ell _0,u_1^\ell ,\dots ,u_{M(\ell )}^\ell = \ell \) from \(\ell _0\) to \(\ell \). By definition, this path satisfies

$$\begin{aligned} \left|u_{j+1}^\ell - u_j^\ell \right|\in (0,\Delta +1] \cup [L-\Delta -1,L), \qquad \text{ for } j = 0,\dots ,M(\ell )-1. \end{aligned}$$

Therefore, there exist sequences \(\sigma _1^\ell ,\dots ,\sigma _{M(\ell )}^\ell \in \{\pm 1\}\) and \(\Delta _1^\ell ,\dots ,\Delta _{M(\ell )}^\ell \in \{1,\dots ,\Delta +1\}\) such that

$$\begin{aligned} u_{j+1}^\ell - u_j^\ell = \sigma _{j+1}^\ell \Delta _{j+1}^\ell \mod L, \qquad \text{ for } j = 0, \dots ,M(\ell )-1. \end{aligned}$$

We let \(\alpha _k \in {\mathbb {R}}\) be chosen in such a way that

$$\begin{aligned} \left|\frac{x(\ell _0)}{|x(\ell _0) |} - \mathrm {e}^{\mathrm {i} \alpha _k} \frac{y(\ell _0)}{|y(\ell _0) |} \right|= 0. \end{aligned}$$

Proceeding as in the proof of Theorem 3.6 (now with \(M(\ell ) \le (L+\Delta )/(2+\Delta )\)), we derive

$$\begin{aligned}&\left( \sum _{\ell \in S_k} |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha _k} \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{1}{\delta ^2} \left( \sum _{\ell \in S_k} \sum _{j=1}^{M(\ell )} \left|x(\ell ) \right|^2 \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell \Delta _j^\ell )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell \Delta _j^\ell )} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

We first treat the case \(2\Delta < L-2\) and use that \(\sigma _j^\ell \Delta _j^\ell \in \{-\Delta -1,\dots ,\Delta +1\}\) to estimate

$$\begin{aligned}&\left( \sum _{\ell \in S_k} |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha _k} \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{1}{\delta ^2} \left( \sum _{m = -\Delta -1}^{\Delta +1} \sum _{\ell \in S_k} \sum _{j=1}^{M(\ell )} \left|x(\ell ) \right|^2 \left|x(u_j^\ell ) \overline{x(u_j^\ell - m)} - y(u_j^\ell ) \overline{y(u_j^\ell - m)} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

We may use that there are no repetitions in the sequences \(u_1^\ell ,\dots , u_{M(\ell )}^\ell \) to obtain

$$\begin{aligned}&\left( \sum _{\ell \in S_k} |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha _k} \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{1}{\delta ^2} \left( \sum _{m = -\Delta -1}^{\Delta +1} \sum _{\ell \in S_k} \sum _{u = 0}^{L-1} \left|x(\ell ) \right|^2 \left|x(u) \overline{x(u - m)} - y(u) \overline{y(u - m)} \right|^2 \right) ^\frac{1}{2} \\&\quad = 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _{\ell ^2(S_k)}}{\delta ^2} \left( \sum _{m = -\Delta -1}^{\Delta +1} \sum _{u = 0}^{L-1} \left|x(u) \overline{x(u - m)} - y(u) \overline{y(u - m)} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

Suppose furthermore that \(4B > L\). According to Plancherel’s theorem, we find that

$$\begin{aligned}&\left( \sum _{\ell \in S_k} |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha _k} \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _{\ell ^2(S_k)}}{\delta ^2} \left( \sum _{m = -\Delta -1}^{\Delta +1} \sum _{n = 0}^{L-1} \left|{\mathcal {A}}[x](m,n) - {\mathcal {A}}[y](m,n) \right|^2 \right) ^\frac{1}{2} \\&\quad = 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _{\ell ^2(S_k)}}{\delta ^2} \left( \sum _{m = -\Delta -1}^{\Delta +1} \sum _{n = -2B}^{2B} \left|{\mathcal {A}}[x](m,n) - {\mathcal {A}}[y](m,n) \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

Next, we use the ambiguity function relation, inequality (4) as well as the symmetry of the ambiguity function of the window around the origin to derive

$$\begin{aligned}&\left( \sum _{\ell \in S_k} |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha _k} \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2c \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _{\ell ^2(S_k)}}{\delta ^2} \left( \sum _{m = -\Delta -1}^{\Delta +1} \sum _{n = -2B}^{2B} \left|{\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] (n,m) \right|^2 \right) ^\frac{1}{2} \\&\quad \le 2c \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _{\ell ^2(S_k)}}{\delta ^2} \left\Vert {\mathcal {F}}\left[ M_\phi [x] - M_\phi [y] \right] \right\Vert _2 \\&\qquad \qquad \qquad \qquad = 2c \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _{\ell ^2(S_k)}}{\delta ^2} \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _2. \end{aligned}$$

Note that we may once again use Jensen’s inequality to show that

$$\begin{aligned} \sum _{k=1}^K \Vert x \Vert _{\ell ^2(S_k)} \le \sqrt{K} \Vert x \Vert _2. \end{aligned}$$

Thus, combining the phase and the magnitude estimates yields

$$\begin{aligned} \inf _{\alpha _1,\dots ,\alpha _K} \sum _{k=1}^K \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha _k} y \right\Vert _{\ell ^2(S_k)} \le \frac{c \sqrt{K}}{\delta } \left( 1 + 2 \sqrt{\frac{L+\Delta }{2+\Delta }} \frac{\Vert x \Vert _2}{\delta } \right) \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _2. \end{aligned}$$

The cases in which \(2\Delta \ge L-2\) or \(4B \ge L\) are dealt with similarly. \(\square \)

Proof of Theorem 4.1

Let \(\alpha \in {\mathbb {R}}\). As in the proof of Theorem 3.6, we start by splitting the estimate into a phase and a magnitude estimate

$$\begin{aligned} \left\Vert x - \mathrm {e}^{\mathrm {i} \alpha _k} y \right\Vert _{\ell ^2(V_\delta )} \le \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )} + \left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2}. \end{aligned}$$

First, noting that

$$\begin{aligned} {\mathcal {F}}\left[ |\phi |^2 \right] (k) = {\mathcal {A}}[\phi ](0,k), \qquad \text{ for } k = 0,\dots ,L-1, \end{aligned}$$

we can apply Lemma 3.4 to obtain the estimate

$$\begin{aligned} \left\Vert |x |- |y |\right\Vert _{\ell ^2(V_\delta )} \le \frac{c}{\delta } \left\Vert M_\phi [x]-M_\phi [y] \right\Vert _\mathrm {F}. \end{aligned}$$

For the estimate on the phase retrieval part, we need to consider a new strategy based on Eq. (1). First, we find that there must exist a vertex \(\ell _0 \in S_\delta \) such that any other vertex \(\ell \in S_\delta \) has graph distance \(M(\ell )\) at most \(|S_\delta |/2\) from \(\ell _0\). So for any \(\ell \in S_\delta \setminus \{\ell _0\}\), there exists a path \(u_0^\ell = \ell _0,u_1^\ell ,\dots ,u_{M(\ell )}^\ell = \ell \) from \(\ell _0\) to \(\ell \). By definition, this path satisfies

$$\begin{aligned} \left|u_{j+1}^\ell - u_j^\ell \right|\in \{\ell _\phi , L-\ell _\phi \}, \qquad \text{ for } j = 0,\dots ,M(\ell )-1. \end{aligned}$$

Therefore, there exists a sequence \(\sigma _1^\ell ,\dots ,\sigma _{M(\ell )}^\ell \in \{\pm 1\}\) such that

$$\begin{aligned} u_{j+1}^\ell - u_j^\ell = \sigma _{j+1}^\ell \ell _\phi \mod L, \qquad \text{ for } j = 0, \dots ,M(\ell )-1. \end{aligned}$$

With this at hand, we proceed similarly to the proof of Theorem 3.6. We let \(\alpha \in {\mathbb {R}}\) be chosen in such a way that

$$\begin{aligned} \left|\frac{x(\ell _0)}{|x(\ell _0) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell _0)}{|y(\ell _0) |} \right|= 0. \end{aligned}$$

Then, we have that for any \(\ell \in S_\delta \)

$$\begin{aligned} \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|\le 2 \sum _{j=1}^{M(\ell )} \frac{ \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell \ell _\phi )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell \ell _\phi )} \right|}{|x(u_j^\ell ) x(u_j^\ell - \sigma _j^\ell \ell _\phi ) |} \end{aligned}$$

and

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{\sqrt{2 |S_\delta |}}{\delta ^2} \left( \sum _{\ell \in S_\delta } \sum _{j=1}^{M(\ell )} \left|x(\ell ) \right|^2 \left|x(u_j^\ell ) \overline{x(u_j^\ell - \sigma _j^\ell \ell _\phi )} - y(u_j^\ell ) \overline{y(u_j^\ell - \sigma _j^\ell \ell _\phi )} \right|^2 \right) ^\frac{1}{2}, \end{aligned}$$

by Jensen’s inequality, \(M(\ell ) \le |S_\delta |/ 2\) and the fact that \(u_j^\ell , u_j^\ell - \sigma _j^\ell \ell _\phi \in S_\delta \), for all \(j \in \{1,\dots ,M(\ell )\}\). As before, we can further employ a crude estimate to derive

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad = \frac{\sqrt{2 |S_\delta |} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta ^2} \left( \sum _{\sigma \in \{\pm 1\}} \sum _{u \in S_\delta } \left|x(u) \overline{x(u - \sigma \ell _\phi )} - y(u) \overline{y(u - \sigma \ell _\phi )} \right|^2 \right) ^\frac{1}{2}, \end{aligned}$$

since \(\sigma _j^\ell \in \{\pm 1\}\), for all \(j \in \{1,\dots ,M(\ell )\}\) and all \(\ell \in S_\delta \), and because for fixed \(\ell \in S_\delta \), the \(u_j^\ell \) are all distinct. Next, we note that due to \({\text {supp}} \phi = \{n_0,\dots ,n_0 + \ell _\phi \} \mod L\), \(2\ell _\phi < L\), and the autocorrelation relation, we have for \(u \in S_\delta \)

$$\begin{aligned}&x(u)\overline{x(u-\ell _\phi )} \phi (n_0) \overline{\phi (n_0 + \ell _\phi )}\\&\quad = \sum _{\ell = 0}^{L-1} x(\ell ) \overline{x(\ell -\ell _\phi )} \phi (\ell + n_0 - u) \overline{ \phi (\ell + n_0 + \ell _\phi - u) } \\&\quad = \sqrt{L} {\mathcal {F}}^{-1} [M_\phi [x](u-n_0-\ell _\phi ,\cdot )](\ell _\phi ), \end{aligned}$$

as well as

$$\begin{aligned}&x(u)\overline{x(u+\ell _\phi )} \phi (n_0+\ell _\phi ) \overline{\phi (n_0)}\\&\quad = \sum _{\ell = 0}^{L-1} x(\ell ) \overline{x(\ell +\ell _\phi )} \phi (\ell + \ell _\phi + n_0 - u) \overline{ \phi (\ell + n_0 - u) } \\&\quad = \sqrt{L} {\mathcal {F}}^{-1} [M_\phi [x](u-n_0,\cdot )](-\ell _\phi ). \end{aligned}$$

This implies

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{\sqrt{2 |S_\delta |L} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta ^2 |\phi (n_0) \phi (n_0 + \ell _\phi ) |}\\&\qquad \Bigg ( \sum _{u \in S_\delta } \Big ( \left|{\mathcal {F}}^{-1} [M_\phi [x](u-n_0-\ell _\phi ,\cdot ) - M_\phi [y](u-n_0-\ell _\phi ,\cdot )](\ell _\phi ) \right|^2 \\&\qquad + \left|{\mathcal {F}}^{-1} [M_\phi [x](u-n_0,\cdot ) - M_\phi [y](u-n_0,\cdot )](-\ell _\phi ) \right|^2 \Big ) \Bigg )^\frac{1}{2}. \end{aligned}$$

Yet another crude estimate results in

$$\begin{aligned}&\left( \sum _{\ell \in S_\delta } |x(\ell ) |^2 \left|\frac{x(\ell )}{|x(\ell ) |} - \mathrm {e}^{\mathrm {i} \alpha } \frac{y(\ell )}{|y(\ell ) |} \right|^2 \right) ^\frac{1}{2} \\&\quad \le \frac{2 \sqrt{|S_\delta |L} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta ^2 |\phi (n_0) \phi (n_0 + \ell _\phi ) |} \left( \sum _{m,n = 0}^{L-1} \left|{\mathcal {F}}^{-1} [M_\phi [x](m,\cdot ) - M_\phi [y](m,\cdot )](n) \right|^2 \right) ^\frac{1}{2} \\&\quad = \frac{2 \sqrt{|S_\delta |L} \Vert x \Vert _{\ell ^2(S_\delta )}}{\delta ^2 |\phi (n_0) \phi (n_0 + \ell _\phi ) |} \left\Vert M_\phi [x] - M_\phi [y] \right\Vert _{\mathrm {F}}. \end{aligned}$$

\(\square \)