Artificial aquifer recharge and pumping: transient analytical solutions for hydraulic head and impact on streamflow rate based on the spatial superposition method

Abstract

The behaviour of transient groundwater mounds in response to infiltration from surface basins has been studied for decades, but some common settings still lack analytical solutions. It has been shown that applying mathematical integration to the line-sink solution developed by Hantush in the 1960s for pumping an unconfined aquifer, considering recharge over the surface of a defined area, is identical to his solution for groundwater mounding below a rectangular basin. This implies that the superposition principle can, generally, be used to directly include pumping wells, as well as aquifer boundaries, to derive a unique solution. Moreover, other line-sink solutions can be used with a spatial superposition method for addressing a variety of hydrogeological settings, provided the behaviour of the relevant partial differential equations is linear. Based on this principle and on existing line-sink solutions, several analytical solutions are proposed that are able to consider a rectangular recharging area and a pumping well in an unconfined aquifer: (1) near a stream, (2) between a stream and a no-flow boundary, with and without the influence of natural recharge, (3) near a stream that partially penetrates an aquifer and (4) for a multi-layer aquifer. For cases including streams, transient solutions of the impact on streamflow rate are also presented. The proposed analytical solutions will be of practical use for managed aquifer recharge, in particular the design of structures for artificially recharging an aquifer, possibly pumped by one or several wells.

Résumé

Le comportement des dômes piézométriques souterrains, en transitoire, suite à l’infiltration d’eau par des bassins de recharge artificielle est étudié depuis des décennies. Cependant, certaines configurations n’ont pas été traitées par des solutions analytiques. Il est d’abord rappelé et montré que l’intégration de la solution développée pour un pompage dans un aquifère libre par Hantush dans les années 1960 sur une surface rectangulaire est identique à sa solution décrivant l’évolution du dôme piézométrique dans l’aquifère sous un bassin de recharge de forme rectangulaire. Ce constat implique que le principe de superposition peut, en général, être utilisé pour inclure directement les puits de pompage, ainsi que les limites des aquifères, dans une unique solution. De plus, d’autres solutions de type puits peuvent être utilisées avec une méthode de superposition spatiale pour traiter diverses situations hydrogéologiques, à condition que le comportement des équations différentielles partielles correspondantes soit linéaire. Sur la base de ce principe et à partir de solutions de type puits existantes, plusieurs solutions analytiques sont proposées. Ces solutions considèrent une zone de recharge rectangulaire et un puits de pompage dans un aquifère libre: (1) près d’un cours d’eau, (2) entre un cours d’eau et une limite étanche, avec et sans influence de la recharge naturelle, (3) près d’un cours d’eau qui n’incise que partiellement l’aquifère et (4) dans un aquifère multicouche. Pour les cas avec cours d’eau, des solutions calculant l’impact sur le débit du cours d’eau, en transitoire, sont également présentées. Ces solutions analytiques sont utiles pour la gestion de la recharge d’aquifères, éventuellement pompés par un ou plusieurs puits, en particulier pour la conception des structures de recharge.

Resumen

El comportamiento de los acuíferos transitorios en respuesta a la infiltración desde las cuencas de superficie se ha estudiado durante décadas, pero algunos escenarios comunes todavía carecen de soluciones analíticas. Se ha demostrado que la aplicación de la integración matemática a la solución de la línea de flotación desarrollada por Hantush en el decenio de 1960 en relación con el bombeo de un acuífero no confinado, considerando la recarga sobre la superficie de un área definida, es idéntica a su solución para las aguas subterráneas que se acumulan debajo de una cuenca rectangular. Esto implica que el principio de superposición puede, en general, utilizarse para incluir directamente los pozos de bombeo, así como los límites del acuífero, para derivar una solución única. Además, pueden utilizarse otras soluciones de sumideros lineales con un método de superposición espacial para abordar una variedad de escenarios hidrogeológicos, siempre que el comportamiento de las ecuaciones diferenciales parciales pertinentes sea lineal. Sobre la base de este principio y de las soluciones de sumidero lineal existentes, se proponen varias soluciones analíticas capaces de considerar un área rectangular de recarga y un pozo de bombeo en un acuífero no confinado: (1) próximo a un curso de agua, (2) entre un curso de agua y un límite sin flujo, con y sin la influencia de la recarga natural, (3) próximo a un curso de agua que penetra parcialmente en un acuífero y (4) para un acuífero multicapa. Para los casos en que se incluyen las aguas fluviales, también se presentan soluciones transitorias del impacto en la cantidad de flujo de las aguas superficiales. Las soluciones analíticas propuestas serán de utilidad práctica para la gestión de la recarga del acuífero, en particular el diseño de estructuras para la recarga artificial de un acuífero, posiblemente bombeadas por uno o varios pozos.

摘要

几十年来,研究了非稳定地下水丘响应地表盆地入渗的行为,但一些常见的问题仍然缺乏解析解。研究表明,将应用数学积分到汉图什(Hantush)在1960年代开发的用于抽取潜水含水层的线汇解时,考虑了在有限区域表层的补给,这与他对矩形盆地下方的地下水丘的解析解类似。这意味着通常可以使用叠加原理直接包括抽水井以及含水层边界,以得出唯一的解析解。此外,如果相关偏微分方程是线性的,则其他线汇解可与空间叠加方法一起使用,以解决各种水文地质问题。基于此原理和现有的线汇解,提出了几种能够考虑矩形补给面积和潜水含水层抽水井的解决解:(1)在河流附近,(2)考虑和不考虑天然入渗时的河流与隔水边界之间;(3)在非完整河附近;(4)多层含水层。对于包括河流的情况,还提出了对河流流速影响的非稳定解析解。提出的解决解将用于含水层回补,特别是用于人工补给含水层(可能由一口或多口井抽水)的结构设计。

Resumo

O comportamento de montículos (mounds) transientes de águas subterrâneas em resposta à infiltração de bacias de superfície tem sido estudado por décadas, mas alguns cenários comuns ainda carecem de soluções analíticas. Foi demonstrado que a aplicação de integração matemática à solução de linha de injeção desenvolvida por Hantush em 1960 para o bombeamento de um aquífero não confinado, considerando a recarga sobre a superfície de uma área definida, é idêntica à sua solução para mounds de águas subterrâneas abaixo de uma bacia retangular. Isso implica que o princípio da superposição pode, geralmente, ser usado para incluir diretamente poços de bombeamento, bem como limites de aquíferos, para derivar a uma solução única. Além disso, outras soluções de linha injeção podem ser usadas com um método de superposição espacial para abordar uma variedade de cenários hidrogeológicos, desde que o comportamento das equações diferenciais parciais relevantes seja linear. Baseado neste princípio e nas soluções existentes para linha de injeção, são propostas várias soluções analíticas capazes de considerar uma área de recarga retangular e um poço de bombeamento em um aquífero não confinado: (1) próximo a um riacho, (2) entre um riacho e um limite sem fluxo, com e sem a influência da recarga natural, (3) próximo a um riacho que penetra parcialmente um aquífero e (4) para um aquífero multicamada. Para casos que incluem fluxos, soluções transientes do impacto na taxa de fluxo também são apresentadas. As soluções analíticas propostas serão de uso prático para a recarga gerenciada de aquíferos, em particular no projeto de estruturas para recarga artificial de um aquífero, possivelmente bombeadas por um ou vários poços.

Appendices

Appendices

Appendix 1

Groundwater flow in the case of groundwater mounding for a rectangular basin with a uniform percolation rate (Fig. 2) is defined by the following nonlinear Boussinesq equation:

$$ \frac{\partial }{\partial x}\left( Kh\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left( Kh\frac{\partial h}{\partial y}\right)+R=S\frac{\partial h}{\partial t} $$

(21)

With K the hydraulic conductivity of the aquifer, S the aquifer storativity and R the recharge rate.

Boundary conditions are h(x, y, 0) = h₀; h(±∞, y, t) = h(x, ±∞, t) = h_0.

Defining Z = h² − h₀², and assuming a homogeneous and isotropic aquifer (K = constant), Hantush (1967) obtained the following approximate partial differential equation:

$$ \frac{\partial^2Z}{\partial {x}^2}+\frac{\partial^2Z}{\partial {y}^2}+\frac{2R}{K}=\frac{1}{\nu}\frac{\partial Z}{\partial t} $$

(22)

with h – h₀ < 0.5h₀, $\nu =\frac{K\overline{b}}{S}$, $\overline{b}$ is a constant of linearization $\overline{b}=\frac{1}{2}\left({h}_0+{h}_t\right)$.

Boundary conditions: Z(x, y, 0) = 0; Z(±∞, y, t) = Z(x, ±∞, t) = 0; $\frac{\partial Z\left(0,y,t\right)}{\partial x}=\frac{\partial Z\left(x,0,t\right)}{\partial y}=0$

Hantush’s approximate partial differential equation for a well pumping an unconfined, infinite and horizontal aquifer (Hantush 1964a, b, 1965).

$$ \frac{\partial^2Z}{\partial {x}^2}+\frac{\partial^2Z}{\partial {y}^2}=\frac{1}{\nu}\frac{\partial Z}{\partial t} $$

(23)

Z = h² − h₀², with h₀– h < 0.5h₀

Boundary conditions:

Z(x, y, 0) = 0; Z(±∞, y, t) = Z(x, ±∞, t) = 0; $\underset{r\to 0}{\mathrm{Lim}}r\frac{\partial Z}{\partial r}=\frac{Q_{\mathrm{Pump}}}{\uppi K}$

Q_Pump is the pumping rate (<0) and r the distance to the pumping well.

Appendix 2

Integration of Eq. (1) over a rectangular surface of dimensions 2x_L × 2y_L and considering that the recharge rate, R, is uniformly distributed over the rectangular recharging area (2x_L × 2y_L), i.e. $R=\frac{Q_{\mathrm{Rech}}}{4{x}_{\mathrm{L}}{y}_{\mathrm{L}}}$, Eq. (2) becomes

$$ {Z}_{\mathrm{Rech}}\left({x}_{\mathrm{o}\mathrm{bs}},{y}_{\mathrm{o}\mathrm{bs}},t\right)={h}^2-{h_{\mathrm{o}}}^2=\frac{R}{2\uppi K}\underset{-{x}_{\mathrm{L}}}{\overset{+{x}_{\mathrm{L}}}{\int }}\underset{-{y}_{\mathrm{L}}}{\overset{+{y}_{\mathrm{L}}}{\int }}\mathrm{W}\left[\frac{{\left(x-{x}_{\mathrm{o}\mathrm{bs}}\right)}^2+{\left(y-{y}_{\mathrm{o}\mathrm{bs}}\right)}^2}{4\nu t}\right] dx\ dy $$

(24)

Then, because of the properties of exponential integrals [$\mathrm{W}\left(\frac{a}{t}\right)=\underset{a/t}{\overset{\infty }{\int }}\frac{{\mathrm{e}}^{-y}}{y} d y=\underset{0}{\overset{t}{\int }}\frac{{\mathrm{e}}^{-a/\tau }}{\tau } d\tau$], it follows that

$$ {Z}_{\mathrm{Rech}}\left({x}_{\mathrm{obs}},{y}_{\mathrm{obs}},t\right)=\frac{R}{2\uppi K}\underset{-{x}_{\mathrm{L}}}{\overset{+{x}_{\mathrm{L}}}{\int }}\underset{-{y}_{\mathrm{L}}}{\overset{+{y}_{\mathrm{L}}}{\int }}\underset{0}{\overset{t}{\int }}\frac{{\mathrm{e}}^{\frac{-{\left(x-{x}_{\mathrm{obs}}\right)}^2-{\left(y-{y}_{\mathrm{obs}}\right)}^2}{4\nu \tau}\kern0.5em }}{\tau } d\tau dxdy\kern0.5em $$

(25)

According to the Fubini theorem (i.e. t, x and y are independent variables), the order of integration can be inverted, resulting in:

Performing a change of variable $\vartheta =\frac{\left(x-{x}_{\mathrm{obs}}\right)}{2\sqrt{\nu t}}$, the (a) term in Eq. (26) can be rewritten as:

$$ \underset{-{x}_{\mathrm{L}}}{\overset{+{x}_{\mathrm{L}}}{\int }}\frac{{\mathrm{e}}^{\frac{-{\left(x-{x}_{\mathrm{obs}}\right)}^2}{4\nu \tau}}}{\sqrt{\tau }} d x=\underset{-\left({x}_{\mathrm{L}}+{x}_{\mathrm{obs}}\right)/2\sqrt{\nu \tau}}{\overset{\left({x}_{\mathrm{L}}-{x}_{\mathrm{obs}}\right)/2\sqrt{\nu \tau}}{\int }}2\sqrt{\nu }\ {\mathrm{e}}^{-{\vartheta}^2} d\vartheta $$

(27)

The right side of Eq. (27) can be separated into two terms related to the Erf function [$\underset{a}{\overset{b}{\int }}{\mathrm{e}}^{-{u}^2} du=\frac{\sqrt{\uppi}}{2}{\left[\mathrm{Erf}(u)\right]}_a^b=\frac{\sqrt{\pi }}{2}\left(\mathrm{Erf}(b)-\mathrm{Erf}(a)\right)$], therefore:

$$ \underset{-\left({x}_{\mathrm{L}}+{x}_{\mathrm{obs}}\right)/2\sqrt{\nu \tau}}{\overset{\left({x}_{\mathrm{L}}-{x}_{\mathrm{obs}}\right)/2\sqrt{\nu \tau}}{\int }}2\sqrt{\nu }\ {\mathrm{e}}^{-{\vartheta}^2} d\vartheta =\sqrt{\uppi \nu}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+{x}_{\mathrm{obs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-{x}_{\mathrm{obs}}}{2\sqrt{\nu \tau}}\right)\right] $$

(28)

Changing the variable $\vartheta^{\prime }=\frac{\left(y-{y}_{\mathrm{obs}}\right)}{2\sqrt{\nu t}}$ in term (b) in Eq. (26), and using the same procedure as described before, the (b) term can be rewritten as

$$ \underset{-{y}_{\mathrm{L}}}{\overset{+{y}_{\mathrm{L}}}{\int }}\frac{{\mathrm{e}}^{\frac{-{\left(y-{y}_{\mathrm{obs}}\right)}^2}{4\nu t}}}{\sqrt{\tau }} dx=\sqrt{\uppi \nu}\left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{obs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{obs}}}{2\sqrt{\nu \tau}}\right)\right] $$

(29)

Finally, combining Eqs. (28) and (29), and since $\nu =\frac{K\overline{b}}{S}$, the following is obtained:

$$ {Z}_{\mathrm{Rech}}\left({x}_{\mathrm{o}\mathrm{bs}},{y}_{\mathrm{o}\mathrm{bs}},t\right)={h}^2-{h_{\mathrm{o}}}^2=\kern0.5em \frac{R\overline{b}}{2S}\underset{0}{\overset{t}{\int }}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right]\kern0.5em \times \left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right] d\tau $$

(30)

Equation (30) demonstrates that the well solution for an unconfined and isotropic aquifer (Hantush 1964a, 1965) integrated over a rectangular plane is exactly the same as Hantush’s analytical solution for a rectangular recharging area with a uniform distribution of the recharge flux (Eq. 13 in Hantush 1967).

Appendix 3

The hydraulic-head solution for a rectangular recharging area and a pumping well between two parallel boundaries (constant head or no-flow boundary).

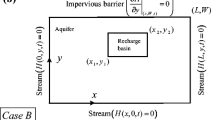
x_w and y_w are coordinates of the pumping well, d is the distance between the centre of the recharging area and the stream. 2 L is the distance between both limits. x = y = 0 at the centre of the recharging area. $\nu =\frac{K\overline{b}}{S}$. The general solutions for hydraulic head between two parallel boundaries are presented below; b and c are coefficients, b or c = 1 for a no-flow boundary, and b or c = –1 for is a constant-head boundary (Dirichlet’s condition).

Term for the pumping well:

$$ {Z}_{2\mathrm{Limit}\_\mathrm{Pump}}\left({x}_{\mathrm{o}\mathrm{bs}},{y}_{\mathrm{o}\mathrm{bs}},t\right)={h}^2-{h_{\mathrm{o}}}^2=\frac{Q}{2\uppi K}\left\{\mathrm{W}\left[\frac{{\left({x}_{\mathrm{o}\mathrm{bs}}-{x}_{\mathrm{w}}\right)}^2+{\left({y}_{\mathrm{o}\mathrm{bs}}-{y}_{\mathrm{w}}\right)}^2}{4\nu t}\right]+\sum \limits_{n=0,2,4..}^{\infty }{b}^{n/2+1}{c}^{n/2}\ \mathrm{W}\left[\frac{{\left(2 nL+2d-{x}_{\mathrm{o}\mathrm{bs}}+{x}_{\mathrm{w}}\right)}^2+{\left({y}_{\mathrm{o}\mathrm{bs}}-{y}_{\mathrm{w}}\right)}^2}{4\nu t}\right]+\sum \limits_{n=2,4..}^{\infty }{(bc)}^{n/2}\ \mathrm{W}\left[\frac{{\left(-2 nL-{x}_{\mathrm{o}\mathrm{bs}}+{x}_{\mathrm{w}}\right)}^2+{\left({y}_{\mathrm{o}\mathrm{bs}}-{y}_{\mathrm{w}}\right)}^2}{4\nu t}\right]+\sum \limits_{n=2,4..}^{\infty }{(bc)}^{n/2}\ \mathrm{W}\left[\frac{{\left(2 nL-{x}_{\mathrm{o}\mathrm{bs}}+{x}_{\mathrm{w}}\right)}^2+{\left({y}_{\mathrm{o}\mathrm{bs}}-{y}_{\mathrm{w}}\right)}^2}{4\nu t}\right]+\sum \limits_{n=2,4..}^{\infty }{b}^{n/2-1}{c}^{n/2}\ \mathrm{W}\left[\frac{{\left(-2 nL+2d-{x}_{\mathrm{o}\mathrm{bs}}+{x}_{\mathrm{w}}\right)}^2+{\left({y}_{\mathrm{o}\mathrm{bs}}-{y}_{\mathrm{w}}\right)}^2}{4\nu t}\right]\right\} $$

(31)

Term for the rectangular recharging area:

$$ {Z}_{2\mathrm{Limi}{\mathrm{t}}_{\mathrm{Rech}}}\left({x}_{\mathrm{o}\mathrm{bs}},{y}_{\mathrm{o}\mathrm{bs}},t\right)={h}^2-{h_{\mathrm{o}}}^2=\frac{R\overline{b}}{2S}\left\{\underset{0}{\overset{t}{\int }}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right]\times \left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right] d\tau +\sum \limits_{n=0,2,4..}^{\infty }{b}^{n/2+1}{c}^{n/2}\ \underset{0}{\overset{t}{\int }}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+2 nL+2d-{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-2 nL-2d+{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right]\times \left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right] d\tau +\sum \limits_{n=2,4..}^{\infty }{(bc)}^{n/2}\ \underset{0}{\overset{t}{\int }}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-2 nL-{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+2 nL+{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right]\times \left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right] d\tau +\sum \limits_{n=2,4..}^{\infty }{(bc)}^{n/2}\ \underset{0}{\overset{t}{\int }}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+2 nL-{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-2 nL+{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right]\times \left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right] d\tau +\sum \limits_{n=2,4..}^{\infty }{b}^{n/2-1}{c}^{n/2}\underset{0}{\overset{t}{\int }}\left[\mathrm{Erf}\left(\frac{x_{\mathrm{L}}-2 nL+2d-{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{x_{\mathrm{L}}+2 nL-2d+{x}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right]\times \left[\mathrm{Erf}\left(\frac{y_{\mathrm{L}}+{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)+\mathrm{Erf}\left(\frac{y_{\mathrm{L}}-{y}_{\mathrm{o}\mathrm{bs}}}{2\sqrt{\nu \tau}}\right)\right] d\tau \right\} $$

(32)

Figure 8 compares the solution of Eq. (32), with b = −1, c = 1, 2x_L = 2 L, d = L, y_L→∞, t→∞, with Bruggeman’s (1999; sol. 21.11, p. 24) steady-state solution.

Fig. 8

Hydraulic-head profile in steady-state condition caused by recharge from precipitation (R) through an infinite strip of width 2 L bounded on one side by a stream and on the other by a no-flow boundary. Aquifer parameters are: K = 10⁻⁴ m/s, S = 0.05, 2 L = 800 m, R = 1.27 × 10⁻⁸ m/s (or 400 mm/year), with h₀ varying from 1.5 to 12 m. The inserted table shows standardized root mean square error values (RMSE-D) for the five cases

Appendix 4

The hydraulic-head solution for a pumping well near a stream with a partially clogged streambed that partially penetrates the aquifer (Hunt 1999), modified for an unconfined aquifer condition (linearized Boussinesq solution as in Hantush 1967), is:

$$ {Z}_{\mathrm{HuntPump}}\left({x}_{\mathrm{o}\mathrm{bs}},{y}_{\mathrm{o}\mathrm{bs}},t\right)={h}^2-{h_{\mathrm{o}}}^2=\frac{Q_{\mathrm{Pump}}}{2\uppi K}\left\{\mathrm{W}\left(\frac{{x_{\mathrm{o}\mathrm{bs}}}^2+{y_{\mathrm{o}\mathrm{bs}}}^2}{4\nu t}\right)-\underset{0}{\overset{\infty }{\int }}{\mathrm{e}}^{-\theta}\mathrm{W}\left[\frac{{\left(d+\left|d-{x}_{\mathrm{o}\mathrm{bs}}\right|+2K\overline{b}\theta /\lambda \right)}^2+{y_{\mathrm{o}\mathrm{bs}}}^2}{4\nu t}\right] d\theta \right\} $$

(33)

with $\lambda =\frac{b}{b^{{\prime\prime} }}k^{{\prime\prime} }$; b = stream width, b″ = streambed thickness and k″ = streambed hydraulic conductivity.

The right part of Eq. (33) can be rearranged with the following change of variable

θ =  –Ln(u) then $=-\frac{1}{\mathrm{u}} du$; Ln = natural logarithm.

Then Eq. (33) becomes:

$$ {Z}_{\mathrm{HuntPump}}\left({x}_{\mathrm{o}\mathrm{bs}},{y}_{\mathrm{o}\mathrm{bs}},t\right)={h}^2-{h_{\mathrm{o}}}^2=\frac{Q}{2\uppi K}\left\{\mathrm{W}\left(\frac{{x_{\mathrm{o}\mathrm{bs}}}^2+{y_{\mathrm{o}\mathrm{bs}}}^2}{4\nu t}\right)-\underset{0}{\overset{1}{\int }}\mathrm{W}\left[\frac{{\left(d+\left|d-{x}_{\mathrm{o}\mathrm{bs}}\right|-2K\overline{b}\mathrm{Ln}(u)/\lambda \right)}^2+{y_{\mathrm{o}\mathrm{bs}}}^2}{4\nu t}\right] du\right\} $$

(34)